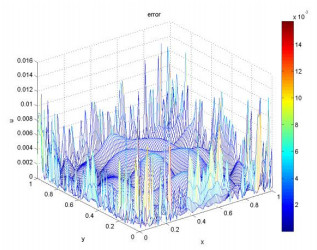
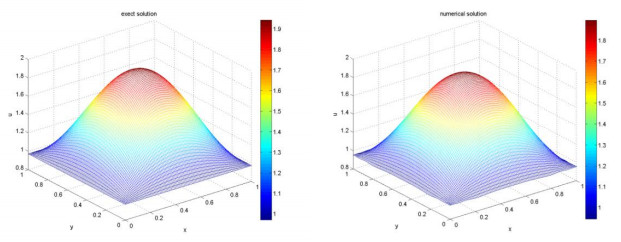
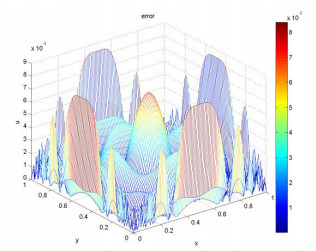
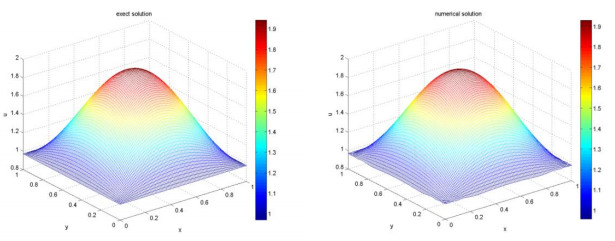
In this paper, we study the inverse problem of identifying the initial value of a two-dimensional degenerate parabolic equation, which often appears in the fields of engineering, physics, and computer image processing. Firstly, the difference scheme of forward problem is established by using the finite volume method. Then stability and convergence of the difference equations are proved rigorously. Finally, the Landweber iteration and conjugate gradient method are used to solve the inverse problem, and some typical numerical examples are shown to verify the validity of our iterative algorithm. Numerical results show that the algorithm is stable and efficient.
1.
Introduction and definitions
Let A denote the family of all functions f which are analytic in the open unit disc U={z:|z|<1} and satisfying the normalization
while by S we mean the class of all functions in A which are univalent in U. Also let S∗ and C denote the familiar classes of starlike and convex functions, respectively. If f and g are analytic functions in U, then we say that f is subordinate to g, denoted by f≺g, if there exists an analytic Schwarz function w in U with w(0)=0 and |w(z)|<1 such that f(z)=g(w(z)). Moreover if the function g is univalent in U, then
For arbitrary fixed numbers A, B and b such that A, B are real with −1≤B<A≤1 and b∈C∖{0}, let P[b,A,B] denote the family of functions
analytic in U such that
Then, p∈P[b,A,B] can be written in terms of the Schwarz function w by
By taking b=1−σ with 0≤σ<1, the class P[b,A,B] coincides with P[σ,A,B], defined by Polatoğ lu [17,18] (see also [2]) and if we take b=1, then P[b,A,B] reduces to the familiar class P[A,B] defined by Janowski [10]. Also by taking A=1, B=−1 and b=1 in P[b,A,B], we get the most valuable and familiar set P of functions having positive real part. Let S∗[A,B,b] denote the class of univalent functions g of the form
in U such that
Then S∗[A,B]:=S∗[A,B,1] and the subclass S∗[1,−1,1] coincides with the usual class of starlike functions.
The set of Bazilevič functions in U was first introduced by Bazilevič [7] in 1955. He defined the Bazilevič function by the relation
where p∈P, g∈S∗, β is real and α>0. In 1979, Campbell and Pearce [8] generalized the Bazilevi č functions by means of the differential equation
where α+iβ∈C−{negative integers}. They associate each generalized Bazilevič functions with the quadruple (α,β,g,p).
Now we define the following subclass.
Definition 1.1. Let g be in the class S∗[A,B] and let p∈P[b,A,B]. Then a function f of the form (1.1) is said to belong to the class of generalized Bazilevič function associated with the quadruple (α,β,g,p) if f satisfies the differential equation
where α+iβ∈C−{negative integers}.
The above differential equation can equivalently be written as
or
Since p∈P[b,A,B], it follows that
where g∈S∗[A,B].
Several research papers have appeared recently on classes related to the Janowski functions, Bazilevič functions and their generalizations, see [3,4,5,13,16,21,22].
2.
Lemmas
The following are some results that would be useful in proving the main results.
Lemma 2.1. Let p∈P[b,A,B] with b≠0, −1≤B<A≤1, and has the form (1.2). Then for z=reiθ,
Proof. The proof of this lemma is straightforward but we include it for the sake of completeness. Since p∈P[b,A,B], we have
Let ˜p(z)=1+∑∞n=1cnzn. Then
Comparing the coefficients of zn, we have
Since |cn|≤A−B [20], it follows that |pn|≤|b|(A−B) and so
Thus the proof is complete.
Lemma 2.2. [1] Let Ω be the family of analytic functions ω on U, normalized by ω(0)=0, satisfying the condition |ω(z)|<1. If ω∈Ω and
then for any complex number t,
The above inequality is sharp for ω(z)=z or ω(z)=z2.
Lemma 2.3. Let p(z)=1+∞∑n=1pnzn∈P[b,A,B], b∈C∖{0}, −1≤B<A≤1. Then for any complex number μ,
This result is sharp.
Proof. Let p∈P[b,A,B]. Then we have
or, equivalently
which would further give
Comparing the coefficients of z and z2, we obtain
By a simple computation,
Now by using Lemma 2.2 with t=μb(A−B)+B, we get the required result. Equality holds for the functions
Now we prove the following result by using a method similar to the one in Libera [12].
Lemma 2.4. Suppose that N and D are analytic in U with N(0)=D(0)=0 and D maps U onto a many sheeted region which is starlike with respect to the origin. If N′(z)D′(z)∈P[b,A,B], then
Proof. Let N′(z)D′(z)∈P[b,A,B]. Then by using a result due to Attiya [6], we have
where c(r)=1−B[B+b(A−B)]r21−B2r2 and d(r)=|b|(A−B)r21−B2r2. We choose A(z) such that |A(z)|<d(r) and
Now for a fixed z0 in U, consider the line segment L joining 0 and D(z0) which remains in one sheet of the starlike image of U by D. Suppose that L−1 is the pre-image of L under D. Then
This implies that
Therefore
For A=−B=b=1, we have the following result due to Libera [12].
Lemma 2.5. If N and D are analytic in U with N(0)=D(0)=0 and D maps U onto a many sheeted region which is starlike with respect to the origin, then
Lemma 2.6. [14] If −1≤B<A≤1,β1>0 and the complex number γ satisfies Re{γ}≥−β1(1−A)/(1−B), then the differential equation
has a univalent solution in U given by
If p(z)=1+p1z+p2z2+⋯ is analytic in U and satisfies
then
and q(z) is the best dominant.
3.
Some auxiliary results
Before proving the results for the generalized Bazilevič functions, let us discuss a few results related to the function g∈S∗[A,B].
Theorem 3.1. Let g∈S∗[A,B] and of the form (1.3). Then for any complex number μ,
Proof. The proof of the result is the same as of Lemma 2.3. The result is sharp and equality holds for the function defined by
or
Theorem 3.2. Let g∈S∗[A,B]. Then for c>0, α>0 and β any real number,
is in S∗[A,B]. In addition
where
Proof. From (3.1), we have
Differentiating and rearranging gives
where p(z)=zG′(z)G(z). Then differentiating (3.2) logarithmically, we have
Since g∈S∗[A,B], it follows that
Now by using Lemma 2.6, for β1=α and γ=c+iβ, we obtain
where
Now by using the properties of the familiar hypergeometric functions proved in [15], we have
This implies that
and
Theorem 3.3. Let g∈S∗[A,B]. Then
is (α+c)-valent starlike, where α>0, c>0 and β is a real number.
Proof. Let D1(z)=zS′(z)=zc+iβgα(z) and N1(z)=S(z). Then
Since g∈S∗[A,B]⊂S∗(1−A1−B), see [10], it follows that
Also
Now by using Lemma 2.5, we have
By the mean value theorem for harmonic functions,
Therefore
Now by using a result due to [9,p 212], we have that S is (c+α)-valent starlike function.
4.
Main results
Now we are ready to discuss some results related to the defined generalized Bazilevič functions.
Theorem 4.1. Let f be a generalized Bazilevič function associated by the quadruple (α,β,g,p), where g∈S∗[A,B] of the form (1.3) and p∈P[b,A,B] of the form (1.2). Then for c>0,
is a generalized Bazilevič function associated by the quadruple (α,β,G,p), where G∈S∗[A,B,δ], as defined by (3.1).
Proof. From (4.1), we have
This implies that
Differentiate both sides and rearrange, we get
and
Now from (3.1), we have
With this, note that
which implies N′(z)D′(z)∈P[b,A,B]. By Theorem 3.3, we know that D(z)=∫z0tc+iβ−1gα(t)dt is (α+c)-valent starlike. Therefore by using Lemma 2.4, we obtain
This is the equivalent form of Definition 1.1. Hence the result follows.
Corollary 4.2. Let A=1,B=−1 and β=0 in Theorem 4.1. Then
belong to S∗(δ1), where
Hence G is starlike when g∈S∗, and
belongs to the class of Bazilevič functions associated by the quadruple (α,0,G,p).
Theorem 4.3. Let f of the form (1.1) be a generalized Bazilevič function associated by the quadruple (α,β,g,p), with g∈S∗[A,B] of the form (1.3) and p∈P[b,A,B] of the form (1.2). Then
This inequality is sharp.
Proof. Since f is a generalized Bazilevič function associated by the quadruple (α,β,g,p), we have
As f, g and p respectively have the form (1.1),(1.3) and (1.2), it is easy to get
Putting these values in (4.2) and comparing the coefficients of z, we obtain
Similarly by comparing the coefficients of z2 and rearranging, we have
From (4.4), we have
Now by using Theorem 3.1 and Lemma 2.3, both with μ=12, we obtain
and
Therefore, we have
The equality
for B≠0 can be obtained for
Similarly, the equality
for B=0 can be obtained for the function g∗(z)= zeA2z2=z+A2z3+⋯. Also equality for the functional |p2−12p21| can be obtained by the functions
Corollary 4.4. For A=1, B=−1 and b=1, we have the result proved in [8]:
For α=1, β=0, we have f∈K, the class of close-to-convex functions, and
The latter result has been proved in [11].
Theorem 4.5. Let f of the form (1.1) be a generalized Bazilevič function associated by the quadruple (α,β,g,p), with g∈S∗[A,B] and of the form (1.3) and p∈P[b,A,B] of the form (1.2). Then
(i)
(ii) If α=0, then
Both the above inequalities are sharp.
Proof. (ⅰ) From (4.3), we have
This implies that
By using the coefficient bound for S∗[A,B] along with the coefficient bound of P[b,A,B], we have
This implies that
Equality can be obtained by the functions
(ⅱ) Let α=0. Then from (4.3) and (4.4), we have
This implies
where μ=12−(3+iβ)2(1+iβ)2. Now by using Lemma 2.3, we obtain
Sharpness can be attained by the functions
Corollary 4.6. For A=1, B=−1 and b=1, we have
and
In the final part of this paper, we look at some results for the generalized Bazilevič functions associated with β=0.
Let Cr denote the closed curve which is the image of the circle |z|=r<1 under the mapping w= f(z), and Lr(f(z)) denote the length of Cr. Also let M(r)=max|z|=r|f(z)| and m(r)=min|z|=r|f(z)|. We now prove the following result.
Theorem 4.7. Let f be a generalized Bazilevič function associated by the quadruple (α,0,g,p). Then for B≠0,
where
Proof. As f is a generalized Bazilevič function associated by the quadruple (α,0,g,p), we have
where g∈S∗[A,B] and p∈P[b,A,B]. Since for z=reiθ, 0<r<1,
we have for 0<α≤1,
where zg′(z)g(z)=h(z)∈P[A,B]. Now by using the distortion theorem for Janowski starlike functions when B≠0 (see [10]) and the Cauchy-Schwarz inequality, we have
Now by using Lemma 2.1 for both the classes P[b,A,B] and P[A,B], along with the result
for p∈P[b,A,B] (see [19]), we can write
Since 1−|B|r≥1−r and 1−B2r2≥1−r2,
where C(α,b,A,B)=2π|b|[(A−B)+(1/α)]B.
When α>1, we can prove similarly as above to get
Corollary 4.8. For g∈S∗ and p∈P(b), we have
Theorem 4.9. Let f be a generalized Bazilevič function associated by the quadruple (α,0,g,p), where g∈S∗[A,B] and p∈P[b,A,B]. Then for B≠0,
Proof. By Cauchy's theorem for z=reiθ, n≥2, we have
Therefore
By using Theorem 4.7 for the case 0<α≤1, we have
Hence, by taking r approaches 1−,
For α>1, we have
Theorem 4.10. Let f be a generalized Bazilevič function represented by the quadruple (α,0,g,p), where g∈S∗[A,B] and p∈P[b,A,B]. Then for B≠0,
Proof. Since f is a generalized Bazilevič function associated by the quadruple (α,0,g,p), by definition, we have
where g∈S∗[A,B] and p∈P[b,A,B]. This implies that
and so
Now by using the results
and
we have
Putting s=ru, we have
where 2F1(a;b;c;z) is the hypergeometric function.
Corollary 4.11. For g∈S∗and p∈P, we have
Acknowledgments
The research for the fourth author is supported by the USM Research University Individual Grant (RUI) 1001/PMATHS/8011038.
Conflict of interest
The authors declare that they have no conflict of interests.
















 DownLoad:
DownLoad: