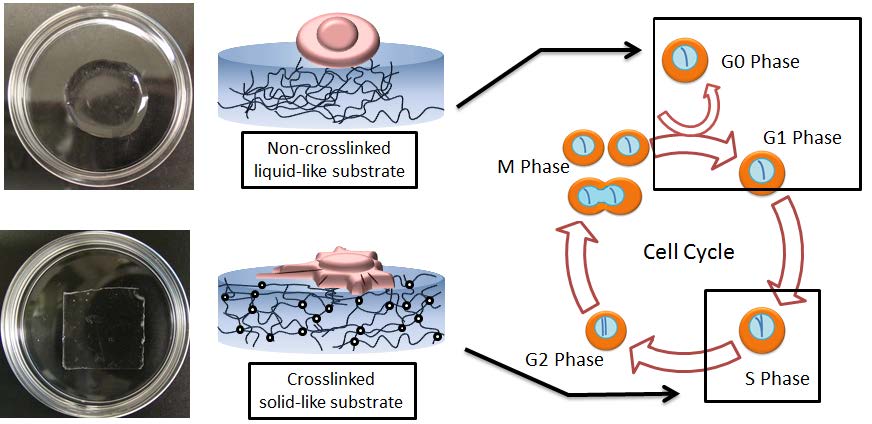
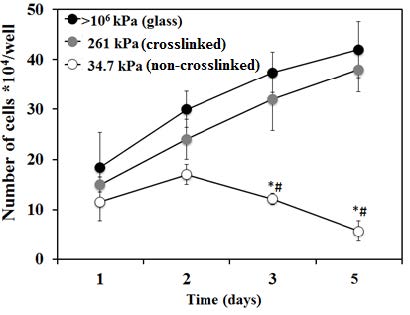
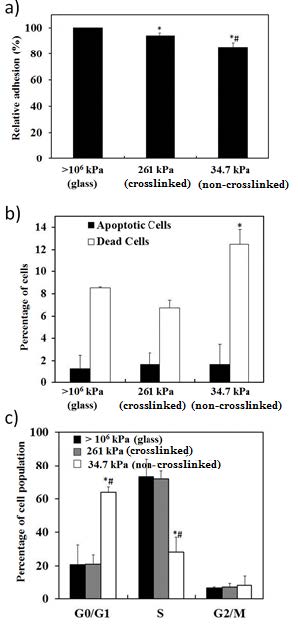
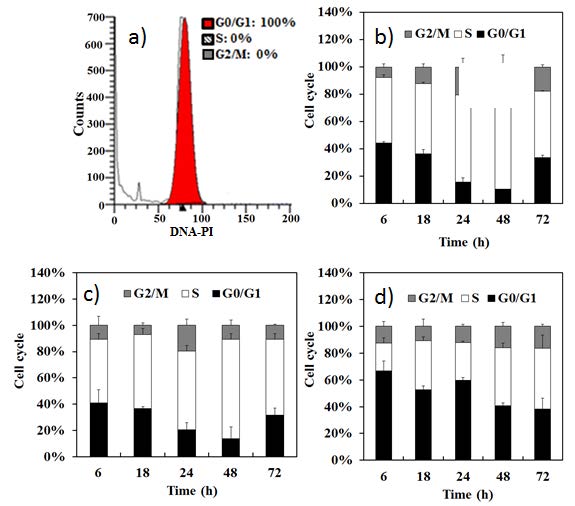
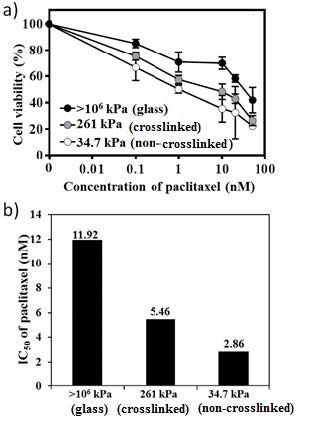
Although various polymeric substrates with different stiffness have been applied for the regulation of cells’ fate, little attention has been given to the effects of substrates’ fluidity. Here, we implement for the first time biodegradable polymer with fluidic property for cancer therapy by investigating cell adhesion, proliferation, apoptosis/death, cycles of cancer cells as well as the anticancer drug efficacy. To achieve this, we prepared crosslinked and non-crosslinked copolymers of ɛ-caprolactone-co-D, L-lactide (P(CL-co-DLLA)). The tensile test showed the crosslinked P(CL-co-DLLA) substrate has the stiffness of 261 kPa while the loss modulus G’’ of the non-crosslinked substrate is always higher than the storage modulus G’ (G’’/G’=3.06), indicating a quasi-liquid state. Human lung epithelial adenocarcinoma cells on crosslinked substrate showed well- spread actin stress fibers and visible focal adhesion with an increased S phase (decreased G0/G1 phase). The cells on non-crosslinked substrate, on the other hand, showed rounded morphology without visible focal adhesion and an accumulated G0/G1 phase (decreased S phase). These results suggest that the behavior of cancer cells not only depends on stiffness but also the fluidity of P(CL-co-DLLA) substrate. In addition, the effects of substrate’s fluidity on anti-cancer drug efficacy were also investigated. The IC50 values of paclitaxel for cancer cells on crosslinked and non-crosslinked substrates are 5.46 and 2.86 nM, respectively. These results clearly indicate that the fluidity of polymeric materials should be considered as one of the crucial factors to study cellular functions and molecular mechanism of cancer progression.
1.
Introduction
Currently it is the digital era where there is a steady flood of information. Such information inundation makes a variety of mass media more important, for example, newspapers, broadcast, social network system media, and public speaking. Before developing mass media, rumors propagated by word of mouth and played a crucial role in communication between people or groups. This process can be understood as a kind of homogenization of information system and social interaction [1]. With the emergence of multimedia and social media, rumors have spread faster and have wide transmissions [5]. However, some harmful and powerful rumor outbreaks arise from such wide transmission via these media [10,14,18]. Moreover, their influence causes multiple effects for a variety of situations rather than the mono effect for localized situations [12].
As a benefit in return for the homogenization, personality is more heavily emphasized and the diversity of people has garnered much attention in our social community. In the microscopic viewpoint of rumor spreading, this variety of characteristics is important. Many researchers already have investigated that the degree of belief is important in rumor spreading [8,16]. From this perspective, we assume that there will be various groups that share the same trust rate. In this paper, we propose an SIR type rumor spreading model with given spreading rate distributions $\lambda_i$, $1\leq i\leq N$. Each spreading rate distribution $\lambda_i$ represents a different character of several classes of groups. With the distribution $\lambda_i$, we present a sufficient condition for the rumor outbreak. To obtain a rumor outbreak, we need a sufficiently large initial quantity that represents the momentum of rumor spreading. We also provide numerical simulations to verify our analysis with several combinations of different parameters. We notice that the authors in [19] studied an SIR type rumor spreading model with a reputation mechanism and considered a probability that represents the reputation of the opinion, where reputation is related to the trust rate. They used a single ignorant SIR model. On the other hand, we consider a model with several classes of ignorants and trust rate distributions $\lambda_i$, $1\leq i\leq N$.
Next we provide a brief historical review of the rumor spreading model. Starting the pioneering studies by Daley and Kendall [3,4], a lot of researchers have studied rumor spreading and tried to build mathematical models [11,17]. Zanette [23,24] numerically obtained the existence of a critical threshold for a rumor spreading model regarding small-world networks. In [13], the authors derived the mean-field equation of complex heterogeneous networks. For other topological settings, see [7,15]. Most mathematical models for rumor spreading are based on the epidemic model. In [27], the authors considered an SIR type rumor spreading model with forgetting mechanism. See also [6,28] for other models with forgetting mechanisms. In [26], the authors added a hibernator variable to the SIR type rumor spreading model. Similarly, in [20,22], the authors adapted several new variables to construct a more realistic model for the rumor spreading phenomena. In [25], the authors employed the probability that ignorants directly become stiflers when they are aware of a rumor. We refer to papers [2,9,29] for other rumor spreading models.
The paper is organized as follows. In Section 2, we present the trust distribution and its mechanism in the SIR type model. In Section 3, we derive a single equation for the rumor size $\phi$. In Section 4, we provide proof of the main theorem. In Section 5, we demonstrate our results by numerical simulations. Finally, we summarize our results in Section 6.
Notation: Throughout the paper, we use the following simplified notation:
2.
Spreading rate distribution model
Let $V$ and $E$ be sets of vertices and edges, respectively. Representing the individuals and contacts as the vertices and edges, a social network leads to an undirected graph $G = (V, E)$. A general social network is close to a small-world network [21]. In [13], the authors derived the mean-field rate equation based on the Poisson distribution of small-world network. As in [13], we consider a rumor spreading model based on the SIR model of a homogeneous network.
There are three groups of populations: ignorants (I), spreaders (S), and stiflers (R). At the first stage, ignorants contact a spreader, realize a rumor, and accept the hearsay. According to the acceptance with rate $\lambda $, some of them become spreaders and then spread the rumor to other ignorants. However, as spreaders lose interest in spreading the rumor, they become stiflers. Based on this mechanism, the SIR rumor spreading model [3,4] is given by
where $k$ is the average degree of the network, $\lambda$ is the spreading rate of the system, $\sigma_1$ is the contact rate between spreaders, and $\sigma_2$ is the contact rate between spreaders and stiflers.
As in [25], we assume that spreaders lose their interest in rumors with probability $\delta$ and become stiflers. Moreover, stiflers interact with spreaders to create other stiflers from other spreaders. Spreaders also have a negative effect on other spreaders because they consider the rumor to be outdated if the spreader meets with other spreaders frequently. For simplicity, we assume that the contact rates $\sigma_1$ and $\sigma_2$ are the same, say $\sigma = \sigma_1 = \sigma_2$. As mentioned before, we consider several groups of ignorants with different spreading rates $\lambda_i$, $i = 1, \ldots, N$, motivated by [8,16]. The mean-field equation is then given by
subject to initial data $~
I_i(0) = \mathring{I}_{i}, i = 1, \ldots, N, S(0) = \mathring{S}, R(0) = \mathring{R}$, where $I_i$ is the population density of the $i$th group of ignorants with spreading (trust) rate $\lambda_i$. $S$ and $R$ are the density of spreaders and stiflers, respectively. Moreover, $\sigma$ is the contact rate between spreaders and stiflers, and $\delta$ denotes the decay rate of spreaders to stiflers.
Throughout this paper, we assume that
(1) $k$, $\sigma$ and $\delta$ are fixed positive constants.
(2) The spreading (trust) rate distribution $\lambda_i $ is nonnegative constant for each $1\leq i\leq N $.
We will consider a family of initial data $\mathring{I}_{1}, \ldots, \mathring{I}_{N}$, $\mathring{S}$ and $\mathring{R}$ such that
for a fixed total initial population $\mathring{T}$.
Next, we define the rumor size, a momentum type quantity of the initial data and rumor outbreak.
Definition 2.1. [19,25,26]For a solution $(I, S, R)$ to system (1), we define the rumor size $\phi$ of $(I, S, R)$:
Definition 2.2. Let $(I, S, R)$ be a solution to system (1) with initial data $\mathring{I}$, $\mathring{S}$ and $\mathring{R}$. We define initial reliability of ignorants $M_1(\mathring{I})$:
and total population with initial $T(0) = \mathring{T}$:
Definition 2.3. Let $(I, S, R)$ be solutions to system (1) subject to initial data $\mathring{I}$, $\mathring{S}$ and $\mathring{R} = 0$. If $\phi(t)$ in Definition 2.1 converges as $t\to \infty$, we define $\phi^\infty$ as the final size of the rumor:
Definition 2.4. For a given initial data $\mathring{I}, \mathring{S}$ and $\mathring{R}$ of system (1) with $\mathring{S} = 0$ and $\mathring{R} = 0$, let $\mathring{I}^n$, $\mathring{S}^n$ and $\mathring{R}^n$ be sequences satisfying
and
We additionally assume that the total populations are the same:
We say that a rumor outbreak occurs if the following limit exists
and $\phi_e(\mathring{I})$ is positive, where $\phi^\infty(\mathring{I}^n, \mathring{S}^n)$ is the final size of the rumor for the initial data $\mathring{I}^n$, $\mathring{S}^n$, $\mathring{R}^n$.
Remark 1. (1) In [13,15,25], the authors define that the rumor outbreak occurs if
This is essentially equivalent to Definition 2.4. We use $\phi(\infty)$ instead of $R(\infty)$, since $R(t) = R(\phi(t))$. See the result in Lemma 3.3.
(2) The rumor spreading begins with one spreader. Therefore, $\mathring{S} = 1/N$, where $N$ is the total population number. Generally, $N$ is a large number and this implies that $\mathring{S}\thickapprox0$. However, if we assume that $\mathring{I} = \mathring{T}$ and $\mathring{S} = \mathring{R} = 0$, then the corresponding solution $(I(t), S(t), R(t))$ is the trivial stationary solution. Therefore, to get an intrinsic property of the system, we have to consider a limit of sequence with initial data $\mathring{S}^n\to 0$.
The following is the main theorem of this paper.
Theorem 2.5. Let $k$, $\sigma$, $\delta$ and $\mathring{T}$ be positive constants and $\mathring{R} = \mathring{R}^n = 0$. Let $\{(I^n(t), S^n(t), R^n(t))\}$ be a sequence of solutions to system (1) subject to initial data $\mathring{I}^n$, $\mathring{S}^n$ and $\mathring{R}^n = 0$, respectively.
We assume that each $\mathring{S}^n$ is positive, $\mathring{I}^n\to \mathring{I}$ and $\mathring{S}^n\to 0$ for an N-dimensional vector $\mathring{I}$, and
Then, there exists the following limit of steady states:
where $\phi^\infty(\mathring{I}^n, \mathring{S}^n)$ is the final size of the rumor for the initial data $\mathring{I}^n$ and $\mathring{S}^n$ with $\mathring{R}^n = 0$.
Furthermore, if $kM_1(\mathring{I})>\delta
$, $\phi_e(\mathring{I})$ is positive and if $kM_1(\mathring{I})\leq\delta
$, $\phi_e(\mathring{I})$ is zero.
Remark 2. An equivalent condition of occurring a rumor outbreak is
3.
An equation for rumor size $\phi$
In this section, we derive a single equation for $\phi$ and consider the steady state analysis for the rumor spreading model (1) via a derived single equation of $\phi$ from the next argument.
Lemma 3.1. Let $(I, S, R)$ be a solution to system (1) with an initial data $\mathring{I}$, $\mathring{S}$ and $\mathring{R}$. Then each $I_i(t)$ satisfies
where $\phi(t)$ is a function defined in Definition 2.1.
Proof. From the first equation of system (1), we have
Integrating the above relation gives
For the population density of $S(t)$, we can obtain the following formula for $I_i$:
Clearly, we have $\displaystyle \frac{d}{dt}\phi(t) = S(t)$, which implies that $\displaystyle \phi(t)-\phi(0) = \int_0^tS(\tau)d\tau$.
Lemma 3.2. Let $(I, S, R)$ be a solution to system (1) with initial data $\mathring{I}$, $\mathring{S}$ and $\mathring{R}$. For the given initial data, the total population $T(t)$ of the solution to system (1) is conserved. Thus, we have
Proof. Note that the summation of all equations in system (1) yields
Integrating the above equation leads to
Remark 3. By the conservation property (3) in Lemma 3.2 and the formula in (2), we easily obtain the following formula for $S(t)$:
Lemma 3.3. Let $(I, S, R)$ be a solution to system (1) with initial data $\mathring{I}$, $\mathring{S}$ and $\mathring{R}$. Then $R(t)$ is a function depending on $\phi$:
Proof. The third equation in system (1) gives us that
From (4) and the definition of $\phi$: $\displaystyle \phi(t) = \int_0^t S(\tau)d\tau$, we get
We directly have $K_1$ and $K_4$ with
For $K_2$, we use $\lambda_i\ne0$ for all $1\leq i\leq N$. By the change of variables and the fact that $\phi(0) = 0$, we obtain
Similarly, we have $K_3$ with
Therefore, the above elementary calculations yield
The formula (4) of $S(t)$ implies that
By the result in Lemma 3.3, we derive a single decoupled equation for $\phi$ such that
For simplicity, we define
Then, $\phi(t)$ is the solution to the following single equation subject to initial data $\phi(0) = 0$.
4.
Steady state analysis
In this section, we use the steady state analysis to obtain the threshold phenomena for asymptotic behavior of the solution to system (1). To obtain the asymptotic behavior of solutions to (6), we first consider a steady state $\phi$ to (6). In other words, the steady state $\phi$ satisfies
where $F(\phi) = F(\phi, \mathring{I}, \mathring{S}, \mathring{R}, \mathring{T})$ is the function defined in (5). Therefore, $\phi$ is one of solutions to equation (7). Using a standard method from [19,25,26], we can obtain a sufficient condition for the existence of nontrivial zeros. We define $G$ and $H$ by
and
Then, we divide $F$ into two parts $G$ and $H$ with $F(\phi) = G(\phi)-H(\phi)$. Note that $F$ is the difference between the exponential part $G$ and the linear part $H$. Hence equation (7) is equivalent to the following:
Lemma 4.1. Let $G(\cdot)$ be a function defined in (8) for a given initial data $\mathring{I}, \mathring{S}, \mathring{R}$ and $\mathring{T}$. If $\mathring{T} = \sum_{i = 1}^N\mathring{I}_i+\mathring{S}+\mathring{R}$, the following properties hold:
Proof. By the definition of $G$, we have $\displaystyle
G(0) = \mathring{T}-\sum_{i = 1}^N \mathring{I}_i -\mathring{R} = \mathring{S}$. Relation (4) yields the first result in this lemma.
For the next result, we take the limit such that
Therefore, we have $\displaystyle
\lim_{\phi\to \infty}G(\phi) = \mathring{S}
+ k \sigma \sum_{\lambda_i\ne 0}\frac{\mathring{I}_i}{ k \lambda_i }$. Notice that the second term on the right hand side of the above equation is finite.
Therefore, we conclude that $\displaystyle \lim_{\phi\to \infty}G(\phi) <\infty$.
Lemma 4.2. Assume that $k$ and $\sigma$ are positive constants, $\lambda_i\geq0$ and $\mathring{I}_i\geq0$ for all $i = 1, \ldots, N$. Let $G(\cdot)$ be the function defined in (8). If $M_1(\mathring{I})>0$, then the derivative $\displaystyle G'(\cdot)$ is positive and
Proof. Note that the derivative of $G$ is
We can calculate the first term in the above as
Thus, if at least one non-zero $\lambda_i\mathring{I}_i $ exists, we have
Lemma 4.3. Let $k$ and $\sigma$ be positive constants and $\delta\geq0$. Let $H(\cdot)$ be the function defined in (9). If $\mathring{T} = \sum_{i = 1}^N\mathring{I}_i+\mathring{S}+\mathring{R}$, and initial data $\mathring{I}_i$, $\mathring{S}$ and $\mathring{R}$ are nonnegative for all $i = 1, \ldots, N$, then $H(\cdot)$ is a linear function with nonnegative slope and $H(0) = 0$.
Proof. Note that
Therefore, $\delta+ k \sigma \mathring{T}- k \sigma
\sum_{\lambda_i = 0}\mathring{I}_i$ is positive and this means that $\displaystyle \delta+ k \sigma \mathring{T} > k \sigma
\sum_{\lambda_i = 0}\mathring{I}_i$. This implies that $H(\cdot)$ is monotone increasing with $H(0) = 0$.
Proposition 1. Let $k$, $\sigma$ and $\delta$ be positive constants. Let $(I, S, R)$ be a solution to system (1) with initial data $\mathring{I}, \mathring{S}$ and $\mathring{R}$. We assume that $\mathring{S}$ is positive, $\mathring{I}\geq 0$, $\mathring{R} = 0$ and $\mathring{T} = \sum_{i = 1}^N\mathring{I}_i+\mathring{S}+\mathring{R}$.
Then there is a final rumor size $\phi^\infty(\mathring{I}, \mathring{S})$ such that
where $\phi(t)$ is the rumor size satisfying (6). Moreover, $\phi^\infty(\mathring{I}, \mathring{S})$ is the smallest positive zero of $F(\cdot)$ such that
Proof. This follows from an elementary result of ordinary differential equations. Note that for given initial data $\mathring{S}>0$, $\mathring{I}\geq 0$ and $\mathring{R} = 0$, the corresponding equation $\dot{\phi} = F(\phi)$ is autonomous. Therefore, we can apply Lyapunov's stability theorem. From the properties of $G(\cdot)$ and $H(\cdot)$ in Lemmas 4.1 and 4.3, we have
and
By the intermediate value theorem, there is at least one positive solution $\psi>0$ such that $0 = F(\psi) = F(\psi, \mathring{I}, \mathring{S}, \mathring{R}, \mathring{T})$ for a given initial data $\mathring{I}$, $\mathring{S}$ and $\mathring{R}$. Let $\phi^\infty$ be the smallest element of the set of positive solutions $\{\psi>0:F(\psi) = 0\}$.
For a fixed $\mathring{S}>0$, $F(0) = \mathring{S}>0$. This shows that $\phi(t)$ is increasing near $t = 0$ and $F(x)>0$ on $\{0<x<\phi^\infty\}$. Moreover, $F(x)$ is differentiable with respect to $x$, which implies that $\phi(t)\to \phi^\infty$ as $t\to \infty$ by an elementary result of ordinary differential equations.
Proposition 2. Let $k$, $\sigma$ and $\delta$ be positive constants and $\lambda_i\geq0$ for all $i = 1, \ldots, N$. Suppose that $\mathring{I}_i\geq0$, $i = 1, \ldots, N$, $\mathring{R} = \mathring{S} = 0$ and $\mathring{T}$ is a fixed positive constant with $\mathring{T} = \sum_{i = 1}^N\mathring{I}_i$. If we assume that $M_1(\mathring{I})>0$, then the following statement holds.
The equation $F(\phi, \mathring{I}, \mathring{S}, \mathring{R}, \mathring{T}) = 0$ has a positive solution $\phi>0$ if and only if $kM_1>\delta$. Moreover, if $kM_1\leq \delta$, then the equation has no positive zero and $\phi = 0$ is a solution to the equation.
Proof. We have, by Lemma 4.1 and 4.3,
and
It follows that $F(0) = 0$ and
Lemma 4.2 implies that the derivative of $G(\phi)$ is positive and
Moreover, if $\mathring{S} = 0$, then we have
Therefore,
So,
This yields
and the continuity of $F$ implies that there is a positive real number $\phi_\epsilon>0$ such that
Thus, the intermediate value theorem and (10) show that $F(\phi, \mathring{I}, \mathring{S}, \mathring{R}, \mathring{T}) = 0$ has a positive solution $\phi>0$.
In order to complete the proof of this proposition, it suffices to verify that the equation has a unique solution $\phi = 0$ on $\{\phi\geq 0\}$ if $kM_1\leq \delta$.
We now assume that $kM_1\leq \delta$. We rewrite (11) by
Since we assume that $\sum_{i = 1}^N k \lambda_i \mathring{I}_i = kM_1\leq \delta$ and $\mathring{T} = \sum_{i = 1}^N \mathring{I}_i$,
This implies that
The fact in (10) with $F(0) = 0$ leads us to
Therefore, we complete the proof.
We are now ready to prove the main theorem.
The proof of the main theorem. Let $\mathring{R}^n = \mathring{R} = 0$ and let $\mathring{I}^n$ and $\mathring{S}^n$ be sequences such that
We denote
First, assume that $kM_1(\mathring{I})>\delta$. By (12), we have
Note that (11) implies that
Therefore,
By (13), there is $N_0\in \mathbb{N}$ such that if $n>N_0$, then
and
Since $\mathring{I}_{i}^n$ is bounded, we can choose $\epsilon_\phi$ such that if $0\leq \phi \leq \epsilon_\phi$, then
Thus, there are constants $\epsilon_\phi>0, N_0\in\mathbb{N}$ such that if $0\leq\phi <\epsilon_\phi$ and $n> N_0$, then
In order to prove convergence, we consider differentiable functions $I(s), S(s)$ and $R(s)$ with respect to $s\in\mathbb{R}$ such that
and
We denote $F_p(\phi, s) = F_p(\phi, I(s), S(s), R(s), \mathring{T})$. Since $\frac{\partial}{\partial\phi}F(\phi, s)\bigg|_{\phi = 0, s = 0}>0$, the implicit function theorem implies that $\phi(s)$ is differentiable near $s = 0$. Thus, $\phi^\infty(\mathring{I}^n, \mathring{S}^n) = \phi(1/n)$ converges.
We now prove that $\phi_n^\infty\to \phi_e>0$. Assume not, that is $\phi_n^\infty\to 0$ as $n\to \infty$. Then there is a $N_1\in\mathbb{N}$ such that $n>N_1$ implies $\phi_n^\infty(\mathring{S}) <\epsilon_\phi$. We may take $N_1\in\mathbb{N}$ such that $N_1>N_0$.
For $n>N_1$, we have $F(0, \mathring{I}^n, \mathring{S}^n, \mathring{R}^n, \mathring{T}) = \mathring{S}^n>0$ and $F(\phi_n^\infty, \mathring{I}^n, \mathring{S}^n, \mathring{R}^n, \mathring{T}) = 0$. However, by (14), $\frac{\partial F}{\partial\phi}(\phi, \mathring{I}^n, \mathring{S}^n, \mathring{R}^n, \mathring{T})>0$. This is a contradiction. Thus we obtain the desired result.
For the last part, we assume that $kM_1\leq \delta$. Then, $\phi = 0$ is the unique nonnegative solution to $F(\phi, \mathring{I}, \mathring{S}, \mathring{R}, \mathring{T}) = 0$. Moreover $\phi^\infty(\mathring{I}^n, \mathring{S}^n)>0$. Let $\{\phi_{n_n}\}$ be any convergent subsequence of $\{\phi^\infty(\mathring{I}^n, \mathring{S}^n)\}$.
Let $\phi_{n_\infty} = \lim_{n\to \infty}\phi_{n_n}\geq0$. Since $F$ is a continuous function,
Therefore, by Proposition 2, $\phi_{n_\infty} = 0$, i.e., $\lim_{n\to \infty}\phi_{n_n} = 0$. We proved that any convergent subsequence of $\{\phi^\infty(\mathring{I}^n, \mathring{S}^n)\}$ converges to zero. Thus, by an elementary theorem in analysis,
5.
Numerical simulation
In this section, we numerically provide the solutions to system (1) with respect to several $\delta$ and compare them with the analytical results in Section 4. The main result in this paper suggests that the condition for rumor outbreak is that $M_1(I_0)$ is less than $\delta/k$.
For the numerical simulations, we used the fourth-order Runge-Kutta method with the following parameters:
We take sufficiently large initial data $\mathring{I}_i$, $i = 1, 2$ and $3$, and sufficiently small $\mathring{S}$ such that
To see the threshold phenomena for $M_1(I_0)$ and $\delta/k$, we consider $\delta = 0.5\times 10^5, 1.5\times 10^5, 2.5\times 10^5, 3.5\times 10^5, 4.5\times 10^5~\mbox{and}~5.5\times 10^5$.
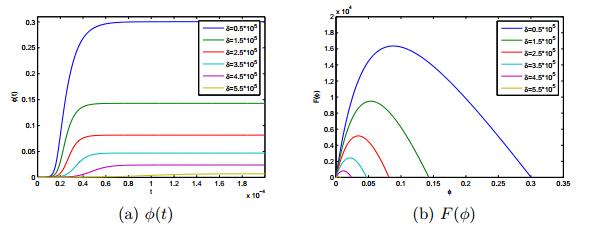
Note that in Proposition 1, we rigorously obtained that the final size of the rumor $\phi^\infty = \lim_{t\to \infty}\phi(t)$ is the smallest positive zero of $F(\phi)$. In Figure 1, we plotted the rumor size $\phi(t)$ and $F(\phi)$ with respect to several $\delta>0$. Here, we can observe that the final size of the rumor $\phi^\infty$ is also the smallest positive zero of $F(\phi)$. Thus the numerical results are consistent with the analytical result.
In Figure 2, we plotted the densities of the spreaders (S) and the stiflers (R) with respect to several $\delta>0$. Thus, we can see that the rumor size are proportional to $1/\delta$.
In Figure 3, we plotted $\phi^\infty$ with respect to $\delta>0$ to see the threshold phenomena for $M_1(I_0)$ and $\delta/k$. Note that $ \mathring{S}\simeq 0, M_1(\mathring{I}) = \lambda_1 \mathring{I}_1+\lambda_2 \mathring{I}_2+\lambda_2 \mathring{I}_2\simeq 6\times 10^4$.
From our analytic results, we can expect that the threshold occurs when $\delta = k M_1(\mathring{I})\simeq 6\times 10^5$. In Figure 3, $\phi^\infty$ decreases almost linearly in $\delta$, and the graph of $\phi^\infty(\delta)$ is very close to the line $\phi^\infty = 0$ as $\delta$ goes to $6\times 10^5$. Therefore, this numerical simulation coincides with our analytic result. By the way, a small error occurs between the analytical and the numerical results. We guess that this error may result from the nonzero assumption for $\mathring{S}>0$.
6.
Conclusion
In this paper, we consider the rumor spreading model with the trust rate distribution. The model consists of several ignorants with trust rates $\lambda_i$, $i = 1, \ldots, N$. We provide the threshold phenomenon for this model by using classical steady state analysis. Fortunately, we can obtain the corresponding equation of rumor size for this model with several types of ignorants. We also present a rigorous proof for the convergence result. As seen from the steady state analysis, we obtain that the threshold phenomena depends on the decay rate $\delta$ of spreaders to stiflers and the momentum type quantity $M_1$ defined in Definition 2.2:$\displaystyle M_1(\mathring{I}) = \sum_{i = 1}^N\lambda_i \mathring{I}_i$. We conclude that a necessary and sufficient condition for rumor outbreak is that the trust momentum $M_1(\mathring{I})$ is greater than some combination of parameters $\delta/k$.









 DownLoad:
DownLoad: