A static multiple detector solar radiation sensor

J. Appelbaum; J. Appelbaum

doi:10.3934/energy.2020.5.802

AIMS Energy

2020, Volume 8, Issue 5: 802-818. doi: 10.3934/energy.2020.5.802

Previous Article Next Article

Research article

A static multiple detector solar radiation sensor

J. Appelbaum ^,

School of Electrical Engineering, Tel Aviv University, Israel

Received: 27 March 2020 Accepted: 03 August 2020 Published: 28 August 2020

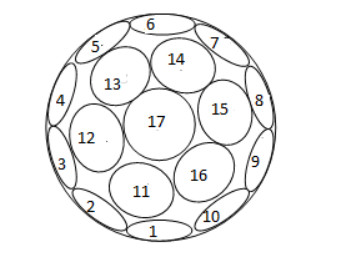
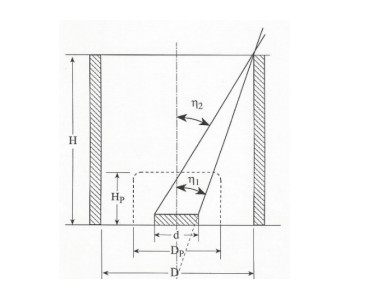
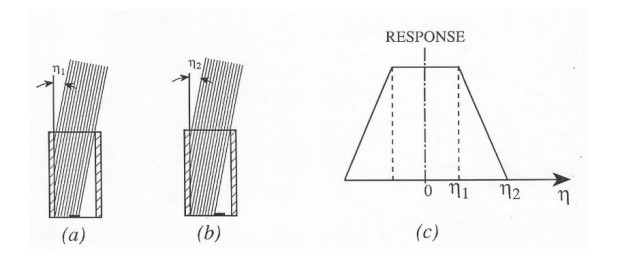
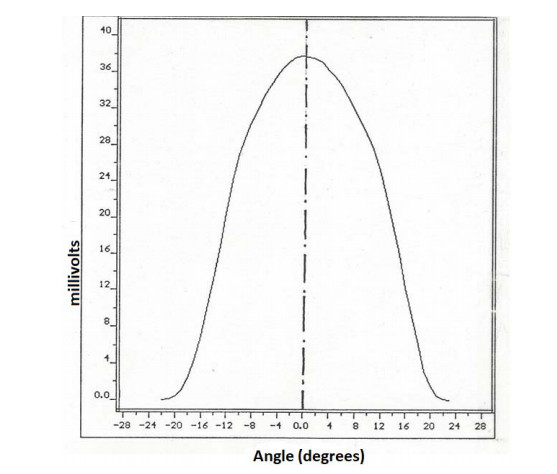
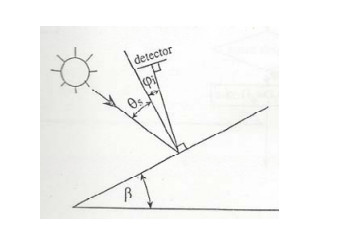
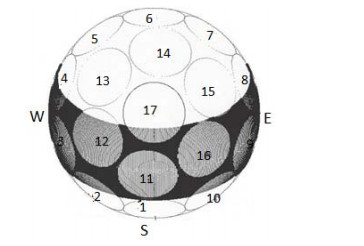
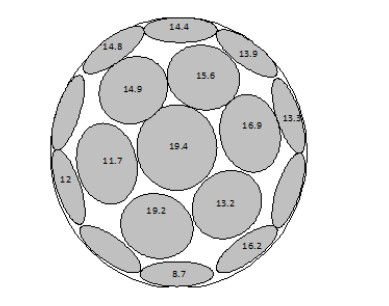
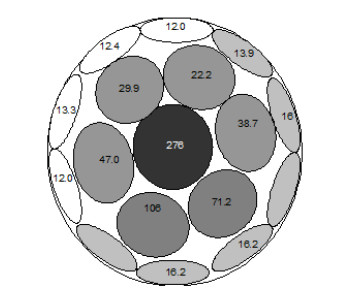
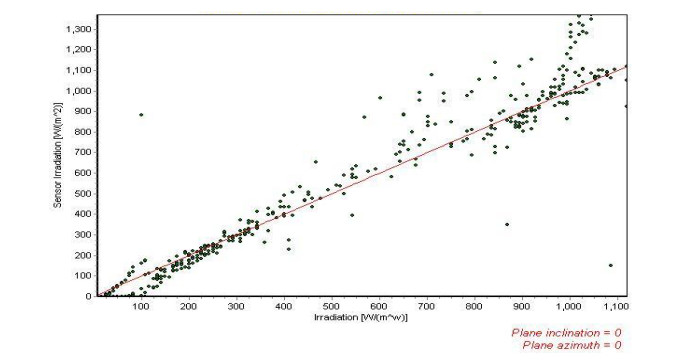
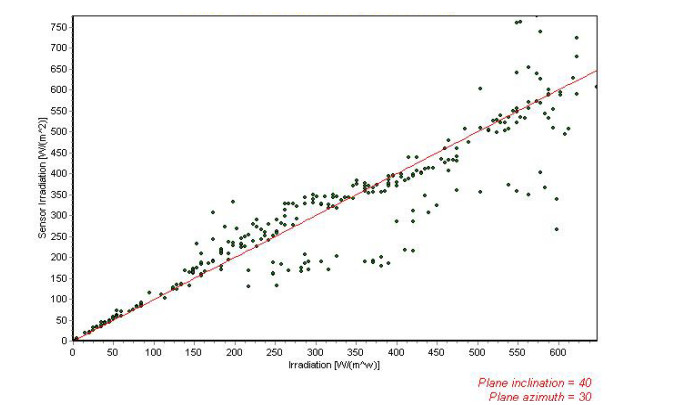
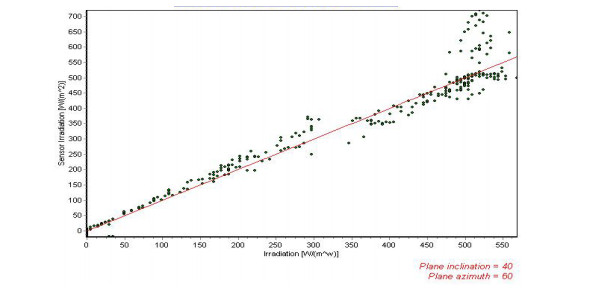
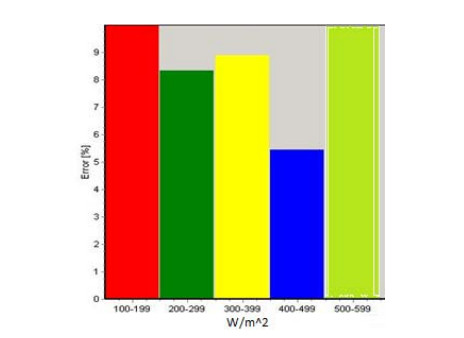
A small static solar radiation sensor comprising of 17 photodiode detectors deployed evenly on a hemispherical-member is proposed. The sensor is capable of measuring the intensity and time dependent of the solar radiation components on any desired inclined and oriented plane, including the distribution of the diffuse radiation in the sky. The sensor may also be used in solar tracking systems for pointing to the highest radiation intensity at any time. An inverted sensor may also measure reflected radiation from different objects. As a first design, the accuracy obtained is about 10 to 15 percent, depending of the solar radiation intensity, and the aiming is to improve the accuracy to about 5 percent. The objective was to construct a static sensor with small dimensions and of light-weight, detectors and hemispherical-dome hermetically sealed and machined close to a prototype product.

Keywords:

static solar radiation sensor,
multiple detector solar radiation sensor,
mapping solar radiation in sky

Citation: J. Appelbaum. A static multiple detector solar radiation sensor[J]. AIMS Energy, 2020, 8(5): 802-818. doi: 10.3934/energy.2020.5.802

Related Papers:

[1]	Boqiang Chen, Zhizhou Zhu, Qiong Li, Daihai He . Resurgence of different influenza types in China and the US in 2021. Mathematical Biosciences and Engineering, 2023, 20(4): 6327-6333. doi: 10.3934/mbe.2023273
[2]	Eunha Shim . Prioritization of delayed vaccination for pandemic influenza. Mathematical Biosciences and Engineering, 2011, 8(1): 95-112. doi: 10.3934/mbe.2011.8.95
[3]	Olivia Prosper, Omar Saucedo, Doria Thompson, Griselle Torres-Garcia, Xiaohong Wang, Carlos Castillo-Chavez . Modeling control strategies for concurrent epidemics of seasonal and pandemic H1N1 influenza. Mathematical Biosciences and Engineering, 2011, 8(1): 141-170. doi: 10.3934/mbe.2011.8.141
[4]	Rodolfo Acuňa-Soto, Luis Castaňeda-Davila, Gerardo Chowell . A perspective on the 2009 A/H1N1 influenza pandemic in Mexico. Mathematical Biosciences and Engineering, 2011, 8(1): 223-238. doi: 10.3934/mbe.2011.8.223
[5]	Oren Barnea, Rami Yaari, Guy Katriel, Lewi Stone . Modelling seasonal influenza in Israel. Mathematical Biosciences and Engineering, 2011, 8(2): 561-573. doi: 10.3934/mbe.2011.8.561
[6]	Gerardo Chowell, Catherine E. Ammon, Nicolas W. Hengartner, James M. Hyman . Estimating the reproduction number from the initial phase of the Spanish flu pandemic waves in Geneva, Switzerland. Mathematical Biosciences and Engineering, 2007, 4(3): 457-470. doi: 10.3934/mbe.2007.4.457
[7]	Marco Arieli Herrera-Valdez, Maytee Cruz-Aponte, Carlos Castillo-Chavez . Multiple outbreaks for the same pandemic: Local transportation and social distancing explain the different "waves" of A-H1N1pdm cases observed in México during 2009. Mathematical Biosciences and Engineering, 2011, 8(1): 21-48. doi: 10.3934/mbe.2011.8.21
[8]	Hiroshi Nishiura . Joint quantification of transmission dynamics and diagnostic accuracy applied to influenza. Mathematical Biosciences and Engineering, 2011, 8(1): 49-64. doi: 10.3934/mbe.2011.8.49
[9]	Eunha Shim . Optimal strategies of social distancing and vaccination against seasonal influenza. Mathematical Biosciences and Engineering, 2013, 10(5&6): 1615-1634. doi: 10.3934/mbe.2013.10.1615
[10]	Julien Arino, Chris Bauch, Fred Brauer, S. Michelle Driedger, Amy L. Greer, S.M. Moghadas, Nick J. Pizzi, Beate Sander, Ashleigh Tuite, P. van den Driessche, James Watmough, Jianhong Wu, Ping Yan . Pandemic influenza: Modelling and public health perspectives. Mathematical Biosciences and Engineering, 2011, 8(1): 1-20. doi: 10.3934/mbe.2011.8.1

Abstract

References

[1]	Faiman D, Feuermann D, Ibbetson P, et al. (1992) A multipyranometer instrument for obtaining the solar beam and diffuse components, and the irradiance on inclined planes. Sol Energy 48: 253-259. doi: 10.1016/0038-092X(92)90099-V
[2]	Curtis P (1993) An analysis of methods for deriving the constituent insolation components from multipyranometer array measurements. J Sol Energy Eng 115: 11-21. doi: 10.1115/1.2930018
[3]	Hamalainen M, Nurkkanen P, Slaen T (1985) A multisensory pyranometer for determination of the direct component and angular distribution of solar radiation. Sol Energy 35: 511-525. doi: 10.1016/0038-092X(85)90120-3
[4]	Appelbaum J, Bergshtein O (1987) Solar radiation distribution Sensor. Sol Energy 39: 1-10. doi: 10.1016/S0038-092X(87)80046-4
[5]	Imamura M, Helm P (1992) A novel method of monitoring global normal irradiance with a stationary sensor. Int J Sol Energy 11: 211-217. doi: 10.1080/01425919208909741
[6]	Heisterkamp N, Orthjohann E, Voss J (1994) A multi-purpose irradiance measuring system. 12^th European photovoltaic solar Energy conference, Amsterdam, The Netherlans.
[7]	Appelbaum J, Weiss Y (1999) The packing of circles on a hemisphere. Meas Sci Technol 10: 1015-1019. doi: 10.1088/0957-0233/10/11/307
[8]	Bany J, Appelbaum J (1987) The effect of shading on the design of a field of solar collectors. Sol Cells 20: 201-228. doi: 10.1016/0379-6787(87)90029-9
[9]	Temp RC, Coulson KL (1977) Solar radiation incident upon slopes of different orientations. Sol Energy 19: 179-184. doi: 10.1016/0038-092X(77)90056-1
[10]	Klucher TM (1979) Evaluation of models to predict insolation on tilted surfaces. Sol Energy 23: 111-114.
[11]	Perez R, Ineichen P, Seal P, et al. (1990) Modeling daylight availability and irradiance componens from direct and global irradiance. Sol Energy 44: 271-289. doi: 10.1016/0038-092X(90)90055-H

This article has been cited by:

1.	Eungyeong Kim, Seok Lee, Young Tae Byun, Hyuk-Jae Lee, Taikjin Lee, Implementation of integrated monitoring system for trace and path prediction of infectious disease, 2013, 14, 1598-0170, 69, 10.7472/jksii.2013.14.5.69
2.	Sergio A. Hojman, Felipe A. Asenjo, Phenomenological dynamics of COVID-19 pandemic: Meta-analysis for adjustment parameters, 2020, 30, 1054-1500, 103120, 10.1063/5.0019742
3.	S. Towers, G. Chowell, Impact of weekday social contact patterns on the modeling of influenza transmission, and determination of the influenza latent period, 2012, 312, 00225193, 87, 10.1016/j.jtbi.2012.07.023
4.	Kirsty J. Bolton, James M. McCaw, Mathew P. Dafilis, Jodie McVernon, Jane M. Heffernan, Seasonality as a driver of pH1N12009 influenza vaccination campaign impact, 2023, 17554365, 100730, 10.1016/j.epidem.2023.100730
5.	Thassakorn Sawetsuthipan, Naraphorn Paoprasert, Papis Wongchaisuwat, A stochastic game model for infectious disease management decisions in schools, 2024, 10293132, 100343, 10.1016/j.apmrv.2024.12.007

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)