Fuzzy permutation entropy derived from a novel distance between segments of time series

1.   Introduction

Over the past decades, the rapid development of communication technology helps to collect massive data from people's daily life. In the coming big data era, it is a hotspot to study how to enhance data processing technology. Data mining for time series plays an important role in this field. Some tools, such as fractal dimension ^[12], Lyapunov exponent ^[27], fractional calculus ^[22], entropy ^[36], etc., have been widely used to characterize essential features of dynamic systems. Fractional calculus brings innovation to both theory and application, and it is a powerful tool that measures memory effects of time series. For example, Yu studies the backward stochastic differential equations driven by fractional Brownian motion ^[35], Zhang establishes limit theorems for the integral functional of fractional Brownian motion ^[34], Zhao proposes a new weak signal detection method based on fractional Fourier transform ^[38] and defines a general fractional derivatives with memory effects ^[39] which can better describe nonlocal phenomena. In fact, memory is one of the manifestations of complexity. Complexity analysis is beneficial to characterize dynamical systems. As another effective tool for complexity analyzing, various entropies based on Shanon's form have been applied in engineering, economic and other disciplines. As we all known, information entropy can be used to quantify indeterminacy from the output of complex systems. In fact, to explore dynamical characteristics and the revolutionary mechanism, researchers have developed diversified tools. Here we show three important ones, and they are Multiple Scale Entropy (MSE) ^[7], Permutation Entropy (PE) ^[5] and Fuzzy Entropy (FE) ^[6]. Readers should know that more than 100 kinds of entropies are widely used in various fields ^[19], such as Cumulative Residual Entropy ^[15,32], Transfer Entropy ^[24,26], Rough Entropy ^[23], Wavelet Entropy ^[10] and so on.

MSE  Based on Sample Entropy(SE), M. Costa takes into account different time lags and proposes MSE which has attract researchers' concerns fascinatingly ^[13,33]. Taking MSE as a feature of the time headway, Z. Xiang studies the relation between the traffic congestion and the complexity ^[30], A. Llenas classifies digital and analog modulated signals with Support Vector Machine(SVM) ^[17]. M. Ahmed generalizes MSE to Multivariate Multiscale Entropy(MMsE) and explores real-world biological systems as well as physical systems ^[18]. Since short time series may cause to undefined MSE, S. Wu has proposed Refined Composite Multiscale Entropy(RCMsE) which contributes to increase the accuracy of estimation ^[28]. What's more, MSE can be applied to biomedicine. For example, F. Liao has found that MSE of the skin blood flow provides a comprehensive assessment of the risk for Diabetic foot ulcer ^[16].

PE  The standard variance, which is used to judge whether a new pattern occurs or not, exerts an important part in the method of MSE. As real-world time series are often non-stationary series, it may lead to unreliable results. PE, which takes the order structure in each segment as a basic criteria, puts forward a different way of identifying new patterns. C. Bandt has proposed the fundamental form of PE and used it to analyze the sensitivity of the noise in speech signals ^[5]. But PE completely neglects the amplitude of time series, which makes it performs barely satisfactory. To overcome this weakness, B. Fadlallah proposes an amendment, Weighted Permutation Entropy(WPE), which takes the amplitude of each fragment as its weight ^[9]. H. Azami has proposed Improvement Multiscale Permutation Entropy(IMPE) by taking the average of WPE over different time lags ^[2]. Both WPE and IMPE are applied to EEG analysis on epilepsy detection, and the results show they are sensitive to impulses or abrupt changes in EEG signals, and the variability of IMPE is smaller than WPE. Moreover, there are some further amendments on WPE and applications in traffic engineering and finance ^[29,37].

FE   Both MSE and PE quantify the complexity of time series by the change of the probability of new patterns in different scales, but ignore the fact that the degree of deviation between different patterns is not invariable. Based on this fact, W. Chen proposes FE as an efficient tool to characterize time series and analyzes its antinoise performance ^[6]. Since the distance between segments is derived from the infinite norm, a lot of details are still abandoned. Researchers have made some improvements on FE. Here we only showcase several recent works. H. Azami puts forward Refined Multiscale Fuzzy Entropy(RMsFE), which enhances the stability and reliability of diagnosing in Alzheimer's disease ^[4]. Later he proposed a multi-dimensional form, Refined Composite Multivariate Multiscale Fuzzy Entropy(RCMMsFE), which is similar to the multi-variable generalizing of MSE. RCMMsFE has been examined on focal and non-focal EEG signals, and it contributes to decrease the running time as well as the sensitivity to the length of time series ^[3]. Fractional Fuzzy Entropy(FFE) demonstrates its effectiveness on analyzing EEG signals from epileptic patients, and S. He discusses how to choose parameters in ^[11]. X. Zhu defines Time-Shift Multiscale Fuzzy Entropy(TSMsFE), which is applied to the single point fault diagnosis for rolling bear system ^[41].

As we have mentioned above, MSE, PE and FE are focus on different scales, ordinal pattern and similarity, respectively. They share similar adjustments to enhance the performance, such as robustness to noise. They still have their own disadvantages. For MSE, it needs long source time series to obtain statistically significant results, because of the process of coarse graining of segments, but it is difficult to collect enough data in some real-time scenarios. In fact, if it is used to measure the complexity of short time series, MSE may induce undefined entropy. For PE, the similarity of different order structures is ignored, which gives rise to a false increasing of the complexity. For FE, since the distance between embedding vectors is derived from the infinite norm, it may no longer be valid if SNR is relatively low. Besides, how to assign optimal parameters of the above three entropies is still unclear. So, we attempt to propose a comprehensive method, Fuzzy Permutation Entropy(FPE), which combines MSE, PE and FE appropriately and this approach can be applied to short time series for real-time problems.

The rest of this paper is organized to 4 sections. In Section 2, we explain key details of FPE as well as some necessary mathematical proofs. Several common signals are examined by FPE, and three comparisons among MSE, PE, FE and FPE are made in Section 3. Then, we apply FPE to the data of traffic simulation to detect the traffic flow congestion in Section 4. Finally, we draw a conclusion in Section 5.

2.   Methodology

In this section, we define a new distance between rearrangement (finite sequence) based on inversion and show the approach of computing this distance, then we introduce the process of calculating FPE.

2.1.   The distance between two ordered array

Let $\pi = ({a_1}\ {a_2}\ \cdots \ {a_n})$ be a rearrangement of the naturally ordered $n$-dimensional array $(1\ 2\ \cdots\ n)$ and $\mathcal{A}$ the set of all rearrangements ^[8]. $\#(\pi)$ denotes its inversion ^[21]. If $\pi_T: \left({T_1}{\rm{\ }}{T_2}{\rm{\ }} \cdots {\rm{\ }}{T_n}\right)$ and $\pi_S: \left({S_1}{\rm{\ }}{S_2}{\rm{\ }} \cdots {\rm{\ }}{S_n}\right)$ belong to $\mathcal{A}$, then

denotes a permutation from $\pi_T$ to $\pi_S$ on $\mathcal{A}$. Obviously, the order of columns in $T$ does not affect its function. In general, $T = \left[\begin{matrix} {{T_1}{\rm{\ }}{T_2}{\rm{\ }} \cdots {\rm{\ }}{T_n}} \cr {{S_1}{\rm{\ }}{S_2}{\rm{\ }} \cdots {\rm{\ }}{S_n}} \cr \end{matrix}\right]$ can be written as $T = \left[\begin{matrix} {T_{k_1}} & {\rm{\ }}{T_{k_2}} & {\rm{\ }} \cdots & {\rm{\ }}{T_{k_n}} \cr {1} & {\rm{\ }}{2} & {\rm{\ }} \cdots & {\rm{\ }}{n} \cr \end{matrix}\right]$, where $k_i$ satisfies to $S_{k_i} = i$. If it does not lead to confusion, $\#(T)$ is still used to represent the inversion of $T$. That is,

If the exchange of elements in a rearrangement is restricted to adjacent elements (in this paper, this restriction always exists), the inversion seems like a kind of distance to some extent, see Theorem 2.1.

Theorem 2.1. Let $\pi = ({a_1}\ {a_2}\ \cdots \ {a_n})$ be a rearrangement, then at least $\#(\pi)$ times exchanges are needed to turn $\pi$ into a natural ordered rearrangement.

Proof: Firstly, each exchange of adjacent elements cause $\pi$ add or minus 1. In particular, if $(a_i, a_{i+1})$ is an inverse pair ^[21] in $\pi$, then

It is a direct corollary of the fact that the exchange of adjacent elements just alter the order relation between themselves.

Secondly, in order to transfer any $\pi$ to natural order, we just need to make sure any pair of adjacent elements can not form inverse pair.

Finally, all we need is to apply the induction on $n$, viz. the length of $\pi$.

1. It is trivial for $n = 2$.

2. Assume it holds for $n\leq k$. For $n = k+1$, let

and

where $a_j = 1$. Thus we have,

For the minimum element "1", if 1 is not in the first place, then each neighbor on the left and itself must be an inverse pair. So it takes at least $j-1$ times exchange to place element 1 at the first place. Using the induction hypotheses, $\pi_0$ needs at least $\#(\pi_0)$ times exchange to form a naturally ordered sequence. Thus $\pi$ needs at least $\#(\pi_0)+j-1$ times exchange to be naturally ordered. From Eq (2.4), the conclusion holds.

Based on the above theorem, the distance between rearrangements can be defined as follow:

Definition 2.1. Let $\pi_a = ({a_1}\ {a_2}\ \cdots \ {a_n})$ and $\pi_b = ({b_1}\ {b_2}\ \cdots \ {b_n})$ be rearrangements, the distance between them can be defined as the inversion of the permutation from $\pi_a$ to $\pi_b$, denoted by $d(\pi_a, \pi_b)$. That is,

$\mathbf{NOTE\ 1:}$ In general, a map to $\mathbb{R}$ is called a distance, if it is non-negative, symmetrical, and satisfies to the triangle inequality. In fact, they can be easily drawn by Theorem 2.1, and $d(\pi_a, \pi_b)$ is the minimum times of exchanges which turn $\pi_a$ to $\pi_b$.

To compute the value of $d(\pi_a, \pi_b)$, we need another kind of transformation which is defined below.

Definition 2.2. Let $\pi_a = ({a_1}\ {a_2}\ \cdots \ {a_n})$ be a rearrangement. For a bijection $OT = [o_1 {\ } o_2 {\ } \cdots {\ } o_n]$ on $\mathcal{A}$ with the property that $OT(\pi_a) = ({a_{o_1}}\ {a_{o_2}}\ \cdots \ {a_{o_n}})$, $OT$ is called an order transformation.

$\mathbf{NOTE\ 2:}$ With order transformation, it is easy to get the value of $d(\pi_a, \pi_b)$. In fact,

where $OT_{\pi_b}$ is an order transformation maps $\pi_b$ into natural order.

$\mathbf{NOTE\ 3:}$ In addition, if $x = (x_1, \ x_2, \ \cdots, \ x_n)$ is a unique real value sequence, we still use $OT_x$ to represent an order transformation, which maps $x$ into natural order. If $x$ is not unique, always assume that the former in $x$ should be still put in front in $OT_x(x)$. For instance, given

then,

2.2.   FPE

Referring to the steps of estimating FE as described in ^[6], the Fuzzy Permutation Entropy of a time series with a fixed scale $\tau$, $FPE(\mathbf{X}, \tau)$, can be figured out soon. The procedure can be described as follows.

1. Let $\mathbf{X} = \{x(i): 1 \leq i \leq N\}$ be a time series with length $N$. For a fixed scale $\tau$, gratitude $m$ and tolerance $r$, construct a temporal vector sequence $\left\{X_{i}^{\tau}, i = 1, 2, \cdots, N-\tau+1\right\}$ in the form as

where $X_{i}^{\tau}$ represents $\tau$ consecutive $x$ values, commencing with the $i$th point.

2. Each $X_{i}^{\tau}$ is transformed to the orderly form $O(X_{i}^{\tau})$, which is defined by

Take the above mentioned $x$ as an example, $O(x) = (4\ 3\ 6\ 2\ 5\ 1)$. For simplification, the symbol $X_{i}^{\tau}$ is still used to represent its orderly form $O(X_{i}^{\tau})$.

3. For each pair of $X_{i}^{\tau}$ and $X_{j}^{\tau}$($i\neq j$), use the Eq (2.6) to calculate the distance $\overline{d_{ij}^{\tau}}$ between them, then standardize the distance set by the maximum. That is,

4. Calculate the similarity degree $S_{ij}^{\tau}$ of each pair of $X_{i}^{\tau}$ and $X_{j}^{\tau}$ through the fuzzy function $\mu(d_{ij}^{\tau}, m, r)$, that is,

In this paper, we fix $m = 2$ and $r = 0.15$.

5. Define a global quantity $\phi^{\tau}$, as the average of $S_{i j}^{\tau}$,

6. Let $\tau = \tau+1$, repeat the above steps 1-5 and define $\phi^{\tau+1}$ as,

7. Finally, $FPE(\mathbf{X}, \tau)$ can be defined by,

3.   Analysis of classical signals

In this section, FPE is used to analyze the complexity of some typical oscillating signals, including white noise, 1/f noise, sine wave, and $x$-coordinates of Rössler system, where white noise and 1/f noise are typical stochastic signals while sine wave and Rössler series represent to deterministic signals. First, we state formulas regarding to sine wave and Rössler system; then, describe the simulation procedure; next, analyze the results under different length of time series; finally, show a comparison of FPE to MSE, PE and FE.

3.1.   Create signals

To verify the function of FPE, several signals have been created, including deterministic and stochastic ones. For random signals, white noise and pink noise(both with $\mu = 0, \sigma = 1$) are produced, as the route described in ^[40]. Here we just showcase the formula of other two deterministic dynamical systems.

Sine wave   For sine waves, different frequencies are utilized to represent different levels of the complexity of deterministic signals. Add another sine wave which has different frequency for disturbing. See Eq (3.1).

where $k$ represents the times of simulation. In every simulation, the gap $\Delta t$ is fixed to 9 constantly. By repeating this process for 10 times, sine waves of different complex degree are produced.

Rössler system

When parameters $a, b$ and $c$ take different values, the Rössler system ^[20] demonstrates distinguishable dynamical behaviors. In this study, we fix $b = 2, c = 4$ with the bifurcation parameter $a = 0.3997$ for 5-period orbit and $a = 0.4002$ for chaotic behavior, respectively.

The fourth/fifth order Runge-Kutta algorithm ^[1] is applied to estimate the numerical solutions of Eq (3.2). For each $a$ in each simulation, let the initial point be $[1,0,1]$ and the simulating timespan $t\in [0, 1500\times k]$ with the step-length for 0.1. The last certain values of $x$-component with gap length for 9 were recorded for further studying.

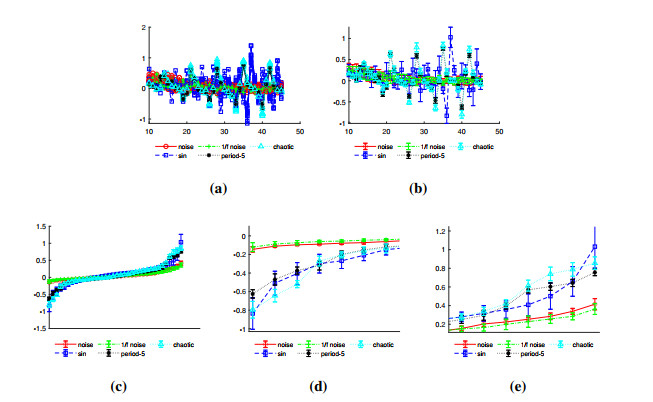
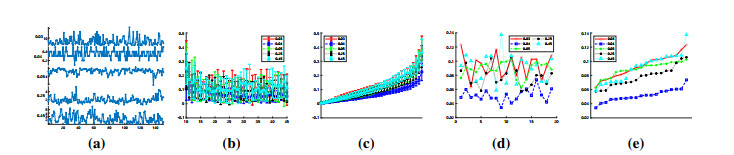
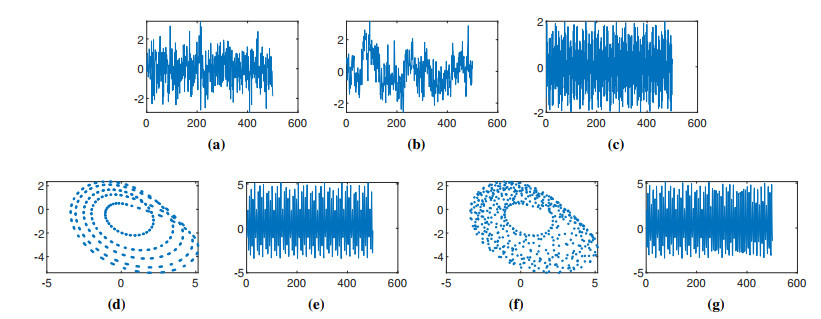
For each signals, a sample displays in Figure 1.

3.2.   Simulation procedure and analysis

Simulation procedure  To begin with, the length of signals is fixed to 500 and the range of scale is between 10 to 45. Next, the simulation is repeated for 10 times. The FPE of each signal in every scale are recorded. Then, the standard variance of FPE over different scales in each simulation are drawn. Finally, in order to analyze the performance of FPE under a variety of length of signals, we repeat the procedure with different signal length for 55, 80, 150 and 300, respectively.

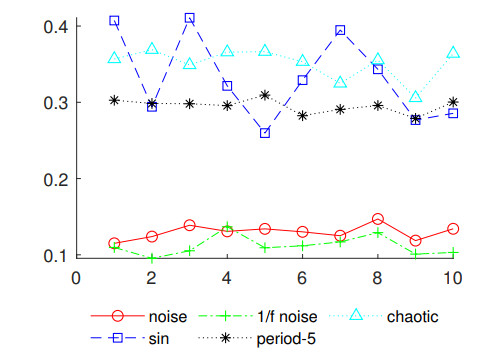
Analysis  Figure 2a and 2b show that FPE values of deterministic signals seem to be oscillating drastically as the scale increases. For stochastic signals, their FPE values are more stable but interweaved and almost indistinguishable. For chaotic and period-5 time series generated by Rössler system, the extreme values of FPE of them are close and locate at same points. For sine waves, the complexity is rising since their frequency increases. For deterministic signals, the reason for this oscillating phenomenon can be attributable to their periodicity which makes $\phi^{\tau+1}$ in Eq (2.14) to be extremely large or small for certain values of $\tau$, thus the volatility of their FPE values increases to some extent along with the window width reaches corresponding values. From Figure 2c one can find different signals can be easily distinguished. Compare with deterministic sequence, if a single point inserts to a fragment of random sequence, the change of its order relation is more concentrated. It leads to the similarity of distributions of $\overline{d_{ij}^{\tau}}$ and $\overline{d_{ij}^{\tau+1}}$ in Eq (2.10), thus the difference between $\phi^{\tau}$ in Eq (2.13) and $\phi^{\tau+1}$ in Eq (2.14) is relative small. As a result, the sorted FPE curves of stochastic signals are smoother. Furthermore, Figure 2d and 2e illustrate the bottom and top 7 with error-bars, respectively. Obviously, extrema of different signals display unique features. The standard variance decreases significantly after sorting. This phenomenon inspire us to investigate the standard variances of FPE values(Std_FPE) of different signals. See Figure 3.

The result shows that Std_FPE can distinguish deterministic or stochastic signals effectively, as a kind of representation of the volatility of complexity of time series. The complexity of stochastic signals is much stabler than that of deterministic ones. The volatility of FPE of 1/f noise is slightly lower than White Gaussian Noise(WGN) and it can be partly attributable to its memorability. The volatility of FPE of chaotic signals is higher than 5-period orbit, although both signals are generated from Rössler system and appear similar in small scale range. This reflects the complexity of chaotic time series. For sine waves with diverse frequency, one may regard that their complexity will increases under the same sample rate as the frequency rises. But in fact, Std_FPE sequence of sine waves is oscillating. The standardization of Eq (2.11) is considered as the main cause. Sine waves are typical periodical signals. Certain values of $\tau$ may cause large $\phi^{\tau+1}$, as we discussed in the above. In short, Std_FPE can be considered as an valid tool to separate time series with various complexity and randomness.

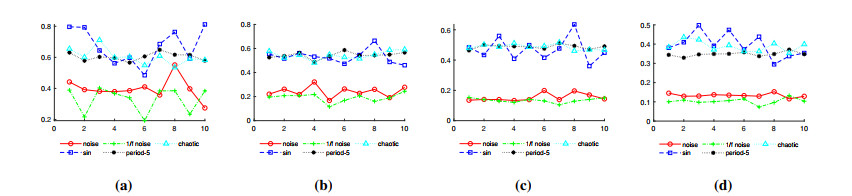
One of the advantage of Std_FPE is that it can also work on shorter sequence, despite lower performance. Signal length of 55, 80, 150, 300 are tested. See Figure 4. It shows that the relative position of each signal remains steady and the differences gradually become remarkable as the length of signals rises.

3.3.   Comparison with other entropies

In this part, FPE is compared with MSE ^[7], PE ^[5] and FE ^[6]. WGN($\mu = 0, \sigma = 1$) and sine waves with the gap $\Delta t = 9$ of different frequency, as described in Eq (3.1), are used to test their performance. The comparison includes three parts: (1) PE, FE and FPE for very short sequences with low-complexity (WGN vs. low-frequency sine-waves); (2)PE, FE and FPE for very short sequences with high-complexity (WGN vs. high-frequency sine-waves); (3) MSE, FE, PE and FPE for short sequences with high-complexity (WGN vs. high-frequency sine-waves).

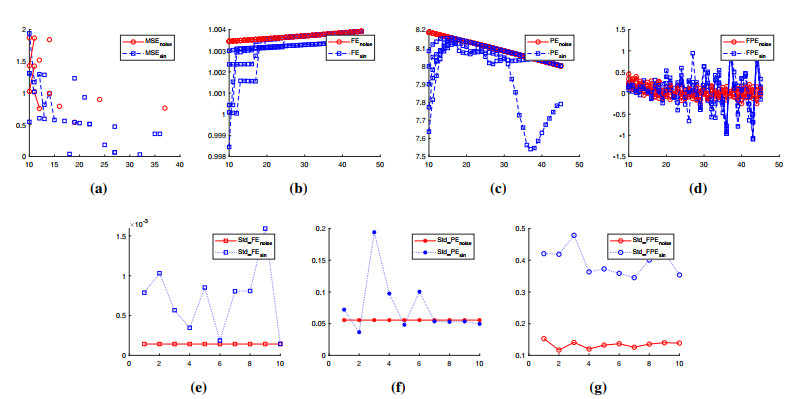
Comparison (1)    The sequence length (SL) is fixed to 100 and repeated for 10 times. The range of scale is between 10 to 45. The result is shown in Figure 5. Note that MSE induced undefined entropy each time, it is invalid for these short time series. We introduce the performance of MSE for longer time series ($SL = 300$) later. Std_FPE is distinguishable for different kinds of signals. In Figure 5a and 5b, $\mathrm{FE}_{noise}$ and $\mathrm{PE}_{noise}$ remain constant in different simulations, and some $\mathrm{FE}_{sin}$ and $\mathrm{PE}_{sin}$ overlap with them on certain scales. As the frequency of sine-wave goes up, $\mathrm{FE}_{sin}$ is coincidence with $\mathrm{FE}_{noise}$. We can see the similar situation in PE. But for FPE, 5c demonstrates significant oscillating behavior. So, $\mathrm{Std_FPE}$ can be used for distinguishing sine-waves from noise as shown 5f. Furthermore, Figure 5d and 5e show that $\mathrm{Std_FE}_{noise}$ and $\mathrm{Std_PE}_{noise}$ are constant, while $\mathrm{Std_FE}_{sin}$ and $\mathrm{Std_PE}_{sin}$ are coincident with them respectively, if the frequency of sine waves reaches certain value. This indicates that it is difficult for FE and PE to distinguish deterministic signals with dramatical oscillation from stochastic signals.

Comparison (2)   In order to compare the function of FE, PE and FPE on more complex time series, sine waves of higher frequency are used for further investigation. Their frequency are adjusted to more than 40, see Eq (3.3).

In Figure 6a, we can see $\mathrm{FE}_{noise}$ and $\mathrm{FE}_{sin}$ are overlapped completely. In Figure 6b, $\mathrm{PE}_{noise}$ and $\mathrm{PE}_{sin}$ are almost overlapped except for a few scales. But in Figure 6c, the oscillation of FPE values of sine-waves is stronger than that of WGN, which is similar to what is shown in Figure 5c. Besides, as shown in Figure 6d and 6e, $\mathrm{Std_FE}$ of noise and sine waves are very close for most of scales, so does $\mathrm{Std_PE}$. It illustrates that both FE and PE are invalid for separating noise from deterministic signals if the complexity of the latter reaches certain levels. In contrary, Figure 6f shows that $\mathrm{Std_FPE}$ is still valid since $\mathrm{Std_FPE_{noise}}$ is significant lower than $\mathrm{Std_FPE_{sin}}$. Compare Figure 6 with Figure 5, one can conclude that FPE is more effective on separating complex deterministic oscillating signals from stochastic ones.

Comparison (3)   At the end of this subsection, we fix the length of time series to 300 to investigate the performance of MSE, FE, PE and FPE on longer signals, where sine waves are generated by Eq (3.3). The results are drawn in Figure 7. From Figure 7a, we can see that most of MSE are undefined entropies. Even for time series with the length of 300, MSE is still invalid. Besides, it can be seen that longer time series lead to better performance for FE, PE and FPE. FPE is still superior to FE and PE. From Figure 5c, 6c and 7d, one can conclude that FPE exhibits similar behaviors, that is, the weaker oscillations for stochastic time series but stronger for deterministic signals.

In short, with longer signals, FE, PE and FPE can distinguish signals of different complexity. If the length of signals is shorten, FPE can hold this ability better than FE and PE. So, FPE can be considered as an effective tool for complexity analysis, especially when the amount of collecting data is restricted.

4.   Simulation analysis

In this section, FPE is used to explore the complexity of traffic evolution. We take the simulated time headway sequence under various states of traffic congestion as the research object. The sequences are generated from a cellular automaton model based on the improved braking light rule (IBLR Model). One can read ^[31], ^[25] and ^[14] for more details. IBLR Model considers the influence of deterministic deceleration, and it describes the behavior of drivers better. By adjusting the traffic density($\rho$), the stable state of the traffic flow (SSTF) can exhibit different characters, such as free flow (FF), synchronized flow (SF) or both coexisting. Several densities and according SSTF are listed in Table 1.

The simulations are performed on a ring with a length of 10 000 cells with the initial homogeneous distribution. As mentioned above, we change $\rho$ to obtain different kinds of traffic flow. The first cell on the left is used as the sampling point and we record 50000 time headway continuously. For each $\rho$ in Table 1, 19 groups of time series with certain lengths are sampled ^[31]. To make sure the time headway sequences are in stable state, start points of sampling are randomly selected after the $25000th$ place.

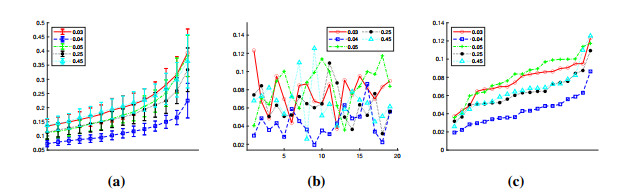
Fix the length of time series to 150 and scale factors are $10\sim45$. Several examples of time headways in different densities are shown in Figure 8a. One can hardly distinguish them. Next, we use FPE to probe their difference in complexity. In Figure 8b, FPE values have oscillated viciously without presenting any significantly regular pattern. Then, by sorting FPE results of each simulation in Figure 8c, we find that $\mathrm{FPE}_{0.04}$ is the least one. It can be contribute to the fact that the traffic density of $0.04$ is the dividing point between FF and SF, thus enhancing the orderliness of time headway. $\mathrm{FPE}_{0.05}$ and $\mathrm{FPE}_{0.25}$ are close, and it can be attributable to their similar SSTF. Furthermore, the curves of $\mathrm{FPE}_{0.03}$ and $\mathrm{FPE}_{0.45}$ are close too, which indicates that FPE values of FSJ are similar to that of FF. Figure 8d displays that $\mathrm{Std_FPE}_{0.04}$ values are significantly smaller than others. Light and heavy SF are distinguishable by using sorted Std_FPE, see Figure 8e.

Figure 8 demonstrates that time headways of different SSTF have various complex extent, although the distinction is not remarkable. Recalling the analysis of Figure 2, we find that using top values can enhance the performance. So, we use top 40% values of every simulating result to analyze the complexity of the system, see Figure 9. Note that in this section we always use same start points as the above experiment for more accurate comparison.

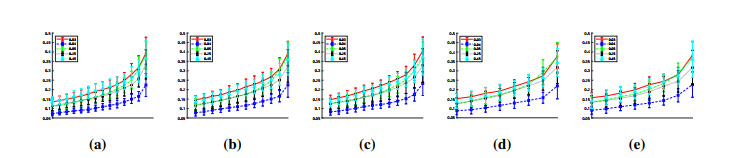
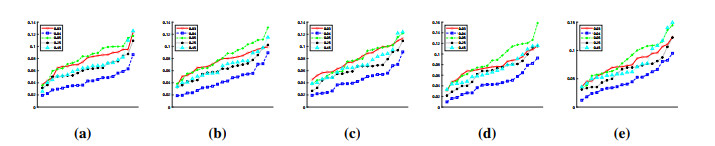
Since the phenomenon of coexisting of FF and SF and Jam, the above FPE method still need to be improved. Obviously, shortening the length of sequence and scale may raise the probability of avoiding the coexistence of different SSTF. But shorter sequence also cause to more unstable FPE_Std, as we have discussed in Section 3.2. To give ideal values of sequence length and scale factors is still very difficult. Here we just conducted several experiments with different length and scales to show the robustness of FPE method. The results are drawn in following charts.

The distributions of top FPE values are less sensitive to the small change of SL and scales, as shown in Figure 10. This property is conducive to choose appropriate SL and scales for a specific purpose. FF is the most sensitive one, since the curve of its mean value become the highest one as SL and scales decrease. Light SF is the secondly sensitive. As the range of scale factors narrows, the range of FPE also reduces. Figure 11 displays the change of Std_FPE. When SL and scales range reduce, the distributions of Std_FPE values are more as the range of scale factors. Std_FPE of light SF has increased, which shows the volatility of its complexity increased too. What's more, it is remarkable that the gap between FF and high SF narrows. The time headways of different density demonstrate specific character as SL and scales altering. It indicates that based on FPE method, the complexity of time headway is conducive to recognize the state of traffic flow. So, FPE method can conduce to Intelligent Transportation Management System.

5.   Conclusion

In this paper, we define a novel distance of rearrangements. Based on it, we introduce the Fuzzy Permutation Entropy (FPE). We have illustrated the behavior of FPE-based approaches, over multiple scale factors, versus WGN, 1/f noise, $x-$component of Rössler system in 5-period or chaotic state, sine waves and simulated time headway of IBLR Model with different densities. Besides, we have compared the performance of MSE, FE, PE and FPE on separating WGN and sine waves. The results show that FPE was an effective tool, which had more sensitive performance on the complexity analysis and more stable effect on identifying deterministic and stochastic signals. Moreover, FPE is conducive to probe various congestion level of traffic flow, such as the free flow, the synchronized flow of different extents or the coexistence of several states. We hope it can be used to enhance Intelligent Transportation Management System.

Acknowledgments

This study is supported by the Doctoral Fund of Hubei University of Automotive Technology (Grant No. BK201703), Local Science and Technology Development Project Guided by Central Government (Grant No. 2018ZYYD007), CERNET Innovation Project (Grant No. NGII20180615). For PE and FE code, thanks to Jesús Monge-Álvarez and Gaoxiang Ouyang, as they have shared their works on MATLAB Central File Exchange.

Conflict of interest

The authors have declared that no conflict of interest exists.