1.
Introduction
Non-alcoholic fatty liver disease (NAFLD) is a multi-system disease that not only causes liver function damage, but also affects other organs [1,2]. For example, patients with NAFLD have a higher mortality rate of liver disease and non-liver disease than ordinary people [3]. Therefore, the accurate assessment of the severity of NAFLD is critical for the prevention, diagnosis and treatment of fatty liver-related diseases. The pathologic definition of NAFLD is that more than 5% of liver hepatocytes have macro steatosis. NAFLD represents a spectrum of diseases ranging from simple steatosis to nonalcoholic steatohepatitis, which can progress to liver fibrosis, cirrhosis, and hepatocellular carcinoma [4].
Even though liver biopsy is considered as the gold standard for NAFLD diagnosis, it has inherent disadvantages such as invasiveness, complications, and being subjective [5,6]. Conventional medical imaging methods for NAFLD diagnosis include computed tomography (CT), magnetic resonance imaging (MRI) and ultrasonography (US) [7,8,9,10]. Among these modalities, US is the most commonly used method for NAFLD diagnosis because it is non-invasive, non-radiative, real-time, and inexpensive. It is suitable for people of all ages, including pregnant women and children, and is not limited by medical history [11]. Conventional ultrasound imaging is a semi-quantitative assessment. Therefore, it is subjective and relies on the experience of the operator [12]. However, quantitative ultrasound (QUS) imaging can provide specific tissue features and increase the specificity of conventional US. It has been widely applied in the liver fat quantification [13,14].
Envelope statistics and spectral-based techniques are two major categories of QUS technique. Both of them have demonstrated success in NAFLD applications, providing additional diagnostic capabilities [13]. The envelope statistics technique utilized the shape and attributes of the envelope of the backscattered ultrasound to estimate the information about the underlying tissue microstructures. Various models and their derivations for the statistics of the envelope, such as the Nakagami model, the Rayleigh model, and the homodyned-K model, have been proposed over the past few decades for the biomedical ultrasound applications [15]. For the NAFLD diagnosis, the Nakagami model is currently the most frequently used one [16,17,18].
Spectral-based techniques include the estimation of attenuation coefficient (AC) and its derivatives, the estimation of backscatter coefficient (BSC) and its derivatives such as the effective scatterer diameter (ESD) and the effective acoustic concentration (EAC) of scatterers. These techniques utilize the amplitude, frequency and phase information in the ultrasonic RF signal and also have the ability to observe tissue microstructures. Paige et al. explored the diagnostic performance of AC and BSC for predicting histology-confirmed steatosis grade in NAFLD patients. Their results suggested that QUS parameters may be more accurate and provide higher interobserver agreement than CUS [19]. Yang et al. used the integral backscatter coefficient to evaluate the liver fat concentration after liver transplantation, and observed that the integrated backscatter coefficient (IBC) has a good correlation with liver fat concentration [17]. Lin et al. investigated the QUS measurements of BSC identify steatosis in animal models and found that BSC can accurately diagnose and quantify hepatic steatosis [21]. Ghoshal et al. studied ESD and EAC and the results indicated that the two parameters are sensitive to fat content in the liver [22].
The primary purpose of this study is to combine multiple QUS parameters using an efficient fusion method to obtain an optimal characteristic parameter. We identified six commonly used QUS parameters to measure different liver fat concentrations, and selected several parameters with better staging effects for combination. The diagnosis performance of the combined parameter was evaluated and compared with that of the single QUS parameter. To the best of our knowledge, this is the first study to combine multiple QUS parameters for evaluating liver steatosis grade.
2.
Methods and materials
2.1. Animal model
The NAFLD rat model was supplied by the Guangdong Experimental Animal Center. The animal experiment obtained the review of the Experimental Animal Ethics Committee of Shenzhen University. The experimental rat weighed between 180 and 200 g. The culture environment of the experimental rat model was sterile and constant, the temperature and humidity of culture environment were maintained at 20−60∘ and 40−70%, respectively. A total of 65 rats were involved in the study. The rats were randomly divided into the control group (8 rats) and the fatty liver group (57 rats). The rats in the control group were fed with a standard diet with sterilized food and water, while for those in the fatty liver group a high fat emulsion (20% lard, 10% cholesterol, 20% sodiumcholate, 0.5% propylthiouracil, and 30% fructose) was given once a day at 1 mL/100 g rat weight, for different numbers of days to induce different severity stages of steatosis. After 2, 4, 6, and 8 weeks, the rats were humanely killed for analysis. Specifically, the right lateral lobe of the liver was used for QUS measurements, while the rest lobes were for histologic assessment. It should be noted that the steatosis grade was ultimately determined by the histologic assessment, rather than the length of feeding time of the rats. Moreover, all procedures conducted in our study had been approved by the Animal Care Committee of Shenzhen University and the Guangdong Medical Laboratory Animal Center.
2.2. Histological assessment
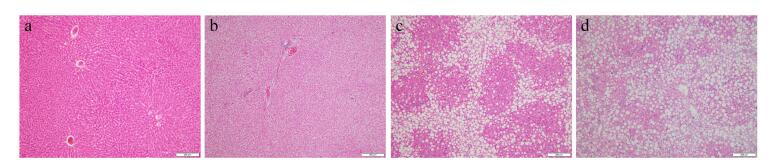
Excised liver tissues were fixed in 10% formalin solution for at least 24 h. After washing and dehydrating, samples were embedded in paraffin and sliced to a thickness of 7 μm. The paraffin slices were stained with hematoxylin-eosin (HE) by histopathology technicians, and analyzed using a microscope (BX41, Olympus, Pittsburgh, PA) by an expert pathologist. According to the percentage of hepatocytes containing macrovesicular fat droplets, the severity grades for steatosis were defined as follows [23]: S0<5%, S1=5%−33%, S2=33−66%, and S3≥67%. For an illustration, example sliced images for liver tissue sections with different steatosis stages are shown in Figure 1, where (a), (b), (c), and (d) represent normal liver, mild fatty liver, moderate fatty liver and severe fatty liver, respectively. It can be seen that hepatocytes containing macrovesicular fat droplets are increasing from (a) to (d) in the figure. The percent of hepatocytes containing macrovesicular fat droplets serves as the quantitative measurement for the determination of steatosis stage.
2.3. Ultrasound measurement
In an ex vivo experiment, the right liver lobe was processed and embedded in a fabricated gelatin phantom (gelatin from porcine skin, G2500, Sigma-Aldrich, St. Louis, MO, USA) in a container (11×11×7 cm). The objective for such design was to simulate the tissues that lie between the ultrasound probe and liver in vivo. A modified ultrasound scanner (M5, Mindray, Guangdong, China) with a linear array probe (7L4S) was used to capture the RF data. The center frequency of the probe is 7.5 MHz and the sampling frequency is 30 MHz. Each rat liver tissue phantom was scanned ten times and the ultrasound images and the corresponding RF data were stored for offline processing.
2.4. QUS parameter estimations
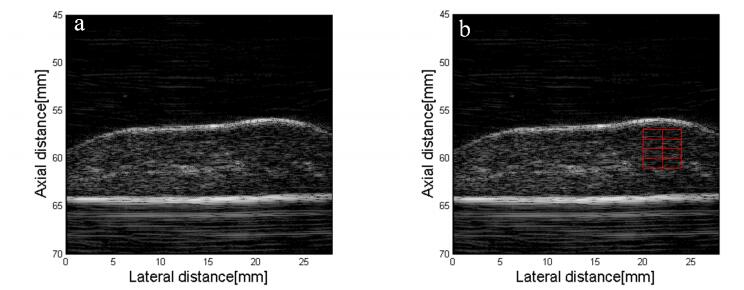
The ultrasound image was reconstructed from the corresponding RF data. Then the region of interest (ROI) is selected in the reconstructed image as shown in Figure 2. Six different QUS parameters were calculated based on the ROI which was divided into several sub-ROIs according to different algorithms. Here we just briefly introduce their definitions.
2.5. Nakagami statistical parameters
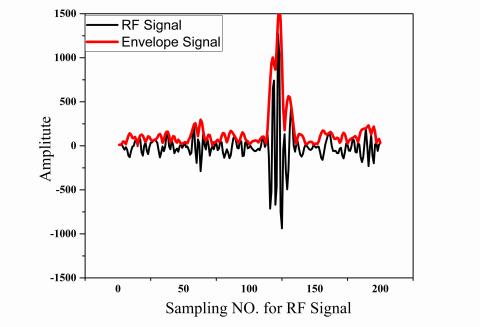
We used the Nakagami statistical model to analyze the envelope and estimate the shape parameter m and the scaling parameter U [24]. The envelope of the RF signal was calculated by the Hilbert transform. The typical relationship between the RF signal and envelope waveform is shown in Figure 3. The probability density function (pdf) of the envelope signal x, which can be approximated as a Nakagami model with two parameters (m,U) as follows:
where τ(⋅) is the gamma function, the parameters m and U are represented as:
2.6. Attenuation coefficient slope (ACS)
The attenuation coefficient slope as a function of frequency is expressed in dB/MHz/cm and is obtained by the following equation [25]:
where S(f,Z1) denotes the power spectrum at depth Z1, S(f,Z2) denotes the power spectrum at depth Z2, f is the frequency, d denotes the distance between Z1 and Z2, d=Z2−Z1, Z1 and Z2 are the distance from the probe to the ROI (in cm). βr and βs denote ACS of reference phantom and tissue (dB/MHz/cm), respectively. We also normalized the power spectrum by dividing the measured power spectrum by the standard power spectrum, which is denoted as
where Ss(f,Z) denotes the measured power spectrum, Sr(f,Z) denotes the reference power spectrum, Z is depth.
2.7. Integrate backscatter coefficient (IBC)
The integrate Backscatter coefficient, expressed in dB, is estimated using [22]:
where BSC(f) is the ultrasonic backscatter coefficient, which is estimated in accordance with the method described by [26]:
where Rp is the reflection coefficient from the plane reflector (assumed to be one), k is the wave vector, a is the transducer radius, F is the transducer focal distance, l is the thickness of segmentation window.
2.8. Effective scatterer diameter (ESD) and effective acoustic concentration (EAC)
From a microscopic point of view, the backscattered theoretical power spectrum can also be expressed as [27]:
where f is the frequency (MHz), aeff denote the effective scatterer diameter (ESD) (mm), p is the scatterer concentration (mm−3), zvar=z−z0z0 is relative acoustic impedance of the scatterer and its surrounding medium, pz2var denote the effective acoustic concentration (EAC), l is the window length (mm), q is the transducer aperture.
The power spectrum is linearly fitted in the bandwidth by the least squares fitting method based on frequency f. The spectral slope and the intermediate frequency amplitude are ms and M, respectively. The effective scatter diameter (ESD) and effective acoustic concentration (EAC) are obtained by the following equation, respectively:
where g1, g2, g3, g4 are constants, b is the fractional bandwidth, E is a constant related to the aperture and focal length, and n is set as 4 for the biological tissue are isotropic scatterers.
2.9. Combination of multiple QUS parameters
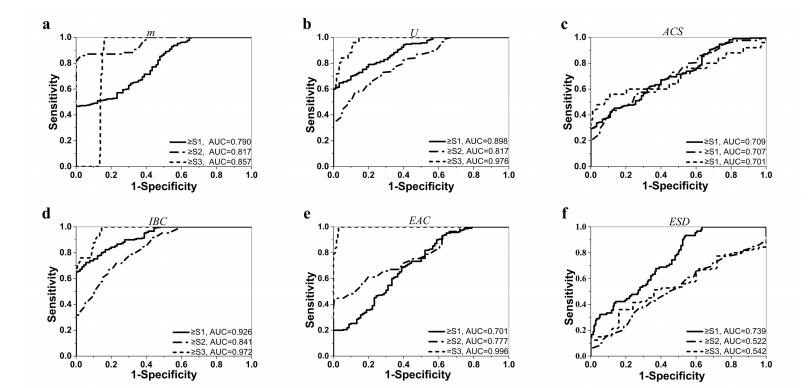
To select the appropriate parameters for predicting NAFLD, a univariate analysis was performed on the parameters mentioned above. Four parameters (m, U, IBC, EAC) showed as the most significant predictors for the NAFLD stage. These four parameters were then used for construct a combination model. An optimal linear combination of the four parameters was used to improve the prediction of mild steatosis (stage ≥ S1). The method proposed by [28,29] was used to determine the optimal linear combination which has the greatest AUROC out of all the possible linear combinations. The combination coefficients and corresponding cut-off values were calculated. Comparisons of the performances between the single parameters and their linear combination were performed.
3.
Results
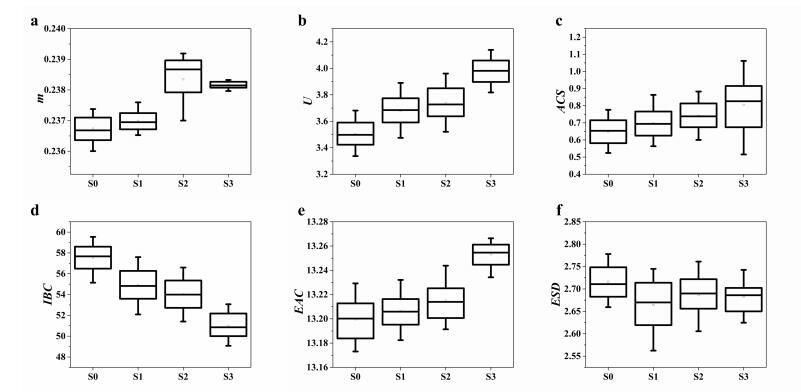
The box plots of the six QUS parameters for different NAFLD stages are shown in Figure 4. In this figure we can clearly observe that the parameter m, U, IBC, EAC are well correlated with the NAFLD stages. The formula of the optimal linear combination was
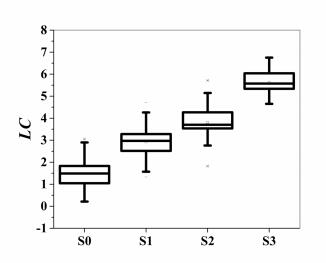
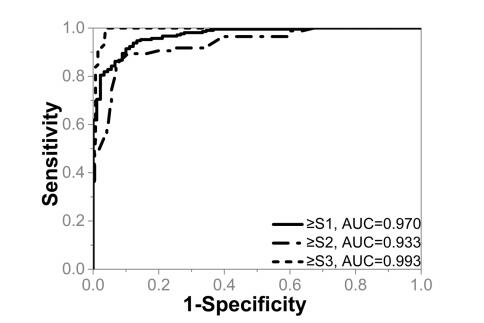
As mentioned earlier, the coefficients in the equation were determined by using the method reported in [28,29], which explores the information carried by the marker values in different testing groups and employs the Fisher's linear discriminant function for the optimization. The resultant linear combination provided us the maximum value of AUROC for better steatosis assessment. The box plot of the combined parameter for different NAFLD stages is shown in Figure 5. The performance of the combined parameter was analyzed and compared with those of the single parameter. The ROC curves of the six QUS parameters and the combined parameters for differentiating NAFLD stages are shown in Figures 6 and 7, respectively. The performance of different parameters are listed in Table 1.
4.
Discussions
Liver fatty deposits not only cause damage to liver tissue, but also cause lesions in other tissues. Studies have shown that NAFLD is more than just a liver disease, it is can also agammaavate the incidence of diabetes and cardiovascular diseases [30]. Moreover, quantitative assessment of donor hepatic steatosis is critical in liver transplantation for the success of surgery [31,32]. Therefore, it is of great clinical importance to accurately assess of the severity of NAFLD.
Various QUS parameters have been developed in previous studies for the NAFLD diagnosis. These parameters can assess the hepatic fat quantification from different aspects. How to combine these parameters for improving the diagnosis performance is still challenging. A recent study explored a multiparametric approach by combining QUS parameters to test the discriminate performance between the stages of liver fibrosis [33]. Linear discriminant analysis was used in that study for combining multiple parameters. This study applied a different combination method which is based on the criteria of maximizing the AUROC. The AUROC is used extensively in research to express discriminating power and diagnostic performance. Therefore, the combination method used in this study has unique advantage. It has the greatest AUROC out of all the possible linear combinations, ensuring that the performance of the combination is better than that of any individual method.
As shown Table 1, the four QUS parameters have different performances in distinguishing different steatosis stages. For distinguishing ≥ S1, ≥ S2, and =S3, IBC, m, EAC have the greatest AUROCs, respectively. Therefore, there is no one single parameter that is completely better than other parameters. The combination method can extract complementary information from different parameters compensate for the lack of a single characteristic parameter. It can be observed that the combination parameter has the highest AUROC than those of any single parameter for distinguishing ≥ S1. For other stages, although the combination parameter cannot achieve the highest AUROC compared with single parameter, it can improve the overall performance.
One limitation of our study comes from the animal model. The effectiveness of the proposed method was demonstrated using the NAFLD rat model. Its performance on human subjects need to be further tested through extra experiments. It would have been ideal to recruit clinical patients who have only varying levels of steatosis severity. However, this was a challenging task because steatosis, inflammation and fibrosis may precede or develop in parallel with the liver disease. Animal models of the spectrum of NAFLD provide the necessary tools to overcome confounding variables, such as genetic heterogeneity, and environmental factors, including diet and lifestyle. Given the difficulty of studying all the factors involved in steatosis in human populations, the animal model may have helped to improve our understanding of the physiopathology of the disease. Another limitation of the study is that ultrasonography was examined in ex vivo samples. In our study, we conducted ex-vivo liver experiments in order to isolate the liver fat factor from the confounding environment experienced in vivo experiments, so that the problem for NALFD can be examined independently. For the assessment of in vivo livers, other factors such as heart beat and blood flow must be considered as well. It could be recognized that the examination of the individual fat factor in ex-vivo livers can provide useful reference information for relevant studies in the in vivo experiments, as the QUS technique explores the microstructures of livers, the changes of which from in vivo to ex vivo are limited. In our future work, we shall deliver more efforts to extent the proposed technique to assess in vivo livers in rats and humans by taking the confounding environment into account. In addition, our work did not include comparisons between quantitative US or their combined parameters and the standard ultrasound techniques utilized clinically. Adding relevant comparisons may provide more comprehensive interpretation of the results. Moreover, it should be noted that quantification of liver fat based on the US technique is one way to assess liver disease in NAFLD. However, liver inflammation cannot be measured with US. Fibrosis is the strongest and most relevant indicator of disease progression and can be more accurately quantified via biopsy and elastography [34].
5.
Conclusion
We have proposed a multiparametric approach to explore the QUS parameters to differentiate between different steatosis stages. The findings show that this approach can make up for the deficiency of single parameter and improve the quantitative staging ability of fatty liver, and thus could play an important role in the diagnosis of NAFLD.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos. 81871429 and 61427806), the Science and Technology Planning Project of Guangdong Province (No. 2017A020215099) and Shenzhen Science and Technology Planning Project (Grant No. JCYJ20160520175319943). We would like to thank the anonymous reviewers for their constructive comments and valuable suggestions.
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this article.









 DownLoad:
DownLoad: