The amplification of the New Keynesian models and robust optimal monetary policy

1.   Introduction

Dynamic stochastic general equilibrium (DSGE) models combined with Bayesian methods of inference have become the mainstream device for research on monetary policy analysis. In its simple form, the shocks are much shorter lived, the responses of the model are too quick than those present in the data. To improve the match of the data, many sources of shocks together with adjustment costs are introduced into the model.¹ Yet, in complex, elaborate DSGE setups containing several frictions, some of these shocks are hard to validate.²

¹Basic setup can be found in Woodford (2003) and Gali (2015). See Smets and Wouters (2007), Fernandez-Villaverde and RubioRamirez (2006), and Fernandez-Villaverde (2010) for a medium-scale model. Also, Gali (2018) provides an overview of some recent developments in New Keynesian modelling including the implications of financial frictions, the zero lower bound on nominal interest rates, household heterogeneity.

²See Chari et al. (2009) for a discussion.

From the perspective of a policymaker, a highly related discussion would be acknowledging the possible uncertainties about the structure of the economy. When one deviates from the assumption of perfect knowledge in several ways, the propagation of shocks hence implied policy suggestion could change substantially. For instance, although the literature on uncertainty has pioneered by Brainard (1967) with an advice on more cautious behavior for the policymaker when faced with ambiguity about parameters of the model, there may be fundamental uncertainties regarding the true data generating process. The monetary authority facing uncertainty regarding the model, or the exogenous disturbances might find it optimal to respond to fluctuations in the economy in a stronger manner. Therefore, introducing uncertainty into an otherwise standard New Keynesian model can improve the propagation of shocks, the fit of the model with the data, and relieve the DSGE models from the criticism of several, unfounded shocks. Further providing a sound economic intuition, allowing model uncertainty can improve the reliability of the policy suggestions derived from the model.

This paper is an attempt to provide additional insights to the optimal policy literature by introducing uncertainty in New Keynesian models with different features with a particular focus on understanding whether and how the extensions of the simple New Keynesian model affect the design of optimal monetary policy under uncertainty. When modelling uncertainty, I exclusively rely on the robust control literature a là Hansen and Sargent (2008). Decision making under robust control can be interpreted as a dynamic game between the policymaker and the nature. In this game, the nature, or the hypothetical evil agent forms the worst-case strategy that would deteriorate the performance of the policymaker as bad as possible, and the policymaker designs the best decision rule given the decision of the nature. The policy recommendations that emerge from this approach are referred to as robust policies, that avoids large losses in all relevant scenarios, irrespective of how likely these outcomes are. Early applications of robust control to monetary policy such as Giordani and Söderlind (2004), Leitemo and Söderström (2008a), Leitemo and Söderström (2008b), Tillman (2009) seemed to contradict the cautious prescription articulated by Brainard (1967), suggesting that policymakers facing uncertainty should respond more agammaessively to news. However, Barlevy (2009), studying a static model, points out that agammaessiveness is not a generic feature of robust control. Also, Cateau (2006) argues that different New Keynesian models implies different monetary policy transmission mechanisms; hence, uncertainty reveals varying responses depending on the model; hence, further study is needed to reveal the effects of model uncertainty.³

³More recent studies include Bask and Proano (2016), Cebula and Boylan (2019), Lengnick and Wohltmann (2017), Pecora and Spelta (2017), Kantur and Özcan (2018), Kantur and Özcan (2019), Andre and Dai (2018).

To that end, habit formation and/or inflation persistence is introduced into the benchmark model, and optimal monetary policy under model uncertainty is derived to analyze how model uncertainty interacts with the additional ingredients of the model. Furthermore, the dynamics these four models are demonstrated and compared in terms of their impulse responses and the design of optimal monetary policy under rational expectations as well as under uncertainty.

I study the optimal commitment policy in response to a supply shock to the Phillips curve as well as in response to a demand shock to the IS equation as the transition equation of the output gap. Following Hansen and Sargent (2008), I characterize optimal policy under Knightian uncertainty. To represent model misspecification, I consider additional disturbances in the shock processes. I show how the problem of the monetary authority differs when she internalizes this type of model uncertainty, and find the optimal policy response in the worst-case realization of the shock process that represents model misspecification. The comparison of the model dynamics from the ones obtained under rational expectations generates a clear picture on how model uncertainty has an impact on the amplification mechanism of the shocks. By adding ⅰ) the habit formation, and ⅱ) indexation to past inflation, I aim to see the contribution of each ingredient one-by-one into the basic framework. ⁴

⁴I restrict the extensions to add persistence in the IS and Phillips relations to keep the results under model uncertainty comparable across encompassing models.

The study proposes some attracting findings on the optimal policy with a concern for robustness to model misspecification in New Keynesian models. First, the concerns about model uncertainty always make the policymaker to attribute less importance to nominal interest rate inertia. Second, the reaction of the policymaker to a demand shock becomes stronger, i.e. more agammaessive under in the presence of habit formation. The monetary authority reacts actively to prevent the fluctuations in marginal utility of the households. However, persistence in inflation smooths out the fluctuations in output, and partially dampens the impact of model uncertainty. Third, the results show that a supply shock is more persistent under model uncertainty. Yet, the initial response of the policymaker depends on the type of the model. The models taking habit persistence into consideration calls for an agammaessive policy. The policymaker keeps the policy rate lower at first compared to the case under rational expectations for the benchmark model and the model with inflation persistence.

The paper is organized as follows. In section 2, the model is constructed and details of the optimal monetary policy design is presented. In section 3, equilibrium dynamics are discussed. Section 4 concludes.

2.   Optimal monetary policy

A welfare criterian for the monetary authority can be derived by taking a second-order approximation to the representative household's utility; however, these are proven to be very model dependent and not robust.⁵ Instead, many central banks are assigned to pursue a simple objective that involves only a small set of economic variables. A simple mandate offers more transparent monetary policy and easier communication with the public. Moreover, a simple objective is found to be more robust to model and parameter uncertainty compared to a complicated state-contingent policy. ⁶

⁵Several papers derive a utility-based welfare criterion following Rotemberg and Woodford (1997). See Edge (2003) for the derivation of a welfare criterion for a model with capital accumulation; Leith et al. (2012) for a model with external habit formation.

⁶Several papers derive a utility-based welfare criterion following Rotemberg and Woodford (1997). See Edge (2003) for the derivation of a welfare criterion for a model with capital accumulation; Leith et al. (2012) for a model with external habit formation.

For a simple New Keynesian model with optimizing agents and sticky prices, the expected welfare criterian can be represented as a fraction of steady state consumption, that is

where $U_{t}$ is the period utility, $U_{c}$ is the marginal utility of consumption, and $\tilde{U}$ and $\tilde{C}$ are the steady state values of the utility and consumption respectively.

Since the aim of this paper is keep the setup as simple as possible to make the results of different models comparable, I assume a simple objective for the central bank so the policy maker chooses $\{y_{t}, \pi_{t}, r_{t} \}$ which minimizes the following standard loss function:

where $\pi$, $y$ and $r$ denotes for the inflation rate, the output gap and the nominal interest rate respectively. $\lambda_{y}, \lambda_{r} > 0$ are relative weights of the stabilization of the output gap, and the change in the nominal interest rate.

This welfare criterion implies triple mandate for the policymaker; namely deviation of the inflation rate from its optimal rate, deviation of output from its natural level and interest rate smoothing. The rationale for assigning some weight for the nominal interest rate in the objective of the central bank can be derived from a model with transaction frictions which justifies the presence of real money balances together with consumption and leisure in utility as shown by Woodford (2003). An ad hoc reason for including the interest rate is to prevent large fluctuations in the short-term nominal rate that might increase the term premium and the long-term interest rate. Hence, by implying a degree of commitment to future rates, interest rate smoothing enables the policymaker to keep agammaegate demand and inflation under control by guiding long-term bond rates. Furthermore, a policymaker incorporating the zero lower bound on the policy rate reduces the likelihood of hitting the bound by decreasing the financial market volatility when the economy is subject to large shocks.

The policymaker designs optimal monetary policy that minimizes the expected loss by using all information available up to the current period and taking the structural equations governing the economy as constraints. I assume credible commitment on the side of the policymaker. By committing to a policy rule, policymaker determines optimality conditions to hold in any future period; hence she takes advantage of being able to affect the formation of private sector expectations. In this section, I will derive optimal commitment policy for a New Keynesian model under rational expectations and under model uncertainty.

2.1.   Extending the basic sticky price New Keynesian model

This section presents an extension of the basic New Keynesian model as presented by Gali (2015). Since the elements are very well known, I only outline the main steps here and leave details to Appendix 8.

The representative household derives utility from consumption, $C_{t}$, and leisure, 1-$L_{t}$, by maximizing the discounted utility $E_{0} \sum_{t = 0}^{\infty}\beta^{t}\{ (C_{t}-hC_{t-1})^{1-\sigma}/(1-\sigma)- L_{t}^{1+\eta}/(1+\eta) \}$where $0 < \beta < 1$ is the discount factor, $\sigma\geq 0$ is the inverse of the intertemporal elasticity of substitution, $\eta\geq 0$ is the inverse of Frisch labor supply elasticity, and $h$ is a parameter that controls the habit persistence. At the beginning of each period $t$, representative household has $B_{t-1}$ nominal bonds, with a nominal gross interest rate of $R_{t-1}$; and buys new bonds $B_{t}$. Also, household earns $w_{t}L_{t}$ labor income, and $\Phi_{t}$ firm's profits. Each household maximize discounted utility subject to the sequence of intertemporal budget constraints, $P_{t}C_{t}+B_{t}\leq B_{t-1}R_{t-1}+P_{t}[w_{t}L_{t}]+\Phi_{t}$.

For the production side, I follow the typical intermediate-final good producer setup. There is a final good sector that uses a continuum of intermediate goods as inputs. Intermediate good firms are monopolistically competitive and use a production function with labor input. Prices are sticky à la Calvo (1983).

When the agammaegate price level is given by $P_{t} = \theta P_{t-1}+(1-\theta)P^{*}_{t}$, the index of newly set prices are defined as $P^{*}_{t} = \omega P^{b}_{t}+(1-\omega)P^{f}_{t},$ where $\omega$ fraction of firms who have a chance to reoptimize their prices are backward-looking and set $P^{b}_{t}\equiv P^{*}_{t-1}+\Pi_{t-1}$ as in Gali and Gertler (1999), and $(1-\omega)$ fraction are forward-looking and choose profit maximizing price $P^{f}_{t}$.

The model gives rise to a hybrid Euler equation and a hybrid Phillips equation in linearized forms which can be written as

where $\kappa_{1} = \lambda(\frac{\alpha+\eta}{1-\alpha}+\frac{\sigma}{1-h})$, $\lambda = {\frac{(1-\omega)(1-\theta)(1-\beta\theta)}{\theta+ \omega[1-\theta(1-\beta)]}}$, $\kappa_{2} = -\lambda\frac{\sigma h}{1-h}$, and $\gamma_{b} = \frac{\omega}{\theta+ \omega[1-\theta(1-\beta)]}$, $\gamma_{f} = \frac{\beta\theta}{\theta+ \omega[1-\theta(1-\beta)]}$, $\delta_{b} = \frac{h}{1+h}$, $\delta_{f} = \frac{1}{1+h}$, $\psi = -\frac{(1-h)}{\sigma(1+h)}$, and variables are expressed as log deviations from the zero-inflation steady state. The backward-looking demand components i.e. $y_{t-1}$ in the IS and the Phillips equations appear due to the habit formation in consumption. In other words, habit persistence parameter, $h$, also reflects the persistence in output dynamics. Note that the above two equations enclose the benchmark New Keynesian model as a special case, when $h = 0$ and $w = 0$. Supply shocks, $e$, are assumed to enter the model through shocks to the markup, and $u$ represents shocks to the agammaegate demand. For ease of exposition, I assume that $u_t$ and $e_t$ follow AR(1) processes with autoregressive coefficients $\rho_{u}$ and $\rho_{e}$.

2.2.   Optimal policy under rational expectations

Following Woodford (2003), I form the Lagrangian of the policymaker as follows:

which leads to the first-order necessary conditions for the commitment problem as follows:

at each date $t\geq 0$, with the initial conditions $s_{1, -1} = s_{3, -1} = 0$ implying that the monetary authority has no previous commitment at the initial period.⁷ Here, $E^{RE}$ is the expectations operator derived from the model under rational expectations (RE).

⁷According to Woodford (2003), the Lagrange multipliers should be specified in a way that makes the policy optimal in a timeless perspective. Time-zero optimal solution is subject to time-inconsistency problem since policymakers are better off by reoptimizing in later periods. By ignoring the first order conditions for the initial period Woodford's approach is time-invariant. I leave the comparison of both types of commitment policies for further research.

The optimal policy under rational expectations for the benchmark model is the solution $\{y_{t}, \pi_{t}, r_{t}, s_{1t}, s_{3t} \}$ to the system of first-order conditions (6), initial conditions of the Lagrange multipliers together with the IS and Phillips equations summarized in (3) and (4).

2.3.   Introducing uncertainty

To allow for model uncertainty, I introduce a second type of disturbances in the shock processes,

which leads:

When (8) are the true shock processes, the error terms in (7) are distributed as $N(v^{e}_{t}, 1)$ and $N(v^{u}_{t}, 1)$ rather than as $N(0, 1)$. Therefore, the misspecification in (7) is captured by allowing the conditional mean of the shock vector (8) that actually generates the data to feed back arbitrarily on the history of the state variables.⁸

⁸In the New Keynesian models studied in this paper, the state variables are the disturbance terms. Thus, the presence of $v^{e}_{t}$ and $v^{u}_{t}$ indicates model misspecification.

Moreover, the model with (7) is assumed to be a good approximation under the following restriction of the distortion.⁹

⁹The distortion can also be interpreted as a measure of the discrepancy between the distorted and approximating models.

Under model uncertainty, the robust policymaker considers the model presented in the previous section as the reference model, which represents the most likely description of the economic structure. However, the policymaker knows that this model could be subject to a wide range of distortions with (8) satisfying (9). Such a policymaker reformulates its optimization problem to obtain a policy rule that performs well even if the underlying structure of the economy deviates from the reference model. Following Hansen and Sargent (2008), to reformulate the problem under robust control, I introduce a fictitious evil agent who shares the same reference model that the policymaker considers and tries to maximize the same objective function (2). Hence the policymaker's problem can be represented by a two-person zero-sum game or a Stackelberg problem. While the evil agent chooses a model from the available set of alternative models, the central bank designs its policy optimally to perform well in this worst-case scenario.

Note that the most likely outcome of the model, the approximating model, is when the policymaker sets policy assuming that the private agents share the same worst-case model and form expectations accordingly, yet there is no such misspecification in reality. To put differently, an approximating model will be the model where the structure of the economy evolves without any misspecification in the disturbances; however, the monetary authority finds it optimal to consider the worst possible scenario when conducting policy. Details of the solution algorithm for the approximating model is described in Appendix 9.

The game between the policymaker and the evil agents is represented by the following extremization problem, i.e. the joint maximization and the minimization problem, subject to the distorted model with shock processes and the entropy constraint.

subject to (8), (9), and

where $E^{RC}$ denotes for the expectations operator from the distorted model, i.e. the model with robust control (RC). To make the model compatible with the rational expectations framework discussed in the previous section, I suppose that the policymaker and the private agents have the same information set, and they form expectations about future variables in a homogeneous manner. Hence, the private agents share the policymaker's degree of concern for robustness and the approximating model as in Giordani and Söderlind (2004). Note that expectations based on the model under model misspecification will differ from those under rational expectations since the former includes the behaviour of the hypothetical evil agent as well.

The monetary authority chooses the paths for $\{ \pi_{t}, y_{t}, r_{t} \}$ that minimizes the loss function (2). Under model misspecification, the evil agent is supposed to choose $v^{e}_{t+1}$ and $v^{u}_{t+1}$ that maximizes the loss function under the budget constraint (9).

Following Walsh (2004), I write the Lagrangian as the multiplier version of the Stackelberg problem defined in Hansen and Sargent (2008) as follows:

where $0 < \Theta < \infty$ represents the monetary authority's preference for the degree of robustness. $\Theta$ can be interpreted as a Lagrange multiplier on the constraint (9) measuring the size of the set of models surrounding the reference model. Hansen and Sargent (2008) show that $\Theta$ is positively related to $\eta_{0}^{-1}$. As $\Theta$ rises (or as $\eta_{0}$ gets smaller in (9)) the policymaker becomes less concerned about model uncertainty, so $\Theta = \infty$ (equivalently $\eta_{0} = 0$) corresponds to the rational expectations solution with $v_{t} = 0$ for all $t$. For now, I take the connection between $\Theta$ and $\eta_{0}$ as given but in Section 3.1.1 I describe how to calibrate a reasonable value for the robustness parameter $\Theta$ using detection probabilities.

I obtain the following first order conditions with respect to the choice variables of the policymaker and the evil agent, $\pi_{t}$, $y_{t}$, $r_{t}$, $v^{e}_{t+1}$, and $v^{u}_{t+1}$ for the optimal commitment policy:

The solution for the optimal paths for $\pi_{t}$, $y_{t}$, $r_{t}$, $v^{e}_{t+1}$, $v^{u}_{t+1}$, $s_{1t}$, $s_{2t}$, $s_{3t}$, $s_{4t}$ are represented by (14) together with the structural Equations (11), (12) and distorted shocks (8). One has to take into consideration the first order condition for the initial period by letting $s_{1, t-1}, s_{2, t-1} = 0$ for $t = 0$. Since there are no previous commitment in the initial period, the monetary authority finds it optimal to consider expectations as fixed for $t = 0$.

3.   Equilibrium dynamics

3.1.   Calibration

3.1.1.   The degree of robustness

As in Hansen and Sargent (2008) and Giordani and Söderlind (2004), I use likelihood ratio test to calculate the detection error probabilities. A detection-error probability is the probability that an econometrician observing equilibrium outcomes would make a wrong deduction about whether two competing models generate the data. The idea is to connect the value of the robustness parameter $\Theta$ to the probability of making the incorrect choice of model between the reference model and the worst-case model. The probability of making this mistake is computed by simulations with

where R and W denotes for the reference model and the worst-case model respectively. $(Pr(L^{A} > L^{B}|B)$ is the probability of the likelihood of model Ai.e. $(L^{A})$, being higher than the probability of the likelihood of model B, i.e. $(L^{B})$, conditional on the hypothesis that model B is the true data generating process.

A detection error probability of $50\%$ implies that two data generating processes are almost the same, and differentiating between the reference model and the worst-case model is not possible. With a detection error probability closer to zero, the econometrician is able to detect the true data generating process since the models are highly different. I choose the value of $\Theta$ to achieve $20\%$ of detection error probability.

3.1.2.   Deep parameters of the model

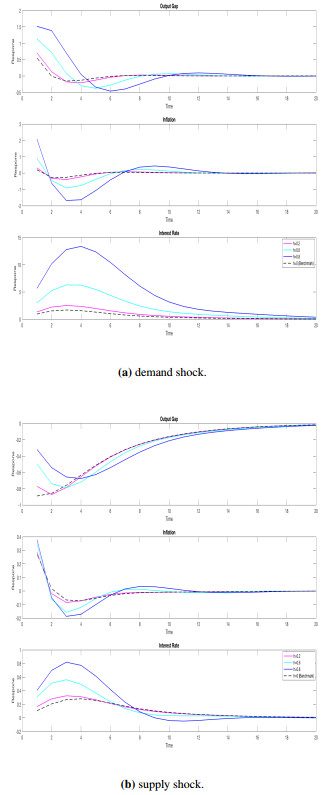
For the baseline calibration, I use the values from Gali (2015). I choose the habit persistence parameter to be consistent with the literature (as in Smets and Wouters (2007)). I calibrate the fraction of the backward-looking firms as 0.25 to produce a backward looking component in the Phillips curve to be quantitatively modest consistent with the estimates of Gali, Gertler and Lopez-Salido (2005). In the Appendix 10, I also present how the dynamics are affected for a variety of parameter values. Yet, the results are quite robust under the specification of the model parameters presented in Table 1.

3.2.   Robust policy rules and comparison with the literature

With a concern for model uncertainty, the policymaker sets the policy rate that would work well under the worst possible model misspecification. Table 2 demonstrates robust optimal policy rule by comparison to the optimal implicit instrument rule without any concern for robustness for each model specification.

To begin with, model uncertainty induces lower response to last period's interest rate; thus, the policymaker attaches less importance to the interest rate inertia. In addition, the robust rule induces caution for the supply shock but agammaessive response for the demand shock under benchmark calibration.

Concerns about model uncertainty always make the policymaker to attribute less importance to nominal interest rate inertia, and to respond agammaessively to the demand shock for the extensions of the benchmark model. Although endogenous persistence in inflation does not bring substantial difference in implicit policy rule, habit formation in consumption reverses the robust rule coefficient to the supply shock.

Recent studies present mixed results whether robust control approach brings attenuation or agammaessiveness to the optimal policy rule as in this study. Leitemo and Söderström (2008a) works in a discretionary solution for the monetary policy and present more agammaessively responses to supply shock but unaltered responses to demand shocks. In a small open economy, the results of Leitemo and Söderström (2008b) indicate that the impact of robustness concerns depends on the type of shock and the source of misspecification. Furthermore, Gerke and Hammermann (2016) introduces uncertainty in a New Keynesian model with financial intermediaries and imperfect interest rate pass-through from the nominal interest rate to the loan rate. They document that the response of the policy rate depends on the source of the shock. Dennis (2010) working on a hybrid New Keynesian model similar to the ones in this paper shows that a discretionary central bank stabilizes inflation and consumption more tightly than the optimal policy under rational expectations. Appendix 11 reports the robust rule and the impulse responses of policy-relevant variables in the benchmark model under discretion, and documents that a robust discretionary policymaker reacts similarly compared to her behavior under commitment.

3.3.   Impulse response analysis

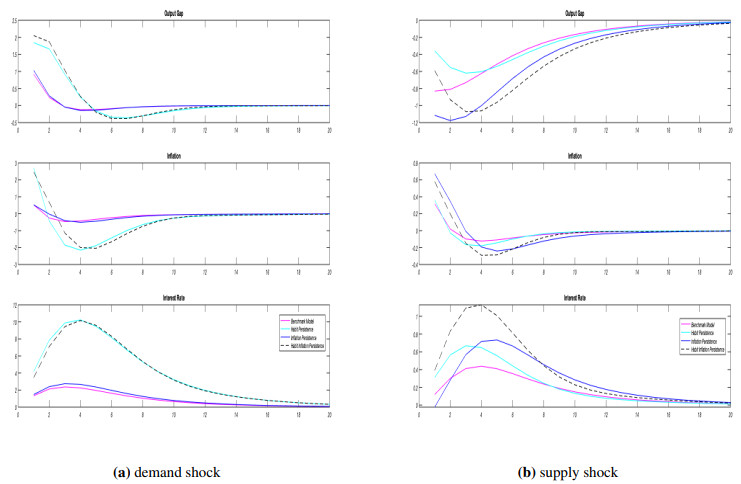
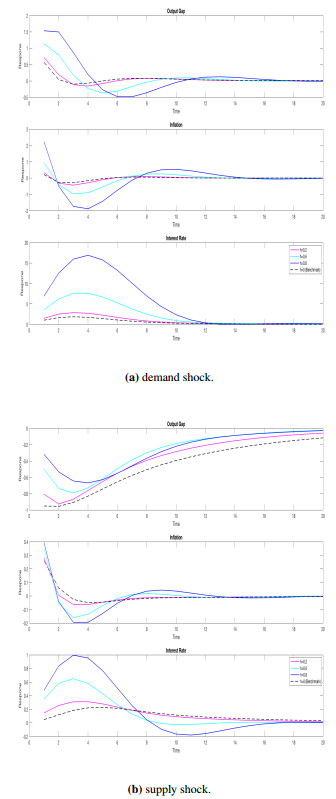
Rational Expectations: I first discuss the responses of the policy relevant variables under the assumption of rational expectations. This analysis is useful for understanding the intuition behind the properties and the amplification mechanism of each model. Figure 1a demonstrates the impulse responses for one standard deviation of a positive shock to the IS equation, i.e. a demand shock.

For the benchmark specification, a demand shock has a direct impact on the output gap and the inflation rate. Both variables increase above their equilibrium values. The policymaker responds to the increase in the agammaegate demand by raising the policy rate. This increase in the interest rate is gradual due to the impact of the policy on future expectations under commitment and the presence of interest rate in the objective function of the policymaker. As the central bank raises the interest rate the output gap and the inflation return to their steady state values.

Allowing household utility to depend on both current consumption and on past consumption reflecting the habit persistence weakens the transmission of the policy rate on agammaegate demand. Under a demand shock, since the initial rise in demand persists, optimal response of the policymaker is to rise the nominal interest rate substantially to keep the fluctuations in the out gap under control by allowing for a disinflationary process for the inflation rate. To put differently, a demand shock is expected to be more persistent due to the hybrid nature of the IS curve unless the central bank makes up for it by keeping the nominal interest rate high for longer compared to its response in the benchmark specification. One can find impulse responses for different degrees of habit persistence in Appendix 10. As the habit persistence parameter increases, the amplification mechanism deepens, and the effect of the shock becomes more persistent.

On the other hand, supposing that some fraction of the firms sets a price indexed to past inflation rate adds a backward-looking component into the agammaegate supply equation, which brings persistence in inflation. Intuitively, when the source of the shock is the demand side of the economy, the policymaker proposes a policy that would decrease the output and the inflation rate in the future. Letting persistence in inflation, by improving the transmission of interest rate on inflation works in favor of the policy of the monetary authority to bring output back to the steady state. Hence, fewer rises in the policy rate will be needed to offset the impact of the shock. Given the current calibration of the parameters, this channel is negligible and indexation to past inflation does not make a significant influence on model dynamics compared to the benchmark specification.

Furthermore, a positive supply shock initially raises inflation rate above its steady state value. As a consequence, the policymaker sets the nominal interest rate high enough to keep the real interest rate positive so that she chooses a path for the output gap that keeps output below its potential for some periods. With credible commitment, the central bank is able to influence private sector expectations of inflation with promises to keep the output gap negative in the future. As time passes, the inflation starts to fall, interest rate declines and output gap rises.

However, the presence of habit formation lowers the effectiveness of monetary policy on the output gap, implying that the transmission mechanism of policy on the inflation rate weakens. Consumption habits calls for a stronger policy, i.e. high interest rate associated with lower volatility in the output gap needed to stabilize the inflation rate.

Similarly, indexation to past inflation ensures stronger responses under a supply shock for the nominal rate, inflation rate and the output gap. More importantly, the policymaker continues to this raise the interest rate gradually until the fifth quarter; although this reaction starts to die out in the third quarter in the benchmark case. Thanks to the stronger reaction, output gap recovers faster and returns to its steady state at the same time with the benchmark.

Finally, inclusion of persistence in both the demand and the price setting shows almost identical dynamics to those under the model with habit formation with a demand shock. Apparent from the figure that letting indexation does not interact with the habit persistence. Only that these features interact with each other with a supply shock. Nominal interest rate peaks at a level twice as much as the one with habit persistence alone.

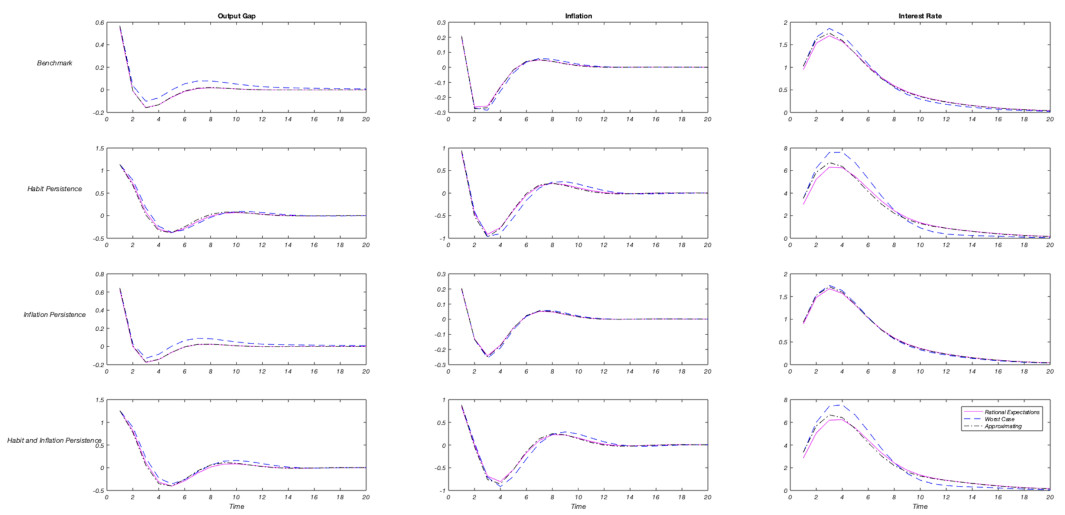
Model Uncertainty: This section presents the impulse response functions for the output, inflation rate and the nominal interest rate under the worst case scenario, as well as under the approximating model matched with the rational expectations responses.

Under model uncertainty, when the economy faces a shock to agammaegate demand, the monetary authority guards against model misspecification and formulates a more agammaessive policy that would work well under the worst possible outcome of the shock. Central bank not only increases the nominal interest rate to a higher level compared to the case under rational expectations but also keeps it that way for a longer time period. Although the responses of output gap and inflation seem close with and without model uncertainty, it takes longer for inflation to go back to the steady state. Yet, as a response to a supply shock, the monetary authority takes a cautious stance.

For the benchmark specification, model uncertainty makes the optimal policy more agammaessive compared to the rational expectations case. When the economy faces a shock to agammaegate demand, the monetary authority guards against model misspecification and formulates a policy that would work well under the worst possible outcome of the shock. Central bank not only increases the nominal interest rate to a higher level compared to the case under rational expectations but also keeps it that way for a longer time. Although the responses of output gap and inflation seem close with and without model uncertainty, it takes longer for inflation to go back to the steady state.

In the worst-case equilibrium, the impact of the supply shock dies out slowly compared to the rational expectations case so inflation is more persistent. Also, the decline in the output gap is more pronounced initially and effect of the shock on the output gap becomes more persistent under model uncertainty. The initial response of the interest rate is the same as the responses under the worst-case model. However, what follows is a lower interest rate and the dynamics follows the rational expectations equilibrium.

The robust central bank fears that inflation responds less strongly to its disturbance. The response of the policymaker under the approximating model, when the fears of the monetary authority do not come true so distortions are not realized, becomes less agammaessive (compared to the response under rational expectations) in order to control inflation.

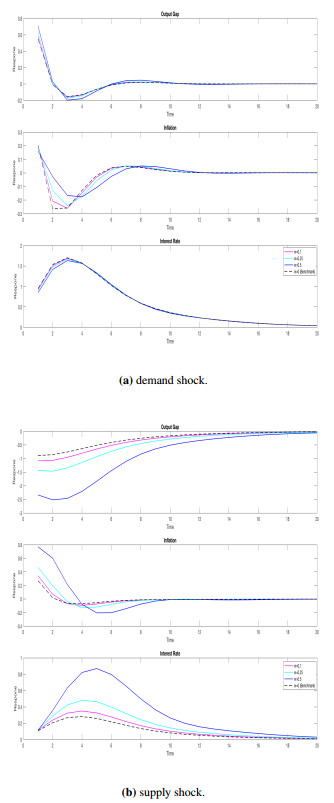
In the presence of habit formation, the reaction of the policymaker to a demand shock always becomes stronger, i.e. more agammaessive as shown in Figure 2. Since the monetary policy transmission on output weakens with habit persistence, the reaction of the policymaker has to be stronger. When coupled with specification doubts, in order to reassure the private sector and signal that it will stabilize the fluctuations in the output gap, the policymaker reacts more agammaessively as habit persistence rises, while keeping the inflation below the steady state for some time.

However, persistence in inflation smooths out the fluctuations in output, and partially dampens the impact of model uncertainty. The results show that a supply shock is more persistent under model uncertainty.

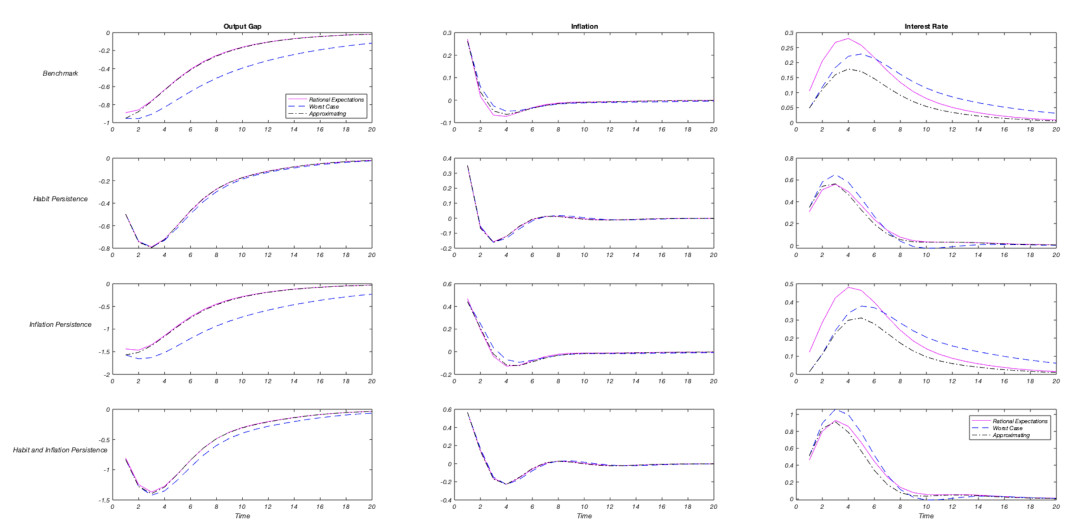
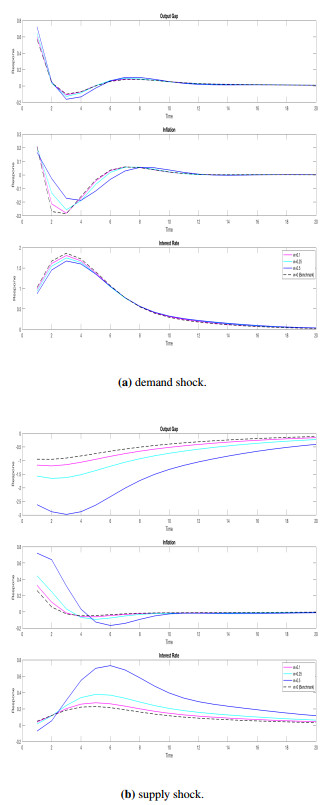
In response to a supply shock, indexation to past inflation does not change the impact of model uncertainty; habit formation in consumption eliminates even reverses the impact of uncertainty on the policy reaction. Although the difference is small, Figure 3 shows an agammaessive monetary policy for the models with habits in consumption.

4.   Conclusions

In this paper, I have discussed whether and how model uncertainty affects the amplification mechanism of New Keynesian models with different features. I present two extensions to a benchmark model with staggered price setting, namely habit formation in consumption, and intrinsic persistence in price setting. With the findings of this study, I aim to shed light on the impact of the concerns for model misspecification on the conduct of optimal policy and dynamics of the New Keynesian models.

Analyzing the optimal commitment policy, I compare the dynamics of models under rational expectations and under model uncertainty via robust control approach. I initially document that allowing for model uncertainty makes the optimal policy always more agammaessive under demand shock. This finding is robust to allowing for habit formation to past consumption. Habit formation generates persistence in the agammaegate demand, deteriorates the ability of the central bank to affect the output gap so calls for a stronger response for the policy. An additional finding is that allowing for inflation persistence represses the effect of model uncertainty. I do not observe a substantial difference between the behaviors of a robust policymaker and the monetary authority acting under the assumption of rational expectations.

Last but not the least, a supply shock brings a cautious behavior for robust policymaker in the benchmark model. Adding indexation to past inflation changes neither the dynamics nor the magnitude under the approximating model. In all other specifications considered in this study, agammaessive policy stance is a general feature of the New Keynesian models with a concern for robustness when forming policy.

Acknowledgments

I am grateful to Refet Gürkaynak and Sang Seok Lee for invaluable support and advice. I benefited from discussions with the seminar participants at Bilkent University and $1^{th}$ Research Conference of the CEPR Network on Macroeconomic Modelling and Model Comparison. I also thank the anonymous referees for their useful comments and suggestions. All remaining errors are mine.

Conflict of interest

The author declares no conflicts of interest in this paper.

Appendices

A.   Model derivation

A.1.   A New Keynesian model with sticky prices, consumption habits and backward-looking firms

Household's problem:

with the first-order conditions:

Equation (A.2) together with Equation (A.3) yields:

Log-linearization¹⁰ gives:

¹⁰The hat above variable denotes its log deviation from steady state.

Equation (A.2) together with Equation (A.4) yields:

One log-linearizes (A.7) as follows:

in terms of habit-adjusted consumption or rearranges as follows:

Inserting the goods market equilibrium condition $Y_{t} = C_{t}$ in log-linearized form ($\hat{y_{t}} = \hat{c_{t}}$) gives the IS equation:

From Equation (A.6), we have

The real marginal cost is:

For the production side, I follow the typical intermediate-final good producer setup. Final good $Y_{t}$ is produced using the following intermediate goods agammaegator:

Intermediate good firms are monopolistically competitive. The corresponding demand for an intermediate good $i$ is:

where $\xi$ denotes for the constant price elasticity, $P_{t}(i)$ is the price of the intermediate good $i$, and $P_{t}$ is the price of the final good. The agammaegate production function is

The first order conditions with respect to the cost minimization problem of firm's yields:

where $z_{t}$ is the marginal cost of production. Prices are sticky à la Calvo (1983). Each period a fraction $(1-\theta)$ of firms gets a signal to reoptimize their prices. Firms maximize the sum of discounted profits:

where $z$ denotes for the marginal cost.

When the agammaegate price level is given by $P_{t} = \theta P_{t-1}+(1-\theta)P^{*}_{t}$, the index of newly set prices are defined as $P^{*}_{t} = \omega P^{b}_{t}+(1-\omega)P^{f}_{t},$ where $\omega$ fraction of firms who have a chance to reoptimize their prices are backward-looking and set $P^{b}_{t}\equiv P^{*}_{t-1}+\Pi_{t-1}$; ¹¹and $(1-\omega)$ fraction are forward-looking and choose profit maximizing price $P^{f}_{t}$.

¹¹As in Gali and Gertler (1999).

As in Gali and Gertler (1999), the profit maximization conditions produce a log-linearized New Keynesian Phillips Curve of the form:

Inserting the marginal cost (A.11) in the Phillips relation yields:

B.   Solution algorithm for the approximating equilibrium

The approximating equilibrium represents the dynamics of the economy under robust decision-making by the policymaker and the private agents. To form the approximating equilibrium, one needs the equilibrium dynamics under the worst-case model. The worst-case model can be represented by the following linear law of motion

where $x_{t}$ and $y_{t}$ represent $n_{1}$ predetermined and $n_{2}$ the forward-looking variables respectively. $u_{t}$ is the control variable of the policymaker. The predetermined variables has shocks $\varepsilon_{t+1}$ ($n_{1}\times 1$ vector with zero mean and identity covariance matrix). $v_{t+1}$ is $n_{1}\times 1$ vector of misspecification which is the control variables of the hypothetical evil agent. The misspecification is bounded as

The policymaker and the evil agent share the following linear quadratic problem:¹²

¹²This is the representation of the multiplier version of the Stackelberg problem defined in the text.

subject to

where $z_{t}' = (x_{t}' \quad y_{t}')$ is the vector of all endogenous variables. ¹³

¹³The control problem under rational expectations corresponds to the case where $\Theta = 0$ (so the maximization is irrelevant) and there is no misspecification, i.e. $v_{t+1} = 0$ in equation (B.4).

The problem can be written in the standard state-space form by defining $R^{*} = \begin{bmatrix} R & 0 \\ 0 & -\beta \Theta I \end{bmatrix}$, $u_{t}^{*} = \begin{bmatrix} u_{t} \\ v_{t+1} \end{bmatrix}$, $B^{*} = \begin{bmatrix} B & C \end{bmatrix}$, and $U^{*} = \begin{bmatrix} U & 0 \end{bmatrix}$ as follows:

subject to

In the worst-case equilibrium, Giordani and Söderlind (2004) shows how to write the evolution of the state variables, the forward-looking variables and the decision rules as follows:

where $\lambda_{t}$ is $n_{2}\times1$ vector of shadow prices of the forward-looking variables with $\lambda_{0} = 0$. $M = P(A-BF_{u}-CF_{v})P^{-1}$, $P = \begin{bmatrix} I & 0\\ \quad N_{1}\end{bmatrix}$ implying $\begin{bmatrix} x_{t}\\y_{t}\end{bmatrix} = P\begin{bmatrix} x_{t}\\\lambda_{t}\end{bmatrix}$

The worst-case model in terms of the state variables is shown below:

where $M = \begin{bmatrix} M_{11} & M_{12}\\ M_{21} & M_{22}\end{bmatrix}$, $\begin{bmatrix} F_{u11} & F_{u21} \end{bmatrix}\equiv -F_{u}P^{-1}$, and $\begin{bmatrix} F_{v11} & F_{v21} \end{bmatrix}\equiv -F_{v}P^{-1}$.

To obtain the approximating model, I first eliminate the worst-case distortions by equating $F_{v11}$ and $F_{v12}$ to zero in equation (B.14). Note that the state variables evolve according to the following equation in the absence of distortions:

Inserting equations (B.13) and (B.14) into (B.14) yields

The approximating equilibrium is summarized by equations (B.12)-(B.14) and (B.16). I calculate the matrices, and implement the procedure using Dynare.

C.   Robustness to calibration

This section shows the dynamics of the model under varying degrees of habit persistence and inflation persistence parameters. While calculating the worst-case model, I use the robustness parameter associated with a detection error probability of $20\%$.

D.   Robust monetary policy under discretion

In this section, I present discretionary solution for the optimal policy in the Benchmark model. Under discretion, a rational policymaker is unable to commit to future policy actions. To stress the point that the policymaker cannot affect the expectations of the private sector about future variables, I reformulate the Lagrangian as

where $\Omega = \{\frac{(1-\theta)(1-\beta\theta)}{\theta}(\frac{\alpha+\eta}{1-\alpha})+\sigma\}$. Here, we assume that the monetary authority optimizes taking expectations of future variables as given, which allows to write $E_{t}\pi_{t+1} = \pi^{e}_{t}$ and $E_{t}y_{t+1} = y^{e}_{t}$ The first-order conditions with respect to $\pi_{t}$, $y_{t}$ and $r_{t}$ are found as:

The optimal policy under rational expectations for the benchmark model is the discretionary solution $\{y_{t}, \pi_{t}, r_{t}, s_{1t}, s_{3t} \}$ to the system of first-order conditions (D.2) initial conditions of the Lagrange multiplier together with the stochastic versions of IS and Phillips equations.

To formulate model misspecification in the policymaker's problem, the concept of robustness is used as a metaphor; thus, the hypothetical evil agent solves his optimization problem when and only when the monetary authority does. Hence while introducing model uncertainty under discretion, one has to take into account the fact that the optimal policy does not have an impact on the private sector expectations so the forward-looking variables are taken as given. Because the planner optimizes every period, I allow the evil agent to apply the same conjecture. In the implied zero-sum-game between the policymaker and the hypothetical evil agent, both players choose their control variables, that are $\{v^{e}_{t}, v^{u}_{t}\}$ and $\{\pi_{t}, y_{t}, y_{t}\}$ sequentially. The Lagrangian for the policy problem under discretion can be written as follows:

One can obtain the following first order conditions:

Table 3 presents the implied optimal implicit instrument rule under discretion.

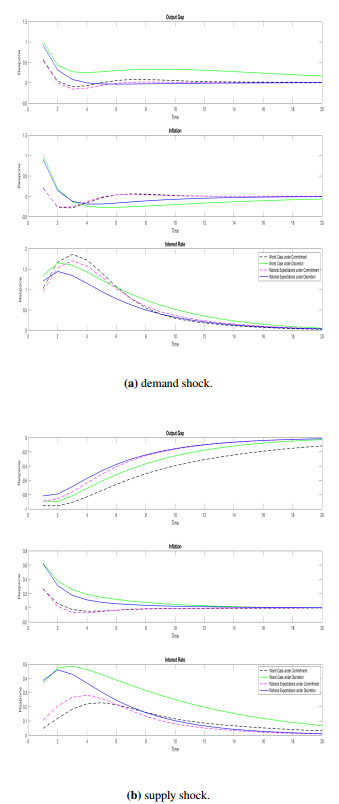
The results are similar with the findings for the commitment case such that concerns for model misspecification calls for attenuation for the policymaker under a supply shock; however policymaker becomes agammaessive when facing a demand shock. Figure 8 shows the impulse responses under commitment and discretion with and without model misspecification for each shock. Although, monetary authority responds more to a demand shock, it takes longer for the output gap to return to the steady state. For the supply shock, nominal interest rate is above compared to the optimal behaviour under rational expectations.

Under commitment, the monetary authority is able to stabilize the economy not only by decreasing the output gap (by adjusting the policy rate gradually) but also promising to keep output gap lower in the future. At the same time, with doubts about model misspecification, both the policymaker and the private sector overestimate the impact of the shocks, which induces a more agammaessive policy.

Under discretion, since policymaker is not able to control expectations regarding future variables, she adjusts the nominal rate sharply to control the effects of the shock immediately, allowing for high deviations of output and the inflation from the steady state in the initial periods. Also, neither the policymaker nor the fictitious evil agent can commit, there will be lower disturbances due to model misspecification compared to the commitment case.