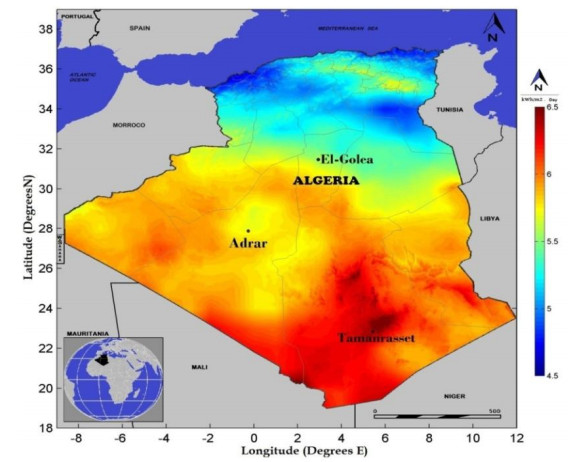
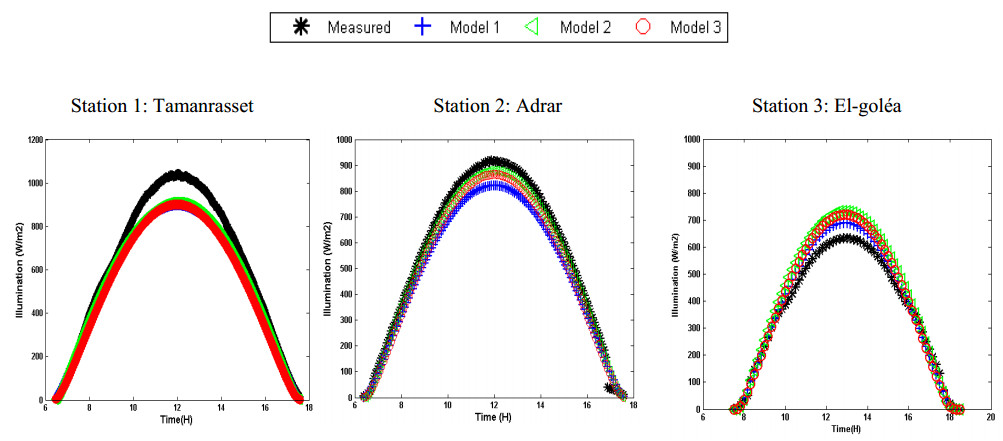
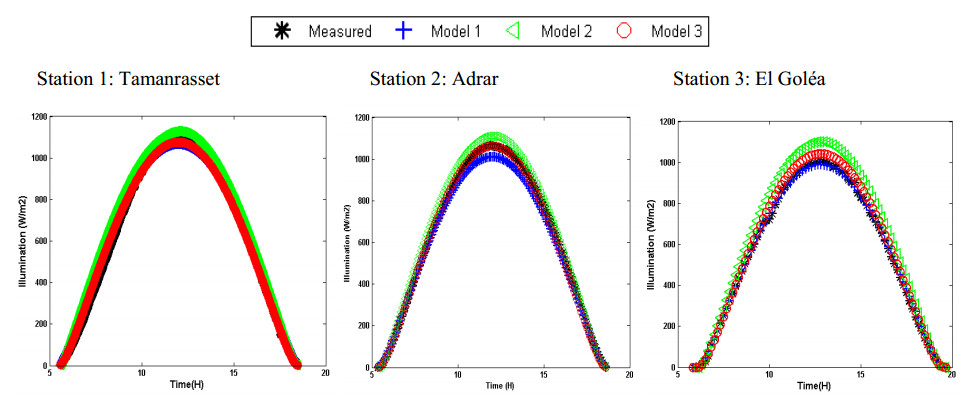
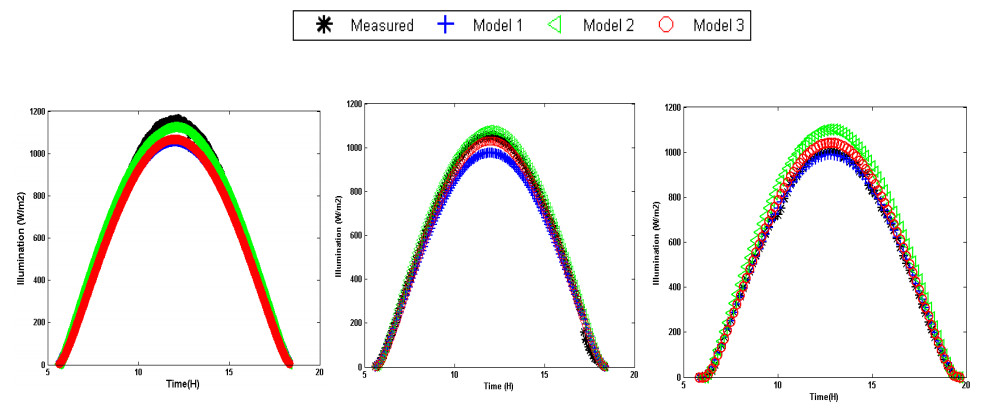
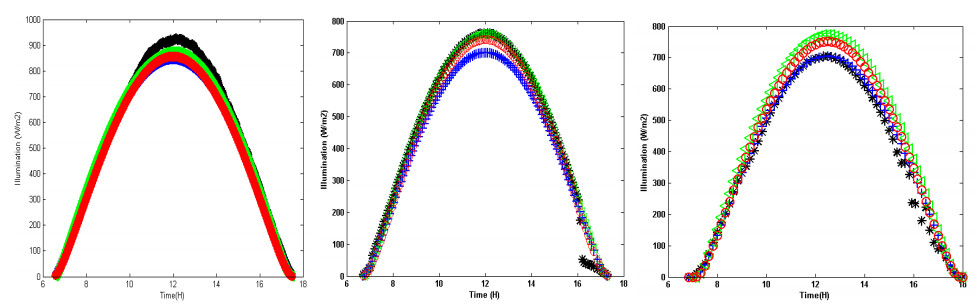
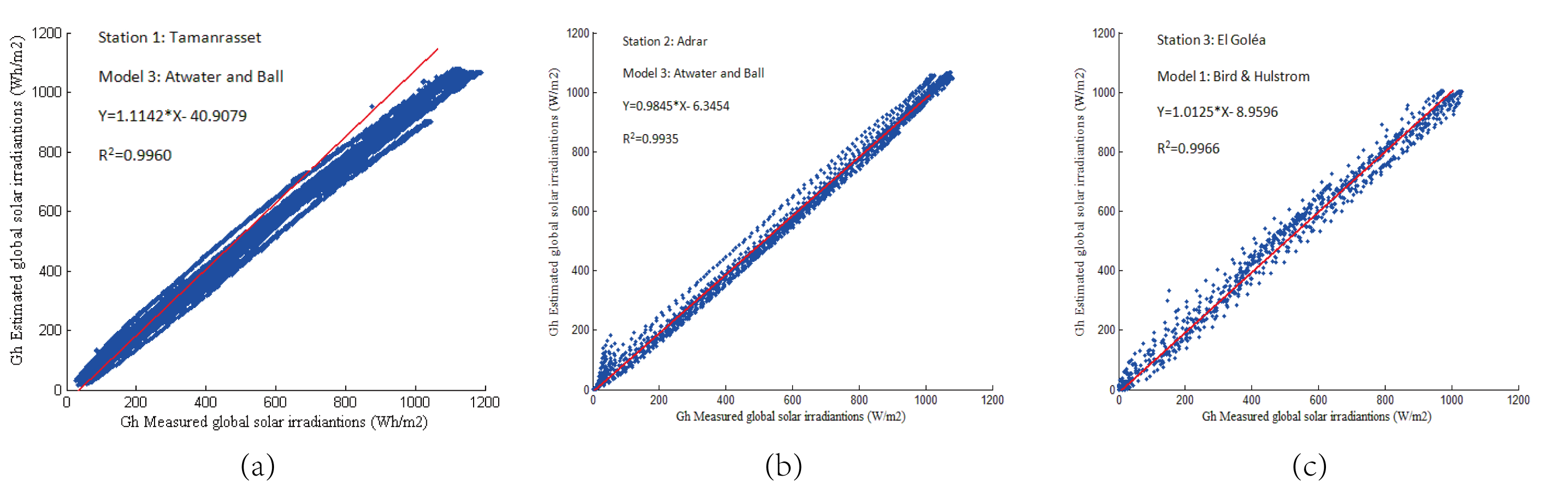
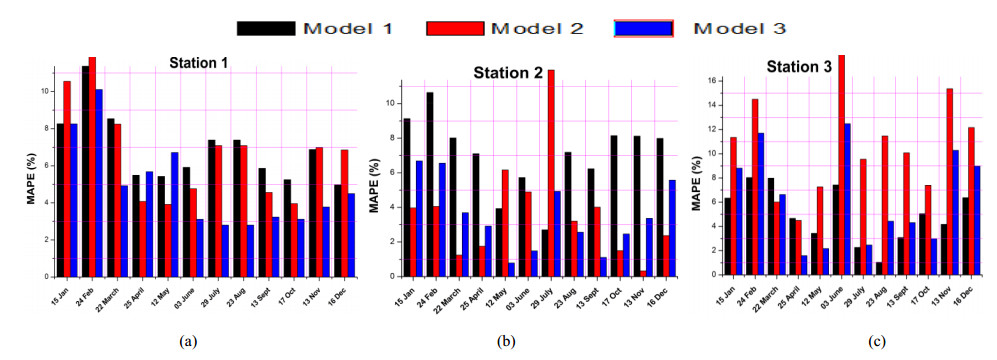
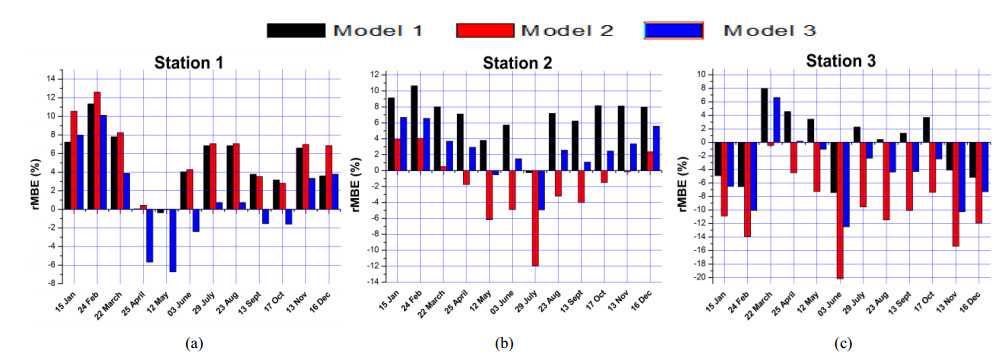
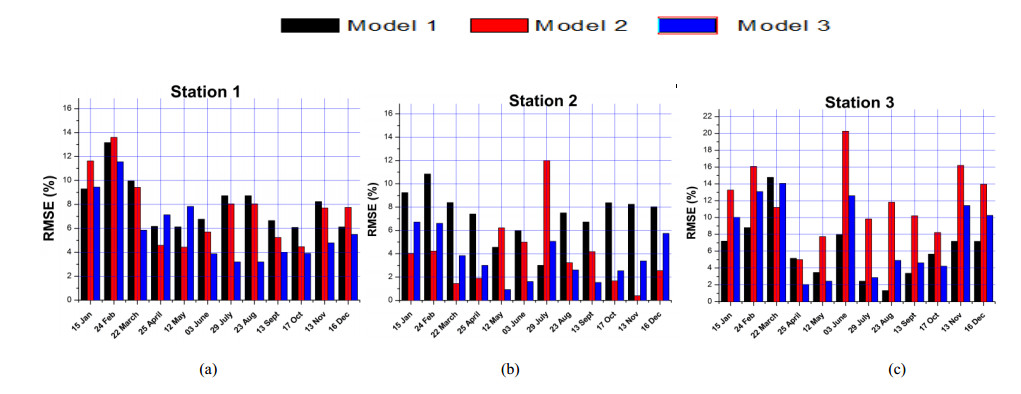
The paper presents the evaluation of performance of three models at three sites for estimating instantaneous clear-sky global solar radiation on a horizontal surface in Algeria. Additionally, recommend it to be used for estimating solar radiation at many locations in similar climates where radiometric measurements are not available and which might be helpful in the selection of the most suitable locations for solar power installations. The results in general exhibit that for global radiation, the daily correlation coefficient is higher than 0.99, whereas the mean absolute percentage error is less than 5%. The daily mean bias error ranges between -3 and +3%. The daily root mean square error is less than 7%. These results represent a precision that indicates that Atwater & Ball and Bird & Hulstrom models can be used successfully to predict solar radiation over three stations in the studied sites.
1.
Introduction
Bankruptcy prediction is the problem of detecting financial distress in businesses which will lead to eventual bankruptcy. Bankruptcy prediction has been studied since at least 1930s. The early models of bankruptcy prediction employed univariate statistical models over financial ratios. The univariate models were followed by multi-variate statistical models such as the famous Altman Z-score model. The recent advances in the field of Machine learning have led to the adoption of Machine learning algorithms for bankruptcy prediction. Machine Learning methods are increasingly being used for bankruptcy prediction using financial ratios. A study by Barboza, Kimura and Altman found that Machine Learning models can outperform classical statistical models like multiple discriminant analysis (MDA) by a significant margin in bankruptcy prediction (Barboza et al., 2017).
1.1. Significance of bankruptcy prediction
Bankruptcy prediction is an important for modern economies because early warnings of bankrupt help not only the investor but also public policy makers to take proactive steps to minimize the impact of bankruptcies. The reasons that add to the significance of bankruptcy prediction are as follows:
(1). Better allocation of resources
Institutional investors, banks, lenders, retail investors are always looking at information that predicts financial distress in publicly traded firms. Early prediction of bankruptcy helps not only the investors and lenders but also the managers of a firm to take corrective action thereby conserving scare economic resources. Efficient allocation of capital is the cornerstone of growth in modern economies.
(2). Input to policy makers
Accurate prediction of bankruptcies of businesses and individuals before they happen gives law makers and policy makers some additional time to alleviate systemic issues that might be causing the bankruptcies. Indeed, with bankruptcies taking center stage in political discourse of many countries, the accurate prediction of bankruptcy is a key input for politicians, bureaucrats and in general for anyone who is making public policy.
(3). Corrective action for business managers
The early prediction of bankruptcy is likely to highlight business issues thereby giving the company's manager additional time to make decisions that will help avoid bankruptcy. This effect is likely to be more profound in public companies where the management has a fiduciary duty to the shareholders.
(4). Identification of sector wide problems
Bankruptcy prediction models that flag firms belonging to a certain sector are likely to be a leading indicator of an upcoming downturn in a certain sector of an economy. With robust models, the business managers and government policy makers would become aware and take corrective action to limit the magnitude and intensity of the downturn in the specific sector. Industry groups in turn has been shown to significantly effect forecasting models (Chava and Jarrow, 2004).
(5). Signal to Investors
Investors can make better and more informed decisions based on the prediction of bankruptcy models. This not only forces the management of firms to take corrective action but also helps to soften the overall economic fallout that results from the bankruptcies. Empirical studies have shown that investment opportunities are significantly related to likelihood of bankruptcy (Lyandres & Zhdanov, 2007).
(6). Relation to adjacent problems
Bankruptcy prediction is often the first step used by ratings agencies to detect financial distress in firms. Based on the predictions of bankruptcy models, ratings agencies investigate and assess credit risk. Getting flagged by bankruptcy prediction models is often the first step that triggers the process of revising credit ratings. A literature survey covering 2000–2013 demonstrates the close relation between bankruptcy prediction and credit risk (García et al., 2015).
1.2. Comparison with past work
Most past studies in bankruptcy prediction including those using Machine Learning have used a relatively small sample of firms and a small number of financial ratios. This study distinguishes itself by using a much larger dataset having data for 21,114 U.S. firms (samples) and 57 financial ratios (features). Our dataset covers US firms from 1970 to 2020. Bankruptcy prediction models have been researched and built since the 1960s. The models built from 1960 to 1990 were primarily statistical models such as univariate, multiple discriminant analysis and logit and probit models. Starting from 1990s machine learning models started outperforming statistical models. Since this study applies the most popular contemporary machine learning algorithms using a big data set, we will compare our model with the machine learning models built since the 1990s. A full listing outlining the comparison with past machine learning studies and models for bankruptcy prediction is shown in the Table 1.
In this study we have used three popular machine learning techniques—Random Forest, Support Vector Machines, and XGBoost to construct forecasting models. We find that Machine Learning models perform very well, with XGBoost being the most successful technique that achieves an accuracy score of more than 99% in out of sample testing.
We also apply our XGBoost model to an important current issue, the task of predicting bankruptcies during the second half of 2020. The depth of the recession caused by the lockdowns that have been imposed to contain the COVID-19 pandemic has raised worries that corporate bankruptcies may rise substantially in the near future. According to a report in the New York Times (2020), Edward Altman, a pioneer of bankruptcy prediction research, and the creator of the famous Z score model, expects a "tsunami of bankruptcies" that will exceed the number of bankruptcies that followed the 2008 financial crisis. The result from our Machine Learning model confirms Prof Altman's fears that corporate bankruptcies will rise substantially in late 2020 and equal the highs seen during the 2008-09 recession. However, this study finds that the elevated level of bankruptcies will not be significantly different from 2010.
1.3. Significance of this study
The previous studies done for bankruptcy prediction have not taken a systematic view of the data used to build the models. The previous studies have been more focused on the models rather than on the data used to build the models. This study offers a much more balanced view where both the data and the models are given equal importance. To begin with, we have use Compustat are a source database to get an exhaustive list of financial ratios over US firms from 1970 to 2020. Compustat is a high-quality database used by several famous finance related papers such as Fama and French (1993). Most of the previous studies have used relatively small datasets as compared to ours. This study takes a systematic look at as many features as possible to train our machine learning models. Our balanced approach is also consistent with the shift from model centric to data centric approach proposed by Andrew Ng (Gil Press, 2021).
The rest of the paper is structured as follows:
Section 2—Describes the existing literature for bankruptcy prediction.
Section 3—Describes the data and the method used to clean, process, and fit the data into our machine learning models. This section also covers the process used to predict the number of bankruptcies using Q2-2020 ratios.
Section 4—Describes the results observed from the experiments
Section 5—Presents our final comments and discusses the implications of the results.
2.
Literature review
Bankruptcy prediction models prior to 1990s were primarily statistical models employing univariate, multivariate and logit & probit techniques. In 1966, Beaver applied univariate analysis in which the predictive ability of 30 financial ratios was tested one at a time to predict bankruptcy (Beaver, 1966). Altman in 1968 performed a multi-variate discriminant analysis (MDA) using 5 ratios to create a linear discriminant function of 5 variables (Altman, 1968). Several variants of MDA were developed in the following years. Edmister used 19 financial ratios to build a linear model for bankruptcy prediction (Edmister, 1972). Deakin found that a linear combination of the 14 ratios could be used to predict bankruptcy five years prior to failure (Deakin, 1972). Ohlson studied the shortcomings of MDA models and built a conditional logit model using maximum likelihood estimation (Ohlson, 1980). The datasets used in all these studies were quite small as compared to modern standards. Ohlson's study for example used a dataset of 2058 firms out of which 105 firms represented the bankrupt class.
The next phase in the evolution of bankruptcy models started in the 1990s with several machine learning algorithms outperforming the older statistical models. Machine learning models such as Random Forests, Support Vector Machines (SVM) and Gradient Boosted Trees were found to be particularly effective for bankruptcy prediction. Barboza, Kimura and Altman compared statistical models with machine learning (ML) models. They found the Random Forests outperformed Alman's Z-score model by a significant margin (Barboza et al., 2017). These results were corroborated by studies (Joshi et al., 2018; Rustam and Saragih, 2018; Gnip and Drotár, 2019). Support Vector Machine (SVM) was also found to be a very effective machine learning algorithm in several studies. Hang et al. (2004) and Chen et al. (2008) achieved superior results for credit rating classification problem by using SVM. Song et al. (2008) used SVM to predict financial distress. Some studies also found boosted trees-based algorithms to outperform SVM. Wang, Ma and Yang proposed a new boosted tree-based algorithm for bankruptcy prediction which they found to be more effective than SVM (Wang et al., 2014). Heo and Yang (2014) used Adaboost algorithm to predict bankruptcy for Korean construction firm. They found Adaboost to have better accuracy than SVM (Heo and Yang, 2014). A more recent study in 2021 has used XGBoost and Random Forest algorithms to predict bankruptcies over 12 months. This study used a medium sized training dataset containing data for 8959 firms registered in Italy (Perboli and Arabnezad, 2021). Another recent study uses a database of Taiwanese firms to predict bankruptcy. This study used data set contain 96 attributes for 6819 firms to train machine learning models (Wang and Liu, 2021). One common attribute shared by all the forementioned studies is the relatively small size of their training data sets. The datasets used by these studies are small as compared to datasets used in the big data era. The largest training dataset in these studies had just 2600 samples which is quite small.
Based on the literature review, the following trends become apparent:
● Machine Learning Models are now consistently outperforming statistical models
● The training data sets used to train the existing machine learning models are relatively small as compared to the data sets used for training models in other application areas.
● Ensemble methods such as Random Forest and Boosted trees have performed better than other models in bankruptcy prediction.
3.
Data and methodology
This study differentiates itself from previous studies by using a substantially larger dataset as compared to previous studies. We use a very standard and well documented dataset called Compustat to retrieve the financial ratios. Compustat is a standard financial dataset used in financial research. Compustat has been used by some very popular papers in finance such as Fama and French (1993). We have used 57 financial ratios that are listed in Table 2. Financial ratios are inputs used to train Bankruptcy prediction models. While most studies use fewer financial ratios, this study applies a large set of financial ratios of US Firms from 1970–2020 (50 years) to train Random Forest, SVM and XGBoost Models. This section discusses the overall methodology which includes data cleaning, balancing, model fitting, and analysis of results.
3.1. Data
Previous studies have used small to medium sized data sets for training Machine learning models. This study sets itself apart by using a much larger training dataset. We used financial ratios data set from Compustat. The financial ratios data set was then joined with another dataset called Bankruptcy data set. The bankruptcy data set contains the data such as date of bankruptcy, bankruptcy reason and GVKEY (primary key) while the financial ratios dataset contains all the financial ratios mentioned in Table A.1. The two datasets were programmatically joined using a common field named GVKEY. GVKEY is a unique identifier assigned to each firm. The relation amongst the two datasets that were used to create our labelled training dataset is best represented by the ER schema diagram shown in Figure 1.
The financial ratios dataset we have used contains 57 financial ratios mentioned in Table A.1 in Appendix A. This is an exhaustive list of features used to train our models. We have included ratios which are often overlooked but are likely to help detect patterns related to edge cases.
3.2. Methodology
3.2.1. Data preprocessing
The first step of building a predictive model is data pre-processing and cleaning. The original data from Compustat had 75 financial ratios for 21,114 US firms. This data covered firms established in the US between 1970 and 2020. The dataset contained firms that belonged to 2 classes: bankrupt and non-bankrupt or continuing enterprises. The dataset contains 1212 bankrupt firms and 19,902 non-bankrupt firms. The distribution of data points (samples) belonging to these two classes is summarized in Table 2. The next step was to drop features which had null values for more than 6000 firms out of 21,114 firms. This step ensured that we don't have more than 30% of null values in any feature. The goal is to ensure that the true distribution generating this data is preserved and learned by our machine learning models. 18 features (financial ratios) were dropped from the data set because they had null values for more than 6000 (30% of total number of firms). The dataset now had 75 − 18 = 57 features. Next, we scaled our data to have mean = 0 and variance = 1 using Scikit-learns Standard Scaler class. Scaling is required to ensure that gradient descent converges on the minima of the loss function. The last step of data cleaning was to impute the missing values in the 57 financial ratios (features). For imputing the missing values, we used the KNN algorithm which used three nearest neighbours to estimate the missing value. Further, the weight assigned to each neighbour is a function of its Euclidean distance from the data point with missing value. KNN with 3-neighbours has been found to be effective in preserving the true distribution of the data (Beretta and Santaniello, 2016).
3.2.2. Balancing the dataset
The cleaned and scaled dataset without any missing values was an imbalanced dataset (see Table 2). The dominant class was the bankruptcy class. Approximately 90% of the samples belonged to the majority class which is non-bankrupt firms. Since the goal of this study is train a classifier to identify bankrupt firms, we decided to balance the classes in our training data. This would ensure that our model would learn about the minority class which is the bankrupt class. This is important in the context of bankruptcy prediction because detecting samples belonging to the bankrupt class. To balance the dataset, we use the Synthetic Minority Over-sampling technique (SMOTE) proposed by Chawla et al. (Chawla et al., 2002). SMOTE generates synthetic samples using the features of the data. The minority class is oversampled by taking a minority class sample and then a line is drawn from this minority class sample to k-nearest minority class samples. Synthetic minority class samples are generated along the line joining the minority class sample to its minority class neighbours. Additionally, to ensure that our balanced dataset facilitated learning of the bankrupt class, we also used Borderline-SVM SMOTE. Borderline-SVM SMOTE technique uses samples close the decision boundary (support vectors) to create synthetic samples (Nguyen et al., 2011). Finally, we used the Adaptive Synthetic Sampling (ADASYN) algorithm of He, Bai, Garcia and Li to generate samples in regions of feature space where the density of minority samples is low (He et al., 2008). The result was a balanced dataset containing 19902 samples of non-bankrupt class and 20,517 bankrupt class. The balanced dataset has 57 financial ratios (features).
3.2.3. Fitting training data into models
The balanced dataset was then shuffled and split into training set containing 70% of the samples and test set containing 30% of the samples. The purpose of creating a test set is to test the accuracy of the models on data that the models have not been trained on. Collecting metrics based on the test set gives practitioners an idea of the generalization performance of machine learning models.
The training data set was fitted into three machine learning models. These models are: Random Forest, Support Vector Machine (SVM) and XGBoost. After fitting, the models were then used to predict for samples in the test set to assess their relative performance.
3.2.4. Performance analysis
For comparing the performance of the models, we decided to use Accuracy score, Receiver Operating Curve (ROC) and Area Under ROC Curve (AUC). Accuracy score can be used because we are training our models using a balanced dataset. However, to get a better idea of the True Positive Rate (TPR) and False Positive Rate (FPR) we decided to employ ROC and AUC metrics as well. It is important to compare the TPR and FPR because it is more to avoid False negatives (FN) as compared to False positives (FP). False negative (FN) would be a firm which would go bankrupt but is wrongly classified by our model as a non-bankrupt sample. False positive (FP) on the other hand would be a firm that is not bankrupt but is wrongly classified as a bankrupt firm.
3.2.5. Predicting bankruptcies
The goal of this study is to predict number of bankruptcies within the next 30, 90 and 180 days. We trained 3 different models to predict the number of bankruptcies within 30, 90 and 180 days. The models were built and analysed using the same approach. The only difference was that the training and test labels for each model were derived from the bankruptcy date. For example, to train the model for predicting number of bankruptcies within 30 days, we used
where
where
else
Therefore, we trained 9 models to predict bankruptcies within 30, 90 and 180 days. For example, for predicting bankruptcy within 30 days we trained Random Forest, SVM and XGBoost. After training the models, we picked the best model based on performance metrics described in previous section and then we used the best model to predict the number of bankruptcies using the latest Q2 2020 financial ratios from Capital IQ. In this final prediction set, we only kept data for firms which did not have any significant gaps or holes. Finally, we used the final prediction set from Q2 2020 to predict the number of bankruptcies we expect to happen over the next 30, 90 and 180 days.
4.
Results
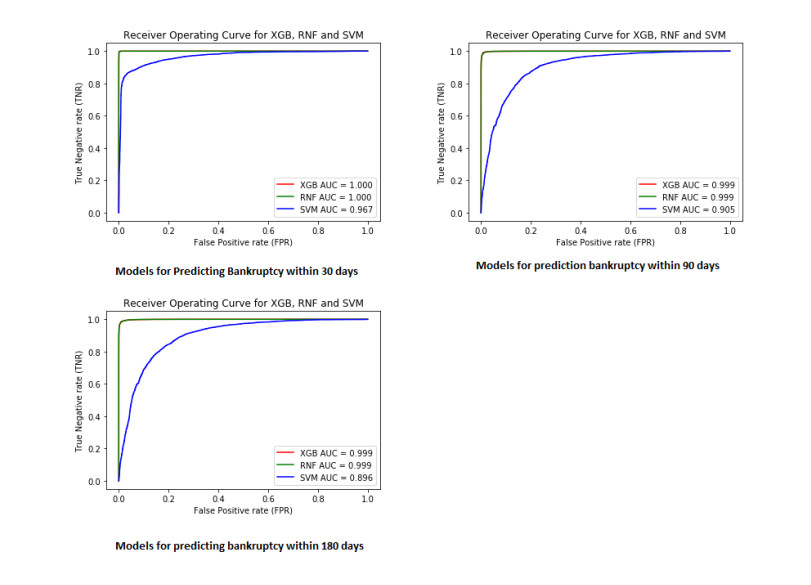
As mentioned in the previous section, we trained 9 models, using three different techniques, RF, SVM, XGBoost, for predicting bankruptcies over 30, 90 and 180 days. Next, we used the test set to make predictions and then assessed the relative performance. Based on the chosen metrics of accuracy score and Area under ROC curve (ROC AUC), XGBoost outperformed the other models for predicting bankruptcy within 30, 90 and 180 days. The actual scores for accuracy and AUC are presented in Table 3.
The accuracy score of XGBoost models is consistently better than SVM and Random Forest. This result is also consistent with the ROC curves which are shown in Figure 2 below.
As seen in Figure 2, the ROC curve for XGBoost is closest to the top left corner thereby covering maximum area under it. XGBoost is therefore the best performing model closely followed by Random Forest. The fact that these metrics are calculated using the test set (containing data which model has not been trained on) gives us confidence in the ability of our models to generalize.
4.1. Comparison of performance with previous studies
We present the performance metrics of previous studies in Table 4. Previous studies have used 2 performance metrics: Test accuracy and Area Under ROC curve (AUC). To keep the comparison consistent, we have computed both test accuracy score and AUC for our models (see Table 3). Our best model built using XGBoost significantly outperforms the models built in previous studies. The accuracy of our XGBoost model for prediction bankruptcy within 180 days is 98.69% which is lower than the test accuracy of our XGBoost models for predicting bankruptcies within 30 and 90 days. However, our model for predicting bankruptcies within 180 days has a higher test accuracy (98.69%) than models built in previous studies. Similarly, our model for predicting bankruptcies within 180 days has an AUC score of 0.99 which is higher than the AUC score reported by previous studies. Our performance metrics of accuracy and AUC score are computed over out of training samples which also indicates to the robustness of our results.
4.2. Predicting bankruptcies caused by Covid
Next, we apply our best model, using XGBoost, to the data from Q2-2020 to evaluate the possibility of a substantial upsurge in business bankruptcies in the second half of 2020 because of the deep 2020 recession caused by the pandemic. We apply this best model to the latest available ratios, for Q2-2020, and classify a firm as going bankrupt during the next 30, 90, or 180 days if the predicted probability of bankruptcy is higher than 0.50.
Using this method, our best model in each category predicted 74 bankruptcies within 30 days, 189 bankruptcies within 90 days and 354 Bankruptcies within 180 days. This prediction is for all firms contained in the S & P Global database, both public and private. The predictions for the number of bankruptcies are summarized in Table 5.
S & P Global has reported a total of 336 actual bankruptcies until the end of June 2020. If we add our prediction of 354 bankruptcies to the actual bankruptcies, then we predict a total of 336 + 354 = 690 bankruptcies in 2020. We summarize our predictions in Table 6 below.
Since the number of firms in the database changes from year to year, we decided to compare the prediction for 2020 with the past by using bankruptcy rates, i.e., the ratio of the number of bankruptcies to the total number of firms. As shown in Table 7, our prediction of 690 bankruptcies in 2020 represents a bankruptcy rate of 4.35% for all US firms. This rate is the highest in the last 10 years. The second highest rate of 4.2%, only slightly lower, was seen in 2010, in the immediate aftermath of the 2008-09 recession. The average rate during the economic expansion years of 2011–2019 was 3.2%, more than a full percentage point lower than the predicted 2020 rate. We conclude that we will indeed see a much higher rate bankruptcies in 2020, but it is unlikely to be substantially larger than in 2010.
5.
Conclusions
We find that two different Machine Learning algorithms, Random Forest (RF) and Extreme Gradient Boosting (XGBoost) produce accurate predictions of whether a firm will go bankrupt within the next 30, 90, or 180 days, using financial ratios as input features. The XGBoost based models perform exceptionally well, with 99% out-of-sample accuracy. Our training dataset uses a large database of public US firms over a period of 49 years, 1970–2019, and 57 financial ratios. This study has used a substantially larger training dataset as compared to previous studies.
An application of our best performing XGBoost model to Q2-2020 financial data for a sample of both private and public U.S. firms shows that the bankruptcy rate will climb substantially higher in 2020 than in the expansion years of 2011–2019. However, our model suggests that the rate will be only marginally higher than in 2010.
5.1. Avenues for future research
We identify the following areas for further research:
● Adding macro-economic features—It will be interesting to add macro-economic features to training data used for training machine learning models for bankruptcy prediction.
● Train deep neural networks with different topologies—Another interesting area of research would be to apply different types of deep neural networks such as TabNet and Recurrent neural networks.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: