Radiative cooling is a well-researched cooling technique based on the ability of terrestrial surfaces to dissipate heat to the cold space. Past research on radiative cooling failed to present subambient temperatures under direct sunlight due to the limited solar reflectance and emissivity in the atmospheric window. Nanostructures developed in recent years have successfully achieved subambient feature during the daytime. The use of electromagnetic simulation in the design of such structures is essential to understand their optical properties and thus optimize the structures and materials selected before manufacture. In this paper, the commonly used software to solve Maxwell’s equations is first reported. Then the numerical techniques are reviewed and their advantages, limitations, and popularity in academic research are compared and analyzed. After that, the application of these numerical techniques in daytime radiative cooling and the extent of the agreement between their results and those of a reference are discussed. The accuracy analysis of these numerical techniques—including the source of errors in the original calculation, how accuracy of the result is evaluated, and explanations for the discrepancies in results between original and reference computations—are discussed in the final part, as well as the characteristics of numerical technique preferred in radiative cooling. The purpose of this paper is to provide strategies for selecting appropriate numerical techniques according to specific needs, evaluating, and analyzing the accuracy of the calculations, and explaining the cause of discrepancies between original and reference computations.
1.
Introduction
Climate change has caused an increase in the ambient temperature and the frequency, magnitude, and duration of extreme heat events [1]. Among all the cooling technologies for buildings and the outdoor environment, materials-related radiative cooling is of great potential since it can be achieved without consuming extra energy or heating the nearby air. It is commonly believed that an ideal radiative cooling material should have (a) extremely high reflectivity in the solar wavelength, mainly in 0.3–2.5 μm and (b) near unity emissivity in the atmospheric window range, which is 8–13 μm [2]. Previous research aimed mainly at discovering natural materials or creating composite materials with the satisfactory optical properties. Radiative coolers were created using polymers, gases, metals, or a simple combination of several materials [3,4,5,6]. The inability to control the optical spectrum precisely significantly constrained the performance of the cooler. Very few structures could achieve sub-ambient temperatures under direct sunlight [7]. In recent years, the maturity of nanofabrication has led to the possibility of increasing spectral reflectivity and emissivity. Some multilayer planar photonic structures [8,9,10,11,12,13,14,15,16,17,18], 2D/3D photonic devices [19,20], metamaterials [21,22], polymers [9,23,24,25] and paints [26,27] have been developed and are reported to have the satisfactory optical properties.
The optical properties of a surface are determined by its structural characteristics at the micro- or nano-scale and the inherent properties, such as refractive index and dielectric constant, of the material it is made of. Restructuring the surface at the micro- or nano-scale can optimize its optical performance [28]. As the manufacture of materials at such scales requires high quantities of resources, the necessity for testing their optical properties in simulations before they are fabricated becomes obvious. Simulation enables researchers to experiment with virtual models beginning at the earliest stages of the design process, compare the performance of different prototypes, and optimize their performance which reduces both cost and time. By numerically solving Maxwell's equations, we can test, study, and optimize the optical properties of radiative cooling surfaces with various combinations of materials, different numbers of layers, or diverse particle size and shape.
The employed numerical method is the most critical feature that differentiates most commercially available electromagnetic (EM) simulation tools. Thus, the emphasis of this paper is on reviewing various numerical methods and their applications to research on daytime radiative cooling. Apart from the numerical methods, the material model and optimizer are also essential parts of the EM simulation and are often integrated into the simulation tool.
The purpose of this paper is to (1) review numerical tools available for electromagnetic simulation and provide information on how to select the appropriate tool based on specific needs, (2) present the application of various numerical methods in daytime radiative cooling research, and (3) provide strategies on finding source of errors in an original simulation, how to evaluate its accuracy, and how to explain discrepancies in results between an original computation and a reference. A brief introduction to commercially available electromagnetic simulation software is followed by a presentation and analysis of numerical methods and their advantages, limitations, and popularity in academic research. The application of these methods to daytime radiative cooling and the extent of agreement between their results and those of the reference are presented in the second part. Accuracy analysis, including where errors come from, how accuracy is evaluated, and how discrepancies can be explained, are discussed in the final part.
2.
Software and numerical techniques in electromagnetic simulation of daytime radiative cooler
2.1. Commercially available software
Various commercially available software (Table 1) has been developed for EM simulation. Most has integrated different material models, numerical methods, and optimizers. Some, like SimSonic, Meep, Lumerical FDTD, ERMES, ANSYS HFSS, BeamPROP, OptiFDTD and OptiBPM, use a single numerical method; others, like OmniSim, CST Studio Suite, COMSOL, S4, and CAMFR, are based on a combination of different types of methods. Various global and local optimizers are employed in the optimization process, as shown in Table 1, while numerical methods act as the foundation of each tools.
2.2. Numerical techniques to simulate electromagnetic wave propagation in devices
A number of numerical methods can be used to calculate the propagation of an EM wave within or around a device, as shown in Figure 1.
2.2.1. Finite-difference-time domain (FDTD) and finite-difference-frequency-domain (FDFD) methods
The finite-difference method solves differential equations by approximating them with difference equations and second order difference can be obtained in central differences. The finite-difference-time domain (FDTD) and finite-difference-frequency-domain (FDFD) methods are based on discretizing differential forms of Maxwell's equations. The FDTD method is based on a direct numerical solution of Maxwell's curl equations in the time-dependent form [45], within which fields are evolved by iterating Maxwell's equations in small time steps. Yee [46] pioneered the application of time domain analysis technique to solve electromagnetic problems in 1966. He used a finite difference algorithm, which became known as the FDTD approach, on a staggered field lattice structure. It is one of the most popular numerical techniques for EM analysis.
FDFD uses the finite-difference method to transform the frequency-domain Maxwell's equations into numerically solvable forms. The time-domain equations are essential for investigating transient states and dynamics while the frequency-domain equations are usually used for studying steady states. Steady-state solutions can be also be reached using time domain methods if a sine source is implemented and sufficient simulation time is guaranteed, but this is inherently inefficient. Similarly, transient solutions can be generated using frequency domain methods if calculate at enough different frequencies and then add the solutions together which is inefficient either. FDFD can handle dispersive materials accurately while transforming the frequency-dependent material parameters into an auxiliary time-domain differential equation can enable FDTD being applied to such materials as well [47]. FDTD can generate a satisfactory result for general dielectric materials. However, FDFD is a better choice for the highly resonant wavelength of some materials. It will take a long time for FDTD to reach the frequency domain solution which makes it inefficient for highly resonant materials.
2.2.2. Rigorous-coupled-wave analysis (RCWA)
Rigorous-coupled-wave analysis (RCWA), which is also referred to as the Fourier modal method (FMM) or the scattering matrix method (SMM), is a mesh-free technique that uses a set of plane waves at different angles to represent fields in each layer. As a semi-analytical method for solving reflection, transmission, and diffraction profiles, it is excellent for modelling periodic structures due to its base in Fourier representation [48].
2.2.3. Discrete dipole approximation (DDA) and the boundary element method (BEM)
Discrete dipole approximation (DDA), which is generally used to predict EM waves scattered by particles, is based on discretizing objects into sub-volumes that behave as electric point dipoles. DDA was initially proposed by Purcell and Pennypacker (PP), who used a set of point dipoles to replace the scatterer [49]. The interaction between these dipoles and the incident field can produce a system of linear equations that can be solved to obtain dipole polarizations. Scattering quantities can be derived from these polarizations.
The boundary element method (BEM) [50,51,52], also known as the method of moments (MoM) and is often referred to as an integral equation method, is used to solve linear partial differential equations in integral form. Harrington [53] was the first to apply MoM in electromagnetics. When applying this method, boundary conditions need to be specified rather than calculated from the differential equations [54]. However, the discretized Maxwell's equations in BEM make it difficult to be applied when the media is inhomogeneous. Moreover, boundary element method often requires the knowledge of Green function, which is hard to calculate, especially for materials having spatially varying parameters.
Yet it is difficult to clearly separate DDA from BEM based only on the volume integral equations of the EM fields. One possible way to make this distinction, according to [55], is that the formulation of DDA can be interpreted as replacing a scatterer with a set of interacting dipoles. This is a fundamental characteristic of DDA that it does not share with MoM.
2.2.4. Transfer matrix method (TMM)
The transfer matrix method (TMM) can be used to study the propagation of EM waves through a stratified material [56]. Since Maxwell's equations indicate the continuity for the electric field at boundaries from one medium to another, if the field is given at the beginning of a layer, the field at the end of the layer can be calculated using a matrix operation. A combination of layers can be regarded as a system of matrices. In the final step, the system matrix is converted back into transmittance and reflectance [57]. It is fast, accurate, robust, and rigorous. Furthermore, because it treats everything as forward propagation, the method itself is inherently unstable. When backward waves or decaying field exist but are treated as forward propagating waves, they grow exponentially, leading to numerical instability. TMM also consumes high amounts of computational resources in 3D simulation because it has to solve a very large group of linear equation in three dimensions.
2.2.5. Plane wave expansion method (PWEM)
The plane wave expansion method (PWEM) [58,59] solves Maxwell's equations by formulating an eigenvalue problem out of the equation. It is rigorous and well suited for modal solution problems; it can calculate both the modes in periodic dielectric structures and the band structure of photonic crystals [60].
2.2.6. Beam propagation method (BPM)
The beam propagation method (BPM) [61,62] is basically a "forward" propagating algorithm in a domain where the dominant propagation direction is longitudinal [63]. It was originally developed in 1970s [64]. It only calculates the field plane at a specific time and does not solve the entire solution space. It also relies on approximate differential equations, which means that it is not a rigorous method and can only be applied to analyze structures for which the influence of the reflected fields on the forward-propagating fields can be neglected. This excludes the use of the BPM for cases in which, for example, the refractive index changes abruptly.
2.2.7. Finite element method (FEM), finite-element-time domain (FETD) method, and the finite-element-frequency-domain (FEFD) method
The finite element method (FEM) is designed for steady-state analysis and can easily be applied to unstructured mesh [65] and deal with extremely complex shapes. Originating from the structural analysis field, FEM was first applied to electromagnetic problems in 1968 [66]. Four basic steps are involved in most finite element analyses: discretizing the solution region; finding governing equations for elements; assembling all elements in the solution region; and solving the equation systems [66].
The finite element time domain (FETD) method is a combination of FEM and FDTD. FETD method approximates the curl operators in Maxwell's equations using FEM, and the time derivatives using finite differences as in FDTD. The main practical difference between FETD and FDTD is the stability condition. Explicit time-stepping requires a stability condition and is limited by the smallest space step. The smallest space step in FDTD is simply the cell size while in the unstructured tetrahedral FETD meshes, the smallest space step can be much smaller, which means the time step can be much smaller as well, leading to the result that many more time steps need to be calculated. The finite element frequency domain (FEFD) method is a steady-state frequency domain solution for complex 3D geometries where the Green function is not known.
2.3. Popularity of different numerical techniques in academic research
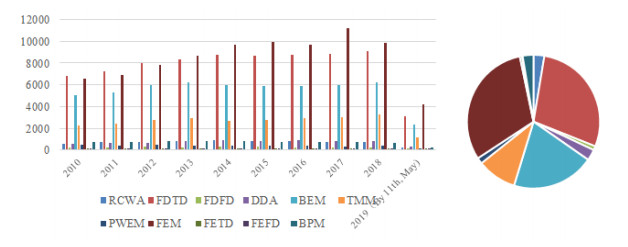
The popularity of the numerical techniques introduced above in academic research is presented in Figure 1. This figure shows, in each year from 2010 to 2019 (by May 11th), the number of academic papers published containing phrase(s): rigorous coupled wave analysis (RCWA), finite difference time domain (FDTD), finite difference frequency domain (FDFD), discrete dipole approximation (DDA), boundary element method (BEM), transfer matrix method (TMM), plane wave expansion method (PWEM), finite element method (FEM), beam propagation method (BPM), finite element time domain (FETD) and finite element frequency domain (FEFD), are counted and shown. According to the result, FEM, FDTD and BEM are more popular than others.
3.
Application of the numerical techniques in daytime radiative cooling
Most of the numerical techniques mentioned above can be employed to predict the optical properties of various radiative cooling materials, as shown in Table 2.
The FDTD method can be used for investigating the optical response of structures with different particle sizes and shapes, thicknesses, and number of layers. In 2017, Bao et al. [9] used Lumerical FDTD to analyze the optical properties of the disordered TiO2 particle system in terms of different thicknesses and particle sizes. Time-domain method was employed since they wanted to get the response for all the wavelengths of interest through a single broadband simulation. Since the simulation yielded a uniform and high reflectance in the solar region when the particle radius was set to 0.5 μm, this size was used for further study. Besides, it was found that the reflectance was high enough at thicknesses greater than 10 μm. Therefore, the thickness of the layer was set to greater than 10 μm in the experiment. In the convergence test, the mesh size contributed a lot to the formation of a converged result. It should be noted that analyzing spherical or ellipsoidal in the regular FDTD grids can lead to bad convergence. As is concluded in [67], the staircasing error due to approximating a sphere by cubic cell was bad that they could not even consistently assign an order of accuracy.
Lumerical FDTD was also used to investigate the effect of hierarchical porous structures on the optical properties of their original structure [27]. However, due to the constraints of computation, they only used a two-dimensional model. In solar wavelengths (0.35–2.5 μm), a total-field scattered-field source was used to simulate the scattering across sections. It was reported that voids with different sizes scatter sunlight in different wavelength ranges. In the atmospheric window range (8–13 μm), the spectral reflectance of both the micro voids and the nano-porous structure were simulated. The nanophase was represented by a Maxwell–Garnett effective medium while 10 μm circular voids were added randomly to the medium in the micro scheme. By excluding randomly varying sizes on the top surface, they mimicked the features of the open porous surface.
Jeong et al. [68] used the thermal regulatory effect of the triangular hairs on Sahara silver ants to create a radiative cooler. They used FDTD simulation before field experiments and optimized the geometry, size, and thickness of the structure. Before studying their own structure, they built a simulation model for validation purpose. They reproduced a paper by Chan et al [69] and found good agreement: their emission peaks had almost the same wavelengths as the results presented in the reference paper although the overall emissivity was slightly over-predicted. A design inspired by the Morpho butterfly used an NF-RT-FDTD algorithm, which was a specially designed computational tool that assesses radiative heat transfer at the nanoscale [70]. This tool considered the fine details of structures with roughness and examined the asperities accurately. As dealing with details at the nanoscale requires utmost accuracy, effective medium theory-based techniques such as RCWA could not be used to yield precise result. The NF-RT-FDTD algorithm was also used in [71,72,73] to solve near-field radiative emissions.
The FDTD method and FEM method were both employed in [74] to ensure the reliability and accuracy of the simulation result. It turned out that the two simulation results agreed well with each other based on the authors' setting.
Shin [75] proposed an acceleration technique for FDFD method which can significantly accelerate the convergence of iterative methods for 3D plasmonic systems. The successful application of this specific technique to the real engineering problems, such as designing novel integrated optical circuit components, was demonstrated as well. Wu et al. [76] also used RCWA to simulate the emissivity of a meta-surface as a function of observation angle and wavelength. The localized nature of plasmonic resonances meant that 23 harmonics were used to obtain a convergent result.
RCWA was used in the optical analysis in [11,19,25,76]. In [11], its code was also based on RETICOLO [77] incorporated with a particle swarm optimization (PSO) algorithm [78]. These tools were used to calculate the optical properties of the multi-layer structure as functions of wavelength and incident angle, optimizing material type, layer thickness, and parameters of grating. They had to choose proper number of Fourier terms as a compromise between precision and calculation time. To obtain the necessary Fourier term number for a good convergence, the emissivity as a function of Fourier terms number was plotted for three different wavelengths. Based on the result, later calculations had 50 iterations. A free EM solver for layered periodic structures, denoted the (Stanford stratified structure solver) S4 was employed in [19]. It was a frequency-domain computational electromagnetics tool and implemented RCWA to simulate electromagnetic propagation in 3D structures with 2D periodicity. S4 was also used in [79] to obtain the emittance spectrum of an emitter. RCWA was compared with FEM for photovoltaic devices with periodically corrugated back-reflectors in [80]. The results showed that the convergence rate of the two methods could be very different for p-polarized light but approximately the same for s-polarized light.
The incoherent transfer-matrix method (TMM) simulated the optical properties of a combined material in the infrared range in [25]. For solar wavelengths, RCWA was used because the extracted parameters were inaccurate when the particle size was greater than the incident wavelength. There were some discrepancies near 3 μm and 16 μm. The authors stated that this was mainly because of the absorbance of water during the FTIR measurement. There was also a slight disagreement in some parts of the solar wavelength (0.8–1.6 μm), within which the simulation gave a little bit higher absorptance than what is measured. TMM was also the simulator that defined the proper thickness of each layer in [81].
Hossain et al. [22] created an array of symmetrically conical metamaterial and a finite element method was implemented (in CST Microwave Studio) to calculate the optical properties of this structure. Both TE and TM polarization had identical results due to the axial symmetry of the structure. They calculated the emissivity spectrum for structures of different bottom diameters. Compared to the measured result, the modelled emissivity had lower valleys and higher peaks. CST Microwave Studio was also employed in [21] to understand absorptivity properties. The absorption was polarization-independent due to the four-fold symmetry of their design. After the material was fabricated, the measured and simulated angular absorption were compared. Compared with the modelled result, the measured absorption angle was wider at 8.8 μm but narrower at the 11.3 μm peak. At 4–7 μm, the simulated absorption was generally low for all incident angles while the measured result had a much higher absorption in 0 to 60°. It was explained that this high absorption could have been caused by power loss through the diffraction and excitations of asymmetric modes. As the designed material has a periodicity of 6.9 µm, diffraction could be observed at a higher order in for wavelengths less than 6.9 µm.
FETD was utilized in [82] to simulate the radiative cooling phenomenon. The rigorous radiation boundary condition [82] was discretized using the FETD method. The same scheme was simulated in COMSOL and there was a good agreement between the two results.
DDA was employed in [83] to discretize the volume integral equation for the electric field. The results calculated using DDA were verified against the exact results; the former was found to have accurately predicted both the locations and magnitudes of resonances accurately. Later, DDA was applied to study near-field radiative heat transfer between an infinite plane and a probe of a complex shape. It was also reported that a large dielectric function negatively affected the convergence of DDA by amplifying the shape error. DDA was also applied in [84] to model the near-field radiative heat transfer of arbitrary three-dimensional geometries. The result was verified against the exact result but the convergence and accuracy needed further study.
4.
Discussion
Accuracy is the major concern in such application. The sources of errors in the original computation processes, methods employed to evaluate the accuracy of the simulation result, and possible explanations about the causations of discrepancies are discussed in this section.
There are two major sources of errors in the original computation process. First, inappropriate settings in the simulations, such as mesh size and time step, are main sources of simulation errors. For example, in the simulation of a system tested with regards to different thicknesses and particle sizes, mesh size is an important contributor to a converged result while time step stability and location of light source have much less influence given the range under consideration [9]. Second, the mismatch between physical scale, like the thickness and particle size of the tested sample, and the simulated wavelength range can produce divergent or inaccurate results. Different techniques can be selected for different wavelengths, based on their inherent suitability, to avoid such errors. Zhai et al. [25] have carried out such work. TMM was employed to simulate the material in infrared ranges; in the solar region it was replaced by RCWA, because when wavelengths are less than the size of the particle, some parameters of the material itself become inaccurate and cannot be used anymore.
Three methods have been employed, to date, to evaluate the accuracy of the simulation results. The first is to compare the simulated result with a real measurement. This method was used in [25], when emissivity simulated by TMM and RCWA were compared to the result from the measurement after the sample was manufactured. This is the most straightforward and reliable method, but the manufactured material is not always available in all cases. The second method is to employ multiple techniques and compare the results generated from these simulations. The agreement of these results can ensure the reliability and accuracy of the result. Wu et al. [74] used FDTD and FEM separately to simulate the same sample to determine whether they could lead to the consistent result. This is a very effective way to eliminate the inaccuracy caused by errors in a single technique. The third method is to reproduce the result from an academic paper. As in [68], the simulation employed was validated by reproducing another experiment; if good agreement is observed, the simulation model is regarded to be reliable and it is then applied to predict the properties of the designed structure.
However, discrepancies can appear when the original computation result is compared with result from a reference. Some possible explanations for that are as follows (1) interference of environmental factors during measurements can contribute to the inaccuracies in the measured result. Such interference was reported in [25], when some discrepancies were observed between the simulation and measurement near 3 μm and 16 μm; the author explained that this was mainly because of the absorbance of water during the FTIR measurement; (2) The reaction of the real sample to light in certain wavelengths had not been considered in the material model or simulation settings. This happened in [21], when power loss due to diffraction and excitations of the asymmetric modes caused diffraction of a higher order for wavelengths smaller than the periodicity of the design (6.9 µm) and led to higher absorptance at these wavelengths than the result predicted in the measurement.
5.
Conclusion
This paper has provided an extensive review of the numerical techniques used in EM simulation and their applications in the calculation of the optical properties of daytime radiative cooling. There are many numerical techniques and different types of commercially available software that can be employed to conduct EM simulation for devices that measure daytime radiative cooling. A good numerical method for radiative cooling analysis should be a broadband solution, being capable of accurately dealing with particles and geometries with arbitrary shapes and sizes in the wavelengths of interest. It should to be selected deliberately based on suitability and limitations for a particular project. In academic research, FEM, FDTD, and BEM are generally more popular than other techniques, while FDTD, RCWA, and TMM are the more frequently used tools in radiative cooling research in particular. In an original computation, errors are mainly due to settings used for the simulation and mismatch between the parameters of the sample tested and the wavelength simulated. The accuracy of the computation can be evaluated by comparing its result with real measurements results, those calculated using other techniques, or results from other papers. Discrepancies between the results of original and reference computations can be caused by interference from environmental factors during the measurement or a reaction between the sample and light of certain wavelengths that had not been considered in the simulation settings. Better selection of simulation tools and understanding of their accuracy can be beneficial, because EM simulation is crucial to the success in a wide range of applications including automobiles, communications, medical equipment, renewable energy, and metamaterials.
Conflict of interests
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: