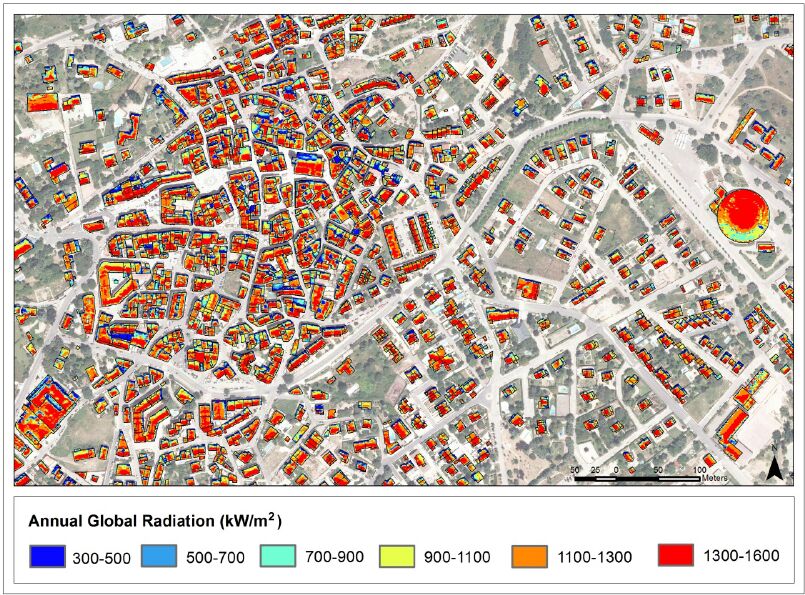
The precise knowledge of the capacity to produce energy from renewable resources requires an adequate study to determine the spatial dimension of the territory. The aim of this paper is to present diverse procedures for the solar potential analysis in urban environments. Models and tools, based on the implementation of geo-information technologies and airborne remote sensing data, have been developed considering a certain level of complexity, where urban structure is composed of different areas characterized by their morphology and function. Before any analysis, establish the available information and define the three-dimensional modeling of the urban environment are the first actions. In addition, techniques for the treatment of data and assess the parameters needed to define the optimal location of solar systems for energy generation, are taken into account. Besides, there is a description of some web services developed to show the results and finally, the advances which may improve the precision and increase the detail degree in these studies.
1.
Introduction
Recently, flight delays at busy airports have caused widespread concern. There are many factors that affect flight delays, including weather, limited resources (i.e., airspace and controllers' workload), and unscientific flight scheduling. Flight scheduling (FS), aims at assigning a set of arrival and departure flights to different runways according to their scheduled time to improve operational efficiency, is one of the most effective ways to reduce number of different planes (i.e., light, medium, and heavy planes) to queue on the runway waiting to take off or land at the same time. Due to the difference in the occupation time of each flight and the waiting time of two adjacent aircraft on the same runway or two independent or dependent runways, such problem is so complex is that civil aviation scientists and engineers need to find the best scheme from the perspective of optimization and simulation. Therefore, this issue has attracted considerable attention in the academic literature recently [1,2,3].
In the real world, a runway incursion may be caused by random events, such as animal intrusion, aircraft or vehicle failure, etc. During an illegal occupation of the runway, aircraft are not allowed to take off or land on the runway. When an incursion event occurs, it is important to predict the incursion time and carry out FS with consideration of incursions (FSI), aiming at minimizing the impact on flight delays. Considering both the location/time of the intrusion and the arrival rate of flights, how to perform scheduling is a new research topic [4]. However, domestic and foreign scholars have paid little attention to this issue.
Another motivation for this study is to study FSI with fuzzy incursion time (FSIFT). In this case, the uncertain occupation time of the runway plays an important role in FS scheduling schemes. Due to the lack of historical and continuous data to evaluate the characteristics of trends in incursion time, it is difficult to obtain the characteristics of random invasion times. With the help of expert knowledge, the characteristics of fuzzy incursion time can be easily analyzed. At present, few existing studies address this issue [5,6].
The primary goal of our research is to present a chance-constrained model with fuzzy parameters for FS with consideration of incursions in order to reveal the optimal relation between the arrival rate of flights and the location and time of the intrusion and delays. The main developments are summarized as follows: 1) optimal coordination of assignment of arrival and departure flights to multiple runways and determination of their actual time by considering how an intrusion might interfere with two adjacent flights covered by a runway; 2) a heuristic-based queuing theory algorithm is proposed to efficiently obtain a set of acceptable solutions. Finally, a case study is used to illustrate the feasibility and effectiveness of the proposed model.
The remainder of the paper is structured as follows. Section 2 reviews and summarizes the related literature both at home and abroad. Section 3 provides the problem description and its mathematical model. Section 4 describes the detail of a novel polynomial algorithm based on queuing theory. A test instance is given to illustrate the applicability and the effectiveness of this study in Section 5. Some critical remarks and possible future developments are discussed in Section 6.
2.
Literature
FS aims at finding an optimal assignment of all flights to different runways [7] to meet some practical constraints, such as safe span time and network flow. The objectives are to balance operational efficiency, safety, fairness, etc. At present, increasing attention has been paid to handling problems with a combination of different objectives and constraints due to practice of FS. In general, these accurate formulations of FS can be abstracted as two classes, i.e., the job shop scheduling model [8,9,10] and the alternative graph model [11]. However, these variants usually do not change the nature of the problem. Aircraft-dependent FS with consideration of delay penalty costs has proven to be an NP-hard problem [11,12]. These approaches can be categorized into two classes: mathematical models and solution methods.
Mathematical models can be divided into two categories: FS with a single runway (FS-SR) [13,14] and FS with multiple runways (FS-MR) [15,16,17,18]. In AADS-MR, if the distance between two adjacent runways is large, they are independent runways, where AADS-MR has an equivalent to FS-SR repeated some operation times [19,20]. If the distance is small in FS-MR, they are runway-dependent, and AADS-MR of interdependent runways should have time deviation between aircraft of flights on separate pairs of runways in FS-SR [8,18]. In FS-SR, any aircraft of arrival or departure flights can take off or land on only one runway. In FS-MR, each runway has a unique operation model, where some runways are only used for taking off or landing and some of them are dedicated to mixed landing and landing aircraft [21]. For instance, Wei etc. [21] revealed the optimal relationship between traffic stream characteristics, operation mode of each runway and flight scheduling to simultaneously minimizing flight delays and maximizing runway utilization. Further, these studies for both FS-SR and FS-MR could be classified as static or dynamic, where static FS schedules landing/departing flights in a static environment to these runways in advance [6,22,23] and dynamic FS reschedules an incomplete set of landing/departing flights in a dynamic environment to runways using the First in First Out (FIFO) rule [11,14,24,25]. For instance, Zhang etc. [25] established an arrival sequencing model was by introducing the concept of alternative approach routes and time-deviation cost.
These approaches can be divided into two categories: exact algorithms [9,15,26,27] and heuristic algorithms. For exact algorithms, standard solvers such as CPLEX are used to solve a mixed-integer programming (MIP) FS problem, but these can only obtain solutions for small/medium instances in a reasonable time. To determine solutions for large instances efficiently, heuristic algorithms are used, which can be further divided into route-building-based heuristics and intelligent algorithms. The former involves dynamic programming [29,30,31,32] and branch- & -price [26,27]. The latter metaheuristics are also often used to contend with FS, including column generation [26,27], Monte-Carlo simulation [6], meta-heuristics [26,27] and genetic algorithms [17,21]. For instance, Liu [17] and Hansen [16] developed a genetic local search (GLS) algorithm for solving the FS with runway dependent attributes; Salehipour etc. [18] designed a hybrid simulated annealing algorithm for resolving FS, and computational results show that it is capable of finding very high quality and comparable solutions for the problems with up to 500 aircrafts and 5 runways in a short time; Bencheikh etc [19] designed a new heuristic for FS with a single runway, and an ant colony algorithm with incorporation of the heuristic to solve FS with the multiple runways; Meng etc [20] designed a novel sliding window algorithm to solve FS, and results are presented for publicly available test problem involving up to 500 aircraft.
However, most of the inexact methods do not consider the characteristics of the problem to narrow the solution search space.
By reviewing the existing literature on the critical issues involved in FS and FSI, some approaches deserve further investigation:
1) Because the aircraft of an arrival flight cannot stay in the air for too long, the scheduling priority of arrival flights is higher than that of departure flights. Actually, there are lots of existing literatures that consider the scheduling priority of arrival flights and departure flights [4]. However, most studies have neglected FSI with consideration of incursions.
2) In FSI, incursion time is an uncertain value, and the use of fuzzy FSI could make it easier to reschedule in practice due to the lack of data to evaluate the characteristics of trends [5,6].
3) FSI is an NP-hard problem. Although heuristic methods are still needed to solve large-scale instances of FSI quickly to find the list of acceptable solutions [21,35], metaheuristic methods are very suitable for this kind of problem.
3.
Methodology
3.1. Research framework
There are multiple runways in an airport. Over a period of time, a set of arrival and departure flights should be assigned to these runways. Each flight has an estimated starting time and occupation time for using a runway. These are related to the type of aircraft (i.e., a light, medium, or heavy plane) and the type of flight (i.e., take-off or landing). These factors also determine the safe span time of two aircraft in a safe operation time. If two flights are assigned to the same runway and they are adjacent in turn, the start time of the former plus its occupation time is less than the start time of the latter, excepting for safe span time. Sometimes an incursion may occur on a certain runway, where flights are not allowed to take off or land at this time. Generally, the start time of an intrusion event is known but the end time is unknown. In view of the lack of historical and continuous data, triangular fuzzy numbers, using the minimum value, involving the most possible value, and the maximum value are used to describe the uncertainty.
To find the optimal relationship between the arrival rate of flights and the location and the time of the intrusion and delays, a fuzzy chance-constrained model based on credibility theory for FSIFT is presented to simultaneously minimize delays in arrival and departure flights. To deal with real-life situations, this study must make several assumptions:
1) The influence of interference between adjacent runways on FS is not considered;
2) A safe span time can be obtained;
3) The influence of the capacity of waypoints on FS is ignored.
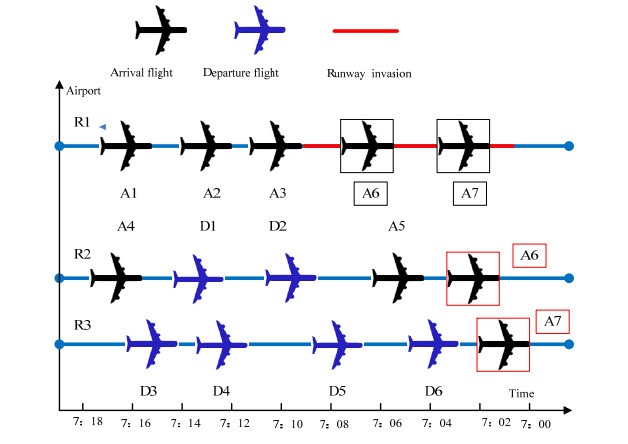
To clarify the basic mechanism of FSI, a small example in Figure 1 aims at assigning seven flights (A1–A7) and six departure flights (D1–D6) to take off or land on three runways (R1–R3). When there is no incursion event at any runway, three flight tasks would be generated in the optimization process, i.e., [A7–A6–A3–A2–A1], [A5–D2–D1–A4], and [D6– D5–D4–D3]. When an incursion occurs in runway R1 between 7:00 and 7:10, three new flight tasks would be generated in the optimization process, i.e., [A3–A2–A1], [A6–A5–D2–D1–A4], and [A7–D6–D5–D4–D3], because runway 1 cannot allow take offs or landings during this time, affecting A7 and A6 in the original flight tasks of R1.
3.2. Model formulation
3.2.1. Notation
To facilitate model presentation, all definitions and notations used hereafter are summarized in Table 1.
3.2.2. Formulation
Using credibility theory, a fuzzy chance-constrained model can be formulated which requires the minimization of:
which is subject to:
In this formulation, the objective function Eq (1) aims at minimizing the total delay time for all arrival flights. The objective function Eq (2) aims at minimizing the total delay time for all departure flights. Constraint Eq (3) guarantees that each flight must be assigned to only one runway. Constraints Eqs (4) and (5) guarantee that the delay of arrival or departure flights does not exceed its maximum value. Constraints Eqs (6) and (7) set that all flights (except virtual flights) served by each runway to have the same incoming and outgoing arcs. Constraint Eq (8) is used for identifying violated subtour elimination constraints. Constraint Eq (9) ensures the safe spacing between aircraft of two adjacent flights. Constraint Eq (10) sets all flights to be prohibited to take off or land within the fuzzy runway's incursion window at a certain level of preference.
Using credibility theory, $ {T}_{r}^{d} $ is a triangular fuzzy number, i.e., $ {T}_{r}^{d} = ({T}_{r}^{d1}, {T}_{r}^{d2}, {T}_{r}^{d3}) $, wherein: $ {T}_{r}^{d1}\le {T}_{r}^{d2}\le {T}_{r}^{d3} $. To satisfy the fuzzy chance constraint Eq (10), the credibility of all flights being prohibited to take off or land within the fuzzy runway's incursion window is defined as follows:
where $ Cr\left\{{T}_{r}^{d}{\le T}_{r}\right\} $ denotes a credibility measure that the fuzzy event holds under the fuzzy metric $ {T}_{r}^{d}{\le T}_{r} $. When α = 1, policymakers are extremely conservative, and the scheduling scheme that considers the worst case of runway incursion is accepted. When α = 0, policymakers are extremely aggressive, and the scheduling schemes under the minimum runway incursion time are accepted and easy to be interrupted.
Definition 1. $Pos$, called as a probability measure, is a set function defined on the power set of a discourse universe $\Gamma $, i.e., $\Pr (\Gamma )$. For any label set (i.e., $I$), if $Pos$ satisfies the following conditions: (i) $Pos(\emptyset ) = 0$, and $Pos(\Gamma ) = 1$; (ii) for any subset $\{ {A_i}|i \in I\} $ of $\Pr (\Gamma )$, $Pos({ \cup _{i \in I}}{A_i}) = {\sup _{i \in I}}Pos({A_i})$.
Definition 2. Let triplet $\{ \Gamma , \Pr (\Gamma ), Pos\} $ be a probability space, and set function $Cr(A) = 0.5(1 + Pos(A) - Pos({A^c}))$ be the credibility measure of event $A$, where ${A^c}$ is the complement of set $A$.
Definition 3. Let triplet $\{ \Gamma , \Pr (\Gamma ), Cr\} $ be a credibility space, and the expectation value of its fuzzy variable $\xi $ is $E[\xi ] = \int_0^\infty {Cr\{ \xi \geqslant r\} } dr - \int_{ - \infty }^0 {Cr\{ \xi \leqslant r\} } dr$.
4.
Heuristic-based queuing algorithm
Since FSI is an NP-hard problem, exact algorithms, such as standard solvers such as CPLEX, cannot be used to resolve large instances efficiently. For heuristic algorithms, although both of route-building-based heuristics and intelligent algorithms are used to obtain solutions for large instances efficiently, the convergence of intelligent algorithms is poor and its solution quality cannot be guaranteed, compared with route-building-based heuristics. Hence, a novel polynomial algorithm based on queuing theory is also proposed to obtain acceptable solutions for large instances efficiently [33,34,35,36].
According to the characteristics of the problem, the scheduling priority of arrival flights is higher than that of departure flights, so this fuzzy chance-constrained problem is a priority multi-objective optimization problem. From each of the target functions, $ \sum _{\forall i\in F}{[t}_{i}^{a}-{t}_{i}^{p}]\to 0 $ decides: 1) $ \left|{t}_{i}^{a}+{t}_{i}^{\mathrm{h}}+{T}_{ij}+\left(1-{z}_{ij}^{r}\right).M-{t}_{j}^{a}\right|\to 0 (i.e., {T}_{ij} = {T}_{ij}^{M}-\mu .({T}_{ij}^{M}-{T}_{ij}^{m}) $; 2) the queue based on a first-come first-served policy. Based on fuzzy credibility theory, the problem is transformed into a deterministic model, and the idea behind the solution to this problem can be considered as follows: at first, arrival flights are allocated to the runways and then departure flights are also assigned on this basis. The details of the heuristic-based queuing algorithm are given below:
Step 1: Set the input of the proposed model, i.e., $ R, {F}_{1} $, $ {F}_{2} $ and $ {T}_{ij}. $ Let $ Server(1:R, [0, +\infty \left]\right) = 0 $
Step 2: Set the parameters of the incursion incident for a runway, i.e., $ {T}_{r}^{s} $ and $ {T}_{r}^{d} $. According to $ Cr\left\{{T}_{r}^{d}{\le T}_{r}\right\}\ge \alpha $ determine $ {T}_{r}^{d} = {Cr}^{-1} $ ($ \alpha $) and $ Server(r, [{T}_{r}^{s}, {{T}_{r}^{s}+T}_{r}^{d}\left]\right) = 1 $.
Step 3: Sort $ {F}_{1} $ and $ {F}_{2} $ respectively according to $ {t}_{i}^{p} $, and let the result be $ {{F}_{1}^{"} = \{{F}_{1}^{"}, {F}_{2}^{"}, \dots , {F}_{\left|{F}_{1}\right|}^{"}\}}^{'} $ and $ {{F}_{2}^{"} = \{{F}_{1}^{"}, {F}_{2}^{"}, \dots , {F}_{\left|{F}_{2}\right|}^{"}\}}^{'} $.
Step 4: Assign an arrival flight $ {\forall i\in F}_{1}^{"} $ to the runway $ \forall r\in R $ and determine $ {t}_{i}^{a} $. Let $ i = 1 $.
Step 4.1: For each flight $ {\forall i\in F}_{1}^{"} $, find the last flight of any runway $ \forall r\in R $, i.e., $ lF\left(r\right) $. According to $ \underset{r}{\mathrm{min}}\{\left|{t}_{lF\left(r\right)}^{a}+{t}_{lF\left(r\right)}^{\mathrm{h}}+{T}_{lF\left(r\right){F}_{i}^{"}}-{t}_{{F}_{i}^{"}}^{p}\right|, Server\left(r, \left[{t}_{{F}_{i}^{"}}^{a}, {t}_{{F}_{i}^{"}}^{a}+{t}_{{F}_{i}^{"}}^{h}\right]\right) = 0, \forall r\in R\} $, determine the assignment of flight $ i $ to runway $ r $, i.e., $ {x}_{i}^{r} $ and $ {t}_{{F}_{i}^{"}}^{a} = \mathrm{m}\mathrm{a}\mathrm{x}({t}_{{F}_{i}^{"}}^{p}, {t}_{lF\left(r\right)}^{a}+{t}_{lF\left(r\right)}^{\mathrm{h}}+{T}_{lF\left(r\right){F}_{i}^{"}}) $.
Step 4.2: For $ {x}_{i}^{r} $ and $ {t}_{{F}_{i}^{"}}^{a} $, let $ Server\left(r, \left[{t}_{{F}_{i}^{"}}^{a}, {t}_{{F}_{i}^{"}}^{a}+{t}_{{F}_{i}^{"}}^{h}\right]\right) = 1 $.
Step 4.3: Let $ i = i+1 $. If $ i\le {|F}_{1}| $, return to Step 4.1; otherwise, the algorithm is terminated to obtain the result.
Step 5: Based on the scheduling of arrival flights, each departure flight $ {\forall i\in F}_{2}^{"} $ is also assigned to the runway $ \forall r\in R $, i.e., determination of $ {x}_{i}^{r} $ and $ {t}_{i}^{a} $. Let $ i = 1 $.
Step 5.1: Similar to Step 4.1, find an optimal runway $ r $ for each departure flight $ {\forall i\in F}_{2}^{"} $, using the rules of $ \underset{r}{\mathrm{min}}\{\left|{t}_{lF\left(r\right)}^{a}+{t}_{lF\left(r\right)}^{\mathrm{h}}+{T}_{lF\left(r\right){F}_{i}^{"}}-{t}_{{F}_{i}^{"}}^{p}\right|, Server\left(r, \left[{t}_{{F}_{i}^{"}}^{a}, {t}_{{F}_{i}^{"}}^{a}+{t}_{{F}_{i}^{"}}^{h}\right]\right) = 0, \forall r\in R\} $, and let $ {x}_{i}^{r} = 1 $ and $ {t}_{{F}_{i}^{"}}^{a} = \mathrm{m}\mathrm{a}\mathrm{x}({t}_{{F}_{i}^{"}}^{p}, {t}_{lF\left(r\right)}^{a}+{t}_{lF\left(r\right)}^{\mathrm{h}}+{T}_{lF\left(r\right){F}_{i}^{"}}) $.
Step 5.2: Let $ Server\left(r, \left[{t}_{{F}_{i}^{"}}^{a}, {t}_{{F}_{i}^{"}}^{a}+{t}_{{F}_{i}^{"}}^{h}\right]\right) = 1 $. Set $ i = i+1 $ . If $ i\le {|F}_{2}| $, return to Step 5.1; otherwise, the algorithm is terminated to obtain the result.
The algorithm complexity is $ o\left({|F}_{1}\right|)+o({|F}_{2}\left|\right) $ and the solution can be obtained in polynomial time.
5.
Numerical example
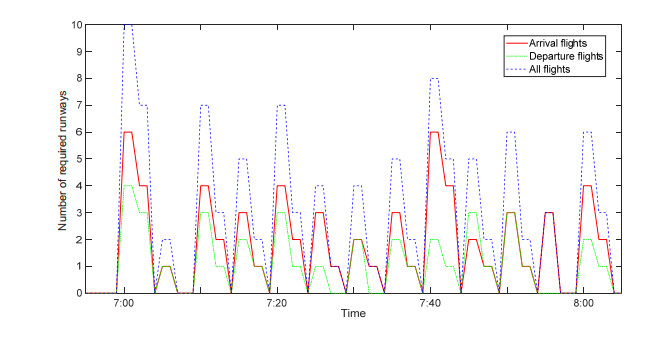
A case study of a real-word example is used to verify the practicality of the model and method. There is a total of 41 arrival flights and 31 departure flights taking off or landing on runways in Beijing Capital International Airport, China, during 7:00 and 8:00 in October 21, 2019. The number of runways required over time is shown in Figure 2. In order for these flights to take off or land according to the planned scheduled time, a maximum of 10 runways and a minimum of 0 runways are required. Therefore, the phenomena of insufficient runway resources and idle runways appear in some periods.
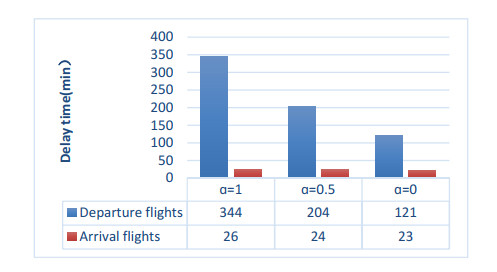
An incursion event occurred on simulated runway 1 at 7:00, and the fuzzy incursion triangle number was (10, 20, 30). When $ \alpha = 1 $, a conservative scheduling scheme that considers the worst case is obtained. To analyze the influence of priority multi-objective optimization on the FSIFT scheduling result, the difference in results between them for different numbers of runways is given in Table 2, from which it can be seen that:
1) As the number of runways increase, the delay time of departure or arrival flights is reduced, resulting in a decrease in the total delay of all flights.
2) For the same number of runways, due to the number of arrival flights being greater than that of departure flights, the delay time in departure or arrival flight of the proposed model is less than that of the traditional model.
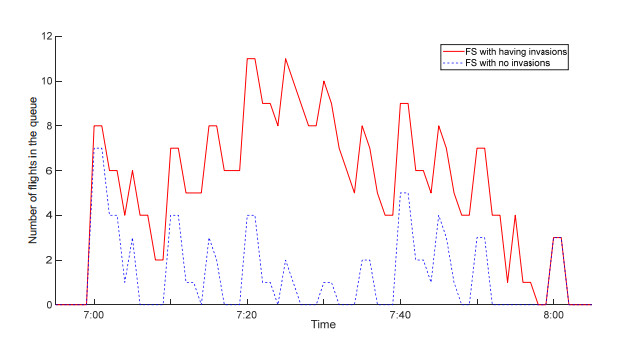
Additionally, the difference in performance of the proposed FS model and traditional model for three runways is displayed in Figure 3. The delay time in departure or arrival flights for the proposed FS approach is better than that of the traditional model. The reason is that runway incursions resulted in reduced runway capacity and increased queues for take-off and landing flights, resulting in flight delays. As shown in Figure 4, the queue length of the improved model at any given time is greater than that of the traditional model, and it takes more time for the queue to dissipate. The result of the calculation is consistent with reality.
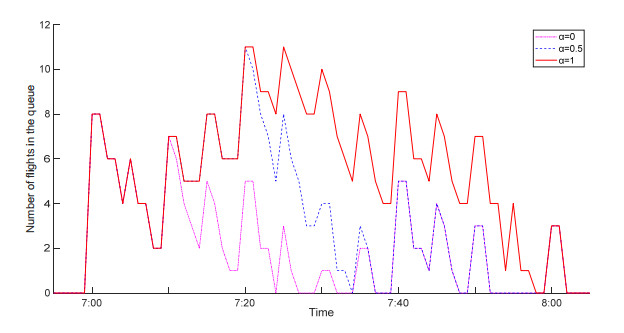
Further, comparing the results of the proposed approach under different preference levels is given in Figure 5. As the preference level $ \alpha $ increases, incursions increase the amount of time spent on available runways, and delays gradually increase. Figure 6 also shows that higher runway incursion times lead to longer queue lengths at any given time, with more dissipation time.
Besides, proposed algorithm is compared with the standard genetic algorithm (GA) and ant colony algorithm (ACO) in order to verify the effectiveness of the algorithm. The core of GA is to code chromosome to assign flights to the runway, and determine the flight take-off and landing sequence according to the flight time. In ACO, the problem is abstracted as a vehicle routing problem, and the solution is constructed by ant traversing different flights. In the three runways of different number of flights, the program was run 50 times. The results are shown in Table 2, from which we can see:
1) As the scale of the test instances increases, proposed algorithm can find a local optimal solution in less than 2 seconds. Because this algorithm is a greedy algorithm, its solution quality is stable.
2) The calculation time and quality of ACO are better than that of GA, but they are worse than proposed algorithm, and the solution quality of ACO and GA decreases rapidly with the increase of problem size. This is because the ACO is to construct the solution, while GA carries out genetic operation on the basis of randomly constructed solution. The problem is extremely complex, which may destroy the solution structure, so the efficiency of GA is poor. To sum up, this algorithm is robust, reliable and efficient.
6.
Conclusions
This study aims at presenting a fuzzy chance-constrained model for FS with consideration of incursions to balance the arrival rate of flights and the location and time of the intrusion and delays. Furthermore, the scheduling priority of arrival flights being higher than that of departure flights is also incorporated into the proposed model in order to represent real-world conditions. A heuristic-based queuing theory algorithm is proposed to obtain efficiently a set of acceptable solutions. The main contributions can be described as follows:
1) As the number of runways increases, the delay time of the arrival flights in this model is better than that of the traditional model, but the delay time of the departure flights in the traditional model is greater than that of this model. With the increase of the number of runways, the total delay time deviation of the two models is gradually reduced.
2) As the preference level α increases, incursions also increase runway occupancy time, resulting in a reduction in the number of aircraft taking off or landing at the runway per hour. Hence, it causes extensive delays to incoming and departing flights.
3) The algorithm proposed in this paper is efficient, stable, and reliable.
However, the premise of the study is that all arrival flights must land at the airport. When an incursion event occurs, even if the scheduling priority of the arrival flight is higher than that of the departure flight, resulting in the queuing time of some arrival flights exceeding their flight time allowed by the remaining fuel, these flights need to choose to make an emergency landing at a nearby airport. Further, IFS with point fusion program is more efficient, compared with the traditional one. Hence, it is worth studying thoroughly the process of extending this model to simultaneously select diverted flights based on point fusion program.
Acknowledgments
This paper is funded by Fundamental Research Funds for the Central Universities of Civil Aviation University of China (3122019126).
Data availability statement
Some or all data, models, or code generated or used during the study are available from the corresponding author by request.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: