1. Introduction

For more than five decades, quasi-two-dimensional structures in the form of quantum semiconductor films (quantum wells) have been intensively studied both theoretically and experimentally ^{[1,2,3,4,5,6,7,8,9,10]}. They very quickly found a variety of instrumental applications and occupy their solid place in modern solid-state electronics ^{[11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]}. Such a wide application of these quasi-two-dimensional quantum structures is mainly due to two factors, the presence of which is fundamentally impossible in a three-dimensional sample. This is the phenomenon of the size quantization of charge carriers in one of the directions of motion ^{[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]} and corresponding to this phenomenon the specificity of the quasi-two-dimensional Fermi distribution of electrons and holes in the film ^{[1,2,29,30,31,32,33,34,35,36,37,38]}. In reality, being a three-dimensional system, a quantum semiconductor film exhibits a number of properties characteristic of 2D systems in the field of multiparticle phenomena (in fact, the two-dimensional nature of the Coulomb coupling in the sample, the two-dimensional dispersion law and the two-dimensional density of states for carriers, etc.).

The object of our consideration in this paper will be precisely questions of the statistics of charge carriers in a quantum semiconductor film. The general questions of the properties of the Fermi-Dirac distribution in a semiconductor film, when dimensional quantization of carriers in one direction takes place are considered in Refs. ^{[1,2,29,30,31,36,37]}. In these papers, the dependence of the chemical potential of the electronic subsystem on the thickness of the film is also considered. The papers ^{[32,33,34,35]} are devoted to the determination of the chemical potential of the electronic subsystem in quasi-two-dimensional systems, and in particular, in quantum semiconductor films.

Chemical potential and internal energy of a noninteracting Fermi gas at low temperature are evaluated using the Sommerfeld method in the fractional-and quasi-two-dimensional spaces in Ref. ^[34]. The effects of low dimensionality on the thermodynamics of a Fermi gas trapped by isotropic power law potentials are analyzed in Ref. ^[38].

Simultaneously it is well known that along with size quantization, one of the powerful external modulating factors is an external homogeneous electrostatic field. In the case of a semiconductor film, the situation where the field is directed along the quantization direction is of greatest physical interest. In this case, the states of the discrete spectrum of charge carriers undergo an additional, field modulation. This leads to a change in the kinetic, optical, and a number of other properties of the semiconductor film ^{[39,40,41,42,43,44]}. Naturally, the external electrostatic field exerts its significant influence also on the statistical properties of a quantum semiconductor film.

In the present paper, the influence of a strong external lateral homogeneous electrostatic field on the statistical properties of the electronic subsystem in a quantum narrow-band semiconductor film is theoretically considered, when a regime of "strong quantization" is realized for charge carriers in a film.

---

2. Single-electron states in the film in the presence of strong electrostatic field

As already noted, in this paper we investigate the case in which a regime of "strong quantization" is realized in a semiconductor film for charge carriers. For this, as is known, at least the following two important physical conditions must be satisfied ^[1,7,43]:

(a) The film thickness (L) must be much less than the Bohr radius of the bulk exciton of the film material (a_ex)

${L^2} \ll a_{ex}^2$

(1)

(b) The distance between the levels of the size quantization $\left( {\Delta {\varepsilon _{n, n + 1}}} \right)$ must significantly exceed the energy of the thermal motion of charge carriers $\left( {{k_B}T} \right)$:

$\Delta {\varepsilon _{n, n + 1}} \gg {k_B}T$

(2)

Here ${k_B}$ is Boltzmann constant and T is the absolute temperature of the sample.

The conditions (1) and (2) dictate the choice of the material under investigation, respectively.

In a number of narrow-gap semiconductors, owing to the large static permittivity and the small effective mass of charge carriers, the Bohr radius of the bulk exciton has a value of the order of several tens of nanometers: PbS (E_g = 0.32 eV) ${{m_e^ * } \mathord{\left/ {\vphantom {{m_e^ * } {{m_0}}}} \right. } {{m_0}}} = 0.04$, a_ex = 20 nm, PbSe (E_g = 0.27 eV) ${{m_e^ * } \mathord{\left/ {\vphantom {{m_e^ * } {{m_0}}}} \right. } {{m_0}}} = 0.08$, a_ex = 47 nm, PbTe (E_g = 0.41 eV) ${{m_e^ * } \mathord{\left/ {\vphantom {{m_e^ * } {{m_0}}}} \right. } {{m_0}}} = 0.04$, a_ex = 150 nm, HgSe (E_g = 0.24 eV) ${{m_e^ * } \mathord{\left/ {\vphantom {{m_e^ * } {{m_0}}}} \right. } {{m_0}}} = 0.016$, a_ex = 52 nm, HgS (E_g = 0.5 eV) ${{m_e^ * } \mathord{\left/ {\vphantom {{m_e^ * } {{m_0}}}} \right. } {{m_0}}} = 0.036$, a_ex = 50 nm, InAs (E_g = 0.354 eV) ${{m_e^ * } \mathord{\left/ {\vphantom {{m_e^ * } {{m_0}}}} \right. } {{m_0}}} = 0.023$, a_ex = 35 nm, InSb (E_g = 0.18 eV) ${{m_e^ * } \mathord{\left/ {\vphantom {{m_e^ * } {{m_0}}}} \right. } {{m_0}}} = 0.014$, a_ex = 60 nm. Here ${m_e^ * } $ is the effective mass of electron, m₀ is the mass of a free electron, E_g is the width of the band gap of a bulk sample (data are taken from Refs. ^{[45,46,47,48]}).

At a film thickness L~10 nm, the condition (1) for such semiconductors begins with sufficient accuracy even at relatively high temperatures, when the temperature of the system T varies, for example, from 100 to 300 K. The energy of the thermal motion of the electrons varies in this case, respectively, in the range from 10 to 25 meV.

We now consider single-particle states in a quantizing film in the presence of a strong transverse electrostatic field. Тhe quantizing film is approximated by the model of an infinitely deep rectangular potential well along the direction of quantization (z) ^[1,7,42]. Such a choice of the form of the model potential of a film is justified by the following physical factors. Firstly, a strong external field creates a deep triangular trap for the particle in the lower part of the well. Secondly, we are interested in the lower levels of quantization. But those levels in this case will be located precisely in the triangular part of the quantum well.

Then, we can write for the potential energy of the electron in the presence of an external electric field $\vec F = \vec F\left( {0;0;F} \right)$ in the film:

$U\left( {z, F} \right) = \left\{ $$\begin{array}{l} \infty ;\;z \le 0, \;z \ge L\\ \left| e \right|Fz;\;0 \le z \le L \end{array}$$ \right.$

(3)

Here e is the charge of an electron, L is the thickness of a film.

In the absence of an external field the energy spectrum of one-electron states in the approximation of an isotropic effective mass, is given by the following expression ^[1,42]:

${\varepsilon _n}\left( {{p_x}, {p_y}} \right) = \frac{{p_x^2 + p_y^2}}{{2m_e^ * }} + \frac{{{\pi ^2}{\hbar ^2}{n^2}}}{{2m_e^ * {L^2}}} \equiv \varepsilon \left( {{p_x}, {p_y}} \right) + {\varepsilon _1}{n^2};\;n = 1, 2, ...$

(4)

Here ${p_x}, {p_y}$ are the components of the quasi-momentum of the particle in the plane of the film.

We regard the external field as strong. Physically, this implies that the energy received by the particle from the field within the film ($\left| e \right|FL$) is much larger than the particle's size quantization energy (${\varepsilon _1}$):

$\left| e \right|FL > > {\varepsilon _1} = {{{\pi ^2}{\hbar ^2}} \mathord{\left/ {\vphantom {{{\pi ^2}{\hbar ^2}} {2m_e^ * {L^2}}}} \right. } {2m_e^ * {L^2}}}$

(5)

It is shown in Ref. ^[42], that the strong-field condition with sufficient accuracy can be written as follows

$\left| e \right|FL \ge 10\varepsilon _1^{}$

(6)

In the case of an InAs film L = 10 nm, we have for ${\varepsilon _1}:{\varepsilon _1} \sim 0.1635$ eV. Accordingly, the condition (6) for the InAs film will be satisfied if the potential difference between the planes of the film is as follows: $\Delta \varphi \ge 1.5$ V.

When the condition (5) is satisfied, the energy spectrum of a particle in a film in the presence of potential Eq 3 can be determined by a variation method ^[42]. Taking into account that it is the lower sub-bands that are important for the manifestation of the quantum size effect, we give the expressions obtained for the first two electronic levels in the film in the presence of a strong electrostatic field:

${\varepsilon _{1, e}}\left( F \right) \simeq 2.345{\left( {\frac{{{\hbar ^2}{e^2}{F^2}}}{{2m_e^ * }}} \right)^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}} = 1.093{\varepsilon _{1, e}}{\left( {\frac{{\left| e \right|FL}}{{{\varepsilon _{1, e}}}}} \right)^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}} \equiv 1.093{\varepsilon _{1, e}}{\eta ^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}}$

(7)

${\varepsilon _{2, e}}\left( F \right) \simeq 4.109{\left( {\frac{{{\hbar ^2}{e^2}{F^2}}}{{2m_e^ * }}} \right)^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}} = 1.931{\varepsilon _{1, e}}{\left( {\frac{{\left| e \right|FL}}{{{\varepsilon _{1, e}}}}} \right)^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}} \equiv 1.931{\varepsilon _{1, e}}{\eta ^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}}$

(8)

Note that the conditions (5) and (6) are, in fact, also the quasi-classical conditions for the potential Eq 3. In view of this circumstance, the energy spectrum of the particle motion in the field (Eq 3) under the conditions (5) and (6) can also be determined from the Bohr-Sommerfeld quantization conditions ^[49]:

$\pi \hbar \left( {l + \frac{3}{4}} \right) = \sqrt {2{m^ * }} \int\limits_0^{{z_0}} {\sqrt {{\varepsilon _l}\left( F \right) - \left| e \right|Fz} } dz;\;\left( {{z_0} = {{{\varepsilon _l}\left( F \right)} \mathord{\left/ {\vphantom {{{\varepsilon _l}\left( F \right)} {\left| e \right|F}}} \right. } {\left| e \right|F}}} \right);$

(9)

Hence we obtain:

${\varepsilon _l}\left( F \right) = {\left[{\frac{3}{2}\frac{{\pi \hbar \left| e \right|F}}{{\sqrt {2{m^ * }} }}\left( {l + \frac{3}{4}} \right)} \right]^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}};\;\;l = 0, 1, 2, ...$

(10)

It is easy to see that both approaches in this case give very similar results. We obtain from the Eq 9:

${\varepsilon _{l = 0}}\left( F \right) = 2.327{\left( {\frac{{{\hbar ^2}{e^2}{F^2}}}{{2{m^ * }}}} \right)^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}};\;\;{\varepsilon _{l = 1}}\left( F \right) = 4.084{\left( {\frac{{{\hbar ^2}{e^2}{F^2}}}{{2{m^ * }}}} \right)^{{1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}}$

(11)

We do not write out the shape of the envelope wave functions, since in the future they will not be needed.

Let us now consider the statistical characteristics of the electron-hole subsystem in a film in the presence of an external field.

All calculations and estimates will be made using the example of an InAs $(m_e^ * \equiv {m_e} = 0.023{m_0}, \;m_{lh}^ * = {m_{lh}} = 0.026{m_0}, \;m_{hh}^ * = {m_{hh}} = 0.41{m_0}, \;\varepsilon _g^{\left( 0 \right)} = 0.354eV)$ quantum film at a film thickness L = 1 nm. In such a sample, the conditions (1) and (2) are satisfied with great accuracy.

The melting temperature of the InAs crystal is equal to ${T_0} = 1215$ K, so that over the entire temperature range of this crystal ($T \in \left[{0, {T_0}} \right]$) this semiconductor is non-degenerate: even when T~1000 K, ${k_B}T = 0.1032eV < {E_g} = 0.354eV.$

We also note that the properties of InAs quantum films are being intensively studied at the present time (for example, ^[49,50]) and the study proposed here is of real interest from this point of view.

---

3. The statistical characteristics of charge carriers in a semiconductor film in the presence of a strong electrostatic field

In the presence of an external field with a strength F for the energy spectrum of an electron in general form, we can now write:

${\varepsilon _n}\left( {\vec p, F} \right) = \frac{{{{\vec p}^2}}}{{2m_e^ * }} + {\varepsilon _n}\left( F \right) = \varepsilon \left( {\vec p} \right) + {\varepsilon _n}\left( F \right) \equiv \varepsilon ;\;\vec p = \vec p\left( {{p_x}, {p_y}, 0} \right)$

(12)

Here the energy ${\varepsilon _n}\left( F \right)$ is given by the Eqs 7–10.

The general form of Fermi-Dirac distribution function for charge carriers in this case is as follows:

$f\left( {{\varepsilon _n}\left( {\vec p, F} \right)} \right) = {\left[{1 + \exp \frac{{{\varepsilon _n}\left( {\vec p, F} \right)-\mu }}{{{k_B}T}}} \right]^{ - 1}}$

(13)

Here $\mu $ is the chemical potential of charge carriers' sub-system.

The effect of size quantization, as already noted, manifests itself most effectively in the conditions when the fewest possible sub-bands are filled. Therefore, we confine ourselves here to considering the filling of only the first two size quantization sub-bands in the presence of an external field.

In the case of the dispersion law from Eq 12, the normalization condition for the distribution function in Eq 13 for electrons and holes is represented in the following forms, respectively:

${N_e} = \sum\limits_{\vec p, {n_e}} {f\left( {{\varepsilon _{{n_e}}}\left( {\vec p, F} \right)} \right);\;\;} {\rho _e} = \frac{{{N_e}}}{V} = \frac{{m_e^ * }}{{\pi {\hbar ^2}L}}\sum\limits_{{n_e}} {\int\limits_{{\varepsilon _{{n_e}}}\left( F \right)}^\infty {\frac{{d{\varepsilon _e}{\kern 1pt} \Theta \left( {{\varepsilon _e} - {\varepsilon _{{n_e}}}\left( F \right)} \right)}}{{1 + \exp \left[{{{\left( {{\varepsilon _e}-\mu } \right)} \mathord{\left/ {\vphantom {{\left( {{\varepsilon _e}-\mu } \right)} {{k_B}T}}} \right. } {{k_B}T}}} \right]}}} } \;\;\;$

(14)

${N_h} = \sum\limits_{\vec p, {n_h}} {f\left( {{\varepsilon _{{n_h}}}\left( {\vec p, F} \right)} \right);\;\;} {\rho _h} = \frac{{{N_h}}}{V} = \frac{{m_h^ * }}{{\pi {\hbar ^2}L}}\sum\limits_{{n_h}} {\int\limits_{{\varepsilon _{{n_h}}}\left( F \right)}^\infty {\frac{{d{\varepsilon _h}{\kern 1pt} \Theta \left( {{\varepsilon _h} - {\varepsilon _{{n_h}}}\left( F \right)} \right)}}{{1 + \exp \left[{{{\left( {\mu-{\varepsilon _h}} \right)} \mathord{\left/ {\vphantom {{\left( {\mu-{\varepsilon _h}} \right)} {{k_B}T}}} \right. } {{k_B}T}}} \right]}}} } \;\;\;$

(15)

Here and below, the index e corresponds to the electronic states, and h to states of the holes, ${N_{e\left( h \right)}}$ is the number of particles, ${\rho _{e\left( h \right)}}$ is the carrier concentration, and $V = SL$ is the volume of the system for area $S$ and thickness $ L$, and $\Theta \left( x \right)$ is the Heaviside step function.

Let us now turn to the calculation of the statistical characteristics of the quasi-two-dimensional sample in question.

---

3.1. Chemical potential and concentration of charge carriers in the film in the presence of external field

We will consider an intrinsic semiconductor with a standard parabolic dispersion law for carriers of the form Eq 12 and confine ourselves to the framework of a simple two-band model.In this case, the splitting of the valence band into bands of heavy (hh) and light (lh) holes will be taken into account. It takes place in the semiconductors cited above, including in InAs.

---

3.1.1. Only the first sub-band of size quantization is filled

As the energy reference point we take the bottom of the first electronic sub-band of size quantization. Then, if only the first sub-band is filled, for the corresponding distribution functions ${f_{e, h}}$ we have:

${f_e}\left( {{\varepsilon _e}} \right) = {\left[{1 + \exp \frac{{{\varepsilon _e}-\mu }}{{{k_B}T}}} \right]^{ - 1}};\;\;{\varepsilon _e} = \frac{{{p^2}}}{{2m_e^ * }}$

(16)

${f_h}\left( {{\varepsilon _h}} \right) = {\left[{1 + \exp \frac{{\mu-{\varepsilon _h}}}{{{k_B}T}}} \right]^{ - 1}};\quad {\varepsilon _h} = - {\varepsilon _{1, e}}\left( F \right) - \varepsilon _g^{\left( 0 \right)} - {\varepsilon _{1, h}}\left( F \right) - \frac{{{p^2}}}{{2m_h^ * }}$

(17)

Here $\varepsilon _g^{\left( 0 \right)}$ is the width of band gap of a bulk sample.

We substitute the distribution functions Eqs 16 and 17 into Eqs 14 and 15, and use after that the electroneutrality condition of the sample:

$ $$\begin{array}{l} \quad \quad \quad \quad \quad \quad \quad \quad \quad {\rho _e} = {\rho _{lh}} + {\rho _{hh}};\\ \left( {{\rho _e} = \frac{{{m_e}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left[{1 + {e^{{{{\mu _1}} \mathord{\left/ {\vphantom {{{\mu _1}} {{k_B}T}}} \right. } {{k_B}T}}}}} \right];\;{\rho _v} = \frac{{{m_v}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left[{1 + \exp \left( {-\frac{{{\mu _1} + \varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, v}}\left( F \right)}}{{{k_B}T}}} \right)} \right]} \right) \end{array}$$ $

(18)

Here $v = lh;hh$, and the index 1 for a chemical potential means that only the first sub-band of size quantization is filled. To determine the chemical potential of charge carriers of a film when only the first sub-band is filled $\left( {{\mu _1}\left( {T, F} \right)} \right)$, we obtain the following equation:

$ $$\begin{array}{l} m_e^ * \ln \left[{1 + \exp \frac{{{\mu _1}}}{{{k_B}T}}} \right] = m_{lh}^ * \ln \left[{1 + \exp \left( {-\frac{{{\mu _1} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, lh}}\left( F \right) + \varepsilon _g^{\left( 0 \right)}}}{{{k_B}T}}} \right)} \right] \\ + m_{hh}^ * \ln \left[{1 + \exp \left( {-\frac{{{\mu _1} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right) + \varepsilon _g^{\left( 0 \right)}}}{{{k_B}T}}} \right)} \right] \end{array}$$ $

(19)

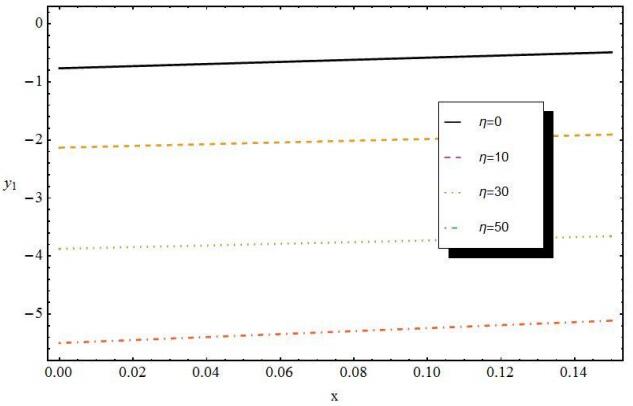
Table 1 lists the values of the chemical potential (in dimensionless units ${y_1} = {{{\mu _1}\left( {T, F} \right)} \mathord{\left/ {\vphantom {{{\mu _1}\left( {T, F} \right)} {\varepsilon _g^{\left( 0 \right)}}}} \right. } {\varepsilon _g^{\left( 0 \right)}}}$) of a narrow-gap InAs semiconductor film for different values of the sample temperature and external field at a film thickness L = 10 nm.

The results are obtained by numerical solution of Eq 19.

As we see, the results of solving Eq 19 clearly show the following:

(a) The chemical potential of the film, when only the first sub-band is filled, in the absence of the field takes its largest absolute negative value at absolute zero.With the increase in temperature ${\mu _1}$ decreasing in modulus, approaches linearly to the zero energy reference level, i.e., to the bottom of the first film sub-band of the conduction band.

(b) Under the influence of an external field the maximum modular value of the chemical potential ${\mu _1}\left( {T, F} \right)$ increases. This is due to the effective broadening of band gap of the sample under the influence of an external field.

(с) At a fixed value of the temperature, the value of the chemical potential is the greater in magnitude, the greater is the intensity of the external field.

(d) In the presence of a field, the chemical potential also increases linearly with increasing the temperature, again approaching the bottom of the conduction band.

Figure 1 shows the graphical dependence ${y_1}\left( T \right) = {{{\mu _1}(T, F)} \mathord{\left/ {\vphantom {{{\mu _1}(T, F)} {\varepsilon _g^{\left( 0 \right)}}}} \right. } {\varepsilon _g^{\left( 0 \right)}}}$ for different values of the external field $\eta = {{eFL} \mathord{\left/ {\vphantom {{eFL} {{\varepsilon _{1, c}}}}} \right. } {{\varepsilon _{1, c}}}}$.

The same results can also be obtained analytically.For this it is necessary to take into account that over the entire temperature range of the existence of the InAs crystal it can be regarded as a nondegenerate semiconductor with great accuracy. Using the approximate formula

$\ln (1 + x){|_{x \ll 1}}\sim x$

(20)

from Eq 19 we arrive to the following analytical expression for the chemical potential:

$ $$\begin{array}{l} {\mu _1}\left( {T, F} \right) = - \frac{{\varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right)}}{2} + \frac{{{k_B}T}}{2}\left\{ {\ln \frac{{{m_{hh}}}}{{{m_e}}} + \frac{{{m_{lh}}}}{{{m_{hh}}}}\exp \left[{-\frac{{{\varepsilon _{1, lh}}\left( F \right)-{\varepsilon _{1, hh}}\left( F \right)}}{{{k_B}T}}} \right]} \right\} \approx \\ -\frac{{\varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right)}}{2} + \frac{{{k_B}T}}{2}\ln \frac{{{m_{hh}}}}{{{m_e}}} \end{array}$$ $

(21)

It is easy to see that for the film thickness L = 10 nm, the results in Table 1 and, accordingly, the graphs of Figure 1 are also obtained from Eq 21. In the intrinsic semiconductor, as is known, the chemical potential of electrons and holes is not a function of the concentration (density) of charge carriers.

However, knowing the chemical potential of the system, it is possible to determine the dependence of the carrier concentration (density) on temperature and in this case, also the dependence on the magnitude of the external field.

Indeed, substituting the value of ${\mu _1}\left( {T, F} \right)$ from Eq 21 into Eq 18, we obtain for the concentration of charge carriers:

$ $$\begin{array}{l} \\ \left. \begin{array}{l} {\rho _{1, e}} = \frac{{{m_e}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left\{ {1 + {{\left( {\frac{{{m_{hh}}}}{{{m_e}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}\exp \left[{-\frac{{\varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right)}}{{2{k_B}T}}} \right]} \right\}\\ {\rho _{1, lh}} = \frac{{{m_{lh}}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left\{ {1 + {{\left( {\frac{{{m_e}}}{{{m_{hh}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}\exp \left[{-\frac{{\varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\varepsilon _{1, lh}}\left( F \right)-{\varepsilon _{1, hh}}\left( F \right)}}{{{k_B}T}}} \right]} \right\}\\ \;{\rho _{1, hh}} = \frac{{{m_{hh}}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left\{ {1 + {{\left( {\frac{{{m_e}}}{{{m_{hh}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}\exp \left[{-\frac{{\varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right)}}{{2{k_B}T}}} \right]} \right\} \end{array}$$ \right\} \end{array}$

(22)

As we see, under the considered conditions and in the approximation Eq 20, the contribution of light holes to the total concentration of positive charge carriers is close to zero, when only the first sub-band of size quantization is filled.

So, if special accuracy is not required, then in calculations one can put:

${\rho _{1, lh}} \approx 0, \;{\rho _{1, e}} = {\rho _{1, hh}} \approx \frac{{\sqrt {{m_e}{m_{hh}}} }}{{\pi {\hbar ^2}L}}{k_B}T\exp \left[{-\frac{{\varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right)}}{{2{k_B}T}}} \right]$

(23)

---

3.1.2. The first and second sub-bands are filled

To determine the chemical potential $\left( {{\mu _2}} \right)$ of the film, when the first and second sub-bands are filled, we now arrive to the following equation (by using Eqs 14, 15 and 18):

$ $$\begin{array}{l} m_e^ * \ln \left\{ {\left[{1 + \exp \frac{{{\mu _2}}}{{{k_B}T}}} \right]\left[{1 + \exp \frac{{{\mu _2}-{\varepsilon _{2, e}}\left( F \right) + {\varepsilon _{1, e}}\left( F \right)}}{{{k_B}T}}} \right]} \right\} = \\ m_{lh}^ * \ln \left\{ {\left[{1 + \exp \left( {-\frac{{{\mu _2} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, lh}}\left( F \right) + \varepsilon _g^{\left( 0 \right)}}}{{{k_B}T}}} \right)} \right]\left[{1 + \exp \left( {-\frac{{{\mu _2} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{2, lh}}\left( F \right) + \varepsilon _g^{\left( 0 \right)}}}{{{k_B}T}}} \right)} \right]} \right\}\\ + m_{hh}^ * \ln \left\{ {\left[{1 + \exp \left( {-\frac{{{\mu _2} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right) + \varepsilon _g^{\left( 0 \right)}}}{{{k_B}T}}} \right)} \right]\left[{1 + \exp \left( {-\frac{{{\mu _2} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{2, hh}}\left( F \right) + \varepsilon _g^{\left( 0 \right)}}}{{{k_B}T}}} \right)} \right]} \right\} \end{array}$$ $

(24)

The numerical solution of this equation leads for to the ${\mu _2}\left( {T, F} \right)$ results that practically coincide with those from Table 1. If we again take advantage of the fact that the semiconductor under consideration is nondegenerate, then we obtain the following equation for ${\mu _2}\left( {T, F} \right)$:

$ $$\begin{array}{l} {\mu _2}\left( {T, F} \right) = - \frac{{\varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}\left( F \right) + {\varepsilon _{1, hh}}\left( F \right)}}{2} + \frac{{{k_B}T}}{2}\ln \frac{{{m_{hh}}}}{{{m_e}}} + \\ \frac{{{k_B}T}}{2}\ln \left[{1 + \exp \left( {-\frac{{{\varepsilon _{2, hh}}\left( F \right)-{\varepsilon _{1, hh}}\left( F \right)}}{{{k_B}T}}} \right) + \frac{{{m_{lh}}}}{{{m_{hh}}}}\exp \left( {-\frac{{{\varepsilon _{1, lh}}\left( F \right) - {\varepsilon _{1, hh}}\left( F \right)}}{{{k_B}T}}} \right)} \right] \end{array}$$ $

(25)

The third term in square brackets can simply be neglected because of its apparent smallness with respect to unity, even in the absence of an external field.

The remaining exponent in the last term makes sense only when F = 0. In the presence of a strong field, this term also tends to zero, i.e., we arrive at the following result:

${\mu _2}\left( {T, F} \right) \sim {\mu _1}\left( {T, F} \right)$

(26)

For carriers' concentrations in the film, when the first and second sub-bands are filled we obtain, respectively:

$\left. $$\begin{array}{l} {\rho _{tot, e}} = {\rho _{1, e}} + {\rho _{2, e}};\;\\ {\rho _{2, e}} = \frac{{{m_e}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left\{ {1 + \sqrt {\frac{{{m_{hh}}}}{{{m_e}}}} \exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\varepsilon _{2, c}}\left( F \right)-{\varepsilon _{1, c}}\left( F \right)}}{{{k_B}T}}} \right]} \right\}\\ {\rho _{tot, lh}} = {\rho _{1, lh}} + {\rho _{2, lh}};\;\\ {\rho _{2, lh}} = \frac{{{m_{lh}}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left\{ {1 + \sqrt {\frac{{{m_e}}}{{{m_{hh}}}}} \exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\varepsilon _{2, lh}}\left( F \right)-{\varepsilon _{1, hh}}\left( F \right)}}{{{k_B}T}}} \right]} \right\}\\ {\rho _{tot, hh}} = {\rho _{1, hh}} + {\rho _{2, hh}};\;\\ {\rho _{2, hh}} = \frac{{{m_{hh}}{k_B}T}}{{\pi {\hbar ^2}L}}\ln \left\{ {1 + \sqrt {\frac{{{m_e}}}{{{m_{hh}}}}} \exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\varepsilon _{2, hh}}\left( F \right)-{\varepsilon _{1, hh}}\left( F \right)}}{{{k_B}T}}} \right]} \right\}\\ \quad \quad \quad \quad \quad \quad {\varepsilon _{g, 1}}(F) = \varepsilon _g^{\left( 0 \right)} + {\varepsilon _{1, e}}(F) + {\varepsilon _{1, hh}}(F) \end{array}$$ \right\}$

(27)

Comparison of the expressions for ${\rho _1}$ and ${\rho _2}$ shows that the concentration of each type of carrier in the second sub-band of size quantization is less than the corresponding concentration in the first sub-band.

---

3.2. Energy and heat capacity of charge carriers in a film in the presence of an external field

For the energy of the system of charge carriers we can write in general form:

$E = \sum\limits_{\vec p, n} {{\varepsilon _n}\left( {\vec p, F} \right)f\left( {{\varepsilon _n}\left( {\vec p, F} \right)} \right)} $

(28)

Here, the particle energy ${\varepsilon _n}\left( {\vec p, F} \right)$ and the distribution function $f\left( {{\varepsilon _n}\left( {\vec p, F} \right)} \right)$ are given by Eqs 12 and 13, respectively.

Let us proceed to a concrete calculation of the energy and heat capacity of charge carriers in a film in the presence of an external field.

---

3.2.1. Only the first sub-band is filled

It was shown above Eq 22 that the concentration of light holes is negligible compared to the concentrations of electrons and heavy holes. Accordingly, we will confine ourselves here to calculating the energy and the heat capacity only for electrons and heavy holes. From Eq 28, taking into account Eqs 7, 8, and 14–17, for the energy (E) and heat capacity (C) of these carriers, we obtain, respectively:

$\left. $$\begin{array}{l} {E_1} \sim {E_{1, e}} + {E_{1, hh}};\;\, {E_{1, e}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{{\left( {{k_B}T} \right)}^2}S}}{{\pi {\hbar ^2}}}\exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}} \right]\\ \\ {E_{1, hh}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}\left( {{k_B}T} \right)S}}{{\pi {\hbar ^2}}}\left[{{\varepsilon _{g, 1}}\left( F \right) + {k_B}T} \right]\exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}} \right] \end{array}$$ \right\}$

(29)

$\left. $$\begin{array}{l} C = {\left( {\frac{{\partial E}}{{\partial T}}} \right)_V};{C_1} \sim {C_{1, e}} + {C_{1, hh}};\;\, {C_{1, e}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{k_B}S}}{{\pi {\hbar ^2}}}\left[{2{k_B}T + \frac{{{\varepsilon _{g, 1}}\left( F \right)}}{2}} \right]\exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}} \right]\\ {C_{1, hh}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{k_B}S}}{{\pi {\hbar ^2}}}\left\{ {{\varepsilon _{g, 1}}\left( F \right) + 2{k_B}T + \frac{{{\varepsilon _{g, 1}}\left( F \right)\left[{{\varepsilon _{g, 1}}\left( F \right) + {k_B}T} \right]}}{{2{k_B}T}}} \right\}\exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}} \right] \end{array}$$ \right\}$

(30)

---

3.2.2. The first and second sub-bands are filled

Using the value of ${\mu _2}(T, F)$ from the Eqs 25 and 26, for the energy and heat capacity of the charge carriers from the second sub-band of size quantization, we get:

$\left. $$\begin{array}{l} {E_{2, e}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}\left( {{k_B}T} \right)S}}{{\pi {\hbar ^2}}}\left[{{\varepsilon _{2, e}}(F)-{\varepsilon _{1, e}}(F) + {k_B}T} \right]\exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\varepsilon _{2, e}}(F)-{\varepsilon _{1, e}}(F)}}{{{k_B}T}}} \right]\\ \\ {E_{2, hh}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}\left( {{k_B}T} \right)S}}{{\pi {\hbar ^2}}}\left[{{\varepsilon _{g, 1}}\left( F \right) + {\varepsilon _{2, hh}}(F)-{\varepsilon _{1, hh}}(F) + {k_B}T} \right] \times \\ \exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\varepsilon _{2, hh}}(F)-{\varepsilon _{1, hh}}(F)}}{{{k_B}T}}} \right] \end{array}$$ \right\}$

(31)

$\left. $$\begin{array}{l} {C_{2, e}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}S{k_B}}}{{\pi {\hbar ^2}}}\left\{ \begin{array}{l} \frac{{\left[{{\varepsilon _{2, e}}(F)-{\varepsilon _{1, e}}(F) + {k_B}T} \right]\left[{{\varepsilon _{g, 1}}\left( F \right) + 2{\varepsilon _{2, e}}(F)-2{\varepsilon _{1, e}}(F)} \right]}}{{2{k_B}T}} + \\ \left[{{\varepsilon _{2, e}}(F)-{\varepsilon _{1, e}}(F) + 2{k_B}T} \right] \end{array}$$ \right\}\\ \times \exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\varepsilon _{2, e}}(F)-{\varepsilon _{1, e}}(F)}}{{{k_B}T}}} \right]\\ \\ {C_{2, hh}} = \frac{{{{\left( {{m_{hh}}{m_e}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}S{k_B}}}{{\pi {\hbar ^2}}}\left\{ $$\begin{array}{l} \frac{{\left[{{\varepsilon _{g, 1}}\left( F \right) + {\Delta _{12, hh}}\left( F \right) + {k_B}T} \right]\left[{{\varepsilon _{g, 1}}\left( F \right) + 2{\Delta _{12, hh}}\left( F \right)} \right]}}{{2{k_B}T}} + \\ \left[{{\varepsilon _{g, 1}}\left( F \right) + {\Delta _{12, hh}}\left( F \right) + 2{k_B}T} \right] \end{array}$$ \right\}\\ \times \exp \left[{-\frac{{{\varepsilon _{g, 1}}\left( F \right)}}{{2{k_B}T}}-\frac{{{\Delta _{12, hh}}\left( F \right)}}{{{k_B}T}}} \right];\;\;\;{\Delta _{12, hh}}\left( F \right) = {\varepsilon _{2, hh}}\left( F \right) - {\varepsilon _{1, hh}}\left( F \right) \end{array} \right\}$

(32)

The total energy and total heat capacity of electrons and holes in the sample will be expressed by the sum of Eqs 29–32, respectively. Let us discuss now the results obtained in this paper.

---

4. Results and discussions

In the quantized film, as it is well known, due to the quantum size effect, an effective broadening of band gap of the sample takes place:

$\varepsilon _g^{\left( 0 \right)} \to {\varepsilon _g}\left( L \right) = \varepsilon _g^{\left( 0 \right)} + \varepsilon _{1, e}^{}\left( L \right) + \varepsilon _{1, v}^{}\left( L \right);\;\, {\Delta _g}\left( L \right) = {\varepsilon _g}\left( L \right) - \varepsilon _g^{\left( 0 \right)} = \varepsilon _{1, e}^{}\left( L \right) + \varepsilon _{1, v}^{}\left( L \right)$

(33)

For a fixed film thickness, under the influence of the external field, there is an additional broadening of band gap of the sample with respect to its previous broadening.

As in the semiconductor InAs, ${m_{hh}} \gg {m_{lh}}$, from the valence band only heavy holes will contribute to this broadening:

${\varepsilon _g}\left( {L, F} \right) - {\varepsilon _g}\left( {L, F = 0} \right) \equiv {\Delta _g}\left( F \right) = \left[{{\varepsilon _{1, c}}\left( F \right)-\varepsilon _{1, c}^{}\left( L \right)} \right] + \left[{{\varepsilon _{1, hh}}\left( F \right)-\varepsilon _{1, hh}^{}(F)} \right]$

(34)

According to Eqs 7, 8, 10 and 11 with the increase in the external field, this broadening increases according to the law у~x^2/3:

${\Delta _g}\left( F \right) \sim {F^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}}$

(35)

As we can see, the action of the external field actually substitutes the process of reducing the thickness of the film. This process naturally has a reasonable technological limit. By superimposing an external field, it becomes possible for a given thickness of the film to vary the energy of the quantized motion of the charge carriers in a controlled manner and, accordingly, to vary the width of the band gap of the sample in a controlled manner.

The chemical potential of a system of electrons and holes depends explicitly on the external field.

According to the Eqs 21, 25 and 26 remaining negative in sign, with the increase in the field it increases in absolute value ($ \sim {F^{{2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}}}$).

Both in the absence and in the presence of an external field, the chemical potential of the electrons and holes decrease by absolute value with the increase in the temperature. In the system under consideration, the contribution of light holes in the statistical characteristics of electrons and holes is negligible.

This is explained by the fact that in the system under consideration, between the first levels of heavy and light holes, there is a significant energy gap (${\Delta _{lh, hh}}(F = 0) = 0.1359eV$) and, in the presence of size quantization, light holes do not participate in the formation of a new forbidden band. Physically, this is quite understandable: the particles tend to occupy the lowest possible energy states, and such are the levels of the size quantization of heavy holes in this case.

We note that in the case of a bulk sample, where the energies of the sub-bands of heavy and light holes in the center of the Brillouin zone coincide, the secondary role of light holes is not so strongly pronounced.

For example, for the chemical potential of a bulk InAs sample, we obtain:

${\mu ^{3D}} \approx - \frac{{\varepsilon _g^{\left( 0 \right)}}}{2} + \frac{{3{k_B}T}}{4}\ln \frac{{{m_{hh}}}}{{{m_e}}} + \frac{{{k_B}T}}{2}\ln \left[{1 + {{\left( {\frac{{{m_{lh}}}}{{{m_{hh}}}}} \right)}^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}} \right]$

(36)

Hence it is clear that in the 3D case the contribution of light holes is not as small as in the quasi-two-dimensional case.

It follows from Eqs 22 and 27 that the concentration of free charge carriers increases with the increase in temperature. At fixed values of the temperature and the external field, the carriers' concentration is maximal for the first sub-band. As the sub-band number increases, the concentration decreases. At a fixed temperature, an increase in the external field leads to a decrease in the concentration of free carriers. This is due to an increase in the width of the band gap under the action of the external field. This makes it possible, by changing the external field, to regulate the concentration of free carriers in the quasi-two-dimensional system under consideration. I.e., with the aid of an external field, we are able to control the degree of population of the sub-bands of the quantized motion of free charge carriers. Since the energy and heat capacity of a system are determined by the number of particles, the concentration behavior mentioned above also determines the behavior of the energy and heat capacity of the system of charge carriers in the film in the presence of an external field.

The contribution of the second sub-band to the energy and heat capacity of electrons and holes is much less (respectively, $\exp \left[{-\frac{{{\varepsilon _{2, e}}\left( F \right)-{\varepsilon _{1, e}}\left( F \right)}}{{2{k_B}T}}} \right]$ and $\exp \left[{-\frac{{{\varepsilon _{2, hh}}\left( F \right)-{\varepsilon _{1, hh}}\left( F \right)}}{{2{k_B}T}}} \right]$ times) than the contribution of the first sub-band.

As we see, the result of the influence of an external strong electric field on the statistical characteristics of a quantum semiconductor film is determined, mainly, by the influence of this field on the first film sub-band.

In particular, as can be seen from Eqs 29–32, the decisive factor for determining the values of the energy and heat capacity of an electron-hole subsystem in a film is the factor $\exp \left[{-{{{\varepsilon _g}\left( {F, L} \right)} \mathord{\left/ {\vphantom {{{\varepsilon _g}\left( {F, L} \right)} {2{k_B}T}}} \right. } {2{k_B}T}}} \right]$. Here ${\varepsilon _g}\left( {F, L} \right)$ is the value of the band gap of the sample, taking into account its effective broadening under the action of size quantization and the external field (see Eqs 7, 8, 33 and 34). It is clear that with increasing of ${\varepsilon _g}\left( {F, L} \right)$ the values of the energy and heat capacity at a given fixed temperature will decrease.

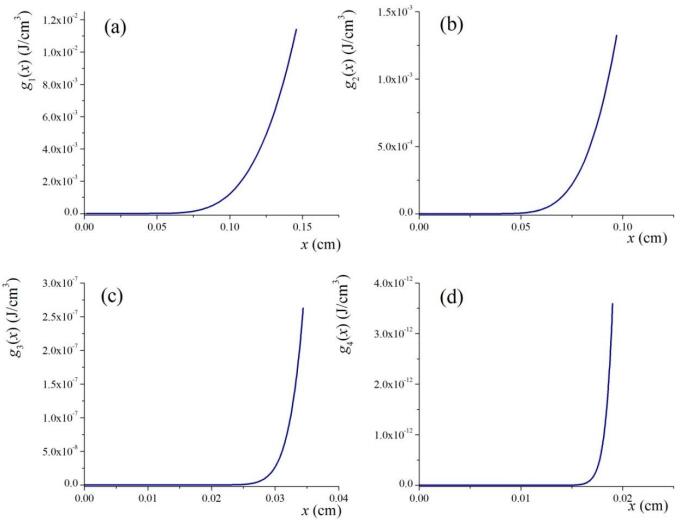
The dependence of the energy of the electron-hole subsystem for the bulk InAs semiconductor (Figure 2a) and for the InAs film (L = 10 nm) in the temperature range from 0 to 600 K for the different values of the external field is shown (Figures 2b–2d).

A similar dependence also holds for the heat capacity of the electron-hole sub-system in a semiconductor film.

In the end, we note that all the calculations and conclusions that have been made are also applicable to semiconductor quasi-two-dimensional structures noted at the beginning of this article.

---

5. Conclusions

In terms of the effect on single-electron states, the presence of an external field makes it possible, for a fixed film thickness and a certain temperature, to obtain for the charge carriers energies unattainable by reducing the film thickness. Simultaneously, by using an external field, the position of the size quantization levels can be moved in a controlled manner.

In terms of the effect on the thermodynamic properties of the electron-hole subsystem, the presence of an external field makes it possible to vary the width of the forbidden band of the sample in a controlled manner. That is, an external strong electrostatic field makes it possible to control the values of such fundamental quantities of a system of free charge carriers in a film as their concentration, energy and heat capacity.

---

Acknowledgments

The author wants to express their gratitude to David Hayrapetyan and Vram Mughnetsyan for helping in numerical calculations.

---

Conflict of interest

Тhere is no conflict of interest

---