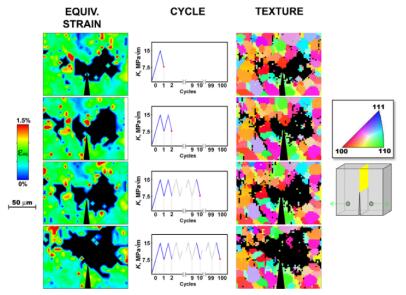
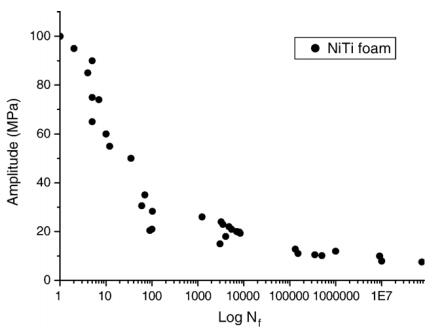
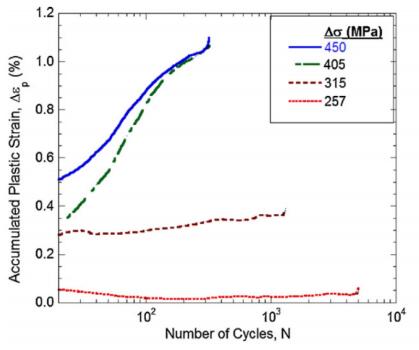
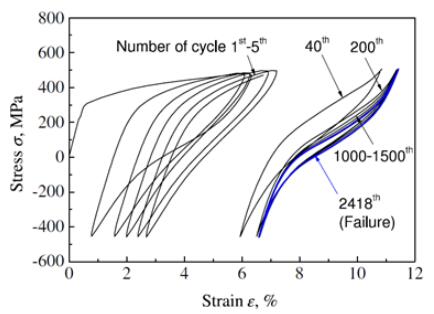
|
[1]
|
Huang WM, Ding Z, Wang CC, et al. (2010) Shape memory materials. Mater Today 13: 54–61.
|
|
[2]
|
Ji F, Zhu Y, Hu J, et al. (2006) Smart polymer fibers with shape memory effect. Smart Mater Struct 15: 1547. doi: 10.1088/0964-1726/15/6/006

|
|
[3]
|
Petrini L, Migliavacca F (2011) Biomedical applications of shape memory alloys. J Metall 2011: 1–14.
|
|
[4]
|
Cho JW, Kim JW, Jung YC, et al. (2005) Electroactive shape-memory polyurethane composites incorporating carbon nanotubes. Macromol Rapid Commun 26: 412–416. doi: 10.1002/marc.200400492

|
|
[5]
|
Lendlein A, Jiang H, Junger O, et al. (2005) Light-induced shape-memory polymers. Nature 434: 879–882. doi: 10.1038/nature03496

|
|
[6]
|
Lendlein A, Schmidt AM, Schroeter M, et al. (2005) Shape-memory polymer networks from oligo (ϵ-caprolactone) dimethacrylates. J Polym Sci, Part A: Polym Chem 43: 1369–1381. doi: 10.1002/pola.20598

|
|
[7]
|
Tzou H, Lee HJ, Arnold S (2004) Smart materials, precision sensors/actuators, smart structures, and structronic systems. Mech Adv Mater Struct 11: 367–393. doi: 10.1080/15376490490451552

|
|
[8]
|
Behl M, Lendlein A (2007) Shape-memory polymers. Mater Today 10: 20–28.
|
|
[9]
|
Wei Z, Sandstroröm R, Miyazaki S (1998) Shape-memory materials and hybrid composites for smart systems: Part I Shape-memory materials. J Mater Sci 33: 3743–3762. doi: 10.1023/A:1004692329247

|
|
[10]
|
El Feninat F, Laroche G, Fiset M, et al. (2002) Shape memory materials for biomedical applications. Adv Eng Mater 4: 91. doi: 10.1002/1527-2648(200203)4:3<91::AID-ADEM91>3.0.CO;2-B

|
|
[11]
|
Hornbogen E (2006) Comparison of shape memory metals and polymers. Adv Eng Mater 8: 101–106. doi: 10.1002/adem.200500193

|
|
[12]
|
Gunes IS, Jana SC (2008) Shape memory polymers and their nanocomposites: A review of science and technology of new multifunctional materials. J Nanosci Nanotechnol 8: 1616–1637. doi: 10.1166/jnn.2008.038

|
|
[13]
|
Ma J, Karaman I, Noebe RD (2010) High temperature shape memory alloys. Int Mater Rev 55: 257–315. doi: 10.1179/095066010X12646898728363

|
|
[14]
|
Tsuchiya K (2011) Mechanisms and properties of shape memory effect and superelasticity in alloys and other materials: A practical guide, In: Shape Memory and Superelastic Alloys, Woodhead Publishing, 3–14.
|
|
[15]
|
Leng J, Lan X, Liu Y, et al. (2011) Shape-memory polymers and their composites: Stimulus methods and applications. Prog Mater Sci 56: 1077–1135. doi: 10.1016/j.pmatsci.2011.03.001

|
|
[16]
|
Rousseau IA (2008) Challenges of shape memory polymers: A review of the progress toward overcoming SMP's limitations. Polym Eng Sci 48: 2075–2089. doi: 10.1002/pen.21213

|
|
[17]
|
Es-Souni M, Fischer-Brandies H (2005) Assessing the biocompatibility of NiTi shape memory alloys used for medical applications. Anal Bioanal Chem 381: 557–567. doi: 10.1007/s00216-004-2888-3

|
|
[18]
|
Geetha M, Singh A, Asokamani R, et al. (2009) Ti based biomaterials, the ultimate choice for orthopaedic implants-a review. Prog Mater Sci 54: 397–425. doi: 10.1016/j.pmatsci.2008.06.004

|
|
[19]
|
De Nardo L, Bertoldi S, Tanzi M, et al. (2011) Shape memory polymer cellular solid design for medical applications. Smart Mater Struct 20: 035004. doi: 10.1088/0964-1726/20/3/035004

|
|
[20]
|
Robertson S, Pelton A, Ritchie R (2012) Mechanical fatigue and fracture of Nitinol. Int Mater Rev 57: 1–37. doi: 10.1179/1743280411Y.0000000009

|
|
[21]
|
Schroeder T, Wayman C (1977) The two-way shape memory effect and other "training" phenomena in Cu-Zn single crystals. Scr Metall 11: 225–230.
|
|
[22]
|
Perkins J, Hodgson D (1990) The two-way shape memory effect. Eng Aspects Shape Mem Alloys 1990: 195–206.
|
|
[23]
|
Huang W, Toh W (2000) Training two-way shape memory alloy by reheat treatment. J Mater Sci Lett 19: 1549–1550. doi: 10.1023/A:1006721022185

|
|
[24]
|
Otsuka K, Ren X (2005) Physical metallurgy of Ti-Ni-based shape memory alloys. Prog Mater Sci 50: 511–678. doi: 10.1016/j.pmatsci.2004.10.001

|
|
[25]
|
Huang W (2002) On the selection of shape memory alloys for actuators. Mater Des 23: 11–19. doi: 10.1016/S0261-3069(01)00039-5

|
|
[26]
|
Huang WM, Song CL, Fu YQ, et al. (2013) Shaping tissue with shape memory materials. Adv Drug Delivery Rev 65: 515–535. doi: 10.1016/j.addr.2012.06.004

|
|
[27]
|
Carroll MC, Somsen C, Eggeler G (2004) Multiple-step martensitic transformations in Ni-rich NiTi shape memory alloys. Scr Mater 50: 187–192. doi: 10.1016/j.scriptamat.2003.09.020

|
|
[28]
|
Zhou Y, Fan G, Zhang J, et al. (2006) Understanding of multi-stage R-phase transformation in aged Ni-rich Ti-Ni shape memory alloys. Mater Sci Eng A S438–440: 602–607.
|
|
[29]
|
Fujishima K, Nishida M, Morizono Y, et al. (2006) Effect of heat treatment atmosphere on the multistage martensitic transformation in aged Ni-rich Ti-Ni alloys. Mater Sci Eng A 438: 489–494.
|
|
[30]
|
Khalil-Allafi J, Dlouhy A, Eggeler G (2002) Ni4Ti3-precipitation during aging of NiTi shape memory alloys and its influence on martensitic phase transformations. Acta Mater 50: 4255–4274. doi: 10.1016/S1359-6454(02)00257-4

|
|
[31]
|
Wagner MFX, Dey SR, Gugel H, et al. (2010) Effect of low-temperature precipitation on the transformation characteristics of Ni-rich NiTi shape memory alloys during thermal cycling. Intermetallics 18: 1172–1179. doi: 10.1016/j.intermet.2010.02.048

|
|
[32]
|
Kim JI, Liu Y, Miyazaki S (2004) Ageing-induced two-stage R-phase transformation in Ti-50.9at.%Ni. Acta Mater 52: 487–499.
|
|
[33]
|
Qin Q, Peng H, Fan Q, et al. (2018) Effect of second phase precipitation on martensitic transformation and hardness in highly Ni-rich NiTi alloys. J Alloys Compd 739: 873–881. doi: 10.1016/j.jallcom.2017.12.128

|
|
[34]
|
Luo J, Bobanga JO, Lewandowski JJ (2017) Microstructural heterogeneity and texture of as-received, vacuum arc-cast, extruded, and re-extruded NiTi shape memory alloy. J Alloys Compd 712: 494–509. doi: 10.1016/j.jallcom.2017.04.152

|
|
[35]
|
Luo J, Ye WJ, Ma XX, et al. (2018) The evolution and effects of second phase particles during hot extrusion and re-extrusion of a NiTi shape memory alloy. J Alloys Compd 735: 1145–1151. doi: 10.1016/j.jallcom.2017.11.133

|
|
[36]
|
Jani JM, Leary M, Subic A, et al. (2014) A review of shape memory alloy research, applications and opportunities. Mater Des 56: 1078–1113. doi: 10.1016/j.matdes.2013.11.084

|
|
[37]
|
Maruyama T, Kubo H (2011) 12-Ferrous (Fe-based) shape memory alloys (SMAs): Properties, processing and applications, In: Shape Memory and Superelastic Alloys, Woodhead Publishing, 141–159.
|
|
[38]
|
Yamauchi K (2011) 3-Development and commercialization of titanium-nickel (Ti-Ni) and copper (Cu)-based shape memory alloys (SMAs), In: Shape Memory and Superelastic Alloys, Woodhead Publishing, 43–52.
|
|
[39]
|
Wadood A (2016) Brief overview on nitinol as biomaterial. Adv Mater Sci Eng 2016: 1–9.
|
|
[40]
|
Buehler WJ, Wang FE (1968) A summary of recent research on the nitinol alloys and their potential application in ocean engineering. Ocean Eng 1: 105–120. doi: 10.1016/0029-8018(68)90019-X

|
|
[41]
|
Dikici B, Esen Z, Duygulu O, et al. (2015) Corrosion of metallic biomaterials, In: Advances in Metallic Biomaterials, Springer, 275–303.
|
|
[42]
|
Mantovani D (2000) Shape memory alloys: Properties and biomedical applications. JOM 52: 36–44.
|
|
[43]
|
Ryhänen J, Kallioinen M, Tuukkanen J, et al. (1998) In vivo biocompatibility evaluation of nickel-titanium shape memory metal alloy: Muscle and perineural tissue responses and encapsule membrane thickness. J Biomed Mater Res 41: 481–488. doi: 10.1002/(SICI)1097-4636(19980905)41:3<481::AID-JBM19>3.0.CO;2-L

|
|
[44]
|
Duerig T, Pelton A, Stöckel D (1999) An overview of nitinol medical applications. Mater Sci Eng A 273: 149–160.
|
|
[45]
|
Morgan N (2004) Medical shape memory alloy applications-the market and its products. Mater Sci Eng A 378: 16–23. doi: 10.1016/j.msea.2003.10.326

|
|
[46]
|
Dahlgren JM, Gelbart D (2009) System for mechanical adjustment of medical implants. Google Patents.
|
|
[47]
|
Pfeifer R, Müller CW, Hurschler C, et al. (2013) Adaptable orthopedic shape memory implants. Procedia Cirp 5: 253–258. doi: 10.1016/j.procir.2013.01.050

|
|
[48]
|
Maynard RS (1999) Distributed activator for a two-dimensional shape memory alloy. Google Patents.
|
|
[49]
|
Zider RB, Krumme JF (1988) Eyeglass frame including shape-memory elements. Google Patents.
|
|
[50]
|
Lim G, Park K, Sugihara M, et al. (1996) Future of active catheters. Sens Actuators A 56: 113–121. doi: 10.1016/0924-4247(96)01279-4

|
|
[51]
|
Tung AT, Park BH, Liang DH, et al. (2008) Laser-machined shape memory alloy sensors for position feedback in active catheters. Sens Actuators A 147: 83–92. doi: 10.1016/j.sna.2008.03.024

|
|
[52]
|
Pelton A, Schroeder V, Mitchell M, et al. (2008) Fatigue and durability of Nitinol stents. J Mech Behav Biomed Mater 1: 153–164. doi: 10.1016/j.jmbbm.2007.08.001

|
|
[53]
|
Dye D (2015) Shape memory alloys: Towards practical actuators. Nat Mater 14: 760–761. doi: 10.1038/nmat4362

|
|
[54]
|
Ogawa Y, Ando D, Sutou Y, et al. (2016) A lightweight shape-memory magnesium alloy. Science 353: 368. doi: 10.1126/science.aaf6524

|
|
[55]
|
Schone AC, Schulz B, Lendlein A (2016) Stimuli responsive and multifunctional polymers: progress in materials and applications. Macromol Rapid Commun 37: 1856–1859. doi: 10.1002/marc.201600650

|
|
[56]
|
Cao Y, Xu S, Li L, et al. (2017) Physically cross-linked networks of POSS-capped poly(acrylate amide)s: Synthesis, morphologies, and shape memory behavior. J Polym Sci, Part B: Polym Phys 55: 587–600. doi: 10.1002/polb.24303

|
|
[57]
|
Momtaz M, Razavi-Nouri M, Barikani M (2014) Effect of block ratio and strain amplitude on thermal, structural, and shape memory properties of segmented polycaprolactone-based polyurethanes. J Mater Sci 49: 7575–7584. doi: 10.1007/s10853-014-8466-y

|
|
[58]
|
Momtaz M, Barikani M, Razavi-Nouri M (2015) Effect of ionic group content on thermal and structural properties of polycaprolactone-based shape memory polyurethane ionomers. Iran Polym J 24: 505–513. doi: 10.1007/s13726-015-0341-4

|
|
[59]
|
Saed MO, Torbati AH, Starr CA, et al. (2017) Thiol-acrylate main-chain liquid-crystalline elastomers with tunable thermomechanical properties and actuation strain. J Polym Sci, Part B: Polym Phys 55: 157–168. doi: 10.1002/polb.24249

|
|
[60]
|
Yang B, Huang WM, Li C, et al. (2006) Effects of moisture on the thermomechanical properties of a polyurethane shape memory polymer. Polymer 47: 1348–1356. doi: 10.1016/j.polymer.2005.12.051

|
|
[61]
|
Gyarmati B, Mészár EZ, Kiss L, et al. (2015) Supermacroporous chemically cross-linked poly(aspartic acid) hydrogels. Acta Biomater 22: 32–38. doi: 10.1016/j.actbio.2015.04.033

|
|
[62]
|
Guo W, Lu CH, Orbach R, et al. (2015) pH-stimulated DNA hydrogels exhibiting shape-memory properties. Adv Mater 27: 73–78. doi: 10.1002/adma.201403702

|
|
[63]
|
Xie H, He MJ, Deng XY, et al. (2016) Design of poly(l-lactide)-poly(ethylene glycol) copolymer with light-induced shape-memory effect triggered by pendant anthracene groups. ACS Appl Mater Interfaces 8: 9431–9439. doi: 10.1021/acsami.6b00704

|
|
[64]
|
Park J, Yoo JW, Seo HW, et al. (2017) Electrically controllable twisted-coiled artificial muscle actuators using surface-modified polyester fibers. Smart Mater Struct 26: 035048. doi: 10.1088/1361-665X/aa5323

|
|
[65]
|
Zou H, Weder C, Simon YC (2015) Shape-Memory Polyurethane Nanocomposites with Single Layer or Bilayer Oleic Acid-Coated Fe3O4 Nanoparticles. Macromol Mater Eng 300: 885–892. doi: 10.1002/mame.201500079

|
|
[66]
|
Voit W, Ware T, Gall K (2010) Radiation crosslinked shape-memory polymers. Polymer 51: 3551–3559. doi: 10.1016/j.polymer.2010.05.049

|
|
[67]
|
Small Iv W, Wilson T, Benett W, et al. (2005) Laser-activated shape memory polymer intravascular thrombectomy device. Opt Express 13: 8204–8213. doi: 10.1364/OPEX.13.008204

|
|
[68]
|
Zhang F, Zhou T, Liu Y, et al. (2015) Microwave synthesis and actuation of shape memory polycaprolactone foams with high speed. Sci Rep 5: 11152. doi: 10.1038/srep11152

|
|
[69]
|
Du H, Song Z, Wang J, et al. (2015) Microwave-induced shape-memory effect of silicon carbide/poly(vinyl alcohol) composite. Sens Actuators A 228: 1–8. doi: 10.1016/j.sna.2015.01.012

|
|
[70]
|
Fang Y, Ni Y, Leo SY, et al. (2015) Reconfigurable photonic crystals enabled by pressure-responsive shape-memory polymers. Nat Commun 6: 7416. doi: 10.1038/ncomms8416

|
|
[71]
|
Fang Y, Ni Y, Choi B, et al. (2015) Chromogenic photonic crystals enabled by novel vapor-responsive shape-memory polymers. Adv Mater 27: 3696–3704. doi: 10.1002/adma.201500835

|
|
[72]
|
Hu J, Zhu Y, Huang H, et al. (2012) Recent advances in shape-memory polymers: Structure, mechanism, functionality, modeling and applications. Prog Polym Sci 37: 1720–1763. doi: 10.1016/j.progpolymsci.2012.06.001

|
|
[73]
|
Liu C, Qin H, Mather P (2007) Review of progress in shape-memory polymers. J Mater Chem 17: 1543–1558. doi: 10.1039/b615954k

|
|
[74]
|
Ahn Sk, Kasi RM (2011) Exploiting microphase-separated morphologies of side-chain liquid crystalline polymer networks for triple shape memory properties. Adv Funct Mater 21: 4543–4549. doi: 10.1002/adfm.201101369

|
|
[75]
|
Luo X, Mather PT (2010) Triple-shape polymeric composites (TSPCs). Adv Funct Mater 20: 2649–2656. doi: 10.1002/adfm.201000052

|
|
[76]
|
Wang L, Yang X, Chen H, et al. (2013) Design of triple-shape memory polyurethane with photo-cross-linking of cinnamon groups. ACS Appl Mater Interfaces 5: 10520–10528. doi: 10.1021/am402091m

|
|
[77]
|
Wang L, Yang X, Chen H, et al. (2013) Multi-stimuli sensitive shape memory poly(vinyl alcohol)-graft-polyurethane. Polym Chem 4: 4461–4468. doi: 10.1039/c3py00519d

|
|
[78]
|
Wang L, Wang W, Di S, et al. (2014) Silver-coordination polymer network combining antibacterial action and shape memory capabilities. RSC Adv 4: 32276–32282. doi: 10.1039/C4RA03829K

|
|
[79]
|
Behl M, Kratz K, Zotzmann J, et al. (2013) Reversible bidirectional shape-memory polymers. Adv Mater 25: 4466–4469. doi: 10.1002/adma.201300880

|
|
[80]
|
Zhou J, Turner SA, Brosnan SM, et al. (2014) Shapeshifting: Reversible shape memory in semicrystalline elastomers. Macromolecules 47: 1768–1776. doi: 10.1021/ma4023185

|
|
[81]
|
Miaudet P, Derré A, Maugey M, et al. (2007) Shape and temperature memory of nanocomposites with broadened glass transition. Science 318: 1294–1296. doi: 10.1126/science.1145593

|
|
[82]
|
Behl M, Kratz K, Noechel U, et al. (2013) Temperature-memory polymer actuators. Proc Natl Acad Sci 110: 12555–12559. doi: 10.1073/pnas.1301895110

|
|
[83]
|
Wang L, Di S, Wang W, et al. (2014) Tunable temperature memory effect of photo-cross-linked star PCL-PEG networks. Macromolecules 47: 1828–1836. doi: 10.1021/ma4023229

|
|
[84]
|
Hu J (2007) Shape memory textiles, In: Shape Memory Polymers and Textiles, Woodhead Publishing, 305–337.
|
|
[85]
|
Yanju L, Haiyang D, Liwu L, et al. (2014) Shape memory polymers and their composites in aerospace applications: A review. Smart Mater Struct 23: 023001. doi: 10.1088/0964-1726/23/2/023001

|
|
[86]
|
Baudis S, Behl M, Lendlein A (2014) Smart polymers for biomedical applications. Macromol Chem Phys 215: 2399–2402. doi: 10.1002/macp.201400561

|
|
[87]
|
Wache HM, Tartakowska DJ, Hentrich A, et al. (2003) Development of a polymer stent with shape memory effect as a drug delivery system. J Mater Sci Mater Med 14: 109–112.
|
|
[88]
|
Small W, Buckley PR, Wilson TS, et al. (2007) Shape memory polymer stent with expandable foam: A new concept for endovascular embolization of fusiform aneurysms. IEEE Trans Biomed Eng 54: 1157–1160. doi: 10.1109/TBME.2006.889771

|
|
[89]
|
Zheng Y, Li Y, Hu X, et al. (2017) Biocompatible shape memory blend for self-expandable stents with potential biomedical applications. ACS Appl Mater Interfaces 9: 13988. doi: 10.1021/acsami.7b04808

|
|
[90]
|
Kularatne RS, Kim H, Boothby JM, et al. (2017) Liquid crystal elastomer actuators: Synthesis, alignment, and applications. J Polym Sci, Part B: Polym Phys 55: 395–411.
|
|
[91]
|
Zhang Y, Gao H, Wang H, et al. (2018) Radiopaque highly stiff and tough shape memory hydrogel microcoils for permanent embolization of arteries. Adv Funct Mater 28: 1705962. doi: 10.1002/adfm.201705962

|
|
[92]
|
Hager MD, Bode S, Weber C, et al. (2015) Shape memory polymers: Past, present and future developments. Prog Polym Sci 49: 3–33.
|
|
[93]
|
Kratz K, Voigt U, Lendlein A (2012) Temperature-memory effect of copolyesterurethanes and their application potential in minimally invasive medical technologies. Adv Funct Mater 22: 3057–3065. doi: 10.1002/adfm.201200211

|
|
[94]
|
Serrano MC, Ameer GA (2012) Recent insights into the biomedical applications of shape-memory polymers. Macromol Biosci 12: 1156–1171. doi: 10.1002/mabi.201200097

|
|
[95]
|
Small W, Singhal P, Wilson TS, et al. (2010) Biomedical applications of thermally activated shape memory polymers. J Mater Chem 20: 3356–3366. doi: 10.1039/b923717h

|
|
[96]
|
Lendlein A, Langer R (2002) Biodegradable, elastic shape-memory polymers for potential biomedical applications. Science 296: 1673–1676. doi: 10.1126/science.1066102

|
|
[97]
|
Wischke C, Neffe AT, Steuer S, et al. (2009) Evaluation of a degradable shape-memory polymer network as matrix for controlled drug release. J Controlled Release 138: 243–250. doi: 10.1016/j.jconrel.2009.05.027

|
|
[98]
|
Balk M, Behl M, Wischke C, et al. (2016) Recent advances in degradable lactide-based shape-memory polymers. Adv Drug Delivery Rev 107: 136–152. doi: 10.1016/j.addr.2016.05.012

|
|
[99]
|
Yu K, Ritchie A, Mao Y, et al. (2015) Controlled sequential shape changing components by 3D printing of shape memory polymer multimaterials. Procedia Iutam 12: 193–203. doi: 10.1016/j.piutam.2014.12.021

|
|
[100]
|
Hardy JG, Palma M, Wind SJ, et al. (2016) Responsive biomaterials: Advances in materials based on shape-memory polymers. Adv Mater 28: 5717–5724. doi: 10.1002/adma.201505417

|
|
[101]
|
Chan BQY, Low ZWK, Heng SJW, et al. (2016) Recent advances in shape memory soft materials for biomedical applications. ACS Appl Mater Interfaces 8: 10070–10087. doi: 10.1021/acsami.6b01295

|
|
[102]
|
Mazza E, Ehret AE (2015) Mechanical biocompatibility of highly deformable biomedical materials. J Mech Behav Biomed Mater 48: 100–124. doi: 10.1016/j.jmbbm.2015.03.023

|
|
[103]
|
Niinomi M, Nakai M, Hieda J (2012) Development of new metallic alloys for biomedical applications. Acta Biomater 8: 3888–3903. doi: 10.1016/j.actbio.2012.06.037

|
|
[104]
|
Niinomi M (2010) Tend and present state of titanium alloys with body centered structure for biomedical applications. Bull Iron Steel Inst Jpn 15: 661–670.
|
|
[105]
|
Tane M, Akita S, Nakano T, et al. (2008) Peculiar elastic behavior of Ti-Nb-Ta-Zr single crystals. Acta Mater 56: 2856–2863. doi: 10.1016/j.actamat.2008.02.017

|
|
[106]
|
Sadrnezhaad SK, Hosseini SA (2009) Fabrication of porous NiTi-shape memory alloy objects by partially hydrided titanium powder for biomedical applications. Mater Des 30: 4483–4487. doi: 10.1016/j.matdes.2009.05.034

|
|
[107]
|
Xiong J, Li Y, Wang X, et al. (2008) Titanium-nickel shape memory alloy foams for bone tissue engineering. J Mech Behav Biomed Mater 1: 269–273. doi: 10.1016/j.jmbbm.2007.09.003

|
|
[108]
|
Oh IH, Nomura N, Hanada S (2002) Microstructures and mechanical properties of porous titanium compacts prepared by powder sintering. Mater Trans 43: 443–446. doi: 10.2320/matertrans.43.443

|
|
[109]
|
Wang M, Jiang M, Liao G, et al. (2012) Martensitic transformation involved mechanical behaviors and wide hysteresis of NiTiNb shape memory alloys. Prog Nat Sci Mater Int 22: 130–138. doi: 10.1016/j.pnsc.2012.03.010

|
|
[110]
|
Chen J, Wang G, Sun W (2005) Investigation on the fracture behavior of shape memory alloy NiTi. Metall Mater Trans A 36: 941–955. doi: 10.1007/s11661-005-0288-8

|
|
[111]
|
Kim HY, Hashimoto S, Kim JI, et al. (2004) Mechanical properties and shape memory behavior of Ti-Nb alloys. Mater Trans 45: 2443–2448. doi: 10.2320/matertrans.45.2443

|
|
[112]
|
Miyazaki S, Kim H, Hosoda H (2006) Development and characterization of Ni-free Ti-base shape memory and superelastic alloys. Mater Sci Eng A 438: 18–24.
|
|
[113]
|
Niinomi M (2003) Recent research and development in titanium alloys for biomedical applications and healthcare goods. Sci Technol Adv Mater 4: 445–454. doi: 10.1016/j.stam.2003.09.002

|
|
[114]
|
Mckelvey A, Ritchie R (2001) Fatigue-crack growth behavior in the superelastic and shape-memory alloy nitinol. Metall Mater Trans A 32: 731–743. doi: 10.1007/s11661-001-1008-7

|
|
[115]
|
Robertson S, Mehta A, Pelton A, et al. (2007) Evolution of crack-tip transformation zones in superelastic nitinol subjected to in situ fatigue: A fracture mechanics and synchrotron X-ray microdiffraction analysis. Acta Mater 55: 6198–6207. doi: 10.1016/j.actamat.2007.07.028

|
|
[116]
|
Figueiredo AM, Modenesi P, Buono V (2009) Low-cycle fatigue life of superelastic NiTi wires. Int J Fatigue 31: 751–758. doi: 10.1016/j.ijfatigue.2008.03.014

|
|
[117]
|
Yu XJ, Kumar KS (2012) Uniaxial, load-controlled cyclic deformation of recrystallized molybdenum sheet. Mater Sci Eng A 540: 187–197. doi: 10.1016/j.msea.2012.01.124

|
|
[118]
|
Yu XJ, Kumar KS (2016) Cyclic tensile response of Mo-27 at% Re and Mo-0.3 at% Si solid solution alloys. Mater Sci Eng A 676: 312–323.
|
|
[119]
|
Kim Y (2002) Fatigue properties of the Ti-Ni base shape memory alloy wire. Mater Trans 43: 1703–1706. doi: 10.2320/matertrans.43.1703

|
|
[120]
|
Pappas P, Bollas D, Parthenios J, et al. (2007) Transformation fatigue and stress relaxation of shape memory alloy wires. Smart Mater Struct 16: 2560. doi: 10.1088/0964-1726/16/6/060

|
|
[121]
|
Barrabés M, Sevilla P, Planell JA, et al. (2008) Mechanical properties of nickel-titanium foams for reconstructive orthopaedics. Mater Sci Eng C 28: 23–27. doi: 10.1016/j.msec.2007.02.001

|
|
[122]
|
Nayan N, Roy D, Buravalla V, et al. (2008) Unnotched fatigue behavior of an austenitic Ni-Ti shape memory alloy. Mater Sci Eng A 497: 333–340. doi: 10.1016/j.msea.2008.07.025

|
|
[123]
|
Kang G, Song D (2015) Review on structural fatigue of NiTi shape memory alloys: Pure mechanical and thermo-mechanical ones. Theor Appl Mech Lett 5: 245–254. doi: 10.1016/j.taml.2015.11.004

|
|
[124]
|
Zhang X, Liu H, Yuan B, et al. (2008) Superelasticity decay of porous NiTi shape memory alloys under cyclic strain-controlled fatigue conditions. Mater Sci Eng A 481: 170–173.
|
|
[125]
|
Fulcher J, Lu Y, Tandon G, et al. (2010) Thermomechanical characterization of shape memory polymers using high temperature nanoindentation. Polym Test 29: 544–552. doi: 10.1016/j.polymertesting.2010.02.001

|
|
[126]
|
Schmidt C, Sarwaruddin Chowdhury AM, Neuking K, et al. (2011) Thermo-mechanical behaviour of shape memory polymers, e.g., Tecoflex® by 1WE method: SEM and IR analysis. J Polym Res 18: 1807–1812.
|
|
[127]
|
Di Prima M, Gall K, Mcdowell D, et al. (2010) Cyclic compression behavior of epoxy shape memory polymer foam. Mech Mater 42: 405–416. doi: 10.1016/j.mechmat.2010.01.004

|
|
[128]
|
Ahmad M, Xu B, Purnawali H, et al. (2012) High performance shape memory polyurethane synthesized with high molecular weight polyol as the soft segment. Appl Sci 2: 535. doi: 10.3390/app2020535

|
|
[129]
|
Kang SM, Lee SJ, Kim BK (2012) Shape memory polyurethane foams. eXPRESS Polym Lett 6: 63–69. doi: 10.3144/expresspolymlett.2012.7

|
|
[130]
|
Zhang H, Wang H, Zhong W, et al. (2009) A novel type of shape memory polymer blend and the shape memory mechanism. Polymer 50: 1596–1601. doi: 10.1016/j.polymer.2009.01.011

|
|
[131]
|
Guo J, Wang Z, Tong L, et al. (2015) Shape memory and thermo-mechanical properties of shape memory polymer/carbon fiber composites. Composites Part A 76: 162–171. doi: 10.1016/j.compositesa.2015.05.026

|
|
[132]
|
Ni QQ, Zhang CS, Fu Y, et al. (2007) Shape memory effect and mechanical properties of carbon nanotube/shape memory polymer nanocomposites. Compos Struct 81: 176–184. doi: 10.1016/j.compstruct.2006.08.017

|
|
[133]
|
Mohr R, Kratz K, Weigel T, et al. (2006) Initiation of shape-memory effect by inductive heating of magnetic nanoparticles in thermoplastic polymers. Proc Natl Acad Sci U S A 103: 3540–3545. doi: 10.1073/pnas.0600079103

|
|
[134]
|
Xu B, Fu YQ, Ahmad M, et al. (2010) Thermo-mechanical properties of polystyrene-based shape memory nanocomposites. J Mater Chem 20: 3442–3448. doi: 10.1039/b923238a

|
|
[135]
|
Zheng X, Zhou S, Li X, et al. (2006) Shape memory properties of poly(d,l-lactide)/hydroxyapatite composites. Biomaterials 27: 4288–4295. doi: 10.1016/j.biomaterials.2006.03.043

|
|
[136]
|
Wei H, Zhang F, Zhang D, et al. (2015) Shape-memory behaviors of electrospun chitosan/poly(ethylene oxide) composite nanofibrous membranes. J Appl Polym Sci 132: n/a.
|
|
[137]
|
Cisse C, Zaki W, Zineb TB (2016) A review of modeling techniques for advanced effects in shape memory alloy behavior. Smart Mater Struct 25: 103001. doi: 10.1088/0964-1726/25/10/103001

|
|
[138]
|
Zhang L, Du H, Liu L, et al. (2014) Analysis and design of smart mandrels using shape memory polymers. Composites Part B 59: 230–237. doi: 10.1016/j.compositesb.2013.10.085

|
|
[139]
|
Mirzaeifar R, DesRoches R, Yavari A (2011) Analysis of the rate-dependent coupled thermo-mechanical response of shape memory alloy bars and wires in tension. Continuum Mech Thermodyn 23: 363–385. doi: 10.1007/s00161-011-0187-8

|
|
[140]
|
Uehara T, Asai C, Ohno N (2009) Molecular dynamics simulation of shape memory behaviour using a multi-grain model. Modell Simul Mater Sci Eng 17: 035011. doi: 10.1088/0965-0393/17/3/035011

|
|
[141]
|
Pun GP, Mishin Y (2010) Molecular dynamics simulation of the martensitic phase transformation in NiAl alloys. J Phys Condens Matter 22: 395403. doi: 10.1088/0953-8984/22/39/395403

|
|
[142]
|
Zhong Y, Zhu T (2014) Phase-field modeling of martensitic microstructure in NiTi shape memory alloys. Acta Mater 75: 337–347. doi: 10.1016/j.actamat.2014.04.013

|
|
[143]
|
Nguyen TD (2013) Modeling shape-memory behavior of polymers. Polym Rev 53: 130–152. doi: 10.1080/15583724.2012.751922

|
|
[144]
|
Leclercq S, Lexcellent C (1996) A general macroscopic description of the thermomechanical behavior of shape memory alloys. J Mech Phys Solids 44: 953–980. doi: 10.1016/0022-5096(96)00013-0

|
|
[145]
|
Falk F (1980) Model free energy, mechanics, and thermodynamics of shape memory alloys. Acta Metall 28: 1773–1780. doi: 10.1016/0001-6160(80)90030-9

|
|
[146]
|
Paiva A, Savi MA (2006) An overview of constitutive models for shape memory alloys. Math Probl Eng 2006: 39–62.
|
|
[147]
|
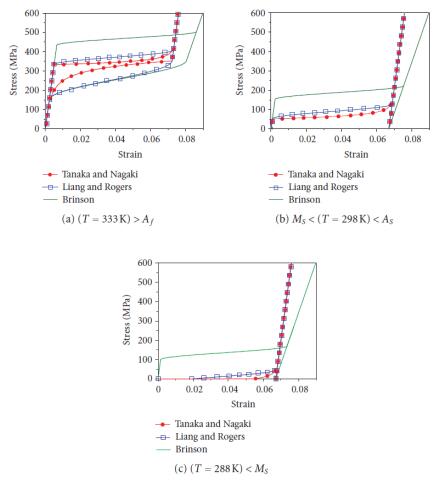
Tanaka K, Nagaki S (1982) A thermomechanical description of materials with internal variables in the process of phase transitions. Ing Arch 51: 287–299. doi: 10.1007/BF00536655

|
|
[148]
|
Liang C, Rogers CA (1990) One-dimensional thermomechanical constitutive relations for shape memory materials. J Intell Mater Syst Struct 1: 207–234. doi: 10.1177/1045389X9000100205

|
|
[149]
|
Brinson LC (1993) One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J Intell Mater Syst Struct 4: 229–242. doi: 10.1177/1045389X9300400213

|
|
[150]
|
Panico M, Brinson L (2007) A three-dimensional phenomenological model for martensite reorientation in shape memory alloys. J Mech Phys Solids 55: 2491–2511. doi: 10.1016/j.jmps.2007.03.010

|
|
[151]
|
Bouvet C, Calloch S, Taillard K, et al. (2004) Experimental determination of initial surface of phase transformation of SMA. J Phys IV Fr 115: 29–36. doi: 10.1051/jp4:2004115004

|
|
[152]
|
Arghavani J, Auricchio F, Naghdabadi R, et al. (2010) A 3-D phenomenological constitutive model for shape memory alloys under multiaxial loadings. Int J Plast 26: 976–991. doi: 10.1016/j.ijplas.2009.12.003

|
|
[153]
|
Moumni Z, Zaki W, Maitournam H (2009) Cyclic behavior and energy approach to the fatigue of shape memory alloys. J Mech Mater Struct 4: 395–411. doi: 10.2140/jomms.2009.4.395

|
|
[154]
|
Zhang Q, Yang QS (2012) Recent advance on constitutive models of thermal-sensitive shape memory polymers. J Appl Polym Sci 123: 1502–1508. doi: 10.1002/app.34307

|
|
[155]
|
Srivastava V, Chester SA, Anand L (2010) Thermally actuated shape-memory polymers: Experiments, theory, and numerical simulations. J Mech Phys Solids 58: 1100–1124. doi: 10.1016/j.jmps.2010.04.004

|
|
[156]
|
Liu Y, Gall K, Dunn ML, et al. (2006) Thermomechanics of shape memory polymers: Uniaxial experiments and constitutive modeling. Int J Plast 22: 279–313. doi: 10.1016/j.ijplas.2005.03.004

|
|
[157]
|
Diani J, Liu Y, Gall K (2006) Finite strain 3D thermoviscoelastic constitutive model for shape memory polymers. Polym Eng Sci 46: 486–492. doi: 10.1002/pen.20497

|
|
[158]
|
Li G, Xu W (2011) Thermomechanical behavior of thermoset shape memory polymer programmed by cold-compression: Testing and constitutive modeling. J Mech Phys Solids 59: 1231–1250. doi: 10.1016/j.jmps.2011.03.001

|
|
[159]
|
Baghani M, Naghdabadi R, Arghavani J, et al. (2012) A thermodynamically-consistent 3D constitutive model for shape memory polymers. Int J Plast 35: 13–30. doi: 10.1016/j.ijplas.2012.01.007

|
|
[160]
|
Wever D, Veldhuizen A, Sanders M, et al. (1997) Cytotoxic, allergic and genotoxic activity of a nickel-titanium alloy. Biomaterials 18: 1115–1120. doi: 10.1016/S0142-9612(97)00041-0

|
|
[161]
|
Shayan M, Chun Y (2015) An overview of thin film nitinol endovascular devices. Acta Biomater 21: 20–34. doi: 10.1016/j.actbio.2015.03.025

|
|
[162]
|
Cui ZD, Man HC, Yang XJ (2005) The corrosion and nickel release behavior of laser surface-melted NiTi shape memory alloy in Hanks' solution. Surf Coat Technol 192: 347–353. doi: 10.1016/j.surfcoat.2004.06.033

|
|
[163]
|
Cheng Y, Cai W, Li H, et al. (2004) Surface characteristics and corrosion resistance properties of TiNi shape memory alloy coated with Ta. Surf Coat Technol 186: 346–352. doi: 10.1016/j.surfcoat.2004.01.012

|
|
[164]
|
Firstov G, Vitchev R, Kumar H, et al. (2002) Surface oxidation of NiTi shape memory alloy. Biomaterials 23: 4863–4871. doi: 10.1016/S0142-9612(02)00244-2

|
|
[165]
|
Poon R, Yeung K, Liu X, et al. (2005) Carbon plasma immersion ion implantation of nickel-titanium shape memory alloys. Biomaterials 26: 2265–2272. doi: 10.1016/j.biomaterials.2004.07.056

|
|
[166]
|
Chen M, Yang X, Liu Y, et al. (2003) Study on the formation of an apatite layer on NiTi shape memory alloy using a chemical treatment method. Surf Coat Technol 173: 229–234. doi: 10.1016/S0257-8972(03)00733-3

|
|
[167]
|
Chu C, Hu T, Wu S, et al. (2007) Surface structure and properties of biomedical NiTi shape memory alloy after Fenton's oxidation. Acta Biomater 3: 795–806. doi: 10.1016/j.actbio.2007.03.002

|
|
[168]
|
Hu T, Wen C, Sun G, et al. (2010) Wear resistance of NiTi alloy after surface mechanical attrition treatment. Surf Coat Technol 205: 506–510. doi: 10.1016/j.surfcoat.2010.07.023

|
|
[169]
|
Walker J, Andani MT, Haberland C, et al. (2014) Additive manufacturing of Nitinol shape memory alloys to overcome challenges in conventional Nitinol fabrication. Proceedings of the ASME 2014 IMECE, V02AT02A037.
|
|
[170]
|
Ge Q, Sakhaei AH, Lee H, et al. (2016) Multimaterial 4D printing with tailorable shape memory polymers. Sci Rep 6: 31110. doi: 10.1038/srep31110

|
|
[171]
|
Hu N, Burgueño R (2015) Buckling-induced smart applications: Recent advances and trends. Smart Mater Struct 24.
|









 DownLoad:
DownLoad: