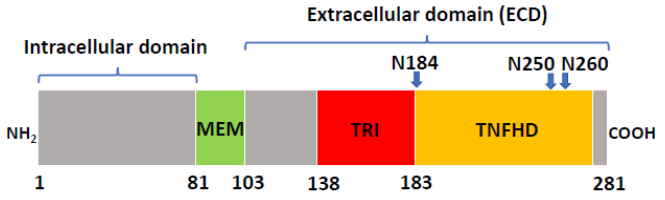
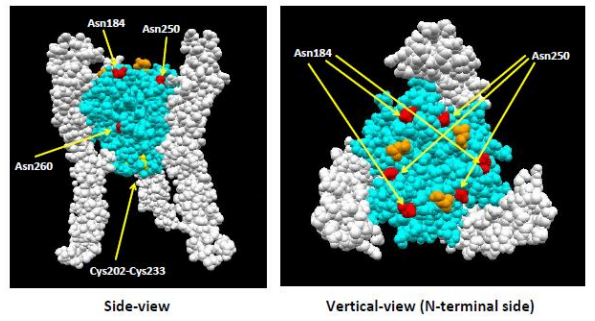
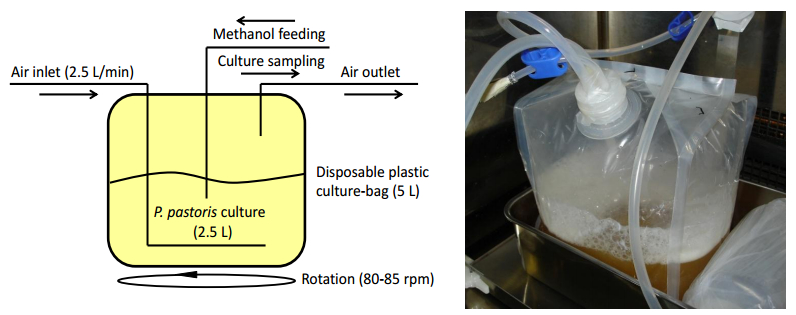
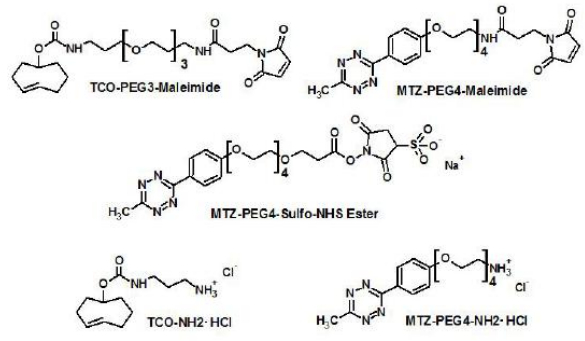
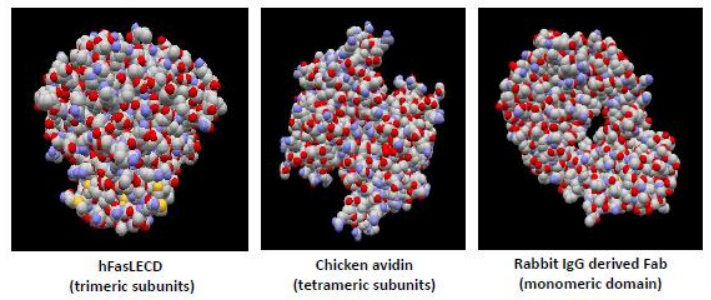
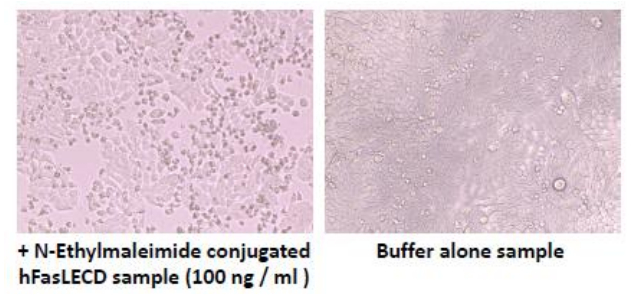
Human Fas ligand extracellular domain (hFasLECD) is a biomedically important glycoprotein with three potential N-linked carbohydrate-chain attachment sites. hFasLECD can induce an apoptotic cell-death in many malignant cells. Hence, the creation of novel molecular tools exhibiting useful biological activities, based on the exploitation of this protein domain as their components, opens up a great possibility of the advancements in future medical applications. This review mainly focuses on the development of expression systems for obtaining various derivatives of recombinant hFasLECD using Pichia pastoris and the preparation of the conjugates by site-specific chemical modifications of the expressed products. Firstly, a brief introduction of human Fas ligand protein and an overview of the previous works, on the heterologous expression systems for recombinant hFasLECD as well as the associated derivatives aimed at medical applications, were described. Then, the experimental results, obtained during our investigations into the development of the expression systems for the recombinant hFasLECD derivatives using chemically synthesized artificial genes in Pichia pastoris, were summarized. After that, the current state of the methodology for preparation of the hFasLECD conjugates by site-specific chemical modifications, and the functional characterizations of the prepared conjugates, were presented. Finally, conclusions, including a relevant discussion and future perspectives, are provided.
1.
Fractional nonlinear Schrödinger equation with harmonic potential
In this paper, we examine the following Schrödinger equation:
where $ 0<s<1 $, $ \sigma>0 $, $ N\geq1 $ and $ \psi: \mathbb{R}^{N}\times [0, \infty)\longrightarrow \mathbb{C} $ is the wave function with initial condition $ \psi_0(x) $ belonging to the following Sobolev space:
with
The fractional Laplacian $ (-\Delta)^{s} $ is defined via a pseudo-differential operator
For the Cauchy problem, formally we have two conserved quantities [17] by multiplying the conjugate of $ \psi $ to both sides and taking the integral: The mass of the wave function:
and the total energy:
In recent years, a great attention has been focused on the study of problems involving the fractional Laplacian, which naturally appears in obstacle problems, phase transition, conservation laws, financial market. Nonlinear fractional Schrödinger equations (FNLS) have been proposed by [20,19,9] in order to expand the Feynman path integral, from the Brownian like to the Lévy like quantum mechanical paths. The stationary solutions of fractional nonlinear Schrödinger equations have also been intensively studied due to their huge importance in nonlinear optics and quantum mechanics [20,19,14,12]. The most interesting solutions have the special form:
They are called the standing waves. These solutions reduce (1) to a semilinear elliptic equation. In fact, after plugging (5) into (1), we need to solve the following equation
The case $ s = 1 $ has been intensively studied by many authors (See [24]). There also exist a considerable amount of results concerning the standing waves and long time behavior of fractional nonlinear Schrödinger equations, we refer the readers to [4,7,6,10,13,16,21,23,22,1] and the references therein.
In this paper, we mainly focus on the solutions to (6). To the best of our knowledge, our results are new and will open the way to solve other classes of fractional Schrödinger equations. This paper has two main parts: In the first part, we address the existence of standing waves through a particular variational form, whose solutions are called ground state solutions. We prove the existence of ground state solutions (Theorem 2.1), and show some qualitative properties like monotonicity and radiality (Lemma 4). We also show that the ground state solutions are orbitally stable (Def 4.2, Theorem 2.2) if we have the uniqueness of the solutions for the Cauchy problem (1) (Theorem 4.3). We have also addressed the critical case $ \sigma = \frac{2s}{N} $, which is consistent with the case $ s = 1 $ in [11]. The second part of this article deals with the numerical method to solve (1) and the existence of ground state solutions as well as the optimality of our conditions. In this part, we were not only able to show the existence of ground state solutions for $ 0<\sigma<\frac{2s}{N} $ but we also gave a characterizing variational problem ((65)-(66)), which was crucial to find the standing waves for the subcritical $ \frac{2s}{N}\leq\sigma< \frac{2s}{N-2s} $. The numerical results provided a good explanation of the effect of $ s $ on the ground state solution. To reach this goal, we showed that the ground state solution is continuous and decreasing with respect to $ s $ in $ L^2 $ and $ L^\infty $ norm (Figure 3), which is a similar phenomenon to [18]. Besides, like Gross–Pitaevskii equation [11], we examined the convergence property of $ \lambda_c $. It turned out that this convergence property also holds in our case. Second, we checked the stability of ground state solutions for different $ s $. If we add a small perturbation to the initial condition, for different $ s $, the absolute value of the solution will always have periodic behavior, which shows the orbital stability (Figure 7). Furthermore, surprisingly, when $ s $ becomes smaller, the stability is worse, which means the oscillation amplitude in the periodic phenomenon becomes larger (Figure 9, 10a). We then address the case where the harmonic potential is not radial, and we obtained nonradial symmetrical ground state solution (Figure 6a, 6b). Finally, we provided interesting numerical results for the time dynamics of the fractional nonlinear Schrödinger equation (FNLS).
The main difficulty of constructing ground state solutions comes from the lack of compactness of the Sobolev embeddings for the unbounded domain $ \mathbb{R}^N $. However, by defining an appropriate function space, in which the norm of the potential is involved, we "recuperate" the compactness (see Lemma 3.1). This fact, combined with rearrangement inequalities is the key point to prove the existence of ground state solutions. In the numerical part, the presence of the harmonic potential term is challenging. One can't take Fourier transform directly on both sides of the equation like [18] because we have the nonlinear term. Unlike in [11], we also can't use finite-difference directly since fractional Laplacian is not a local term. Consequently, we use the splitting method and adopt an idea from [8], where they numerically solve fractional Schrödinger equation without potential energy. By our splitting, we can obtain specific solutions in each small step and also preserve the mass (3). For the ground state solutions, the classical Newton's method [11] is too slow because we have to deal with fractional Laplacian. To overcome this, we borrow an idea from [2] and use normalized gradient flow (NGF) to find the ground state solutions. Moreover, for the case $ \frac{2s}{N}\leq\sigma\leq \frac{2s}{N-2s} $, we have noticed that the energy in the original variational problem can not be bounded from below, therefore, we present a new characterizing variational problem ((65)-(66)) to establish the existence of ground state solutions.
The paper is organized as follows. In section 2, we give our main results about the existence of ground state solutions and the orbital stability of standing waves. In section 3, we provide proof of existence. Then, in section 4, we discuss the orbital stability. In section 5, we use Split-Step Fourier Spectral method to solve (1) numerically. In section 6, instead of using common iterative Newton's method, we use the NGF method to find ground states when $ 0<\sigma\leq \frac{2s}{N-2s} $. Finally, in section 7, we present our numerical results for the dynamics (1) and compare them with other kinds of Schrödinger equations ([11,18]).
2.
Main results
We use a variational formulation to examine the solution to (6). First, note that if $ \lambda = 0 $, we can find solutions $ u(x) $ to (6) from the critical points of the functional $ \mathcal{J}: H_{s}(\mathbb{R}^{N})\longrightarrow \mathbb{R} $ defined as:
where $ \|.\|_{L^2(\mathbb{R}^{N})} $ is the $ L^{2} $-norm and $ \|\nabla_{s}u\|_{L^{2}({\mathbb{R}^{N}})} $ is defined by
with some normalization constant $ C_{N, s} $.
We can derive (7) by multiplying smooth enough test function $ v(x) $ on both sides of (6) and taking the integral over $ x $. However, instead of directly finding the critical points of (7), we consider a reconstructed variational problem, which can help us find solutions with different $ \lambda $ and any energy. Specifically, for a fixed number $ c>0 $, we need to solve the following constrained minimization problem.
with
where
is a Hilbert space, with corresponding natural inner product.
We claim that for each minimizer $ u(x) $ of the constrained minimization problem (8), there exists some $ \lambda $ such that $ (u(x), \lambda) $ is a solution to (6). To prove the claim, we consider $ \lambda $ as a Lagrange multiplier and define
The minimizer to problem (8) must be the critical point of (11), satisfying:
and
where (12) implies (6) and (13) implies (9). In this paper, we will mainly focus on the minimizers of problem (8). The following theorem discusses the existence of such minimizers.
Theorem 2.1. If $ 0<\sigma<\frac{2s}{N} $, then (8) admits a nonnegative, radial and radially decreasing minimizer.
Remark 1. There were some works considering standing waves for fractional nonlinear Schrödinger equation with different potential enery and nonlinearity terms. In [6], the authors focus on the case where the nonlinearity term is asymptotically linear with $ \psi\rightarrow \infty $. In [7], the author considers strictly positive potential energy. In our case, the nonlinearity term increases polynomially with $ \psi $ and potential energy is not strictly positive, therefore previous technics can not be applied here directly.
Remark 2. The condition $ 0<\sigma<\frac{2s}{N} $ is important in our proof for the existence of minimizers. For the critical case $ \sigma = \frac{2s}{N} $, we were able to obtain interesting results (section 7).
After we construct the ground state solutions, we further investigate their stability. By the definition of (5), the ground state solution moves around a circle when the time changes. Therefore we consider and prove the orbital stability of ground state solution (Def 4.2).
Theorem 2.2. Suppose that $ 0<\sigma<\frac{2s}{N} $ and (1) has a unique solution with conserved mass (3) and energy (4), then the ground state solutions constructed in Theorem 2.1 are orbitally stable.
3.
The minimization problem
In this section, we will establish the existence of ground state solutions of (6), the main difficulty comes from the lack of compactness of the Sobolev embeddings. Usually, at least when the potential in (1) is radially symmetric and radially increasing, such difficulty is overcome by considering the appropriate function space. More precisely, we have
Lemma 3.1. Let $ 2\leq p< \frac{2N}{N-2s} $, then the embedding $ \Sigma_{s}({\mathbb{R}^{N}})\subset L^p(\mathbb{R}^N) $ is compact.
Proof. First, when $ p = 2 $, choose $ R>0 $, then for any $ u(x)\neq 0\in \Sigma_s({\mathbb{R}^{N}}) $, we have
By the classical Sobolev embedding theorem, for any fixed $ R $, $ H_{s}(|x|<R) $ is compactly embedded in $ L^2(|x|<R) $. Therefore, for any bounded sequence in $ \Sigma_s $, we choose $ R_n>0\rightarrow \infty $. And for each $ n $, we pick out the subsequence that converges in $ L^2(|x|<R_n) $ from former convergence sequence in $ L^2(|x|<R_{n-1}) $. Finally, using the diagonal method combined with (14), we find the convergence sequence in $ L^2(\mathbb{R}^N) $.
Second, for $ p>2 $, using the fractional Gagliardo-Nirenberg inequality [14], we have
for some positive constant $ K $, where $ \theta = \frac{N(p-2)}{2sp}<1 $. Since $ \Sigma_s(\mathbb{R}^N) $ is compactly embedded into $ L^2(\mathbb{R}^N) $, (15) directly implies $ \Sigma_s(\mathbb{R}^N) $ is compactly embedded into $ L^p(\mathbb{R}^N) $ for $ 2\leq p<\frac{2N}{N-2s} $.
Then we have a lemma showing the existence of $ I_{c} $ and the boundedness of the minimizing sequences.
Lemma 3.2. If $ 0<\sigma<\frac{2s}{N} $, then $ I_{c}>-\infty $ and all the minimizing sequences of (8) are bounded in $ \Sigma_{s}(\mathbb{R}^{N}) $.
Proof. First, we prove that $ \mathcal{J}(u) $ is bounded from below. Using the fractional Gagliardo-Nirenberg inequality [14], we certainly have
for some positive constant $ K $, where $ \theta = \frac{N\sigma}{2s(\sigma+1)}. $
On the other hand, let $ \epsilon>0 $, and $ p, q>1 $ such that $ \frac{1}{p}+\frac{1}{q} = 1 $, then, using Young's inequality, one gets that
Combining (16) and (17), we obtain that for any $ u\in S_{c} $,
where $ p = \frac{1}{\theta(1+\sigma)} = \frac{2s}{N\sigma}, \ q = \frac{1}{1-\theta(1+\sigma)} $.
Hence, from (18) we get:
Then we choose $ \epsilon $ small enough in (23) to make $ \left(\frac{1}{2}-\frac{\epsilon^{p}K^{2\sigma+2}}{2p(\sigma+1)}\right)>0 $, which implies that $ I_{c}>-\infty $. Finally, for all minimizing sequences $ \{u_n\} $, since $ \mathcal{J}(u_n) $ is bounded from below, $ \{u_n\} $ is bounded in $ \Sigma_{s}(\mathbb{R}^{N}) $ by (23).
Now, we can use compactness (Lemma 3.1) and boundedness (Lemma 3.2) to prove our existence Theorem 2.1.
Proof. Let $ \{u_{n}\} $ be a minimizing sequence of (8). By Lemma 3.2, $ \{u_{n}\} $ is bounded in $ \Sigma_{s}(\mathbb{R}^{N}) $. Up to a subsequence, there exists $ u $ such that $ u_{n} $ converges weakly to $ u $ in $ \Sigma_{s}(\mathbb{R}^{N}) $.
Since $ 2\sigma+2<\frac{2N}{N-2s} $ and $ \Sigma_{s}(\mathbb{R}^{N}) $ is compactly embedded in $ L^{p}(\mathbb{R}^{N}) $ for any $ p $ such that $ 2\leq p<\frac{2N}{N-2s} $, we can further prove that $ u_{n} $ will converge strongly to $ u $ in $ L^2({\mathbb{R}^{N}}) $ and $ L^{2\sigma+2}({\mathbb{R}^{N}}) $ (Lemma 3.1). In particular, $ u_n\rightarrow u $ in $ L^2({\mathbb{R}^{N}}) $, which implies that $ u\in \mathcal{S}_c $.
On the other hand, thanks to the lower semi-continuity, we have
Therefore
which yields that $ u $ is a minimizer.
The second step consists of constructing a nonnegative, radial, and radially decreasing minimizer. First, we note that:
which implies that $ \mathcal{J}(|u|)\leq\mathcal{J}(u) $. Using the Schwarz symmetrization [15], we construct a symmetrization function $ u^{\ast} $, which is a radially-decreasing function from $ \mathbb{R}^{N} $ into $ \mathbb{R} $ with the property that
It is well-known [15] that
Besides, from [3] Lemma 6.3, we also have
Combining (26) and (27), we obtain that
Remark 3. By (24) and the weakly convergence, we can also see that:
which implies that there is a minimizing subseqence $ u_{n_k} $ converging to $ u $ in $ \Sigma_s(\mathbb{R}^N) $.
Remark 4. If $ u\in\Sigma_s(\mathbb{R}^N) $ is a minimizer to (8), we must have
By (27) and (28), we obtain that
which implies that $ u $ doesn't change sign almost everywhere. Furthermore, we also have
which further implies $ |u| = |u|^* $ a.e. by [11]. In conlusion, we obtain a minimizer $ u $ that doesn't change sign and is radially decreasing almost everywhere.
4.
Orbital stability
In this section, we will deal with the orbital stability of the ground state solutions. Let us introduce the appropriate Hilbert space:
equipped with the norm $ \|\omega\|^{2}_{\widetilde{\Sigma}_{s}(\mathbb{R}^{N})} = \|u\|^{2}_{\Sigma_{s}(\mathbb{R}^{N})}+\|v\|^{2}_{\Sigma_{s}(\mathbb{R}^{N})} $, which is a Hilbert space.
In term of the new coordinates, the energy functional reads
where $ \|\nabla_s\omega\|_{{L^2({\mathbb{R}^{N}})}}^{2} = \|\nabla_{s}u\|_{{L^2({\mathbb{R}^{N}})}}^{2}+\|\nabla_{s}v\|_{{L^2({\mathbb{R}^{N}})}}^{2} $, we can also prove that $ \widetilde{\mathcal{J}}(\omega) $ remains as a constant with time $ t $ if $ \omega(t, x) $ is a solution to $ (1) $.
Then, for all $ c>0 $, we set a similar constrained minimization problem
where $ \mathcal{\widetilde{S}}_{c} $ is defined by:
We also introduce the following sets
Proceeding as in [4,16], we have the following lemma:
Lemma 4.1. If $ 0<\sigma<\frac{2s}{N} $, then the following properties hold true:
(i) The energy functional $ \mathcal{J} $ and $ \widetilde{\mathcal{J}} $ are of class $ C^{1} $ on $ \Sigma_{s}(\mathbb{R}^{N}) $ and $ \widetilde{\Sigma}_{s}(\mathbb{R}^{N}) $ respectively.
(ii) There exists a constant $ C > 0 $ such that
(iii) All minimizing sequences for $ \widetilde{\mathcal{I}}_{c} $ are bounded in $ \widetilde{\Sigma}_{s}(\mathbb{R}^{N}) $ and all minimizing sequences for $ \mathcal{I}_{c} $ are bounded in $ \Sigma_{s}(\mathbb{R}^{N}) $.
(iv) The mappings $ c\longmapsto \mathcal{I}_{c}, \, \widetilde{\mathcal{I}}_{c} $ are continuous.
(v) Any minimizing sequence of $ \mathcal{I}_{c} $, $ \widetilde{\mathcal{I}}_{c} $ are relatively compact in $ \Sigma_{s}(\mathbb{R}^{N}) $, $ \widetilde{\Sigma_{s}}(\mathbb{R}^{N}) $.
(vi) For any $ c>0 $,
Proof. (i) We follow the steps of Proposition 2.3 [16] by choosing $ g(x, t) = -t^{\sigma} $. For any $ u, v\in \Sigma_{s}(\mathbb{R}^{N}) $, we can see that the last term of functional
is of class $ C^{1} $ on $ \Sigma_{s}(\mathbb{R}^{N}) $. Then by the definition of $ \Sigma_{s}(\mathbb{R}^{N}) $ (see (10)), the first two terms of the functional are of class $ C^1 $ on $ \Sigma_{s}(\mathbb{R}^{N}) $.
(ii) From (i), $ \mathcal{J} $ is of class $ C^{1} $ on $ \Sigma_{s}(\mathbb{R}^{N}) $. Moreover, for all $ u, v\in \Sigma_{s}(\mathbb{R}^{N}) $, we have
For the last term, by Hölder's inequality, we have
Therefore, there exists $ C>0 $ such that
(iii) This is a direct result of Lemma 3.2.
(iv) Let $ c>0 $ and $ \{c_{n}\}\subset (0, \infty) $ such that $ c_{n}\rightarrow c $. It suffices to prove that $ \mathcal{I}_{c_{n}}\rightarrow \mathcal{I}_{c} $. By the definition of $ \mathcal{I}_{c_{n}} $, for any $ n $, there exists $ u_{n}\in S_{c_{n}} $ such that
From (iii), there exists a constant $ C_{1}>0 $ such that for all $ n $, we have
Setting $ v_{n} = \frac{c}{c_{n}}u_{n} $, then we have that for all $ n\in \mathbb{N} $
which implies that
We deduce by part (ii) that there exists a positive constant $ K: = K(C_{1}) $ such that
By (32) and (33), we get that
Then, from (31) and (34), we obtain that
Combining this with the fact that $ \lim_{n\rightarrow \infty}c_{n} = c $, it yields
Now, from Lemma 3.2 and by the definition of $ \mathcal{I}_{c} $, there exists a positive constant $ C_{2} $ and a sequence $ \{u_{n}\}\subset \mathcal{S}_{c} $ such that
Set $ v_{n} = \frac{c_{n}}{c}u_{n} $, then $ v_{n}\in S_{c_{n}} $, there exists a constant $ L = L(C_{2}) $ such that
Combining this with (31), we obtain that
Since $ \lim_{n\rightarrow \infty}c_{n} = c $, we have
It follows from (35) and (36) that
(v) This is a direct result of Remark 3.
(vi) First, we can see $ \Sigma_s(\mathbb{R}^{N})\subset\widetilde{\Sigma}_s(\mathbb{R}^{N}) $. And for any $ \omega\in\Sigma_s(\mathbb{R}^{N}) $, we have
which implies that
Second, for any $ \omega\in\widetilde{\Sigma}_s(\mathbb{R}^N) $, we have
which implies that
and
Combining (37) and (38), we finally have $ \widetilde{\mathcal{I}}_c = \mathcal{I}_c. $
Now, for a fixed $ c > 0 $, we use the following definition of stability (see [5]):
Definition 4.2 We say that $ \widetilde{\mathcal{O}}_{c} $ is stable if
● $ \widetilde{\mathcal{O}}_{c} $ is not empty.
● For all $ \omega_0\in\widetilde{\mathcal{O}}_{c} $ and $ \varepsilon>0, $ there exists $ \delta>0 $ such that for all $ \psi_{0}\in \widetilde{\Sigma}_s(\mathbb{R}^{N}) $, we have
where $ \psi $ denotes the solution of (1) corresponding to the initial data $ \psi_{0} $.
If $ \widetilde{\mathcal{O}}_{c} $ is stable, we say that the ground state solutions in $ \widetilde{\mathcal{O}}_{c} $ are orbitally stable. The following theorem states the orbital stability of $ \widetilde{\mathcal{O}}_c $.
Theorem 4.3. Suppose that $ 0<\sigma<\frac{2s}{N} $, and (1) with initial data $ \psi_{0} \in\widetilde{\Sigma}_s(\mathbb{R}^{N}) $ has a unique solution $ \psi(t, x)\in \widetilde{\Sigma}_s(\mathbb{R}^{N}) $ with
then $ \widetilde{\mathcal{O}}_{c} $ is stable.
Proof. The proof is by contradiction: Suppose that $ \widetilde{\mathcal{O}}_{c} $ is not stable, then there exists $ \epsilon_{0}>0, \;\omega_0\in\widetilde{\mathcal{O}}_{c} $ and a sequence $ \Phi_{0}^{n}\in \widetilde{\Sigma}_s(\mathbb{R}^{N}) $ such that $ \|\omega_0-\Phi^{n}_{0}\|_{\widetilde{\Sigma}_{s}(\mathbb{R}^{N})}\rightarrow 0\;{\rm{as}}\;n\rightarrow \infty $, but
for some sequence $ \{t_{n}\}\subset \mathbb{R} $, where $ \Phi^{n}(t, .) $ is the unique solution of problem (1) corresponding to the initial condition $ \Phi^{n}_{0} $.
Let $ \omega_{n} = \Phi^{n}(t_{n}, .) = (u_{n}, v_{n})\in \widetilde{\Sigma}_{s}(\mathbb{R}^{N}) $. Since $ \omega\in\widetilde{\mathcal{S}}_{c} $ and $ \widetilde{\mathcal{J}}(\omega) = \widetilde{\mathcal{I}}_{c} $, it follows from the continuity of $ \|.\|_{L^2(\mathbb{R}^{N})} $ and $ \widetilde{\mathcal{J}} $ in $ \widetilde{\Sigma}_{s}(\mathbb{R}^{N}) $ that
Thus, we deduce from (39) that
Since $ \{\omega_{n}\}\subset \widetilde{\Sigma}_{s}(\mathbb{R}^{N}) $, it is easy to see that $ \{|\omega_{n}|\}\subset \Sigma_{s}(\mathbb{R}^{N}) $. On the other hand, Lemma 4.1 (iii) and the proof of Lemma 3.2 imply that $ \{\omega_{n}\} $ is bounded in $ \widetilde{\Sigma}_{s}(\mathbb{R}^{N}) $. Hence, by passing to a subsequence, there exists $ \omega = (u, v)\in\widetilde{\Sigma}_{s}(\mathbb{R}^{N}) $ such that
Now, by a straightforward computation, we obtain that
which implies that
Besides, by (41),
It follows from Lemma 4.1 that we have
Hence
It follows from (42), (43) and (44) that
which is equivalent to say that
The boundedness of $ \omega_n $ in $ \widetilde{\Sigma_s}(\mathbb{R}^{N}) $ and (45) imply that $ |w_{n}| $ is bounded in $ \Sigma_{s}(\mathbb{R}^{N}) $. Using a similar argument to Lemma 3.1, there exists $ \varphi\in \Sigma_{s}(\mathbb{R}^{N}) $ such that
Next, let us prove $ \varphi = |\omega| = \left(|u|^2+|v|^2\right)^{1/2} $. Using (42), it follows that
Since $ \left|(u_{n}^{2}+v_{n}^{2})^{\frac{1}{2}}-(u^{2}+v^{2})^{\frac{1}{2}}\right|\leq |u_{n}-u|^{2}+|v_{n}-v|^{2} $, one has
But $ |\omega_n| = (u_{n}^{2}+v_{n}^{2})^{\frac{1}{2}}\longrightarrow \varphi\;{\rm{in}}\;\Sigma_s(\mathbb{R}^N)\subset L^{2}(\mathbb{R}^N). $ Thus, we certainly have
This further implies that
and
Additionally, by the lower semi-continuity, we further have
Combining (48) with (49) and $ \omega\in\widetilde{\mathcal{S}}_c $, we finally obtain that
which implies that
Finally, by (46), (47), and (50), we obtain that
which contradicts to (40).
5.
Numerical method for fractional NLS with harmonic potential
In this section, we consider numerical methods to solve (1) and introduce the Split-Step Fourier Spectral method.
First, we truncate (1) into a finite computational domain $ [-L, L]^N $ with periodic boundary conditions:
for $ \textbf{x}\in[-L, L]^N $.
Let $ \tau>0 $ be the time step, and define the time sequence $ t_n = n\tau $ for $ n\geq0 $ and the mesh size $ h = 2L/J $, where $ J $ is a positive even integer. The spatial grid points are
where $ \textbf{j} $ is a $ N $-dimension integer vector with each component between 0 and $ J $.
Denote $ \psi^n_{\textbf{j}} $ the numerical approximation of the solution $ \psi(\textbf{x}^{\textbf{j}}, t_n) $. By the definition of fractional Laplacian in (2), we use the Fourier spectral method for spatial discretization. Hence, we assume the ansatz:
where $ \textbf{K} = \left\{\textbf{k}\in \mathbb{R}^N|-J/2\leq \textbf{k}_l\leq J/2-1, 1\leq l\leq N\right\} $, $ \left(\mu^{\textbf{k}}\right)_k = \textbf{k}_k\pi/L $, $ 1\leq k\leq N $.
Now, we introduce the Split-step Fourier Spectral method. The main idea of this method is to solve (51) in two splitting steps from $ t = t_n $ to $ t = t_{n+1} $ :
First, by multiplying $ \psi^* $ on both sides of (54) and subtracting it from its conjugate, we obtain that $ |\psi(\textbf{x}, t)| = |\psi(\textbf{x}, t_n)| $ for any $ t\in[t_n, t_{n+1}) $. Then (54) can be simplified to
Second, taking Fourier transform on both sides of (55), we obtain that
We use the second order Strang splitting method with (56) and (57) as follows:
where $ \textbf{j} $ comes from (52) and $ n\geq 0 $. For $ n = 0 $, initial condition (51) is discretized as:
This method has spectral order accuracy in space and second order in time. Similar to [8], this method preserves discrete mass corresponding to (3) defined as
6.
Numerical method to solve ground state solutions
To find ground state solutions, we have to solve the following equation corresponding to $ u(x) $:
As discussed previously, for $ \sigma<\frac{2s}{N} $, we can solve (8)-(10) to find a solution to (63). In order to calculate the minimizer of $ \mathcal{J}(u) $ in $ S_c $, we use the normalized gradient flow method (NGF) [2]. We first apply the steepest gradient decent method to the energy functional $ \mathcal{J}(u) $ without constraint. Then we project the solution back onto the sphere $ \mathcal{S}_c $ to make sure that the constraint $ ||u||_{L^2(\mathbb{R}^{N})} = c $ is satisfied.
Thus, for a given sequence of time $ 0 = t_0 < t_1 < ... < t_n $ with fixed time step $ \tau $, we compute the approximated solution $ u^{(n)} $ of the partial differential equation
and project it onto $ \mathcal{S}_c $ at each step. Specifically,
Here, we use semi-implicity time discretization scheme:
with
to discretize fractional Laplacian, where $ \textbf{K} $, $ \mu^{\textbf{k}} $ are defined in (53).
In conlusion, in each step, we solve:
where $ M^n $ is defined in (62), $ \textbf{j} $ comes from (52) and $ n\geq 0 $. For $ n = 0 $, we guess a starting function and discretize it as (61).
We need to notice that we can only solve (8) for $ \sigma<\frac{2s}{N} $. If $ \sigma\geq \frac{2s}{N} $, $ \|u\|_{L^{2\sigma+2}(\mathbb{R}^N)} $ can not be bounded by $ \|\cdot\|_{\Sigma_s(\mathbb{R}^N)} $, which causes $ I_c = -\infty $ in $ \mathcal{S}_c $. However, we can use another characterizing variational form and find standing waves to (1) for $ \frac{2s}{N}\leq \sigma<\frac{2s}{N-2s} $.
For $ \sigma<\frac{2s}{N-2s} $, we define the following constrained minimization problem:
with
where $ \Sigma_s(\mathbb{R}^{N}) $ is defined as (10).
For $ u\in T_c $, we have the estimate
where $ C_{R, \delta} $ depends on $ R, \delta $. Hence, for $ \omega<0 $, if we choose $ R $ large enough to make $ \left(\frac{1}{2}+\frac{\omega}{R^2}\right)>0 $, we obtain that
for $ u\in T_c $. Besides, if $ \omega>0 $, (67) is greater than $ 0 $. Similar to Lemma 3.2 and Theorem 2.1, there exists a local minimizer for (65) with any $ \omega $ and $ c $.
Now we see $ \lambda $ as the Lagrange multiplier like (11) but with a different functional
then the critical points $ u^* $ and $ \lambda^* $ satisfy
by $ \frac{\partial\mathcal{K}^*(u)}{\partial u} = 0 $. If $ \omega>0 $, by multiplying $ \overline{u^*} $ on both sides of (68) and taking the integral, we can see that:
which implies that $ \lambda>0 $. Defining $ u_{\omega, c} = \lambda^{1/2\sigma}u^* $, when $ \omega>0 $, we obtain that
which means $ u_{\omega, c}e^{i\omega t} $ is one standing wave solution to (1). We need to mention that (69), (70) actually showed that we can find a ground state solution by solving (66) if $ L_c = \mathcal{K}(u^*)>0 $. In fact, we have $ \mathcal{K}(u^*)>0 $ with $ \omega<0 $ but not very small. This is related with the smallest eigenvalue of $ \left(-\Delta\right)^s+|x|^2 $ (see detail [11]).
Now, for $ \frac{2s}{N}\leq\sigma<\frac{2s}{N-2s} $, we use the NGF method and the semi-implicity time discretization scheme to solve the constrained problem (65). Similar to (64), the scheme is
where $ M^n_{2\sigma+2} $ is discrete $ L^{2\sigma+2}(\mathbb{R}^N) $ norm
and $ \textbf{j} $ comes from (52) for $ n\geq 0 $. For $ n = 0 $, we guess a starting function and discretize it as (61).
7.
Numerical results
In this section, we show some numerical results, which can help us understand the ground state solution and also illustrate theoretical results. We have mainly investigated: 1. Ground state solutions with different $ s $. 2. Ground state solutions with non-symmetric potentials. 3. Stability and dynamics.
7.1. Numerical results of ground state solutions
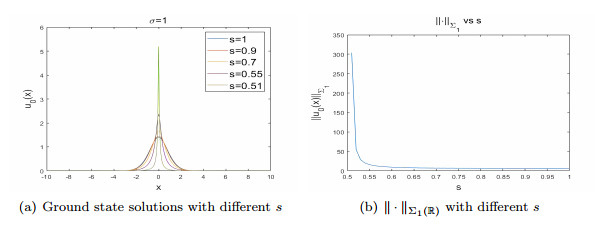
First, we solve (8) numerically by (64) in one dimension $ N = 1 $ for the case $ s = 0.8 $ and $ \sigma = 1 $ to obtain a ground state solution $ u_0(x) $. From figure 1a we see that $ u_0(x) $ is radially decreasing as Remark 4.
Second, we use $ u_0(x) $ as initial condition in (1) and investigate time evolution of the standing wave (figure 1b, 2a, 2b). As expected, we see that $ |\psi(x, t)| $ is conserved. And the real and imaginary part of the solution change periodicly with time $ t $.
By Theorem 2.1, we can obtain the existence of ground state solutions with $ \sigma<\frac{2s}{N} $. We change $ s $ but keep $ \sigma = 1 $ to obtain ground state solutions with different $ s $. From figure 3a, we can see when $ s $ approaches to $ 0.5 $, ground state solutions become peaked with faster spatial decay. This is a similar result to the case without potential [18]. We also check $ \|\cdot\|_{\Sigma_1(\mathbb{R})} $ of ground state solutions when $ s\rightarrow 0.5 $ in (figure 3b), whose growth shows regularity of the solution becomes worse.
From figure 3a and figure 3b, it seems ground state solutions change continuously with $ s $. We use $ L^2 $ distance between $ u^s_0(x)-u^1(x) $ to check and see the convergence of ground state solutions in $ L^2 $ space with $ s\rightarrow 1 $ (figure 4).
Then, we test another two things. The first is the relationship between the constrained minimal energy in (8) and $ s $. We calculate the discrete energy by
From figure 5a, we find the energy's dependence $ (E(s)) $ on $ s $ is monotonic. When $ s $ approaches to $ 0.5 $, the energy will approach to $ -\infty $ because of the nonlinear term. There are two reasons. First, we keep the $ L^2 $ norm of $ u $ (we test with the same mass $ c $), but the potential term becomes small since $ u $ gathers around $ 0 $. Second, in Lemma 3.2, we need $ \sigma<\frac{2s}{N} $ to bound $ \|u\|_{L^{2\sigma+2}(\mathbb{R}^N)} $, whose boundedness becomes worse when $ s\rightarrow0.5 $. This is different from [18], where they didn't use the variation form and keep the $ L^2 $ norm.
Second, we test the relationship between $ c $ and $ \lambda_c $, where $ c $, $ \lambda_c $ are mass and Lagrange multiplier corresponding to the minimizer (8)-(10). By [11], in the case $ s = 1 $, there exists $ \lambda_0 $ such that for any $ \sigma $,
We also test this with $ s = 0.8 $. From figure 5b, for different $ \sigma $, when $ c\rightarrow 0 $, $ \lambda_c $ will also converge to a same value $ \lambda_0 $.
Up to now, we only consider the case with radially symmetrical potential. However, when the potential is not radially symmetric, we can still find a standing wave to (1) using (8). We tried cases where the potential has the form $ |x|^2+a\sin(2\pi x) $ with $ a = 1 $ and $ a = 5 $. From figure 6a and 6b, if we add a nonsymmetrical perturbation to potential, we won't get radially symmetrical ground state solutions.
7.2. Dynamics and stability of ground state solution
First, we consider the case $ s>\frac{N\sigma}{2} $, which is covered by our Theorem 2.2. From the theoretical results and figure 1b, we see that standing waves preserve $ |\psi(x, t)| $ with time $ t $. Therefore, we use $ |\psi(x, t)| $ to draw graphs and test its stability. We consider the case $ s = 0.8 $ and $ \sigma = 1 $. We first test condition (39) in Theorem 2.2 with the initial condition $ \psi_0(x) = (1+e)*u_0(x) $. Because the scheme is mass preserving, it suffices to test energy preservation, which is showed in figure 7a, 7b. Then, we test the stability of the solution, where $ e $ is a constant number. From figure 7c, 7d, when $ e = 0.05 $, the solution almost preserves $ |\psi(x, t)| $ as we desired. When $ e = 0.2 $, the solution shows large perturbation but still has the periodic behavior, similar to [11] and [18]. In figure 8, we compare the $ \|\cdot\|_{\widetilde{\Sigma}_s(\mathbb{R})} $ distance between ground state solutions and perturbed solutions. We can see from figure 3b and theoretical results that when $ s\rightarrow \frac{\sigma N}{2} $, the regularity of ground state solutions becomes worse. This inspires us to investigate its stability relationship with $ s $. By Theorem 2.2, Def 4.2, the orbital stability means we can find $ \omega\in\widetilde{\mathcal{O}}_{c} $ such that $ \|\omega-\psi\|_{\widetilde{\Sigma}_{s}(\mathbb{R})} $ is small when we only have a small perturbation in initial condition. This definition is hard to measure. Instead of checking the exact definition of the orbital stability, we test classical stability by comparing the distance between perturbed solutions and ground state solutions using the normalized $ \|\cdot\|_{\widetilde{\Sigma}_s(\mathbb{R})} $ distance:
We test initial conditions $ \psi_0(x) = 0.9*u_0(x) $ with $ s = 0.8 $ and $ s = 0.6 $. From figure 9, 10a, as expected, when $ s $ is small, its stability seems worse. To be complete, we test $ D(s, 1) $ with $ s $ between $ 0.51 $ and $ 1 $ in figure 10b. We can see $ D(1, s) $ increases when $ s $ approaches to $ 0.5 $, which implies worse stability.
Second, we try to obtain some numerical results when we touch the critical point $ s = \frac{\sigma N}{2} $. In this case, we can't find the ground state solution through (8) because $ I_c = -\infty $. However, as we discussed before, we can find a ground state solution related to another constrained minimization problem (65). Here, we try to use the NGF method to find a ground state solution with $ s = 0.5 $, $ \sigma = 1 $. We first tried positive $ \omega $, but the projection step dominated the process (71). Therefore, we tried $ \omega = -0.5 $ and find the method does converge to a solution. From figure 11b-11d, we can see $ |\psi(x, t)| $ is almost preserved with time $ t $ and it has periodical real and imaginary part. We use it to test the finite blowup phenomenon ($ \psi_0(x) = 2u_0(x) $) appeared in the case without potential [18], and this also happens with potential (figure 11e). We note here that we still can't find a perfect ground state solution, which is caused by the stability of (1) is very bad when $ s = 0.5 $.
Finally, we test some simple time dynamics of FNLS, we let $ \psi_0(x) = u_0(x)e^{ikx} $, which changes its phase but not absolute value. If $ s = 0.8 $ and $ k = 1, 20 $ (Figure 12a, 12b), the maximum point of $ |\psi(x, t)| $ will move along $ x $ periodically. We also test the $ L^\infty $ norm of $ \psi(x, t) $ (Figure 13a). We find that it decreases first and then approaches to some limits, which is similar to the case without potential [18].









 DownLoad:
DownLoad: