1. Introduction
The function of the immune system rests largely on interactions of protein superfamilies. The ties that bind a particular superfamily together can be based on either sequence homology, structural similarity, or function/mechanism of action [1]. As a classification scheme, superfamily designations identify successful core scaffolding features with deep evolutionary roots. While extensive diversification is often evident, a semblance of core continuity is always maintained. With some justification, present-day immunotherapeutic approaches view the most relevant protein interactions as involving two superfamilies, the immunoglobulin superfamily and the tumor necrosis factor receptor superfamily. The immunoglobulin superfamily (IgSF) is represented by 29 members and the tumor necrosis factor receptor superfamily (TNFRSF) by 26 members on T cells [2]. Because many of these, such as CTLA-4, PD-1, TNF-α receptors and Fas/FasL (CD95/CD95L) are now immunotherapeutic superstars [3,4,5,6], these two superfamilies dominate discussions of T cell immunotherapy.
There is, however, another important immunotherapeutic superfamily, the C-type (Ca2+-dependent) lectin-type (CLEC) receptors [7]. Most, if not all, immune cells express one or more of this large family [8,9,10]. CLECs, based on a scaffold categorization as lectins, are proteins that non-catalytically bind carbohydrate moieties with high specificity, most of which require Ca2+ to achieve high affinity binding. They impact the behavior of numerous myeloid [11] and lymphoid [12] cell types and have prominent roles in disease [13,14,15,16,17]. The primary function of these receptors on antigen-presenting cells (APCs) is "pattern-recognition", usually through recognition of carbohydrate structures, by which they bind and internalize pathogens (non-self) for degradation [11]. A coincident role of CLEC receptors is cell-to-cell adhesion for enhancement of intercellular communication. CLEC's widespread influence is rooted in Nature's reliance on the superior structural recognition diversity that sugars provide.
The purpose of this review is to highlight the selective endocytosis and subsequent calcium signaling that can be triggered by binding of a ligand to members of the CLEC family of receptors. Andersen and Moestrup [18] brought attention to the possibility that ligand-dependent endocytosis of CLEC receptors presents a unique opportunity to initiate a Ca2+-induced, signal-transduction response. Indeed, because these receptors bind Ca2+, they constitutively initiate a Ca2+ signal upon endocytosis.
2. The Endosomal Pathway to Antigen Presentation
Most cells are capable of antigen presentation through MHC class Ⅰ complexes to specific CD8+ T cells, whereas the main APCs are capable of MHC class Ⅱ presentation primarily to CD4+ T cells. Peptides that are presented by the MHC class Ⅰ complexes generally arise from the turnover of intracellular proteins by proteosomes in the cytosol and subsequent transfer into the endoplasmic reticulum (ER) through the transporter-associated-with-antigen-processing (TAP) complex [19]. Within the ER, the peptide is loaded onto membrane-bound MHC class Ⅰ complexes that travel through the secretory pathway to the cell surface. Many different proteins that are resident in the ER, such as calnexin, TAP, calreticulin, and tapasin, are integral to MHC class Ⅰ assembly. Overall, assembly of MHC class Ⅰ complexes is now understood to involve the interplay of multiple intra-and intermolecular events in a defined chronological order that ensures continual reporting of cellular contents to cytotoxic T lymphocytes. Among the APCs, dendritic cells (DCs) were thought to have a unique pathway for transferring exogenous antigens, after endocytosis into early endosomes, to the cytosol for eventual loading onto MHC class Ⅰ complexes [20]. This process, termed "cross-presentation" [21,22,23,24,25,26], is an ability shared, but with much less effectiveness by monocytes and macrophages [27,28]. Antigen-specific CD8+ T cells become cytotoxic, capable of recognizing cells that bear that antigen. Calcium is known to play a prominent role in these processes [29,30,31].
The initial step in selective presentation of a non-self antigen to the immune system is binding of a pathogen/antigen to endocytic receptors expressed by dermal DCs, immature DCs and macrophages. Binding of the ligand triggers endocytosis/phagocytosis, which leads to formation of early endosomes that develop into late endosomes and lysosomes where degradation of the pathogen occurs, while the receptor is recycled to the cell surface. Degradation in late endosomes/lysosomes leads to loading of the antigen onto the MHC class Ⅱ complex and transport to the cell surface as vesicles that fuse with the plasma membrane [32,33]. DCs subsequently migrate to lymphoid tissues and antigens are presented to antigen-specific receptors (TCRs) on T cells [33,34]. Internalization by DCs is blocked by cytochalasin D and the kinase inhibitor staurosporine [35], an indication that active cytoskeletal rearrangements are required for these processes. Approximately an hour passes from the moment of endocytosis until an antigen first appears on the surface of an APC. Analysis of fluid-phase endocytosis of a marker dye found that the half-life is about 5 min for early endosomes and 100 min for late endosomes [36].
Antigen presentation can be selective or non-selective [37,38], as DCs can utilize macropinocytosis, receptor-mediated endocytosis, and phagocytosis to capture exogenous antigens for presentation to T cells. Although induction of glucocorticoid-induced leucine zipper (GILZ) [39,40] by the synthetic glucocorticoid dexamethasone is viewed as controlling non-selective macropinocytosis in DCs [38], constitutive macropinocytosis is stringently calcium dependent, as extracellular calcium is sensed by G-protein-coupled calcium-sensing receptors (CaSR) that signal macropinocytosis through Gα-, phosphatidylinositol 3-kinase and phospholipase C. CaSR-induced constitutive macropinocytosis facilitates the sentinel function of macrophages, promoting the efficient delivery of ligands to cytoplasmic pattern-recognition receptors [41]. An important recent study revealed the striking difference between anti-inflammatory macrophages that perform vigorous macropinocytosis constitutively, while pro-inflammatory cells are virtually inactive [42]. These processes carry extracellular fluid into the cell, with subsequent transfer of Ca2+ into the cytosol. When ligand-bound CLEC receptors are enclosed within an endocytic vesicle, Ca2+ in the carbohydrate-recognition domain (CRD) of the receptor dissociates from each monomer and adds free Ca2+ to the interior of the cell. Calcium is uniquely suited to act as the universal intracellular second messenger [43] and has even been proposed as an extracellular "third messenger" [44]. Receptor-mediated endocytosis provides the opportunity to target these receptors for selective initiation of a therapeutic approach.
3. CLEC Superfamily: Diversity and Impact
Drickamer introduced the C-type (Ca2+-dependent) lectin classification scheme in 1988 [45], and has updated its understanding with excellent reviews [46,47,48]. His early efforts evolved to yield other helpful summaries of CLEC diversity such as Zelensky and Gready [7] and a 2013 review of myeloid receptors by Sancho and Reis e Sousa [11]. These reviews aided in fostering more tightly-focused studies on important, individual family members and signaling modalities [49,50,51,52]. Particularly noteworthy, Drickamer and the Imperial College maintain an extremely informative C-type lectin domain database [53], which lists 86 members divided into 16 groups. A common feature is a conserved CRD that binds three or four Ca2+ ions (Figure 1). Reference [54] provides an excellent introduction to the structure and function of the subgroups of CLEC receptors.
While the extracellular calcium-dependency of CLEC receptors is largely understood, the intracellular aspect of signal transduction has remained less clear. Sancho and Reis e Sousa in a comprehensive 2012 review [55] grouped CLEC receptors according to the presence or absence of motifs within the cytoplasmic domain that are known to regulate cellular activity. Sequences that define an ITAM (immunoreceptor tyrosine-based activation motif) or an ITIM (immunoreceptor tyrosine-based inhibitory motif) have been studied extensively [56,57,58]. When the tyrosine residues in an ITAM (YxxI/Lx6–12YxxI/L) are phosphorylated, the motif binds Src and Syk family kinases and activates downstream signaling intermediates by phosphorylation, which leads to stimulation of cellular activity and proliferation [59]. Conversely, tyrosine residues in an ITIM (S/I/V/LxYxxI/V/L) sequence attract the phosphatases SHP1 and SHP2, which inactivate signaling intermediates [60]. Nevertheless, some of these receptors are also endocytic.
A third group of CLECs was described by Sancho and Reis e Sousa [55] that lacks an ITAM or ITIM yet also initiates responses to a ligand. Most of these receptors are within the large Group 2 clade of the C-type lectin family as described by Drickamer and Taylor [48]. These receptors contain an endocytosis motif in their cytoplasmic domain and, although these motifs lack a generalized sequence, several contain an essential tyrosine residue, e.g., the YENF motif in CLEC10A [61] and ASGPR1 [62], and YKSL in DC-SIGN [52]. These receptors also contain additional signals, such as the LL sequence in CLEC10A and LLEEE motif in DC-SIGN that are required for efficient endocytosis. To contrast our discussion in the second part of this review of the immunologically important Group 2 type Ⅱ endocytic receptors, we first describe the type Ⅰ M subfamily (Group 6). These groups illustrate the extremes of the topological features of these receptors.
4. Functional Analysis of the Type Ⅰ CLEC Receptor Family
4.1. The mannose receptor (MR, CD206)
The four-membered M family, named for the macrophage mannose receptor (MMR or MR), has inherent structural complexity. East and Isacke [63] provided an extensive review of the structure and function of this family. These receptors bind glycans containing mannose, fucose, glucose, or N-acetylglucosamine [63,64]. They are topologically single-pass, type Ⅰ membrane proteins with the N-terminus on the extracellular surface and the C-terminal domain in the cytosol (Figure 2). A fibronectin-like type Ⅱ domain near the N-terminus binds collagen [63]. The extracellular heterodomain contains 8 tandemly arranged CRD structures that may play a role in what has been termed cooperative complexity [65], in which the endocytic candidates are shuttled from the most distal binding domain through the glycocalyx to more membrane proximal locations. As for the parent MR (CD206), noteworthy features are the diverse ligand specificity of its various CRDs. Whereas CRDs 1 to 3 are considered to bind very weakly to ligands, CRD4 binds with the highest affinity and has multi-specificity for a variety of monosaccharides. At least three CRDs (4, 5, and 7) are required for high affinity binding and endocytosis of multivalent glycoconjugates [63]. A soluble form of the macrophage-related mannose receptor (CD206) is present in human serum and is elevated in critical illness [66].
The initial crystal structure of CRD4 was revealed as a relaxed conformation that was expected after release of Ca2+ in an acidified endosome [67]. The structure was similar to that of the CRD of the serum mannose-binding protein, which was resolved with two, one or no Ca2+ ions bound [68]. One of the Ca2+ ions coordinated directly with hydroxyl groups 3 and 4 of bound mannose [69,70]. Analyses of the crystal structures and mutagenesis studies showed that the triplet sequence Glu-Pro-Asn (EPN) in the long loop of the CRD determined specificity for mannose and glucose, and when replaced with the sequence Gln-Pro-Asp (QPD) provided specificity for galactose and N-acetylgalactosamine [70,71]. The tyrosine-containing, endocytic motif in the C-terminal domain of MR, as FENTLY, is required for efficient endocytosis of a receptor-bound ligand [52,63]. Interestingly, MR, with its multiple CRDs, preferentially binds a single mannose residue.
Apostolopoulos and colleagues [72] made a remarkable observation that conjugation of the tumor-associated, glycoprotein MUC1 to periodate-oxidized mannan induced a CD8+ cytotoxic lymphocyte response when injected into mice, which was characterized by high secretion of IFN-γ but low level of IgG antibody production [73]. Moreover, the aldehyde groups generated by oxidation of the vicinal hydroxyl groups in the mannose residues of mannan were required for the strong MHC class Ⅰ response; reduction of these groups to alcohols by sodium borohydride after conjugation with MUC1 induced a MHC class Ⅱ response, with a high level of antibody production but no IFN-γ. Both mannan-MUC1 conjugates bound to MR on DCs and the oxidized conjugate was highly effective in inducing an immune response and extending survival in clinical trials with patients with adenocarcinomas [74]. These studies highlighted the possibility of inducing specifically a MHC class Ⅰ or MHC class Ⅱ response with appropriately chosen ligands for CLECs on DCs.
DCs initiate activation of antigen-specific T cells and generation of antibodies by B cells, but DCs can also induce tolerance, particularly to self-antigens and under conditions in which "danger" signals are not present [75,76,77]. Binding of an activating antibody to MR induces maturation of immature DCs, as indicated by upregulation of CD80, CD83 and CD86, but continued incubation with the antibody strongly polarizes the cells to secrete the Th2 cytokine IL-10 while inhibiting secretion of Th1 cytokines such as IL-12 [78]. The antibody ligand induces T cell anergy in co-cultures with matured DCs, and the T cells become unresponsive to subsequent challenge [79]. Thus persistent presentation of the same antigen leads to tolerance, a process related to "self" tolerance in peripheral tissues [75,76,77,78,79]. These results suggest that targeting a CLEC receptor without a co-stimulatory factor leads to T cell anergy. Members of the other superfamilies, the Ig and TNFR families, are essential co-stimulating molecules for sustaining an active immune response [80,81].
An interesting observation was the involvement of MR in internalization of ADAMTS13 (A Disintegrin And Metalloproteinase with a ThromboSpondin type 1 motif, member 13)—also known as von Willebrand factor-cleaving protease). ADAMTS13 is a metalloprotease in plasma that is activated cooperatively by zinc and calcium ions [82] and regulates platelet adhesion and aggregation by cleaving ultra-large von Willebrand factor multimers on the surfaces of endothelial cells. An autoimmune response to ADAMTS13 inhibits the processing of von Willebrand factor, which is required for normal blood clotting, and leads to a disorder called acquired thrombotic thrombocytopenic purpura. This process requires binding by MR on DCs of mannose residues on ADAMTS13, endocytosis into early endosomes, and subsequent processing of ADAMTS13 into peptides that are presented on MHC class Ⅱ molecules to CD4+ T cells [83].
4.2. CLEC13B (DEC-205, CD205, LY75)
CLEC13B (DEC-205) has 10 tandemly-repeated, extracellular CRDs and contains an endocytic motif as FSSVRY along with a tri-acidic targeting motif EDE in the C-terminal, cytoplasmic domain [52,84]. Whereas MR targets more peripheral, early endosomes, DEC-205 expressed by DCs delivers antigens to late endosomes and lysosomes [84,85]. While endocytic activity and non-specific maropinocytosis are generally down-regulated by DCs during maturation, DEC-205 is up-regulated by mature bone marrow-derived DCs and delivers immune complexes to late endosomes/lysosomes within 2 hours after internalization. In contrast, an antibody against DEC-205 is internalized rapidly and appears in the lysosomal compartment after only 15 min, which indicates that receptor-mediated uptake by DEC-205 is maintained in mature DCs [85]. DEC-205 also mediates antigen uptake and presentation by both resting and activated human plasmacytoid DCs [86]. Delivery of antigens by receptor-mediated endocytosis was much more efficient in inducing T cell activation and proliferation than free peptide [84,87]. Similar to results found with MR, non-responsive T cells were obtained with a chimeric protein in which a fragment of hen egg lysozyme (HEL) was fused to an antibody against DEC-205. The HEL peptide conjugated to the antibody induced a strong proliferative response by T cells isolated from mice 2 days after a subcutaneous injection of the same chimeric ligand. When isolated 7 days after the injection, the T cells failed to respond to this challenge, whereas T cells exhibited a strong response when the mice were initially immunized by injecting the peptide with complete Freund's adjuvant. Within 7 days after injection of the ligand-antibody conjugate, the number of antigen-specific T cells was dramatically reduced and the remaining T cells were not responsive to repeated challenge. Steinman and colleagues [76,87] concluded that the initial expansion of T cells in response to antigen presented by DCs in vivo was not sustained without a co-stimulatory factor. Thus when an agonistic anti-CD40 antibody, which binds to CD40 (a member of TNFRSF) on DCs, macrophages and B cells, was injected along with the anti-DEC-205/HEL antibody conjugate, activity of the T cells was maintained. Signaling through CD40 induces changes in DCs that allow them to be effective in antigen presentation [88,89]. Sartorius et al. [90] designed a unique approach to achieve activation of DCs by conjugating the filamentous bacteriophage fd, constructed to include an epitope of ovalbumin, to a single-chain variable fragment of the antibody against DEC-205. The receptor delivered this package to the late endosomal/lysosomal compartment where the bacteriophage, the DNA of which is rich in CpG motifs, triggered a TLR9-mediated response for production of IL-6 and IFN-α while the OVA epitope was processed for presentation to T cells through the MHC class Ⅰ and MHC class Ⅱ pathways. By providing co-stimulatory factors through the TLR9 receptor in the lysosomal compartment, the immune response to the antigen internalized by DEC-205 was sustained.
4.3. CLEC13E (ENDO180)
Family member CLEC13E (Endo180) is proving to be centrally involved in glioblastoma multiforme [91] and bone cancer [92]. Through binding to the fibronectin domain, endocytosis of collagen or large collagen fragments serves to direct this protein to lysosomal degradation. This capacity endows Endo180 with a critical role in development and homeostasis, as well as in pathological disruptions of the extracellular matrix structure. Calcium-dependent conformational changes associated with ligand-binding domains 1 to 4 are viewed as likely key structural determinants [93]. Studies of CLEC13E have also provided insight into the complexity of carbohydrate ligand recognition. CLEC13E contains eight CRDs and binds mannose, fucose and N-acetylglucosamine in a Ca2+-dependent manner, but not galactose. This activity is mediated by only one of the eight CRDs, CRD2, which is similar in its monosaccharide binding specificity to that of MR CRD4 [94]. Although Endo180 and the MR are mannose-binding lectins, each receptor is likely to have a distinct set of glycoprotein ligands in vivo.
4.4. CLEC13C (PLA2R)
The least well-known M family member is CLEC13C (PLA2R), a phospholipase A2 receptor that was identified as a potential tumor suppressor that acts through the p53 pathway [95]. CLEC13C was reported to be a target antigen in idiopathic membranous nephropathy [96]. Similar to Endo180, PLA2R has been shown to bind collagen, utilizing the fibronectin-like type Ⅱ domain and C-type lectin domains 1 and 2, a functionality beyond binding secretory PLA2 [97]. A recent study established its differential overexpression in children with atopic asthma, suggesting that PLA2R is involved in regulation of hyper-responsiveness and airway inflammation [98]. Interestingly, PLA2R binds to the annexin A2-S100A10 complex [99] and suggests that the S100 proteins, the largest and most distinctive EF hand-containing, calcium-binding subfamily, may have a role to play in CLEC family function [100].
5. Functional Analysis of Type Ⅱ CLEC Receptors
The numerous type Ⅱ receptors are single-pass, membrane proteins that have their N-terminus in the cytosol and the C-terminal domain on the extracellular surface [101,102]. Synthesis of typical membrane and secreted proteins is initiated as a "hair-pin" structure that contains a signal sequence at the N-terminus, which guides the ribosome to the ER membrane. As the protein elongates, the protein is extruded into ER lumen. Cleavage of the signal sequence releases the protein into the ER for eventual secretion. Extensive, internal hydrophobic sequences serve as a membrane-anchor and after completion of synthesis holds the protein within the membrane bilayer, with the N-terminus in the interior of the ER. The hydrophobic sequence is often flanked at the trailing end by positively charged arginine or lysine residues that act as a "stop-transfer" signal. Vesicular transfer of membranes through the secretory pathway will eventually expose the N-terminus of these proteins on the cell surface as type Ⅰ receptors. A type Ⅱ membrane protein lacks a typical signal sequence that would guide the N-terminus of the nascent protein into the ER lumen. As these proteins are synthesized, a single internal hydrophobic sequence is embedded into the ER membrane, with the nascent polypeptide again as a "hair-pin" structure. This internal, single hydrophobic sequence functions as both an ER stop-transfer and membrane-anchor sequence. As synthesis proceeds, the C-terminal domain of the growing chain is extruded into the ER lumen via cotranslational transport while the N-terminus remains in the cytosol. Internal signal-anchor sequences are not cleaved and after synthesis is completed the protein remains within the membrane to maintain the type Ⅱ topological orientation. Several examples of the most extensively studied receptors are described in the following.
5.1. DC-SIGN (CLEC4L, CD209)
The type Ⅰ MR binds to single mannose residues, whereas the type Ⅱ DC-SIGN (dendritic cell-specific intercellular adhesion molecule (ICAM)-3 grabbing non-integrin, CD209), a tetrameric protein with a single CRD per subunit [52,103], preferentially binds high-mannose oligosaccharides [52,104,105]. The CRD contains four Ca2+, with three Ca2+ in the carbohydrate binding site, two of which directly coordinate with sugar residues. DC-SIGN is highly expressed on DCs [52], where ligation results in ERK and PI3K activation and modulates cytokine production [106]. DC-SIGN is also expressed on macrophages [105]. The receptor actively internalizes oligosaccharide-containing pathogens such as viruses and delivers the pathogen for degradation to late endosomes and lysosomes that stain for MHC class Ⅱ complexes [52]. DC-SIGN expression is maintained during maturation of DCs in keeping with its role in adhesion of DCs to enhance transfer of antigen to T cells in lymph nodes. Depending on the ligand, DC-SIGN can promote a pro-inflammatory response with release of cytokines IL-6 and IL-12 or an alternate pathway resulting in the production of IL-10 [55]. The cytoplasmic domain contains endocytic motifs YKSL in addition to dileucine and tri-glutamate sequences [52]. As with other C-type lectin receptors, binding of ligand is sensitive to pH and is lost at a pH of 5.5 [105]. Interestingly, a related protein, DC-SIGNR, which also has three Ca2+ in the binding site, retains full binding ability at pH 5.0 [105]. The DC-SIGN Ca2+-binding site has been shown to influence phagocytosis of E. coli [107]. DC-SIGN also exhibits cooperative interaction with soluble surfactant protein D (SP-D) to modulate HIV-1 capture and transfer antigens to CD4+ T cells [108,109]. As with CLEC13C (PLA2R), the N-linked mannose-rich glycan of annexin A2 is a documented ligand for DC-SIGN. Annexin A2 on nasopharygeal carcinoma cells bound to DC-SIGN, which inhibited DC maturation and IL-12 production but stimulated production of the immunosuppressive IL-10 [110].
5.2. ASGPR1 (CLEC4H) and CLEC10A (CD301)
Terminal galactose (Gal) or N-acetylgalactosamine (GalNAc) residues on glycans attached to proteins, with the primary exception of the blood group substances, result from removal of sialic acid from O-glycans or a shift in regulatory pathways that lead to incomplete synthesis [111]. The Tn antigen (GalNAc-OSer/Thr-) is a rare structure in healthy tissues but relatively common on tumor-associated glycoproteins [9,10,112]. The terminal GalNAc is generally restricted to tissues such as cancer cells or pathogens, which makes CLEC10A a very specific detector of pathogens and a highly sensitive modulator of DCs. A total of 96 glycoproteins bearing one or more Tn antigens was identified on human T lymphoblastoid cells (Jurkat) and 33 glycoproteins were identified on human breast adenocarcinoma cells (MCF7 cell line) [112]. GalNAc is the preferred ligand for the hepatic asialoglycoprotein receptor-1 (ASGPR1, also called the Ashwell-Morell receptor), with a 60-fold greater affinity for GalNAc over Gal [113]. ASGPR1 was the first lectin-type cellular receptor to be identified in mammals [114,115], and has been studied extensively over the past several decades since its discovery [116]. The GalNAc specificity of ASGPR1 is also shared by the endocytic receptors CLEC4F, expressed by liver Kupfer cells [117], and CLEC10A (CD301, also designated the macrophage galactose-type lectin, MGL) [10,49,118]. The mouse expresses two isoforms of MGL, MGL1 (CD301a) that is specific for Gal and MGL2 (CD301b) that is specific for GalNAc [118].
The function of the endocytic ASGPR1 is to bind serum proteins and cells whose attached glycans have lost terminal sialic acid residues, which exposes the penultimate Gal or GalNAc moieties. Weigel and Yik [116] presented an extensive review of the hepatic ASGPR. With isolated hepatocytes, internalization occurs rapidly, with a half-life of 2 to 4 min and a half-life of degradation of the protein of 15 to 20 min. The receptor is rapidly recycled and reappears on the cell surface within 5 to 7 min. Based on the biphasic kinetics of dissociation of ligand-receptor complexes, two pathways were proposed, with half of the internalized complex dissociated in 2.5 min whereas the other half was dissociated in about 50 min, which suggested separate compartments. The rapid dissociation occurred without a significant decrease in endosomal pH. To explain why all structures with terminal Gal or GalNAc are not taken up by ASGPR1, Weigel offered the Galactosyl Homeostasis Hypothesis that proposed essential cell-to-cell communications functions are provided by these sugars and their lectin-type receptors. Removal from circulation may thus depend upon avidity of binding to various receptors.
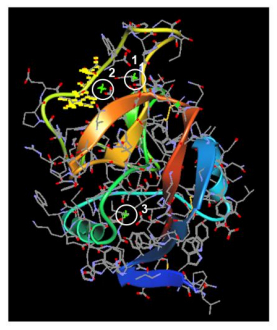
The extracellular domain of ASGPR1 (CLEC4H1) and the highly homologous CLEC10A (CD301) is a particularly cogent example from a structural and functional standpoint. It embodies and defines the essential details of carbohydrate ligand recognition and Ca2+ binding, with relatively well-known protein functions. The structure of the H1 subunit [119,120] provides a prototypic understanding of the GalNAc-specific CLECs (see Figure 1). Two Ca2+ ions are within the binding site of the carbohydrate-recognition domain (CRD) and a third occurs at the base of the CRD [120]. Ca2+ is required for stability of the CRD and Ca2+(2) directly coordinates with hydroxyl groups 3 and 4 of a bound carbohydrate ligand. The sequence QPD in the long loop of the sugar-binding site defines the specificity for Gal and GalNAc (see Figure 1).
The Group 2 CLEC family usually contains three disulfide bonds that define the CRD [120]. ASGPR1 contains disulfide bonds between cysteines 154↔165,182↔277 and 255↔269. The 255↔269 disulfide bond perhaps qualifies as the more central defining feature for diverse ligand specificity because of its proximity to the two high-affinity Ca2+ binding sites. This bond is also located within an integral region of the characteristic long loop, containing other highly conserved scaffold features such as a bend motif (W-hydrophobicX-G-L) and the calcium/sugar binding QPD motif. A particularly noteworthy feature of the high-affinity calcium-binding region is the density (loop region > 10%) of tryptophan (W) residues, especially in the CRD of ASGPR1 and CLEC10A. Conservation of such an energetically expensive amino acid at such high levels likely speaks to functional necessity.
CLEC10A is expressed predominantly by dermal DCs, immature DCs and alternatively-activated (M2) macrophages [10,49,121]. CLEC10A is also expressed by basophils [122], mast cells [123], CD8+ lymphocytes in patients with rheumatoid arthritis and with large granular leukaemia [124], and is upregulated several-fold in patients with juvenile idiopathic arthritis [125]. CLEC10A is expressed at the 8-cell stage of embryogenesis [126] and by hematopoietic stem cells during differentiation of multipotent progenitors to myeloid committed cells [127]. It also identifies subpopulations induced by allergen [128] and ozone exposure [129]. CD301b+ DCs stimulate tissue-resident memory CD8+ T cells to protect against genital HSV-2 [130], and specialized DCs induce Th17 formation [131]. CLEC10A is a marker for intermediate monocytes, a population between CD14++ and CD16++ monocytes [132,133], which incidentally is a target for the Zika virus [134]. In obese patients, a macrophage population arises that has been designated M1½ and is shifted from the suppressive M2 toward an M1 inflammatory phenotype but retains expression of CLEC10A [135], a M2a macrophage marker [136].
CD45 is a ubiquitous, highly glycosylated, receptor-like type 1 membrane protein that is expressed by T cells and other leukocytes. CD45 is a phosphatase required for cell activation and survival [137] and was identified as an endogenous ligand for CLEC10A (MGL) [138]. Several isoforms of CD45 are expressed as the result of alternative transcript splicing, e.g., CD45RO, CD45RA, CD45RAB or CD45RABC in order of increasing size and glycosylation. CLEC10A binds to isoforms that contain exon B [138]. CD45 bears O-linked GalNAc (the Tn-antigen) at two positions, 137 and 140 in the full protein, which lie in exon B [112]. Resting naive T cells express the larger, heavily glycosylated isoforms that have the highest protein-tyrosine phosphatase activity, whereas activated, mature cells express more of the smaller isoforms, CD45RA and CD45RO, which have low phosphatase activity [139,140,141]. Interaction of CLEC10A with CD45 has been described as a cause of suppression of T cell activity and apoptosis [138]. However, as immature DCs migrate to lymphoid tissues and mature, expression of CLEC10A is down-regulated and nearly absent in mature DCs [138,142]. T cells that undergo clonal expansion after activation express the shorter isoforms of CD45 and thus would be impervious to the presence of cells that express CLEC10A. The same reasoning applies to tumors in which infiltrating lymphocytes would not be suppressed by CLEC10A expressed by the immunosuppressive, tumor-associated M2a macrophages [136]. However, CLEC10A expression is induced in DCs by glucocorticoids [138,142], which may be a factor in the immunosuppressive activity of these steroids.
6. Endocytosis
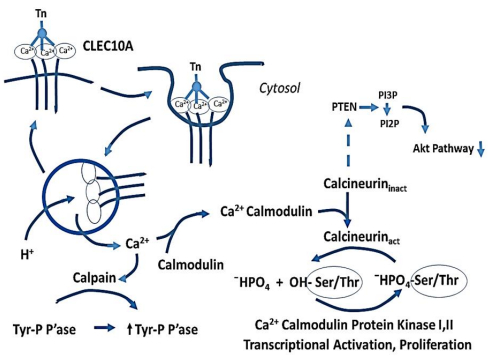
Lectins generally have a relatively low affinity to sugars. The KD of α-methyl Gal binding to CLEC10A, determined by saturation-transfer-difference NMR, was 900 µM, whereas the affinity for α-methyl GalNAc, determined as the KI for inhibition of α-methyl Gal binding, was 12 µM [143,144]. These results demonstrate the remarkable specificity of CLEC10A for GalNAc. Multivalency dramatically increases avidity of binding to the receptor, largely by lowering the off rate. The strong effect of multivalency on avidity of binding of ligands to ASGPR1 is illustrated by the KD values of 10–3, 10–6, 5 × 10–9 and 10–9 M for mono-, di-, tri-or tetra-antennary GalNAc-containing structures, respectively [116,145,146]. Synthetic multivalent Tn structures bind with several orders of magnitude greater avidity to CLEC10A than the monovalent structure [147,148]. When a peptide antigen was presented to antigen-specific T cells by A20 cells, a B cell lymphoma cell line as the APC, the T cell response was increased 10,000-fold when attached to a multivalent Tn structure and was achieved at peptide concentrations of approximately 1 nM [147]. Thus the in vivo dynamics of antigen presentation occur a much lower concentrations of antigen than determined by in vitro, chemical systems.
Following endocytosis, dissociation of the ligand from a receptor requires a change in the endosomal environment. A process of acidification begins in the early endosome, which continues through late endosomes and eventually in the lysosomes where pathogens are degraded by catabolic enzymes with acidic pH optima [18,149]. Although dissociation of Ca2+ and the ligand from the receptor in vitro as a function of lowering of the pH is well documented, with half-maximal binding near pH 6 and essentially no binding activity at pH 5 [61,105,150], the cation is completely dissociated from ASGPR in vivo with only a modest decrease in pH from 7.4 to 6.9 [151]. Dissociation in vivo results from the rapid extrusion of Ca2+ from the endosome [152] through several mechanisms, including a Ca2+/ATPase pump and a Ca2+/H+ antiporter [149,153]. The concentration of Ca2+ within the endosome drops from the extracellular value near 1.2 mM to 30 µM within 3 min [151]. The KD of Ca2+ (1) and (2) in the CRD of ASGPR1 is 330 µM at pH 6.9, the pH of the early endosome, and thus Ca2+ dissociates from the receptor as the concentration of free Ca2+ is lowered. Because Ca2+ is required for binding, the ligand is released. After dissociation, the receptor recycles back to the cell surface while the ligand generally is degraded and processed to either late endosomes/lysosomes, the MHC Ⅱ pathway, or translocated to the cytosol and the MHC Ⅰ pathway [18,19,21,22,23,24].
An antibody against the receptor CLEC10A was initially localized after endocytosis within early endosomes in DCs and was detected in late, MHC class Ⅱ-positive endosomes only after several hours [154]. Modified forms of the glycoprotein MUC1 that express short glycans with terminally exposed GalNAc bound to CLEC10A and after endocytosis progressed through to the late endosomes but then were processed no further [155,156]. The positions of glycans on the protein may block proteolytic cleavage sites, which prevents generation of presentable antigens [156]. Whereas antigens in the late endosomal/lysosomal compartments are loaded onto MHC Ⅱ complexes for presentation to CD4+ T cells, those that escape into the cytosol are loaded onto MHC Ⅰ complexes in the ER, move to the cell surface, and are presented to CD8+ T cells. Shorter fragments of MUC1 with attached GalNAc residues can escape the endosomes and enter the cytosol, where they are recognized as foreign peptides, and transferred through TAP into the ER [18,19,32]. A synthetic, branched molecule containing multiple GalNAc moieties (Tn antigens) strongly promoted a Th2 immune response and an elevated release of IL-10 when presented to T cells by APCs [157,158]. Similar results were obtained when an antigen was targeted to DC-ASGPR by an antibody [159]. This receptor was characterized previously and shown to deliver antigen to early endosomes [160]. IL-10 induces immunosuppression, and continued stimulation of this pathway can lead to tolerance and even T cell deletion.
The heavily glycosylated, tumor-produced MUC1 glycoprotein bound to the MR and was internalized by DCs, but the protein remained within the early endosome or was recycled to the cell surface along with the receptor [63]. In contrast, DEC-205 targeted ligands to late endosomes and lysosomes that stain for MHC class Ⅱ complexes [84,85]. MR is expressed by DCs in the dermis, whereas DEC-205 is expressed more strongly in the basal layer of the epidermis [52]. DEC-205 delivered antigens to CD4+ T cells significantly more efficiently than MR [84,85]. Endocytosis of DC-SIGN is induced upon ligand binding, which in immature DCs also delivered antigen to late endosomes/lysosomes, with a compartment pH of 5.47, but in mature DCs the ligand was internalized to early endosomes that had a pH of 6.45 [52].
Internalization of a pathogen or an immunogen by a dermal DC starts migration of the cell to a draining lymph node, a trip that takes 3 to 4 days [161,162,163]. The pathogen is processed for loading onto MHC class Ⅰ or MHC class Ⅱ complexes along the way. This process of maturation includes down-regulation of receptors and preparation of the DC for efficient presentation to antigen-specific T cells. In lymph nodes, a DC scans about 500 different T cells an hour, seeking the rare (1 in 105 to 106) antigen-specific T cell, over a period of several days [26]. When recognition occurs, the antigen is transferred to the specific T cell receptor (TCR), which activates the T cell for clonal expansion and release of cytokines [25]. In the presence of IL-12, MHC class Ⅱ-activated CD4+ T cells differentiate into Th1 cells that produce IFN-γ. In the presence of IL-4, CD4+ T cells become Th2 cells that release IL-4, IL-5, IL-10 and IL-13 [164], which promote transfer of the antigen to B cells for subsequent differentiation into antibody-producing plasma cells [165].
7. Calcium
DCs are the most powerful antigen presenting cell and achieve antigen-specific activation of CD4+and CD8+ T cells. C-Type lectin receptors are excellent mediators of entry of pathogens/antigens and Ca2+ into the cell. Calcium is critical for the overall function of DCs [166]. An extensive literature supports the hypothesis that a major outcome of ligand-induced endocytosis of CLEC receptors is activation of DCs by the transfer of Ca2+ into the cell interior. In addition to the Ca2+ bound to the CLEC receptors, the endocytic vesicles also delivers extracellular fluid, in which the free Ca2+ concentration is approximately four orders of magnitude greater than the intracellular concentration, i.e., 1.2 mM outside of the cell and less than 0.1 μM inside, to the endosome [149,153,167]. Antigen processing, including endosome traffic, pathogen digestion, migration to lymph nodes during maturation of DCs and antigen presentation to T cells requires Ca2+ [166]. A recent report describes the control of DC migration as a response to release of Ca2+ from lysosomes [168]. Ca2+ is released through TRPML1 (transient receptor potential cation channel, mucolipin subfamily, member 1), activates actin-based motor protein myosin Ⅱ to promote fast and directional migration and leads to down-regulation of macropinocytosis.
Immature DCs exhibit spontaneous oscillations in cytosolic Ca2+ with a periodicity of 12.5 sec at 37 ℃, a behavior that is lost as DCs mature [169]. A source of the cytosolic Ca2+ is release from internal sources, mediated by the inositol 1, 4, 5-triphosphate receptor on the ER and to a lesser extent from influx from extracellular fluid [169]. As Figure 3 illustrates, ligand-induced transfer of CLEC receptors into endosomes contributes to cytosolic Ca2+. The increase in cytosolic Ca2+ drives activation of Ca2+-dependent phosphatases and kinases that result in rapid changes in the rates of a plethora of reactions, including gene transcription, cell proliferation, cytoskeleton activities, migration and apoptosis [171,172,173,174]. Many of these processes are mediated by calmodulin, which binds Ca2+ with very high affinity [175]. MHC class Ⅱ antigen maturation and presentation in human DCs is regulated by Ca2+-calmodulin kinase Ⅱ [176,177]. The interplay of phosphatases and kinases in response to the concentration of Ca2+ regulates the levels of activation of signal transduction intermediates. A large number of signal transduction intermediates that are rapidly dephosphorylated (within minutes) carry phosphate on Ser or Thr residues, which indicates activation of Ser/Thr phosphatases such as protein phosphatase-2B (PP2B, calcineurin) [178], PTEN [179], PP1 and PP2A [180]. The Ca2+ oscillations in immature DCs induced migration of NFAT into the nucleus, which requires dephosphorylation of cytosolic NFAT by calcineurin [181,182]. NFAT is rapidly rephosphorylated by glycogen synthase kinase-3 (GSK-3), a Ser/Thr protein kinase in the nucleus, and returned to the cytosol. A metabolically important kinase, the 5'-AMP-activated protein kinase (AMPK), is activated by Ca2+-activated protein kinase kinase β (CaMKKβ). In turn, AMPK phosphorylates a Thr residue on CaMKKβ to render the latter enzyme completely dependent upon Ca2+/calmodulin [183]. Many signal transduction intermediates and cellular processes are also regulated by phosphorylation of tyrosine residues [184,185,186,187,188]. The regulation of signal transduction pathways and subsequent consequences for the cell were extensively reviewed by Bononi et al. [189]. Activation of tyrosine kinases can also lead in turn to an increase in intracellular Ca2+, a major event occurring after MHC class Ⅰ ligation of T cells [31]. In addition, proteases such as the Ca2+-dependent calpain are activated by Ca2+ [190], whose activity regulates the activity of other phosphatases and kinases [191].
The transient rise in the cytosolic Ca2+ is rapidly reversed by Ca2+-ATPases in the plasma membrane to pump Ca2+ out of the cell or on the ER membrane to pump Ca2+ back into the ER [149,153]. When the ER store becomes depleted, ER membrane proteins (STIM1 and STIM2) interact with subunits (ORA1) of calcium release-activated channels (CRAC) in the plasma membrane to allow Ca2+ entry into the cell from the extracellular fluid, the process of store-operated Ca2+ entry (SOCE) [192]. Upon activation of T cells, CRAC initiates production of inositol 1, 4, 5-triphosphate, which is the primary signal to release Ca2+ from the ER store. However, Vaeth et al. [193] demonstrated that when SOCE is inhibited by deletion of Stim1 and Stim2 genes, T cell activation is preserved. Interestingly, an influx of Ca2+ causes a spike in ATP production by mitochondria and release of ATP into the extracellular space. ATP metabolites then bind to purinergic receptors and contribute to the influx of Ca2+ and T cell activation [194].
8. Conclusion
The ability to initiate an immune response by ligand presentation to C-type lectin-type receptors is a potentially valuable means to therapeutically treat a variety of diseases. Particularly important is the ability to tune the response dependent upon the ligand toward a MHC class Ⅰ or MHC class Ⅱ presentation to T cells, generating a Th1 or Th2 state, processes that were excellently reviewed by Zizzari et al. [195]. CLEC receptor-mediated endocytosis triggers a Ca2+ influx that leads to a plethora of cellular responses [10,51,196]. The outcomes vary from activation of phagocytosis and cell killing [197] to suppression [198]. Whereas these receptors are characterized by a carbohydrate ligand, immunotherapeutic responses can be achieved in vivo with synthetic peptide mimetics of the natural ligand, as found in models of glioblastoma multiforme [199,200] and ovarian cancer [201], which offers a novel approach to drug design. There is yet much to learn.
Acknowledgements
The work was supported by Susavion Biosciences, Inc. The funders had no role in the literature research, collection, interpretation, decision to publish, or preparation of the manuscript. LLE and JKH declare that they are inventors of intellectual property that has been assigned to Susavion Biosciences, Inc., in which these authors hold shares.
Conflict of Interest
All authors declare that no conflicts of interest in this paper.









 DownLoad:
DownLoad: