Citation: Dumisani Chirambo. Increasing the value of climate finance in an uncertain environment: Diaspora financial resources as a source of climate finance for Sub-Saharan Africa[J]. AIMS Environmental Science, 2017, 4(6): 730-742. doi: 10.3934/environsci.2017.6.730
| [1] | Ruchira R N Ghormare, Sana Fatima, Priya Grover, Nidhi Phutela, Vinay Kandpal, Ernesto D. R. Santibanez Gonzalez . Exploring the paradigm shift towards sustainability: A systematic literature review on circular economy and eco-innovation. AIMS Environmental Science, 2024, 11(6): 940-959. doi: 10.3934/environsci.2024047 |
| [2] | Filippo Sgroi . Circular economy and environmental protection. AIMS Environmental Science, 2022, 9(2): 122-127. doi: 10.3934/environsci.2022009 |
| [3] | Sergey Orlov, Elena Rovenskaya, Julia Puaschunder, Willi Semmler . Green bonds, transition to a low-carbon economy, and intertemporal welfare allocation: Evidence from an extended DICE model. AIMS Environmental Science, 2024, 11(4): 628-648. doi: 10.3934/environsci.2024031 |
| [4] | Filippo Sgroi . Landscape management and economic evaluation of the ecosystem services of the vineyards. AIMS Environmental Science, 2021, 8(4): 393-402. doi: 10.3934/environsci.2021025 |
| [5] | Majid Ibrahim Alsaggaf . The dynamic nexus between economic factors, socioeconomic factors, green growth factors, and ecological footprint: evidence from GCC economies. AIMS Environmental Science, 2024, 11(5): 797-830. doi: 10.3934/environsci.2024040 |
| [6] | Filippo Sgroi . Agriculture and tourism: economic evaluation of sustainable land management. AIMS Environmental Science, 2022, 9(1): 83-94. doi: 10.3934/environsci.2022006 |
| [7] | Simon Bergsma, Efthymios Poulios, Nikolaos Charalampogiannis, Spyridon Achinas . Lactic acid bacteria as bioprotective agents: A mini-review on biotechnological-and human health-based facets. AIMS Environmental Science, 2023, 10(2): 206-225. doi: 10.3934/environsci.2023012 |
| [8] | Serpil Guran . Options to feed plastic waste back into the manufacturing industry to achieve a circular carbon economy. AIMS Environmental Science, 2019, 6(5): 341-355. doi: 10.3934/environsci.2019.5.341 |
| [9] | Philipp Braun, Timm Faulwasser, Lars Grüne, Christopher M. Kellett, Willi Semmler, Steven R. Weller . On the social cost of carbon and discounting in the DICE model. AIMS Environmental Science, 2024, 11(3): 471-495. doi: 10.3934/environsci.2024024 |
| [10] | María Santos-Corrada, Rafael Méndez-Tejeda . Public perception of climate change in a period of economic crisis in Puerto Rico. AIMS Environmental Science, 2017, 4(1): 83-93. doi: 10.3934/environsci.2017.1.83 |
During the last decades there is an increasing interest and a rapid development of new nanomaterials for various industrial and technological applications. Indeed, up-to-date nanostructured materials have been successfully applied, either as coatings or bulk materials, in a wide range of technological fields such as in electronics, catalysis, magnetic data storage, structural and mechanical components etc. [1]. Their wide applicability is due to their superior properties [1], when compared to conventional micro-crystalline materials.
One of the recently developed nanomaterials is the Ni-W system. Ni-W based alloy coatings having different wt.% W content have been deposited onto metallic substrates either by sputtering [2], or electrolytic [3] techniques. However electrodeposition is considered as one of the most important deposition processes for the production of pure and alloyed metallic coatings. It can be easily understood that nanocrystalline Ni-W coatings due to their excellent properties [4, 5] have attracted a lot of attention in the scientific and industrial community. It should be noted that the existing scientific literature focuses more on the surface properties [4, 5, 6], rather than the bulk properties [7, 8] of Ni-W coatings.
This scientific work deals with the properties of Ni-W coated copper and not of bulk Ni-W e.g. foils [7, 8]. In industrial applications and especially in the electronics industry Ni-W is used as a coating on copper and not as a bulk material. Thus, it is considered very important to study the properties of the coated system and not just of the coating itself. For example, in many cases involving mechanical loading, failure occurs at the interface between thee coating and thee substrate and not in the coating. In this perspective the behaviour of the coated system needs to be addressed.
Furthermore, the effect of the coating thickness on mechanical properties of the coated system is investigated. Most of the existing articles focus only on the effect of e.g. composition and microstructure, but they neglect the effect of coating thickness on the mechanical properties of the system. In this work, an attempt is made to illustrate how changes in the thickness of the coating can have an important influence on the microstructure and mechanical properties of the coated system. In this way a structure-property relationship is established for this type of nanostructured coated materials. Finally, research data on the tensile properties of Ni - 40 wt.% W coatings are presented. In existing literature information on the mechanical properties can be found only for Ni-W coatings having a W content up to 30 wt.%.
The substrate material used in this study was a commercially pure copper sheet. From this sheet copper substrates with length 40 mm, width 10 mm and thickness 1.5 mm were produced for the structural study and microhardness experiments, whereas standard tensile specimens were prepared for the tensile experiments. These specimens then were grinded and polished to an average roughness of 1 μm and then annealed at 350 oC for 2 hrs in an Ar-inert atmosphere, in order to remove residual stresses, brought about by the mechanical machining of the samples.
Prior to the electrodeposition process, the copper substrates were ultrasonically cleaned with acetone for 5 min and then rinsed with distilled water. Nickel-tungsten alloy coatings were then electrodeposited on the copper substrates from a sodium citrate aqueous solution, using a two electrodes configuration [9]. Cathode was the copper substrate, whereas the anode was a nickel electrode. The copper substrate and the nickel anode were placed vertically, facing each other. The in-between distance was approximately 30 mm. The used plating bath composition and conditions are given in Table 1. Magnetic agitation was conducted at 200 rpm.
| Bath composition(g/L) | 17 NiSO4*7H2O, 147 Na3C6H5O7*2H2O, 46 Na2WO4*2H2O, 27 NH4Cl, 15 NaBr |
| Current density (mA/cm2) | 40 |
| Deposition time (min) | 30, 60, 90, or 120 |
| pH | 6 |
| Temperature (o) | 75 ± 3ºC |
| Agitation (rpm) | 200 |
| Anode | Nickel |
DownLoad: CSVThe surface and the cross-sections of the coatings were studied with the aid of a JEOL 6100 Scanning Electron Microscope (SEM). The chemical composition of the produced coatings was examined with the aid of a NORAN TS 5500 Electron Dispersive Spectrometer (EDS), which was connected to the SEM. With the aid of a SIEMENS D5000 X-ray diffractometer, giving a CuKa radiation from a graphite monochromator, the crystal structure of the grown coatings was studied. Analysis of the obtained X-ray Diffraction patterns was performed with the use of X’Pert HighScore Plus Software. The root mean square (RMS) roughness of the coatings was measured with the aid of a DME Dualscope DS95 Atomic Force Microscope (AFM). The current efficiency (ηc) of the electodeposition process was calculated by applying the following formulas, which are based on Faraday’s law:
| ηc = (W1/W2) × 100 | (I) |
where W1 is the weight deposited in g and W2 is the weight expected in g.
| W2 = ItM/nF | (II) |
where I is the current in A, t is in s, M is the molecular weight in g, n is the number of electrons involved in the electrochemical reaction and F is Faraday’s constant.
The microhardness of the Ni-W alloy coatings was examined in the cross section with the help of a SHIMADZU HMV 2000 microhardness tester, imposing 0.15 N for 15 s. The tensile behavior of the copper substrates with Ni-W alloy coating, having approximately 40 wt.% and various thicknesses, was studied with the aid of an INSTRON 4482 testing system. All tensile experiments were performed at a strain rate of 10−4 s−1, in laboratory air at room temperature. Extensive metallurgical microscopy was performed on the surfaceof Ni-W coated copper specimens after applying various values of tensile elongation. For each set of experimental conditions, five independent tests were carried out.
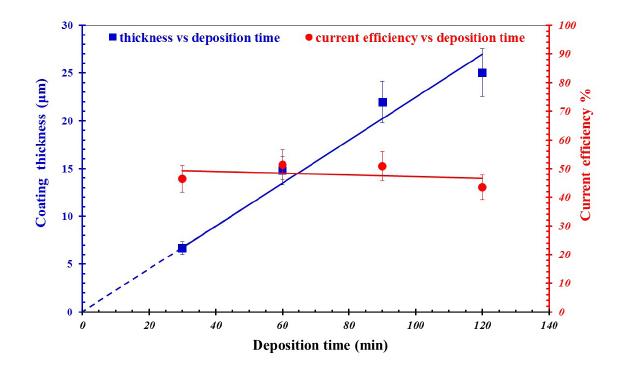
The cross section of Ni-W coated copper specimens, deposited for (a) 30, (b) 60, (c) 90 and (d) 120 minutes are presented in Figure 1. All coatings were free of intensive pores or cracks, especially at the interface of the electrodeposited alloy coating with the copper substrate. This observation is indicative of good adhesion between the coating and the substrate. In addition, the average thickness of the studied Ni-W coatings was calculated by using Image Analyzer Program and is presented as a function of deposition time in Figure 2. The thickness of Ni-W coatings increases almost linearly with deposition time, indicating a relatively constant deposition rate throughout the deposition process. In Figure 2, the effect of deposition time on the current efficiency of the deposition process is presented. No significant influence of the current efficiency with deposition time (for the examined deposition conditions) was observed. Furthermore, the calculated current efficiency values are in agreement with those reported in literature [3] and in other research articles [10, 11].
Figure 1. Cross sectional micrographs of Ni-W coated copper deposited for: (a) 30, (b) 60, (c) 90 and (d) 120 min.
Figure 2. Effect of plating time on thickness and current efficiency of Ni-W electrocoatings.
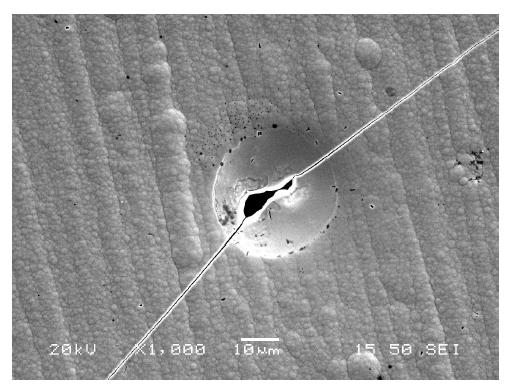
Surface analysis of the Ni-W electrodeposits, having different thicknesses, showed that in all cases a typical nodular structure was obtained, Figures 3(a), 3(b), and 3(c). For the used experimental conditions, the size of nodulus is seen to increase with increasing deposition time, whereas for the growth of the coating follows the topography of the copper substrate. However, for deposition times equal to 120 min localized cracking of the coating was observed, Figure 4. This phenomenon can be attributed to the residual stresses, which are brought about mainly by hydrogen uptake during the electrodeposition process. Indeed, it has been proposed [12] that during the electrodeposition process hydrogen dissolution into metallic matrixes leads to an expansion of the materials lattice. However, subsequent release of the diffused hydrogen causes the occurrence of tensile stress, due to a shrinkage of the lattice. In addition, higher tensile stresses are observed with increasing deposition time, for the same plating conditions, as a higher hydrogen fugacity in the surface layers of the material occurs [13]. If the tensile stresses exceeded the Ultimate Tensile Strength (UTS) of material localized rupture and the formation of cracks occurs, as seen in Figure 4.
Figure 3. Effect of plating time on surface morphology of Ni-W coatings (a) 30, (b) 60, and (c) 120 min.
Figure 4. Localized cracking due to hydrogen evolution during electrodeposition process observed after 120 min of deposition.
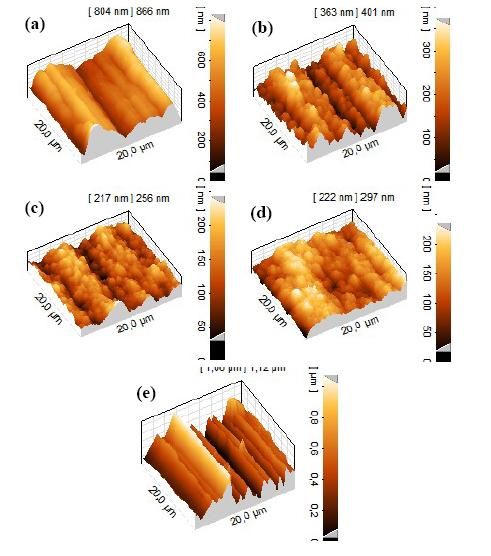
The surface topography of the electrodeposited Ni-W coatings was investigated by AFM analysis. Typical 3D profiles of the surface of Ni-W coatings deposited for 30, 60, 90 and 120 min are presented in Figure 5(a), 5(b), 5(c) and 5(d) respectively. It can be clearly seen that during the initial steps of the electrodeposition process, the coating growth is following the surface topography of the copper substrate, Figure 5(e). An increase of deposition time results in a more homogenous growth of the coating and to a smoother surface finishing. Indeed, the surface roughness (RMS) of Ni-W coatings was observed to decrease with increasing deposition time, for the selected plating conditions, Figure 5.
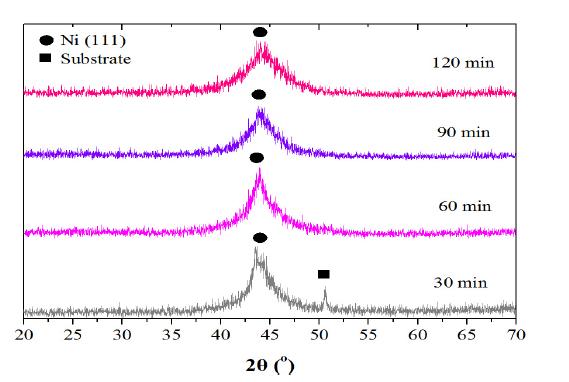
Figure 5. Effect of plating time on surface morphology of Ni-W coatings (a) 30, (b) 60, (c) 90, (d) 120 min and (e) bare copper substrate.From the X-ray diffraction spectra, presented in Figure 6, the following can be observed:
Figure 6. X-ray diffraction spectrographs of Ni-W coated copper samples deposited for: (a) 30, (b) 60, (c) 90 and (d) 120 min.
· Peaks from the Cu substrate can be detected for a deposition time equal to or lower than 30 min. This is due to the fact that the penetration depth of X-rays (10 μm) is greater than the thickness of the coating (about 6 μm). Due to overlapping of X-ray peaks of Ni (111) from the Ni-W coating and Cu (111) from the copper substrate an asymmetrical spectrum is obtained for the deposition time of 30 min. However as of the coating becomes thicker the symmetry is also increased.
· Ni-W alloy coatings containing approximately 40 wt.% tungsten are consisted of solid solution of tungsten in nickel. This finding is in partial agreement with nickel-tungsten equilibrium phase diagram [14], as no Ni4W intermetallic phase was detected. This can be due to the relatively low resolution of X-ray Diffraction techniques which can detect metallurgical phases with a higher than 5 Vol.% concentration.
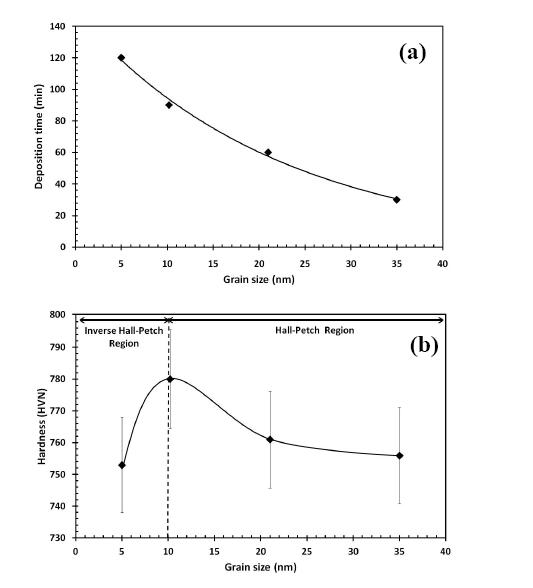
· With the aid of the Debye-Scherrer equation [15], the grain size of the coatings was calculated, Figure 7(a). It can be observed that the increase of deposition time resulted in a decrease of the average grain size of Ni-W coatings. This phenomenon can be possibly due to epitaxial phenomena (micro-crystalline substrate) during the growth of the coating and to the increase of stresses with increasing deposition time, as described previously. The calculated grain size values are in agreement with the experimental work of Auerswald and Fecht [16].
Figure 7. (a) Effect of deposition time on average grain size of Ni-W electrocoatings. (b) Effect of grain size on micro-hardness of Ni-W electrocoatings.· A shift of the main Ni peak in comparison to the theoretical Ni (111) peak, towards smaller diffraction angles, is observed. This is mainly due to macro-strain residual stresses brought about by the synergetic effect of solid solution formation [16] and hydrogen diffusion [17].
The average microhardness values of the produced Ni-W alloy coatings as a function of their grain size are presented in Figure 7(b). Indeed, a grain refinement of the coating was observed with increasing deposition time, Figure 7(a). Thus, according to Hall-Petch theory a higher hardness is expected [18]. However, further increase of the thickness results in lower microhardness values. This decrease can be attributed to:
(a) the existence of micro-cracks in the samples deposited for 120 min which degrade the mechanical characteristics of the coating (see Figure 3)
(b) the grain size is about 5 nm, thus the coating is in inverse Hall-Petch region. It has been proved that Hall-Petch relationship is only valid for grain sizes up to approximately 10 nm [19] for electrodeposited Ni coatings. From this critical value on, further grain size refinement leads to softening of the nanocrystalline material. Several interpretations for this softening behavior have been proposed. The most common explanation is that below the critical grain size, the nanocrystalline materials cannot support the dislocations anymore [20]. Hence the deformation mechanism changes from dislocation movement (up to critical grain size) in the Hall-Petch regime to grain boundary sliding (below critical grain size) in the inverse Hall-Petch regime, as indicated in Figure 7.
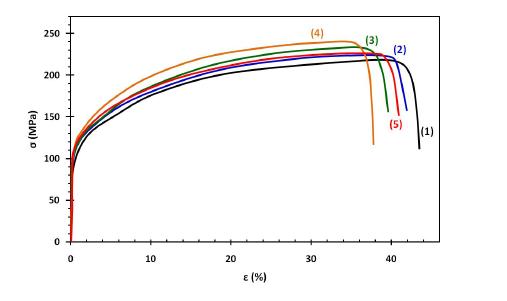
Figure 8 shows the engineering stress-strain curves for the copper specimen in comparison to Ni-W (with different thicknesses) coated copper specimens. From this figure, it can be observed that the Ni-W coated copper specimens had a higher UTS than bare copper. It has been proposed [21] that the UTS of a composite laminate material can be given by the following equation:
Figure 8. Engineering stress-strain curves for: (1) bare copper and Ni-W coated copper samples with (2) 5 μm, (3) 10 μm, (4) 21 μm and (5) 35 μm.
| Pt = PsVs+ PcVc | (III) |
where: Pt is the UTS of the laminate material, Ps is the UTS of the substrate (copper), Pc is the UTS of the coating (Ni-W coating) and Vs and Vc are the % Volume of the substrate and coating respectively, when compared to the total volume of the laminate material. In addition, is widely known that the yield strength (σ) of metallic materials can be related to their Vickers hardness (HVΝ) by the experimental equation [22]:
| σ ≈ 2.9 HVΝ | (IV) |
Therefore, by taking into consideration equations (III), (IV) and the microhardness values given previously (Figure 7), it could be said that the deposition of Ni-W coatings on the copper substrate will possibly lead to higher UTS values, when compared to those of bare copper. In addition, the higher the hardness and/or volume of the coating the higher the UTS of Ni-W coated copper.
Despite the fact that the presented experimental results are in complete agreement with “classical” macroscopic deformation theories, the microscopic phenomena occurring during tensile deformation are much more complicated. Up to now no universal approach has been established on the deformation mechanisms occurring in materials having a grain size between 10 nm up to 1µm [22]. This is due to the fact that various phenomena such as grain boundary sliding, localized dislocation generation and movement, shear-band formation, twinning etc. can coexist in nanomaterials [23]. Furthermore, the existence of defects are found to have a detrimental effect on the properties of nanomaterials.
From figure 8 it could also be said that the ductility of Ni-W coated copper was found to be lower than the ductility of bare copper. The above observation can be attributed to the fact that the presence of surface layers block the egress of dislocations from the metallic substrate to the surface layer [24]. Thus, the lower the movement and multiplication of dislocation in the bulk substrate results in the decrease of ductility of the coated specimen. Another observation that could be made from figure 8 is that the ductility of Ni-W coated copper decreased with increasing thickness. This observation can be attributed to low fracture toughness [25] of the brittle Ni-W coatings in comparison to the ductile copper substrate. Indeed, analysis of the fractured surfaces by SEM technique indicates the brittle fracture of the coating by cleavage and the ductile fracture of the copper substrate, as it consists of dimples, Figure 9. This experimental finding is in complete agreement with the work of Panagopoulos et al. [9] on the scratch testing of nanocrystalline Ni-W coatings on copper. According to these investigators intensive brittle fracture and delamination of the Ni-W coatings is observed even at an early stage of the scratch test, indicating that the difference between the fracture toughness of the coating and the substrate is the main reason for mechanical failure of these coatings. Furthermore, it has been reported that the ductility of nanomaterials is lower that of conventional micro-crystalline materials mainly due the presence of defects from the synthesis process, and to tensile and shear instability [23].
Figure 9. SEM micrograph of the fractured surface of Ni-W coated copper, having a 21 μm thickness.A number of tensile tests were also conducted on the Ni-W coated copper specimens, with an average thickness of 21 μm, in order to study the appearance of surface cracks with increasing applied strain on the laminate material. Figure 10(a), 10(b), 10(c) and 6(d) show the density of cracks formed in the center of the coatings surface, for applied strains of 7%, 14%, 21% and 30% respectively. By comparing these figures it could be said that the increase in applied strain during tensile testing has led to an increase in number and size of surface cracks formed on the surface of the coated specimen, Figure 11. The higher crack densities acquired with increasing applied strain values are attributed to the difference ability of deformation between the substrate and the coating [26]. An approximate calculation of the number of cracks per coatings length and the width of cracks as a function of applied strain is presented in Figure 11.
Figure 10. Metallurgical micrographs of the surface adjacent (1 cm) to the fracture area of Ni-W electrocoating with 21 μm thickness, for applied strains of (a) 7%, (b) 14%, (c) 21% and (d) 30%.
Figure 11. Effect of applied strain on the number and width of cracks formed on the surface of the coating adjacent (1 cm) to the fracture area of Ni-W electrocoating with 21 μm thickness.
In this work, the mechanical behaviour of Ni-W coated copper was studied. The main conclusions are the following:
1. Ni-W coatings having 40 wt.% tungsten and a thickness of 5 up to 25 μm were electrodeposited onto copper substrates. In all cases a nodular morphology was observed, whereas the coatings were consisted of a nanocrystalline solid solution of tungsten in nickel. In addition, the surface roughness was observed to decrease with increasing coating thickness, for the selected plating conditions.
2. The microhardness of these Ni-W coatings was found to increase with increasing coating thickness up to 21 μm. This is mainly to the grain refinement of the coating. Further increase of the thickness results in a lower microhardness of Ni-W coating, due to the propagation of cracks during the deposition process and to the formation an average grain size within the inverse Hall-Petch region.
3. The ultimate tensile strength (UTS) of Ni-W coated copper specimen was higher than that of bare copper. This phenomenon can be attributed to the presence of surface layers which block the egress of dislocations from the metallic substrate to the surface layer.
4. The ductility of Ni-W coated copper was significantly lower than that of bare copper. This decrease was attributed to the brittle fracture of the Ni-W coating.
5. The increase of applied strain during tensile testing has led to an increase in number and size of surface cracks formed on the surface of the coated Ni-W specimen. This is attributed to the difference ability of deformation between the substrate and the coating.
Authors declare that there is not conflict of interest.
| [1] |
Lau LC, Lee KT, Mohamed AR (2012) Global warming mitigation and renewable energy policy development from the Kyoto Protocol to the Copenhagen Accord-A comment. Renew Sust Energ Rev 16: 5280-5284. doi: 10.1016/j.rser.2012.04.006
|
| [2] |
Cobbinah PB, Erdiaw-Kwasie MO, Amoateng P (2015) Africa's urbanisation: implications for sustainable development. Cities 47: 62-72. doi: 10.1016/j.cities.2015.03.013
|
| [3] |
de Oliveira JAP (2009) The implementation of climate change related policies at the subnational level: An analysis of three countries. Habitat Int 33: 253-259. doi: 10.1016/j.habitatint.2008.10.006
|
| [4] |
Abadie LM, Galarraga I, Rübbelke D (2013) An analysis of the causes of the mitigation bias in international climate finance. Mitig Adapt Strat GL 18: 943-955. doi: 10.1007/s11027-012-9401-7
|
| [5] |
Morton TA, Rabinovich A, Marshall D, et al. (2011) The future that may (or may not) come: How framing changes responses to uncertainty in climate change communications. Global Environ Change 21: 103-109. doi: 10.1016/j.gloenvcha.2010.09.013
|
| [6] | Wilson RH, Smith TG, Urban resilience to climate change challenges in Africa. Working Paper No.4., The Robert S. Strauss Centre for International Security and Law, Texas. 2014. |
| [7] |
Scrieciu SS, Barker T, Ackerman F (2013) Pushing the boundaries of climate economics: critical issues to consider in climate policy analysis. Ecol Econ 85: 155-165. doi: 10.1016/j.ecolecon.2011.10.016
|
| [8] |
Hu Y, Monroy CR (2012) Chinese energy and climate policies after Durban: Save the Kyoto Protocol. Renew Sust Energ Rev 16: 3243-3250. doi: 10.1016/j.rser.2012.02.048
|
| [9] |
Rong F (2010) Understanding developing country stances on post-2012 climate change negotiations: Comparative analysis of Brazil, China, India, Mexico, and South Africa. Energy Policy 38: 4582-4591. doi: 10.1016/j.enpol.2010.04.014
|
| [10] | Howlett M (2014) Why are policy innovations rare and so often negative? Blame avoidance and problem denial in climate change policy-making. Global Environ Change 29: 395-403. |
| [11] |
Masini A, Menichetti E (2013) Investment decisions in the renewable energy sector: An analysis of nonfinancial drivers. Tech Forecast Soc Change 80: 510-524. doi: 10.1016/j.techfore.2012.08.003
|
| [12] | Hallegatte S, Bangalore M, Bonzanigo L, et al., Shock Waves: Managing the Impacts of Climate Change on Poverty. Climate Change and Development Series, World Bank, Washington, DC. 2016. |
| [13] |
Buurman J, Babovic V (2016) Adaptation Pathways and Real Options Analysis: An approach to deep uncertainty in climate change adaptation policies. Policy Soc 35: 137-150. doi: 10.1016/j.polsoc.2016.05.002
|
| [14] | Buchner B, Falconer A, Hervé-Mignucci M, et al., The Landscape of Climate Finance: A CPI report. Climate Policy Initiative, Venice, 2011. Available from: http://climatepolicyinitiative.org/wp-content/uploads/2011/10/The-Landscape-of-Climate-Finance-120120.pdf. |
| [15] | UN (United Nations), Transforming our world: the 2030 Agenda for Sustainable Development. United Nations, New York. 2015. |
| [16] |
Glemarec Y (2012) Financing off-grid sustainable energy access for the poor. Energy Policy 47: 87-93. doi: 10.1016/j.enpol.2012.03.032
|
| [17] | Yu Y (2014) Climate finance, Africa and China's role. Afr East-Asian Affair 1: 36-57. |
| [18] | Kato T, Ellis J, Pauw P, et al., Scaling up and replicating effective climate Finance interventions. Climate Change Expert Group Paper 2014 (1), OECD, Paris. 2014. |
| [19] | Mbeva K, Ochieng C, Atela J, et al., Intended Nationally Determined Contributions as a Means to Strengthening Africa's Engagement in International Climate Negotiations. Climate Resilient Economies Working Paper no. 001/2015, African Centre for Technology Studies (ACTS), ACTS Press, Nairobi. 2015. |
| [20] | Campillo G, Mullan M, Vallejo L, Climate Change Adaptation and Financial Protection: Synthesis of Key Findings from Colombia and Senegal. OECD Environment Working Papers No. 120, OECD Publishing, Paris. 2017. |
| [21] | World Bank, Africa's Pulse, Oct 2015, vol. 12, World Bank, Washington, DC. 2015. |
| [22] |
Eriksen S, Aldunce P, Bahinipati CS, et al. (2011) When not every response to climate change is a good one: Identifying principles for sustainable adaptation. Climate Dev 3:7-20. doi: 10.3763/cdev.2010.0060
|
| [23] |
Pasquini L, Cowling RM, Ziervogel G (2013) Facing the heat: Barriers to mainstreaming climate change adaptation in local government in the Western Cape Province, South Africa. Habitat Int 40: 225-232. doi: 10.1016/j.habitatint.2013.05.003
|
| [24] | AfDB (African Development Bank), Available from: http://www.afdb.org/en/cop/programme/climate-finance-for-africa/. |
| [25] |
Mitchell TD, Hulme M (1999) Predicting regional climate change: living with uncertainty. Prog Physl Geog 23: 57-78. doi: 10.1191/030913399672023346
|
| [26] | UNFCCC (United Nations Framework Convention on Climate Change), Report of the conference of the parties on its sixteenth session; addendum: part two: action taken by the conference of the parties at its sixteenth session. FCCC/CP/2010/7/Add.1. 2011. |
| [27] | Buchner B, Stadelmann M, Wilkinson J, et al., The Global Landscape of Climate Finance 2014. Climate Policy Initiative, Venice. 2014. |
| [28] |
Zhang W, Pan X (2016) Study on the demand of climate finance for developing countries based on submitted INDC. Adv Climate Change Res 7: 99-104. doi: 10.1016/j.accre.2016.05.002
|
| [29] |
Marwan NF, Kadir NA, Hussin A, et al. (2013) Export, aid, remittance and growth: Evidence from Sudan. Procedia Econ Financ 7: 3-10. doi: 10.1016/S2212-5671(13)00211-6
|
| [30] | Centre for Environmental Policy and Advocacy, Draft Position Paper: Towards Development of Climate Change Policy in Malawi. Centre for Environmental Policy and Advocacy, Blantyre. 2012. Available from: http://www.cepa.org.mw/documents/ECRP_documents/CEPA_Draft_Position_Paper_Climate_Change_Policy.pdf. |
| [31] | Bird N, Asante F, Bawakyillenuo S, et al., Public spending on climate change in Africa: Experiences from Ethiopia, Ghana, Tanzania and Uganda. Overseas Development Institute, London. 2016. |
| [32] | Niang I, Ruppel OC, Abdrabo MA, et al., Africa. In: Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp. 1199-1265. 2014. |
| [33] |
Arezki R, Brückner M (2012) Rainfall financial development, and remittances: Evidence from Sub-Saharan Africa. J Int Econ 87: 377-385. doi: 10.1016/j.jinteco.2011.12.010
|
| [34] | Watkins K, Quattri M, Lost in intermediation: How excessive charges undermine the benefits of remittances for Africa, Overseas Development Institute, London. 2014. |
| [35] |
Kriegler E, O'Neill BC, Hallegatte S, et al. (2012) The need for and use of socio-economic scenarios for climate change analysis: A new approach based on shared socio-economic pathways. Global Environ Change 22: 807-822. doi: 10.1016/j.gloenvcha.2012.05.005
|
| [36] |
Anda J, Golub A, Strukova E (2009) Economics of climate change under uncertainty: Benefits of flexibility. Energy Policy 37: 1345-1355. doi: 10.1016/j.enpol.2008.11.034
|
| [37] |
Engels A, Hüther O, Schäfer M, et al. (2013) Public climate-change skepticism, energy preferences and political participation. Global Environ Change 23: 1018-1027. doi: 10.1016/j.gloenvcha.2013.05.008
|
| [38] |
Grafakos S, Flamos A, Oikonomou V, et al. (2010) Multi-criteria analysis weighting methodology to incorporate stakeholders' preferences in energy and climate policy interactions. Int J Energy Sec Manag 4: 434-461. doi: 10.1108/17506221011073851
|
| [39] |
Broughton EK, Brent AC, Haywood L (2012) Application of A Multi-Criteria Analysis Approach for Decision-Making in the Energy Sector: The Case of Concentrating Solar Power in South Africa. Energy Environ 23: 1221-1231. doi: 10.1260/0958-305X.23.8.1221
|
| [40] | Konidari P, Mavrakis D (2007) Multi-criteria evaluation of climate policy interactions. J Multi-criteria Decis Anal 14: 35-53. |
| [41] |
Kalim PFHB, Shah U (2011) A multi-criteria evaluation of policy instruments for climate change mitigation in the power generation sector of Trinidad and Tobago. Energy Policy 39: 6331-6343. doi: 10.1016/j.enpol.2011.07.034
|
| [42] | Röser F, Day T, Kurdziel M, After Paris: What is next for Intended Nationally Determined Contributions (INDCs)? International Partnership on Mitigation and MRV and New Climate Institute, 2016. |
| [43] | Day T, Röser F, Kurdziel M, Conditionality of Intended Nationally Determined Contributions (INDCs). International Partnership on Mitigation and MRV and New Climate Institute. 2016. |
| [44] | Hood C, Adkins L, Levina E, Overview of INDCs Submitted by 31 August 2015. Paper No. 2015(4). Climate Change Expert Group. Organisation for Economic Co-operation and Development (OECD), Paris. 2015. |
| [45] | Viljoen W (2013) Addressing climate change issue in eastern and southern Africa: EAC, COMESA, SADC and the TFTA. In Cape to Cairo: Exploring the Tripartite FTA agenda. Trade Law Centre and the Swedish Embassy, Nairobi. 1-35. |
| [46] |
Mohammed YS, Mustafa MW, Bashir N (2013) Status of renewable energy consumption and developmental challenges in Sub-Sahara Africa. Renew Sust Energ Rev 27: 453-463. doi: 10.1016/j.rser.2013.06.044
|
| [47] |
Javadi FS, Rismanchi B, Sarraf M, et al. (2013) Global policy of rural electrification. Renew Sust Energ Rev 19: 402-416. doi: 10.1016/j.rser.2012.11.053
|
| [48] | International Energy Agency (IEA), Boosting the Power Sector in Sub-Saharan Africa: China's involvement. IEA, Paris. 2016. |
| [49] | African Development Bank (AfDB), Sustainable Energy for All Africa Hub: Annual Report 2015–2016, African Development Bank, Abidjan, 2016. |
| [50] |
Winkelman AG, Moore MR (2011) Explaining the differential distribution of Clean Development Mechanism projects across host countries. Energy Policy 39: 1132-1143. doi: 10.1016/j.enpol.2010.11.036
|
| [51] | Burian M, Aren C, Sterk W, et al. Integrating Africa's Least Developed Countries into the Global Carbon Market: Analyzing CDM Implementation Barriers, Federal Ministry for the Environment, Nature Conservation and Nuclear Safety (BMU). 2011. |
| [52] | Arens C, Wang-Helmreich H, Hodes GS, et al., Assessing Support Activities by International Donors for CDM Development in Sub-Saharan Africa with Focus on Selected Least Developed Countries, Federal Ministry for the Environment, Nature Conservation and Nuclear Safety (BMU). 2011. |
| [53] |
Afful-Koomson T (2015) The Green Climate Fund in Africa: what should be different? Climate Dev 7: 367-379. doi: 10.1080/17565529.2014.951015
|
| [54] |
Greening LA, Bernow S (2004) Design of coordinated energy and environmental policies: use of multi-criteria decision-making. Energy Policy 32: 721-735. doi: 10.1016/j.enpol.2003.08.017
|
| [55] |
McKibbin WJ, Wilcoxen PJ (2009) Uncertainty and climate change policy design. J Policy Model 31: 463-477. doi: 10.1016/j.jpolmod.2008.12.001
|
| [56] |
Ha S, Hale T, Ogden P (2016) Climate finance in and between developing countries: an emerging opportunity to build on. Global Policy 7: 102-108. doi: 10.1111/1758-5899.12293
|
| [57] | Weigel M, China's Climate Change South-South Cooperation: Track Record and Future Direction, United Nations Development Programme in China, Beijing. 2016. |
| [58] | Chirambo D (2017) Enhancing Climate Change Resilience through Microfinance: Redefining the Climate Finance Paradigm to Promote Inclusive Growth in Africa. J Dev Soc 33: 1-24. |
| [59] | Wibeck V (2014) Enhancing learning, communication and public engagement about climate change-some lessons from recent literature. Environ Edu Res 20: 387-411. |
| [60] |
Nisbet MC (2009) Communicating Climate Change: Why Frames Matter for Public Engagement. Environ Sci Policy Sustain Dev 51: 12-23. doi: 10.3200/ENVT.51.2.12-23
|
| 1. | Ruba Towiargi, Lama Fetyani, Naila Aljahdali, Adnan Alnofeie, Yahya Alnoamy, Reham Ghandorah, Abrar Abduljawad, Njood Alharbi, Alanoud Alghanmi, Hala AlButi, Assessment of the Safety, Efficacy, and Benefit of Empagliflozin in Patients With Type 2 Diabetes Mellitus (T2DM) and Heart Failure With Reduced Ejection Fraction (HFrEF) at High Risk for Cardiovascular Events, 2022, 2168-8184, 10.7759/cureus.33070 |
Figures(1) / Tables(1)
Dumisani Chirambo. Increasing the value of climate finance in an uncertain environment: Diaspora financial resources as a source of climate finance for Sub-Saharan Africa[J]. AIMS Environmental Science, 2017, 4(6): 730-742. doi: 10.3934/environsci.2017.6.730
| Bath composition(g/L) | 17 NiSO4*7H2O, 147 Na3C6H5O7*2H2O, 46 Na2WO4*2H2O, 27 NH4Cl, 15 NaBr |
| Current density (mA/cm2) | 40 |
| Deposition time (min) | 30, 60, 90, or 120 |
| pH | 6 |
| Temperature (o) | 75 ± 3ºC |
| Agitation (rpm) | 200 |
| Anode | Nickel |
DownLoad: CSV
