1. Introduction
Radiotherapy, mainly using X-rays, is one of the main treatment options in oncology and is administered to about 50% of the patients with localized malignant tumors [1]. The idea of using charged particles instead of photons is mainly addressed to maximizing the tumor control probability while sparing normal tissues, thus limiting toxicity and side effects. Although the number of patients treated with ions is still small if compared to the total, this practice, known as hadron therapy, is rapidly diffusing worldwide. More than 60 facilities are currently in operation and more than 50 are under construction or in a planning stage; moreover, more than 150,000 patients have been treated till now [2]. The use of protons and carbon ions, and possibly other charged particles [3], has a strong rationale, mainly based on their physical properties. Their depth-dose profile, culminating with a sharp decrease beyond the Bragg peak (especially for protons), and the high collimation of ions along their path through tissues, allow for a high conformity to the tumor [4,5,6]. However, also the biological effectiveness of these particles needs to be taken into account. In particular, while protons have a similar biological effectiveness compared to photons, except for those in the distal part of the SOBP (Spread Out Bragg Peak), carbon ions have a highly non-constant depth profile of RBE (Relative Biological Effectiveness). In the latter case, along the entrance channel the LET values are lower than 20 keV/μm and the RBE is around 1, while only in the last few cm (about 4 in the case of a 26-cm-range beam) the LET reaches values around 100 keV/μm and the RBE becomes higher and higher in the tumor region.
Beam delivery and dose distribution into the patient are established through a process called treatment planning, which has the aim of "balancing" high dose conformation to the target while sparing healthy tissues. Thanks to imaging techniques the Clinical Target Volume (CTV) and Organs At Risk (OAR) are delineated, and afterwards the maximum doses to the tumor and to healthy tissues are established. Moreover a Planning Treatment Volume (PTV) is defined, in order to take into account any geometrical variation during the therapy and all possible physical uncertainties. Then the beam directions are selected and the dose optimization is performed. The absorbed dose is calculated by a Treatment Planning System (TPS) on the basis of CT data, which provide the X-ray absorption coefficient at each location in the patient. The total dose is then calculated as a superposition of several Bragg Peaks [7]. However the purpose is not just to deliver a high dose in the tumor and a low dose in healthy tissues (and thus to produce a constant dose level along the SOBP), but more generally to have a conformity regarding the biological effectiveness. This is quantified by the product of absorbed dose and RBE, which is expressed in GyE. The integration of a RBE model into treatment planning, especially for heavy ions, is therefore essential.
A Treatment Planning System (in the case of clinical applications) or a radiation transport code like FLUKA [8], PHITS [9] or GEANT4 [10] (mainly used for research purposes or plan validation), providing the dose distribution in the patient, need therefore to be coupled with a biophysical model. The two main models currently used worldwide for carbon-ion therapy are the Local Effect Model (LEM), developed at GSI in Germany [11], and the Microdosimetric-Kinetic Model (MKM), used in Japan [12]. These two approaches will be described in the first part of this review. Concerning protons, however, radiobiological models are not commonly included into Treatment Planning Systems, and a constant RBE value of 1.1 is generally assumed along the whole SOBP. Nevertheless there are many experimental studies, basing on both in vitro and in vivo irradiation, indicating that this is only an approximation since proton RBE depends on several factors, such as the particle type and energy, the dose level [13] and the irradiated tissue type or cell line [14]. In particular, many experimental data show that proton RBE is not constant with depth along a SOBP, but is characterized by a significant increase in the distal region, due to an excess of low energy (and thus higher LET) protons [15,16,17,18]. In vivo, the mean RBE at mid-SOBP was evaluated as ~1.1, ranging from 0.7 to 1.6; in vitro cell survival data indicate a mean value at mid-SOBP of ~1.2, ranging from 0.9 to 2.1. Furthermore, both in vitro and in vivo data tend to show a significant RBE increase for lower fractional doses, especially in the case of low α/β ratio. This may explain why in vivo experiments, many of which have been performed at higher doses, indicated lower RBE values than in vitro studies. A recent and extensive analysis of proton RBE experiments, which is beyond the scope of the present paper, can be found in [19], where the predictions of the Local Effect Model (LEM) were compared considering 19 publications with in vitro experiments and 10 publications with in vivo experiments.
On the other hand, the currently available results are affected by uncertainties, and it is fundamental to integrate the experimental data with theoretical approaches, in order to have information covering a wide range of conditions and values of dose, LET and radio-sensitivity. Various models exist taking into account RBE deviations from the 1.1 constant value used in clinics; these approaches will be discussed in the second part of this review. Finally, a biophysical model called BIANCA (BIophysical ANalysis of Cell death and chromosome Aberrations), developed at the University of Pavia and the INFN Section of Pavia, Italy, will be described.
2. The Local Effect Model
The Local Effect Model (LEM) is currently used for the radiobiological optimization of carbon-ion treatment planning in Germany and at CNAO in Pavia, Italy. The LEM was initially proposed by Scholz and Kraft at GSI in Darmstadt, Germany, in 1994 [11]. The basic assumption is that the local biological effect, that is the damage in a small cellular sub-volume, is determined by the expectation value of energy deposition in that sub-volume, and is independent of the radiation type. Thus, for a fixed biological target, the only difference relies on the different radiation track structures. In the model, the various particle tracks are assumed to have a radial dose distribution given by
|
D(r)={λLET∞1r2minr<rminλLET∞1r2rmin≤r≤rmax0r>rmax
|
(1)
|
According to [20], LET∞ is the unrestricted LET in water and λ is a normalization constant, which is adjusted so that the integral over the whole track yields the LET as given by the tables reported in [21] and [22].
The track core with radius rmin represents the region where the dose is constant. In the first model version, rmin had a fixed value of 10 nm, taking into account also the diffusion of free radicals. On the contrary in the third version of the model [23], the authors took into account that the extension of the track core should increase with the primary particle velocity, since the distance of the primary excitation and ionization events from the trajectory is energy-dependent. The velocity-dependent radius of the inner part of the track was thus parametrized as follows:
where β = v/c, and rc is the largest extension of the track core in the limit v = c. On the other hand rmax represents the maximum radial distance travelled by the d-electrons with the highest energy. It is parametrized as a function of the ion energy (E, expressed in MeV/u), according to the following empirical formula [24]:
where
|
γ=0.062μm(MeV/u)δδ=1.7
|
(4)
|
Once the dose deposition is known, it is possible to compute the surviving probability for ion irradiation if the response of the same cell line to photons is known. The phenomenological modelization assumed for X-ray survival curves is linear-quadratic, with an exponential tail for doses exceeding a threshold Dt, as follows:
|
−lnSX(D)={αXD+βXD2D<DtαXDt+βXD2t+smax(D−Dt)D≥Dt
|
(5)
|
where smax = aX+ 2βXDt is the slope of the exponential tail. Dt is a semi-free parameter; it is difficult to measure but, from experimental data, it is known to lie between 10 and 40 Gy.
The first step in order to calculate the survival probability for ion irradiation is the Poisson assumption for lethal events, leading to the following survival probability for X-rays:
where NX (D) is the mean number of lethal events per cell after D. Therefore,
Since ions and photons are assumed to interact locally with the cell in the same way and the only difference relies in the dose distribution within the cell nucleus, the local effect in each sub-volume of the nucleus can be calculated by the only knowledge of the dose deposited within it, and of the X-ray survival probability for that dose level. The total dose will then be given by the sum of the contributions of all the ion tracks. The average number of lethal events induced per cell by ion irradiation can be obtained by integration of the local density v(d(x; y; z)) for the production of lethal events (assumed to be identical for ions and photons).
|
ˉNIon=∫v(d(x,y,z))dVNucleus=∫−ln(SX(d(x,y,z)))VNucleusdVNucleus
|
(8)
|
where SX(d) denotes the X-ray dose response curve. It is thus sufficient to know SX(d) and the ion dose distribution to calculate the ion surviving fraction through the relationship:
Simulations over a large number of cells are usually performed in order to obtain a reliable value for Sion.
The model has been tested against several experimental data sets, such as survival curves for Chinese Hamster Ovary (CHO) cells, V79 and XRS cells exposed to carbon and oxygen mono-energetic beams, and for CHO cells exposed to a 270 MeV/u carbon Spread-Out Bragg Peak (SOBP) [25,26]. Comparisons with RBEα experimental data for two different mammalian cell lines (V79 and CHO) were also performed [26]. Moreover, the model predictions were tested against in vivo data on the tolerance of the rat spinal cord [23].
Table 1 reports comparisons between model predictions obtained by the first three LEM versions and experimental data taken from the literature. Such comparisons are based on a work reported in [23], where deviations of predicted values of RBEα (i.e., RBE for the survival curve initial slope) from experimental values were evaluated for different cell lines at two Carbon LET values (13 and 77 keV/µm, representative of the entrance channel and the Bragg peak region, respectively). While LEM Ⅰ (as well as LEM Ⅱ, although in a reduced fashion) underestimates the therapeutic ratio of Carbon ions (i.e. the ratio of RBE in the Bragg peak region as compared with the RBE in the entrance channel), LEM Ⅲ almost completely compensates these systematic deviations.
Table 1. Comparisons of LEM predictions with experimental data. Adapted from ref. [23].
|
ΔRBEα* (13 keV/µm) |
ΔRBEα* (77 keV/µm) |
| LEM Ⅰ |
0.45 ± 0.07 |
–0.17 ± 0.06 |
| LEM Ⅱ |
0.29 ± 0.07 |
–0.10 ± 0.06 |
| LEM Ⅲ |
0.11 ± 0.03 |
–0.02 ± 0.06 |
| * the values of ΔRBEα reported in the table represent average deviations with respect to the various cell lines considered in [23], where the deviation for each cell line was calculated as ΔRBE = (RBELEM – RBEExp)/RBEExp. |
Finally, in 2010 the approach was generalized by directly relating the biological response to double-strand break (DSB) patterns (LEM Ⅳ) [27]. Cell damage was assumed to depend on the local DSB density, regardless of the primary particle type. Two types of damage were distinguished: isolated DSBs (iDSBs) and clustered DSBs (cDSBs). The latter were defined as at least 2 DSBs occurring in the same cubic sub-volume with side length lDSB= 540 nm, corresponding to a DNA giant loop (which consists of approximately 2 Mega-base-pairs). A complexity index was defined as follows:
where N denotes the number of a specific damage type. The ion-induced effect was then calculated on the basis of the equivalent photon dose corresponding to the same complexity index.
This model version was validated through the comparison of simulation results with several experimental data, such as CHO survival data in a typical two-port irradiation with protons and carbon ions and after irradiation with a mono-directional 4-cm extended Bragg peak of Helium ions. Predictions were also performed on the RBE variability along different carbon SOBPs [28]. This work showed that the differences in the prediction of RBE-weighted doses and iso-effective doses between LEM Ⅰ and LEM Ⅳ for typical tumor volumes (i.e. averaged over the patient population in the GSI pilot project) are less than 10%. The authors therefore concluded that the transition to LEM Ⅳ is not expected to lead to significant differences in the TCP dose-response relationship for chordoma as compared to the analysis based on LEM Ⅰ.
3. The NIRS Approach
At NIRS in Chiba, Japan, the RBE is calculated by means of a method proposed by Kanai et al. [29], basing on the linear-quadratic (LQ) model. More specifically, dose-averaged values of the α and β coefficients for a mixed beam are calculated starting from the coefficients for mono-energetic beams derived from empirical tables:
|
αmix=∑fiαi√βmix=∑fi√βi
|
(11)
|
where αi and βi are the parameter values for mono-energetic beams, and fi = di/D is the fraction of dose delivered by the ith mono-energetic beam.
For patient treatment planning [30], in vitro human salivary gland (HSG) tumor cells were used, assuming that the moderate radio-sensitivity of this cell line is representative of a typical tumor response. The RBE for the survival of HSG cells was measured at different depths of different HIMAC SOBPs; the distributions of relative physical and biological dose obtained using HSG cells were assumed to be maintained for the various clinical cases, obtaining a nearly universal SOBP profile for different Carbon energies and different SOBP widths, which allowed obtaining a flat response for HSG survival [31]. To account for the difference between the in vitro and the in vivo response, the radiobiological RBE values were then rescaled to values of "clinical RBE", according to the RBE observed in previous clinical experience with fast neutrons. More specifically, since the neutron therapy experience indicated a neutron clinical RBE of 3.0, the clinical RBE at the neutron-equivalent position of a carbon SOBP was also determined to be 3.0. To determine the neutron-equivalent position, the RBE measurements for Carbon were compared with RBE measurements for neutrons; such comparison suggested that NIRS neutrons were biologically equivalent (in terms of HSG survival) to C-ions at a SOBP depth where the (dose-averaged) LET is ~80 keV/µm. The dose level of the flat top of the biological dose distribution was prescribed by a medical doctor, and the physical dose at the neutron-equivalent position was determined using the RBE = 3.0 assumption, that is dividing the prescribed biological dose by 3.0. Knowledge of the physical dose at the neutron-equivalent position allowed deriving the entire SOBP physical-dose distribution, which was normalized with respect to the neutron-equivalent position. In particular, this allowed obtaining the physical dose at the SOBP center, and thus the RBE at the SOBP center, which was derived by dividing the prescribed biological dose by the physical dose.
In Phase Ⅰ/Ⅱ trials, the prescribed dose was gradually escalated from a relatively lower level to a higher level, to seek the optimum dose level while not causing any severe complication to surrounding normal tissues. These studies allowed verifying that carbon ions could be safely and effectively used for radiotherapy [32]. Furthermore [33], a retrospective analysis of clinical results was carried out by means of TCP (tumor control probability) curves for non-small cell lung cancer, comparing the outcome to the original biophysical parameters.
4. The Microdosimetric Kinetic Model (MKM)
Another approach for predicting cell survival following ion irradiation is the Microdosimetric Kinetic Model (MKM), developed by Hawkins [34,35] basing on the Theory of Dual Radiation Action (TDRA) by Kellerer and Rossi [36]. However, while the latter assumes that a lethal lesion is due to the association of two sub-lethal lesions, according to the former also a sub-lethal lesion that has not been repaired after a certain amount of time can lead to cell death. According to the MKM, cell killing depends on the distribution of energy imparted to a sub-nuclear region, called "domain". The mean number of lethal lesions in a domain is given by
where z is the specific energy, that is the ratio between the energy imparted in the domain and the domain mass. Assuming a Poisson distribution of lethal lesions among the cells, the mean number of lethal lesions in the nucleus, L (which is related to the surviving fraction S by the relationship S = exp(-L)), can be expressed as follows:
|
L=N⟨Ld⟩=(α0+βz1D)D+βD2
|
(13)
|
where N is the number of domains in the nucleus, D is the radiation dose, α0 is the slope in the limit LET = 0, β is assumed to be independent of radiation quality, and z1D is the dose-mean specific energy by single energy deposition in a domain, taking into account that < z2 > = (z1DD + D2). Modelling the nucleus as a cylinder of radius R composed by a certain number of domains of radius r, z1Dcan be expressed as:
where m, ρ and l are the mass, density and mean chord length of the domain, respectively, and yD is the domain "lineal energy", defined as the ratio between the energy imparted for a single event and the domain mean chord length.
To account for the so-called "over-killing effect", Kase et al. [12] replaced z1D by z1D* = ly*/m, where y* was calculated from the probability density of y, f(y), and a coefficient called y0. More specifically:
|
y∗=y20∫[1−exp(−y2/y20)]f(y)dy∫yf(y)dy
|
(15)
|
When the y spectrum was a δ function, y0 could be calculated by
Denoting by α the quantity (α0 + βz1D*) and calling Dx the photon dose (considering photons as a reference radiation) to obtain S, the radiobiological RBE can thus be written as follows:
|
RBE=2βDx−α+√α2−4βlnS
|
(17)
|
Apart from β, which is determined by the photon response since it is assumed to be independent of radiation quality, the parameters of the model are thus α0 (slope of the survival curve in the limit LET = 0), r (domain radius) and R (nucleus radius). Using amorphous track-structure models for the MKM calculations, the same group of authors [37] showed that the MKM approach can predict in vitro cell survival for mono-energetic 12C beams, as well as 3He and 20Ne.
Subsequently, Inaniwa et al. [38] developed a method to calculate the RBE of mixed fields based on the modified MKM, and integrated the modified MKM into a research version of a treatment planning system. D10 values calculated for different combinations of the three model parameters were compared with published D10 data of in vitro HSG cells exposed to mono-energetic 3He-, 12C-or 20Ne-ions [39], leading to R = 3.9 mm, r = 0.32 µm and α0 = 0.172 Gy–1 following best fit. This allowed producing a table with z1D* values for many different mono-energetic ions. The z1D* value for a scanned carbon beam at a given position was then derived by "weighting" the various z1D* values delivered by the different beams at that position (provided by Monte Carlo simulations based on Geant4) by the corresponding doses and beam intensities. The method was then integrated into the research version of a treatment planning system [40]. To verify the method, HSG cell survival irradiation experiments were performed at different depths for a scanned carbon beam. Good agreement was found between the predicted and observed cell survival, as well as the planned and measured dose distributions.
In addition to the aforementioned works, further modifications were performed, leading to new MKM versions that were applied to the estimation of cell survival for both targeted and non-targeted effects [41,42,43].
Comparisons between cell survival calculations performed by the LEM or the MKM approach can be found in [37], where amorphous track-structure models—instead of stochastic models—were used for MKM calculations, finding that such calculations can predict mammalian cell survival curves for He-3, C-12 and Ne-20 beams. Cell survival calculations were also performed by two different implementations of LEM, which is inherently based on an amorphous track-structure model, finding good agreement with the considered experimental data. In the context of the amorphous track-structure model, the differences between LEM and MKM were mainly ascribed to different approaches in calculating the biological effects of the very high local dose delivered in the center of ion tracks. A direct comparison between cell survival calculations performed by LEM (using the LEM-oriented track-structure model) or MKM (using the Kiefer-Chatterjee model) for Carbon-irradiated CHO cells can be found in figure 13 of the original paper, which reports 1%, 10% and 50% survival doses as a function of LET calculated by MKM or two different LEM versions, compared to experimental data. According to the authors, MKM calculations were found to reflect the 1%, 10% and 50% survival doses, and LEM calculations showed reasonably good agreement with the considered experimental data for all considered LET values except 100 and 150 keV/µm. These two LET values showed a relatively large mismatch at 10% and 1% survival, respectively, which was partly compensated by the modified LEM. However, for other cell lines such as HSG cells, and according to other experiments more closely related to cancer therapy [44], the agreement of high-LET particles representative of the SOBP with experimental data was much better, although the effectiveness of low-LET particles was overestimated to some extent.
Other comparisons between LEM and MKM can be found in [45], which describes the coupling of the NIRS clinical dose to the FLUKA Monte Carlo code. A high level of agreement was found with published data by exploring a range of values for the MKM input parameters, whereas some differences were found in forward recalculations of NIRS patient plans, mainly attributable to differences with the analytical TPS dose engine in describing the mixed radiation field. In addition to the NIRS approach, LEM-Ⅰ and LEM-Ⅳ RBE tables (both related to α/β = 2 Gy) were used, allowing to compare profiles of effective dose and RBE for a prostate cancer as computed by the NIRS approach, LEM-Ⅰ or LEM-Ⅳ coupled with FLUKA. Such comparisons, which can be found in figure 5 of the original paper, showed that both LEM-Ⅰ and LEM-Ⅳ effective-dose profiles reached a similar dose level at the target center, in the middle of the modulated region. LEM-Ⅳ-based calculations showed a pronounced peak at the distal end of the SOBP if compared with LEM-Ⅰ. Furthermore, RBE values based on LEM-Ⅳ and NIRS already matched in the SOBP region, whereas RBE values based on LEM-Ⅰ were 64% higher than those based on the NIRS approach. More generally, this work showed that Monte Carlo tools can provide an important contribution in model inter-comparison.
5. Proton-specific Approaches
5.1. Model description
Unlike the case of carbon therapy, biophysical models are not currently implemented in proton therapy treatment planning systems. However, to take into account the possible variations of proton RBE, different theoretical approaches may be applied to the proton case, such as the previously described LEM and MKM and the repair-misrepair-fixation (RMF) model [46]. Recently, various phenomenological models specific for protons have also been proposed. The starting point of all these approaches is the Linear-Quadratic (LQ) formulation, according to which the general dependence of the surviving fraction on the absorbed dose D is given by
where α and β are two parameters. According to this approach, a given proton dose (Dp) will produce the same effect of a given dose of a reference radiation (Dx in the case of X-rays) if the following condition is satisfied:
|
αxDx+βxD2x=αpDp+βpD2p
|
(19)
|
where the index p denotes proton irradiation and the index x denotes photon irradiation. To obtain an expression for the explicit dependence of RBE on the photon dose and the cell-specific ratio αx/βx, equation (19) can be divided by Dx and βx, thus obtaining
|
(αxβx+Dx)RBE2−αpβxRBE−βpβxDx=0
|
(20)
|
where the definition of RBE, which is the ratio between the photon and proton dose to obtain the same effect, has been applied. By solving this equation, and by pointing out the role of αx/βx, we obtain
|
RBE=αxβxαpαx+√(αxβx)2(αpαx)2+4αxβxβpβxDx+4βpβxD2x2(αxβx+Dx)
|
(21)
|
Equivalently, to make explicit the dependence of RBE on the proton dose and the αx/βx ratio, equation (19) can be divided by Dp2, thus obtaining the following expression
|
RBE=−αxβx+√(αxβx)2+4αxβxαpαxDp+4βpβxD2p2Dp
|
(22)
|
It is now convenient to introduce the two quantities RBEmax and RBEmin, which represent the asymptotic values of RBE in the limit of 0 and ∞ dose, respectively: in the limit 0 dose, the quadratic terms of Equation (1) can be neglected, leading to αxDx
= αpDp, and thus
On the contrary, in the limit of ∞ dose, one can neglect the linear terms, leading to βxDx2
= βpDp2, and thus
Equations (21) and (22) thus become
|
RBE=αxβxRBEmax+√(αxβx)2RBEmax2+4αxβxRBEmin2Dx+4RBEmin2D2x2(αxβx+Dx)
|
(25)
|
and
|
RBE=−αxβx+√(αxβx)2+4αxβxRBEmaxDp+4RBEmin2D2p2Dp
|
(26)
|
respectively.
At this level, the various phenomenological models differ in the assumed dependence of RBEmax and RBEmin on the radiation LET and on the tissue type (that is, on αx/βx), and on the experimental data used to obtain these dependences.
For example, the approach of Tilly et al. [47], based on experimental data by Belli et al. [48,49,50], Folkard et al.
[51] and Bettega et al. [52] regarding different cell lines over a wide LET range, assumed a linear dependence of RBEmax on LET, with a slope depending on the αx/βx ratio. In particular, the data were divided into two groups (with αx/βx ~ 2 and ~10, respectively) and fitted separately. The β value was found to be almost constant up to a LET value of about 30 keV/µm. Another similar approach is that of Frese et al. [53], who started from the same ideas of a previous work [54] assuming a linear dependence of α on dose-average LET, as follows:
Here α0 is a normalization parameter representing the initial value of αp, which should be equal to αx.
It was thus assumed that
where 0.5 keV/µm represents the LET value in the entrance channel of a clinical proton beam, according to ICRU report 49 [55]. A single λ value for all tissues was derived by imposing a similar mean RBE value in the target with respect to treatment plans based on a fixed RBE of 1.1. Basing on the treatment plans of four patients, an average λ value of 0.008 µm/(keV·Gy) was found. Concerning the βp parameter, it was considered constant and equal to βx. The expression for RBE thus becomes:
|
RBE=−αxβx+√(αxβx)2+4αxβx(1+λαx(LET−0.5keV/μm))Dp+4D2p2Dp
|
(29)
|
A different approach was adopted by Carabe et al. [56], who assumed for both RBEmax and RBEmin, that is for both αp and βp, a linear dependence on LET and an inverse dependence on the tissue-specific parameter αx/βx. The resulting expressions were:
|
RBEmax=0.843+0.1542.686(αx╱βx)LET
|
(30)
|
and
|
RBEmin=1.09+0.0062.686(αx╱βx)LET
|
(31)
|
The numerical parameters were obtained by fitting experimental data [13,48,51,57,58,59] relating RBE and LET for V79 cells. The value 2.686 represents the average αx/βx resulting from the experiments. Wedenberg et al. [60] assumed a similar behaviour for RBEmax, described by the following equation:
|
RBEmax=1+qLET(αx╱βx)
|
(32)
|
This equation holds for LET values lower than 30 keV/µm. RBEmin, on the contrary, was assumed to be constant and equal to 1. The best value for the q parameter was found to be 0.434 Gy/(keV/µm). This value, as well as the qualitative behaviours of αp and βp, was obtained by statistical analyses of experimental data of 10 different cell lines, irradiated with near mono-energetic proton beams with LET values ranging from 6 to 30 keV/µm. The resulting expression for RBE was
|
RBE=−αxβx+√(αxβx)2+4(αxβx+qLET)Dp+4D2p2Dp
|
(33)
|
A wider experimental data set was used by Paganetti [61], with 76 literature papers on cell survival considered. The RBE was linearly fitted as a function of LET, that is
The fit was performed for four different bins of αx/βx (specifically: αx/βx < 3 Gy; 3 Gy ≤ αx/βx < 6 Gy; 6 Gy ≤ αx/βx < 9 Gy; αx/βx ≥ 9 Gy) and for two different proton doses (2 and 6 Gy). Only data for LET < 15 keV/µm were chosen. The author found a positive slope, which decreased with increasing dose. The slopes were similar for all the αx/βx regions. Concerning the dependence of RBE on αx/βx, the data were linearly fitted for four different LET bins (specifically: LET < 3 keV/µm; 3 keV/µm ≤ LET < 6 keV/µm; 6 keV/µm ≤ LET < 9 keV/µm; 9 keV/µm ≤ LET ≤ 15 keV/µm), two different dose levels (2 and 6 Gy), and for αx/βx < 20 Gy. Unexpectedly, the results do not fully confirm the theoretical prediction of a RBE increase with decreasing αx/βx, with some negative and some positive slopes. Finally, RBEmax and RBEmin as a function of LET were fitted by linear functions; the former showed a positive slope decreasing with increasing αx/βx, whereas values around zero were found for the slope of the latter.
The comprehensive collection of data in [61] was exploited to develop a new phenomenological model aimed to explicitly parametrize the dependence of RBE on dose, LET and αx/βx. [62]. Only data points with LET < 20 keV/µm and αx/βx < 30 Gy were considered. The main assumptions of the model were the dependence of RBEmaxon LET and on the inverse of αx/βx (like in the models by Carabe and Wedenberg), and the dependence of RBEmin on LET and on √αx/βx, as follows:
|
RBEmax=p0+p1(αx╱βx)LET
|
(35)
|
|
RBEmin=p2+p3√(αxβx)LET
|
(36)
|
where p0-3 are the fit parameters of the model. The expression for RBE can be deduced by modifying Equation (26) according to (35) and (36). After fitting the experimental data, the parameter values were found to be p0 ≈ 0.991, p1 ≈ 0.356, p2 ≈ 1.101, p3
≈ –0.004, with their associated uncertainties. The resulting expression for RBE is thus
|
RBE=−αxβx+√(αxβx)2+4αxβx(0.991+0.356(αx╱βx)LET)Dp+4(1.101−0.004√(αxβx)LET)2D2p2Dp
|
(37)
|
According to the model, RBE increases with increasing LET, and decreases with increasing dose and αx/βx ratio.
5.2. Model applications
Although these models are not currently integrated into treatment plans routinely used in clinics, their authors investigated the consequences of applying a constant RBE instead of taking into account its variations. For instance, Tilly et al. [47] applied their study to a clinical case of advanced hypopharynx cancer: when applying a variable RBE, its value was found to be higher both in the tumour region and in the spinal cord, an organ at risk, compared to the 1.1 constant value. However, the NTCP (Normal Tissue Complication Probability) for the spinal cord came out to be still zero. Nevertheless, the NTCP for the other normal tissues outside the CTV (Clinical Tumour Volume) was much higher with respect to the constant RBE case. The authors concluded that it is worth considering RBE variations in clinical proton therapy planning, especially when organs at risk are located immediately behind the tumour region.
Frese et al. [53] performed a study on four patients with nasopharyngeal carcinoma, previously treated with intensity-modulated radiotherapy at the German Cancer Research Center (Heidelberg, Germany). For each patient an IMPT (Intensity Modulated Protontherapy Therapy) plan was calculated assuming RBE = 1.1. By keeping the same dose, a variable RBE was then applied, as computed by their phenomenological model in agreement with Equation (29). Finally, a biologically optimized plan was calculated, in order to obtain a treatment plan having at least the same quality as the physically optimized plan. They observed important RBE variations in the treated volumes, when calculating it with the model; moreover, when performing the biological optimization, a higher inhomogeneity in the dose distributions was obtained, due to LET variations within the volumes. Nevertheless, a biological optimization of IMPT plans was found to be possible, since the optimizations in the four considered cases led to plans of at least as good quality as physically optimized plans. Moreover, the authors highlighted how "radio-resistant normal tissues have a higher risk of overdosage than radio-sensitive tissues".
Carabe et al. [56] investigated the differences in the use of a variable or a constant RBE in terms of biological range shifts, by studying the Dose-Volume Histograms (DVH) for the case of a patient with an adenoid cystic carcinoma (ACC) in the lachrymal gland. In this specific case the tumour was surrounded by normal tissues with low αx/βx. The largest differences between the constant and variable RBE cases were observed in the case of low αx/βx volumes receiving low dose. In the opposite case of large doses and large values of αx/βx, variable RBE values even smaller of 1.1 were observed. Moreover, the biological doses in the low αx/βx organs at risks (optic nerve, chiasm and brainstem) were higher for the variable RBE case. Finally, since the uncertainty in the range of the biological dose profile is smaller at higher doses, the authors observed that hypo-fractionated treatment plans may allow for a reduction of the overall range uncertainty.
Wedenberg et al. [60] pointed out that late-responding tissues (low αx/βx) are more sensitive to LET changes than early-responding tissues (high αx/βx). Moreover, since the highest RBE values, in agreement with Equation (33), are expected for low αx/βx, high LET and low dose per fraction, particular attention should be devoted to late-responding normal tissues positioned just behind tumours and to the lateral peripheral parts of the beam, where these conditions may be satisfied. In a subsequent work [63] the authors applied their model to three brain tumour cases, by comparing a photon IMRT (Intensity-Modulated Radiation Therapy) plan, a IMPT plan with RBE = 1.1 and another proton plan with the same dose distribution but with variable RBE. When using a constant RBE value, the proton plans showed higher doses to the tumour and lower doses to the normal tissues, as compared to the photon plans. However, when the variable RBE was taken into account, the proton dose to the tumour was generally lower than the photon dose, and hot spots were found in the organs at risk (such as in the optic nerve). The authors also evaluated NTCP for some different endpoints (such as blindness and necrosis in the brain stem): the general tendency was to obtain a lower probability for constant RBE proton plans than for photon plans, but a significantly higher probability for variable RBE proton plans than for both the other cases. Such evaluation was performed for three brain tumor cases; as an example, table 2 reports NTCP estimates, in percent, for three regions of interest (R.o.I.) for case 1. In conclusion, the results indicated that the use of a constant RBE may produce sub-optimal proton treatment plans.
Table 2. NTCP estimates (in percent) for a brain tumour case, comparing three different plans: IMRT photons, protons with constant RBE and protons with variable RBE. Adapted from [63].
| R. o. I. |
Photon |
constant RBE |
variable RBE |
| Brain stem |
0.84 |
0.57 |
2.13 |
| Optic chiasm |
0.88 |
0.18 |
0.91 |
| Optic nerve |
1.21 |
1.13 |
4.21 |
According to [61], the assumption of a constant RBE value of 1.1 at 2 Gy is not unreasonable, since they found an average value of 1.15 in the centre of a typical SOBP. However, caution is needed "for small modulation widths and/or low αx/βx, where the average RBE could be higher". Moreover, RBE was found to increase with depth up to typical average values of ~1.7 in the distal fall-off. In general, a trend of a RBE increase with decreasing αx/βx and with decreasing dose was observed. Finally, the authors performed a study on endpoints different from cell survival, concluding that experimental NTCP values are not sufficient to define a clear RBE behaviour, and that they are not in disagreement with a general value of 1.1, although the selected endpoints showed important deviations from that value.
McNamara et al. [62] performed an interesting comparison between their model and the models by Carabe and by Wedenberg, applying them to the case of a SOBP with a modulation width of 10 cm and a range of 25 cm. The dose-average LET in the middle of the plateau region of the SOBP (depth: ~160–220 mm) ranged from ~1.4 to ~3.1 keV/µm, and from ~1.4 to ~10 keV/µm over the entire plateau region. Tissues with a different radio-sensitivity (αx/βx = 1 Gy, αx/βx = 2 Gy and αx/βx = 10 Gy) were considered. The McNamara and Wedenberg models predicted very similar results, whereas the Carabe model showed some discrepancies. However, each considered RBE model, with only slight differences, predicted an increase in biological dose at the distal edge of the SOBP. According to the McNamara model, for the case of low αx/βx ratio, this increase was of about 30% compared to the biological dose used in clinics (RBE = 1.1), which is a much higher value than for the case of high αx/βx (about 4%). In the same work, the authors also simulated two different proton treatment plans, a prostate and a paediatric head-and-neck case. They were two opposite situations: for the first case the prostate αx/βx value was ~1.5 Gy and the rectum and the surrounding tissue αx/βx was ~3.1 Gy, whereas for the second case the target volume αx/βx was ~11 Gy and the αx/βx of the rest of the brain was ~2.1 Gy. In both cases, the total prescribed dose was 1.8 Gy per fraction. In the case of the prostate treatment plan, the RBE calculated within the target was ~1.2, whereas that calculated just outside the target region was 1.3. This trend was even amplified in the head-and-neck treatment plan case, for which the RBE values within the target were ~1.1, whereas those calculated just outside the target volume, in the brainstem (which is a critical structure), were ~1.5. These studies may also have an impact on the comparison between proton and photon therapy in terms of tumour control and toxicities.
Another model inter-comparison was performed by Giovannini et al. [64], who compared the predictions of LEM-Ⅳ [27] and the approaches proposed by Carabe et al. [56] and Wedenberg et al. [60], in the framework of a variable versus constant RBE. Using the considered models, a proton SOBP and two exemplary clinical cases for cranial proton irradiation, all delivered with pencil-beam scanning, were analyzed in terms of absorbed dose, dose-averaged LET (LETD), RBE-weighted dose (DRBE), and shift of biological range. A detailed analysis, which is beyond the scope of the present work, can be found in the original paper, including the figures and tables therein reported. Herein, it is worth reporting that: (1) comparison of the RBE predictions showed different levels of agreement depending on the values of (α/β)X and LET; (2) the SOBP study emphasized the variation of LETD and RBE not only as a function of depth but also of the lateral distance from the central beam axis; (3) application to clinical-like scenario showed consistent discrepancies from the values obtained assuming a constant RBE of 1.1, when using a variable RBE scheme for proton irradiation in tissues with low (α/β)x (regardless of the model); (4) shifts of biological range of 0.6–2.4 mm (for high (α/β)x) and 3.0–5.4 mm (for low (α/β)x) were found from the fall-off analysis of individual profiles of RBE-weighted fraction dose along the beam penetration depth. Concerning issue (1), Table 3 reports the resulting minimum RBE (minRBE), maximum RBE (maxRBE) and mean RBE (meanRBE) values in the PTV for one of the two patient cases analysed in [64], calculated either by LEM-Ⅳ (for two different values of the threshold dose, i.e. Dt = 10 Gy and Dt = 40 Gy), or by the Wedenberg (WED) or Carabe (CAR) models. The results are shown both for (α/β)X = 2 Gy and for (α/β)X = 10 Gy except for the Carabe model, which was considered as not applicable for (α/β)X
= 10 Gy [64]. Table 4 reports analogous results in terms of shift of biological range (issue 4) above. More specifically, the biological range shift (in mm) calculated by the various models in correspondence of three different dose values beyond the dose fall off (corresponding to 90% Dpresc, 80% Dpresc and 50% Dpresc, respectively) are reported. Analogous to Table 3, the results are shown both for (α/β)X = 2 Gy and for (α/β)X
= 10 Gy except for the Carabe model, which was considered as not applicable for (α/β)X = 10 Gy.
Table 3. Minimum, maximum and mean RBE in the PTV for (α/β)X = 2 Gy and (α/β)X = 10 Gy for the first patient case analysed in [64] (adapted from ref. [64]).
|
|
(α/β)X =2 Gy |
|
(α/β)X =10 Gy |
| Model |
minRBE |
maxRBE |
meanRBE |
minRBE |
maxRBE |
meanRBE |
| LEM Dt=10 Gy |
|
1.10 |
1.70 |
1.19 |
|
1.05 |
1.34 |
1.09 |
| LEM Dt=40 Gy |
1.15 |
1.90 |
1.27 |
1.05 |
1.45 |
1.12 |
| WED |
1.20 |
1.64 |
1.24 |
1.10 |
1.26 |
1.11 |
| CAR |
1.20 |
1.60 |
1.27 |
|
|
|
Table 4. Mean shift of biological range (in mm) for (α/β)X = 2 Gy and (α/β)X
= 10 Gy for the first patient case analysed in [64] (adapted from ref. [64]).
|
|
(α/β)X =2 Gy |
|
(α/β)X =10 Gy |
| Model |
90% Dpresc |
80% Dpresc |
50% Dpresc |
90% Dpresc |
80% Dpresc |
50% Dpresc |
| LEM Dt=10 Gy |
|
3.74 |
4.33 |
4.07 |
|
1.73 |
1.81 |
1.64 |
| LEM Dt=40 Gy |
4.75 |
5.42 |
4.97 |
2.30 |
2.44 |
2.10 |
| WED |
3.16 |
3.64 |
3.39 |
1.11 |
1.16 |
1.03 |
| CAR |
3.10 |
3.51 |
3.17 |
|
|
|
From this analysis the authors concluded that, although more experimental evidence is needed to validate the accuracy of the investigated models and their input parameters, their main RBE dependencies (dose, LET and (α/β)x) should be included in treatment planning. As a first step, simpler models based on the linear-quadratic formalism and LETD might already be sufficient to reproduce important RBE dependencies for re-evaluation of plans optimized with the current RBE = 1.1 approximation.
6. The BIANCA Approach
The model presented in this section [65,66,67,68,69,70,71,72] deals both with light ions like protons and with heavier ions, including not only Carbon but also Iron, which is of great interest for space research [73,74,75,76]. The model, called BIANCA (BIophysical ANalysis of Cell death and chromosome Aberrations), takes into account some fundamental features of the processes leading from energy deposition by radiation to DNA/chromosome damage and cell death, but at the same time requires two adjustable parameters only. According to this approach, the cell survival probability after a dose D is directly calculated from the yields of specific chromosome aberration types (dicentrics, rings and deletions, see below). In turn, chromosome aberrations are assumed to derive from mis-rejoining, or un-rejoining, of chromosome fragments, which are produced by DNA "Cluster Lesions" (CL). More specifically, the following basic assumptions are adopted:
(1) ionizing radiation induces DNA "cluster lesions", defined as DNA breaks that are severe enough to produce two independent chromosome free-ends;
(2) each free-end either remains un-rejoined (which occurs with probability f), or can be rejoined with another free-end, provided that the initial distance from the "partner" is smaller than a threshold d;
(3) dicentrics, rings and large deletions (where "large" means visible in metaphase, see below) lead to clonogenic cell death.
Since the critical DNA lesion(s) leading to important endpoints like chromosome aberrations and cell death have not been fully characterized yet, the mean number of CLs per unit dose and per unit DNA mass (mean number of CLs per Gy and per Dalton, which can be easily converted into CLs per Gy and per cell) was left as an adjustable parameter. Such parameter mainly depends on radiation quality, basically particle type and energy, and thus LET. Unless the LET is so high to be in the so-called "over-killing" region, for a given particle type the CL yield was found to increase with LET; furthermore, at a given LET, there was a tendency for lighter particles to induce more CLs than heavier particles of the same LET. The CL yield was also found to be modulated by the target cell features: more radio-resistant cells showed lower CL yields, whereas more radiosensitive cells showed higher CL yields.
Assumption (2), according to which each chromosome fragment has a certain probability of remaining un-rejoined, was recently introduced to account for the so-called "incomplete" chromosome exchanges [77]. This un-rejoining probability is likely to vary with the considered cell line, consistent with the observation that more radiosensitive cells tend to show higher frequencies of deletions [78]. Concerning a possible dependence of the un-rejoining probability on radiation quality, contradicting results are available in the literature: while in some works the percentage of incomplete exchanges was found to increase with LET [77], other studies failed to reveal such a LET-dependence [79]. Therefore, as a starting point, the value of f was assumed to be cell-line dependent but radiation-quality independent. Concerning the threshold distance for chromosome-fragment rejoining, in the most recent model version (called BIANCA Ⅱ) it was set equal to the mean distance between two adjacent chromosome territories, since the occurrence of aberrations involving chromosomes located far apart in the cell nucleus is unlikely, although not impossible. Of course this distance depends on the shape and dimensions of the cell nucleus, as well as the total number of chromosomes. For instance, d was found to be ~1.6 µm for human lymphocytes (modelled as spheres with 3.0-µm radius), and ~3.0 µm for AG1522 human fibroblasts (modelled as 4.0-µm-height cylinders with elliptical base having major and minor axes of 20 and 10 µm, respectively). This approach allowed to reproduce very well yields, distributions and ratios of inter-chromosome and inter-arm exchanges (typically dicentrics and centric rings), as well as total deletion yields, although interstitial deletions were underestimated and terminal deletions were overestimated. This suggests that representing the distance-dependence of chromosome fragment rejoining by a step function, which has similarities with the so-called "site approach" [80], allows taking into account the relationship between inter-chromosome and intra-chromosome aberrations, whereas a more detailed approach (for instance a continuously decreasing function) is necessary to account for the relationship between inter-arm and intra-arm exchanges in the same chromosome. Concerning the rejoining process, since the model applies to chromosome aberrations formed following irradiation during the G0/G1 of the cell cycle, it is assumed that repair mainly occurs via Non-Homologous End Joining (NHEJ). No distinction is made between different repair pathways, such as the so-called "canonical" or "alternative" DNA repair. Although in principle this could be done and the model would become more realistic from a biological point of view, we chose not to make this distinction to avoid introducing other free parameters in the model, which is characterized by the fact that it makes use of two adjustable parameters only.
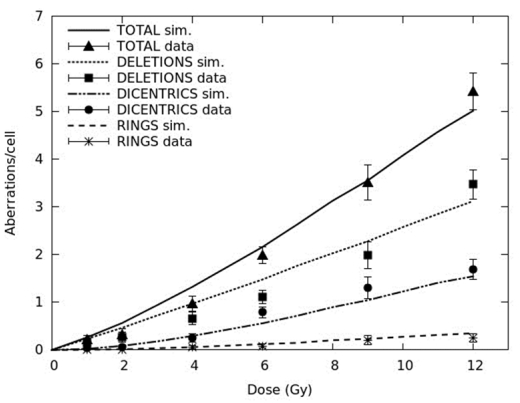
Examples of comparisons between simulations and data are reported in Figure 1, which shows dose-response curves for dicentrics, rings and deletions induced in X-irradiated AG1522 normal human fibroblasts. The lines are simulation outcomes, the points are experimental data taken from the literature [81]. For both dicentrics and rings, the calculated yields were within the experimental errors, with the only exception of dicentrics at 6 Gy; the capability of reproducing separately the yields of dicentrics and rings supports the assumption adopted for d, since higher d values overestimated the ratio of dicentrics to rings (the so-called "F-ratio"), whereas lower d values underestimated the F-ratio. Concerning deletions, while the simulated response is basically linear, the experimental one shows a non-negligible quadratic component. This may be explained considering that in the simulations most deletions were "terminal deletions", which being due to a single chromosome break involve a single-particle mechanism proportional to dose, whereas most experimental deletions were of the "interstitial" type, which requiring two chromosome breaks (also) involves a two-particle mechanism proportional to the square of dose. This issue requires further investigations. The curves reported in figure 1 were obtained with a f value of ~0.2, and a CL yield of ~1.3 CL·Gy–1·cell–1. Lower f values (associated to higher CL yields) led to an underestimation of deletions and an overestimation of dicentrics, whereas higher f values (associated to lower CL yields) led to an overestimation of deletions and an underestimation of dicentrics.
Concerning assumption (3), it is based on the fact that, in X-ray-exposed AG1522 human fibroblasts, Cornforth and Bedford [81] observed a one-to-one relationship between the mean number per cell of the so-called "lethal aberrations" (dicentrics, rings and deletions visible in metaphase) and the logarithm of the surviving fraction, which therefore was expressed as:
where LA is the mean number of lethal aberrations per cell after a dose D. A similar relationship was observed in V79 Chinese hamster fibroblasts [82]. Although this result cannot be generalized, it is reasonable to assume that it holds also for other cells, basically those cells for which clonogenic inactivation is the main death pathway, whereas other forms of cell death like apoptosis and necrosis do not play an important role. More specifically, the so-called "asymmetrical aberrations" (like dicentrics and centric rings) are capable of forming a "bridge" at anaphase, and in turn the bridge can lead to failure of cytokinesis and thus cell death. On the other hand, an acentric fragment (deletion) either is transmitted (as a paired structure) to one of the two daughter cells, or is not transmitted at all, thus leading to loss of genetic material in the cell progeny; such loss probably plays a small role for cell death in the generation immediately following the loss, but death caused by loss of acentric fragment(s) becomes more important in subsequent generations [82]. These findings explain why dicentrics, centric rings, and (excess) acentric fragments (at least, those fragments that are large enough to cause a significant loss of genetic material [81]), have a high probability of leading to clonogenic cell death, as observed e.g. by Cornforth and Bedford [81]. Of course cell death can also derive from other pathways than (asymmetrical) chromosome aberrations, such as apoptosis, necrosis, etc. As a consequence, the current version of our model is specific for cell types in which cell death via apoptosis and/or necrosis does not play an important role, as is the case of AG1522 and V79 normal cells and of many tumour cells.
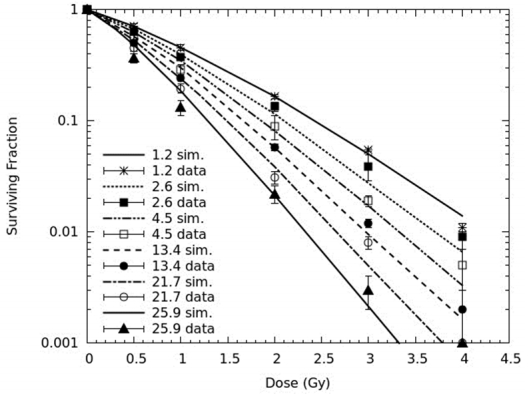
After testing against chromosome aberration data and photon survival data, recently the model was applied to ion cell survival, starting with protons. In particular, experimental survival curves [17] were reproduced for AG01522 normal human cells exposed at different depth positions of a 62-MeV proton beam available at INFN-LNS in Catania, Italy, where ocular melanoma is treated [83]. All simulations were performed adopting the same f value used to calculate chromosome aberrations in AG1522 cells, whereas the CL yield was separately adjusted for each curve. Figure 2 reports simulated survival curves compared with experimental data obtained by Chaudhary et al. [17] at six depth positions along a proton SOBP, corresponding to LET values in the range 1.2–25.9 keV/µm. Despite a tendency to underestimate the experimental survival at high doses, a satisfactory agreement between simulations and data was obtained.
While for the depth positions considered in the experimental work the cell killing calculations did not add substantial information with respect to the experimental data, the model allowed for full prediction of cell survival also for positions not considered in the experiments, with focus on the dose fall-off region that can be critical for normal tissue damage. Moreover, the model also predicted yields of chromosome aberrations, which were not investigated in the experimental work and may be useful for normal tissue damage evaluation, since there may be a link between chromosome aberrations in normal cells and second tumours [84]. In line with the experimental data reported in [17] and with many other works available in the literature, the beam effectiveness—both for cell death and for chromosome aberrations -was found to increase with depth along the SOBP plateau, and high levels of biological damage were found also beyond the distal dose fall-off. This is due to proton slowing down, which implies an increase in LET and thus in biological effectiveness. Interestingly, the increase in chromosome aberrations with depth was more pronounced than the increase in cell killing. Predictions of cell death and chromosome aberrations were also performed assuming different plateau doses. Increasing the physical dose from 2 to 4 Gy reduced the increase in biological effectiveness along the plateau, whereas decreasing the dose from 2 to 1 Gy led to an even more pronounced increase in effectiveness. This is consistent with the well known dose-dependence of RBE, which tends to be higher at lower doses and vice-versa. However, while for cell death the highest considered dose (4 Gy) led to an almost flat biological effectiveness along the plateau, for chromosome aberrations even that dose implied an increase in effectiveness.
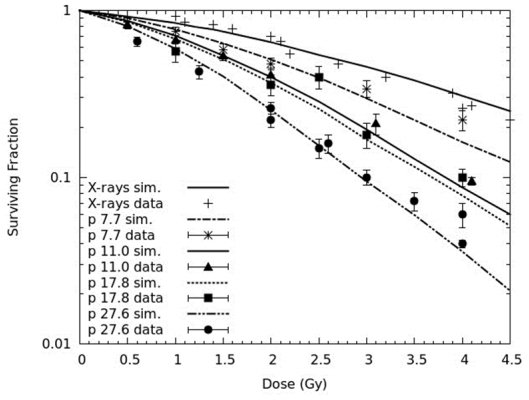
The model was also applied to V79 cells, which are rather radio-resistant and have been widely used to characterize many hadrontherapy beams. First, experimental survival curves obtained by different mono-energetic beams [49,51] were successfully reproduced, adjusting the CL yield for each energy. For a given LET, the CL yields adjusted for V79 cells were lower than those for AG01522, reflecting the lower radio-sensitivity of V79 cells. In fact, as mentioned above, although the CL yield mainly depends on radiation quality, it is also modulated by the specific target cell features. Figure 3 reports calculated survival curves for four monoenergetic proton beams (with LET values in the range 7.7–27.6 keV/mm), as well as X-rays as a reference radiation; the points represent experimental data taken from [49,51]. The X-ray curve was obtained using a CL yield of 1.5 CL·Gy–1·cell–1, whereas the four proton curves were obtained with CL yields in the range ~2.0–3.2 CL·Gy–1·cell–1, increasing with LET. With these values, the general agreement between the simulation outcomes and the experimental data was satisfactory.
Afterwards, full predictions of cell death and chromosome aberrations for V79 cells exposed to the Catania hadrontherapy beam were performed. Analogous to AG01522 cells, the beam effectiveness was found to increase along the SOBP plateau, and high levels of biological damage were also found beyond the distal dose fall-off. However, the increase in biological effectiveness was more pronounced for V79 cells than for AG01522 cells. This is consistent with the higher RBE generally shown by cells exhibiting smaller α/β ratios [16], which is the case of V79 cells.
The application of the model to other ions, including carbon, is in progress. Preliminary results on V79 cells irradiated at different depth positions of a Carbon SOBP at the CNAO hadrontherapy centre in Pavia are encouraging. This approach represents a starting point for possible future works in which treatment plan optimization may be directly based on the calculated level of biological effect. To be of practical use, of course the model needs to be interfaced to a TPS and/or a radiation transport code; to this aim, a collaboration has recently started to develop an interface with the FLUKA code [8] within the MC-INFN project funded by the Italian National Institute of Nuclear Physics. Moreover, the model should be further refined and tested for other cell lines and radiation qualities.
7. Conclusions
Some approaches adopted to evaluate the biological effectiveness of proton and Carbon ions were reviewed. Far from being exhaustive, this review has the main aim of summarizing and discussing the main aspects of the various approaches, also outlining similarities and differences. When possible, the application of these approaches in cancer therapy was also discussed. In addition to the well-known approaches used for Carbon, some examples of biophysical models specifically developed for protons were presented, as well as a model of cell death and chromosome aberrations developed in Pavia. In particular, the analysis concerning protons outlined that, although adopting a constant RBE = 1.1 still seems a reasonable choice, further studies aimed at increasing the accuracy of RBE evaluation in proton therapy are desirable with the final objective of implementing biological models in proton therapy treatment planning, as also suggested by others [85]. Comparing the various approaches to choose the model(s) to be implemented in TPS is not trivial, because the differences in the results are related not only to the approach adopted for modelling the particle biological effectiveness, but also to the physics models underlying the simulation of the various particle interactions in matter. To perform such comparisons, it is therefore desirable that different radiobiological models are implemented in the same radiation transport code.
Acknowledgements
This work was partially supported by the Italian National Institute of Nuclear Physics (INFN), under the projects "ETHICS" and MC-INFN/FLUKA. The authors are also grateful to the Reviewers for their valuable comments.
Conflict of Interest
All authors declare no conflicts of interest in this paper









 DownLoad:
DownLoad: