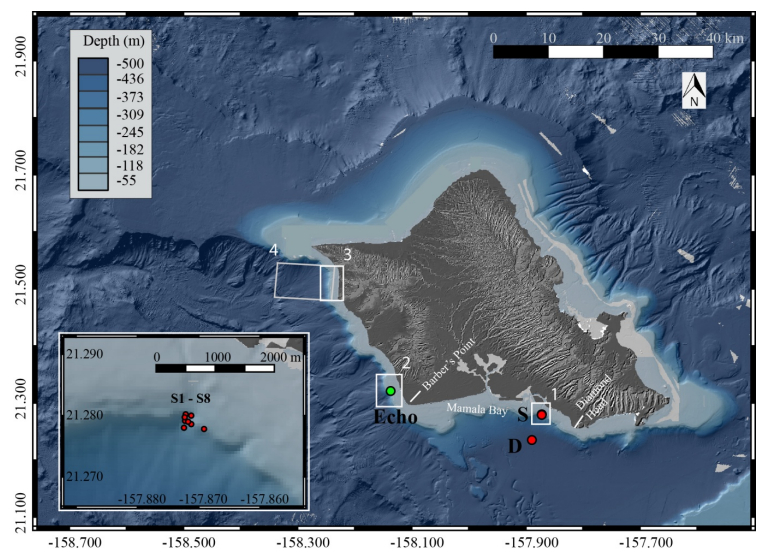
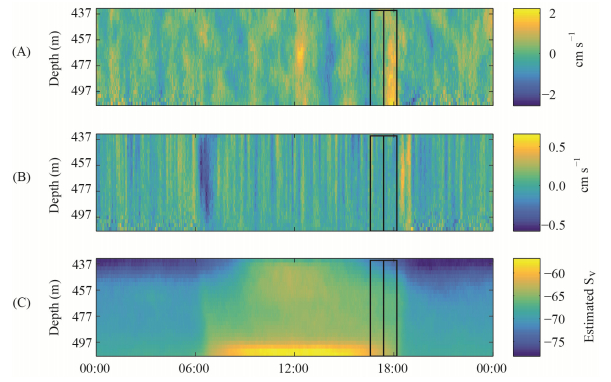
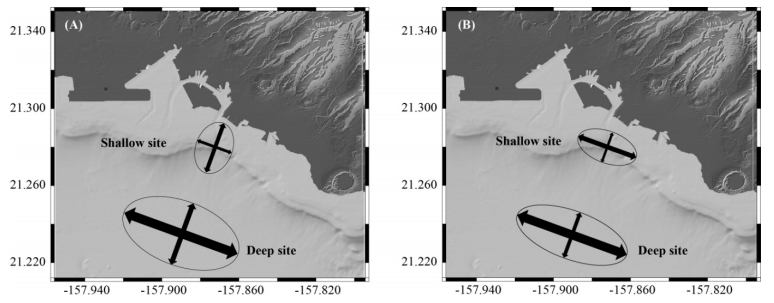
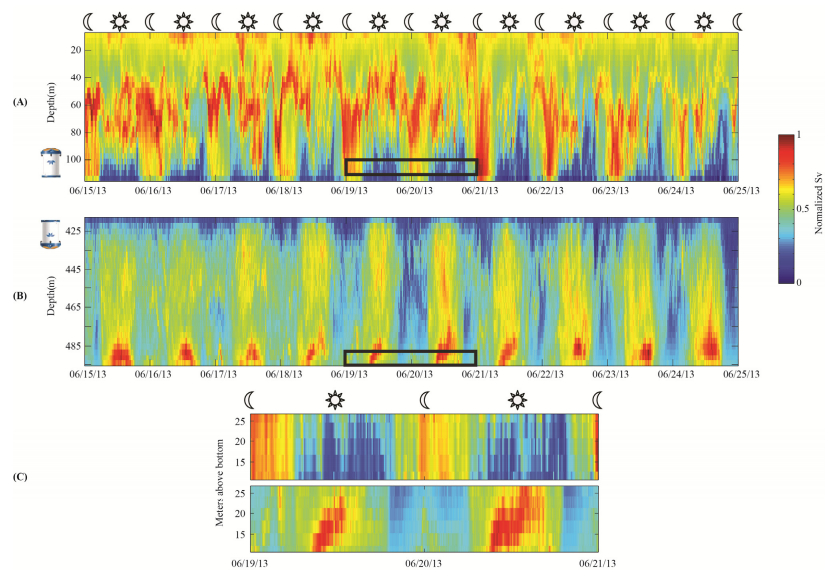
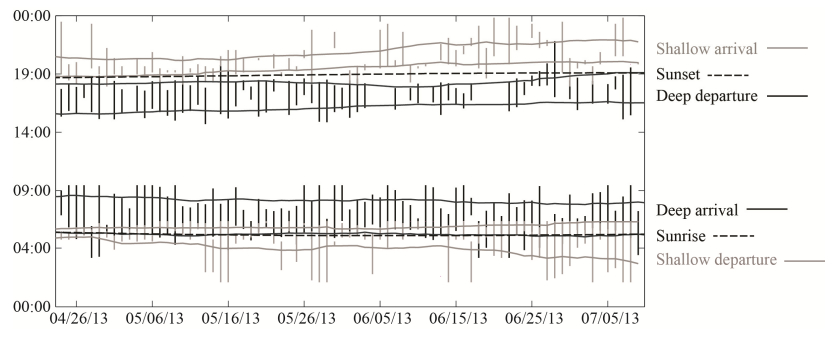
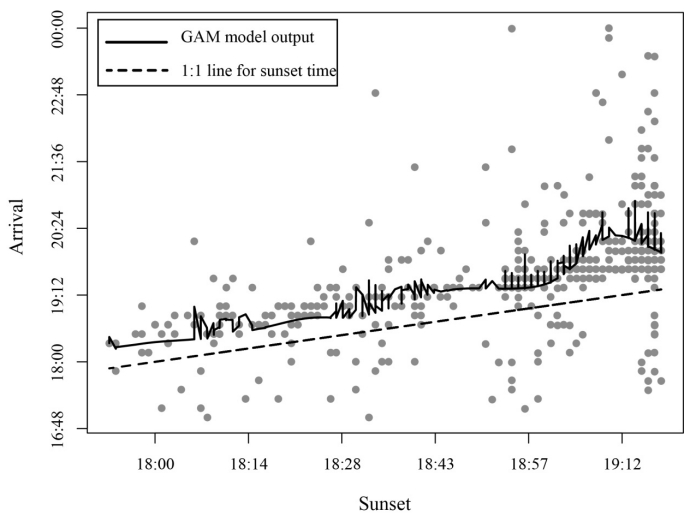
Observations of the Hawaiian Mesopelagic Boundary Community in Daytime and Nighttime Habitats Using Estimated Backscatter

1.   Introduction

In the present paper, we consider numerical solution of the time fractional Fokker-Planck equations (TFFPEs):

where $\Omega\in \mathbb{R}^d\; (d = 1, 2, 3)$, $\boldsymbol{x} = {(x_1, x_2, \ldots, x_d)}$, $u_0(\boldsymbol{x})$ is smooth on $\Omega$, $\boldsymbol{p}: = (p_1, p_2, \ldots, p_d)$ with $p_i: = p_i(\boldsymbol{x}, t) \; (i = 1, 2, \ldots, d)$ and $q: = q(\boldsymbol{x}, t)$ are continuous functions. ${\partial}_t^{\alpha}u$ represents the Caputo derivative of order $\alpha \in (0, 1)$. When $\alpha = 1$ in Eq (1.1), the corresponding equations are a class of very useful models of statistical physics to describe some practical phenomena. TFFPEs are widely used in statistical physics to describes the probability density function of position and the evolution of the velocity of a particle, see e.g., ^[1,2,3,4]. The TFFPEs also represent the continuous limit of a continuous time random walk with a Mittag-Leffler residence time density. For a deeper understanding of TFFPEs, we refer the readers to ^[5,6]. In addition, the regularity of the solutions of the TFFPE (1.1) can be found in ^[7].

For the past few years, many numerical methods were used to solve the TFFPEs. For example, Deng ^[8] proposed an efficient predictor-corrector scheme. Vong and Wang ^[9] constructed a compact finite difference scheme. Mahdy ^[10] used two different techniques to study the approximate solution of TFFPEs, namely the fractional power series method and the new iterative method. Yang et al. ^[11] proposed a nonlinear finite volume format to solve the two-dimensional TFFPEs. More details can refer to ^{[12,13,14,15]}. Besides, it is difficult that analysing the convergence and stability properties of the numerical schemes for TFFPEs, when convective and diffusion terms exist at the same time. In the study of TFFPEs, the conditions imposed on $\boldsymbol{p}$ and $q$ were somewhat restrictive. For example, for solving the one-dimensional TFFPEs, Deng ^[16] proved the stability and convergence under the conditions that $p_1$ was a monotonically decreasing function and $q \leq 0$. Chen et al. ^[17] obtained the stability and convergence properties of the method with the conditions that $p_1$ was monotone or a constant and $q$ was a constant.

To solve the time Caputo fractional equations, one of the keys is the treatment of the Caputo derivative, which raised challenges in both theoretical and numerical aspects. Under the initial singularity of the solutions of the equations, many numerical schemes are only proved to be of $\tau^\alpha$ in temporal direction, e.g., convolution quadrature (CQ) BDF method ^[18], CQ Euler method ^[19], uniform $L1$ method et al. ^[20,21]. Here $\tau$ represents the temporal stepsize. Considering the singularity of solutions, different numerical formats were established to obtain high convergence orders, e.g., the Alikhanov scheme (originally proposed in ^[22]) and the $L1$ scheme (see e.g., ^[23]) by employing the graded mesh (i.e., $t_n = T(n/K)^r, n = 1, 2, \ldots, K$, $r$ is mesh parameter). It was proved that the optimal convergence of those methods can be $2$ and $2-\alpha$ iff $r\geq 2/\alpha$ and $r\geq(2-\alpha)/\alpha$, respectively (see e.g., ^{[24,25,26,27,28,29]}). The $\overline{{\rm L}1}$ scheme studied in ^[30,31,32] was another high-order scheme for Caputo fractional derivative. There were also some fast schemes for Caputo fractional derivative, see ^{[33,34,35,36]}. When $\alpha$ was small, the grids at the beginning would become very dense. It may lead to the so-called round-off errors. Recently, taking the small $\alpha$ and the initial singularity into account, Li et al. ^[37] introduced the transformation $s = t^{\alpha}$ for the time variable, and derived and analyzed the equivalent fractional differential equation. They constructed the $TL1$ discrete scheme, and obtained that the convergence order of the $TL1$ scheme is of $2-\alpha$. Based on the previous research, Qin et al. ^[38] studied the nonlinear fractional order problem, and established the discrete fractional order Grönwall inequality. Besides, discontinuous Galerkin methods were also effective to solve the similar problems with weak singular solutions ^[39,40,41].

Much of the past study of TFFPEs (i.e., in ^{[16,17,42,43]}) has been based on many restrictions on $q$ and $p_i, \; i = 1, 2, \ldots, d$. This reduces the versatility of the equations. In the paper, we consider the more general TFFPE (1.1), i.e., $q$ and $p_i, \; i = 1, 2, \ldots, d,$ are variable coefficients, and $q$ is independent of $p_i$. We draw on the treatment of the Caputo derivative in ^[37], introduce variable substitution, and construct the $TL1$ Legendre-Galerkin spectral scheme to solve the equivalent $s$-fractional equation. For time discreteness, we take into account the initial singularity, and obtain that the optimal convergence order is $2-\alpha$. In terms of spatial discreteness, unlike other schemes ^[16,17], which impose restrictions on coefficients, the Legendre-Galerkin spectral scheme does not require $p_i$ and $q$ to be constants or to be monotonic. Besides, we obtain the following theoretical results. The order of convergence in $L^2$-norm of the method is exponential order convergent in spatial direction and ($2-\alpha$)-th order convergent in the temporal direction. And the scheme is valid for equations with small parameter $\alpha$.

The structure of the paper is as follows. In Section 2, we propose the $TL1$ Legendre-Galerkin spectral scheme for solving TFFPEs. In Section 3, the detailed proof of our main results is presented. In Section 4, two numerical examples are given to verify our obtained theoretical results. Some conclusion remarks are shown in Section 5.

2.   Numerical scheme

We denote $W^{m, p}(\Omega)$ and $||\cdot||_{W^{m, p}\;(\Omega)}$ as the Sobolev space of any functions defined on $\Omega$ and the corresponding Sobolev norm, respectively, where $m\geq0$ and $1\leq p\leq \infty$. Especially, denote $L^2(\Omega): = W^{0, 2}(\Omega)$ and $H^m(\Omega): = W^{m, 2}(\Omega)$. Define $C^{\infty}_0(\Omega)$ as the space of infinitely differentiable functions which are nonzero only on a compact subset of $\Omega$ and $H^1_0(\Omega)$ as the completion of $C^{\infty}_0(\Omega)$. For convenience, denote $||\cdot||_0: = ||\cdot||_{L^2(\Omega)}$, $||\cdot||_m: = ||\cdot||_{H^m(\Omega)}$.

For simplicity, we suppose that $\Omega = (-1, 1)^d$, and $u(\boldsymbol{x}, t)\in H_0^1(\Omega)\cap H^m(\Omega)$ for $0\leq t\leq T$. First of all, we introduce $TL1$ scheme to discrete the Caputo fractional derivative. Introducing the change of variable as follows ^[21,37,44]:

By this, then the Caputo derivative of $u(\boldsymbol{x}, t)$ becomes

Hence, Eq (1.1) can be rewritten as

where $\tilde{\boldsymbol{p}} = (\tilde{p}_1, \tilde{p}_2, \ldots, \tilde{p}_d)$, $\tilde{p}_d: = p_d(\boldsymbol{x}, s^{1/\alpha}), \; \tilde{q}: = q(\boldsymbol{x}, s^{1/\alpha})$, and $\tilde{f}(\boldsymbol{x}, s) = f(\boldsymbol{x}, s^{1/\alpha})$. Let $s_n = T^\alpha n/K, \; n = 0, 1, \ldots, K$, and the uniform mesh on $[0, T^\alpha]$ with $\tau_s = s_n-s_{n-1}$. For convenience, $K_i$, $i\geq 1$ represent the positive constants independent of $\tau_s$ and $N$, where $N$ represents polynomial degree. In addition, we define the following notations

Applying the $TL1$ approximation, we have

Here the coefficients $a_{n, n-l} = \frac{1}{\tau_s\Gamma(1-\alpha)}\int_{s_{l-1}}^{s_l}\frac{dr}{(s_n^{1/\alpha}-r^{1/\alpha})^\alpha}$, and $Q^n$ represents the truncation error. For more details, we refer to ^[37,38]. By Eq (2.6), then Eq (2.3) arrives at

For spatial discretization, we introduce the following basis functions:

where $\boldsymbol{k} = {(k_1, k_2, \ldots, k_d)}$, $I_N = {\{0, 1, 2, \ldots, N-2\}}$. For $\psi_{k_i}({x_i}), \; i = 1, 2, \ldots, d$, one has

where $\{L_j(x)\}_{j = 0}^N$ are the Legendre orthogonal polynomials, given by the following recurrence relationship ^[45]:

Define the finite-dimensional approximation space

where $\boldsymbol{N} = (\underbrace {N, N, \ldots, N}_{d})$. For any function $w_{\boldsymbol{N}}(x)$, write

By Eqs (2.7) and (2.8), we have

Then, the $TL1$ Legendre-Galerkin spectral scheme is to seek $W^{n}\in X_{\boldsymbol{N}}$, such that

Here $W^0 = \pi_{\boldsymbol{N}} w^0$, and $\pi_{\boldsymbol{N}}$ is the Ritz projection operator given in Lemma 2. For instance, if $d = 1$, we solve Eqs (2.3) and (2.4) by

where $\hat{\boldsymbol{w}}^n = (\hat{w}^n_0, \hat{w}^n_1, \hat{w}^n_2, \dots, \hat{w}^n_{N-2})^T$, $\boldsymbol{A1}_{j, h} = (\psi_{h}(x), \psi_{j}(x))$, $j, h \in I_N$, $\boldsymbol{A2}_{j, h} = (\psi'_{h}(x), \psi'_{j}(x))$, $\boldsymbol{A3}^n_{j, h} = (\tilde{p}^n\psi'_{h}(x), \psi_{j}(x))$, $\boldsymbol{A4}^n_{j, h} = (\tilde{q}^n\psi_{h}(x), \psi_{j}(x))$, and $\boldsymbol{F}^n_{j, 1} = (\tilde{f}^n, \psi_{j}(x))$.

The typical solution of Eq (1.1) meets ^[18,46,47]

then, with the help of the changes of variable (2.1), one has (see e.g., ^[38])

where $C > 0$ is a constant independent of $s$ and $\boldsymbol{x}$. From [37, Lemma 2.2] and [38, Lemma 2.1], the solution becomes smoother at the beginning.

Now, the convergence results of $TL1$ Legendre-Galerkin spectral scheme (2.9) is given as follows.

Theorem 1. Assume that $\tilde{q}$ and $\tilde{p_i}, \; i = 1, 2, \ldots, d,$ in (2.3) are bounded, and that the unique solution $w$ of Eqs (2.3) and (2.4) satisfying Eq (2.11) and $w(\boldsymbol{x}, s)\in H_0^1(\Omega)\cap H^m(\Omega)$. Then, there exist $N_0 > 0$ and $\tau_0 > 0$ such that when $N\geq N_0$ and $\tau_s\leq\tau_0$, Eq (2.9) has a unique solution $W^n\; (n = 0, 1, \ldots, K)$, which satisfies

where $K^* > 0$ is a constant independent of $\tau_s$ and $N$.

3.   Proof of the main results

3.1.   Preliminaries

We will present the detailed proof of Theorem 1 in this section. For this, we first introduce the following several lemmas.

Lemma 1. ^[37,38] For $n\geq 1$, we get

Lemma 2. If we given the Ritz projection operator $\pi_{\boldsymbol{N}}:H_0^1(\Omega) \rightarrow X_{\boldsymbol{N}}$ by

then, one can get that ^[48]

with $d \leq m\leq N+1$, where $C_{\Omega} > 0$ is a constant independent of $N$.

Lemma 3. ^[49] For any $s_K = T^{\alpha} > 0$ and given nonnegative sequence $\left\{\lambda_i\right\}^{K-1}_{i = 0}$, assume that there exists a constant $\lambda^* > 0$ independent of $\tau_s$ such that $\lambda^*\geq\sum^{K-1}_{i = 0}\lambda_i$. Assume also that the grid function $\{{w^n|n\geq0}\}$ satisfies

where $\{Q^n|n\geq1\}$ is well defined in Eq (2.6). Then, there exists a constant $\tau_s^* > 0$ such that, when $\tau_s\leq\tau_s^*$,

where $C_1^*$ is a constant and $E_\alpha(x) = \sum_{k = 0}^\infty\frac{x^k}{\Gamma(1+k\alpha)}$.

3.2.   Proof of Theorem 1

We will offer the proof of Theorem 1 in this section. The projection $\pi_{\boldsymbol{N}} w^n$ of the exact solution $w^n$ satisfies

Here $R^n = D_\tau^\alpha(w^n-\pi_{\boldsymbol{N}} w^n)-\Delta(w^n-\pi_{\boldsymbol{N}} w^n)+\tilde {\boldsymbol{p}}^n \cdot \nabla(w^n-\pi_{\boldsymbol{N}} w^n)+\tilde{q}^n(w^n-\pi_{\boldsymbol{N}} w^n)$, and $Q^n$ is the truncation error for approximating the fractional derivative defined in Eq (2.6).

The error between numerical solution $W^n$ and exact solution $w^n$ can be divided into

Let

Subtracting Eq (2.9) from Eq (3.2), we get that

Setting $v = e^n$ in Eq (3.4), we obtain

By Lemma 1, we have

By Cauchy-Schwartz inequality, one can obtain that

Here $K_1 = \mathop{\max}\limits_{0\leq n\leq K}\left\lbrace ||\tilde {\boldsymbol{p}}(\boldsymbol{x}, s_n)||_0 \right\rbrace$, and $K_2 = \mathop{\max}\limits_{0\leq n\leq K}\left\lbrace \mathop{\max}\limits_{\boldsymbol{x}\in \Omega}|\tilde{q}(\boldsymbol{x}, s_n)| \right\rbrace$. Similarly, we see that

Noting that $e^n\in X_{\boldsymbol{N}}$ and by Lemma 2, one has

Then

Here $K_3 = \mathop{\max}\limits_{0\leq n\leq K}\left\lbrace C_{\Omega}||D_\tau^\alpha w^n||_m, K_1C_{\Omega}||w^n||_m, K_2C_{\Omega}||w^n||_m\right\rbrace$, and Lemma 2 is applied. Substituting Eqs (3.6)–(3.9) into Eq (3.5), one gets

Noting that $e^0 = 0$ and by Lemma 3, it follows that

By Eq (3.3), we observe

where $K^* = \mathop{\max}\limits_{0\leq n\leq K}{\big\{C_{\Omega}||w^n||_m, \; 4K_3C_1^*E_\alpha\big(4(K_1^2/4+K_2)s_n\big)\big\}}$. This completes the proof.

4.   Numerical results

In this section, two numerical examples are given to verify our theoretical results. We define the maximal $L^2$ error and the convergence order in time, respectively, as

Example 1. Consider the one-dimensional TFFPEs:

where the initial-boundary conditions and the forcing term function $f$ are choosen by the analytical solution

In this case, $q$ is independent of $p_1$, furthermore, $p_1$ and $q$ are not monotone functions.

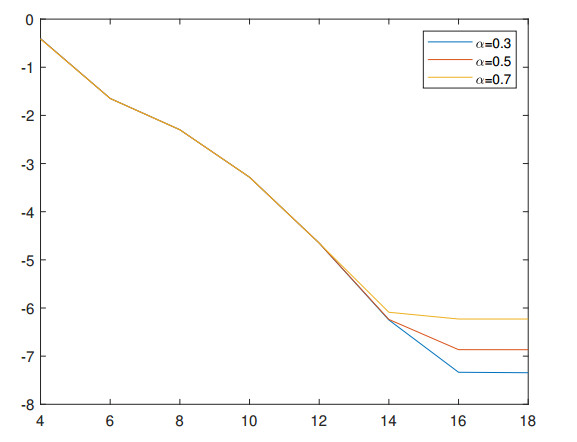
We solve this problem with the $TL1$ Legendre-Galerkin spectral method. Table 1 gives the maximal $L^2$ errors, the convergence orders in time and the CPU times with $N = 14$. The temporal convergence orders are close to $2-\alpha$ in Table 1. For the spatial convergence test, we set $K = 8192$. In Figure 1, we give the errors as a function of $N$ with $\alpha = 0.3, \; 0.5, \; 0.7$ in logarithmic scale. We can observe that the errors indicate an exponential decay.

Table 1.  Maximal $L^2$ errors, convergence orders in time and CPU times with $N = 14$ for Example 1.

	$\alpha=0.1$				$\alpha=0.3$				$\alpha=0.5$
$K$	$e(K)$	order	CPU(s)		$e(K)$	order	CPU(s)		$e(K)$	order	CPU(s)
4	5.3660e-03	*	1.12e-02		7.5697e-03	*	9.76e-03		8.5571e-03	*	9.92e-03
16	1.3833e-03	0.98	2.45e-02		1.1574e-03	1.35	2.19e-02		1.3367e-03	1.34	2.25e-02
64	1.7352e-04	1.50	8.06e-02		1.3606e-04	1.54	7.53e-02		1.8311e-04	1.43	7.40e-02
256	1.6850e-05	1.68	2.90e-01		1.4476e-05	1.62	3.00e-01		2.3859e-05	1.47	3.01e-01

---

 | Show Table

DownLoad: CSV

Figure 1.  Errors in space with $\alpha = 0.3, 0.5, 0.7$ and different $N$ for Example 1.

DownLoad: Full-Size Img PowerPoint

Example 2. Consider the two-dimensional TFFPEs:

where the initial-boundary conditions and the forcing term function $f$ are choosen by the analytical solution

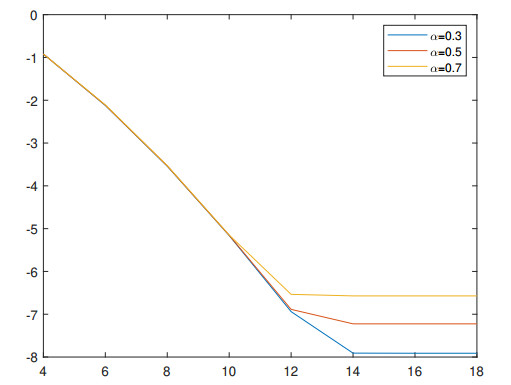
Table 2 gives the maximal $L^2$ errors, the convergence orders in time and the CPU times with $N = 14$. The temporal convergence orders are close to $2-\alpha$ in Table 2. For the spatial convergence test, we give the errors as a function of $N$ for $\alpha = 0.3, \; 0.5, \; 0.7$ and $K = 8192$ in Figure 2. We use the logarithmic scale for the error-axis. Again, we observe that the errors indicate an exponential decay.

Table 2.  Maximal $L^2$ errors, convergence orders in time and CPU times with $N = 14$ for Example 2.

	$\alpha=0.3$				$\alpha=0.5$				$\alpha=0.7$
$K$	$e(K)$	order	CPU(s)		$e(K)$	order	CPU(s)		$e(K)$	order	CPU(s)
32	7.0619e-05	*	2.08e-01		1.7386e-04	*	1.73e-01		3.1316e-04	*	1.69e-01
256	3.3124e-06	1.47	1.34e+00		9.7836e-06	1.38	1.28e+00		2.3617e-05	1.24	1.31e+00
2048	1.1965e-07	1.60	1.29e+01		4.6734e-07	1.46	1.28e+01		1.6199e-06	1.29	1.30e+01
8192	1.2339e-08	1.64	8.59e+01		5.9649e-08	1.48	8.54e+01		2.6824e-07	1.30	8.83e+01

---

 | Show Table

DownLoad: CSV

Figure 2.  Errors in space with $\alpha = 0.3, 0.5, 0.7$ and different $N$ for Example 2.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

We present a $TL1$ Legendre-Galerkin spectral method to solve TFFPEs in this paper. The new scheme is convergent with $O(\tau_s^{2-\alpha}+ N^{1-m})$, where $\tau_s$, $N$ and $m$ are the time step size, the polynomial degree and the regularity of the analytical solution, respectively. In addition, this $TL1$ Legendre-Galerkin spectral method still holds for problems with small $\alpha$ and gives better numerical solutions near the initial time. The new scheme can achieve a better convergence result on a relatively sparse grid point.

Acknowledgments

The work of Yongtao Zhou is partially supported by the NSFC (12101037) and the China Postdoctoral Science Foundation (2021M690322).

Conflict of interest

The authors declare that they have no conflicts of interest.