Associations among living alone, social support and social activity in older adults

1.   Introduction

At present, infectious diseases are still one of the most important diseases threatening human health. Faced with emerging and emerging infectious diseases, such as novel coronavirus pneumonia (NCP), AIDS, Ebola virus, avian influenza, hepatitis B, and tuberculosis. In the absence of specific drug treatment and vaccine prevention, inappropriate behavior may accelerate the speed and extent of disease spread ^[1,2,3]. We need to take active precautions to avoid the potential risk of infection. Conscious defensive behaviors, such as paying attention to personal hygiene, wearing masks, and staying away from gathering places, are especially important during epidemics. As the epidemic evolves, people are getting information about the disease from close friends, public health authorities and the media. People from different social backgrounds may take different actions to protect themselves, but awareness of the disease will accumulate. When a type of disease begins to spread, the importance people attach to it determines their actions. Quarantine measures should also be considered during a severe outbreak. Studies of infectious disease models with conscious constraints on human behavior have shown that even the absence of effective treatments can slow transmission ^[4]. Therefore, during multiple epidemics, authorities have strengthened people's awareness of the disease through media publicity and taken necessary measures to reduce exposure to the source of infection. For example, the 2009 influenza A (H1N1), the global spread of COVID-19 in 2020. Through the theoretical analysis and simulation of the model, it was found that with the increase in the proportion of infected people, people's awareness of prevention also increased, and people's susceptibility decreased. However, due to the slow response mechanism to information, and the attenuating degree of attention to the disease, the epidemic would also show oscillating behavior. But increased awareness could control the epidemic threshold for outbreaks ^[5].

It is found that people's consciousness accumulation is closely related to media propaganda. In the face of the epidemic, authorities should regularly update and release information, and publicize the ways of infection and prevention methods through various media in a timely manner, so as to promote people's awareness of prevention and reduce their contact with the source of infection. In addition, measures such as isolation have been taken to control the floating population. Media publicity plays an extremely important role in controlling the spread of the epidemic ^[6,7].

In recent years, considering that the media contributes to the accumulation of awareness, the idea of media propaganda and reducing the exposure rate of susceptible people were substituted into the infectious disease model. Some achievements have been made in predicting the epidemic trend and formulating prevention and control strategies by using the epidemic model with the media publicity effect. In response to a sudden outbreak, media campaigns can increase awareness and encourage people to take preventive measures, thereby reducing infection rates. The results show that when the contact rate between healthy people and infected people is reduced to a manageable level, the number of infected people can be greatly reduced and the peak time of the epidemic can be delayed ^[8,9]. For some seasonal and chronic infectious diseases, the expected epidemic prevention effect can also be achieved by adjusting the media propaganda strategy ^[10,11]. In the early days of the outbreak, media publicity will increase people's awareness of the disease and make susceptible persons take active quarantine measures. However, the long-term media publicity response may be attenuated, which will gradually reduce the awareness of epidemic preparedness among susceptible persons. Therefore, many scholars divided susceptible people into two categories: unguarded consciousness and guarded consciousness. Due to the difference in the cumulative density M of consciousness, the contact rates of the two susceptible persons SS and infected persons I would also be different. The SISM infectious disease model was established, the conditions for the existence of the model equilibrium were given, and the global stability of the equilibrium was proved by constructing Liapunov function ^[12,13]. Misra et al. considered that media publicity made susceptible people form a conscious group to avoid contact with infected people, proposed a nonlinear mathematical model of the influence of media publicity on the spread of influenza and other infectious diseases, and provided stability conditions of the equilibrium point. Their results showed that media publicity could control the spread of infectious diseases, but that immigration was likely to spread them ^[14]. Wang Xiaona et al. considered that unconscious susceptible persons become conscious susceptible persons after the effect of media information, and established a time-lag model of media reports for the control of a class of infectious diseases with an incubation period. They found that changes in awareness caused by media activities could prevent contact with infected people and effectively stop the spread of infectious diseases. However, due to the consumption of consciousness with time and the lag of the incubation period, Hopf bifurcation would also occur ^[15]. In ^[16], a nonlinear mathematical model with time delay was proposed by considering that media reports would contribute to the accumulation of disease knowledge of susceptible persons and make them consciously stay away from the infected persons. The lag in reporting caused by the slow acquisition of statistical data of infected cases was studied, we found that the lag would make the model unstable and cause the emergence of Hopf bifurcation. Numerical simulations showed that accumulation of consciousness did not eradicate infection, but it helped control the epidemic. According to people's cognitive differences in diseases, Samanta and Rana et al. divided susceptible people into conscious and unconscious groups, believing that there were differences in their possibility of being infected. They proposed a mathematical model to analyze the existence and stability of the equilibrium point. It is found that the change of consciousness accumulation rate may produce Hopf bifurcation, and the numerical simulation also supported the analysis results. The results of the model also showed that the media promoted people to change their behavior and played a role in controlling the epidemic of infectious diseases ^[17]. Greenhalgh and Rana et al. studied a double-delay infectious disease model by introducing two time-delay factors, one for the time lag in memory fading of aware people and one for the delay between cases of disease occurring and mounting awareness programs. The existence of Hopf bifurcation was proved. Numerical simulation verified the rationality of the model ^[18]. Considering the lag of consciousness accumulation caused by media publicity delay, some scholars proposed an infectious disease model with time delay, proved the global asymptotic stability of the two equilibrium points of the model, and found that the media coverage of infectious diseases would affect consciousness accumulation. The numerical simulation results also showed that media publicity could reduce the proportion of disease transmission rate and realization rate ^[19,20]. When a disease occurs, people take a series of preventive measures to avoid infection. The accumulation of disease awareness is particularly important, as it is affected by the lag time of media reports, the incubation period of the disease, and the duration of consciousness fatigue. Through the study of infectious disease model with time delay, it is of great significance to explore the role of media publicity in controlling the spread of infectious diseases.

In section 2 of this paper, considering the incubation period of the disease and the influence of the time lag of media publicity on the awareness rate of the epidemic, a SISM infectious disease model with double-time delay is established. In section 3, the stability of two equilibrium points and the existence condition of the Hopf branch are studied. In section 4, the influence of media propaganda time delay on the change of epidemic law is numerically simulated. In section 5, after the outbreak of A (H1N1), the model is used to analyze the influence of media coverage lag on the outbreak control.

2.   Model establishment

After the occurrence of the disease, the health and epidemic prevention departments take various prevention and control methods to isolate the source of infection and prevent the spread of the epidemic. The scholars used the infectious disease model to study the dynamical behavior of the epidemic situation, simulated the epidemic evolution under different prevention and control measures, and put forward the suggested strategies for further improving the prevention and control effect ^[21,22,23]. The incubation period of many infectious diseases is infectious, and a lack of understanding of the mode of transmission can lead to the potential spread of the epidemic. Therefore, it is particularly important to strengthen media propaganda in time to improve the awareness rate. The media publicity has a lag time h and the incubation period $\tau$ after infection. The SISM infectious disease model affected by media publicity with double-time delay is as follows:

where ${S_1}(t)$, ${S_2}(t)$ and $I(t)$ represent the density of the susceptible individuals without preventive consciousness, the density of susceptible persons with preventive consciousness and the density of infected persons at time $t$ respectively. $M(t)$ indicates the cumulative density of consciousness caused by the media at time $t$. $\lambda$ represents the population input rate $c$ represents the natural mortality rate for the total population. $\beta$ indicates an effective exposure rate between the susceptible person and the infected person. ${\xi _0}$ represents the rate of transfer of from aware susceptible individuals to unaware. $\xi$ represents the rate of transfer of from unaware susceptible individuals to aware. $v$ indicates the recovery rate of the infected person, with probability $p$ restored to the conscious susceptibility. $\mu$ indicates the implementation rate of media propaganda. ${\mu _0}$ denotes the dissipation rate of ineffective media coverage. All parameters are non-negative.

Let $N(t) = {S_1}(t) + I(t) + {S_2}(t)$, summing up the four equations of model (1), we have $\frac{{dN(t)}}{{dt}} = \lambda - cN(t)$, then

Considering the limit equation of model (1)

Let $l = \max (\tau, h)$, supposing that $C$ represents all continuous mapping: $\varphi :[-l, 0] \to {R^3}$ constitutes a Banach space, and denoting norm $\left\| \varphi \right\| = \max \{ \mathop {\sup}\limits_{ - l \leqslant \theta \leqslant 0} \left| {{\varphi _1}(\theta)} \right|, \mathop {\sup}\limits_{ - l \leqslant \theta \leqslant 0} \left| {{\varphi _2}(\theta)} \right|, \mathop {\sup}\limits_{ - l \leqslant \theta \leqslant 0} \left| {{\varphi _3}(\theta)} \right|\}$, where $\varphi = ({\varphi _1}, {\varphi _2}, {\varphi _3})$.

According to the mean of biology, it follows that $\varphi = ({\varphi _1}, {\varphi _2}, {\varphi _3}) \in {C_ + }$, ${C_ + } = \{ {\phi _i}(\theta) \geqslant 0, \forall \theta \in [-l, 0], i = 1, 2, 3\}$.

The initial condition of model (3) is

3.   The main research results

Theorem 1 If $(I(t), {S_2}(t), M(t))$ is a solution to model (3) and satisfies the initial condition (4), then $I(t), {S_2}(t), M(t)$ is non-negative and ultimately bounded.

Proof. From the first equation of model (3), when $t \geqslant 0$, we get

An integration of inequality (5) yields

From the third equation of model (3), we get

Therefore,

From the second equation of model (3), we get

Solving the Eq (6), we get

Thus, When $t \geqslant 0$, the solution to model (3) is nonnegative.

According to Eq (2) and the third equation of model (3), we get

Solving the equation, we get

Hence, all solutions to model (3) are bounded. For $t \geqslant 0$, there is a feasible region

The basic reproduction number of model (3) is defined by

The equilibria of model (3) satisfies the following equations

We obtain the disease-free equilibrium ${E_0}(0, 0, 0)$ and the endemic equilibrium ${E^*}({I^*}, S_2^*, {M^*})$.

Where

Theorem 2 The model (3) exists disease-free equilibrium ${E_0}(0, 0, 0)$. If ${R_0} > 1$, then the model (3) exists a unique endemic equilibrium ${E^*}({I^*}, S_2^*, {M^*})$.

Theorem 3 If ${R_0} \leqslant 1$, then the disease-free equilibrium ${E_0}$ of model (3) is globally asymptotically stable in $\Gamma$.

Proof. The linearization equation of model (3) at ${E_0}$ as follows

The corresponding characteristic equation of Eq (7) is

with characteristic roots ${\lambda _1} = - {\mu _0}$, ${\lambda _2} = - ({\xi _0} + c)$.

Next, we consider equation as follows

Suppose that the Eq (8) has a complex root with non-negative real part $\lambda = \alpha + i\omega$, i.e., $\alpha > 0$. Substituting it into Eq (8), and separating real and imaginary parts of Eq (8) gives that

We square both sides of the Eq (9) and add squared above equations to obtain the following equation

It follows from ${R_0} \leqslant 1$ that $k\beta \leqslant v + c$, so we have $k\beta {e^{ - \alpha \tau }} \leqslant v + c$, it is in contradiction with Eq (10), then the roots of Eq (8) only have a negative real part. Consequently, the disease-free equilibrium of model (3) is locally asymptotically stable.

Define the Lyapunov function

where $A = \frac{{pv{\mu _0} + \xi k\mu }}{{\xi k{\mu _0}}}$.

Calculating the derivative of $V(t)$, we get

Define

In the feasible region $\Gamma$, when ${S_2} = I \equiv 0$, $V'(t) = 0$. Let ${\rm H}$ be the largest compact invariant set in $\Lambda$. $V'{|_{(3)}} = 0$ implies ${S_2} = I = 0$. Substituting ${S_2} = I = 0$ into model (3), and we get that $M = 0$. Therefore, ${\rm H} = \{ {E_0}\}$. By the LaSalle invariance principle for delay systems [24], the equilibrium point ${E_0}$ of model (3) is globally asymptotically stable in $\Gamma$. This completes the proof.

Let $I = {I^*} + i$, ${S_2} = S_2^* + {s_2}$, $M = {M^*} + m$, we obtain the linearization system of model (3) at ${E^*}$

The characteristic equation of Eq (11) is

According to the different values of parameter $\tau, h$, it can be divided into the following situations to discuss the characteristic roots of Eq (12) and judge the stability of model (3) the equilibrium $E^*$ of endemic diseases.

Case (I) $\tau = h = 0$

Simplifying the characteristic Eq (12), we have

where

According to the Routh-Hurwitz Criterion, we have the following theorem.

Theorem 4 When ${R_0} > 1$ and $\tau = h = 0$, the endemic equilibrium ${E^*}$ of model (3) is locally asymptotically stable, if and only if ${a_1}{a_2} > {a_3}$.

Case (II) $\tau = 0$, $h > 0$

Simplifying the characteristic Eq (12), we have

Suppose that $\lambda = \pm i\omega (h)(\omega > 0)$ is purely imaginary complex roots of Eq (14). Substituting it into Eq (13), and separating real and imaginary parts of Eq (14) gives that

We square both sides of each equation above and add the squared above equations to obtain the following equation

where

It is knowing that $f(0) = {q_3}$ and $\mathop {\lim }\limits_{{\omega ^2} \to + \infty } f({\omega ^2}) = + \infty$.

When ${q_3} < 0$, then Eq (16) at least exists a positive root.

When ${q_3} > 0$, we take the derivative to both sides of the Eq (16) about ${\omega ^2}$, so

Let $\Delta$ be discriminant, then $\Delta = 4(q_1^2 - 3{q_2})$.

When $\Delta < 0$, Eq (17) has no real root, then Eq (16) has no positive real root.

When $\Delta \geqslant 0$, if ${q_1} > 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_2} > 0$, Eq (17) has no positive real root, then Eq (16) has no positive real root; if ${q_1}$ and ${q_2}$ are the other cases, Eq (17) has at least a positive real root ${\bar \omega ^2}$. So $f({\bar \omega ^2}) \leqslant 0$, then Eq (16) has at least a positive root.

Suppose that Eq (16) has finite positive roots $\omega _k^2 \in [0, {\bar \omega ^2}]{\rm{ }}(k = 1, 2, \cdots, m)$ in the interval $[0, {\bar \omega ^2}]$, substituting it into the second formula of Eq (15). We obtain

Let $h_k^j$ satisfy $\alpha (h_k^j) = 0, {\rm{ }}\omega (h_k^j) = {\omega _k}$ and $h_1^0 = \min \{ h_k^j\}$.

Then, we have

Theorem 5 If $R_{0}>1, \quad \tau=0, \quad h>0$ hold, then

(I) When ${q_3} > 0$, $\Delta < 0$ or $\Delta \geqslant 0$ and ${q_i} > 0(i = 1, 2)$, for all $h \geqslant 0$, the endemic equilibrium ${E^*}$ of model (3) is asymptotically stable.

(II) When ${q_3} < 0$ or $\Delta \geqslant 0$, ${q_i}(i = 1, 2)$ are non-positive at the same time, the limit point of $f({\omega ^2})$ is ${\bar \omega ^2}$, and when $f({\omega ^2}) \leqslant 0$, for each $h \in [0, h_1^0)$, the endemic equilibrium ${E^*}$ of model (3) is asymptotically stable. When $h > h_1^0$, the characteristic roots of Eq (14) have a positive real part, then the endemic equilibrium ${E^*}$ of model (3) is unstable.

(III) If condition (Ⅱ) holds, when $h = h_k^j(k = 1, 2, 3, ..., m;{\rm{ }}j \in N)$, then there exists Hopf bifurcation around the endemic equilibrium ${E^*}$ of the model (3).

Proof. (I) According to the roots existence conditions of cubic polynomial, when ${q_3} > 0$, $\Delta < 0$ or $\Delta \geqslant 0$ and ${q_i} > 0(i = 1, 2)$, then Eq (15) has no positive root. By the Cook Theorem [25] we know that all characteristic roots of Eq (13) have negative real parts, then ${E^*}$ is asymptotically stable, conclusion (I) holds.

(II) Suppose that $\lambda (h) = \alpha (h) + i\omega (h)$ is the positive root of Eq (13). When $\Delta \geqslant 0$, ${q_1}$ and ${q_2}$ are non-positive at the same time, $f'({\omega ^2})$ has a positive root ${\bar \omega ^2}$, and $f({\omega ^2}) \leqslant 0$, it follows that Eq (15) exists positive roots $\omega _k^2(k = 1, 2, \cdots, m)$ in $[0, \bar \omega]$, let ${\omega _0}$ satisfy $\alpha (h_1^0) = 0, {\rm{ }}\omega (h_1^0) = {\omega _0}$. According to the continuous dependence of characteristic root $\alpha (h)$ to $h$ and the choice of $h_1^0$, it follows that the critical value $h_1^0$ is $h$ which makes the characteristic root firstly through to the imaginary axis. According to the Cook Theorem [25], for each $h \in [0, h_1^0)$, it follows that all the roots of Eq (13) have a strict negative real part, so ${E^*}$ is asymptotically stable. When $h > h_1^0$, then the characteristic roots of Eq (13) exist positive real part, the endemic equilibrium ${E^*}$ of model (3) is unstable, conclusion (II) holds.

(III) If condition (II) holds, now differentiating Eq (13) with respect to $h$, we get

Solving the above equation, we have

Substituting $\lambda = i{\omega _k}$ into Eq (17) and combining Eq (14), we get

Due to the choice of ${\omega _k}$ and the property of quadratic function, we get $f'(\omega _k^2) \ne 0$. Combining transversality condition [12], $sign{\left({{{d\operatorname{Re} \lambda (h_k^j)} \mathord{\left/ {\vphantom {{d\operatorname{Re} \lambda (h_k^j)} {dh}}} \right. } {dh}}} \right)^{ - 1}} \ne 0$ holds. According to Hopf bifurcation theorem [26], it follows that Hopf bifurcation appears if $h$ through to $h_k^j$, conclusion (III) holds. This completes the proof of Theorem 4.

Case (III) $\tau > 0$, $h = 0$

Simplifying the characteristic Eq (11), we have

Suppose that $\lambda = \pm i\omega (h)(\omega > 0)$ is a pair of purely imaginary roots of Eq (19). Substituting it into Eq (19), and separating real and imaginary parts, we have

Where

When ${R_0} > 1$, then ${p_3} > 0$. Now differentiating Eq (18) with respect to ${\omega ^2}$, we have

Let $\Delta = 4(p_1^2 - 3{p_2})$ be the discriminant of Eq (21).

Suppose that ${\bar \omega ^2}$ is the positive root of Eq (21), so $f'({\bar \omega ^2}) = 0$, and $f({\bar \omega ^2}) < 0$, then Eq (20) have positive roots $\omega _l^2(l = 1, 2, \cdots, n)$ in $[0, {\bar \omega ^2}]$, we obtain

where

Let $\tau _l^i$ satisfy $\alpha (\tau _l^i) = 0, {\rm{ }}\omega (\tau _l^i) = {\omega _l}$, $\tau _1^0 = \min \{ \tau _l^i\}$. We have the following theorem.

Theorem 6 If $R_{0}>1, \quad \tau>0, \quad h=0$ holds, we have

(I) When $\Delta < 0$ or $\Delta \geqslant 0$ and ${p_1}, {\rm{ }}{p_2} > 0$, for all $\tau \geqslant 0$, the endemic equilibrium ${E^*}$ of model (3) is asymptotically stable;

(II) When $\Delta \geqslant 0$, ${p_i}(i = 1, 2)$ are not positive at the same time, the limit point of $f({\omega ^2})$ is ${\bar \omega ^2}$, and when $f({\omega ^2}) \leqslant 0$, for each $\tau \in [0, \tau _1^0)$, the endemic equilibrium ${E^*}$ of model (3) is asymptotically stable; when $\tau > \tau _1^0$, the characteristic roots of Eq (19) have a positive real part, then the endemic equilibrium ${E^*}$ is unstable;

(III) If condition (II) and

holds, when $\tau = \tau _l^i(l = 1, 2, 3, ..., n;{\rm{ }}i \in N)$, then there exists Hopf bifurcation around the endemic equilibrium ${E^*}$ of the model (3).

Proof. The proof of this theorem can be complete by the method analogous to that used above proof.

(III) Now differentiating Eq (18) with respect to $\tau$, we get

Substituting $\lambda = i{\omega _l}$ into Eq (22), we have

It follows from the transversality condition that $sign{\left({{{d\operatorname{Re} \lambda (h_k^j)} \mathord{\left/ {\vphantom {{d\operatorname{Re} \lambda (h_k^j)} {dh}}} \right. } {dh}}} \right)^{ - 1}} \ne 0$ holds. According to the Hopf bifurcation theorem, it follows that the model (3) undergoes Hopf bifurcation around the endemic equilibrium ${E^*}$ if $\tau$ through to $\tau _l^i$. So conclusion (III) holds. This completes the proof of Theorem 6.

Cas (IV) $\tau > 0, {\rm{ }}h > 0$

Based on the above research methods, two different conditions are discussed.

(I) Let time delay $\tau$ be research parameter, and fix ${h^{\rm{*}}} \in [0, h_1^0)$, Eq (10) becomes

Let $\lambda = i\omega {\rm{ }}(\omega > 0)$ be the root of Eq (24), substituting it into Eq (24). And separating real and imaginary part, we have

where

${m_3}, {\rm{ }}{m_4}$ are shown in Eq (22).

Supposed that there exist positive roots ${\omega _l}(l = 0, 1, 2, ..., n)$ of $f(\omega)$, substituting it into Eq (26), we have

Let $\alpha (\tau _{1l}^i) = 0, {\rm{ }}\omega (\tau _{1l}^i) = {\omega _l}$, $\tau _{10}^0 = \min \{ \tau _{1l}^i\}$.

(II) Let time delay $h$ be research parameter, and fix ${\tau ^{\rm{*}}} \in [0, \tau _1^0)$, Eq (11) becomes

Let $\lambda = i\omega (\omega > 0)$ be the root of Eq (27), substituting it into Eq (27). And separating real and imaginary parts, we have

And removing $\sin \omega h$ and $\cos \omega h$, we obtain

where

Supposed that there exist positive roots ${\omega _k}(k = 0, 1, 2, ..., m)$ of $f(\omega)$, substituting it into Eq (28), we have

Let $\alpha (h_{1k}^j) = 0, {\rm{ }}\omega (h_{1k}^j) = {\omega _k}$ and $h_{10}^0 = \min \{ h_{1k}^j\}$.

In similar to the proof of Theorem 5, we obtain

Theorem 7 If holds, we have

(I) If ${h^*} \in [0, h_1^0)$, and Eq (25) exists positive roots, when $\tau \in [0, \tau _{10}^0)$, the positive equilibrium point ${E^*}$ of model (3) is asymptotically stable. When $\tau > \tau _{10}^0$, the Eq (24) has at least a positive real part characteristic root, then the positive equilibrium point ${E^*}$ of model (3) is unstable. When $\tau = \tau _{1l}^i{\rm{ }}(l = 0, 1, 2, ..., n;{\rm{ }}i \in N)$, then the model (3) undergoes Hopf bifurcation around the positive equilibrium point ${E^*}$.

(II) If ${\tau ^*} \in [0, \tau _1^0)$, and Eq (29) exists positive roots, when $h \in [0, h_{10}^0)$, the positive equilibrium point ${E^*}$ of model (3) is asymptotically stable. When $h > h_{10}^0$, the Eq (27) has at least a positive real part characteristic root, then the positive equilibrium point ${E^*}$ of model (3) is unstable. When $h = h_{1k}^j, {\rm{ }}k = 0, 1, 2, ..., m;{\rm{ }}j \in N$, then there exists Hopf bifurcation around the endemic equilibrium ${E^*}$ of the model (3).

According to the conclusion of Theorems 5-7, the change of time delay affects the stability of the equilibrium point, and branching phenomenon occurs. In [27,28], the switching criterion of stability is given according to the distribution of characteristic roots for the stability problem of systems with double delays. The influence of time delay on stability switching is further analyzed according to Eq (12).

By simplifying Eq (12), we get

where

According to the conditions of Theorem 4, there is no imaginary root of ${P_0}(\lambda)$, that is to say, ${P_0}(i\omega) \ne 0$. Substituting $\lambda = i\omega$ into Eq (30), we get

where

Suppose the imaginary roots $\pm i\omega$ of Eq (31) exist, and $\Omega$ is the set of the roots of Eq (31). According to the operation of vector amplitude angle and [28], the time delay $\tau$ and $h$ can be calculated by given $\lambda = i\omega$ as follows

where ${\theta _1}$ and ${\theta _2}$ respectively represent the angle between vector ${a_1}(i\omega){e^{ - i\omega \tau }}$ and 1, and the angle between vector ${a_2}(i\omega){e^{ - i\omega h}}$ and 1.

Based on the above analysis and the method of [28], we can know ${P_i}(i\omega) \ne 0, i = 0, 1, 2$，$\omega \in \Omega$. And ${a_1}(i\omega)$ and ${a_1}(i\omega)$ can be computed. Thus, the time delay $\tau$ and $h$ can be calculated from Eq (30). The difference of time delay $\tau$ and $h$ leads to the switch of equilibrium stability. When the characteristic root $\lambda$ crosses the imaginary axis, the sign of the real part can be determined by the sign of the following expression:

where

According to Theorem 5.4 in [28], the following conclusions can be drawn:

Property: Suppose that $\pm i{\omega ^*}$ is a pair of imaginary roots of Eq (31), $({\tau ^*}, {h^*})$ is a parameter determined by Eq (32), the corresponding characteristic root $\lambda ({\tau ^*}, {h^*}) = \alpha ({\tau ^*}, {h^*}) \pm i\omega ({\tau ^*}, {h^*})$ of model (3) satisfies $\alpha ({\tau ^*}, {h^*}) = 0, \omega ({\tau ^*}, {h^*}) = {\omega ^*}$. When $G(\tau, h) > 0(<0)$, the characteristic root crosses the imaginary axis from the left (right) side to the right (left) side.

4.   Numerical simulations

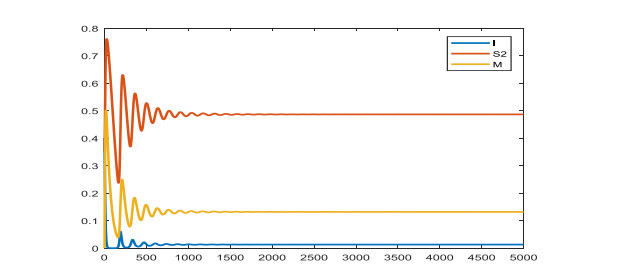
To analyze the rationality of the theorem, we present some numerical computations in the section by using MATLAB. To do the numerical simulation of the disease-free equilibrium ${E_0}$, we choose the parameter values as follows: $c = 0.007$, $\beta = 0.2$, $\xi = 0.6$, ${\xi _0} = 0.3$, $p = 0.6$, $v = 0.29$, $\mu = 0.2$, ${\mu _0} = 0.6$. And let $(0.4, 0.3, 0)$ be initial value, we can obtain ${R_0} < 1$. According to Theorem 3, it follows that the disease-free equilibrium ${E_0}$ of model (3) is globally asymptotically stable, and it has nothing to do with the value of $\tau$ and $h$. At this time, the infected people tend to be extinct, the epidemic is over. The simulation results are shown in Figure 1.

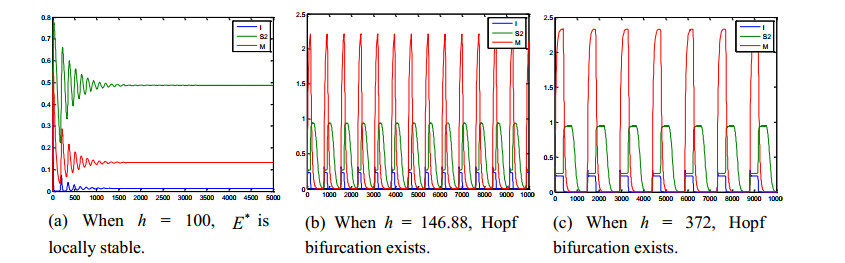
The stability of the equilibrium point of endemic disease in model (3) is analyzed as follows. We choose the following set of parameter values $c = 0.005$, $\beta = 0.5$, $\xi = 0.5$, ${\xi _0} = 0.02$, $p = 0.4$, $v = 0.2$, $\mu = 0.2$, ${\mu _0} = 0.02$. According to the different values of parameter $\tau, h$, the equilibrium points of endemic diseases are discussed. By calculating the basic reproduction number, we have ${R_0} > 1$, then the unique endemic equilibrium ${E^*}(0.013, 0.487, 0.13)$ of model (3) exists. According to the different values of time-delay parameters, the simulation results can be divided into the following cases.

Case (I) $\tau = h = 0$

According to the condition of Theorem 4, it follows that the endemic equilibrium ${E^*}$ of model (3) is stable. The numerical simulation is shown in Figure 2.

Case (II) $\tau = 0$, $h > 0$

By calculations, we obtain $\pm i{\omega _0} \approx \pm 0.045i$ and $h_1^0 \approx 146.88$. And we select $h = 100 < h_1^0$, $h = 372 > h_1^0$. According to the conditions in Theorem 5, with the increase of $h$, the stability of endemic disease equilibrium point changes from local stability to the emergence of Hopf bifurcation. The amplitude of orbit oscillation increases with the increase of $h$. Its mimetic diagrams are illustrated in Figure 3.

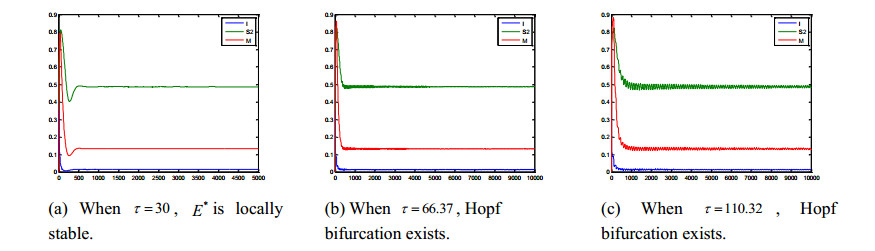
Case (III) $\tau > 0$, $h = 0$

We obtain $\pm i{\omega _0} \approx \pm 0.3627i$ and $\tau _1^0 \approx 66.37$. And we select $\tau = 30 < \tau _1^0$, $\tau = 110.32 > \tau _1^0$. According to the conditions in Theorem 6, with the increase of $\tau$, the stability of the equilibrium point of endemic disease in model (3) changes from local stability to the emergence of Hopf bifurcation, and the amplitude increases with the increase of $\tau$. However, the amplitude decreases gradually with the increase of time. Its mimetic diagrams are illustrated in Figure 4.

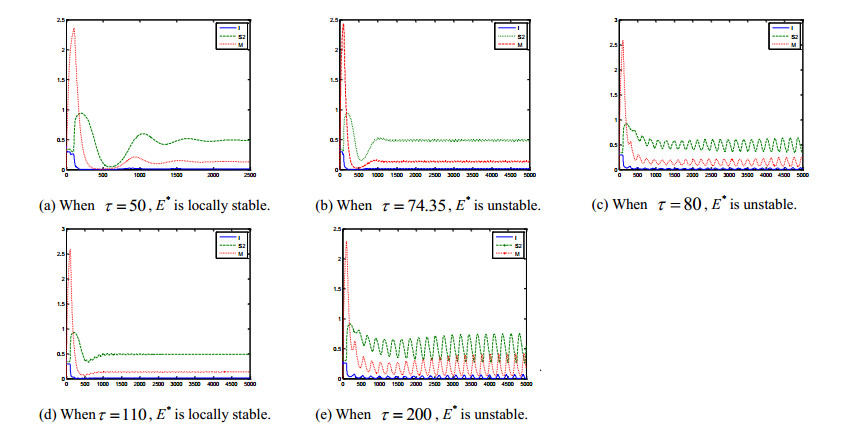
Case (IV) $\tau > 0$, $h > 0$

Firstly, let $h = 100$, we calculate $\tau _{10}^0 \approx 74.35$, And we select $\tau = 50 < \tau _{10}^0$, $\tau = 80, 110, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 200 > \tau _{10}^0$. According to the condition of Theorem 7, the trajectory of the endemic equilibrium point of model (3) is simulated, as shown in Figure 5.

With the increase of $\tau$, the stability of the equilibrium point changes from stable to unstable (Figure 5). To increase the value of $\tau$, the curve tends to be stable. Compared with Figure 5a, the time of tending to ${E^*}$ is shorted (Figure 5d). To increase the value of $\tau$ again, the curve appears oscillation (Figure 5e). Based on a given parameter $h$, it can be seen that delay time $\tau$ makes the endemic equilibrium ${E^*}$ from stable to unstable or from unstable to stable. As a result, the time delay $\tau$ plays a role in adjusting the stability of endemic equilibrium ${E^*}$.

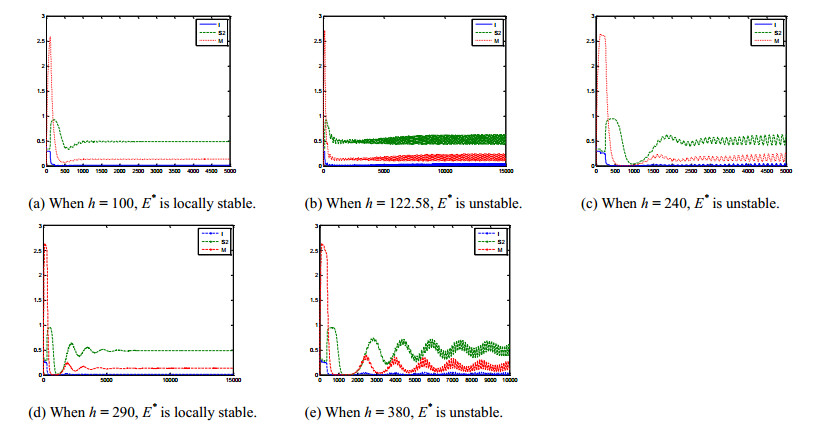
Let $\tau = 110$, we calculate $h_{10}^0 \approx 122.58$, and we select $h = 100 < h_{10}^0$, $h = 240, 290, 380 > h_{10}^0$, see Figure 6.

From Figure 6, we obtain that with the increase of $h$, the stability of the equilibrium point ${E^*}$ changes from a stable state to an unstable state. When h is increased again, it will change from an unstable state to a stable state, indicating that time delay h can also adjust the stability of the equilibrium point.

The numerical simulation shows that the incubation period and the lag of media publicity will affect the stability of the equilibrium point of endemic diseases. Comparing case (Ⅱ) with case (Ⅳ), we find that when the media's lag time is the same, the incubation period lag increases to a certain value, and the stability of the equilibrium point changes from stable state to unstable state. However, after the latency period continues to increase, the stability of the equilibrium point changes from an unstable state to a stable state, and so on. Comparing case (III) with case (Ⅳ), we find that when the incubation period is the same, the media's lag time increases to a certain value, and the stability of the equilibrium point changes from stable state to unstable state, the media's lag time continues to increase, the stability of the equilibrium point changes from unstable state to stable state. The mutual transformation between the stability and instability of the equilibrium point indicates that in practical problems, timely adjustment of publicity time should be made according to the incubation time of infectious diseases, so as to effectively control the development of the epidemic and finally reach a controllable range.

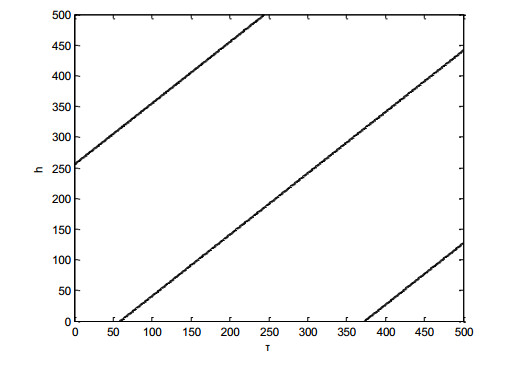
Situations (Ⅱ)-(Ⅳ) are aimed at a fixed time delay, change another delay discussions, model (3) stability switch phenomenon is simulated. Due to the different understanding of infectious diseases, the mutual interference between the two-time lags will be caused, which affects the controllability of the disease to a certain extent. The numerical simulation method is still used to intuitively understand how the value of $(\tau, h)$ changes the stability of model (3). In the model (3), the values of the above parameters are still applied. According to the calculation method in [27,28], the interval $\Omega = (0, 0.01879]$ of the existence of the root of Eq (31) can be obtained.

The value of $\omega$ is set as 0.01. On plane $(\tau, h)$, the curve L of $G(\tau, h) = 0$ is simulated numerically. The simulation results are shown in Figure 7:

The curve L in Figure 7 divides the first quadrant of the plane into several regions. In different regions, the $G(\tau, h)$ symbol can be calculated according to Eq (33). For example, $G(50, 100) > 0$, $G(200, 100) < 0$, $G(0, 100) > 0$, $G(30, 0) > 0$, $G(100, 240) < 0$. Situations (Ⅱ)-(Ⅳ) on the stability of the equilibrium point switch conclusions are verified. According to different values of $\tau$ and $h$, the stability of the equilibrium point is different.

5.   The application of the model of in influenza A (H1N1) virus

Influenza A (H1N1) virus includes gene fragments of three kinds of influenza virus of human, avian, swine flu, it spreads mainly through body fluids, droplets and air, latent period is generally 1 to 7 days [29]. In the early stage of the outbreak of A (H1N1) in 2009, government departments at all levels attached great importance to it. Through media propaganda and active intervention measures, people were made aware of the transmission route of H1N1, and their awareness of prevention was enhanced to protect themselves. The isolation of those with a history of contact with the source of the infection allowed the outbreak to be contained and eventually ended in a short time [30]. Many scholars use established models of infectious diseases and historical data to identify the parameters in the model, and use numerical simulation to predict the trend of the epidemic, and analyze and evaluate better epidemic prevention and control plans based on the statistics of the number of infected and suspected people reported every day [31,32]. Take A (H1N1) as an example to simulate the impact of media publicity on epidemic prevention and control.

The parameters of population birth rate, mortality rate, natural growth rate, constant input rate and natural mortality rate in the model are selected from paper ^{[33,34,35,36]}. The selection of parameters is shown in Table 1.

The following models can be obtained from model (3) and Table 1.

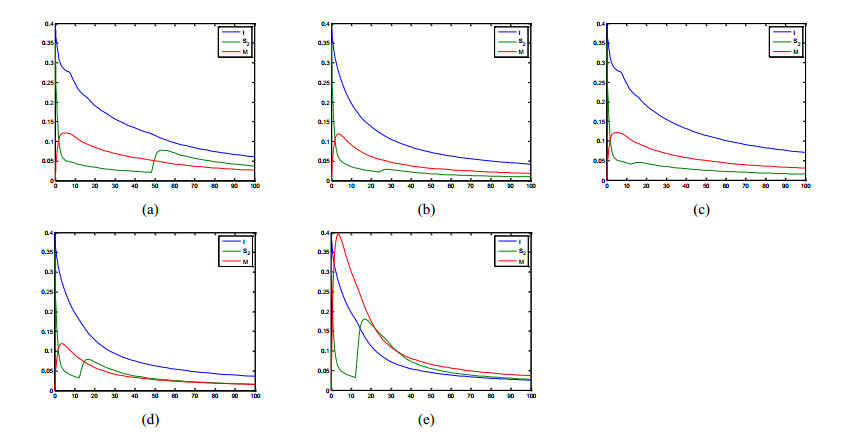
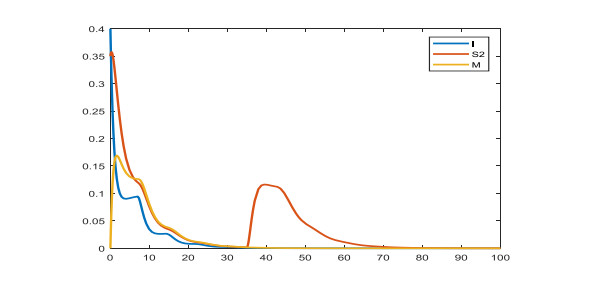
The awareness transfer rate $\xi$, media project implementation rate $\mu$, time delay $\tau$ and $h$ in model (34) are undetermined parameters. It is hoped that numerical simulation can be used to analyze the impact of these parameters on disease control and to propose feasible and effective control strategies. The values of the parameters are shown in Table 2 and the initial values $(0.4, 0.3, 0)$ are selected. The simulation results of model (33) are shown in Figure 8.

According to the numerical simulation results of model (33), when an outbreak occurs, the government should reduce the lag time of media propaganda, increase the propaganda intensity of media, let people know the transmission route of the disease as soon as possible, and take preventive measures, so as to effectively control the epidemic.

6.   Conclusions and suggestions on epidemic prevention and control

In this paper, the influence of media propaganda lag was considered, the infectious disease model with media propaganda was established, and the sufficient conditions for the existence and stability of the model equilibrium were given. Under different conditions of media propaganda time delay, the dynamical behavior of the epidemic was simulated, and the simulation results showed that the epidemic can be effectively controlled in a short time when the propaganda time delay is reduced and the awareness rate of the epidemic is improved.

After the outbreak of the epidemic, the media should respond quickly and timely to report the relevant information on the epidemic. Epidemic prevention propaganda can improve people's awareness rate and strengthen people's awareness of prevention. The hospital should isolate the infected in time and provide medical assistance to improve the cure rate. The tracing and isolation of those who have close contact with the infected person can effectively reduce or even prevent the further spread of the virus. By increasing the media propaganda, increasing the rate of consciousness transfer and media implementation, the proportion of the infected people is significantly reduced, and the disease can be well controlled. People are also advised to strengthen self-protection, pay attention to personal hygiene, change bad habits, and avoid going to public places as much as possible to reduce the chance of being infected.

Acknowledgments

This work was supported by the project of Nature Scientific Foundation of Heilongjiang Province (A2016004).

Conflict of interest

The authors declare there is no conflict of interest.