1.
Introduction
The aim of this work is to prove convergence of energies and corrector results for an elliptic problem with nonlinear Robin conditions and L1 data in a periodically perforated domain. This study completes the homogenization results given by the authors in [11], where the convergence of the solutions to a limit problem explicitly described, including its unfolded version, is proved.
More precisely, we consider the following elliptic problem in a periodically perforated domain Ω∗ε:
where f∈L1(Ω), g∈L1(∂T), A(⋅,t) is a coercive Y-periodic matrix which is bounded where t is bounded, h is a monotone continuous function verifying a sign condition and τ is a positive function in L∞(∂T).
Here, as in [11] (see also [4] and the references therein), the perforated domain is obtained by removing from a fixed domain Ω a set of ε-periodic holes of size ε. Its boundary consists of two parts on which we prescribe two different boundary conditions. Roughly speaking, on the boundary of the holes which are completely contained in Ω, we prescribe the nonlinear Robin condition, and on the remaining part of the boundary is a homogeneous Dirichlet condition. We refer the reader to Section 2 for a rigorous definition of the domain.
Heterogeneous media are widely studied since they have many interesting applications in sciences, in industry and, more recently, even in biology and environmental sciences. Let us recall that the mathematical homogenization theory (see, for instance, [3,8]) allows to describe the microscopical behavior of a problem with periodic oscillations in the coefficients and/or in the domain. Theory provides a limit homogenized problem described through a problem posed in the periodicity reference cell. It represents a good approximation of the initial problem, and it is easier to compute since it does not present oscillations anymore.
It is well known already, in the classical case where f∈L2, that the gradient of the solution uε converges weakly (never strongly) in L2 to that of the solution u0 of the homogenized problem. This is the reason why one looks for corrector results improving the weak convergence. To do that, one replaces ∇u0 by Cε∇u0, where Cε is the corrector matrix field, described via the cell problem. Hence, one proves that ∇uε−Cε∇u0 strongly converges to zero in L1. As a first step of the proof, one has to prove the convergence of the energy of the problem to the one of the homogenized problem.
In this paper, we prove similar results in the more delicate case where f is only in L1. For physical motivations and references of related works, we refer the reader to [11].
As usual, the presence of the L1 data requires a specific framework: we use here that of renormalized solutions (see [9] and the references therein and Definition 2.1 below). Since, in this case, the solution does not belong to H1, the notion of a renormalized solution consists first of imposing the regularity of the truncations of the solution, and second, of making use of test functions of the type S(u)φ where S∈C1(R) has a compact support and φ∈L∞∩H1. The test functions depend on the solution and vanish for large values of the solution. To counterbalance the lack of information where |u| is large, a decay of the truncated energy is imposed.
The existence and the uniqueness of a renormalized solution of this problem have been proved in [12]. Successively, in [11], the authors, using the periodic unfolding method introduced in [5] (see for a complete presentation the book [7]), studied the homogenization of problem (1.1), proving that the renormalized solution converges to the renormalized solution of a homogenized problem posed in the whole domain.
We prove first the convergence of the energies for problem (1.1) (see Theorem 3.1 and Theorem 3.3), and then a corrector result (Theorem 4.1) for the corresponding linear equation, where the matrix field does not depend on the solution that is A(y,t)=A(y) (see Remark 4.2). As far as we know, the results presented here are new, even in the case of a fixed domain (where there are no holes, so that Ω∗ε=Ω). With respect to the classical situation with L2 data, since the solutions are not in H1, we cannot expect to have for the renormalized solutions a convergence result for ∇uε−Cε∇u0, and we can only describe the convergences in terms of the truncated solutions and of the truncated limit function (at a fixed level). Our corrector result states the following convergence:
where u0 is the solution of the homogenized problem, Tk is the truncation at level k and Cε is the corrector matrix of the classical linear case in perforated domains (see [10]). This is not surprising, since, in the homogenization results proved in [11] for the case f∈L1, all of the convergences concern the truncations Tk(uε). In fact, the use of the truncation is standard in the literature of renormalized solutions.
The proofs are quite technical, since one cannot merely replace the solutions by their truncations and follow the usual arguments because the definition of a renormalized solution (see (2.21) in Definition 2.1) contains test functions which are nonlinear functions of the solution itself. This is the main difficulty all along the proofs. In addition, since the truncation function is not differentiable, we need to approach it by using suitable and more regular functions.
In Section 2, we introduce the problem and we recall some results on the periodic unfolding method, as well as the homogenization results from [11]. In Section 3, we prove the convergence of both (unfolded and not) types of truncated energy to those of the homogenized problem. Section 4 and 5 are devoted to the statement of the corrector result, and to the related proofs.
2.
Position of the problem and preliminaries
In this paper, we study some corrector results for an elliptic problem with nonlinear Robin conditions and L1 data, in a periodically perforated domain Ω∗ε.
In Subsection 2.1, we define the perforated domain and set the problem, together with its variational formulation. In Subsection 2.2, we recall the definition of the periodic unfolding operator and the homogenization results obtained in [11].
2.1. Position of the problem
Let us introduce the geometrical framework used in [11] (see also [4]). In what follows, Ω is a connected open bounded subset of RN (N≥2) with a Lipschitz-continuous boundary and b=(b1,…,bN) as a given basis of RN.
We define the reference periodicity cell Y by
and denote by {ε}ε>0 a positive sequence converging to zero. We set
As is usual in the periodic unfolding method, (see for instance [6], and the exhaustive book [7]), we construct the interior of the largest union of cells ε(ξ+¯Y) contained in Ω, as well as its complement, that is,
We now denote by T the reference hole, which is a compact subset of Y, and by Y∗=Y∖T the perforated reference cell. We suppose that the boundary ∂T is Lipschitz-continuous with a finite number of connected components.
Then, the holes and the perforated domain Ω∗ε (see Figure 1) are defined by
respectively, while the perforated sets corresponding to (2.1) are
Finally, we decompose the boundary of the perforated domain Ω∗ε as
In the sequel, we denote by
● ˜v, the extension by zero outside B of a function v defined on any set B,
● θ=|Y∗||Y|, the proportion of the material,
● χA, the characteristic function of a measurable set A,
● M∂T(v)=1|∂T|∫∂Tv(y)dσy, the mean value over ∂T of a function v∈L1(∂T).
Let us recall that, as ε→0,
We are concerned with the following problem:
where γ≥1 and n is the unit exterior normal to Ω∗ε.
We suppose that the following assumptions hold true:
● The functions f, g, h and τ are such that
(i) gε(x)=εg(xε), with g∈L1(∂T) Y-periodic with M∂T(g)≠0
or
(ii) gε≡0.
● Let A:(y,t)∈Y×R⟼A(y,t)∈RN2 be a real matrix field such that the matrix field A(⋅,t)={aij(⋅,t)}i,j=1...N is Y-periodic for every t.
We suppose that A is a Carathéodory function, i.e., for almost every y∈Y, the map t↦A(y,t) is continuous, and for every t∈R, the map y↦A(y,t) is measurable.
For some constant α>0, we suppose further that the matrix A satisfies the following:
3. The matrix field A(y,t) is locally Lipschitz-continuous with respect to the second variable, that is, for every r>0, there exists a positive constant Mr such that
and we set
In order to define a renormalized solution of problem (2.6), let us introduce the space
equipped with the norm
Observe that (2.16) defines a norm since a Poincaré inequality holds in Vε, namely,
where the constant C is independent of ε. Also, the Sobolev continuous and compact embedding theorems on Vε hold with constants independent of ε.
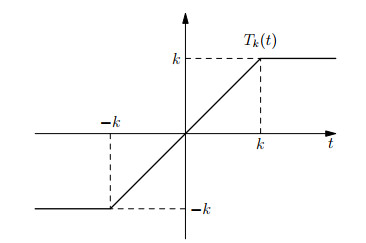
We recall now the definition of the truncation, which plays a crucial role in our work. For any k>0, the truncation function Tk:R→R at height ±k is given by
for all t∈R (see Figure 2).
Let us now present the definition of a renormalized solution to our problem, introduced in [12].
Definition 2.1. We say that uε is a renormalized solution of (2.6) if
and for any ψ∈C1(R) (or equivalently for any ψ∈W1,∞(R)) with compact support, uε satisfies
for all v∈Vε∩L∞(Ω∗ε).
Remark 2.2.
1. Proposition 2.3 in [12] (see also [2]) guarantees that the gradient and the trace along the boundaries of any function verifying (2.19) and (2.20) are well defined almost everywhere in Ω∗ε and Γε1, respectively. This shows that every term in (2.21) is well defined.
2. Observe that, for every k>0, we have
for any function v such that Tk(v)∈Vε for all k>0.
3. It has been proved in [12] that, under assumptions (2.7)–(2.12), there exists a renormalized solution to (2.6) in the sense of Definition 2.1. Moreover, assumption (2.13) provides the uniqueness of a solution.
2.2. Review of homogenization results
In this subsection, we recall the homogenization results proved in [11] by using the periodic unfolding method, and we state them in the particular case where assumption (2.13) holds. This condition is needed in the following sections, since it provides the uniqueness of the solution to the problem we consider here.
Let us start by recalling the definitions of the unfolding operator and the boundary unfolding operator. For a detailed and extensive presentation of the method, see [6,4,7]. For the properties used in this paper, we refer the reader to [11,Section 3].
For a.e. z∈RN, we denote by [z]Y=∑Ni=1libi, li∈Z for i=1,…,n, the unique integer combination such that z−[z]Y∈Y and set {z}Y=z−[z]Y∈Y.
Thus, for a positive ε, we can write
Definition 2.3. Suppose φ is a Lebesgue-measurable function. The unfolding operator T∗ε is defined as
Definition 2.4. Suppose that φ is a Lebesgue-measurable function on ∂ˆΩ∗ε∩∂Tε. The boundary unfolding operator Tbε is defined as
Remark 2.5. For a given a continuous function r(x), with r(0)=0, one has
in Ω×Y∗.
Nevertheless, for any Lebesgue measurable function φ, we can write
even if r(0)≠0. This is due to the fact that, if (x,y)∈Λε×Y∗, equality is still obtained since T∗ε(φ)(x,y)=0. Further, this implies that (2.26) holds for all (x,y)∈Ω×Y∗.
Similar properties hold for Tbε.
Let us state now the homogenization results proved in [11].
Theorem 2.6 ([11]). Let uε be the renormalized solution of (2.6) under assumptions (2.7)–(2.14), with γ≥1. Set J(γ)
Then, as ε tends to zero, there exists u0:Ω→R, measurable and finite almost everywhere, and for every k∈N, ^uk∈L2(Ω,H1 per (Y∗)) with MY∗(^uk)=0 satisfying
and
Further, there exists a unique measurable function ˆu:Ω×Y∗→R such that, for every function R∈W1,∞(R) with compact support such that suppR⊂[−n,n] for some n∈N, we have
Moreover, if S,S1 are functions in C1(R) with compact supports, then the pair (u0,ˆu) is the unique solution of the limit problem
We also have the convergence
As a consequence, we prove the following result, used in the sequel:
Corollary 2.7. Under the assumptions of Theorem 2.6, for any bounded continuous function H:R→R such that H(0)=0, we have
Consequently, using (2.5),
Proof. Using the properties of H, from Remark 2.5, convergence (2.28)(i) and the dominated convergence Lebesgue theorem, we get
Applying Corollary 1.19 of [4], from the boundedness of H we derive convergence (2.33). Convergence (2.34) is then straightforward.□
We also recall the next theorem, which identifies ˆu in terms of the limit function u0.
Theorem 2.8 ([11]). Under the same assumptions and notations of Theorem 2.6, the function ˆu can be expressed as
where (ej)Nj=1 is the canonical basis of RN and ^χej(⋅,t) is the solution of
for every t∈R and λ∈RN.
The next result shows that u0 is a renormalized solution to a homogenized elliptic problem corresponding to the homogenized matrix A0.
Theorem 2.9 ([11]). Let u0 be the function given in Theorem 2.6. Then, u0 is the renormalized solution of the problem
that is, u0 satisfies
and for every S∈C1(R) with compact support, u0 satisfies
for all η0∈H10(Ω)∩L∞(Ω).
The homogenized matrix A0(t) is defined, for every fixed t∈R, as
in which
and where the function ^χλ(⋅,t) is the solution of the problem (2.36).
Consequently, in view of Theorem 2.8,
The result below, proved in [11] (Proposition 6.1), plays an important role in the proof of the corrector results to our problem.
Proposition 2.10. Under the assumptions of Theorem 2.6, for every k∈N and ε>0, we have
3.
Convergence of the energies
The first result of this section states the convergence of the truncated energies associated with our problem. This convergence is important in itself, and it is essential in the proof of our corrector results.
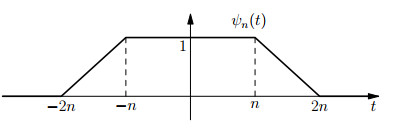
To this aim, for n∈N, we define the function ψn (see Figure 3) by
which is Lipschitz-continuous and has a compact support given by suppψn=[−2n,2n].
Further, ψn satisfies
Theorem 3.1. Under assumptions (2.7)–(2.14), let uε be the renormalized solution to (2.6). Let also G∈W1,∞(R) be a nondecreasing function such that G′ has a compact support and G(0)=0.
Then,
as ε tends to zero, where u0 and A0 are given by Theorem 2.6.
In particular, for every fixed k∈N,
as ε tends to zero.
Proof. Let G∈W1,∞(R) be a nondecreasing function such that, for some k∈N, supp G′⊂[−k,k]. Since, for n≥k,
it suffices to prove that
where ψn is defined by (3.1). Using ψ=ψn and v=G(uε) in (2.21), we have
Let us first prove that, for any n∈N,
where J(γ) is given by (2.27).
Corollary 2.7 applied to ψnG, and the first convergence in (2.28), give
From the properties of the boundary unfolding operator (see [4]) and Remark 2.5, we have
Using convergence (ii) of (2.28), we obtain
Also, from the assumptions on h and Remark 2.5, we have
Thus, combining the convergences above, equality (3.10) gives
since u0 is independent of y. When γ>1, we deduce from (3.14) that
Concerning the second integral on the left-hand side of (3.8), for the case M∂T(g)≠0, we again use (2.10), Remark 2.5 and properties of the boundary unfolding operator to write
Arguing as above, we obtain
which completes the proof of (3.8).
Now, using the properties of ψn and setting mG=maxR|G|, we obtain
Then, from Proposition 2.10, we deduce that
where ω1(n) goes to zero as n→∞. On the other hand, taking η0=G(u0) and S=ψn as test functions in (2.40) gives
This, combined with (3.7), and using (3.8) and (3.17), yields
Now, since ψn→1 as n→∞, by the Lebesgue dominated convergence theorem,
Therefore, passing to the limit as n→+∞ in (3.19), we get (3.6), which, in view of (3.5), proves (3.3).□
Proposition 3.2. Under the assumptions of Theorem 3.1, for every k∈N, we have
and
as ε tends to zero.
Proof. We prove first the following inequality for the two energies:
Observe that
Then, using (2.30) and equality (2.43) from Theorem 2.8, we can write
Hence, to prove the equality in (3.22), it suffices to show that
where, again, we used (2.30) in the first equality.
To do that, for any δ>0, let S1δ∈C1(R) be a bounded sequence function with compact support contained in [−k,k], and such that
Then, choosing in (2.31) η0=0, Ψ=^uk and S1=S1δ, we obtain
Passing to the limit as δ→0, from (3.25), we deduce (3.24), which concludes the proof of (3.22).
Let us prove now convergence (3.21). From (2.11)–(2.12), by the lower semi-continuity of the limit and using convergence (2.29)(ii), the properties of the unfolding operator and convergence (3.4) from Theorem 3.1, we have
where we also used (3.22). This implies the equality of all terms above and proves both equality (3.20) and convergence (3.21).□
The following result shows that convergence (ii) of (2.29) is actually strong.
Theorem 3.3. Under the assumptions of Theorem 3.1, for all k∈N,
Proof. By the ellipticity of A, we have
where
It suffices to show that
Now, from (3.28), we can write Jε as
where
By Proposition 3.2, we get
From the convergences of (2.29) in Theorem 2.6, we also have
Hence, using (3.31)–(3.33), from (3.30), we get (3.29).□
4.
The corrector result
In this section, we suppose that the equation is linear, that is, A(y,t)=A(y). Then, (2.12) reads as A∈(L∞(Y))N×N, and we set
Moreover, the homogenized matrix A0 is constant and is given by
We recall the well-known inequality (see, for instance, [8,Prop. 8.3])
In this case, the functions ^χλ and ^wλ defined in (2.36) and (2.42), respectively, are the classical functions used in the linear homogenization. That is, for any λ∈RN, the function ^χλ is the unique solution of
and ^wλ is defined in Y∗ by
Moreover, setting
in Ω∗ε, one has
and
For any ε, the corrector matrix for perforated domain Cε=(Cεij)1≤i,j≤N, introduced in [10], is defined by
where ^wj=^wej and {ej}Nj=1 is the canonical basis of RN.
We are now ready to present our main corrector result.
Theorem 4.1. Let uε be the renormalized solution to (2.6) under the assumptions of Theorem 2.6. Then, for any fixed k∈N, we have
The proof of Theorem 4.1 is given at the end of this section and makes use of the following results whose proof is given in next section. It makes use of a somehow "regularized truncation" function Hδk (see (4.12)–(4.13)).
Remark 4.2. Let us observe that, in the quasilinear case, the corrector would have the form Cε(x,t)=C(xε,t), and then, in the corrector result, one should replace t by a function of x. To do that, it is necessary to have at least the measurability of C with respect to t, and the proof requires that C (hence, each derivative of wj) is Lipschitz-continuous in t. This is not the case under our assumptions on A, since this regularity is essentially true only under very strong and global regularity assumptions on A, as proved in [1]. This is not adapted to homogenization, and this is why, in this section, we suppose that A is independent of t.
Theorem 4.3. Let uε be the renormalized solution to (2.6) under the assumptions of Theorem 2.6. Let k∈N be fixed, and let H be a nondecreasing function in C2(R) such that H(0)=0, and such that H′ has a compact support included in [−k,k]. Then, for any Φ=(Φ1,Φ2,…,ΦN)∈(D(Ω))N,
where α and β are given by (2.11) and (4.1), respectively.
Proof of Theorem 4.1. For a fixed k, for all δ>0, there exists Φδ∈(D(Ω))N such that
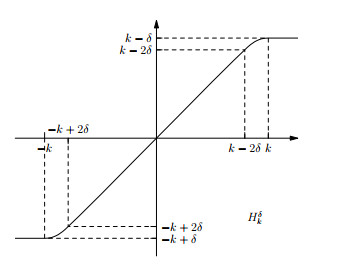
Further, for any δ>0, let Hδk∈C2(R) be a smooth approximation of Tk verifying (see Figure 4)
with
Observe that, by construction, Hδk satisfies the assumptions of Theorem 4.3; in particular, its support is contained in [−k,k].
In view of the regularity of Tk(u0), and by construction of the function Hδk, we have
with limδ→0ω2(δ)=0. Let us prove that
By the definitions of Hδk and Tk, and using the ellipticity condition (2.11), we have
where
Since the function G=Gδk satisfies the assumptions of Theorem 3.1, from (2.12) and (4.16), and by using (4.3), we obtain
which proves (4.15).
Hence, from Theorem 4.3, (4.11) and (4.15), we have
where, for a fixed k, limδ→0ω3(δ)=0. This proves (4.10).□
5.
Proof of Theorem 4.3
For any ε>0, let uε be a renormalized solution of (2.6). Let k∈N be fixed, and let H be a nondecreasing function in C2(R) such that H(0)=0 and H′ has a compact support included in [−k,k]; it follows that H(uε)=H(Tk(uε)) belongs to L∞(Ω⋆ε)∩H10(Ω⋆ε).
In the whole proof of Theorem 4.3, to shorten the notations, we set
We consider the quantity α‖∇H(uε)−CεΦ‖2L2(Ω∗ε), where Φ=(Φ1,Φ2,…,ΦN)∈(D(Ω))N.
Since Aε is uniformly coercive,
We will pass to the limit in (5.1) in each term as ε→0.
Let us point out that the difficulties in our situation concern the first three terms studied below in Step 1, Step 2 and Step 3, respectively. In particular, Step 2 requires the most delicate arguments due to the fact that we are dealing with renormalized solutions. Passing to the limit in the last term is standard.
Step 1. Limit of I1ε
By defining G(r)=∫r0H′(s)2ds and recalling that the support of H′ is included in [−k,k], we can write
Since G is a nondecreasing element of W1,∞(R) such that G(0)=0, Theorem 3.1 leads to
Step 2. Limit of I2ε
For the second integral I2ε on the right-hand side of (5.1), by the definition (4.9) of Cε, we have
Since H′ belongs to C1(R) and has a compact support, we have ∇H(uε)=H′(uε)∇uε almost everywhere in Ω⋆ε. On the other hand, the function ^wεi given by (4.6) belongs to L∞(Ω⋆ε)∩H1(Ω⋆ε), so that Φi^wεi∈L∞(Ω⋆ε)∩H10(Ω⋆ε). Then, choosing Φi^wεi as a test function and ψ=H′ in (2.21), we get, for 1≤i≤N,
Thus, to study the behavior of I2ε, it remains to determine the limit of ∫Ω⋆εAε∇H(uε)∇Φi^wεidx and the limit of the right hand-side of (5.4) as ε goes to zero.
By the properties of the unfolding operator, Remark 2.5, the convergences in (2.29) and definition (4.6), we compute
We now study the behavior of the terms on the right-hand side of (5.4) when ε goes to zero. In view of (4.6) and the properties of H′, and applying Corollary 2.7, we have
The boundary unfolding operator properties and Remark 2.5 give
Next, due to (3.11) and the properties of the boundary unfolding operator, we obtain
Since H′(u0), Φi and x↦xi are independent of y, we get, at last,
Using similar arguments, we get
where J(γ) is given by (2.27).
We now turn to the last term of the right-hand side of (5.4). Again, the unfolding operator and Remark 2.5 allow us to write
From Theorem 3.3, we have
and since H″ is a continuous and bounded function, convergence (2.28) implies that
By the properties of the unfolding operator, the function T∗ε(Φi) goes to Φ in L∞(Ω×Y∗) weak star as ε→0. It follows that
Gathering (5.3), (5.4), (5.5), (5.6), (5.7), (5.8) and (5.10), we obtain
For 1≤i≤N, using η0=Φixi and Ψ=^ukΦixi as test functions in (2.31) with S=H′ and S1=H″, and recalling that supp(H′)⊂[−k,k], we get
Because ∇(Φixi)=∇Φixi+Φiei, using (2.43) written for Tk(u0), we obtain
Step 3. Limit of I3ε and I4ε
From (4.8), we have
Using convergence (2.34) given in Corollary 2.7, and (4.7), we can pass to the limit in (5.13). Since, here, A0 is constant, we obtain
On the other hand, it has been proved in [10] that
which ends this step.
Step 4. Conclusion
Collecting (5.2), (5.12), (5.14) and (5.15), we have
From (5.1), the ellipticity of the matrix A (see (2.11)) and (4.3), we obtain
which concludes the proof.□
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: