Traveling waves for conservation laws with nonlocal flux for traffic flow on rough roads

Wen Shen; Wen Shen

doi:10.3934/nhm.2019028

Networks and Heterogeneous Media

2019, Volume 14, Issue 4: 709-732. doi: 10.3934/nhm.2019028

Previous Article Next Article

Traveling waves for conservation laws with nonlocal flux for traffic flow on rough roads

Wen Shen ^,

Mathematics Department, Pennsylvania State University, University Park, PA 16802, USA

Received: 01 September 2018 Revised: 01 March 2019
Primary: 65M20, 35L02, 35L65; Secondary: 34B99, 35Q99

We consider two scalar conservation laws with non-local flux functions, describing traffic flow on roads with rough conditions. In the first model, the velocity of the car depends on an averaged downstream density, while in the second model one considers an averaged downstream velocity. The road condition is piecewise constant with a jump at $ x = 0 $. We study stationary traveling wave profiles cross $ x = 0 $, for all possible cases. We show that, depending on the case, there could exit infinitely many profiles, a unique profile, or no profiles at all. Furthermore, some of the profiles are time asymptotic solutions for the Cauchy problem of the conservation laws under mild assumption on the initial data, while other profiles are unstable.

Keywords:

Citation: Wen Shen. Traveling waves for conservation laws with nonlocal flux for traffic flow on rough roads[J]. Networks and Heterogeneous Media, 2019, 14(4): 709-732. doi: 10.3934/nhm.2019028

Related Papers:

[1]	Ravi Agarwal, Snezhana Hristova, Donal O'Regan . Integral presentations of the solution of a boundary value problem for impulsive fractional integro-differential equations with Riemann-Liouville derivatives. AIMS Mathematics, 2022, 7(2): 2973-2988. doi: 10.3934/math.2022164
[2]	Ravi P. Agarwal, Snezhana Hristova . Stability of delay Hopfield neural networks with generalized proportional Riemann-Liouville fractional derivative. AIMS Mathematics, 2023, 8(11): 26801-26820. doi: 10.3934/math.20231372
[3]	Wei Liu, Qinghua Zuo, Chen Xu . Finite-time and global Mittag-Leffler stability of fractional-order neural networks with S-type distributed delays. AIMS Mathematics, 2024, 9(4): 8339-8352. doi: 10.3934/math.2024405
[4]	Khalid K. Ali, K. R. Raslan, Amira Abd-Elall Ibrahim, Mohamed S. Mohamed . On study the fractional Caputo-Fabrizio integro differential equation including the fractional q-integral of the Riemann-Liouville type. AIMS Mathematics, 2023, 8(8): 18206-18222. doi: 10.3934/math.2023925
[5]	Md. Asaduzzaman, Md. Zulfikar Ali . Existence of positive solution to the boundary value problems for coupled system of nonlinear fractional differential equations. AIMS Mathematics, 2019, 4(3): 880-895. doi: 10.3934/math.2019.3.880
[6]	Hasanen A. Hammad, Hassen Aydi, Manuel De la Sen . The existence and stability results of multi-order boundary value problems involving Riemann-Liouville fractional operators. AIMS Mathematics, 2023, 8(5): 11325-11349. doi: 10.3934/math.2023574
[7]	Iman Ben Othmane, Lamine Nisse, Thabet Abdeljawad . On Cauchy-type problems with weighted R-L fractional derivatives of a function with respect to another function and comparison theorems. AIMS Mathematics, 2024, 9(6): 14106-14129. doi: 10.3934/math.2024686
[8]	Yucai Ding, Hui Liu . A new fixed-time stability criterion for fractional-order systems. AIMS Mathematics, 2022, 7(4): 6173-6181. doi: 10.3934/math.2022343
[9]	Thabet Abdeljawad, Sabri T. M. Thabet, Imed Kedim, Miguel Vivas-Cortez . On a new structure of multi-term Hilfer fractional impulsive neutral Levin-Nohel integrodifferential system with variable time delay. AIMS Mathematics, 2024, 9(3): 7372-7395. doi: 10.3934/math.2024357
[10]	Lakhlifa Sadek, Tania A Lazǎr . On Hilfer cotangent fractional derivative and a particular class of fractional problems. AIMS Mathematics, 2023, 8(12): 28334-28352. doi: 10.3934/math.20231450

Abstract

1. Introduction

Differential equations with various types of fractional derivatives such as Caputo fractional derivative, Riemann-Liouville fractional derivative, are intensively studied theoretically and applied to varies models in the last decades. For example, they are successfully applied to study various types of neural networks (see, for example, ^[1,2,3]). Fractional differential equations with delays are rapidly developed. One of the main studied qualitative questions about fractional delay differential equation is the one about stability. In 1961, Dorato ^[4] introduced a concept of finite time stability (FTS). FTS is different from asymptotic stability. However, it is regarded as one of the core problems in delay systems from practical considerations. Later this type of stability has been applied to different types of differential equations. Recently, it is applied for Caputo delta fractional difference equations ^[5,6], for Caputo fractional differential equations ^[7] for -Hilfer fractional differential equation ^[8].

The investigations of the properties of the solutions of Riemann-Liouville (RL) fractional differential equations with delays are still at his initial stage. The asymptotic stability of the zero solution of the linear homogeneous differential system with Riemann-Liouville fractional derivative is studied in ^[9]. Li and Wang introduced the concept of a delayed Mittag-Leffler type matrix function, and then they presented the finite-time stability results by virtue of a delayed Mittag-Leffler type matrix in ^[10,11,12]. In connection with the presence of the bounded delay the initial condition is given on a whole finite interval called initial interval. In the above mentioned papers (^[10,11,12]) the authors study the case when the lower limit of the RL fractional derivative coincides with the left side end of the initial interval. It changes the meaning of the initial condition in differential equations. In connection with this in the paper we set up an initial condition satisfying two main properties: first, it is similar to the initial condition in differential equations with ordinary derivatives and, second, the RL fractional condition is defined at the right side end of the initial interval which is connected with the presence of RL fractional derivative.

In this paper we study initial value problems for scalar nonlinear RL fractional differential equations with constant delays. Similarly to the case of ordinary derivative, the differential equation is given to the right of the initial time interval. It requires the lower bound of the RL fractional derivative to coincides with the right side end of the initial time interval. We present an integral representation of of the studied initial value problem. By the help of fractional generalization of Gronwall inequality we study the existence, continuous dependence and finite time stability of the scalar nonlinear RL fractional differential equations.

The main contributions of the current paper include:

(ⅰ) An appropriate initial value problem for nonlinear RL fractional differential equations is set up based on the idea of the initial time interval for delay differential equations with ordinary derivatives.

(ⅱ) A mild solution of the considered initial value problem is defined based on an appropriate integral representation of the solution.

(ⅲ) The existence, continuous dependence and finite time stability of the scalar nonlinear RL fractional differential equations is studied by the help of fractional generalization of Gronwall inequality.

The rest of this paper is organized as follows. In Section 2, some notations and preliminary lemmas are presented. In Section 3, main results are obtained. In Section 3.1. mild solution of the studied initial value problem is defined and some sufficient conditions by Banach contraction principle are obtained. In Section 3.2. continuous dependence on the initial functions is investigated based on the fractional extension of Gronwall inequality. In Section 3.3. some sufficient conditions for finite time stability are given.

2. Preliminary notes

Let $ J = [-{\tau}, T] $, $ I = [0, T] $ where $ {\tau} > 0 $ is a constant, $ T < \infty $. Without loss of generality we can assume there exists a natural number $ N $ such that $ T = (N+1){\tau} $. Let $ L^{\it loc}_1(I, \mathbb{R}) $ be the linear space of all locally Lebesgue integrable functions $ m: I\to\mathbb{R} $, $ PC(J) = C([-{\tau}, 0), \mathbb{R})\cup C((0, T], \mathbb{R}) $.

Let $ x\in PC(J, \mathbb{R}) $. Denote $ ||x||_{J} = \sup_{t\in J} |x(t)| $.

In this paper we will use the following definitions for fractional derivatives and integrals:

$ - $ Riemann - Liouville fractional integral of order $ q\in(0, 1) $ (^[13,14])

$\begin{equation} \label{{2299}} _{0}I^{q}_tm(t) = \frac{1}{\Gamma( q)}\int\limits_{0}^{t}\frac{m(s)}{( t-s) ^{1-q}}ds,\ \ \ \ \ t\in I, \nonumber \end{equation}$ $

where $ \Gamma(.) $ is the Gamma function.

$ - $Riemann - Liouville fractional derivative of order $ q\in (0, 1) $ (^[13,14])

$\begin{equation} \label{{23}} _{0}^{RL}D^{q}_tm(t) = \frac{d}{dt}\big(\ _{0}I^{1-q}_tm(t)\big) = \frac{1}{\Gamma \left( 1-q\right)}\frac{d}{dt}\int\limits_{0}^{t}\left( t-s\right) ^{-q}m(s)ds,\ \ \ \ \ t\in I. \nonumber \end{equation}$ $

We will give fractional integrals and RL fractional derivatives of some elementary functions which will be used later:

Proposition 1. The following equalities are true:

$ _{0}^{RL}D^{q}_tt^{{\beta}} = \frac{\Gamma(1+{\beta})}{\Gamma(1+{\beta}-q)} t^{{\beta}-q},\ \ \ \ \ \ \ _{0}I^{1-q}t^{{\beta}-1} = \frac{\Gamma({\beta})}{\Gamma(1+{\beta}-q)}t^{{\beta}-q}, $

$ _{0}I^{1-q}t^{q-1} = \Gamma(q), \ \ \ \ \ \ \ _{0}^{RL}D^{q}_tt^{q-1} = 0. $

The definitions of the initial condition for fractional differential equations with RL-derivatives are based on the following result:

Proposition 2. (Lemma 3.2 ^[15]). Let $ q\in (0, 1) $, and $ m\in L^{\it loc}_1([0, T], \mathbb{R}) $.

(a) If there exists a.e. a limit $ \lim_{t\to 0+}[t^{q-1}m(t)] = c $, then there also exists a limit

$ _{0}I^{1-q}_tm(t)|_{t = 0}: = \lim\limits_{t\to 0+}\ _{0}I^{1-q}_tm(t) = c\Gamma(q). $

(b) If there exists a.e. a limit $ _{0}I^{1-q}_tm(t)|_{t = 0} = b $ and if there exists the limit $ \lim_{t\to 0+}[t^{1-q}m(t)] $ then

$ \lim\limits_{t\to 0+}[t^{1-q}m(t)] = \frac{b}{\Gamma(q)}. $

We will use the Mittag - Leffler functions with one and with two parameters, respectively, (see, for example, ^[14]) given by $ E_{p}(z) = \sum_{j = 0}^\infty \frac{z^j}{\Gamma(jp+1)} $ and $ E_{p, q}(z) = \sum_{j = 0}^\infty \frac{z^j}{\Gamma(jp+q)} $.

Proposition 3. ^[16] (Gronwall fractional inequality) Suppose $ a(t) $ is a nonnegative function locally integrable on $ [0, T) $ (some $ T\leq \infty $) and $ b(t) $ is a nonnegative, nondecreasing continuous function defined on $ [0, T) $, $ b(t)\leq M $ (constant), and suppose $ u(t) $ is nonnegative and locally integrable on $ [0, T) $ with

$ u(t)\leq a(t)+b(t)\int_0^t (t-s)^{q-1}u(s)ds,\ \ \ t\in [0,T). $

Then

$ u(t)\leq a(t)+\int_0^t\Big(\sum\limits_{n = 1}^\infty\frac{(b(t)\Gamma(q))^n}{\Gamma(n q)}(t-s)^{n q-1}a(s)\Big)ds, \ t\in[0,T). $

Recently, in ^[17] the non-homogeneous scalar linear Riemann-Liouville fractional differential equations with a constant delay :

$\begin{equation} \label{{22}} \begin{split} &\ _{0}^{RL}D_t^{q}x(t) = Ax(t)+ Bx(t-{\tau})+f(t) \ \mbox {for} \ t \gt 0. \end{split} \end{equation}$ $

(2.1)

with the initial conditions

$\begin{equation} \label{{2}} x(t) = g(t),\ \ \ t\in[-{\tau},0], \end{equation}$ $

(2.2)

$\begin{equation} \label{{3}} \lim\limits_{t\to 0+}\Big(t^{1-q}x(t)\Big) = \frac{g(0)}{\Gamma(q)} \end{equation}$ $

(2.3)

where $ f\in C(\mathbb{R}_+, \mathbb{R}) $, $ g\in C([-{\tau}, 0], \mathbb{R}) $ was studied. It was proved the solution is given by the function

$\begin{equation} \label{{112233}}\begin{split} \ \Lambda_q(t) = \begin{cases} g(t) & t\in (-{\tau},0]\\ g(0) E_{q,q}(At^q)t^{q-1}+\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)\Big(Bg(s-{\tau})+f(s)\Big)ds& \ t\in(0,{\tau}] \\ g(0)E_{q,q}(At^q)t^{q-1}+\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)f(s)ds\\ \ \ \ \ \ \ \ \ +B\sum\limits_{i = 0}^{n-1}\int_{i{\tau}}^{(i+1){\tau}} (t-s)^{q-1}E_{q,q}(A(t-s)^q)\Lambda_q(s-{\tau})ds\\ \ \ \ \ \ \ \ \ +B\int_{n{\tau}}^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)\Lambda_q(s-{\tau})ds\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mbox{for}\ \ \ t\in (n{\tau},(n+1){\tau}], n = 1,2,\dots \end{cases} \end{split} \end{equation}$ $

(2.4)

where $ E_{q, q}(z) = \sum_{i = 0}^\infty\frac{z^i}{\Gamma(iq+q)} $ and $ E_{q }(z) = \sum_{i = 0}^\infty\frac{z^i}{\Gamma(iq+1)} $ are Mittag-Leffler functions with two and one parameter, respectively.

Now, we will study the following nonlinear fractional delay differential equations

$\begin{equation} \label{{1}} \begin{split} &\ _{0}^{RL}D_t^{q}x(t) = Ax(t)+ Bx(t-{\tau})+f(t,x(t)) \ \mbox {for} \ t\in I. \end{split} \end{equation}$ $

(2.5)

with the initial conditions (2.2), (2.3) where $ A, B\in \mathbb{R} $ are given constants, $ f:I\times\mathbb{R}\to \mathbb{R} $.

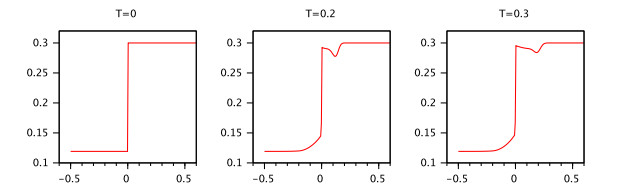
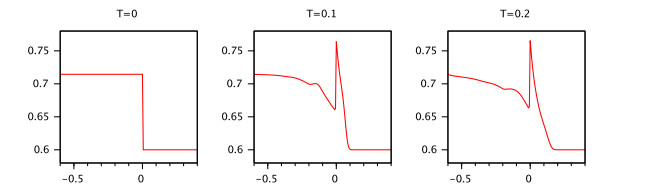
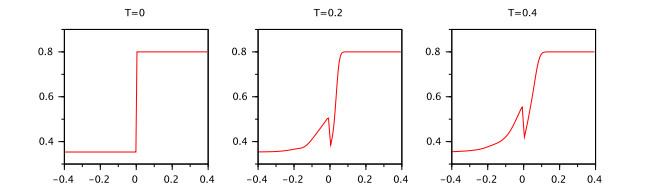
Remark 1. Note that in the case of the linear equation (2.1) we have formula (2.4) for the explicit solution since in the case of nonlinear equation (2.5) we are not able to obtain an explicit formula, we could provide only an integral presentation of the solution (see Example 1 and Example 2).

Example 1. Consider the special case of (2.1):

$\begin{equation} \label{{222}} \begin{split} &\ _{0}^{RL}D_t^{0.5}x(t) = x(t-1)+t \ \mbox {for} \ t \gt 0\\ &x(t) = t,\ \ \ t\in[-1,0],\\ &\lim\limits_{t\to 0+}\Big(t^{0.5}x(t)\Big) = 0.\end{split} \end{equation}$ $

(2.6)

Then applying $ E_{q, q}(0) = \frac{1}{\Gamma(q)} $ we obtain the solution of (2.6):

$\begin{equation} \label{{923}}\begin{split} \ x(t) = \begin{cases} t,\ \ \ \ \ \ \ \ \ t\in (-1,0]\\ \frac{1}{\sqrt{\pi}}\int_0^t(t-s)^{-0.5}\Big(s-1+s\Big)ds = \frac{2\sqrt{t}}{\sqrt{\pi}}( \frac{4}{3}t-1),\ \ \ \ \ \ t\in(0,1] \\ \frac{1}{\sqrt{\pi}}\int_0^t(t-s)^{-0.5}sds+\frac{1}{\sqrt{\pi}}\int_{0}^{1} (t-s)^{-0.5}(s-1)ds+\frac{1}{\sqrt{\pi}}\int_{{\tau}}^t(t-s)^{-0.5}x(s-1)ds\\ \ \ \ \ = \frac{4}{3\sqrt{\pi}} t^{1.5} -\frac{4}{3\sqrt{\pi}}(t-1)^{1.5} + \frac{4}{3\sqrt{\pi}} \sqrt{t} (t-1.5 )+ t (t-1) + \frac{4 }{3\pi\sqrt{ t}}\ _2F_1[0.5, 1.5, 2.5, \frac{1}{t}] \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ - \frac{16 }{15\pi\sqrt{ t}} \ _2F_1[0.5, 2.5, 3.5,\frac{1}{t}] , \ \ \ \ \ t\in (1,2]. \end{cases} \end{split} \end{equation}$ $

(2.7)

3. Main result

3.1. Existence of mild solutions of the IVP (2.5), (2.2), (2.3)

In connection with Remark 1 we will define a mild solution:

Definition 1. A function $ x\in PC(J, \mathbb{R}) $ is called a mild solution of the IVP (2.5), (2.2), (2.3) if it satisfies the following integral equation

$ \ x(t) =

$\begin{cases} g(t)\ \ \ \mbox{for}\ \ \ t\in [-{\tau},0],\\ g(0) E_{q,q}(At^q)t^{q-1}+B\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)g(s-{\tau})ds\\ \ \ \ \ \ \ \ \ +\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)f(s,x(s))ds\ \ \ \mbox{for}\ \ \ t\in(0,{\tau}], \\ g(0) E_{q,q}(At^q)t^{q-1}+\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)f(s,x(s))ds\\ \ \ \ \ \ \ \ \ +B\sum\limits_{i = 0}^{n-1}\int_{i{\tau}}^{(i+1){\tau}} (t-s)^{q-1}E_{q,q}(A(t-s)^q)x(s-{\tau})ds\\ \ \ \ \ \ \ \ \ +B\int_{n{\tau}}^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)x(s-{\tau})ds\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mbox{for}\ \ \ t\in (n{\tau},(n+1){\tau}], n = 1,2,\dots,N \end{cases}$ $

Example 2. Consider the partial case of (2.5) (compare with (2.6):

$\begin{equation} \label{{2211}} \begin{split} &\ _{0}^{RL}D_t^{0.5}x(t) = x(t-1)+\sin(x(t)) \ \mbox {for} \ t \gt 0\\ &x(t) = t,\ \ \ t\in[-1,0],\\ &\lim\limits_{t\to 0+}\Big(t^{0.5}x(t)\Big) = 0.\end{split} \end{equation}$ $

(3.1)

Now similarly to Example 1 we are not able to obtain the exact solution of (2.6). But using Definition 1 we can consider the mild solution $ x(t) $ of the IVP (3.1) satisfying:

$\begin{equation} \label{{9231}}\begin{split} \ x(t) = \begin{cases} t,\ \ \ \ \ \ \ \ \ t\in (-1,0]\\ \frac{1}{\sqrt{\pi}}\int_0^t(t-s)^{-0.5}(s-1)ds+\frac{1}{\sqrt{\pi}}\int_0^t(t-s)^{-0.5}\sin(x(s))ds\\ \ \ \ \ \ \ = \frac{2\sqrt{t}}{\sqrt{\pi}}( \frac{2}{3}t-1)+\frac{1}{\sqrt{\pi}}\int_0^t(t-s)^{-0.5}\sin(x(s))ds,\ \ \ \ \ \ t\in(0,1] \\ \frac{1}{\sqrt{\pi}}\int_0^t(t-s)^{-0.5}\sin(x(s))ds+\frac{1}{\sqrt{\pi}}\int_{0}^{1} (t-s)^{-0.5}(s-1)ds+\frac{1}{\sqrt{\pi}}\int_{{\tau}}^t(t-s)^{-0.5}x(s-1)ds\\ \ \ \ \ = \frac{1}{\sqrt{\pi}}\int_0^t(t-s)^{-0.5}\sin(x(s))ds -\frac{4}{3\sqrt{\pi}}(t-1)^{1.5} + \frac{4}{3\sqrt{\pi}} \sqrt{t} (t-1.5 )\\ \ \ \ \ \ \ \ \ +\frac{1}{\sqrt{\pi}}\int_{{\tau}}^t(t-s)^{-0.5}x(s-1)ds, \ \ \ \ \ t\in (1,2]. \end{cases} \end{split} \end{equation}$ $

(3.2)

Examples 1 and 2 show the main difference between the linear RL fractional differential equations and the nonlinear RL fractional differential equations with a linear part.

We will introduce the following conditions:

(A1). The function $ f\in C([0, T]\times \mathbb{R}, \mathbb{R}) $ and there exists a function $ w\in C(I, \mathbb{R}_+) $ such that $ |f(t, x)|\leq w(t) $ for all $ t\in I, x\in \mathbb{R} $.

(A2). The function $ f\in C([0, T]\times \mathbb{R}, \mathbb{R}) $ and there exists a constant $ L > 0 $ such that $ |f(t, x)-f(t, y)|\leq L|x-y| $ for all $ t\in I, x, y\in \mathbb{R} $. First, we will consider the case of Lipschitz nonlinear function.

Theorem 1. Let $ A\not = 0 $, the condition (A2) be satisfied and

1. The function $ g\in C([{\tau}, 0], \mathbb{R} $ and $ |g(0)| < \infty $.

2. $ \rho = \frac{Lh_1+|B|h_2}{|A|} < 1 $ where $ h_1 = \max_{t\in [0, T]}|E_q(At^q)-1|, $

$ h_2 = \max\limits_{n = 0,1,2,\dots,N}\{\max\limits_{t\in (n{\tau},(n+1){\tau}]}\Big(|E_q(A(t-n{\tau})^q)-1|+ \sum\limits_{j = 0}^{n-1}|E_q(A(t-j{\tau})^q)-E_q(A(t-(j+1){\tau})^q)| \Big)\}. $

Then the the IVP (2.5), (2.2), (2.3) has a unique mild solution $ x\in PC(J, \mathbb{R}) $.

${{\rm{P\ r\ o\ o\ f:} }}$ Existence. Define the operator $ \Xi: PC(J, \mathbb{R})\to PC(J, \mathbb{R}) $ by the equality

$ \ \Xi(x(t)) =

$\begin{cases} g(t)\ \ \ \ \ \ \ \ \ \ \ \ t\in[-{\tau},0]\\ g(0) E_{q,q}(At^q)t^{q-1}+B\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)g(s-{\tau})ds\\ \ \ \ \ \ \ \ \ +\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)f(s,x(s))ds\ \ \ \mbox{for}\ \ \ t\in(0,{\tau}], \\ g(0) E_{q,q}(At^q)t^{q-1}+\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)f(s,x(s))ds\\ \ \ \ \ \ \ \ \ +B\sum\limits_{i = 0}^{n-1}\int_{i{\tau}}^{(i+1){\tau}} (t-s)^{q-1}E_{q,q}(A(t-s)^q)x(s-{\tau})ds\\ \ \ \ \ \ \ \ \ +B\int_{n{\tau}}^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)x(s-{\tau})ds\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mbox{for}\ \ \ t\in (n{\tau},(n+1){\tau}], n = 1,2,\dots,N \end{cases}$ $

Let $ z, y\in PC(J, \mathbb{R}) $. We will prove that

$\begin{equation} \label{{823}}\begin{split} &|\Xi(z(t))-\Xi(y(t))|\\ &\leq \Big(L\frac{|E_q(At^q)-1|}{|A|} +|B| \frac{\sum_{j = 0}^{n-1}|E_q(A(t-{j{\tau}})^q)-E_q(A(t-{(j+1){\tau}})^q)|}{|A|}\\ &\ \ \ \ \ \ \ \ +|B| \frac{|E_q(A(t-{n{\tau}})^q)-1|}{|A|}\Big)||z -y||_{J}\ \mbox{for}\ \ \ t\in (n{\tau},(n+1){\tau}], \ n = 0,1,2,\dots,N \end{split} \end{equation}$ $

(3.3)

Let $ t\in(0, {\tau}] $. Then applying Definition 1 and the equality

$\begin{equation} \label{{111}}\begin{split} &\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds = \sum\limits_{i = 0}^\infty \frac{A^i}{\Gamma((i+1)q)}\int_0^t(t-s)^{(i+1)q-1}ds\\ & = \sum\limits_{i = 0}^\infty \frac{A^i}{(1 + i)q\Gamma((i+1)q)} t^{(i+1)q} = \frac{E_q(At^q)-1}{A}, \ \ \ t\in (0,{\tau}], \end{split} \end{equation}$ $

(3.4)

we obtain

$\begin{equation} \label{{12}}\begin{split} |\Xi(z(t))-\Xi(y(t))|&\leq|\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)|f(s,z(s))-f(s,y(s))|ds|\\ &\leq L|\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)|z(s)-y(s)|ds|\\ &\leq L||z -y||_{J}|\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds|\\ & = L\frac{|E_q(At^q)-1|}{|A|} ||z -y||_{J}\end{split} \end{equation}$ $

(3.5)

Let $ t\in({\tau}, 2{\tau}] $. Then according to Definition 1 and the equality

$\begin{equation} \label{{1113}}\begin{split} &\int_{\tau}^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds = \sum\limits_{i = 0}^\infty \frac{A^i}{\Gamma((i+1)q)}\int_{\tau}^t(t-s)^{(i+1)q-1}ds\\ & = \sum\limits_{i = 0}^\infty \frac{A^i}{(1 + i)q\Gamma((i+1)q)} (t-{\tau})^{(i+1)q} = \frac{E_q(A(t-{\tau})^q)-1}{A},\ \ \ \ t\in({\tau},2{\tau}], \end{split} \end{equation}$ $

(3.6)

we have

$\begin{equation} \label{{13}}\begin{split} |\Xi(z(t))-\Xi(y(t))|&\leq|\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)|f(s,z(s))-f(s,t(s))|ds|\\ &\ \ \ \ \ \ \ \ +|B|\ |\int_{0}^{{\tau}} (t-s)^{q-1}E_{q,q}(A(t-s)^q)|z(s-{\tau})-y(s-{\tau})|ds|\\ & \ \ \ \ \ \ \ \ +|B|\ |\int_{ {\tau}}^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)|z(s-{\tau})-y(s-{\tau})|ds|\\ &\leq \Big(L\frac{|E_q(At^q)-1|}{A} +|B|\ |\int_{ {\tau}}^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds|\Big)||z -y||_{J}\\ &\leq \Big(L\frac{|E_q(At^q)-1|}{|A|} +|B|\frac{|E_q(A(t-{\tau})^q)-1|}{|A|}\Big)||z -y||_{J}. \end{split} \end{equation}$ $

(3.7)

Let $ t\in(2{\tau}, 3{\tau}] $. Then according to Definition 1 and the equalities

$\begin{equation} \label{{11136}}\begin{split} &\int_{2{\tau}}^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds = \sum\limits_{i = 0}^\infty \frac{A^i}{\Gamma((i+1)q)}\int_{2{\tau}}^t(t-s)^{(i+1)q-1}ds\\ & = \sum\limits_{i = 0}^\infty \frac{A^i}{(1 + i)q\Gamma((i+1)q)} (t-{\tau})^{(i+1)q} = \frac{E_q(A(t-{2{\tau}})^q)-1}{A},\ \ \ \ t\in(2{\tau},3{\tau}], \end{split} \end{equation}$ $

(3.8)

and

$\begin{equation} \label{{11137}}\begin{split} &\int_{ {\tau}}^{2{\tau}}(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds = \sum\limits_{i = 0}^\infty \frac{A^i}{\Gamma((i+1)q)}\int_{{\tau}}^{2{\tau}}(t-s)^{(i+1)q-1}ds\\ & = \sum\limits_{i = 0}^\infty \frac{A^i}{(1 + i)q\Gamma((i+1)q)} (t-{\tau})^{(i+1)q}-\sum\limits_{i = 0}^\infty \frac{A^i}{(1 + i)q\Gamma((i+1)q)} (t-2{\tau})^{(i+1)q}\\ & = \frac{E_q(A(t-{{\tau}})^q)-E_q(A(t-{2{\tau}})^q)}{A}, \end{split} \end{equation}$ $

(3.9)

we have

$\begin{equation} \label{{136}}\begin{split} |\Xi(z(t))-\Xi(y(t))|&\leq|\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)|f(s,z(s))-f(s,t(s))|ds|\\ &\ \ \ \ \ \ \ \ +|B|\ |\int_{0}^{{\tau}} (t-s)^{q-1}E_{q,q}(A(t-s)^q)|z(s-{\tau})-y(s-{\tau})|ds|\\ & \ \ \ \ \ \ \ \ +|B|\ |\int_{ {\tau}}^{2{\tau}}(t-s)^{q-1}E_{q,q}(A(t-s)^q)|z(s-{\tau})-y(s-{\tau})|ds|\\ & \ \ \ \ \ \ \ \ +|B|\ |\int_{ 2{\tau}}^{t}(t-s)^{q-1}E_{q,q}(A(t-s)^q)|z(s-{\tau})-y(s-{\tau})|ds|\\ &\leq \Big(L\frac{|E_q(At^q)-1|}{|A|} +|B|\ |\int_{ {\tau}}^{2{\tau}}(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds|\\ &\ \ \ \ \ \ \ \ \ +|B|\ |\int_{ 2{\tau}}^{t}(t-s)^{q-1}E_{q,q}(A(t-s)^q)ds|\Big)||z -y||_{J}\\ &\leq \Big(L\frac{|E_q(At^q)-1|}{|A|} +|B| \frac{|E_q(A(t-{{\tau}})^q)-E_q(A(t-{2{\tau}})^q)|}{|A|}\\ &\ \ \ \ \ \ \ +|B|\frac{|E_q(A(t-2{\tau})^q)-1|}{|A|}\Big)||z -y||_{J}. \end{split} \end{equation}$ $

(3.10)

Following the induction process and the definition of $ \rho $ we obtain that $ ||\Xi(z(t))-\Xi(y(t))||_J\leq \rho||z-y||_J. $ Therefore, the operator $ \Xi:PC(J, \mathbb{R})\to PC(J, \mathbb{R}) $ is a contraction.

Uniqueness. Let $ z(t), y(t) $ be two mild solutions of the IVP (2.5), (2.2), (2.3). Applying induction process w.r.t. the intervals and from condition 2 we obtain that $ ||z-y||_{(k{\tau}, (k+1){\tau}]} < \rho ||z-y||_{(k{\tau}, (k+1){\tau}]} $ for $ k = 0, 1, \dots, N $ which proves the uniqueness.

Remark 2. It is obvious that the condition $ A\not = 0 $ in Theorem 1 is not a restriction because the nonzero term $ Ax $ could be added to the nonlinear part without losing the Lipschitz property.

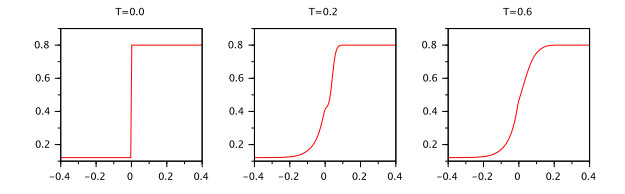
Example 3. Consider the IVP (3.1) In this case $ A = 0.1, f(t, x) = \sin(x)-0.1x, B = 1 $. Then the condition (A2) is satisfied with $ L = 1.1 $ but the condition 2 of Theorem 1 is not satisfied.

Now, we change the equation in the IVP (3.1) to $ \ _{0}^{RL}D_t^{0.5}x(t) = 0.1x(t-1)+0.01\sin(x(t)) $. In this case $ A = 0.1, f(t, x) = 0.01\sin(x)-0.1x, B = 0.1 $, $ h_1 = h_2 = 0.43581 $ and $ \rho = \frac{(0.11+0.1)0.43581}{0.1} < 1 $. According to Theorem the IVP (3.1) has unique mild solution which is satisfying the integral presentation given in Definition 1.

In the case of a bounded nonlinear function we have the following result:

Theorem 2. Let the condition (A1) be satisfied and

1. The function $ g\in C([{\tau}, 0], \mathbb{R} $ and $ |g(0)| < \infty $.

2. $ \rho = \frac{2||w||_Ih_1+|B|h_2}{|A|} < 1 $ where $ h_1 $ and $ h_2 $ are defined in Theorem 1.

Then the the IVP (2.5), (2.2), (2.3) has a unique solution $ x\in PC(J, \mathbb{R}) $.

The proof of Theorem 2 is similar to the one of Theorem 1 and we omit it.

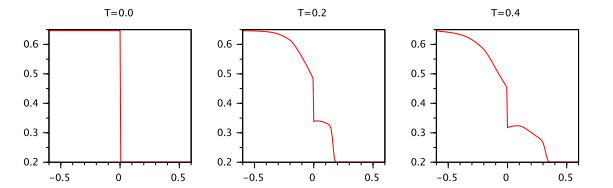
3.2. Continuous dependence on the initial functions

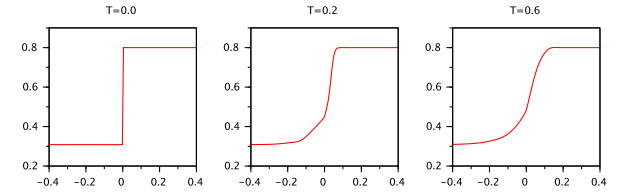
We will study the continuous dependence of mild solutions of the IVP (2.5), (2.2), (2.3) on the initial functions.

Consider IVP (2.5), (2.2), (2.3) and the RL fractional equation (2.5) with initial conditions

$\begin{equation} \label{{212}} x(t) = p(t),\ \ \ t\in[-{\tau},0], \end{equation}$ $

(3.11)

$\begin{equation} \label{{312}} \lim\limits_{t\to 0+}\Big(t^{1-q}x(t)\Big) = \frac{p(0)}{\Gamma(q)} \end{equation}$ $

(3.12)

Theorem 3. Let the following conditions be satisfied:

1. The functions $ g, p\in C([-{\tau}, 0], \mathbb{R} $, $ |g(0)| < \infty $, $ |p(0)| < \infty $.

2. The function $ f\in C([0, T]\times \mathbb{R}, \mathbb{R}) $ and it is Lipschitz with a constant $ L > 0 $ on $ [0, T]\times \mathbb{R} $.

Then for any number $ \delta > 0 $ there exist numbers $ K_k, C_k > 0, \ k = 0, 1, 2, \dots, N $ such that the inequality $ ||g-p||_{[-{\tau}, 0]} < \delta $ implies

$\begin{equation} \label{{11111}} |x(t)-y(t)|\leq \delta\Big( K_k(t-k{\tau})^{q-1}+C_k\Big) \ \mathit{\mbox{for}}\ \ t\in(k{\tau},(k+1){\tau}],\ \ k = 0,1,2,\dots,N \end{equation}$ $

(3.13)

where $ x(t), y(t) $ are mild solutions of the IVPs (2.5), (2.2), (2.3) and (2.5), (3.11), (3.12) respectively.

${{\rm{P\ r\ o\ o\ f:} }}$ We will use the induction w.r.t. the intervals to prove the claim.

Let $ M = \sup_{t\in J}|E_{q, q}(At^q)|. $

Let $ t\in(0, {\tau}] $. Then from Definition 1 and Eq. (3.4) we get

$\begin{equation} \label{{456}}\begin{split} |x(t)-y(t)|&\leq \delta Mt^{q-1}+|B|M\delta \int_0^t(t-s)^{q-1}ds\\ &+LM\int_0^t(t-s)^{q-1}| x(s)-y(s)| ds\\ &\leq \delta Mt^{q-1}+\delta M\frac{|B|{\tau}^q}{q}+LM\int_0^t(t-s)^{q-1}| x(s)-y(s)| ds\\ &\leq \delta Mt^{q-1}+\delta P_0+LM\int_0^t(t-s)^{q-1}| x(s)-y(s)| ds\end{split} \end{equation}$ $

(3.14)

where $ P_0 = M\frac{|B|{\tau}^q}{q} $.

According to Proposition 3, the inequality $ \int_0^t (t-s)^{n q-1} s^{q-1} ds = \frac{t^{nq+q-1}\; \Gamma(q) \Gamma(nq)}{\Gamma(nq+q)} $ we obtain

$\begin{equation} \label{{467}}\begin{split} |x(t)-y(t)|&\leq \delta Mt^{q-1}+\delta P_0+ \delta P_0\int_0^t \sum\limits_{n = 1}^\infty\Big(ML\Gamma(q)\Big)^n\frac{(t-s)^{n q-1}}{\Gamma(n q)} ds\\ &+\delta M\int_0^t \sum\limits_{n = 1}^\infty\Big(ML\Gamma(q)\Big)^n\frac{(t-s)^{n q-1}}{\Gamma(n q)} s^{q-1} ds\\ &\leq \delta P_0 \sum\limits_{n = 0}^\infty\Big(ML\Gamma(q)\Big)^n\frac{t^{n q }}{ \Gamma(n q+1)}+\delta M t^{ q -1} \Gamma(q)\sum\limits_{n = 0}^\infty\Big(ML\Gamma(q)\Big)^n\ \frac{t^{ n q} }{ \Gamma(nq+q)}\\ & = \delta(K_0t^{q-1 }+C_0),\ \ \ t\in(0,{\tau}] \end{split} \end{equation}$ $

(3.15)

where $ K_0 = M \Gamma(q) E_{q, q}(ML\Gamma(q){\tau}^{q}) $, $ C_0 = M\frac{|B|{\tau}^q}{q} E_q(ML\Gamma(q){\tau}^{ q }) $.

Let $ t\in({\tau}, 2{\tau}] $. Then applying Definition 1, (3.15), the inequalities $ \int_0^{\tau} ({\tau}-s)^{q-1} s^{q-1} ds = \frac{{\tau}^{2q-1} \Gamma(q) \Gamma(q)}{\Gamma(2q)} $, $ \frac{q \Gamma^2(q)}{\Gamma(2q)}\leq 2 $ we get

$\begin{equation} \label{{1212}}\begin{split} |x(t)-y(t)|&\leq \delta Mt^{q-1}+LM\int_0^t(t-s)^{q-1}| x(s) - y(s)|ds+|B|\delta M\int_{0}^{{\tau}} (t-s)^{q-1}ds\\ & +|B|M\int_{ {\tau} }^t(t-s)^{q-1}(\delta K_0(s-{\tau})^{q-1} + \delta C_0)ds\\ &\leq \delta M{\tau}^{q-1}+LM\delta K_0\frac{(t-{\tau})^{2q-1}\Gamma^2(q)}{\Gamma(2q)}+LM\delta C_0\frac{(2{\tau})^q}{q}\\ & +|B|\delta M\frac{{\tau}^q}{q}+\delta|B|MK_0\frac{(t-{\tau})^{2q-1} \Gamma^2(q)}{\Gamma(2q)} +\delta |B|MC_0\frac{(t-{\tau})^q}{q}\\ &+LM\int_{\tau}^t(t-s)^{q-1}| x(s) - y(s)|ds\\ &\leq \delta M{\tau}^{q-1}+2\delta(L+|B|)MK_0 (t-{\tau})^{q-1}\frac{ ({\tau})^q }{q} +\delta|B|MC_0\frac{{\tau}^q}{q}+|B|\delta M\frac{({\tau})^q}{q}\\ & +\delta LMK_0 \frac{{\tau}^{2q-1} \Gamma(q) \Gamma(q)}{\Gamma(2q)}+LM \int_{\tau}^t(t-s)^{q-1}| x(s) - y(s)|ds\\ &\leq 2\delta |B|MK_0 \frac{ {\tau}^q }{q}(t-{\tau})^{q-1}+\delta P_1+LM\int_{\tau}^t(t-s)^{q-1}| x(s) - y(s)|ds\\ \end{split} \end{equation}$ $

(3.16)

where $ P_1 = M{\tau}^{q-1} +|B|MC_0\frac{{\tau}^q}{q}+|B| M\frac{({\tau})^q}{q} +LMK_0 \frac{{\tau}^{2q-1} \Gamma(q) \Gamma(q)}{\Gamma(2q)}. $

According to Proposition 3 we obtain

$\begin{equation} \label{{46719}}\begin{split} |x(t)-y(t)|&\leq 2|B|MK_0 \frac{ {\tau}^q }{q}(t-{\tau})^{q-1}+P_1+ \\ &+ \int_{\tau}^t\Big[\sum\limits_{n = 1}^\infty\Big(ML\Gamma(q)\Big)^n\frac{(t-s)^{n q-1}}{\Gamma(n q)}(2|B|MK_0 \frac{ {\tau}^q }{q}(s-{\tau})^{q-1}+P_1\Big]ds\\ &\leq 2|B|MK_0 \frac{ {\tau}^q }{q}(t-{\tau})^{q-1} +P_1 E_q( ML\Gamma(q)(t-{\tau})^q) \\ & +2|B|MK_0 \frac{ {\tau}^q }{q}\sum\limits_{n = 1}^\infty\Big(ML\Gamma(q)\Big)^n \frac{(t-{\tau})^{-1 + q + n q} \Gamma(q)}{\Gamma(nq+q)}\\ &\leq P_1 E_q( ML\Gamma(q)(t-{\tau})^q) +2|B|MK_0\Gamma(q) \frac{ {\tau}^q }{q}(t-{\tau})^{q-1}E_{q,q}(ML\Gamma(q)(t-{\tau})^{ q} )\\ &\leq P_1 E_q( ML\Gamma(q){\tau}^q) +2|B|MK_0\Gamma(q) \frac{ {\tau}^q }{q}(t-{\tau})^{q-1}E_{q,q}(ML\Gamma(q){\tau}^{ q} )\\ & = \delta\Big(K_1(t-{\tau})^{q-1} +C_1\Big) ,\ \ t\in({\tau},2{\tau}] \end{split} \end{equation}$ $

(3.17)

where $ K_1 = 2|B|M^2\Gamma^2(q) E_{q, q}^2(ML\Gamma(q){\tau}^{q}) \frac{ {\tau}^q }{q} $ and $ C_1 = P_1E_q(ML\Gamma(q){\tau}^q) $.

Let $ t\in(2{\tau}, 3{\tau}] $. Then applying Definition 1 and (3.6) we get

$\begin{equation} \label{{1219}}\begin{split} |x(t)-y(t)|&\leq \delta Mt^{q-1}+L M\delta\int_0^{\tau} (t-s)^{q-1}(K_0s^{q-1}+C_0)ds\\ &+LM\delta\int_{\tau}^{2{\tau}}(t-s)^{q-1}(K_1(s-{\tau})^{q-1} +C_1)ds \\ &+LM\int_{2{\tau}}^t(t-s)^{q-1}| x(s) - y(s)|ds\\ & +|B|M\delta\int_{0}^{{\tau}} (t-s)^{q-1}ds+|B|M\delta\int_{{\tau}}^{2{\tau}} (t-s)^{q-1}(K_0(s-{\tau})^{q-1}+C_0)ds\\ & +|B|M\delta\int_{ 2{\tau}}^t(t-s)^{q-1}(K_1(s-2{\tau})^{q-1} +C_1)ds\\ &\leq \delta M(2{\tau})^{q-1}+\delta L M K_0 (3{\tau})^{2q-1} Beta[1/3, q, q]+\delta LMC_0 \frac{(3{\tau})^q}{q}-\\ &+\delta LMK_1(2{\tau})^{2q-1} Beta[1/2, q, q]+\delta LMC_1 \frac{(2q)^q}{q} \\ &+LM\int_{2{\tau}}^t(t-s)^{q-1}| x(s) - y(s)|ds\\ & +|B|M\delta\frac{(3{\tau})^q}{q}+|B|M\delta K_0 (2{\tau})^{2q-1} Beta[1/2, q, q]+|B|M\delta C_0 \frac{(2{\tau})^q}{q}\\ & +\delta |B|MK_1 \frac{{\tau}^{q}\Gamma^2(q)}{\Gamma(2 q)}(t-2{\tau})^{q-1} +\delta |B|MC_1\frac{{\tau}^q}{q}\\ &\leq\delta |B|MK_1 \frac{{\tau}^{q}\Gamma^2(q)}{\Gamma(2 q)}(t-2{\tau})^{q-1}+\delta P_2+ LM\int_{2{\tau}}^t(t-s)^{q-1}| x(s) - y(s)|ds\nonumber \end{split} \end{equation}$ $

where $ Beta[x, q, q] $ is the incomplete beta function.

According to Proposition 3 we obtain

$\begin{equation} \label{{46712}}\begin{split} |x(t)-y(t)|&\leq\delta |B|MK_1 \frac{{\tau}^{q}\Gamma^2(q)}{\Gamma(2 q)}(t-2{\tau})^{q-1}+ \delta P_2+ \delta P_2 \int_{2{\tau}}^t\Big[\sum\limits_{n = 1}^\infty\Big(ML\Gamma(q)\Big)^n\frac{(t-s)^{n q-1}}{\Gamma(n q)} \Big]ds\\ &+\delta |B|MK_1 \frac{{\tau}^{q}\Gamma^2(q)}{\Gamma(2 q)} \int_{2{\tau}}^t\Big[\sum\limits_{n = 1}^\infty\Big(ML\Gamma(q)\Big)^n\frac{(t-s)^{n q-1}}{\Gamma(n q)} (s-2{\tau})^{q-1}\Big]ds\\ &\leq \delta P_2 \sum\limits_{n = 0}^\infty\Big(ML\Gamma(q)\Big)^n\frac{(t-2{\tau})^{n q}}{\Gamma(n q+1)} \\&+\delta |B|MK_1 \frac{{\tau}^{q}\Gamma^3(q)}{\Gamma(2 q)} (t-2 {\tau})^{q-1} \sum\limits_{n = 0}^\infty\Big(ML\Gamma(q)\Big)^n\frac{(t-2 {\tau})^{n q} }{\Gamma(q + n q)}\\ & = \delta |B|MK_1 \frac{{\tau}^{q}\Gamma^3(q)}{\Gamma(2 q)} E_{q,q}(ML\Gamma(q)(t-2 {\tau})^{ q}) (t-2 {\tau})^{q-1}+\delta P_2 E_q(ML\Gamma(q)(t-2{\tau})^{ q}) \\ & = K_2 (t-2 {\tau})^{q-1}+C_2,\ \ \ t\in( 2{\tau},3{\tau}],\nonumber \end{split} \end{equation}$ $

where $ K_2 = \delta |B|MK_1 \frac{{\tau}^{q}\Gamma^3(q)}{\Gamma(2 q)} E_{q, q}(ML\Gamma(q)(t-2 {\tau})^{ q}) $ and $ C_2 = \delta P_2 E_q(ML\Gamma(q)({\tau})^{q}). $

Continue the induction process we prove the claim.

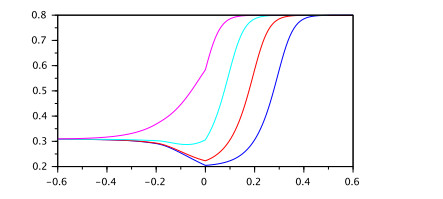
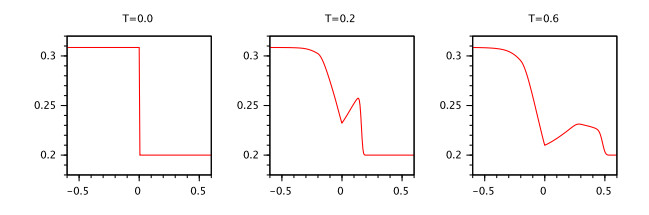
Corollary 1. Let the conditions of Theorem 3 be satisfied and $ q > 0.5 $.

Then for any positive numbers $ \delta, {\varepsilon}: \ {\varepsilon} < {\tau} $ there exists a number $ K, C > 0 $ such that the inequality $ ||g-p||_{[-{\tau}, 0]} < \delta $ implies

$\begin{equation} \label{{1199}} |x(t)-y(t)|\leq \delta K \ \mathit{\mbox{for}}\ \ t\in({\varepsilon},T], \end{equation}$ $

(3.18)

where $ x(t), y(t) $ are mild solutions of the IVPs (2.5), (2.2), (2.3) and (2.5), (3.11), (3.12) respectively.

${{\rm{P\ r\ o\ o\ f:} }}$ The proof is similar to the one of Theorem 3 applying the inequality $ \frac{(t-k{\tau})^{2q-1}}{q}\leq \frac{{\tau}^q}{q} $ for $ t\in(k{\tau}, (k+1){\tau}], \ k = 0, 1, \dots, N $.

3.3. Finite time stability

In this section we will define and study the finite time stability of mild solutions of the IVP for Riemann-Liouville (2.5), (2.2), (2.3).

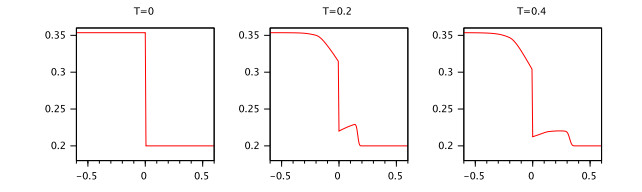
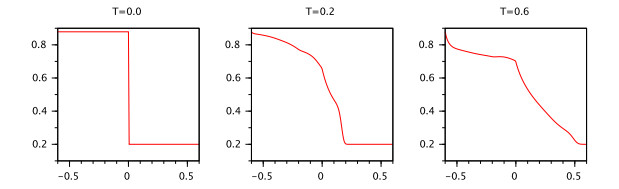
Note that because of the singularity of $ t^{q-1} $ at 0, we could prove the FTS on an interval which does not contain 0.

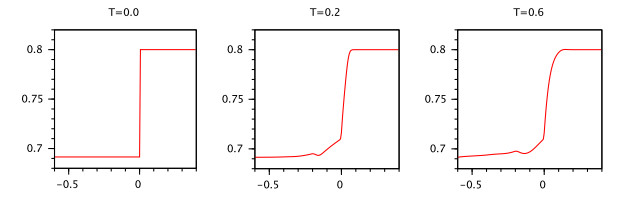
Theorem 4. Let the function $ g\in C([{\tau}, 0], \mathbb{R} $, $ |g(0)| < \infty $, $ q > 0.5 $ and the condition (A1) be satisfied.

Then for any real positive numbers $ \delta, {\varepsilon}:\ {\varepsilon} < {\tau} $ there exists a number $ K $ depending on $ \delta $ and $ {\varepsilon} $ such that the inequality $ ||g||_{[-{\tau}, 0]} < \delta $ implies $ |x(t)| < K $ for $ t\in ({\varepsilon}, T] $ where $ x(t) $ is the mild solution of the IVP (2.5), (2.2), (2.3).

${{\rm{P\ r\ o\ o\ f:} }}$ Let $ ||g||_{[-{\tau}, 0]} < \delta $ and $ M = \sup_{t\in J}|E_{q, q}(At^q)|. $

Let $ t\in(0, {\tau}] $. Then according to Definition 1 we have

$\begin{equation} \label{{678}}\begin{split} |x(t)|&\leq \delta E_{q,q}(At^q)t^{q-1}+|B|\delta\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)| ds\\ & \ \ \ \ \ \ \ \ +\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)|f(s,x(s))|ds\\ &\leq \delta Mt^{q-1}+|B|M\delta\int_0^t(t-s)^{q-1} ds +M||w||_I\int_0^t(t-s)^{q-1}ds\\ &\leq \delta Mt^{q-1}+M(|B|\delta +||w||_I)\frac{{\tau}^q}{q},\ \ \ t\in(0,{\tau}]. \end{split} \end{equation}$ $

(3.19)

From (3.19) it follows that

$\begin{equation} \label{{1678}} |x(t)|\leq \delta M{\varepsilon}^{q-1}+M(|B|\delta +||w||_I)\frac{{\tau}^q}{q},\ \ \ t\in({\varepsilon},{\tau}]. \end{equation}$ $

(3.20)

Let $ t\in({\tau}, 2{\tau}] $. Then we have

$\begin{equation} \label{{139}}\begin{split} |x(t)|&\leq \delta M{\tau}^{q-1}+ M \int_0^t(t-s)^{q-1} |f(s,x(s))| ds\\ &\ \ \ \ \ \ \ \ +|B| M\delta\int_{0}^{{\tau}} (t-s)^{q-1}ds+|B|M\int_{ {\tau}}^t(t-s)^{q-1}x(s-{\tau})ds\\ &\leq \delta M{\tau}^{q-1}+ M \Big((||w||_I+|B|\delta)\frac{(2{\tau})^q}{q}+|B|M\Big(\delta M\frac{{\tau}^{2q-1}}{2q-1}+ M(||w||_I+|B|\delta)(\frac{{\tau}^q}{q})^2\Big)\\ & = K_1.\nonumber \end{split} \end{equation}$ $

Let $ t\in(2{\tau}, 3{\tau}] $. Then we have

$\begin{equation} \label{{13911}}\begin{split} |x(t)|&\leq \delta M(2{\tau})^{q-1}+ M \int_0^t(t-s)^{q-1} |f(s,x(s))| ds +|B| M\delta\int_{0}^{{\tau}} (t-s)^{q-1}ds\\ & +|B| M\int_{{\tau}}^{2{\tau}} ({\tau}-s)^{q-1}(\delta M(s-{\tau})^{q-1}+M(|B|\delta +||w||_I)\frac{{\tau}^q}{q})ds+|B|MK_1\int_{ 2{\tau}}^t(t-s)^{q-1}ds\\ &\leq \delta M(2{\tau})^{q-1}+| M (|w||_I +|B|\delta)\frac{(3{\tau})^q}{q}+ |B| M(\delta M\frac{{\tau}^{2q-1}}{2q-1}+M(|B|\delta +||w||_I)(\frac{{\tau}^q}{q}))^2 + K_1\frac{{\tau}}{q}\Big)\\ & = K_2.\nonumber \end{split} \end{equation}$ $

Let $ t\in(3{\tau}, 4{\tau}] $. Then we have

$\begin{equation} \label{{1394}}\begin{split} |x(t)| &\leq \delta M(3{\tau})^{q-1}+| M (|w||_I +|B|\delta)\frac{(4{\tau})^q}{q}+ |B| M\Big(\delta M\frac{{\tau}^{2q-1}}{2q-1}+M(|B|\delta +||w||_I)(\frac{{\tau}^q}{q})^2 \Big)\\ &+ |B| M\frac{{\tau}}{q}\Big(K_1+ K_2\Big) = K_3.\nonumber \end{split} \end{equation}$ $

Following the induction process we prove the claim with $ K = \delta M(N{\tau})^{q-1}+| M (|w||_I +|B|\delta)\frac{(N{\tau})^q}{q}+ |B| M\Big(\delta M\frac{{\tau}^{2q-1}}{2q-1}+M(|B|\delta +||w||_I)(\frac{{\tau}^q}{q})^2 \Big)+ |B| M\frac{{\tau}}{q}\sum_{i = 1}^{N}K_i $.

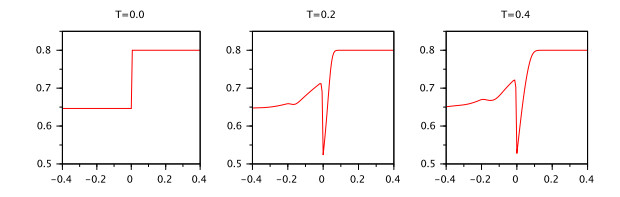
In the case the nonlinear Lipschitz functions we obtain the following result:

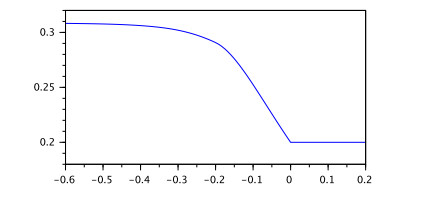
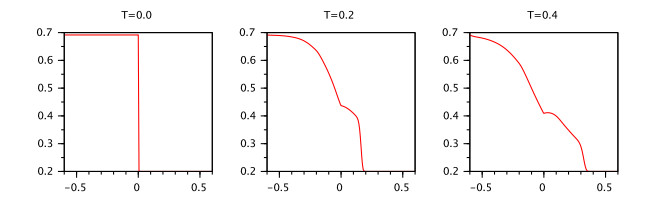
Theorem 5. Let the function $ g\in C([{\tau}, 0], \mathbb{R} $, $ |g(0)| < \infty $, $ q > 0.5 $ and the condition (A2) be satisfied.

${{\rm{P\ r\ o\ o\ f:} }}$ According to Theorem 1 the the IVP (2.5), (2.2), (2.3) has a unique solution $ x\in PC(J, \mathbb{R}) $. Let $ ||g||_{[-{\tau}, 0]} < \delta $ and $ M = \sup_{t\in J}|E_{q, q}(At^q)|. $

Let $ t\in({\varepsilon}, {\tau}] $. Then according to Definition 1 we have

$\begin{equation} \label{{6786}}\begin{split} |x(t)|&\leq \delta E_{q,q}(At^q)t^{q-1}+|B|\delta\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q) ds\\ & \ \ \ \ \ \ \ \ +L\int_0^t(t-s)^{q-1}E_{q,q}(A(t-s)^q)|x(s)| ds\\ &\leq \delta Mt^{q-1}+|B|M\delta\frac{{\tau}^q}{q} +LM\int_0^t(t-s)^{q-1}|x(s)| ds. \end{split} \end{equation}$ $

(3.21)

From (3.21) and Proposition 3 it follows that

$\begin{equation} \label{{561}}\begin{split}|x(t)|&\leq \delta Mt^{q-1}+|B|M\delta\frac{{\tau}^q}{q} +\int_0^t\Big(\sum\limits_{n = 1}^\infty\frac{(LM\Gamma(q))^n}{\Gamma(n q)}(t-s)^{n q-1}(\delta Ms^{q-1}+|B|M\delta\frac{{\tau}^q}{q})\Big)ds\\ &\leq \delta Mt^{q-1}+|B|M\delta\frac{{\tau}^q}{q} +\delta M t^{q-1}\Gamma(q) \sum\limits_{n = 1}^\infty\frac{(LM\Gamma(q))^n}{\Gamma(n q+q)} t^{nq}+|B|M\delta\frac{{\tau}^q}{q} \sum\limits_{n = 1}^\infty\frac{(LM\Gamma(q))^n}{\Gamma(n q+1)}(t )^{n q }\\ &\leq \delta Mt^{q-1}+|B|M\delta\frac{{\tau}^q}{q} +\delta M {\varepsilon}^{q-1}\Gamma(q) \sum\limits_{n = 1}^\infty\frac{(LM\Gamma(q))^n}{\Gamma(n q+q)} t^{nq}+|B|M\delta\frac{{\tau}^q}{q} \sum\limits_{n = 1}^\infty\frac{(LM\Gamma(q))^n}{\Gamma(n q+1)}(t )^{n q }\\ &\leq \delta M t^{q-1}\Gamma(q)E_{q,q}(LM\Gamma(q))t^q)+|B|M\delta\frac{{\tau}^q}{q}E_q(LM\Gamma(q))t^q). \end{split} \end{equation}$ $

(3.22)

Therefore,

$\begin{equation} \label{{67}}x(t)\leq \delta \Big(M {\varepsilon}^{q-1}\Gamma(q)+|B|M\frac{{\tau}^q}{q}\Big)E_q(LM\Gamma(q)){\tau}^q) = \delta K_0,\ \ t\in({\varepsilon},{\tau}]. \end{equation}$ $

(3.23)

Let $ t\in({\tau}, 2{\tau}] $. Then from (3.23) we have

$\begin{equation} \label{{13922}}\begin{split} |x(t)|&\leq \delta Mt^{q-1}+ ML \int_0^t(t-s)^{q-1} |x(s)| ds\\ &\ \ \ \ \ \ \ \ +|B| M\delta\int_{0}^{{\tau}} (t-s)^{q-1}ds+|B|M\int_{ {\tau}}^t(t-s)^{q-1}x(s-{\tau})ds\\ &\leq \delta Mt^{q-1}+|B| M\delta(1+K_0)\frac{{\tau}^q}{q}+ ML \int_0^t(t-s)^{q-1} |x(s)| ds.\nonumber \end{split} \end{equation}$ $

From (3.24) and Proposition 3 it follows that

$\begin{equation} \label{{5614}}\begin{split}|x(t)|&\leq \delta Mt^{q-1}+|B| M\delta(1+K_0)\frac{{\tau}^q}{q} +\int_{\tau}^t\Big(\sum\limits_{n = 1}^\infty\frac{(ML\Gamma(q))^n}{\Gamma(n q)}(t-s)^{n q-1}(\delta Ms^{q-1}+|B| M\delta(1+K_0)\frac{{\tau}^q}{q})\Big)ds\\ &\leq \delta M t^{q-1}\Gamma(q)E_{q,q}(LM\Gamma(q))t^q)+|B|M\delta(1+K_0)\frac{{\tau}^q}{q}]E_q(LM\Gamma(q))t^q). \end{split} \end{equation}$ $

(3.24)

Therefore,

$\begin{equation} \label{{600}} |x(t)| \leq\delta \Big(M {\varepsilon}^{q-1}\Gamma(q)+|B|M(1+K_0)\frac{{\tau}^q}{q}\Big)E_q(LM\Gamma(q)){\tau}^q) = \delta K_1,\ \ t\in({\tau},2{\tau}] \end{equation}$ $

(3.25)

Following the induction process we obtain

$\begin{equation} \label{{13923}}\begin{split} |x(t)|&\leq \delta \Big(M {\varepsilon}^{q-1}\Gamma(q)+|B|M(1+K_{k-1})\frac{{\tau}^q}{q}\Big)E_q(LM\Gamma(q)){\tau}^q) = \delta K_k,\ \ t\in(k{\tau},(k+1){\tau}], \nonumber \end{split} \end{equation}$ $

where $ K_k = \Big(M {\varepsilon}^{q-1}\Gamma(q)+|B|M(1+K_{k-1})\frac{{\tau}^q}{q}\Big)E_q(LM\Gamma(q)){\tau}^q), \ k = 1, 2, \dots, N $.

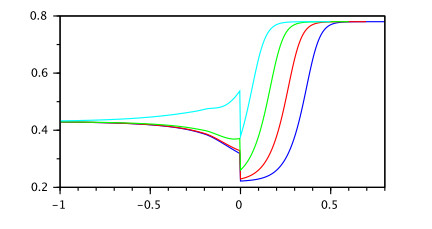
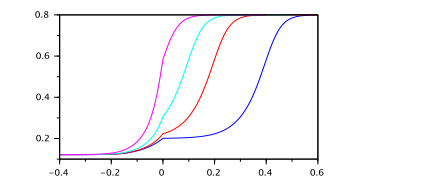
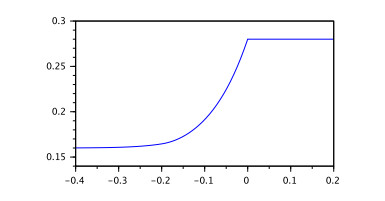
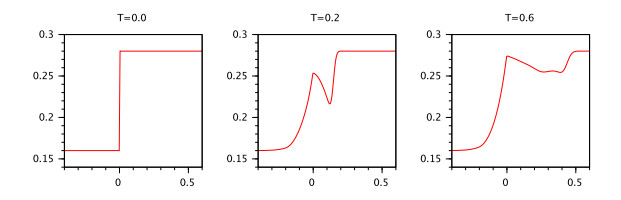
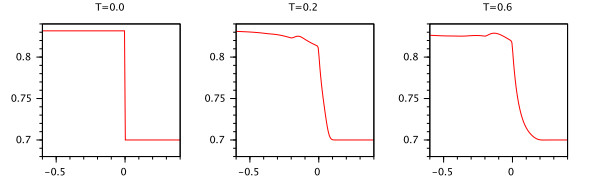
Example 4. Consider the IVP (3.1) with RL fractional equation $ \ _{0}^{RL}D_t^{0.5}x(t) = 0.1x(t-1)+0.01\sin(x(t)) $. According to Example 3 it has unique mild solution $ x(t) $ which is satisfying the integral presentation given in Definition 1. Also, according to Theorem 5 for $ \delta = 1 $, $ {\varepsilon} = 0.001 $ the inequality $ |x(t)| < K $ holds for $ t\in[0.001, 3] $ where $ M = sup_{[0, 3]}E_{0.5, 0.5}(0.1t^{0.5}) = 0.7772 $, $ K_0 = \Big(0.7772* 0.001^{0.5-1}\Gamma(0.5)+0.1 * 0.7772\frac{1}{0.5}\Big)E_q(0.11 *0.7772\Gamma(0.5)) = 52.321 $, $ K_1 = 62.0518 $ and $ K = K_2 = 63.8615 $.

4. Conclusions

We study scalar nonlinear RL fractional differential equations with constant delays. An appropriate initial value problem for studd equations is set up based on the idea of the initial time interval for delay differential equations with ordinary derivatives. A mild solution is defined based on an appropriate integral representation of the solution. The existence, continuous dependence and finite time stability of the scalar nonlinear RL fractional differential equations is studied by the help of fractional generalization of Gronwall inequality. The obtained integral representations could be successfully applied to study many qualitative investigation of the properties of the solutions of nonlinear RL fractional differential equations.

Acknowledgments

Research was partially supported by Fund Scientific Research MU19-FMI-009, Plovdiv University.

Conflict of interest

All authors declare no conflicts of interest in this paper.

References

[1]	Nonlocal systems of conservation laws in several space dimensions. SIAM J. Numer. Anal. (2015) 53: 963-983.
[2]	On the global well-posedness of BV weak solutions to the Kuramoto-Sakaguchi equation. J. Differential Equations (2017) 262: 978-1022.
[3]	Front tracking approximations for slow erosion. Dicrete Contin. Dyn. Syst. (2012) 32: 1481-1502.
[4]	On the numerical integration of scalar nonlocal conservation laws. ESAIM Math. Model. Numer. Anal. (2015) 49: 19-37.
[5]	On nonlocal conservation laws modelling sedimentation. Nonlinearity (2011) 27: 855-885.
[6]	Well-posedness of a conservation law with non-local flux arising in traffic flow modeling. Numer. Math. (2016) 132: 217-241.
[7]	Solutions for a nonlocal conservation law with fading memory. Proc. Amer. Math. Soc. (2007) 135: 3905-3915.
[8]	J. Chien and W. Shen, Traveling Waves for nonlocal particle models of traffic flow on rough roads, Discrete Contin. Dyn. Syst., 39 (2019), 4001—4040, arXiv: 1902.08537.
[9]	M. Colombo, G. Crippa and L. V. Spinolo, On the singular local limit for conservation laws with nonlocal fluxes, Arch. Ration. Mech. Anal., 233 (2019), 1131–1167, arXiv: 1710.04547.
[10]	M. Colombo, G. Crippa and L. V. Spinolo, Blow-up of the total variation in the local limit of a nonlocal traffic model, Preprint, arXiv: 1808.03529.
[11]	Nonlocal crowd dynamics models for several populations. Acta Math. Sci. (2012) 32: 177-196.
[12]	Existence and stability of solutions of a delay-differential system. Arch. Rational Mech. Anal. (1962) 10: 401-426.
[13]	R. D. Driver, Ordinary and Delay Differential Equations, Applied Mathematical Sciences, Vol. 20. Springer-Verlag, New York-Heidelberg, 1977.
[14]	A new approach for a nonlocal, nonlinear conservation law. SIAM J. Appl. Math. (2012) 72: 464-487.
[15]	J. Friedrich, O. Kolb and S. Göttlich, A Godunov type scheme for a class of LWR traffic flow models with non-local flux, Netw. Heterog. Media, 13 (2018), 531–547, arXiv: 1802.07484.
[16]	Existence and stability of traveling waves for an integro-differential equation for slow erosion. J. Differential Equations (2014) 256: 253-282.
[17]	On kinematic waves. Ⅱ. A theory of traffic flow on long crowded roads. Proc. Roy. Soc. London. Ser. A (1955) 229: 317-345.
[18]	J. Ridder and W. Shen, Traveling waves for nonlocal models of traffic flow, Discrete Contin. Dyn. Syst., 39 (2019), 4001–4040, arXiv: 1808.03734.
[19]	Traveling wave profiles for a follow-the-leader model for traffic flow with rough road condition. Netw. Heterog. Media (2018) 13: 449-478.
[20]	Traveling waves for a microscopic model of traffic flow. Discrete Contin. Dyn. Syst. (2018) 38: 2571-2589.
[21]	Erosion profile by a global model for granular flow. Arch. Rational Mech. Anal. (2012) 204: 837-879.
[22]	On a nonlocal dispersive equation modeling particle suspensions. Q. Appl. Math. (1999) 57: 573-600.

This article has been cited by:

1.	S. Hristova, T. Donchev, 2021, 2321, 0094-243X, 030012, 10.1063/5.0040075
2.	Fouzia Bekada, Saïd Abbas, Mouffak Benchohra, Juan J. Nieto, Dynamics and stability for Katugampola random fractional differential equations, 2021, 6, 2473-6988, 8654, 10.3934/math.2021503
3.	Sinan Serkan Bilgici, Müfit ŞAN, Existence and uniqueness results for a nonlinear singular fractional differential equation of order $ \sigma\in(1, 2) $, 2021, 6, 2473-6988, 13041, 10.3934/math.2021754
4.	Chen Chen, Qixiang Dong, Existence and Hyers–Ulam Stability for a Multi-Term Fractional Differential Equation with Infinite Delay, 2022, 10, 2227-7390, 1013, 10.3390/math10071013

Reader Comments

Your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)