The interaction network
.In this paper, we present a multiscale model reduction framework within Generalized Multiscale Finite Element Method (GMsFEM) for nonlinear elliptic problems. We consider an exemplary problem, which consists of nonlinear p-Laplacian with heterogeneous coefficients. The main challenging feature of this problem is that local subgrid models are nonlinear involving the gradient of the solution (e.g., in the case of scale separation, when using homogenization). Our main objective is to develop snapshots and local spectral problems, which are the main ingredients of GMsFEM, for these problems. Our contributions can be summarized as follows. (1) We re-cast the multiscale model reduction problem onto the boundaries of coarse cells. This is important and allows capturing separable scales as discussed. (2) We introduce nonlinear eigenvalue problems in the snapshot space for these nonlinear "harmonic" functions. (3) We present convergence analysis and numerical results, which show that our approaches can recover the fine-scale solution with a few degrees of freedom. The proposed methods can, in general, be used for more general nonlinear problems, where one needs nonlinear local spectral decomposition.
Citation: Eric Chung, Yalchin Efendiev, Ke Shi, Shuai Ye. A multiscale model reduction method for nonlinear monotone elliptic equations in heterogeneous media[J]. Networks and Heterogeneous Media, 2017, 12(4): 619-642. doi: 10.3934/nhm.2017025
| [1] | Tingting Zhu . Synchronization of the generalized Kuramoto model with time delay and frustration. Networks and Heterogeneous Media, 2023, 18(4): 1772-1798. doi: 10.3934/nhm.2023077 |
| [2] | Xiaoxue Zhao, Zhuchun Li . Synchronization of a Kuramoto-like model for power grids with frustration. Networks and Heterogeneous Media, 2020, 15(3): 543-553. doi: 10.3934/nhm.2020030 |
| [3] | Seung-Yeal Ha, Yongduck Kim, Zhuchun Li . Asymptotic synchronous behavior of Kuramoto type models with frustrations. Networks and Heterogeneous Media, 2014, 9(1): 33-64. doi: 10.3934/nhm.2014.9.33 |
| [4] | Seung-Yeal Ha, Jaeseung Lee, Zhuchun Li . Emergence of local synchronization in an ensemble of heterogeneous Kuramoto oscillators. Networks and Heterogeneous Media, 2017, 12(1): 1-24. doi: 10.3934/nhm.2017001 |
| [5] | Seung-Yeal Ha, Se Eun Noh, Jinyeong Park . Practical synchronization of generalized Kuramoto systems with an intrinsic dynamics. Networks and Heterogeneous Media, 2015, 10(4): 787-807. doi: 10.3934/nhm.2015.10.787 |
| [6] | Seung-Yeal Ha, Jeongho Kim, Jinyeong Park, Xiongtao Zhang . Uniform stability and mean-field limit for the augmented Kuramoto model. Networks and Heterogeneous Media, 2018, 13(2): 297-322. doi: 10.3934/nhm.2018013 |
| [7] | Seung-Yeal Ha, Hansol Park, Yinglong Zhang . Nonlinear stability of stationary solutions to the Kuramoto-Sakaguchi equation with frustration. Networks and Heterogeneous Media, 2020, 15(3): 427-461. doi: 10.3934/nhm.2020026 |
| [8] | Young-Pil Choi, Seung-Yeal Ha, Seok-Bae Yun . Global existence and asymptotic behavior of measure valued solutions to the kinetic Kuramoto--Daido model with inertia. Networks and Heterogeneous Media, 2013, 8(4): 943-968. doi: 10.3934/nhm.2013.8.943 |
| [9] | Vladimir Jaćimović, Aladin Crnkić . The General Non-Abelian Kuramoto Model on the 3-sphere. Networks and Heterogeneous Media, 2020, 15(1): 111-124. doi: 10.3934/nhm.2020005 |
| [10] | Wenlian Lu, Fatihcan M. Atay, Jürgen Jost . Consensus and synchronization in discrete-time networks of multi-agents with stochastically switching topologies and time delays. Networks and Heterogeneous Media, 2011, 6(2): 329-349. doi: 10.3934/nhm.2011.6.329 |
In this paper, we present a multiscale model reduction framework within Generalized Multiscale Finite Element Method (GMsFEM) for nonlinear elliptic problems. We consider an exemplary problem, which consists of nonlinear p-Laplacian with heterogeneous coefficients. The main challenging feature of this problem is that local subgrid models are nonlinear involving the gradient of the solution (e.g., in the case of scale separation, when using homogenization). Our main objective is to develop snapshots and local spectral problems, which are the main ingredients of GMsFEM, for these problems. Our contributions can be summarized as follows. (1) We re-cast the multiscale model reduction problem onto the boundaries of coarse cells. This is important and allows capturing separable scales as discussed. (2) We introduce nonlinear eigenvalue problems in the snapshot space for these nonlinear "harmonic" functions. (3) We present convergence analysis and numerical results, which show that our approaches can recover the fine-scale solution with a few degrees of freedom. The proposed methods can, in general, be used for more general nonlinear problems, where one needs nonlinear local spectral decomposition.
Synchronized behavior in complex systems is ubiquitous and has been extensively investigated in various academic communities such as physics, biology, engineering [2,7,29,36,37,39,40,42], etc. Recently, sychronization mechanism has been applied in control of robot systems and power systems [12,13,34]. The rigorous mathematical treatment of synchronization phenomena was started by two pioneers Winfree [43] and Kuramoto [27,28] several decades ago, who introduced different types of first-order systems of ordinary differential equations to describe the synchronous behaviors. These models contain rich emergent behaviors such as synchronization, partially phase-lcoking and nonlinear stability, etc., and have been extensively studied in both theoretical and numerical level [3,5,11,14,15,16,17,19,26,32,39].
In this paper, we address the synchronous problem of Kuramoto model on a general graph under the effect of frustration. To fix the idea, we consider a digraph
| χij={1if thejth oscillator influences theith oscillator,0otherwise. |
Then, the set of neighbors of
| {˙θi(t)=Ωi+K∑j∈Nisin(θj(t)−θi(t)+α),t>0,i∈V,θi(0)=θi0, | (1) |
where
Comparing to the original Kuramoto model, there are two additional structures, i.e., frustration and general digraph. The frustration was introduced by Sakaguchi and Kuramoto [38], due to the observation that a pair of strongly coupled oscillators eventually oscillate with a common frequency that deviates from the average of their natural frequencies. On the other hand, the original all-to-all symmetric network is an ideal setting, thus it is natural to further consider general digraph case. Therefore, the frustration model with general digraph is more realistic in some sense. Moreover, these two structures also lead to richer phenomenon. For instance, the author in [6] observed that the frustration is common in disordered interactions, and the author in [44] found that frustration can induce the desynchronization through varying the value of
However, mathematically, for the Kuramoto model, the frustration and general digraph structures generate a lot of difficulties in rigorous analysis. For instance, the conservation law and gradient flow structure are lost, and thus the asymptotic states and dissipation mechanism become non-trivial. For all-to-all and symmetric case with frustration, in [20], the authors provided sufficient frameworks leading to complete synchronization under the effect of uniform frustration. In their work, they required initial configuration to be confined in half circle. Furthermore, the authors in [31] dealt with the stability and uniqueness of emergent phase-locked states. In particular, the authors in [22] exploited order parameter approach to study the identical Kuramoto oscillators with frustration. They showed that an initial configuration whose order parameter is bounded below will evolve to the complete phase synchronization or the bipolar state exponentially fast. On the other hand, for non-all-to-all case without frustration, the authors in [9] lifted the Kuramoto model to second-order system such that the second-order formulation enjoys several similar mathematical structures to that of Cucker-Smale flocking model [8]. But this method only works when the size of initial phases is less than a quarter circle, as we know the cosine function becomes negative if
Our interest in this paper is studying the system (1) with uniform frustration on a general digraph. As far as the authors know, when the ensemble is distributed in half circle, the dissipation structure of the Kuramoto type model with general digragh is still unclear. The main difficulty comes from the loss of uniform coercive inequality, which is due to the non-all-to-all and non-symmetric interactions. Thus we cannot expect to capture the dissipation from Gronwall-type inequality of phase diameter. For example, the time derivative of the phase diameter may be zero at some time for general digraph case. To this end, we switch to apply the idea of node decomposition in [25] to gain the dissipation through hypo-coercivity. Due to the lack of monotonicity of sine function in half circle, we follow the delicate constructions and estimates of the convex combinations in [45]. Eventually, we have the following main theorem.
Theorem 1.1. Suppose the network topology
| D(θ(0))<π. |
Then for sufficient large coupling strength
| D(θ(t))≤D∞,∀t∈[t∗,∞), |
and
| D(ω(t))≤C1e−C2(t−t∗),t≥t∗, |
where
Remark 1. The first part of Theorem 1.1 claims that all oscillators confined initially in half circle will enter into a region less than quarter cirlce after some finite time. It is natural to ask how large
| tanα<1(1+(d+1)ζζ−D(θ(0)))2Ncβd+1D∞[4(2N+1)c]d,D∞+α<π2,1>(1+(d+1)ζζ−D(θ(0)))c[4(2N+1)c]dβd+1D∞(D(Ω)Kcosα+2Nsinαcosα), | (2) |
where
| D(θ(0))<ζ<γ<π,η>max{1sinγ,21−ζγ},β=1−2η,c=(N−1∑j=1ηjA(2N,j)+1)γsinγ, | (3) |
where
Remark 2. For
The rest of the paper is organized as follows. In Section 2, we recall some concepts on the network topology and provide a priori local-in-time estimate on the phase diameter of whole ensemble with frustration. In Section 3, we consider a strongly connected ensemble with frustration for which the initial phases are distributed in a half circle. We show that for large coupling strength and small frustration, the phase diameter is uniformly bounded by a value less than
In this section, we first introduce some fundamental concepts such as synchronization, spanning tree and node decomposition of a general network (1). Then, we will provide some necessary notations and a priori estimate that will be frequently used in later sections.
For the Kuramoto-type model, we recall the definition of synchronization as follows.
Definition 2.1. Let
| limt→∞|˙θi(t)−˙θj(t)|=0,∀ i≠j. |
Let the network topology be registered by the neighbor set
Definition 2.2. (1)The Kuramoto digraph
(2)A path in
| is∈Nis+1for 1≤s≤k−1. |
If there exists a path from
(3)The Kuramoto digraph contains a spanning tree if we can find a vertex such that any other vertex of
In order to guarantee the emergence of synchronization, we will always assume the existence of a spanning tree throughout the paper. Now we recall the concepts of root and general root introduced in [25]. Let
| ci≥0,l≤i≤kandk∑i=lci=1. |
For an ensembel of
| Lkl(Cl,k):=k∑i=lciθi. |
Note that each
Definition 2.3. (Root and general root)
1. We say
2. We say
Lemma 2.4.[25] The following assertions hold.
1. If the network contains a spanning tree, then there is at most one root.
2. Assume the network contains a spanning tree. If
In this part, we will recall the concept of maximum node introduced in [25]. Then, we can follow node decomposition introduced in [25] to represent the whole graph
Definition 2.5. [25] (Node) Let
Intuitively, a node can be understood through a way that a set of oscillators can be viewed as a "large" oscillator. The concept of node can be exploited to simplify the structure of the digraph, which indeed helps us to catch the attraction effect more clearly in the network topology.
Lemma 2.6.[25] Any digraph
Lemma 2.7.[25] (Node decomposition)Let
1.
2. For any
Proof. As
Remark 3. Lemma 2.7 shows a clear hierarchical structure on a general digraph. For the convenience of later analysis, we make some comments on important notations and properties that are used throughout the paper.
1. From the definition of maximum node, for
| G=d⋃i=0Gi, |
where
2.For a given oscillator
In this part, for notational simplicity, we introduce some notations, such as the extreme phase, phase diameter of
| θ=(θ1,θ2,…,θN),ω=(ω1,ω2,…,ωN),Ω=(Ω1,Ω2,…,ΩN),θM=max1≤k≤N{θk}=max0≤i≤dmax1≤j≤Ni{θij},θm=min1≤k≤N{θk}=min0≤i≤dmin1≤j≤Ni{θij},D(θ)=θM−θm,Dk(θ)=max0≤i≤kmax1≤j≤Ni{θij}−min0≤i≤kmin1≤j≤Ni{θij},ΩM=max0≤i≤dmax1≤j≤Ni{Ωij},Ωm=min0≤i≤dmin1≤j≤Ni{Ωij},D(Ω)=ΩM−Ωm,Ni=|Gi|,Sk=k∑i=0Ni,0≤k≤d,d∑i=0Ni=N. |
Finally, we provide a priori local-in-time estimate on the phase diameter to finish this section, which states that all oscillators can be confined in half circle in short time.
Lemma 2.8. Let
| D(θ(0))<ζ<γ<π, |
where
| D(θ(t))<ζ,t∈[0,ˉt)whereˉt=ζ−D(θ(0))D(Ω)+2NKsinα. |
Proof. From system (1), we see that the dynamics of extreme phases is given by the following equations
| ˙θM(t)=ΩM+K∑j∈NMsin(θj(t)−θM(t)+α),˙θm(t)=Ωm+K∑j∈Nmsin(θj(t)−θm(t)+α), |
where
| ˙D(θ(t))=˙θM(t)−˙θm(t)=ΩM−Ωm+K∑j∈NMsin(θj−θM+α)−K∑j∈Nmsin(θj−θm+α)≤D(Ω)+K∑j∈NM[sin(θj−θM)cosα+cos(θj−θM)sinα]−K∑j∈Nm[sin(θj−θm)cosα+cos(θj−θm)sinα]=D(Ω)+Kcosα(∑j∈NMsin(θj−θM)−∑j∈Nmsin(θj−θm))+Ksinα(∑j∈NMcos(θj−θM)−∑j∈Nmcos(θj−θm)), | (4) |
where
| sin(x+y)=sinxcosy+cosxsiny |
When the phase diameter satisfies
| sin(θj−θM)≤0, j∈NMandsin(θj−θm)≥0, j∈Nm. |
Then we see from (4) that
| ˙D(θ)≤D(Ω)+2NKsinα. | (5) |
That is to say, when
| D(θ(t))≤D(θ(0))+(D(Ω)+2NKsinα)t. |
Therefore, it yields that there exists a finite time
| D(θ(t))<ζ,∀ t∈[0,ˉt), |
where
| ˉt=ζ−D(θ(0))D(Ω)+2NKsinα. |
We will first study the special case, i.e., the network is strongly connected. Without loss of generality, we denote by
Step 1. For any given time
| θ01(t)≤θ02(t)≤…≤θ0N0(t). | (6) |
In order to introduce the following steps, we first provide the process of iterations for
| ˉLN0k−1(ˉCk−1,N0)=ˉak−1ˉLN0k(ˉCk,N0)+θ0k−1ˉak−1+1. |
| L_l+11(C_1,l+1)=a_l+1L_l1(C_1,l)+θ0l+1a_l+1+1 |
Step 2. According to the strong connectivity of
Step 3. Similarly, we know that
It is worth emphasizing that the order of the oscillators may change along time
Lemma 3.1. Let
| D0(θ(t))<γ<π,η>max{1sinγ,21−ζγ}, |
where
| {N0∑i=n(ηi−nminj∈N0i(0)j≤isin(θ0j−θ0i))≤sin(θ0ˉkn−θ0N0), ˉkn=minj∈∪N0i=nN0i(0)j, 1≤n≤N0,n∑i=1(ηn−imaxj∈N0i(0)j≥isin(θ0j−θ0i))≥sin(θ0k_n−θ01), k_n=maxj∈∪ni=1N0i(0)j, 1≤n≤N0. |
Proof. For the proof of this lemma, please see [45] for details.
Recall the strongly connected ensemble
| θ01(t)≤θ02(t)≤…≤θ0N0(t). |
Then we apply the process
| ˉLN0k−1(ˉCk−1,N0) with ˉa0N0=0, ˉa0k−1=η(2N0−k+2)(ˉa0k+1),2≤k≤N0,L_k+11(C_1,k+1) with a_01=0, a_0k+1=η(k+1+N0)(a_0k+1),1≤k≤N0−1, | (7) |
where
| ˉa0k−1=N0−k+1∑j=1ηjA(2N0−k+2,j),2≤k≤N0,a_0k+1=k∑j=1ηjA(k+1+N0,j),1≤k≤N0−1. |
Note that
| ˉθ0k:=ˉLN0k(ˉCk,N0),θ_0k:=L_k1(C_1,k),1≤k≤N0. | (8) |
We define a non-negative quantity
Lemma 3.2. Let
| βD0(θ(t))≤Q0(t)≤D0(θ(t)),β=1−2η, |
where
Proof. As we choose the same design for coefficients of convex combination as that in [45], the proof of this lemma is same as that in [45], please see [45] for details.
From Lemma 3.2, we see that the quantity
Lemma 3.3. Let
| D0(θ(0))<ζ<γ<π,η>max{1sinγ,21−ζγ},tanα<1(1+ζζ−D(θ(0)))2N0cβD∞,D∞+α<π2,K>(1+ζζ−D0(θ(0))(D(Ω)+2N0Ksinα)ccosα1βD∞, | (9) |
where
| D0(θ(t))<γ,t∈[0,+∞), |
and the dynamics of
| ˙Q0(t)≤D(Ω)+2N0Ksinα−KcosαcQ0(t),t∈[0,+∞). |
Proof. The proof is similar to [45] under the assumption that the frustration
Lemma 3.3 states that the phase diameter of the digraph
Lemma 3.4. Let
| D0(θ(t))≤D∞,for t∈[t0,+∞), |
where
| t0<ζKcosαcβD∞−(D(Ω)+2N0Ksinα)<ˉt. | (10) |
Remark 4. According to Lemma 2.8, we see that
Proof. From Lemma 3.3, we see that the dynamics of quantity
| ˙Q0(t)≤D(Ω)+2N0Ksinα−KcosαcQ0(t),t∈[0,+∞). | (11) |
We next show that there exists some time
| ˙Q0(t)≤D(Ω)+2N0Ksinα−KcosαcQ0(t)≤D(Ω)+2N0Ksinα−KcosαcβD∞<0. | (12) |
That is to say, when
| t0=inf{t≥0 | Q0(t)≤βD∞}. |
And based on the definition of
| Q0(t0)=βD∞. | (13) |
Moerover, from (12), it is easy to see that the stopping time
| t0≤Q0(0)−βD∞KcosαcβD∞−(D(Ω)+2N0Ksinα). | (14) |
Now we study the upper bound of
| Q0(t)≤βD∞, t∈[t0,+∞). | (15) |
| Q0(t)≤βD∞,t∈[0,+∞). | (16) |
Then in this case, we directly set
Therefore, from (15), (16), and Lemma 3.2, we derive the upper bound of
| D0(θ(t))≤Q0(t)β≤D∞,for t∈[t0,+∞). | (17) |
On the other hand, in order to verify (10), we further study
| t0<ζKcosαcβD∞−(D(Ω)+2N0Ksinα). | (18) |
Here, we use the truth that
| K>(1+ζζ−D0(θ(0))(D(Ω)+2N0Ksinα)ccosα1βD∞, |
it yields the following estimate about
| t0<ζ(1+ζζ−D0(θ(0)))(D(Ω)+2N0Ksinα)−(D(Ω)+2N0Ksinα)=ζ−D0(θ(0))D(Ω)+2N0Ksinα=ˉt, | (19) |
where in this special strongly connected case, it's clear that
Thus, combining (17), (18) and (19), we derive the desired results.
In this section, we investigate the general network with a spanning tree structure, and prove our main result Theorem 1.1, which state that synchronization will emerge for Kuramoto model with frustration. According to Definition 2.5 and Lemma 2.6, we see that the digraph
We have studied the situation
From Remark 3 and node decomposition, the graph
| G=d⋃k=0Gk,|Gk|=Nk, |
and we denote the oscillators in
| θk1(t)≤θk2(t)≤…≤θkNk(t),0≤k≤d. |
For each subdigraph
| {ˉLNkl−1(ˉCl−1,Nk) with ˉakNk=0, ˉakl−1=η(2N−l+2)(ˉakl+1),2≤l≤Nk,L_l+11(C_1,l+1) with a_k1=0, a_kl+1=η(l+1+2N−Nk)(a_kl+1),1≤l≤Nk−1. | (20) |
By induction principle, we deduce that
| {ˉakl−1=Nk−l+1∑j=1ηjA(2N−l+2,j),2≤l≤Nk,a_kl+1=l∑j=1ηjA(l+1+2N−Nk,j),1≤l≤Nk−1. |
Note that
| ˉak1=Nk−1∑j=1(ηjA(2N,j)),ˉak1≤N−1∑j=1(ηjA(2N,j)),0≤k≤d. | (21) |
And we further introduce the following notations,
| ˉθkl:=ˉLNkl(ˉCl,Nk),θ_kl:=L_l1(C_1,l),1≤l≤Nk,0≤k≤d, | (22) |
| ˉθk:=ˉLNk1(ˉC1,Nk),θ_k:=L_Nk1(C_1,Nk),0≤k≤d, | (23) |
| Qk(t):=max0≤i≤k{ˉθi}−min0≤i≤k{θ_i},0≤k≤d. | (24) |
Due to the analyticity of the solution,
Lemma 4.1. Let
| βDk(θ(t))≤Qk(t)≤Dk(θ(t)),0≤k≤d,β=1−2η, |
where
Proof. As we adopt the same construction of coefficients of convex combination in [45] which deals with the Kuramoto model without frustration on a general network, thus for the detailed proof of this lemma, please see [45].
Now we are ready to prove our main Theorem 1.1. To this end, we will follow similar arguments in Section 3 to complete the proof. Actually, we will investigate the dynamics of the constructed quantity
Lemma 4.2. Suppose that the network topology contains a spanning tree, and let
| D(θ(0))<ζ<γ<π,η>max{1sinγ,21−ζγ}, | (25) |
where
| tanα<1(1+(d+1)ζζ−D(θ(0)))2Ncβd+1D∞[4(2N+1)c]d,D∞+α<π2,K>(1+(d+1)ζζ−D(θ(0)))(D(Ω)+2NKsinα)ccosα[4(2N+1)c]dβd+1D∞, | (26) |
where
1. The dynamics of
| ˙Q0(t)≤D(Ω)+2NKsinα−KcosαcQ0(t),t∈[0,+∞), |
2. there exists time
| D0(θ(t))≤βdD∞[4(2N+1)c]d,for t∈[t0,+∞), |
where
| t0<ζKcosαcβd+1D∞[4(2N+1)c]d−(D(Ω)+2NKsinα)<ˉt. |
Next, inspiring from Lemma 4.2, we make the following reasonable ansatz for
Ansatz:
1. The dynamics of quantity
| ˙Qk(t)≤D(Ω)+2NKsinα+(2N+1)KcosαDk−1(θ(t))−KcosαcQk(t), | (27) |
where we assume
2. There exists a finite time
| Dk(θ(t))≤βd−kD∞[4(2N+1)c]d−k,∀ t∈[tk,+∞), | (28) |
where
| tk<(k+1)ζKcosαcβd+1D∞[4(2N+1)c]d−(D(Ω)+2NKsinα)<ˉt=ζ−D(θ(0))D(Ω)+2NKsinα. | (29) |
In the subsequence, we will split the proof of the ansatz into two lemmas by induction criteria. More precisely, based on the results in Lemma 4.2 as the initial step, we suppose the ansatz holds for
Lemma 4.3. Suppose the assumptions in Lemma 4.2 are fulfilled, and the ansatz in (27), (28) and (29) holds for some
Proof. We will use proof by contradiction criteria to verify the ansatz for
| Bk+1={T>0 : Dk+1(θ(t))<γ, ∀ t∈[0,T)}. |
From Lemma 2.8, we see that
| Dk+1(θ(t))≤D(θ(t))<ζ<γ,∀ t∈[0,ˉt). |
It is clear that
| ˉt≤T∗,Dk+1(θ(t))<γ, ∀ t∈[0,T∗),Dk+1(θ(T∗))=γ. | (30) |
As the solution to system (1) is analytic, in the finite time interval
| [0,T∗)=r⋃l=1Jl,Jl=[tl−1,tl). |
such that in each interval
| ˙Qk+1(t)≤D(Ω)+2NKsinα+(2N+1)KcosαDk(θ(t))−KcosαcQk+1(t). | (31) |
As the proof is slightly different from that in [45] and rather lengthy, we put the detailed proof in Appendix B.
| ˙Qk+1(t)≤−Kcosαc(Qk+1(t)−(2N+1)cDk(θ(t))−(D(Ω)+2NKsinα)cKcosα), | (32) |
where
| c=(∑N−1j=1ηjA(2N,j)+1)γsinγ. | (33) |
For the term
| Dk(θ(t))≤βd−kD∞[4(2N+1)c]d−k, t∈[tk,+∞),tk<ˉt. | (34) |
And from the condition (26), it is obvious that
| K>(1+(d+1)ζζ−D(θ(0)))(D(Ω)+2NKsinα)ccosα[4(2N+1)c]dβd+1D∞>(D(Ω)+2NKsinα)ccosα[4(2N+1)c]dβd+1D∞. |
This directly yields that
| (D(Ω)+2NKsinα)cKcosα<βd+1D∞[4(2N+1)c]d<βd−kD∞4d−k[(2N+1)c]d−k−1, | (35) |
where
| (2N+1)cDk(θ(t))+(D(Ω)+2NKsinα)cKcosα≤(2N+1)cβd−kD∞[4(2N+1)c]d−k+βd−kD∞4d−k[(2N+1)c]d−k−1≤βd−kD∞2[4(2N+1)c]d−k−1<βd−kD∞[4(2N+1)c]d−k−1,t∈[tk,+∞). | (36) |
From Lemma 2.8, we have
| Qk+1(t)≤max{Qk+1(tk),βd−kD∞[4(2N+1)c]d−k−1}:=Mk+1,t∈[tk,T∗). | (37) |
Suppose not, then there exists some
| Ck+1:={tk≤t<˜t:Qk+1(t)≤Mk+1}. |
Since
| t∗<˜t,Qk+1(t∗)=Mk+1,Qk+1(t)>Mk+1for t∈(t∗,˜t]. | (38) |
From the construction of
| −Kcosαc(Qk+1(t)−(2N+1)cDk(θ(t))−(D(Ω)+2NKsinα)cKcosα)<−Kcosαc(Mk+1−βd−kD∞[4(2N+1)c]d−k−1)≤0. |
Wen apply the above inequality and integrate on both sides of (32) from
| Qk+1(˜t)−Mk+1=Qk+1(˜t)−Qk+1(t∗)≤−∫˜tt∗Kcosαc(Qk+1(t)−(2N+1)cDk(θ(t))−(D(Ω)+2NKsinα)cKcosα)dt<0, |
which contradicts to the truth
| βd−kD∞[4(2N+1)c]d−k−1<D∞,tk<ˉt,Qk+1(tk)≤Dk+1(θ(tk))≤D(θ(tk))<ζ, |
we directly obtain
| Qk+1(t)≤max{Qk+1(tk),βd−kD∞[4(2N+1)c]d−k−1}<max{ζ,D∞}=ζ,t∈[tk,T∗). |
From Lemma 4.1 and the condition (25), it yields that
| Dk+1(θ(t))≤Qk+1(t)β<ζβ<γ,t∈[tk,T∗). |
Since
| Dk+1(θ(T∗))=limt→(T∗)−Dk+1(θ(t))≤ζβ<γ, |
which obviously contradicts to the assumption
Thus, we combine all above analysis to conclude that
| Dk+1(θ(t))<γ,∀ t∈[0,+∞). | (39) |
Then for any finite time
| ˙Qk+1(t)≤D(Ω)+2NKsinα+(2N+1)KcosαDk(θ(t))−KcosαcQk+1(t). | (40) |
Therefore, we complete the proof of the Ansatz (27) for
Lemma 4.4. Suppose the conditions in Lemma 4.2 are fulfilled, and the ansatz in (27), (28) and (29) holds for some
Proof. From Lemma 4.3, we know the dynamic of
| ˙Qk+1(t)≤−Kcosαc(Qk+1(t)−(2N+1)cDk(θ(t))−(D(Ω)+2NKsinα)cKcosα), | (41) |
where
| ˙Qk+1(t)≤−Kcosαc(βd−kD∞[4(2N+1)c]d−k−1−βd−kD∞2[4(2N+1)c]d−k−1)=−Kcosαcβd−kD∞2[4(2N+1)c]d−k−1<0. | (42) |
That is to say, when
| tk+1=inf{t≥tk | Qk+1(t)≤βd−kD∞[4(2N+1)c]d−k−1}. |
Then, based on (42) and the definition of
| Qk+1(tk+1)=βd−kD∞[4(2N+1)c]d−k−1. | (43) |
Moreover, from (42), it yields that the stopping time
| tk+1≤Qk+1(tk)−βd−kD∞[4(2N+1)c]d−k−1Kcosαcβd−kD∞2[4(2N+1)c]d−k−1+tk. | (44) |
Now we study the upper bound of
| Qk+1(t)≤βd−kD∞[4(2N+1)c]d−k−1,t∈[tk+1,+∞). | (45) |
On the other hand, in order to verify (29), we further study
| Qk+1(tk)≤Dk+1(θ(tk))≤D(θ(tk))<ζ,βd−kD∞2[4(2N+1)c]d−k−1>βd+1D∞[4(2N+1)c]d, |
we have the following estimates
| Qk+1(tk)−βd−kD∞[4(2N+1)c]d−k−1Kcosαcβd−kD∞2[4(2N+1)c]d−k−1<ζKcosαcβd+1D∞[4(2N+1)c]d−(D(Ω)+2NKsinα), | (46) |
where the denominator on the right-hand side of above inequality is positive from the conditions about
| tk<(k+1)ζKcosαcβd+1D∞[4(2N+1)c]d−(D(Ω)+2NKsinα)<ˉt=ζ−D(θ(0))D(Ω)+2NKsinα. | (47) |
Thus it yields from (44), (46) and (47) that the time
| tk+1<(k+2)ζKcosαcβd+1D∞[4(2N+1)c]d−(D(Ω)+2NKsinα). | (48) |
Moreover, from (26), it is easy to see that the coupling strength
| K>(1+(d+1)ζζ−D(θ(0)))(D(Ω)+2NKsinα)ccosα[4(2N+1)c]dβd+1D∞≥(1+(k+2)ζζ−D(θ(0)))(D(Ω)+2NKsinα)ccosα[4(2N+1)c]dβd+1D∞,0≤k≤d−1. | (49) |
Thus we combine (48) and (49) to verify the Ansatz (29) for
| tk+1<ˉt=ζ−D(θ(0))D(Ω)+2NKsinα. | (50) |
| Qk+1(t)≤βd−kD∞[4(2N+1)c]d−k−1,t∈[tk,+∞). | (51) |
In this case, we directly set
Finally, we are ready to verify the ansatz (28) for
| Dk+1(θ(t))≤Qk+1(t)β≤βd−k−1D∞[4(2N+1)c]d−k−1,t∈[tk+1,+∞). | (52) |
Then we combine (48), (50) and (52) in Case 1 and similar analysis in Case 2 to conclude that the Ansatz (28) and (29) is true for
Now, we are ready to prove our main result.
Lemma 4.5. Let
| D(θ(t))≤D∞,for t∈[t∗,+∞), |
where
Proof. Combining Lemma 4.2, Lemma 4.3 and Lemma 4.4, we apply inductive criteria to conclude that the Ansatz (27) –(29) hold for all
| D(θ(t))=Dd(θ(t))≤D∞,for t∈[td,+∞). |
Thus we set
Remark 5. For the Kuramoto model with frustration, in Lemma 4.5, we show the phase diameter of whole ensemble will be uniformly bounded by a value
More precisely, we can introduce phase velocity or frequency
| {˙θi(t)=ωi(t),t>0,i=1,2,…,N,˙ωi(t)=K∑j∈Nicos(θj(t)−θi(t)+α)(ωj(t)−ωi(t)),(θi(0),ωi(0))=(θi(0),˙θi(0)). | (53) |
Now for the second-order system (53), we apply the results in [9] for Kuramoto model without frustration on a general digraph and present the frequency synchronization for Kuramoto model with frustrations.
Lemma 4.6. Let
| D(ω(t))≤C1e−C2(t−t∗),t≥t∗, |
where
Proof. According to Lemma 4.5 and the condition
| D(θ(t))+α≤D∞+α<π2,t∈[t∗,+∞). |
Therefore, we can apply the methods and results in the work of Dong et al. [9] for Kuramoto model without frustration to yield the emergence of exponentially fast synchronization. As the proof is almost the same as that in [9], we omit its details.
Proof of Theorem 1.1: Combining Lemma 4.5 and Lemma 4.6, we ultimately derive the desired result in Theorem 1.1.
In this section, we present several numerical simulations to illustrate the main results in Theorem 1.1, which state that in sufficiently large coupling strength and small frustration regimes, synchronous behavior will emerge for the Kuramoto model with frustration in half circle case.
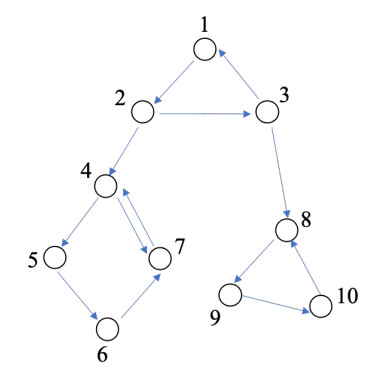
For the simulation, we use the fourth-order Runge-Kutta method and employ the parameter
| (χij)=(1010000000110000000001100000000101001000000110000000001100000001011000001000010100000001100000000011). |
For the fixed digraph in Figure 1, we choose large
In Figure 3, we fix the coupling strength
In Figure 4, we fix the frustration
Moreover, for
In this paper, under the effect of frustration, we provide sufficient frameworks leading to the complete synchronization for the Kuramoto model with general network containing a spanning tree. To this end, we follow a node decomposition introduced in [25] and construct hypo-coercive inequalities through which we can study the upper bounds of phase diameters. When the initial configuration is confined in a half circle, for sufficiently small frustration and sufficiently large coupling strength, we show that the relative differences of Kuramoto oscillators adding a phase shift will be confined into a region of quarter circle in finite time, thus we can directly apply the methods and results in [9] to prove that the complete frequency synchronization emerges exponentially fast. And we provide some numerical simulations to illustrate the main results.
We really appreciate the editors and reviewers for their thorough reviews and insightful suggestions.
We will split the proof into six steps. In the first step, we suppose by contrary that the phase diameter of
| B0:={T>0: D0(θ(t))<γ, ∀ t∈[0,T)}. |
From Lemma 2.8 where
| D0(θ(t))=D(θ(t))<ζ<γ,∀ t∈[0,ˉt), |
which directly yields that
| D0(θ(t))<γ,∀ t∈[0,T∗),D0(θ(T∗))=γ. | (54) |
In particular, we have
| [0,T∗)=r⋃l=1Jl,Jl=[tl−1,tl), |
where the end point
| θ01(t)≤θ02(t)≤…≤θ0N0(t),t∈Jl. |
| ˙θ0N0(t)=Ω0N0+K∑j∈N0N0(0)sin(θ0j−θ0N0+α)≤ΩM+K∑j∈N0N0(0)[sin(θ0j−θ0N0)cosα+cos(θ0j−θ0N0)sinα]≤ΩM+N0Ksinα+Kcosαminj∈N0N0(0)sin(θ0j−θ0N0). | (55) |
For the dynamics of
| ˙ˉθ0N0−1=ddt(ˉa0N0−1θ0N0+θ0N0−1ˉa0N0−1+1)=ˉa0N0−1ˉa0N0−1+1˙θ0N0+1ˉa0N0−1+1˙θ0N0−1≤ˉa0N0−1ˉa0N0−1+1(ΩM+N0Ksinα+Kcosαminj∈N0N0(0)sin(θ0j−θ0N0))+1ˉa0N0−1+1(Ω0N0−1+K∑j∈N0N0−1(0)sin(θ0j−θ0N0−1+α))≤ΩM+Kcosα1ˉa0N0−1+1η(N0+2)minj∈N0N0(0)sin(θ0j−θ0N0)+ˉa0N0−1ˉa0N0−1+1N0Ksinα+Kcosα1ˉa0N0−1+1∑j∈N0N0−1(0)sin(θ0j−θ0N0−1)+Ksinα1ˉa0N0−1+1∑j∈N0N0−1(0)cos(θ0j−θ0N0−1)≤ΩM+Kcosα1ˉa0N0−1+12ηminj∈N0N0(0)sin(θ0j−θ0N0)+ˉa0N0−1ˉa0N0−1+1N0Ksinα+Kcosα1ˉa0N0−1+1(∑j∈N0N0−1(0)j≤N0−1sin(θ0j−θ0N0−1)+sin(θ0N0−θ0N0−1))+1ˉa0N0−1+1N0Ksinα≤ΩM+Kcosα1ˉa0N0−1+1ηminj∈N0N0(0)sin(θ0j−θ0N0)+Kcosα1ˉa0N0−1+1minj∈N0N0−1(0)j≤N0−1sin(θ0j−θ0N0−1)+Kcosα1ˉa0N0−1+1(ηminj∈N0N0(0)sin(θ0j−θ0N0)+sin(θ0N0−θ0N0−1))⏟I1+N0Ksinα, | (56) |
where we use
| |∑j∈N0N0−1(0)cos(θ0j−θ0N0−1)|≤N0, Kcosα1ˉa0N0−1+1ηN0minj∈N0N0(0)sin(θ0j−θ0N0)≤0,∑j∈N0N0−1(0)j≤N0−1sin(θ0j−θ0N0−1)≤minj∈N0N0−1(0)j≤N0−1sin(θ0j−θ0N0−1). |
Next we show the term
| minj∈N0N0(0)sin(θ0j−θ0N0)≤sin(θ0ˉkN0−θ0N0)where ˉkN0=minj∈N0N0(0)j. |
Note that
| 0≤θ0N0(t)−θ0N0−1(t)≤θ0N0(t)−θ0ˉkN0(t)≤π2, |
which implies that
| I1≤ηsin(θ0ˉkN0−θ0N0)+sin(θ0N0−θ0N0−1)≤sin(θ0ˉkN0−θ0N0)+sin(θ0N0−θ0N0−1)≤0. |
On the other hand, if
| η>1sinγandsin(θ0N0(t)−θ0ˉkN0(t))>sinγ, |
to conclude that
| I1≤ηsin(θ0ˉkN0−θ0N0)+sin(θ0N0−θ0N0−1)≤−1+1≤0. |
Thus, for
| I1=ηminj∈N0N0(0)sin(θ0j−θ0N0)+sin(θ0N0−θ0N0−1)≤0. | (57) |
Then combining (56) and (57), we derive that
| ˙ˉθ0N0−1≤ΩM+N0Ksinα+Kcosα1ˉa0N0−1+1(ηminj∈N0N0(0)sin(θ0j−θ0N0)+minj∈N0N0−1(0)j≤N0−1sin(θ0j−θ0N0−1)). | (58) |
| ˙ˉθ0n(t)≤ΩM+N0Ksinα+Kcosα1ˉa0n+1N0∑i=nηi−nminj∈N0i(0)j≤isin(θ0j(t)−θ0i(t)). | (59) |
In fact, it is known that (59) already holds for
| ˙ˉθ0n−1≤ΩM+N0Ksinα+Kcosα1ˉa0n−1+1ηN0∑i=nηi−nminj∈N0i(0)j≤isin(θ0j−θ0i)+Kcosα1ˉa0n−1+1minj∈N0n−1(0)j≤n−1sin(θ0j−θ0n−1)+Kcosα1ˉa0n−1+1×(η(N0−n+1)N0∑i=nηi−nminj∈N0i(0)j≤isin(θ0j−θ0i)+∑j∈N0n−1(0)j>n−1sin(θ0j−θ0n−1)⏟I2). | (60) |
Moreover, we can prove the term
| ˙ˉθ01≤ΩM+N0Ksinα+Kcosα1ˉa01+1N0∑i=1ηi−1minj∈N0i(0)j≤isin(θ0j−θ0i)≤ΩM+N0Ksinα+Kcosα1ˉa01+1sin(θ0ˉk1−θ0N0)=ΩM+N0Ksinα+Kcosα1ˉa01+1sin(θ01−θ0N0), | (61) |
where
| ddtθ_0N0(t)≥Ωm−N0Ksinα+Kcosα1ˉa01+1sin(θ0N0−θ01). | (62) |
Then we recall the notations
| ˙Q0(t)=ddt(ˉθ0−θ_0)≤D(Ω)+2N0Ksinα−Kcosα2ˉa01+1sin(θ0N0−θ01)≤D(Ω)+2N0Ksinα−Kcosα1∑N0−1j=1ηjA(2N0,j)+1sin(θ0N0−θ01), |
where we use the property
| ˉa01=N0−1∑j=1ηjA(2N0,j). |
As the function
| sin(θ0N0−θ01)≥sinγγ(θ0N0−θ01). |
Moreover, due to the fact
| ˙Q0(t)≤D(Ω)+2N0Ksinα−Kcosα1∑N0−1j=1ηjA(2N0,j)+1sinγγ(θ0N0−θ01)≤D(Ω)+2N0Ksinα−Kcosα1∑N0−1j=1ηjA(2N0,j)+1sinγγQ0(t),t∈Jl. | (63) |
Note that the constructed quantity
| M0=max{Q0(0),βD∞}. |
We claim that
| Q0(t)≤M0for all t∈[0,T∗). | (64) |
Suppose not, then there exists some
| C0:={t<˜t | Q0(t)≤M0}. |
Since
| t∗<˜t,Q0(t∗)=M0,Q0(t)>M0for t∈(t∗,˜t]. | (65) |
For the given constant
| K>(1+ζζ−D(θ(0))(D(Ω)+2N0Ksinα)ccosα1βD∞>(D(Ω)+2N0Ksinα)ccosα1βD∞, | (66) |
where
| D(Ω)+2N0Ksinα−Kcosα1∑N0−1j=1ηjA(2N0,j)+1sinγγQ0(t)<D(Ω)+2N0Ksinα−Kcosα1∑N0−1j=1ηjA(2N0,j)+1sinγγβD∞<0. |
Then, we apply the above inequality and integrate on the both sides of (63) from
| Q0(˜t)−M0=Q0(˜t)−Q0(t∗)≤∫˜tt∗(D(Ω)+2N0Ksinα−Kcosα1∑N0−1j=1ηjA(2N0,j)+1sinγγQ0(t))dt<0, |
which obviously contradicts to the fact
| Q0(t)≤M0=max{Q0(0),βD∞}<ζ,t∈[0,T∗). |
Then we apply the relation
| D0(θ(t))≤Q0(t)β<ζβ<γ,t∈[0,T∗)where β=1−2η. |
As
| D0(θ(T∗))=limt→(T∗)−D0(θ(t))≤ζβ<γ, |
which contradicts to the situation that
| D0(θ(t))<γ,for all t∈[0,+∞). | (67) |
Then for any finite time
| ˙Q0(t)≤D(Ω)+2N0Ksinα−Kcosα1∑N0−1j=1ηjA(2N0,j)+1sinγγQ0(t), t∈[0,+∞). |
We will show the detailed proof of Step 1 in Lemma 4.3. Now we pick out any interval
Figure 5 shows the four possible relations between
| max0≤i≤k+1{ˉθi}=ˉθk+1,min0≤i≤k+1{θ_i}=θ_k+1fort∈Jl. |
Without loss of generality, we assume that
| θk+11≤θk+12≤⋯≤θk+1Nk+1,for t∈Jl. |
| ddtˉθk+1n(t)≤ΩM+Sk+1Ksinα+SkKcosαDk(θ(t))+Kcosα1ˉak+1n+1Nk+1∑i=n(ηi−nminj∈Nk+1i(k+1)j≤isin(θk+1j(t)−θk+1i(t))), | (68) |
where
| ddtˉθk+1Nk+1=Ωk+1Nk+1+Kcosα∑j∈Nk+1Nk+1(k+1)sin(θk+1j−θk+1Nk+1)+Kcosαk∑l=0∑j∈Nk+1Nk+1(l)sin(θlj−θk+1Nk+1)+Ksinαk+1∑l=0∑j∈Nk+1Nk+1(l)cos(θlj−θk+1Nk+1)≤ΩM+Sk+1Ksinα+Kcosα∑j∈Nk+1Nk+1(k+1)sin(θk+1j−θk+1Nk+1)⏟I11+Kcosαk∑l=0∑j∈Nk+1Nk+1(l)sin(θlj−θk+1Nk+1)⏟I12, | (69) |
where we use
| |k+1∑l=0∑j∈Nk+1Nk+1(l)cos(θlj−θk+1Nk+1)|≤k+1∑l=0Nl=Sk+1. |
| sin(θk+1j−θk+1Nk+1)≤0,for j∈Nk+1Nk+1(k+1). |
Then we immediately have
| I11=∑j∈Nk+1Nk+1(k+1)sin(θk+1j−θk+1Nk+1)≤minj∈Nk+1Nk+1(k+1)sin(θk+1j−θk+1Nk+1). | (70) |
If
| sin(θlj−θk+1Nk+1)≤0. |
If
| θiNi≥ˉθi≥θ_i≥θi1,0≤i≤d, |
we immediately obtain
| θk+1Nk+1≥ˉθk+1=max0≤i≤k+1{ˉθi}≥max0≤i≤k{ˉθi}≥min0≤i≤k{θ_i}≥min0≤i≤kmin1≤j≤Ni{θij}. | (71) |
Thus we use the property of
| sin(θlj−θk+1Nk+1)≤θlj−θk+1Nk+1≤θlj−min0≤i≤kmin1≤j≤Ni{θij}≤Dk(θ(t)). |
Therefore, combining the above discussion, we have
| I12=k∑l=0∑j∈Nk+1Nk+1(l)sin(θlj−θk+1Nk+1)≤SkDk(θ(t)). | (72) |
From (69), (70) and (72), it yields that (68) holds for
| ˙ˉθk+1n−1≤ΩM+ˉak+1n−1ˉak+1n−1+1Sk+1Ksinα+ˉak+1n−1ˉak+1n−1+1SkKcosαDk(θ(t))+Ksinα1ˉak+1n−1+1Sk+1+Kcosα1ˉak+1n−1+1η(Nk+1−n+2+Sk)Nk+1∑i=n(ηi−nminj∈Nk+1i(k+1)j≤isin(θk+1j−θk+1i))+Kcosα1ˉak+1n−1+1minj∈Nk+1n−1(k+1)j≤n−1sin(θk+1j−θk+1n−1)+Kcosα1ˉak+1n−1+1∑j∈Nk+1n−1(k+1)j>n−1sin(θk+1j−θk+1n−1)⏟I21+Kcosα1ˉak+1n−1+1k∑l=0∑j∈Nk+1n−1(l)sin(θlj−θk+1n−1)⏟I22. | (73) |
Next we do some estimates about the terms
| \begin{equation} \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j(t) - \theta^{k+1}_{i}(t))\right) \le \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}), \end{equation} | (74) |
where
(i) For the first case that
| \begin{equation} 0 \le \theta^{k+1}_{j}(t) - \theta^{k+1}_{n-1}(t) \le \theta^{k+1}_{N_{k+1}}(t) - \theta^{k+1}_{n-1}(t) \le \theta^{k+1}_{N_{k+1}}(t) - \theta^{k+1}_{\bar{k}_{n}}(t) \le \frac{\pi}{2}. \end{equation} | (75) |
Then it yieldst from (74), (75) and
| \begin{equation*} \begin{aligned} &\eta(N_{k+1} - n + 1) \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j(t) - \theta^{k+1}_{i}(t))\right) + \mathcal{I}_{21} \\ & \le \eta(N_{k+1} - n + 1) \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}) + \underset{j > n-1}{\sum\limits_{j\in \mathcal{N}_{n-1}^{k+1}(k+1)}}\sin (\theta^{k+1}_j - \theta^{k+1}_{n-1}) \\ & \le (N_{k+1} - n + 1) \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}) + (N_{k+1} - n + 1) \sin (\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{n-1}) \\ &\le 0. \end{aligned} \end{equation*} |
(ii) For the second case that
| \begin{equation} \eta > \frac{1}{\sin \gamma} \quad \mbox{and} \quad \sin(\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{\bar{k}_{n}}) > \sin \gamma, \end{equation} | (76) |
which yields
| \begin{equation*} \begin{aligned} &\eta(N_{k+1} - n + 1) \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j(t) - \theta^{k+1}_{i}(t))\right) + \mathcal{I}_{21} \\ & \le \eta(N_{k+1} - n + 1) \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}) + \underset{j > n-1}{\sum\limits_{j\in \mathcal{N}_{n-1}^{k+1}(k+1)}}\sin (\theta^{k+1}_j - \theta^{k+1}_{n-1}) \\ & \le -(N_{k+1} - n + 1) +(N_{k+1} - n + 1) = 0. \end{aligned} \end{equation*} |
Then, we combine the above arguments in (i) and (ii) to obtain
| \begin{equation} \eta(N_{k+1} - n + 1) \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j - \theta^{k+1}_{i})\right) + \mathcal{I}_{21} \le 0. \end{equation} | (77) |
(i) If
(ii) If
(a) For the case that
| 0 \le \theta^l_j - \theta^{k+1}_{n-1} \le \theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{n-1}\le \theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{\bar{k}_{n}} \le \frac{\pi}{2}. |
Thus from the above inequality and (74), we have
| \begin{equation*} \begin{aligned} &\eta \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j(t) - \theta^{k+1}_{i}(t))\right) + \sin (\theta^l_j - \theta^{k+1}_{n-1}) \\ &\le \eta \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}) + \sin (\theta^l_j - \theta^{k+1}_{n-1}) \\ &\le \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}) + \sin(\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{\bar{k}_{n}}) = 0. \end{aligned} \end{equation*} |
(b) For another case that
| \begin{equation*} \begin{aligned} &\eta \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j(t) - \theta^{k+1}_{i}(t))\right) + \sin (\theta^l_j - \theta^{k+1}_{n-1}) \\ &\le \eta \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}) + \sin (\theta^l_j - \theta^{k+1}_{n-1}) \\ &\le -1 + 1 = 0. \end{aligned} \end{equation*} |
Hence, combining the above arguments in (a) and (b), we obtain that
| \eta \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j(t) - \theta^{k+1}_{i}(t))\right) + \sin (\theta^l_j - \theta^{k+1}_{n-1}) \le 0. |
(iii) If
| \begin{equation} \sin (\theta^l_j - \theta^{k+1}_{n-1}) \le \sin (\theta^l_j - \theta^{k+1}_{N_{k+1}}) + \sin (\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{n-1}). \end{equation} | (78) |
For the second part on the right-hand side of above inequality (78), we apply the same analysis in (ii) to obtain
| \eta \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j - \theta^{k+1}_{i})\right) + \sin (\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{n-1}) \le 0. |
For the first part on the right-hand side of (78), the calculation is the same as (72), thus we have
| \begin{equation*} \sin (\theta^{l}_j - \theta^{k+1}_{N_{k+1}}) \le \theta^{l}_j - \theta^{k+1}_{N_{k+1}} \le \theta^{l}_j - \min\limits_{0 \le i \le k}\min\limits_{1 \le j \le N_i} \{\theta^i_j\} \le D_k(\theta(t)). \end{equation*} |
Therefore, we combine the above estimates to obtain
| \begin{equation} \begin{aligned} &\eta S_k \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j(t) - \theta^{k+1}_{i}(t))\right) + \mathcal{I}_{22} \\ & \le \eta S_k \sin(\theta^{k+1}_{\bar{k}_{n}} - \theta^{k+1}_{N_{k+1}}) + \sum\limits_{l = 0}^k \sum\limits_{j\in \mathcal{N}_{n-1}^{k+1}(l)} \sin (\theta^{l}_j - \theta^{k+1}_{n-1}) \\ & \le S_k D_k(\theta(t)). \end{aligned} \end{equation} | (79) |
Then from (73), (77), and (79), it yields that
| \begin{equation*} \begin{aligned} &\frac{d}{dt} \bar{\theta}^{k+1}_{n-1}\\ &\le \Omega_M + S_{k+1}K \sin\alpha + \frac{\bar{a}^{k+1}_{n-1}}{\bar{a}^{k+1}_{n-1}+1} S_kK \cos \alpha D_k (\theta(t)) + + K\cos\alpha \frac{1}{\bar{a}^{k+1}_{n-1} + 1} S_kD_k(\theta(t))\\ &+ K\cos \alpha \frac{1}{\bar{a}^{k+1}_{n-1} + 1} \eta \sum\limits_{i = n}^{N_{k+1}}\left( \eta^{i-n} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j - \theta^{k+1}_{i})\right)\\ &+K \cos\alpha \frac{1}{\bar{a}^{k+1}_{n-1}+1} \underset{j \le n-1}{\min\limits_{j\in \mathcal{N}_{n-1}^{k+1}(k+1)}} \sin (\theta^{k+1}_j - \theta^{k+1}_{n-1})\\ &\le \Omega_M + S_{k+1}K\sin\alpha + S_kK\cos\alpha D_k(\theta(t))\\ &+K\cos \alpha \frac{1}{\bar{a}^{k+1}_{n-1} + 1} \sum\limits_{i = n-1}^{N_{k+1}}\left( \eta^{i-(n-1)} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j - \theta^{k+1}_{i})\right). \end{aligned} \end{equation*} |
This means that the claim (68) does hold for
| \begin{equation*} \sum\limits_{i = 1}^{N_{k+1}}\left( \eta^{i-1} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j - \theta^{k+1}_{i})\right) \le \sin(\theta^{k+1}_1 - \theta^{k+1}_{N_{k+1}}). \end{equation*} |
From the notations in (22) and (23), it is known that
| \begin{equation*} \bar{\theta}_1^{k+1} = \bar{\theta}_{k+1}, \quad \underline{\theta}_{N_{k+1}}^{k+1} = \underline{\theta}_{k+1}. \end{equation*} |
Thus, we exploit the above inequality and set
| \begin{equation} \begin{aligned} &\frac{d}{dt} \bar{\theta}_{k+1} = \frac{d}{dt} \bar{\theta}^{k+1}_1\\ &\le \Omega_M + S_{k+1}K \sin\alpha + S_kK\cos\alpha D_k(\theta(t))\\ &+ K\cos \alpha \frac{1}{\bar{a}^{k+1}_{1} + 1} \sum\limits_{i = 1}^{N_{k+1}}\left( \eta^{i-1} \underset{j \le i}{\min\limits_{j\in \mathcal{N}_{i}^{k+1}(k+1)}} \sin (\theta^{k+1}_j - \theta^{k+1}_{i})\right) \\ &\le \Omega_M + S_{k+1}K \sin\alpha + S_kK\cos\alpha D_k(\theta(t)) + K\cos \alpha \frac{1}{\bar{a}^{k+1}_{1} + 1} \sin(\theta^{k+1}_1 - \theta^{k+1}_{N_{k+1}}). \end{aligned} \end{equation} | (80) |
We further apply the similar arguments in (80) to derive the differential inequality of
| \begin{equation} \frac{d}{dt} \underline{\theta}_{k+1} \ge \Omega_m - S_{k+1}K\sin \alpha - S_kK\cos\alpha D_k(\theta(t)) + K\cos \alpha \frac{1}{\bar{a}^{k+1}_{1} + 1} \sin (\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_1). \end{equation} | (81) |
Due to the monotone decreasing property of
| \sin (\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_1) \ge \frac{\sin \gamma}{\gamma}(\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_{1}). |
Then we combine the above inequality, (80), (81) and (21) to get
| \begin{equation*} \begin{aligned} \dot{Q}^{k+1}(t) & = \frac{d}{dt} (\bar{\theta}_{k+1} - \underline{\theta}_{k+1}) \\ &\le D(\Omega) + 2S_{k+1}K\sin\alpha + 2S_kK\cos\alpha D_k(\theta(t)) \\ &- K\cos \alpha \frac{2}{\bar{a}^{k+1}_{1} + 1} \sin (\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_1) \\ &\le D(\Omega) + 2S_{k+1}K\sin\alpha + 2S_kK\cos\alpha D_k(\theta(t)) \\ &- K\cos \alpha \frac{1}{\bar{a}^{k+1}_{1} + 1} \frac{\sin \gamma}{\gamma} (\theta^{k+1}_{N_{k+1}} - \theta^{k+1}_1)\\ &\le D(\Omega) + 2NK\sin \alpha + (2N+1)K \cos \alpha D_k(\theta(t)) \\ &- K\cos \alpha \frac{1}{\sum\limits_{j = 1}^{N-1}\eta^jA(2N,j) + 1} \frac{\sin \gamma}{\gamma}Q^{k+1}(t),\qquad t \in J_l, \end{aligned} \end{equation*} |
where we use the fact that
| \begin{equation} \begin{aligned} \dot{Q}^{k+1}(t) &\le D(\Omega) + 2NK\sin\alpha + (2N+1)K\cos\alpha D_k(\theta(t)) - \frac{K\cos\alpha}{c}Q^{k+1}(t). \end{aligned} \end{equation} | (82) |
As our analysis does not depend on the choice of
| [1] |
Analysis of the finite element heterogeneous multiscale method for quasilinear elliptic homogenization problems. Mathematics of Computation (2014) 83: 513-536. 
|
| [2] |
A multiscale finite element method for numerical homogenization. SIAM J. Multiscale Modeling and Simulation (2005) 4: 790-812. 
|
| [3] |
Homogenization and two-scale convergence. SIAM Journal on Mathematical Analysis (1992) 23: 1482-1518. 
|
| [4] |
Analysis of a two-scale, locally conservative subgrid upscaling for elliptic problems. SIAM J. Numer. Anal. (2004) 42: 576-598 (electronic). 
|
| [5] |
An "empirical interpolation" method: Application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathematique (2004) 339: 667-672. 
|
| [6] |
Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Computer Methods in Applied Mechanics and Engineering (2007) 197: 173-201. 
|
| [7] |
Discrete network approximation for highly-packed composites with irregular geometry in three dimensions. In Multiscale Methids in Science and Engineering, Spring (2005) 44: 21-57. 
|
| [8] | L. Berlyand, A. G. Kolpakov and A. Novikov, Introduction to the Network Approximation Method for Materials Modeling, Number 148. Cambridge University Press, 2013. |
| [9] |
Error of the network approximation for densely packed composites with irregular geometry. SIAM Journal on Mathematical Analysis (2002) 34: 385-408. 
|
| [10] |
Flux norm approach to finite dimensional homogenization approximations with non-separated scales and high contrast. Archive for Rational Mechanics and Analysis (2010) 198: 677-721. 
|
| [11] |
Multiscale empirical interpolation for solving nonlinear PDEs. Journal of Computational Physics (2014) 278: 204-220. 
|
| [12] |
Randomized oversampling for generalized multiscale finite element methods. Multiscale Model. Simul. (2016) 14: 482-501. http://arxiv.org/pdf/1409.7114.pdf. 
|
| [13] |
Homogenization of monotone operators. Nonlinear Analysis: Theory, Methods & Applications (1990) 14: 717-732. 
|
| [14] |
A new multiscale finite element method for high-contrast elliptic interface problems. Math. Comp. (2010) 79: 1915-1955. 
|
| [15] |
The staggered dg method is the limit of a hybridizable dg method. SIAM Journal on Numerical Analysis (2014) 52: 915-932. 
|
| [16] |
E. T. Chung, Y. Efendiev and W. T. Leung, An adaptive generalized multiscale discontinuous galerkin method (GMsDGM) for high-contrast flow problems arXiv preprint, arXiv: 1409.3474, 2014. doi: 10.1016/j.jcp.2014.05.007

|
| [17] |
Residual-driven online generalized multiscale finite element methods. J. Comput. Phys. (2015) 302: 176-190. 
|
| [18] |
An adaptive GMsFEM for high-contrast flow problems. Journal of Computational Physics (2014) 273: 54-76. 
|
| [19] |
P. G. Ciarlet,
The Finite Element Method for Elliptic Problems, volume 40. Siam, 2002. doi: 10.1137/1.9780898719208

|
| [20] |
Unified hybridization of discontinuous galerkin, mixed, and continuous galerkin methods for second order elliptic problems. SIAM Journal on Numerical Analysis (2009) 47: 1319-1365. 
|
| [21] |
Numerical calculation of equivalent grid block permeability tensors for heterogeneous porous media. Water Resour. Res. (1991) 27: 699-708. 
|
| [22] |
Heterogeneous multiscale methods. Comm. Math. Sci. (2003) 1: 87-132. 
|
| [23] |
Coarse-grid multiscale model reduction techniques for flows in heterogeneous media and applications. Numerical Analysis of Multiscale Problems, Lecture Notes in Computational Science and Engineering (2012) 83: 97-125. 
|
| [24] |
Generalized multiscale finite element methods. Journal of Computational Physics (2013) 251: 116-135. 
|
| [25] |
Robust multiscale iterative solvers for nonlinear flows in highly heterogeneous media. Numer. Math. Theory Methods Appl. (2012) 5: 359-383. 
|
| [26] |
Generalized multiscale finite element methods. Oversampling strategies. International Journal for Multiscale Computational Engineering, accepted (2014) 12: 465-484. 
|
| [27] |
Multiscale finite element methods for high-contrast problems using local spectral basis functions. Journal of Computational Physics (2011) 230: 937-955. 
|
| [28] | Y. Efendiev and T. Hou, Multiscale Finite Element Methods: Theory and Applications, Springer, 2009. |
| [29] |
Multiscale finite element methods for nonlinear problems and their applications. Comm. Math. Sci. (2004) 2: 553-589. 
|
| [30] |
Numerical homogenization and correctors for nonlinear elliptic equations. SIAM J. Appl. Math. (2004) 65: 43-68. 
|
| [31] |
A multiscale enrichment procedure for nonlinear monotone operators. ESAIM: Mathematical Modelling and Numerical Analysis (2014) 48: 475-491. 
|
| [32] |
A spectral multiscale hybridizable discontinuous Galerkin method for second order elliptic problems. Computer Methods in Applied Mechanics and Engineering (2015) 292: 243-256. 
|
| [33] |
Domain decomposition preconditioners for multiscale flows in high-contrast media. Multiscale Model. Simul. (2010) 8: 1461-1483. 
|
| [34] |
Domain decomposition preconditioners for multiscale flows in high contrast media: reduced dimension coarse spaces. Multiscale Model. Simul. (2010) 8: 1621-1644. 
|
| [35] | Sur l'approximation, par éléments finis d'ordre un, et la résolution, par pénalisation-dualité d'une classe de problémes de dirichlet non linéaires. Revue française d'automatique, informatique, recherche opérationnelle. Analyse numérique (1975) 9: 41-76. |
| [36] | P. Henning, Heterogeneous multiscale finite element methods for advection-diffusion and nonlinear elliptic multiscale problems, Münster: Univ. Münster, Mathematisch-Naturwissenschaftliche Fakultät, Fachbereich Mathematik und Informatik (Diss.). ii, (2011), page 63. |
| [37] |
Error control and adaptivity for heterogeneous multiscale approximations of nonlinear monotone problems. Discrete and Continuous Dynamical Systems-Serie S. Special Issue on Numerical Methods based on Homogenization and Two-Scale Convergence (2015) 8: 119-150. 
|
| [38] |
Multiscale phenomena: Green's functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Computer Methods in Applied Mechanics and Engineering (1995) 127: 387-401. 
|
| [39] |
The variational multiscale methoda paradigm for computational mechanics. Comput. Methods Appl. Mech. Engrg. (1998) 166: 3-24. 
|
| [40] |
Variational multiscale analysis: the fine-scale Green's function, projection, optimization, localization, and stabilized methods. SIAM Journal on Numerical Analysis (2007) 45: 539-557. 
|
| [41] |
V. V. Jikov, S. M. Kozlov and O. A. Oleinik,
Homogenization of Differential Operators and Integral Functionals, Springer-Verlag, Berlin, 1994. doi: 10.1007/978-3-642-84659-5

|
| [42] |
Reiterated homogenization of nonlinear monotone operators. Chinese Annals of Mathematics (2001) 22: 1-12. 
|
| [43] |
Analysis of the heterogeneous multiscale method for elliptic homogenization problems. Journal of the American Mathematical Society (2005) 18: 121-156. 
|
| [44] | Homogenization of nonlinear monotone operators beyond the periodic setting. Electr. J. of Diff. Eqns (2003) 36: 1-24. |
| [45] |
Polyharmonic homogenization, rough polyharmonic splines and sparse super-localization. ESAIM: Mathematical Modelling and Numerical Analysis (2014) 48: 517-552. 
|
| [46] |
A. A. Pankov,
G-convergence and Homogenization of Nonlinear Partial Differential Operators, volume 422. Mathematics and its Applications, 422. Kluwer Academic Publishers, Dordrecht, 1997. doi: 10.1007/978-94-015-8957-4

|
| [47] | G. Papanicolau, A. Bensoussan and J. -L. Lions, Asymptotic Analysis for Periodic Structures, Elsevier, 1978. |
| [48] |
Reduced-order multiscale modeling of nonlinear p-Laplacian flows in high-contrast media. Computational Geosciences (2015) 19: 921-932. 
|
| [49] |
Analysis of upscaling absolute permeability. Discrete and Continuous Dynamical Systems, Series B. (2002) 2: 185-204. 
|
| [50] |
E. Zeidler,
Nonlinear Functional Analysis and Its Applications: Ⅲ: Variational Methods and Optimization, Springer-Verlag, New York, 1985. doi: 10.1007/978-1-4612-5020-3

|
| 1. | Conor Carty, Young-Pil Choi, Chiara Cicolani, Cristina Pignotti, Asymptotic synchronization of Kuramoto oscillators with time delay and non-universal interaction, 2025, 76, 0044-2275, 10.1007/s00033-024-02406-5 |