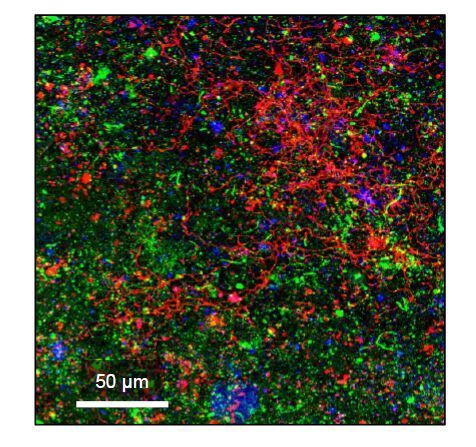
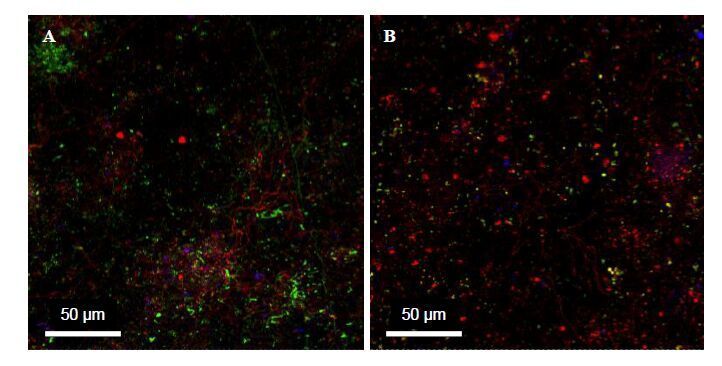
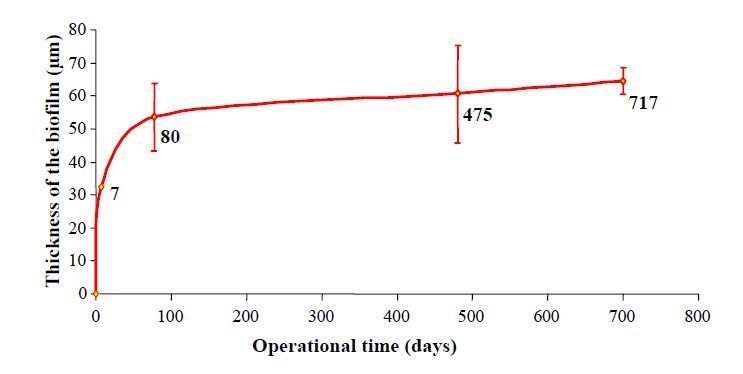
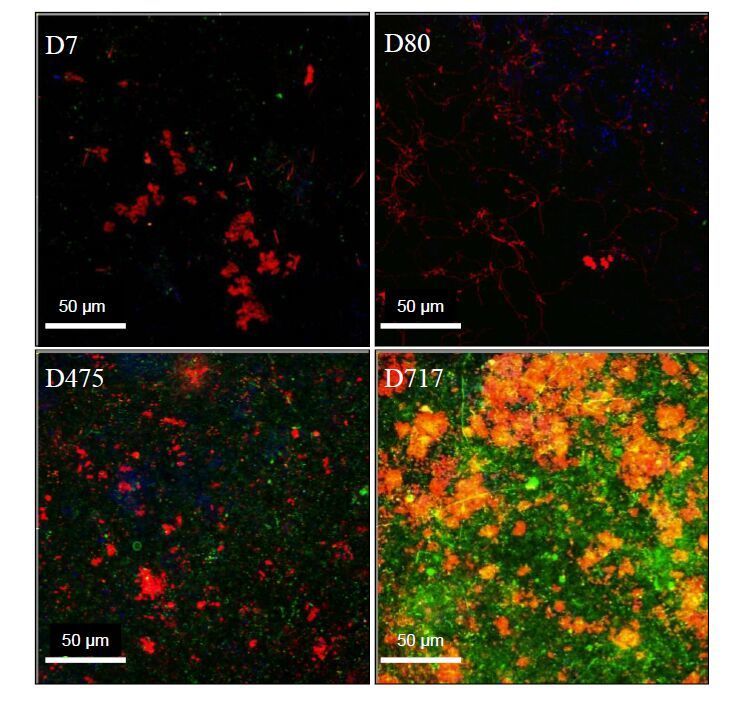
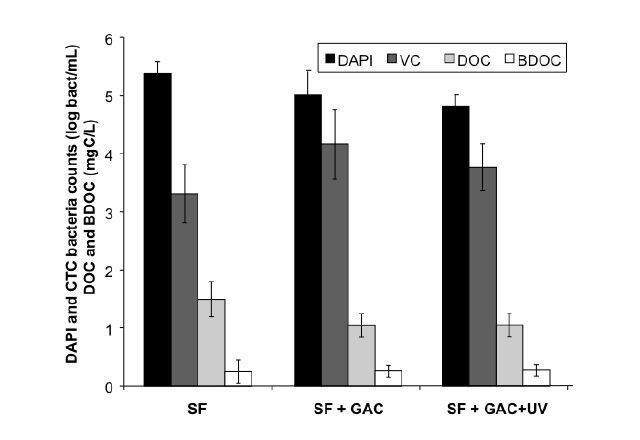
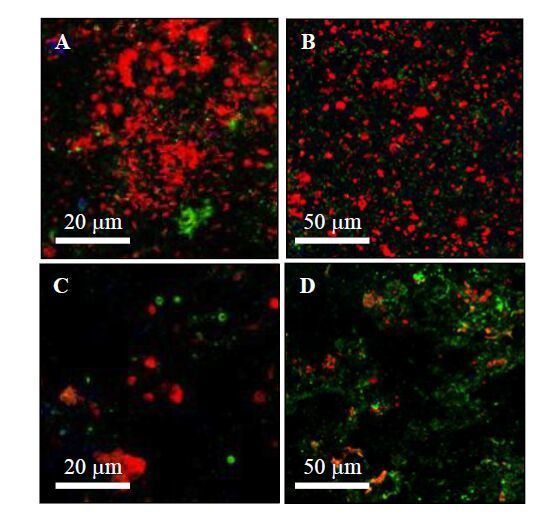
The biofilm state is the dominant microbial lifestyle in nature. A biofilm can be defined as cells organised as microcolonies embedded in an organic polymer matrix of microbial origin living at an interface between two different liquids, air and liquid, or solid and liquid. The biofilm matrix is made of extracellular polymeric substances, polysaccharides being considered as the major structural components of the matrix. Fluorescently labelled lectins have been widely used to stain microbial extracellular glycoconjugates in natural and artificial environments, and to study specific bacterial species or highly complex environments. Biofilm development at the membrane surface conducting to biofouling is one of the major problems encountered during drinking water production by filtration. Biofouling affects the durability and effectiveness of filtration membranes. Biofouling can be reduced by pretreatments in order to control two key parameters of water, the bioavailable organic matter concentration and the concentration of live bacteria. Nanofiltration (NF) is a high technology process particularly suited to the treatment of surface waters to produce drinking water that is highly sensitive to biofouling. The development of strategies for fouling prevention and control requires characterizing the fouling material composition and organisation before and after NF membrane cleaning. The aim of this review is to present basics of biofilm analyses after staining with fluorescently labelled lectins and to focus on the use of fluorescent lectins and confocal laser scanning microscopy to analyse NF membrane biofouling.
1.
Introduction
Complex dynamical networks (CDNs) refer to systems composed of interconnected nodes or entities, where the relationships between nodes are not trivial and often exhibit nontrivial patterns or structures, e.g., transport networks and 5G communication networks, social networks and Covid-19 epidemic networks. The study of complex networks has become a significant interdisciplinary field, drawing insights and methodologies from mathematics, computer science, physics, biology, sociology, and other disciplines [1,2,3]. Complex networks have found applications in diverse fields, including biology (e.g., gene regulatory networks, protein-protein interaction networks), social sciences (e.g., social networks, collaboration networks), transportation (road networks, air traffic networks), and information systems (e.g., the World Wide Web, citation networks); see papers [4,5,6]. Researchers in this field often use tools from graph theory, statistical physics, and machine learning to analyze and model the intricate structures and behaviors of complex systems (see refs. [7,8,9]).
A system composed of nonidentical networks may refer to a heterogeneous network. It consists of different types of nodes or entities with diverse characteristics, and the connections between them can vary in nature. Examples include multiplex networks, where nodes can have different types of relationships in different layers, and interdependent networks, where the failure of nodes in one network can affect nodes in another. The synchronization of nonidentical networks is a complex and interdisciplinary topic that spans various fields, including physics, engineering, and network science. In the context of nonidentical networks, achieving synchronization implies that nodes with different dynamics or characteristics become correlated or coordinated in their behavior. A common approach is to consider a drive network influencing the behavior of a response network. The drive network might have more influence or a different role compared to the response network, and achieving synchronization involves aligning the dynamics of the two networks. For the synchronization issues of nonidentical CDNs, the readers could refer to the literatures [10,11,12,13,14].
Anti-synchronization of networks involves achieving a specific type of coordination or correlation between nodes in a network. In synchronization, nodes in a network tend to evolve in a coordinated manner. In contrast, anti-synchronization is a state where the nodes exhibit an antiphase relationship, meaning that their dynamics are such that when one node is in a certain state, the other is in the opposite state; see refs. [15,16,17,18,19,20]. Adaptive anti-synchronization involves incorporating mechanisms that allow the network to adapt to changes in its internal or external conditions. These adaptive mechanisms can include adjusting parameters, coupling strengths, or introducing control signals based on feedback from the system or external measurements. Adaptive anti-synchronization has potential applications in various fields, including secure communication systems, networked control systems, and complex systems where maintaining a specific antiphase relationship between components is important, see refs. [18,19,20].
Stochastic network plays a significant role in the evolution of the network. These uncertainties can arise from various sources, including random events, probabilistic interactions, or dynamic processes. Analyzing and modeling stochastic networks is essential for understanding their behavior and making informed decisions in scenarios where uncertainty is inherent; see refs. [21,22,23,24,25,26]. Uncertain networks refer to network structures where there is uncertainty or variability in the connections between nodes, the strengths of these connections, or other properties of the network. This uncertainty can arise from various sources, including incomplete information, dynamic changes in network topology, or random fluctuations. Understanding and modeling uncertain networks are crucial for various applications, and researchers often employ different approaches to address the challenges associated with uncertainty. Researchers have developed various approaches and methodologies to address these challenges; please see publications [27,28,29,30,31,32].
Discrete space or discrete time networks, as opposed to continuous space or continuous time networks, have distinct advantages in various applications. For example, discrete time systems are often easier to synchronize and coordinate. Events or updates can be synchronized at specific time intervals, simplifying the management of network-wide activities. Discrete time models are often simpler to develop and analyze. In signal processing applications, discrete time signals are often preferred for digital signal processing. Discrete time allows for the application of powerful digital filtering techniques and efficient algorithms [33]. On the other hand, discretizing space simplifies computations, making it more computationally efficient, especially for systems with a large number of nodes or complex interactions. Nodes in the network are located at specific points in space, simplifying the description of their positions and connections. In certain applications, discretizing space allows for more efficient utilization of resources [34]. To the authors' knowledge, despite numerous reports having focused on the research of discrete-time complex networks [9,15,35,36,37] or continuous-time complex networks with reaction diffusions [5,38,39,40,41,42], the studies of the discrete networks in both time and space are very few; please see ref. [43]. Specifically, almost no paper involves the adaptive anti-synchronization of time-space discrete drive-response nonidentical CDNs.
Based on the above discussion, the primary purpose of this paper is to study the adaptive anti-synchronization problems of space-time discrete heterogeneous stochastic multilayer CDNs with multiple delays. To achieve this, a space-time discrete Lyapunov-Krasovskii functional and the linear matrix inequality (LMI) method are used to design an adaptive updated law for unknown parameter and feedback controller that incorporates boundary information. In particular, the adaptive parameter in the response networks can achieve the accuracy identification to the unknown information in the drive networks. This document presents key contributions that are distinct from existing works. These contributions are briefly summarized.
1) This paper differs from the continuous time networks in [6,7,8,10,11,12,13,14,44,45,46] or reaction-diffusion networks in [5,38,39,40,41,42]; a CDNs in time and space is modeled by a discrete way.
2) In contrast to the feedback controller in the networks presented in previous reports [9,15,35,36,37], a feedback controller in the boundary is built to discrete space-time CDNs, which is a more effective and low-cost control technique for the networks.
3) In contrast to previous work on the incomplete synchronization to heterogeneous CDNs, e.g., quasi-synchronization [10,11,12,13,14], the present paper addresses the problem of anti-synchronization to heterogeneous discrete space-time CDNs, which belongs to the category of the complete synchronization.
4) In order to fill the gap that no report had been published for the adaptive control of discrete space-time CDNs until now, this paper considers the uncertainty in the model of CDNs and designs an adaptive updated rule. The adaptive parameter in the response networks can achieve the accuracy identification to the uncertain factor.
This article has the following structure. In Section 2, the drive-response discrete space-time heterogeneous CDNs with multiple delays have been established. The adaptive updated law of the unknown parameter and adaptive anti-synchronization of the drive-response heterogeneous CDNs are discussed in Section 3. In Section 4, the theoretical results are confirmed by a numerical example. A brief summary is given in Section 5.
Notations: Denote R0=[0,+∞), Z0={0,1,2,…}; Z+=Z0∖{0}. We use symbol ⊗ to denote the Kronecker product. Define ‖A‖∞=max1≤i≤m,1≤j≤n|aij| for A=(aij)m×n∈Rm×n. For any sets I,J, IJ stands for set I∩J. I represents some suitable dimensional identical matrix. Also, denote
where z=z[δ]k:Z2→RM, (δ,k)∈Z2, ℏ>0.
2.
Digital scheme of space-time CDNs
In the following model, F,σ∈RM are the activation and noise functions in sequence; Γl∈RM×M and Gl=(Gij,l)m×m represent the inner and outer linking matrix in sequence l=1,2,…,p, i,j=1,2,…,m; w∈R denotes the Brownian motion on certain probability space. This paper discusses the general CDNs with reaction diffusions, unknown dynamics, and multiple delays, which are constructed by
where (x,t)∈(0,L)×R0 for some L>0, or in a discrete form
where (δ,k)∈(0,L)Z×Z0, L≥2 is some integer; wi=(wi1,wi2,…,wiM)T∈RM stands for the state of the ith transportation node; γk is adaptive; w[δ]i,k and wk are the simplified forms of wi(δℏ,kh) and w(kh) in sequence i=1,2,…,m; Δhwk=wk+1−wk√h; ℏ and h denote the space and time steps' length, respectively; A∈RM×M, C is nonsingular M-order square matrix; cl≥0, ˆσ(⋅)=√hσ(⋅), τl∈[1,+∞)Z is the time delay, l=1,2,…,p; ζ∈RM is a corrective vector. Furthermore, CDNs (2.2) possesses the following initial and controlling boundary values:
where τ∞:=maxδ=1,2,…,pτl<∞, ξi denotes the boundary input, i=1,2,…,m.
Remark 2.1. CDNs (2.2) is the discrete form of CDNs (2.1) by using the exponential Euler difference (see [33]) for variable t and the central finite difference (see [47,48]) for variable x.
Remark 2.2. It can be seen from the boundary control described above that, in contrast to the feedback controls (FCs) that are designed within the networks, the boundary control described in this study is only active at the boundary point L−1. This control method is a more effective and low-cost technique than the FCs described in the paper [48], which occurs for all values of δ∈[1,L−1]Z.
Let the matrix G⋅, and the activation and noise functions F,σ meet the following assumptions.
(c1) Gl=(Gij,l)m×m is irreducible and Gij,l=Gji,l≥0 for i≠j, Gii,l=−∑mj=1,j≠iGij,l, i,j=1,2,…,m, l=1,2,…,p.
(c2) F(⋅) and σ(⋅) are odd, and there exist positive constant F0, and M-order matrices Lf,Lσ≥0 such that
where z,y∈RM.
Let us consider the drive CDNs below:
where (δ,k)∈(0,L)Z×Z0; γ is an unknown parameter. The initial and boundary values are described by
CDNs (2.2) can be regarded as the response networks of the drive networks (2.3). Let the anti-synchronous error between the drive-response networks (2.3) and (2.2) be represented by ei=wi+z for i=1,2,…,m. From CDNs (2.3) and (2.2), it follows
where i=1,2,…,m, or in a compact form
where (δ,k)∈(0,L)Z×Z0, ˉe=(eT1,…,eTm)T, C∗=(eCh−I)C−1,
In the model above, (A)⊗m:=Im⊗A and (A)⊗B:=B⊗A for suitable dimensional matrices A,B and the m-order identical matrix Im.
According to the initial and boundary values in CDNs (2.2) and (2.3), the error system (2.4) possesses the initial and controlling boundary conditions
where φ=(ϕ1+ψ,…,ϕm+ψ)T, ˉξ=(ξ1,…,ξm)T.
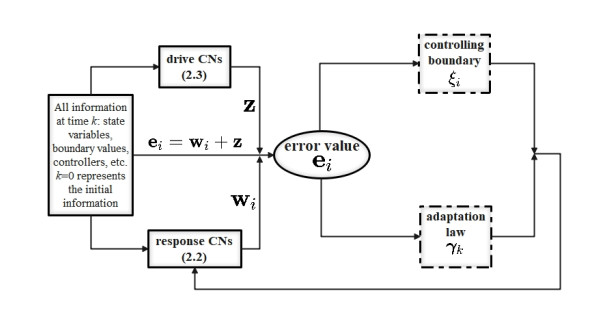
The framework of the drive-response-error CDNs (2.2)–(2.4) is figured as that in Figure 1.
Remark 2.3. In [43], Zhang and Li discussed a class of discrete space-time CDNs and the issue of switching clusters' synchronization had been addressed perfectly in this article. Compared with the work above, this paper possesses some merits below. First, CDNs (2.2) of this paper is involved with the stochastic disturbances. Second, the drive-response networks (2.2) and (2.3) are heterogeneous, but the CDNs in [43] were homogeneous. Finally, it exists the uncertainty in CDNs (2.2), which extensively increases the researching difficulty and the applicable categories of the networks.
Remark 2.4. Literatures [44,45,46] used adaptive methods to identify and estimate unknown parameters of continuous time transportation networks without spatial variables. However, identifying uncertain parameters in spatiotemporal discrete heterogeneous networks presents two challenges that must be overcome. In the first, the introduction of spatial diffusion will complicate the research of this topic. Additionally, based on the applicant's recent research experience in [43], the calculation of the time discrete Lyapunov function is more complex than that of the continuous time Lyapunov function. You can see this point in Eq (3.6), where the term £k exists, but remember that there is no £k in the continuous case.
Definition 2.1 ([49]). The drive-response networks (2.3) and (2.2) are said to be mean squared asymptotic anti-synchronization (MSAAS) via boundary control ˉξk in (2.5) if
Remark 2.5. In the existing publications, papers [9,15,35,36,37] investigated single discrete-time CDNs and reports [5,38,39,40,41,42] considered the continuous-time CDNs with reaction diffusions. The drive-response CDNs (2.3) and (2.2) are distinct with them by discussing both time and space discretizations in the model of CDNs. Although the time-space discrete CDNs has been considered in our work in literature [43], it has some clear distinctions. The biggest difference is that the drive-response CDNs in literature [43] are identical, but drive-response CDNs (2.3) and (2.2) are nonidentical. Besides, this paper considers MSAAS with adaptive updated rule, which is different from the synchronization in literature [43].
Throughout this article, suppose that
where s∈[−τ∞,0]Z. By right of initial values (2.5), it has
In view of Corollary 3.1 of [50], Subsection 2.3, and Inequalities 3.2.1 and 3.2.3 of [51], one has the following lemma.
Lemma 2.1. ([50,51]). The inequalities below are valid for m-dimensional vector z and m-order positive definitive matrix G.
(i) L−1∑δ=0Δℏz[δ]TGΔℏz[δ]≤μLℏ2L∑δ=0z[δ]TGz[δ] when z0=0, where μL=4cos2π2L+1.
(ii) L−1∑δ=1Δℏz[δ]TGΔℏz[δ]≥χLℏ2L∑δ=1z[δ]TGz[δ]−1ℏ2(z1+zL)TG(z1+zL), where χL=4sin2π2L.
(iii) L−1∑δ=1Δℏz[δ]TGΔℏz[δ]+1ℏ2[z1+(−1)LzL]TG[z1+(−1)LzL]≤4−χLℏ2L∑δ=1z[δ]TGz[δ].
3.
Adaptive anti-synchronization with parameter identification
This section constructs the space-time discrete stochastic Lyapunov-Krasovskii functional to the error CDNs (2.4). Subsequently, an adaptive update law of uncertain parameter γ is designed. Further, boundary input and controlling gain are designed to perform mean squared asymptotic anti-synchronization of the drive-response networks (2.3) and (2.2), i.e., some asymptotical stability criterions in mean squared sense are established to the error CDNs (2.4). Meanwhile, it achieves the identification of the uncertain parameter.
In accordance with the error CDNs (2.4), a space-time discrete Lyapunov-Krasovskii functional candidate is constructed by
where
where P>0 is an M-order matrix, and d2,d3,α are some positive constants.
The chief research scheme of this paper can be summarized in the flowchart described by Figure 2.
3.1. Adaptive updated law
Set η[δ]k=ˉe[δ]k+1−ˉe[δ]k, ∀(δ,k)∈(0,L)Z×Z0. We design the adaptive updated law for unknown parameter γk as below:
where k∈Z0. Hereby, Q is a positive definitive M-order matrix, which will be calculated by some LMIs later. Remarkably, it follows from (c2) that
where u,v∈RM,w∈RmM,H∈RM×M. So, it implies
for all k∈Z0. Suppose that
(c3) Constants α,α∗ satisfy 0<2α(mM)3F20Lmax{‖PC∗‖2∞,‖QC∗‖2∞}<α∗.
According to (3.3) and assumption (c3), it yields
Remark 3.1. In the designation of adaptive updated law (3.1), it is dependent of the value of η[δ]k=ˉe[δ]k+1−ˉe[δ]k, namely, the value of ˉe at time k+1. If the current time is k, by the iterative relationship (3.1), the states' values of the response network (2.2) at time k+1 can be determined by the whole relative values at time k or before the time k, and so are the states' values of the response network (2.3).
Remark 3.2. In the construction of adaptation rules for continuous CDNs ([44,45,46]), it was observed that all of them were not involved with the term η[δ]k. In other words, it was ascertained that the second term on the righthand side of Υk in (3.1) does not exist. Why? The rationale will be expounded in the ensuing discourse on heterogeneous anti-synchronization. The calculations of inequalities (3.3) and (3.4) demonstrate that the presence of term η[δ]k greatly increases the complexity and difficulty of the current research.
Remark 3.3. In the studies of nonidentical CDNs [10,11,12,13,14], nobody designs the adaptive updated rule such as Eq (3.1), so the concept of quasi-synchronization was proposed and researched. In this article, an adaptive parameter with updated rule Eq (3.1) has been designed to perform the complete MSAAS for the drive-response CDNs (2.3) and (2.2).
3.2. Heterogeneous anti-synchronization with uncertain recognition
The boundary controlling input is designed by
where Π∈RM×M represents the controlling gain.
Theorem 3.1. Let assumptions (c1)–(c3) hold, det(A)≠0, det(C)≠0, ε∈(0,1), and the updated law for adaptive parameter γ and the boundary controlling input be designed as those in (3.1) and (3.5), respectively. Suppose further that
(c4) Eγ20<∞ and |γ|≤γ∗, where γ∗ is a known constant.
(c5) There exist matrices P>0, Q>0, R>0, Φ>0, ℧>0 and positive numbers α∗,d1,d2,d3 so that
where
Then, the response CDNs (2.2) asymptotically inversely synchronizes the drive CDNs (2.3) in the mean squared sense, and E|γk−γ|2→0 as k→∞. Moreover, the controlling gain Π=[PC∗A]−1Φ.
Proof. Taking α fulfills assumption (c3). Based on the Lyapunov-Krasovskii functional as before and the error networks (2.4), it attains
where
Via the discrete formula of integration by parts and boundary values in (2.5), it computes
Define ˆˉe[δ]k=ˉe[L]k−ˉe[δ]k, ∀(δ,k)∈[0,L]Z×Z0. It should be noted that
Together with the discrete Wirtinger's inequalities in item (ii) of Lemma 2.1, it results in
which indicates
According to the error CDNs (2.4), it gets
where (δ,k)∈(0,L)×Z0. It induces from (3.10) that
According to the elementary inequality in Lemma 1.13 of [52], i.e., 2XTY≤εXTX+1εYTY for any X,Y∈RmM and ε>0, it generates
and, similarly,
From (3.11), we have
where k∈Z0. In (3.14), note that Δhwk is independent of ˉe[⋅]s for all s≤k, and we use the fact of E(Δhw⋅)2=1.
In terms of assumption (c2), it deduces
where k∈Z0. Based on the definition of V2,k, we have
where k∈Z0.
From Lemma 2.1, we have
In view of (3.8) and by boundary input (3.5), it has
Set
On the grounds of (3.4), (3.6)–(3.20), and assumption (c5), it induces ˜Ω<0 and
where
for any (δ,k)∈(0,L)Z×Z0. Obviously,
which implies
as k\rightarrow \infty. Hereby, \lambda_\Omega^+ denotes the maximum eigenvalue of \Omega . According to boundary information in (3.5), it exists constant M_1 > 0 so that
Additionally,
Together with (3.21) and (3.22), it causes
Videlicet, the error CDNs (2.4) achieves global asymptotic stability in the mean squared sense. To wit, the response CDNs (2.2) asymptotically inversely synchronizes the drive CDNs (2.3). Based on the error CDNs (2.4) and the same discussions in [52, Theorem 4.20], it directly gains {\boldsymbol\gamma}_k\rightarrow \gamma, as k\rightarrow \infty. This achieves the proof. □
3.3. Homogeneous anti-synchronization
If {\boldsymbol\gamma}_k\equiv\gamma for all k\in\mathbb{Z}_0 , then the error CDNs (2.4) is transformed into
where (\delta, k)\in(0, \mathcal{L})_{\mathbb{Z}}\times\mathbb{Z}_0.
By a similar proof to Theorem 3.1, we can gain the corollary below.
Corollary 3.1. Let assumptions (c_1) – (c_3) hold, \mathrm{det}(A)\neq0 , \mathrm{det}(C)\neq0 , \varepsilon\in(0, 1) , and the boundary input be designed as that in (3.5). Assume that
( c_6 ) {\boldsymbol\gamma}_k\equiv\gamma for all k\in\mathbb{Z}_0 .
( c_7 ) Assumption ( c_5 ) is valid with \alpha_* = 0 .
Furthermore, the controlling gain is designed as before. Then, the response CDNs (2.2) asymptotically anti-synchronizes the drive CDNs (2.3) in the mean squared sense.
According to Theorem 3.1, a realizable algorithm for adaptive anti-synchronization of the drive-response CDNs (2.2) and (2.3) is designed as follows.
Remark 3.4. Discrete-time CDNs have been the focus of the authors' previous works [9,15,35,36,37]. This article deals with discrete-time CDNs with discrete spatial diffusion. The associated calculations, such as the Lyapunov-Krasovskii functional, are more complex than the case of a single time-variable. In this paper, we present a boundary feedback controller for discrete-time and spatial CDNs, whereas previous reports [9,15,35,36,37] have used a traditional feedback controller for CDNs. Previous studies [9,15,35,36,37] have focused on homogeneous CDNs, whereas this article examines heterogeneous CDNs.
Remark 3.5. Previous publications [10,11,12,13,14] have examined continuous-time heterogeneous networks. In contrast, this article addresses the following aspects: 1) The paper considers the issue of discrete space transportation networks, taking into account their heterogeneity. 2) It achieves mean squared asymptotic anti-synchronization for the networks, which differs significantly from the quasi-synchronization discussed in previous publications [10,11,12,13,14]. 3) The response networks in these publications [10,11,12,13,14] have a predetermined heterogeneous coefficient. We have designed an adaptive parameter in the response networks that tends to drive-response CDNs homogeneously by continuously adjusting it according to the updated law. At this moment, the adaptive parameter in the response CDNs can perfectly identify the unknown parameter in the drive CDNs according to the updated law.
4.
Experiments
Supposing the drive CDNs are expressed by
where \mathbf{z} = \left[\begin{array}{c} \mathbf{z}_1 \\ \mathbf{z}_2 \\ \end{array} \right], C = -\left[\begin{array}{cc} 8 & 0 \\ 8 & 24 \\ \end{array} \right], h = 0.01, \hbar = 0.25 , \gamma = 0.1 . The boundary values of the drive CDNs (4.1) are given by \Delta_{\hbar} \mathbf{z}_{k}^{[0]} = \Delta_{\hbar} \mathbf{z}_{k}^{[5]} = 0, \forall k\in\mathbb{Z}_0. The response CDNs of the drive CDNs (4.1) are described as
where (\delta, k)\in(0, 6)_{\mathbb{Z}}\times\mathbb{Z}_0, \tilde{\gamma}_0 = 0 ,
The boundary values of the response CDNs (4.2) are given by \Delta_{\delta} \mathbf{w}_{1, k}^{[0]} = \Delta_{\delta} \mathbf{w}_{2, k}^{[0]} = 0 , \Delta_{\delta} \mathbf{w}_{1, k}^{[5]} = \xi_{1, k} , \Delta_{\delta} \mathbf{w}_{2, k}^{[5]} = \xi_{2, k} , \forall k\in\mathbb{Z}_0.
According to the information above and Algorithm 1, a flow diagram of achieving the adaptive anti-synchronization of the drive-response CDNs (4.1) and (4.2) is drawn in Figure 3.
Obviously, ( c_1 )–( c_2 ) in Theorem 3.1 hold. Taking \varepsilon = 0.5 , \gamma_* = 0.2 and computing the LMIs in Theorem 3.1, the LMIs in ( c_5 ) are valid for \alpha_* = 1.5763 , d_1 = 29.0039 , d_2 = 9.1156 , d_3 = 10.6818 ,
Further, taking \alpha in ( c_3 ) small enough, it is easy to ensure that ( c_3 ) is satisfied.
So, the gain and controller are determined as
where \mathbf{e}_{11, k}^{[\delta]} = \mathbf{w}_{11, k}^{[\delta]}+ \mathbf{z}_{1, k}^{[\delta]} , \mathbf{e}_{12, k}^{[\delta]} = \mathbf{w}_{12, k}^{[\delta]}+ \mathbf{z}_{2, k}^{[\delta]} , \mathbf{e}_{21, k}^{[\delta]} = \mathbf{w}_{21, k}^{[\delta]}+ \mathbf{z}_{1, k}^{[\delta]} , \mathbf{e}_{22, k}^{[\delta]} = \mathbf{w}_{22, k}^{[\delta]}+ \mathbf{z}_{2, k}^{[\delta]} , (\delta, k)\in(0, 6)_{\mathbb{Z}}\times\mathbb{Z}_0. The update law for the adaptive parameter \tilde{\gamma}_k is outlined as
where the initial value is \tilde{\gamma}_{0} = 0 , k\in\mathbb{Z}_+ . Apparently, ( c_4 ) holds. In sum, all assumptions in Theorem 3.1 are valid. By Theorem 3.1, the response CDNs (4.2) asymptotically inversely synchronizes the drive CDNs (4.1); please see Figures 4–19.
In Figures 4–11, we picture the 3-dimensional asymptotical anti-synchronization of the drive-response CDNs (4.1) and (4.2). Specifically, by taking the space variable \delta = 3 , we also show the trajectories of the errors between the drive-response CDNs (4.1) and (4.2) in the 2-dimensional space; see Figures 12–19. Finally, based upon the update law (4.3) for adaptive parameter \tilde{\gamma}_k , we give a variational curve in Figure 20, which tends to \gamma = 0.1 over time.
5.
Conclusions
In the first place, by using mixed approaches of Euler time-difference and finite central space-difference, we consider a delayed multivariable discrete stochastic transportation networks with unknown parameter. In the second place, based on the theory of matrix, the compact drive-response nonidentical stochastic transportation networks with the adaptive parameter are built. Via the method of the Lyapunov-Krasovskii functional and the designation of the update law for the unknown parameter in the response networks, the article performs the mean squared asymptotic anti-synchronization for the drive-response nonidentical stochastic transportation networks. Besides, by designing an adaptive parameter updated rule, the adaptive parameter in the response networks can achieve the accuracy identification to the unknown information in the drive networks. The current work establishes a theory of the problem of asymptotic anti-synchronization for the drive-response nonidentical stochastic transportation networks under the framework of space-time discrete schemes.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by the Scientific Research Funds of Educational Department of Yunnan Province under Grant No. 2024J1169.
Conflict of interest
The authors declare there is no conflicts of interest.









 DownLoad:
DownLoad: