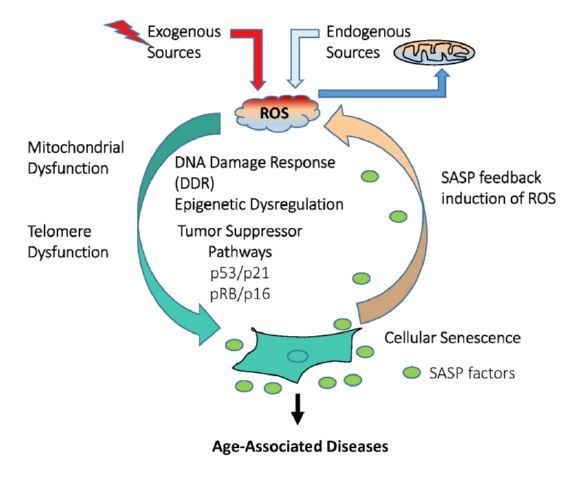
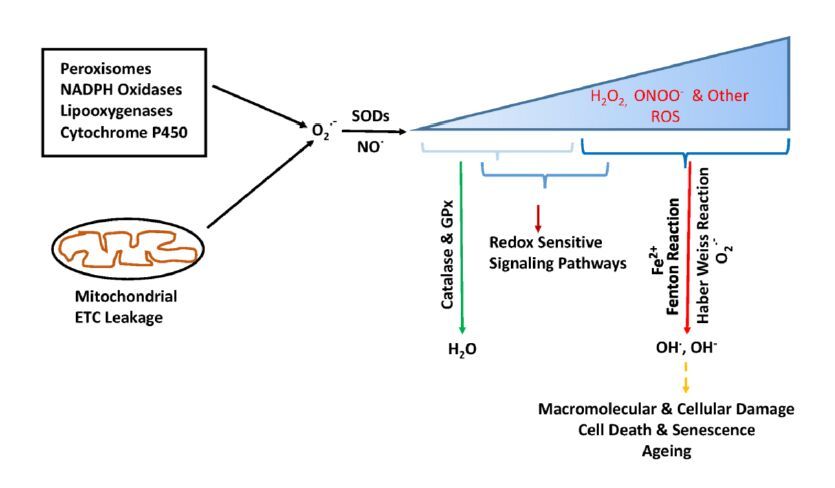
Almost a half century ago, the free radical theory of ageing proposed that the reactive oxygen species (ROS) is a key component which contributes to the pathophysiology of ageing in mammalian cells. Over the years, numerous studies have documented the role of oxidative stress caused by ROS in the ageing process of higher organisms. In particular, several age-associated disease models suggest that ROS and oxidative stress modulate the incidence of age-related pathologies, and that it can strongly influence the ageing process and possibly lifespan. The exact mechanism of ROS and oxidative stress-induced age-related pathologies is not yet very clear. Damage to biological macromolecules caused by ROS is thought to result in many age-related chronic diseases. At the cellular level, increased ROS leads to cellular senescence among other cellular fates including apoptosis, necrosis and autophagy. Cellular senescence is a stable growth arrest phase of cells characterized by the secretion of senescence-associated secretory phenotype (SASP) factors. Recent evidence suggests that cellular senescence via its growth arrest phenotype and SASP factors is a strong contributing factor in the development of age-associated diseases. In addition, we suggest that SASP factors play an important role in the maintenance of age-associated pathologies via a positive feedback mechanism. This review aims to provide an overview of ROS mechanics and its possible role in the ageing process via induction of cellular senescence.
1.
Introduction
HIV (Human immunodeficiency Virus), the causative agent of AIDS (acquired immune deficiency syndrome), infects nearly 40 million people worldwide [1] and represents one of the highest overall global burdens of disease [2]. HIV is a virus that attacks the immune system. Over time, HIV can lead to a weakened immune systems, making individuals more susceptible to opportunistic infections and certain cancers [3].
HIV predominantly infects immune system cells, specifically targeting CD4+T cellls (a type of white blood cell) that play pivotal roles in orchestrating and executing the body's defense mechanisms against infections. Once the virus enters immune system cells, the viral RNA is reversely transcribed into DNA by the enzyme reverse transcriptase. When the host cell becomes activated, it begins to transcribe and translate the proviral DNA, producing new viral RNA and proteins. These viral components are assembled into new virus particles. The newly formed virus particles bud from the host cell's membrane, acquiring an outer envelope derived from the host cell membrane [4]. After HIV infects host cells, in addition to immediately starting to replicate and destroy CD4+T lymphocytes of the immune system, it can also enter the latent state of the cells. This latent state allows the virus to hide within host cells and avoid detection by the immune system, making HIV infection a chronic, sustainable disease [5]. Given the intricate nature of HIV transmission within the human body, experimental study of the entire process poses significant challenges. In contrast, the development of viral dynamics models stands as a valuable and rigorous approach for investigating the virus's transmission processes and pathogenic mechanisms within the host.
Numerous studies based on virus models have been conducted to investigate the interactions between virus and host [6,7,8]. With the development of modern medicine and scientific research, researchers have completed the model from adding the virus, infected cells and susceptible cells [9,10], to gradually put more infection patterns processes into consideration [11,12,13,14], so that the model can accurately describe the dynamic process of HIV transmission in the body. The diversity of these models, as well as the corresponding theories and experiments, have made significant progress. Perelson et al. [15] proposed an ODE model of cell-free viral spread of human immunodeficiency virus in a well-mixed compartment. Using this model, they explain the characteristics of virus spread under different steady states. Müller et al. [16] also proposed a model incorporating the activation of latently infected cells. They concluded through model predictions that the residual virus after long-term suppressive treatment is likely to originate from latently infected cells. Wang et al. [17] investigated a class of HIV-1 infection models with different infection rates and latently infected cells, and obtained sufficient conditions for the global stability of both the infection-free and chronic-infection equilibria of the model.
These investigations are based on a system of ordinary differential equations and intuitively describe the trend of viral infection. However, the activities of viruses and cells within the human body are subject to changes over both time and space. Further consideration of spatial factors in modeling can provide further insight into the viral pathogenesis. Based on the spatial model, Wang et al. [18] proposed a virus infection model with multiple target cells and discussed the threshold dynamics through semigroup theory. Wang et al. [19] introduced a mathematical model to simulate hepatitis B virus infection, incorporating spatial dependence. Considering the free movement of viruses, they introduce the random mobility for viruses.
In addition, we note that the virus infection model in [19] is investigated under conditions of a well-mixed or homogeneous environment. These studies ignore the heterogeneous mobility of cells [20] and the differences in the diffusion ability of virus particle in different environments [21,22,23]. Under the assumption of homogeneity, there is a possibility of either underestimating or overestimating critical factors in viral pathogenesis. Wu et al. [24] argued that the use of the spatially averaged parameters may underestimate HIV infection, and explored the effect of two time delays (latency caused by latently infected cells) on the HIV infection process in a heterogeneous environment. Based on the research of [19], Wang et al. [25] further considered an virus dynamics model with spatial heterogeneity under homogeneous boundary conditions. This extension involved allowing all parameters to exhibit spatial dependence, except for the diffusion coefficient. We note that few previous models have simultaneously considered spatial heterogeneity and infection modes of both target cells. There is a lack of theoretical justification for the dynamic behavior of the model when considering susceptible and infected cell mobility.
The purpose of HIV modeling research is to inhibit the transmission and diffusion of HIV within the human body, and optimal control strategy is an effective method to explore and simulate the changes in the transmission of the virus under certain control. This method is often used to explore the optimal action time of drugs and prevent the spread of diseases. In fact, optimal control theory has been used to study HIV treatment both at the cellular level [26,27] and at the level of individual patients [28,29]. However, existing mathematical models have not been used to study the effects of multiple drug combination treatments and optimal control on HIV infection.
Based on the considerations mentioned above, we established an HIV model incorporating spatial heterogeneity and conducted optimization control studies. In the next section (Section 2), we will propose a spatially heterogeneous model and explain the parameters in the model. Given that the dynamical behavior of the model is crucial for investigating optimal control, we first conducted a viral dynamics analysis of the proposed model in Section 3. We discuss the threshold dynamics of the basic reproduction number R0 and demonstrate the uniform persistence of the solution in Section 4. In Section 5, We further understand the impact of pharmacological interventions on the dynamics of HIV infection and investigate key strategies for controlling infection. In the final section (Section 6), we obtained the optimal solution of the control system through numerical simulations and presented the spatiotemporal variations of the control. Some conclusions and discussions are presented.
2.
Model formulation
Mathematical models are useful to interpret the different profiles, providing quantitative information about the kinetics of virus replication. In a recent survey, Hill et al. [30] summarized the contributions that viral dynamic models have made to understand the pathophysiology of HIV infection and to design effective therapies and proposing basic viral dynamics model:
which tracks levels of the virus V and the CD4+T cells that it infects. Uninfected target cells T are assumed to enter the system at a constant rate λ, and die with rate constant μT (equivalent to an average lifespan of 1/μT). Infected cells I are produced with a rate proportion to levels of both virus and target cells and the infectivity parameter β. Infected cells produce free virus at a rate k and die with rate μI. Free virus is cleared at rate c.
With further research on the pathogenesis of HIV, more complicated facets of infection can be inferred from looking at viral load decay curves under different types of treatments. This decay can be explained using mathematical models, and in general the multiple phases are believed to reflect distinct populations of infected cells [31,32]. Cardozo et al. [33] modeled proviral integration in short- and long-lived infected cells, which suggests that "HIV infects two different cell subsets, one of which has a fast rate and the other a slow fusion rate". Based on the work of Hill [30] and Cardozo [33], Wang [10] considered the more general situation when the infectivity parameters of two target cells are different and then proposed the following equations to describe an HIV infection model containing two different cell subsets:
Two separate populations of target cells are hypothesized to exist, with the second type T2, I2 being longer lived and proceeding to integrate virus more slowly. Infected cells of either type can be divided up into those who have not yet completed the phase of the viral lifecycle where integration occurs Ii, and those mature infected cells M, which allows investigation of different dynamics in the presence and absence of integrase inhibitor drugs.
Despite our meticulous consideration in the modeling process, the speed of virus propagation within the human body varies significantly depending on its environment. Concurrently, studies have revealed that the virus spreads at different rates within the body, and the spatial movement plays a crucial role in the dissemination of the pathogenic agent. In light of these considerations, we incorporate spatial reactivity diffusion into the model to simulate the diverse spread rates of the virus among different tissues. This enhancement renders the model more practical and provides greater reference value for guiding realistic treatment plans. In addition, since what we really care about is the effect of HIV virus on the sum of two target cell concentrations, we build the model based on the following considerations:
(1) The infection process of T1 can be regarded as a special form of the infection process of T2. When f=0, the cell subsets with a slow fusion rate will not enter the latency period, and we can regard them as the cell subsets with a fast fusion rate.
(2) From a virological perspective, when the sum of the concentrations of two types of target cells is considered, the variables and parameters of each compartment in the model can be considered together, which is beneficial to simplifying the proof of the properties of the model.
(3) If target cells are not considered together, there will be two susceptible compartments, making it challenging to analyze the global existence of a system solution.
(4) The amalgamation of two cell types has simplified the objective function for optimum control, resulting in a reduction of computational workload for numerical simulations.
Finally, we establish the following spatially heterogeneous reaction-diffusion model of HIV in human body:
with (x,t)∈ΩΓ=Ω × (0,Γ). Moreover, as a complement to the system (2.3), we introduce the no-flux condition:
with the positive initial conditions:
The outward normal vector to ∂Ω is denoted by ∂v. Given the complexity of describing the architecture, composition of target tissues, and the diversity of the human internal environment, the domain Ω is considered as the target tissues. The interpretation of the variables are listed in Table 1. Moreover, all parameters and their respective meanings can be found in Table 2, where θi(i=0,1,2,3,4) represents the diffusion rate of each compartment, indicating that the local diffusion rate vary across different compartments. Under the condition of x∈Ω, we suppose that position-dependent parameters are functions that are continuous, strictly positive, and uniformly bounded.
3.
Some basic properties for system
In this section, we encompasse an exploration of the well-posedness of the solutions as well as an analysis of dynamic behavior of the model. Similar to Zhao's method [34] in the article, we consider the following scalar reaction-diffusion equation:
According to the method of Lemma 1 in [34], similarly, we have the following lemma:
Lemma 3.1. System (3.1) admits a unique positive steady state w∗(x), which is globally asymptotically stable in the function space C(ˉΩ,R). Furthermore, w∗=λμT if λ and μT are positive constants.
Let D=C(ˉΩ,R5) equip with the uniform norm denoted by ||⋅||D, D+=C(ˉΩ,R5+). Then we will obtain an Banach space which is denoted as (D,D+). We set a mapping relation Ti(t):C(ˉΩ,R)→C(ˉΩ,R)(i=1,2,3,4,5) to represent the C0 semigroups. C0 semigroups is associated with ∇(θi(x)∇)−mi(⋅), where m0(⋅)=μT(⋅), m1(⋅)=μI(⋅)+n(⋅), m2(⋅)=μL(⋅)+a(⋅), m3(⋅)=μM(⋅),m4(⋅)=c(⋅). Thus, it comes that:
The function Gi(t,x,y) denotes the Green function corresponding to the operator ∇(θi(x)∇)−mi(⋅) under the Neumann boundary conditions. Building upon the theorem presented in Smith's work (1995, Corollary 7.2.3) [35], the operator Ti(t) (i=1,2,3,4,5) is compact and strictly positive for all t>0. Obviously, we can find a positive constant M>0 that when αi⩽0 and t⩾0 satisfies ||Ti(t)||⩽Meαit. Here, αi represents the main eigenvalue of ∇(θi(x)∇)−mi(⋅). Define operator F=(F1,F2,F3,F4,F5)T:D+→D by
where ψ=(ψ1,ψ2,ψ3,ψ4,ψ5)T∈D+. Subsequently, we rewrite the system (2.3):
where E(t)=(T(t),I(t),L(t),M(t),V(t))T,E∗(t)=diag(T1(t),T2(t),T3(t),T4(t),T5(t)).
According to the conclusion of Martin and Smith (1990, Corollary 4) [36], the subtangential conditions are satisfied, and then, the following lemma is applicable:
Lemma 3.2. For system (2.3)–(2.5) with initial condition ψ∈D+, when the maximum interval [0,τ∞),τ∞⩽+∞ is provided, the solution u(t,ψ)∈D+ is mild and also unique. Furthermore, this solution to the system (2.3) is classical.
Next we give proofs for the dynamical behavior and the existence of the global attractor.
Theorem 3.3. There exist unique and mild solution u(x,t,ψ)∈D+ on [0,∞) to the system (2.3)–(2.5), when it fits the initial condition ψ∈D+. In addition, we can find the solution semiflow Ψ(t)=u(t,⋅,ψ):D+→D+, t⩾0 exist a global compact attractor.
Proof. For the sake of later discussion, we first set g_=minx∈ˉΩg(⋅) and ˉg=maxx∈ˉΩg(⋅), where g(⋅)=λ(⋅),β(⋅),n(⋅),f(⋅) ,a(⋅),k(⋅),c(⋅),μT(⋅),μI(⋅),μL(⋅),μM(⋅). According to the theory of Lemma 3.2, we can easily find the solution to the system (2.3) exists and is also unique and positive. Next, we can obtain the following conclusion: ||u(x,t,ψ)||→+∞ for τ∞<+∞ refer to Martin and Smith (1990, Theorem 2) [36]. It follows from the system (2.3) that
By the comparison principle and Lemma 3.1, we obtain that there admits M1>0 such that
Then, a series of equations can be established:
Consider the following problem:
We can find that the strictly positive eigenfunction ϕ=(ϕ1,ϕ2,ϕ3,ϕ4) correspond to A which is principal eigenvalue to the system (3.4) based on the standard Krein-Rutman theorem. Hence, if t⩾0, systems (3.4) has a solution σeAtϕ(x), where σϕ=(v1(x,0),v2(x,0),v3(x,0),v4(x,0)⩾(I(x,0),L(x,0),M(x,0),V(x,0)) for x∈ˉΩ. Then we will get by referring the comparison principle:
Then, there exists M2>0 that satisfies the following inequality:
When the τ∞<+∞ is given, we find that it contradicts the previous conclusion (||u(x,t,ψ)||→+∞ when τ∞<+∞). Therefore, we have proved the solution is globally existed. Furthermore, we can prove that the semiflow of solution is dissipative. Refer to the comparison principle and Lemma 3.1, there exist N1>0 and t1>0 satisfies
Denote S(t)=∫Ω(T(x,t)+I(x,t)+L(x,t)+M(x,t)+μM(x)k(x)V(x,t))dx, then we have that
Thus there exist N2>0 and t2>0 such that S(t)⩽N2 for all t⩾t2.
It follows from Guenther and Lee [37] that G2(t,x,y)=∑n⩾1eτntφn(x)φn(y), where φn(x) means the eigenfunction and the eigenvalue of ∇⋅(θ1(x)∇)−μI(x)−n(x) is τi. Moreover, τi satisfies τ1>τ2⩾τ3⩾⋯⩾τn⩾⋯. Then
for some ω1>0 since φn is uniformly bounded. Let νn(n=1,2…) be the eigenvalue of ∇⋅(θ1_∇)−μI_(x)−n_(x) and satisfy ν1=−μI_−n_>ν2⩾ν3⩾⋯⩾νn⩾⋯. According to the Theorem 2.4.7 in Wang [38], we can obtain that νi⩾τi for any i∈N+. Considering the trend of νn is similar to −n2, we can obtain that
for t>0 some ω>0.
Here we set t3=max{t1,t2}. If t⩾t3, we can also have refer to the comparison principle:
Thus, lim supt→∞||I(x,t)||⩽ωN1N2⋅ˉβ⋅ˉk/μM_(μI_+n_). Moreover, follow the same method, there admits N3>0 such that lim supt→∞||L(x,t)||⩽N3. Therefore, we can show that the system is point dissipative. Furthermore, in the condition of t>0, the solution semiflow Ψ(t) is compact and also globally attracted based on Wu (Theorem 2.2.6) [39] and Hale (Theorem 3.4.8) [40]. □
4.
Threshold dynamics behavior
In this section, we delve into the fundamental concept of the reproduction number. Based on Lemma 3.1, it can be concluded that system (2.3) amdits a unique infection-free equilibrium state E0=(T0(x),0,0,0,0), where T0=ω∗(x). At the infection-free equilibrium state E0, we can derive a set of linearized equations:
Letting (P2,P3,P4,P5)=eAt(ψ2(t),ψ3(t),ψ4(t),ψ5(t)), the above system can be rewritten as:
From the above equations we know the system is cooperative. According to the Krein-Rutman theorem, we find the strictly positive eigenfunction (φ2(x),φ3(x),φ4(x),φ5(x)) and its unique principal eigenvalue A0(T0). Suppose the solution semigroup Φ(t):C(ˉΩ,R4)→C(ˉΩ,R4) associated with the following system:
We set that:
We define the distribution of the infected with starting conditions ψ=(ψ2,ψ3,ψ4,ψ5). With time goes by, the distribution of infection is denoted by Φ(t)ψ. Then, the total number of cells infected and the number of viruses is:
According to the method in next generation matrix theory, we get the basic reproduction number:
where we use κ(L) to denote the spectral radius of L.
According to the proof of Theorem 3.1 in Wang and Zhao [41], we use a similar method to establish the following lemma:
Lemma 4.1. R0−1 and A0 have the same sign. When R0<1, the state E0 is asymptoticallyis stable, or not when R0>1.
The basic reproduction number serves as a critical threshold, determining whether the virus can persist or not.
Theorem 4.2. When R0<1, E0 exhibits further globally asymptotic stability.
Proof. There admits a δ>0 such that A0(T0+δ)<0. Consider the first equation in the system (2.3):
Refer to the principle of the comparison, given t1 is positive, we know that T(x,t)⩽T0+δ when t⩾t1 and x∈Ω. Then,
Suppose that α(¯ϕ2(x),¯ϕ3(x),¯ϕ4(x),¯ϕ5(x))⩾(I(x,t),L(x,t),M(x,t),V(x,t)). A0(T0+δ) is negative and is the principal eigenvalue of the eigenfunction (¯ϕ2(x),¯ϕ3(x),¯ϕ4(x),¯ϕ5(x)). Thenthe comparison principle implies that:
Therefore, limt→∞(I(x,t),L(x,t),M(x,t),V(x,t))=0. According to the theory in (Corollary 4.3 in Thieme [42]), we know that limt→∞T(x,t)=T0. These findings are all available by Lemma 4.1.
□
Theorem 4.3. When R0 is greater than 1, there admits a positive number η such that any solution (T(x,t),I(x,t),L(x,t),M(x,t),V(x,t)) with T(x,0)≢0,I(x,0)≢0,L(x,0)≢0,M(x,0)≢0 and V(x,0)≢0 satisfies
uniformly for all x∈ˉΩ. Moreover, it is obvious that there at least exists one stable state which is also positive.
Proof. Set D0={ψ=(T,I,L,M,V)∈D+:I(⋅)≢0,L(⋅)≢0,M(⋅)≢0,V(⋅)≢0}. Obviously,
D0 is fixed and positive for the semiflow of solution Ψ(t) based on the theory of Hopf boundary and the maximum eigenvalue. We suppose the set of forward orbit γ+(ϕ)={Ψ(t)(ϕ):t⩾0} where its limit set is denoted by ω(ϕ), and set N∂={ϕ∈∂D0:Ψ(t)∈∂D0}.
Claim 1. ⋃ϕ∈N∂ω(ϕ)=E0.
Given that ϕ belongs to N∂, it implies that either I(x,t,ϕ)≡0, L(x,t,ϕ)≡0, M(x,t,ϕ)≡0 or V(x,t,ϕ)≡0. Assuming V(x,t,ϕ)≡0, from the fifth equation in (2.3), we deduce that M(x,t,ϕ)≡0. Moreover, the fourth equation implies I(x,t,ϕ)≡0 and L(x,t,ϕ)≡0. Hence, as t→∞, T(x,t,ϕ) converges to T0. If there exists a t0⩾0 that satisfies V(x,t0,ϕ)≢0, then we can prove that V(x,t,ϕ)>0 for all t>t0 using the Hopf bifurcation theory and the maximum principle. Thus, we know that M(x,t,ϕ)≡0, L(x,t,ϕ)≡0, I(x,t,ϕ)≡0 for all t⩾t0. From the fifth equation of (2.3), as t→∞, it can be inferred that V(x,t0,ϕ) converges to 0. Consequently, Then T(x,t,ϕ) asymptotically approaches the solution given by Eq (3.1). Utilizing the Corollary 4.3 in [42], it follows that T(x,t) converges to T0 uniformly for x∈ˉΩ as t→∞. Given that R0>1, there exists a ς>0 such that A0(T0−ς)>0.
Claim 2. E0 is a uniform weak repeller in the sense that lim supt→∞||Ψ(t)(ϕ)−E0||⩾ς where ϕ∈D0.
While, there comes a contradiction, there exist a ϕ0∈D0 such that lim supt→∞||Ψ(t)(ϕ)−E0||<ς. Then, for t1>0:
Therefore, we can deduce that:
The eigenfunction is supposed to be (¯ϕ2(x),¯ϕ3(x),¯ϕ4(x),¯ϕ5(x)) and the principal eigenvalue is A0(T0−ς)>0. Assume that α>0 and fulfills the condition α(¯ϕ2(x), ¯ϕ3(x), ¯ϕ4(x), ¯ϕ5(x))⩽(I(x,t),L(x,t),M(x,t),V(x,t)). Then,
This is contradictory to limt→∞(I(x,t),L(x,t),M(x,t),V(x,t))=(+∞,+∞,+∞,+∞).
Given a function K:D+→[0,+∞]:
It is evident that K−1(0,∞)⊆D0. Moreover, we obtain K(Ψ(t)ϕ)>0 when K satisfies the condition: K(ϕ)=0 and ϕ∈D0 or K(ϕ)>0. Therefore, we obtain the function K to the semiflow Ψ(t):D+→D+ (Smith and Zhao 2001) [43]. So it comes a conclusion that any forward orbit of Ψ(t) in M∂ converges to E0. The intersection of the stable subset Ws(E0) with D0 is empty. Moreover, E0 is an isolated invariant set in D+ and the set of ∂D0 only contains the disease-free equilibrium E0. According to Smith and Zhao (Theorem 3), it follows that there exist a ς1>0 satisfies: min{p(ψ):ψ∈ω(ϕ)}>ς1 for any ϕ∈D0. This implies that
According to the method in the Theorem 3.3, it can be established that there exist M>0 and t2>0 satisfies the following inequality:
For T(x,t):
Thus, we can get lim inft→∞T(x,t,ϕ)⩾ς2:=A_/(ˉμT+ˉβM). Then, set ς3:=min{ς1,ς2}. we know that the uniform persistence.
According to Magal and Zhao [44], it follows that system (2.3) has at least one equilibrium in D0. Now, we demonstrate that these equilibrium are positive. Let (ψ1.ψ2,ψ3,ψ4,ψ5) be a equilibrium in D0. Then ψ2≢0,ψ3≢0,ψ4≢0,ψ5≢0, implying ψ2>0,ψ3>0,ψ4>0,ψ5>0. Through the maximum principle we can get ψ1>0 or ψ1≡0. Suppose ψ1≡0. Then ψ2≡0, contradicting the second equation of the steady state system (2.3) and the maximum principle. We final know that(ψ1.ψ2,ψ3,ψ4,ψ5) is a positive equilibrium. □
5.
Optimal control of model
In addition to analyzing the global nature of the equation of HIV kinematics with spatial heterogeneity, we would like to further understand how the dynamic process of HIV transmission in the human body is affected by the action of antiviral drugs. Next, when the mathematical modeling of AIDS dynamic behavior has been completed, the role of optimal disease control can be fully exploited. Combined with optimal control theory, the help of viral infection modeling enables one to find key strategies and methods for controlling infection or enhancing prevention.
The investigation conducted by Kirschner et al. [45] delved into optimal chemotherapy strategies for a specific category of HIV models, employing methodologies rooted in optimal control theories. To reduce the number of infected people and minimize the cost of pharmacological interventions, Zhou et al. [46] considered an optimal control problem of partial differential equations based on the SIR model. Combining the above research and the purpose of this paper to establish optimal control, we want to investigate the optimal effect of drug administration while minimizing the cost and side effects of drug administration. Therefore, we introduce w1,w2,w3 in the following system. The w1(x,t) represents the role of reverse transcriptase inhibitors, which are used to prevent HIV particles from transcribing RNA through susceptible cells, which means that susceptible cells will be less likely to transform into infected cells. The w2(x,t) denotes the action of a protease inhibitor that primarily disables the process involved in the integration of proteins within the virus. This allows a portion of the free virus to be removed from the matured infected cells. The w3(x,t) represents the role of Flavonoid Compounds, which can inhibit HIV activation in latently infected cells. Then, the controlled system is as follows.
The system (5.1) exists only under the condition (x, t)∈ΩΓ=Ω×(0,Γ). Moreover, as a complement to the system, we introduce the no-flux condition and initial conditions:
The control variable can be obtained:
The aim of the system with control is to reduce the HIV virus concentration and the cost of taking medication as much as possible. To achieve this goal, the cost function was set by us to:
where the weight functions are denoted by ϱi(x,t)∈L∞(ΩΓ) and εi(x)∈L∞(ΩΓ),i=1,2,3,4,5; lk∈L∞(ΩΓ) and pk∈L∞(ΩΓ),k=1,2,3 represent the cost of pharmacological interventions. To solve the optimal control problem, we are supposed to determine an optimal control u∗∈U that minimizes the control cost function (5.3).
In this part of this article, we establish the uniqueness and existence of the solution. Additionally, we prove that the optimal control problem can be established under the system (5.1) and give the first-order necessary conditions.
5.1. Preliminaries and basic assumptions
We use the H=(L2(Ω))3 as Hilbert space and set a linear operator A:D(A)⊆H→H where A is:
with
Denote by Q=(T,I,L,M,V),Θ(t,Q)=(Θ1(t,Q),Θ2(t,Q),Θ3(t,Q),Θ4(t,Q),Θ5(t,Q)) with
where Q=(T,I,L,M,V)∈D(Q)≜{Q∈H:Θ(t,Q)∈H,∀t∈[0,Γ]}. Then systems (5.1) with (5.2) can be reformulated as:
To give the proof of the uniqueness and the existence of the solutions to the system, we present some conclusions next.
Theorem 5.1. We define the infinitesimal generator of C0-semigroup as A:D(A)⊆B→B, where B represent the Banach space. Consequently, it can be deduced the uniqueness of the solution Q∈C([0,Γ];B) when Q0∈B of Cauchy problem (5.5):
Furthermore, if A is dissipative on the Hilbert space H and also self-adjoint, then the mild solution meet the conditions Q∈W1,2(0,Γ;B)∩L2(0,Γ;D(A)).
Assumption 5.1. Assume that the functionsT0(x),I0(x),L0(x),M0(x),V0(x)∈H2(Ω), T0(x)>0,T0(x)>0,I0(x)>0,L0(x)>0,M0(x)>0,V0(x)>0 and ∂T0(x)∂ν=∂I0(x)∂ν=∂L0(x)∂ν=∂M0(x)∂ν=∂V0(x)∂ν=0, x∈∂Ω.
We can deduce the uniqueness of the solution in the system (5.1) based on the similar arguments provided in Zhou et al. [46].
Theorem 5.2. In Rk,k⩽5, we first set a bounded domain which is denoted as Ω. Meanwhile, class C2+ϵ,ϵ>0 is the boundary of Ω. It is assumed that Assumption 5.1 holds, and for a optimal control pairs w=(w1,w2,w3)∈W, we can obtain that the solution Q of the system (5.1) is globally positive and unique with Q=(T,I,L,M,V)∈W1,2(0,T;H).
Furthermore, there exists a C>0 such that:
and
5.2. The existence of optimal solution
Theorem 5.3. If Assumption 5.1 is valid, in that case, system (5.1) exists an optimal control (T∗,I∗,L∗,M∗,V∗,w∗1,w∗2,w∗3).
Proof. Set
Then
It can be referred from (5.7) that C(T,I,L,M,V,w) is proved to be bounded. Thus, there exist a minimizing sequence {wm1,wm2,wm3}m⩾1 and a positive constant η=infw∈WC(T,I,L,M,V,w) such that
Here, (Tm,Im,Lm,Mm,Vm,wm) represents the solution of the system given by
Utilizing the results of Theorem 5.2, we can verify that Tm,Im,Lm,Mm,Vm∈W1,2(0,Γ;H), which implies that Tm,Im,Lm,Mm,Vm∈C([0,Γ];L2(Ω)). Furthermore, from (5.7)–(5.8), the uniformly boundedness of Tm,Im,Lm,Mm,Vm follows; Tm,Im,Lm,Mm,Vm are both proved to be uniformly bounded. Then given C>0 and is not dependent on m satisfies that:
From the above Eq (5.8), we know that {(Tm(t),Im(t),Lm(t),Mm(t),Vm(t))} is the family of equicontinuous functions. Considering H1(Ω) is compactly embedded into L2(Ω), we get {(Tm(t),Im(t),Lm(t),Mm(t),Vm(t))}m⩾1 is relatively compact in (L2(Ω))5 and ||Tm||L2(Ω)⩽C,||Im||L2(Ω)⩽C,||Lm||L2(Ω)⩽C,||Mm||L2(Ω)⩽C,||Vm||L2(Ω)⩽C,∀t∈[0,Γ]. From Ascoli-Arzela Theorem [47], we obtain there exists (T∗,I∗,L∗,M∗,V∗)∈(C([0,Γ]:L2(Ω)))5 and {(Tm(t),Im(t),Lm(t),Mm(t),Vm(t))}m⩾1, such that
Therefore, under the condition m→∞ the optimal control problem (5.1)–(5.4) admits a optimal control variable (T∗,I∗,L∗,M∗,V∗). From the estimate (5.10), there admits a {(Tm(t),Im(t),Lm(t),Mm(t),Vm(t))} such that
Furthermore, since wmi,i=1,2,3 are all bounded in L2(ΩΓ), we can get an optimal control pairs {wmi;m⩾1,i=1,2,3} which fit:
At the same time, we find W is a weak closed set since W is a convex closed set in L2(ΩΓ). Hence, based on w∗i∈W (5.14), we can further prove that
and
Then, we know that: TmIm−T∗I∗=Tm(Im−I∗)+I∗(Tm−T∗), TmLm−T∗L∗=Tm(Lm−L∗)+L∗(Tm−T∗), TmMm−T∗M∗=Tm(Mm−M∗)+M∗(Tm−T∗), TmVm−T∗V∗=Tm(Vm−V∗)+V∗(Tm−T∗) and wm1Tm−w∗1T∗=wm1(Tm−T∗)+T∗(wm1−w∗1), wm2Tm−w∗2T∗=wm2(Tm−T∗)+T∗(wm2−w∗2), wm3Tm−w∗3T∗=wm3(Tm−T∗)+T∗(wm3−w∗3). We can deduce that Tm strictly converge to T∗ in L2(ΩΓ) based on formula (5.11), (5.13) and the Theorem 3.1.1 in Zheng [48]. Furthermore, consider the uniformly boundedness of Tm,Im,Lm,Mm,Vm,wm1,wm2,wm3 in L∞(ΩΓ), we have (5.15) and (5.16). As m→∞, then we obtain an optimal control variable (T∗,I∗,L∗,M∗,V∗) of the system (5.9). □
5.3. First-order necessary conditions of HIV intervention therapy with optimal control
We will introduce the adjoint equations of state variables at the beginning of this section. Let (ˆT,ˆI,ˆL,ˆM,ˆV) denote the adjoint variable:
We get an optimal control pair (T∗,I∗,L∗,M∗,V∗). Make a transformation: substituting the variable t with Γ−t and letting ζ1(x,t)=ˆT(x,Γ−t),ζ2(x,t)=ˆI(x,Γ−t),ζ3(x,t)=ˆL(x,Γ−t)ζ4(x,t)=ˆM(x,Γ−t),ζ5(x,t)=ˆV(x,Γ−t),(x,t)∈ΩΓ, system (5.17) then becomes
Refer to a similar process in Theorem 5.2, the solution to the system (5.18), is proved to be existed and strictly positive, and its dynamical behavior and the well-posedness of system (5.17) is also analyzed. Consequently, we will have these conclusions based on Theorem 5.2.
Lemma 5.4. Remain all the conditions which make Theorem 5.2 valid the same, then get a control variable combination (T∗,I∗,L∗,M∗,V∗). Then we can get that the solution (ˆT,ˆI,ˆL,ˆM,ˆV) to the system (5.17) such that ˆT,ˆI,ˆL,ˆM,ˆV∈W1,2(0,Γ;H). Further, ˆT,ˆI,ˆL,ˆM,ˆV∈L∞(ΩΓ)∩L2(0,Γ;H2(Ω)∩L∞(0,Γ;H1(Ω))
Lemma 5.5. Remain all the conditions which make Theorem 5.2 valid the same. For ˜w1,˜w2,˜w3∈L2(ΩΓ) and a positive κ, suppose that wκ1=w∗1+κ˜w1,wκ2=w∗1+κ˜w2,wκ3=w∗3+κ˜w3∈W. Then the problem (5.1) with w=wκ=(wκ1,wκ2,wκ3) has a unique solution Qκ=(Tκ,Iκ,Lκ,Mκ,Vκ). Furthermore, it can be proved that the uniformly boundedness of ||Qκ||L∞(Ω).
Proof. The positive strong solution's existence and uniqueness can be established using methods similar to those employed in Theorem 5.2. To demonstrate the uniform boundedness of ||Qκ||L∞(Ω), consider the following equations.
Consider the system (5.19) and system (5.1) with w=wκ, along with the use of the comparison principle and Gronwall's inequality, we find that
Here, ϖ1 represent positive constants and is not related to κ. Therefore, we will get the uniformly boundedness of ||Tκ||L∞(Ω). Using similar methods, we know that ||Iκ||L∞(Ω),||Lκ||L∞(Ω),||Mκ||L∞(Ω),||Vκ||L∞(Ω) are all bounded in regard to κ in ΩΓ. □
Next, we assume that (T∗,I∗,L∗,M∗,V∗,w∗1,w∗2,w∗3) is an optimal pair and Qκ=(Tκ,Iκ,Lκ,Mκ,Vκ) is the solution to the problem (5.1) with wκ=(wκ1,wκ2,wκ3) written in Lemma 5.5. If we let ZκT=Tκ−T∗κ,ZκI=Iκ−I∗κ,ZκL=Lκ−L∗κ,ZκM=Mκ−M∗κ,ZκV=Vκ−V∗κ, then we have
Lemma 5.6. Remain all the conditions which make Theorem 5.2 valid the same. Then the uniqueness of strong solution Z^\kappa of control system problem (5.20), which satisfying Z^\kappa = (Z^{\kappa}_{T}, Z^{\kappa}_{I}, Z^{\kappa}_{L}, Z^{\kappa}_{M}, Z^{\kappa}_{V})^T \in W^{1, 2}(0, \Gamma; \mathscr H) and Z^{\kappa}_{T}, Z^{\kappa}_{I}, Z^{\kappa}_{L}, Z^{\kappa}_{M}, Z^{\kappa}_{V}\in L^2(0, \Gamma; \mathscr H^2(\Omega))\cap L^\infty(0, \Gamma; \mathscr H^1(\Omega)) can be proved. Moreover, we can prove that T^\kappa\rightarrow T^*, I^\kappa\rightarrow I^*, L^\kappa\rightarrow L^* M^\kappa\rightarrow M^*, V^\kappa\rightarrow V^* , in L^2(\Omega_\Gamma) and Z^\kappa\rightarrow Z as \kappa\rightarrow 0 . Here, Z = (Z_T, Z_I, Z_L, Z_M, Z_V)^T is the solution to this problem:
Proof. According to the method in Theorem 5.2, we can prove that there admits a strong solution. Next, we need to prove that Z^{\kappa}_{T}, Z^{\kappa}_{I}, Z^{\kappa}_{L}, Z^{\kappa}_{M}, Z^{\kappa}_{V} are all bounded in L^2(\Omega_\Gamma) uniformly with regard to \kappa and lim_{\kappa\rightarrow0}||T^\kappa-T^*||_{L^2(\Omega_\Gamma)} = 0, lim_{\kappa\rightarrow0}||I^\kappa-I^*||_{L^2(\Omega_\Gamma)} = 0, lim_{\kappa\rightarrow0}||L^\kappa-L^*||_{L^2(\Omega_\Gamma)} = 0, lim_{\kappa\rightarrow0}||M^\kappa-M^*||_{L^2(\Omega_\Gamma)} = 0, lim_{\kappa\rightarrow0}||V^\kappa-V^*||_{L^2(\Omega_\Gamma)} = 0 . For this purpose, let
and
Then system (5.20) can be rewritten as
Assuming \mathscr{A} has semigroup \left\{T(t):t\geqslant 0\right\} , it can be deduced from Lions [49] that the solution of (5.22) can be formulated as
Moreover, considering Lemma 5.4, 5.5 and Theorem 5.2, we will obtain the uniformly boundedness of \mathscr{T} and U . Hence, there admits B_1 > 0 and B_2 > 0 such that
According to inequality of Gronwall that is Z^\kappa bounded in L^2(\Omega_\Gamma) . Thus we have
We next further show Z^\kappa\rightarrow Z , in L^2(\Omega_\Gamma) . System (5.21)can be expressed as
Next, the solution of system (5.24):
Consider both the (5.23) and (5.25):
In addition, The elements of matrix T^\kappa(t) tend to the corresponding elements of matrix T^*(t) in L^2(\Omega_\Gamma) , and it is also bounded. We can speculate that Z^\kappa\rightarrow Z in L^2(\Omega_\Gamma) by the inequality of Gronwall. □
Theorem 5.7. Remain all the conditions which make Theorem 5.2 valid the same. If (T^*, I^*, L^*, M^*, V^*, w^{*}_{1}, w^{*}_{2}, w^{*}_{3}) is an control combination of problem (5.1)–(5.4) and (\hat{T}, \hat{I}, \hat{L}, \hat{M}, \hat{V}) is the solution to the adjoint system, then we have
Furthermore, if p_1(x) = p_2(x) = p_3(x)\equiv 0 in \Omega , we can choose the following strategy:
and
Proof. Assume that the optimal control pair (T^*, I^*, L^*, M^*, V^*, w^{*}_{1}, w^{*}_{2}, w^{*}_{3}) and the control cost function \mathscr{C}(T, I, L, M, V, w) , which is given by (5.3). Hence,
That is
Multiply both sides of the inequality by 1/\kappa :
Moreover, refer to Lemma 5.6, it holds that
Hence, it holds that
Similarly, we can prove that
Then, sending \kappa\rightarrow 0 :
From system (5.17) and (5.21), we can obtain that
Let the expression (5.28) be integrated over \Omega_\Gamma . Then, considering the initial boundary conditions of \hat{T}, \hat{I}, \hat{L}, \hat{M}, \hat{V}, Z_T, Z_I, Z_L, Z_M, Z_V , we can get:
From the last equation of (5.17), we can get
Then, by (5.27), one has
Given that \tilde{w} = (\tilde{w}_1, \tilde{w}_2, \tilde{w}_3)\in L^2(\Omega_\Gamma) is arbitrary, make equality transformation such as \hat{w}_i = \tilde{w}_i-\tilde{w}^{*}_i, \forall \tilde{w}^{*}_i\in\mathscr{W}, i = 1, 2, 3 . We can get the formula (5.26) from the Theorem 5.7.
□
6.
Numerical simulations
6.1. Model parameters and its initial values
In this section, our focus is on the concentration dynamics of each compartment under the optimal control strategy. In numerous studies and experiments, the estimated parameter values are invariant and independent of the spatial dimension, and these values can reflect the mean level of these factors. Hence, it is reasonable to use mean values to estimate parameters. The parameter values for model (2.3) are chosen from Table 3, and the mean value of b(x) over \bar\Omega is set to \tilde b , where b = \lambda, \beta, n, f, a, k, c, \mu_T, \mu_I, \mu_L, \mu_M . Moreover, the mean values of these parameters refer to the literature listed in Table 3. We assume that the one-dimensional bounded space area \Omega_\Gamma can be regarded as an abstract projection of the two-dimensional space.
Considering that the basic reproduction number of HIV transmission in the human body is generally between 8 and 10 , we assume that \tilde\beta = 3.2 \times 10^{-10} , which implies that R_0 = 8.4492 . The diffusion coefficient of the uninfected cells can be set to \tilde\theta_0 = 0.006 mm ^2 day ^{-1} . Given that infected cells exhibit slower movement compared to uninfected cells, we hypothesized that \tilde\theta_1 = 0.005 mm ^2 day ^{-1} , \tilde\theta_2 = 0.005 mm ^2 day ^{-1} , \tilde\theta_3 = 0.003 mm ^2 day ^{-1} , \tilde\theta_4 = 0.006 mm ^2 day ^{-1} .
6.2. Numerical simulation of dynamic behavior
In Section 5, we explain that the reverse transcriptase inhibitors, protease inhibitor, and Flavonoid Compounds treatments are likely effective to prevent virus-to-cell transmission. Therefore, we assume that when these interventions are taken, the production rate of virus in infected cells and the speed of virus infection will be reduced, that is, k(x) and \beta(x) will be reduced. Now, set \beta(x) = 0.25 \tilde\beta , the remaining parameters are set according to Table 3. Then we can calculate R_0\approx 2.1123 and the virus is persistent (Figure 1(a) with T_0(x) = 5.0\times10^7 , I_0(x) = 0 , L_0(x) = 0 , M_0(x) = 0 , V_0(x) = 25\times(1+x(1-x)^2(2-x)^3) for x\in (0, 1] ). Set \beta(x) = 0.125\tilde\beta , k(x) = 0.5 \tilde k for x\in (0, 1] and The remaining parameters remain consistent with those illustrated in Figure 1(a). Then use the same method to calculate, we calculate R_0\approx 0.5281 and observe that the virions are becoming extinct (Figure 1(b)). By comparison we find that the increase in R_0 is clearly associated with an elevated risk of HIV transmission.
To study the effect of spatial heterogeneity, we assume that parameter \beta is spatial dependent. Under the condition that the mean value of parameter \beta(x) is equal to 0.25\tilde\beta ( x \in (0, 1] ), we assume that \beta(x) = 8 \times 10^{-11}(1+sin(2\pi x)) . The remaining parameters are consistent with the experimental parameters in Figure 1 (a). We set the following initial values: T_0(x) = 5\times10^7(1+x(1-x)^2(2-x)^3) , I_0(x) = 10 \times (1+x(1-x)^2(2-x)^3) L_0(x) = 10 \times (1+x(1-x)^2(2-x)^3) , M_0(x) = 50 \times (1+x(1-x)^2(2-x)^3) , V_0(x) = 25 \times (1+x(1-x)^2(2-x)^3) . Under the influence of heterogeneous parameters, we obtain the concentration changes in each compartment as shown in Figure 2. In addition, Figure 3 is a graph of the change in concentration of each compartment when \beta is a spatial homogeneous parameter (\beta(x) = 0.25\tilde\beta) .
In Figures 2 and 3, the compartments representing infected cells and virions are both beyond normal levels due to infection. Susceptible compartment shows no significant changes in the short term. Comparing the cases of heterogeneous and homogeneous parameters, we find that the concentrations of the infected compartments (I, L, M, V) are significantly higher under heterogeneous parameters than under homogeneous parameters. This indicates that using spatially averaged parameters will underestimate the extent of HIV infection.
6.3. Numerical simulation of optimal control in HIV transmission
In the context of researching optimal control problems for reaction-diffusion models, it is crucial to consider the rational selection of parameters within the objective functional \mathscr{C}(T, I, L, M, V, w) . The values for the parameters are as follows: \varrho_1 = 1 , \varrho_2 = 1 , \varrho_3 = 1 , \varrho_4 = 1 , \varrho_5 = 1 , l_1 = 0.4 , l_2 = 0.3 , l_3 = 0.3 , l_4 = 0.3 , l_5 = 0.35 , \varepsilon_1 = 100 , \varepsilon_2 = 100 , \varepsilon_3 = 100 . The initial values are the same as those in Figure 3. Based on the given parameter values, we employ the finite difference method (Crank-Nicolson) to numerically simulate the optimal control problem (5.1)–(5.4). For the numerical solution of the adjoint system (5.17), we use the iterative solution of the control system (5.1) to solve backward in time by the Crank-Nicolson method.
The solution surface of the control system (5.1) is shown in Figure 4. After adding controls, we found that the load of immature infected cells, latent infected cells, mature infected cells and viral particles all decreased significantly under the optimal treatment strategy. This indicated that the optimal treatment strategy is very effective in controlling HIV infection in the host. Susceptible compartments ( CD4^{+} T ) did not change significantly in the short term. The base number of susceptible cells is large, and the early spread of the virus has little impact on the concentration of susceptible cells (Figure 4(a)).
The optimal control w^{*}_{i} , i = 1, 2, 3 is shown in Figure 5. We found that the optimal control strategies are Bang-Bang control forms. For w_1 and w_3 control, the optimal control is interrupted for a certain distance at the early time, the maximum control intensity is reached near the mid-range moment. For w_2 control, the maximum control intensity is reached near the terminal time. When the w_1 variable and w_3 variable are not controlled in the later stage, they lead to an increase in the concentration of latent infected cells and mature infected cells respectively. The free viral particle compartment converged to lower concentrations after the addition of the control term w_2 , and it suggest that the ability of infected cells to produce virus was controlled at low levels. This indicates that pharmacological interventions can slow down the process of viral infection in humans and reduce the severity of the disease in the early stages of HIV transmission.
In addition, the values of optimal control are different at different spatial locations x , which means that the intensity of measures taken depends on the different spatial locations. During the clinical treatment of HIV, the differences in human body organs and tissues should be taken into consideration in the dosage. Large doses should be used in areas with a high degree of infection, and less medication should be used in areas with a mild degree of infection. In this way, on the one hand, HIV infection in the body can be accurately controlled, and on the other hand, the cost of treatment can be reduced. A treatment process that does not take heterogeneity into account is equivalent to completely equalizing medication, which is not conducive to suppressing the spread of the virus and also increases the cost.
7.
Conclusions
In this paper, we develop a dynamic model of HIV transmission in human body that includes a spatially heterogeneous diffusion term to study combination effect of reverse transcriptase inhibitors, protease inhibitor and Flavonoid Compound. We study the case of bounded spaces with Neumann boundaries to obtain the persistence conditions of viruses in heterogeneous spaces. First, we discuss the case of well-posedness under Neumann boundary conditions and prove the existence of the global attractor of the system, and we derive a biologically meaningful threshold index, the basic reproduction ratio R_0 . We prove that the threshold dynamics of R_0 : The virus persists in body when R_0 > 1 and is eventually eliminated when R_0 < 1 . The basic reproduction ratio for this model is characterized as the spectral radius of the next generation operator and can be numerically calculated when the model parameters are spatially independent.
To further investigate the optimal control strategy for pharmacological intervention in the HIV infection, we introduced control variables representing reverse transcriptase inhibitors, protease inhibitor and Flavonoid Compounds, respectively. An objective function that minimizes the number of infected cells and intervention costs while maximizing the number of susceptible cells was established. Finally, We prove the first-order necessary conditions.
In the numerical simulation section, we initially compared the changes in virus concentration under different basic reproduction number values, and that experimental and theoretical results are consistent. Next, we compared the variations in concentration over time and position in different compartments with and without control. It is shown that the implementation of the optimal treatment strategies in this paper can significantly reduce the load of infected cell and free virus, so as to effectively control HIV infection in the host.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgement
The paper was supported by Natural Science Foundation of Guangxi (No. 2022GXNSFAA035584), Guangxi Medical and health key cultivation discipline construction project(cultivation, 2019-19), National Natural Science Foundation of China (No.12201007).
Conflict of interest
The authors declare there is no conflicts of interest.









 DownLoad:
DownLoad: