1. Introduction
We are interested in the time-harmonic Maxwell equations in and near a composite material with boundary conditions modeling electromagnetic field radiated by an electromagnetic pulse (EMP). An electromagnetic pulse is a short burst of electromagnetic energy. It may be generated by a natural occurrence such like a lightning strike, meteoric EMP, EMP caused by geomagnetic Storm or nuclear EMP. This focuses on what happens over a period of time of a millisecond during the peak of the first return stroke. We study the electromagnetic pulse caused by this lightning strike. This is the first step of a larger study which goal is to understand the behavior of the electromagnetic field and its interaction with a composite material.
EMP interference is generally damaging to electronic equipment. A lightning strike can damage physical objects such as aircraft structures, either through heating effects or disruptive effects of the very large magnetic field generated by the current. Structures and systems require some form of protection against lightning. Every commercial aircraft is struck by lightning at least once a year on average. Aircraft lightning protection is a major concern for aircraft manufacturers. Increasing its use of composite materials, up to 53% for the latest Airbus A350, and 50% for the Boeing B787, aircrafts offer increased vulnerability facing lightning. Earlier generation aircrafts, whose fuselages were predominantly composed of aluminum, behave like a Faraday cage and offer maximum protection for the internal equipment. Currently, in aircrafts, composite materials consisting of a resin enclosing carbon fibers have significant advantages in terms of weight gain and therefore fuel saving. Yet, because aluminium conducts 100 to 1000 times more than composite, we lose the Faraday effect. Modern aircrafts have seen also the increasing reliance on electronic avionics systems instead of mechanical controls and electromechanical instrumentation. For these reasons, aircraft manufacturers are very sensitive to lightning protection and pay special attention to aircraft certification through testing and analysis.
There are two types of lightning strikes to aircraft: the first one is the interception by the aircraft of a lightning leader. The second one, which makes about 90% of the cases, is when the aircraft initiates the lightning discharge by emitting two leaders when it is found in the intense electric field region produced by a thundercloud, our approach applies in this case. When the aircraft flies through a cloud region where the atmospheric electric field is large enough, an ionized channel, called a positive leader, merges from the aircraft in the direction of the ambient electric field. Laroche et al. [15], at an altitude of 6000 m, observed an atmospheric electric field close to 50 kV/m inside the storm clouds, 100 kV/m to the ground. When upward leader connects with the downward negative leader of the cloud, a return stroke is produced and a bright return stroked wave travels from aircraft to cloud. The lightning return strokes radiate powerful electromagnetic fields which may cause damage to aircraft electronic equipment. Our work is devoted to the study of the electromagnetic waves propagation in the air and in the composite material. In this artificial periodic material, the electromagnetic field satisfies the Maxwell equations.
We evaluate the electromagnetic field within and near a periodic structure when the period of this microstructure is small compared to the wavelength of the electromagnetic wave. Our model is composed by air above the composite fuselage and we study the behavior of the electromagnetic wave in the domain filled by the composite material, representing the skin aircraft, and the air. We build the 3D model, under simplifying assumptions, using linear time-harmonic Maxwell equations and constitutive relations for electric and magnetic fields. Composite materials consist of conducting carbon fibers, distributed as periodic inclusions in a matrix (epoxy resin). We impose a magnetic permeability μ0 uniform and an electrical permittivity ϵ=ϵ0ϵ⋆, where ϵ⋆ is the relative permittivity depending of the medium. In the future, we will enrich this model by adding complexity and we will consider non uniform magnetic permeability and electrical permittivity.
Now, we account for some characteristic values. In the first place we focus on the boundary conditions as we consider them as the source. Then, we use on the upper frontier, the magnetic field induced by the peak of the current of the first return stroke
with current intensity I=200 kA and r the radius of the lightning strike, this is the worst aggression that can suffer an aircraft, and we deduce a characteristic electric field ¯E=20 kV/m. In our model we consider that we have very conductive-but not perfect conductors-carbon fibers and an epoxy resin whose conduction depends on its doping rate. The conductivity of the air is non-linear. Air is a strong insulator [29] with conductivity of the order of 10−14 S.m−1 but beyond some electric solicitation, the air loses its insulating nature and locally becomes suddenly conductive. The ionization phenomenon is the only cause that can make the air conductor of electricity. The ionized channel becomes very conductive.
Our mathematical context is periodic homogenization. We consider a microscopic scale ε, which represents the ratio between the diameter of the fiber and thickness of the composite material. So, we are trying to understand how the microscopic structure affects the macroscopic electromagnetic field behavior. Homogenization of Maxwell equations with periodically oscillating coefficients was studied in many papers. N. Wellander homogenized linear and non-linear Maxwell equations with perfect conducting boundary conditions using two-scale convergence in[26] and [27]. N. Wellander and B. Kristensson homogenized the full time-harmonic Maxwell equation with penetrable boundary conditions and at fixed frequency in [28]. The homogenized time-harmonic Maxwell equation for the scattering problem was done in F. Guenneau, S. Zolla and A. Nicolet [12]. Y. Amirat and V. Shelukhin perform two-scale homogenization time-harmonic Maxwell equations for a periodical structure in [5]. They calculate the effective dielectric ε and effective electric conductivity σ. They proved that homogenized Maxwell equations are different in low and high frequencies. The result obtained by two-scale convergence approach takes into account the characteristic sizes of skin thickness and wavelength around the material.
On of the parameter we account for in our model: δ=1√¯ω ¯σμ0, where ¯σ is the characteristic conductivity and ¯ω the order of the magnitude of the pulsation shares much with the definition of theoretical thickness skin δ=√2¯ω¯σμ0. The thickness skin is the depth at which the surface current moves to a factor of e−1. Indeed, at high frequency, the skin effect phenomenon appears because the current tends to concentrate at the periphery of the conductor. On the other side, at low frequencies the penetration depth is much greater than the thickness of the plate which means that a part of the electric field penetrates the composite plate. We use the theory of two-scale convergence introduced by G. Nguetseng [12] and developed by G. Allaire [3].
The paper is organized as follows : in Section 2 we specify the geometry of the model and the dimensionless equations converting the problem into an equivalent one with which we work in the following sections. In Section 3 we perform the mathematical analysis of the model. In particular, we introduce the weak formulation of the problem for the electric field and we regularize it using divergence term. We establish the existence and uniqueness result for the regularized Maxwell equations thanks to Lax-Milgram Theorem. We conclude this section by estimate of the electric field. The last section is devoted to the homogenization of the problems for electric field using the two-scale convergence concept.
2. Modeling
This section is dedicated to the complete mathematical model we will study in this paper. First, we consider a problem that seems relevant with the perspective of propagation of the electromagnetic field in the air and in the skin of aircraft fuselage made of composite material. Secondly, we make a scaling of this model and finally we operate simplifications. If desired, the reader can go directly to the mathematical analysis knowing that the problem to be studied is given by (63), (68) equipped with boundary conditions (66), (67).
2.1. Notations and setting of the problem
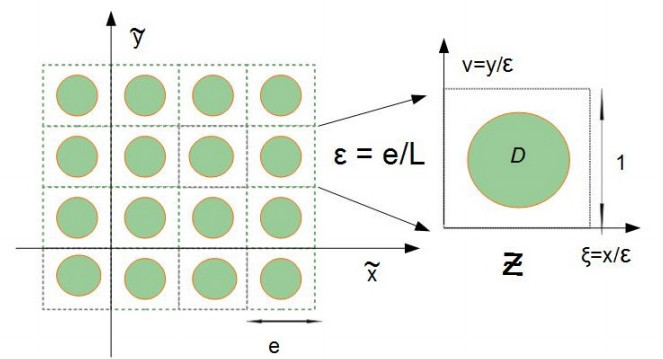
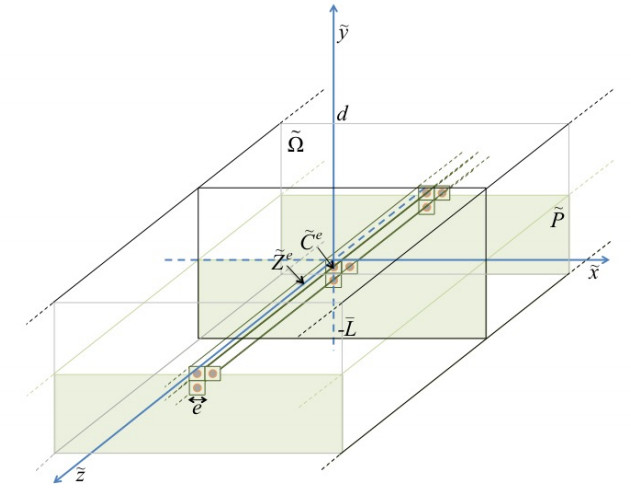
We consider set ˜Ω={(˜x,˜y,˜z)∈R3, ˜y∈(−¯L,d)} for ¯L and d two positive constants, with two open subsets ˜Ωa and ˜P (see Figure 1). The air fills ˜Ωa and we consider that the composite material, with two materials periodically distributed, stands in domain ˜P.
We assume that the thickness ¯L of the composite material is much smaller than its horizontal size. We denote by e the lateral size of the basic cell ˜Ye of the periodic microstructure of the material. The cell is composed of a carbon fiber in the resin. We define now more precisely the material, introducing:
|
˜P={(˜x,˜y,˜z)∈R3/−¯L<˜y<0},
|
(2)
|
which is the domain containing the material. Now we describe precisely the basic cell. For this we first introduce the following cylinder with square base:
|
˜Ze=[−e2,e2]×[−e,0]×R,
|
(3)
|
We consider α such that 0<α<1, and ˜Re=αe2. We set
|
˜De={(˜x,˜y)∈R2/(˜x2+(˜y+e2)2)<(˜Re)2}.
|
(4)
|
We define the cylinder containing the fiber as (see fig 1):
Then the part of the basic cell containing the matrix is
and by definition, the basic cell ˜Ye is the couple
The composite material results from a periodic extension of the basic cell. More precisely the part of the material that contains the carbon fibers is
|
˜Ωc=˜P∩{(ie,je,0)+˜Ce,i∈Z,j∈Z−},
|
(8)
|
where the intersection with ˜P limits the periodic extension to the area where stands the material. Set {(ie,je,0)+˜Ce,i∈Z,j∈Z−} is a short notation for
|
{(˜x,˜y,˜z)∈R3,∃i∈Z,∃j∈Z−,∃(xb,yb,zb)∈˜Ce;˜x=xb+ie,˜y=yb+je,˜z=zb}.
|
(9)
|
In the same way the part of the material that contains the resin is
|
˜Ωr=˜P∩{(ie,je,0)+˜YeR},
|
(10)
|
or equivalently
|
˜Ωr=˜P∩{(ie,je,0)+˜Ze∖˜Ce}=(R×(−¯L,0)×R)∖˜Ωc.
|
(11)
|
So the geometrical model of our composite material is couple (˜Ωc,˜Ωr). Now, it remains to set the domain that contains the air:
|
˜Ωa={(˜x,˜y,˜z)/0⩽˜y<d}.
|
(12)
|
We consider that d is of the same order as ¯L and we introduce the upper frontier ˜Γd={(˜x,˜y,˜z)/˜y=d} of domain ˜Ω. On this frontier we will consider that the electric field and magnetic field are given. We also introduce the lower frontier ˜ΓL={(˜x,˜y,˜z)/˜y=−¯L} with those definitions we have ˜Ωa∩˜P=∅, ˜Ωc∩˜Ωr=∅, ˜P=Ωr∪Ωc, ˜Ω=Ωa∪˜P=Ωa∪Ωr∪Ωc, and for any (˜x,˜y,˜z)∈∂˜Ω=˜Γd∪˜ΓL and, we write ˜n, the unit vector, orthogonal to ∂˜Ω and pointing outside ˜Ω. We have:
|
˜n=e2on˜Γd˜n=−e2on˜ΓL.
|
(13)
|
In the following we need to describe what happens at the interfaces between resin and carbon fibers, and resin and air. So we define Γra={(˜x,˜y,˜z) / ˜y=0} and Γcr the boundary of the set defined by (9).
2.2. Maxwell equations
In ˜Ω, we now write a PDE model that has to do with electromagnetic waves radiated from return stroke. We are well aware that the model we write is a simplified one. Nonetheless, it seems to be well dimensioned for our problem which consists in making homogenization. It is well known see Maxwell [17] the propagation of the electromagnetic field is described by the Maxwell equations which write:
in RטΩ.
In (14)-(17), ∇ and ∇ are the curl and divergence operators. ˜E⋆(t,x,y,z) is the electric field, ˜H⋆(t,x,y,z) the magnetic field, ˜D⋆(t,x,y,z) the electric induction, ˜B⋆(t,x,y,z) the magnetic induction and ˜ρ⋆(t,x,y,z) is the charges density see T. Abboud and I. Terrasse [1].
System of Maxwell equations ((14)-(17)) is completed by the constitutive laws which are given in R×˜Ω by:
where μ0 and ϵ0 are the permeability and permittivity of free space. ϵ⋆ is the relative permittivity of the domains defined by
|
ϵ⋆|~Ωa=1,ϵ⋆|~Ωr=ϵr,ϵ⋆|~Ωc=ϵc,
|
(20)
|
where ϵr and ϵc are positives constants. In order to account for energy transfer between the electromagnetic compartment and the propagation of the electric charges, we take for granted the Ohmic law, in RטΩ
where σ is the electric conductivity. Its value depends on the location:
|
σ|~Ωa=σa,σ|~Ωr=σr,σ|~Ωc=σc,
|
(22)
|
where ~Ωa, ~Ωr and ~Ωc were defined in (12), (10) and (8).
2.3. Boundary conditions
For mathematical as well as physical reasons we have to set boundary conditions on ~Γd and ~ΓL. On ~Γd we will write conditions that translate that ˜E⋆ and ˜H⋆ are given by the source located in ˜y=d. The way we chose consists in setting:
|
˜E⋆טn=˜E⋆dטn;˜H⋆טn=˜H⋆dטnonR×~Γd,
|
(23)
|
where ˜E⋆d, ˜H⋆d are functions defined on ˜Γd for any t∈R. On ˜ΓL, we chose something simple, i.e:
that translate that ˜E⋆ does not vary in the ˜y-direction near ˜ΓL.
Problem (14)-(21) supplemented with (23) and (24), is considered as containing all physics we want to account for. In the following we will consider simplifications of it.
2.4. Time-harmonic Maxwell equations
The first simplification we make, consists in considering the harmonic version of the Maxwell equations (14)-(22). This simplification is used in many references studying electromagnetic phenomena and especially for lightning applications [14], in spite of the fact that it considers implicitly that every fields and currents are waves of the form, for all ˜ω ∈ R:
|
a(˜x,˜y,˜z)cos(−˜ωt+ϕ(˜x,˜y,˜z))=ℜe[a(˜x,˜y,˜z)expi˜ωtexpiϕ(˜x,˜y,˜z)],
|
(25)
|
where ˜ω is the pulsation, ϕ(˜x,˜y,˜z) is the phase shift of the wave and a(˜x,˜y,˜z) is its amplitude. In particular, it supposes ˜E⋆d, ˜H⋆d in (23) are of the form, for all ˜w∈R:
|
˜E⋆d(t,˜x,˜z)=ℜe(˜Ed(˜x,˜z)expi˜ωt),
|
(26)
|
|
˜H⋆d(t,˜x,˜z)=ℜe(˜Hd(˜x,˜z)expi˜ωt),
|
(27)
|
where ˜Ed and ˜Hd take into account the amplitude and the phase shift of their corresponding fields. Taking (21) into account, the time-harmonic Maxwell equations, which describe the electromagnetic radiation, are written:
|
∇טH−i˜ωϵ0ϵ⋆˜E=σ˜E, Maxwell - Ampere equation
|
(28)
|
|
∇טE+i˜ωμ0˜H=0, Maxwell - Faraday equation
|
(29)
|
where ˜E⋆(t,˜x,˜y,˜z)=ℜe(˜E(˜x,˜y,˜z)expi˜ωt) and ˜H⋆(t,˜x,˜y,˜z)=ℜe(˜H(˜x,˜y,˜z)expi˜ωt), (˜x,˜y,˜z)∈˜Ω. The magnetic field ˜H can be directly computed from the electric field ˜E
Now, for the electric approach, taking the curl of equation (32) yields an expression of ∇טH in term of ∇×∇טE. Inserting ∇טH in (28) we get the following equation for the electric field:
|
∇×∇טE+(−˜ω2μ0ϵ0ϵ⋆+i˜ωμ0σ)˜E=0in˜Ω.
|
(33)
|
Taking the divergence of the equation (28) yields the natural gauge condition:
|
∇⋅[(i˜ωϵ0ϵ⋆+σ)˜E]=0in˜Ω.
|
(34)
|
Notice that i˜ωϵ0+σ is equal to i˜ωϵ0+σa in ~Ωa, to i˜ωϵ0ϵr+σr in ~Ωr and to i˜ωϵ0ϵc+σc in ~Ωc, those quantities being all nonzero. Then (34) is equivalent to:
|
∇⋅˜E|Ωa=0 in ~Ωa, ∇⋅˜E|Ωr=0 in ~Ωr, ∇⋅˜E|Ωc=0 in ~Ωc.
|
(35)
|
with the transmission conditions
|
(i˜ωϵ0+σa)˜E|~Ωa.˜n=(i˜ωϵ0ϵr+σr)˜E|~Ωr.˜n on ~Γra,(i˜ωϵ0ϵr+σr)˜E|~Ωr.˜n=(i˜ωϵ0ϵc+σc)˜E|~Ωc.˜n on ~Γcr.
|
(36)
|
Summarizing, we finally obtain the PDE model:
|
∇×∇טE+(−˜ω2μ0ϵ0ϵ⋆+i˜ωμ0σ)˜E=0in˜Ω.
|
(37)
|
According to the tangential trace of the Maxwell-Faraday equation (29) we obviously obtain that using boundary condition (23), is equivalent to using:
|
∇טE×e2=−i˜ωμ0˜Hd(˜x,˜z)×e2on~Γd
|
(38)
|
where ˜Hd is defined in (27) and where we used (13). And on ~ΓL we have the following boundary condition:
2.5. Scaling
In this subsection we propose a rescaling of system ((37)-(39)), we will consider a set of characteristic sizes related to our problem. Physical factors are then rewritten using those values leading to a new set of dimensionless and unitless variables and fields in which the system is rewritten. The considered characteristic sizes are : ¯ω the characteristic pulsation, ¯σ the characteristic electric conductivity, ¯E the characteristic electric magnitude, ¯H the characteristic magnetic magnitude. We also use the already introduced thickness ¯L of the plate ˜P. We then introduce the dimensionless variables: x=(x,y,z) with x=˜x¯L, y=˜y¯L, z=˜z¯L and fields E, H and σ that are such that
|
{E(ω,x)=1¯E˜E(¯ωω,¯Lx,¯Ly,¯Lz),H(ω,x)=1¯H˜H(¯ωω,¯Lx,¯Ly,¯Lz),σ(x)=1¯σ˜σ(¯Lx,¯Ly,¯Lz),
|
(40)
|
Taking (22) into account, σ also reads:
|
σ(x)=σa¯σif0≤¯Ly≤d,σ(x)=σr¯σif(¯Lx,¯Ly,¯Lz)∈˜Ωr,σ(x)=σc¯σif(¯Lx,¯Ly,¯Lz)∈˜Ωc.
|
(41)
|
Doing this gives the status of units to the characteristic sizes. Since, for instance:
|
∂E∂x(ω,x)=¯L¯E∂˜E∂˜x(¯ωω,¯Lx,¯Ly,¯Lz),
|
(42)
|
using those dimensionless variables and fields and taking (41) into account, equation (37) gives:
|
¯E ∇×∇×E(ω,x)−(¯L2¯ω2c2ϵ⋆ω2+i¯σ ¯ω ω¯L2μ0σ(x,ω))¯EE(ω,x,y,z)=0,
|
(43)
|
for any (ω,x) such that (¯ωω,¯Lx,¯Ly,¯Lz)∈˜Ω. Now we exhibit
which is the characteristic wave length and
which is the characteristic skin thickness. Using those quantities equation (43) reads, for any (ω,x)∈Ω:
|
∇×∇×E(ω,x)+(−4π2¯L2¯λ2ω2+i¯L2¯δ2σa¯σω)E(ω,x)=0when0≤¯Ly≤d,∇×∇×E(ω,x)+(−4π2¯L2¯λ2ϵr ω2+i¯L2¯δ2σr¯σω)E(ω,x)=0when(¯Lx,¯Ly,¯Lz)∈˜Ωr,∇×∇×E(ω,x)+(−4π2¯L2¯λ2ϵc ω2+i¯L2¯δ2σc¯σω)E(ω,x)=0when(¯Lx,¯Ly,¯Lz)∈˜Ωc.
|
(46)
|
In the following expressions, ¯L¯λ and ¯L¯δ appearing in the equations above will be rewritten in terms of a small parameter ε.
The boundary conditions are written
|
∇×E(ω,x)×e2=−iω¯ωμ0¯L¯E~Hd(¯Lx,¯Lz)×e2 when (¯Lx,¯Ly,¯Lz)∈~Γd,∇×E(ω,x)×e2=0 when (¯Lx,¯Ly,¯Lz)∈~ΓL.
|
(47)
|
The characteristic thickness of the plate ¯L is about 10−3m and the size of the basic cell e is about 10−5m. Since e is much smaller than the thickness of the plate ¯L, it is pertinent to assume the ratio e¯L equals a small parameter ε:
Then, in what concerns the characteristic pulsation ¯ω, in the tables below we consider several values. The lightning is seen as a low frequency phenomenon. Indeed, energy associated with radiation tracers and return stroke are mainly burn by low and very low frequencies (from 1 kHz to 300 kHz). Components of the frequency spectrum are however observed beyond 1GHz (see [16]). So, in the case when we want to catch low frequency ie we consider ¯ω=100 rad/s, (in our study we will consider ¯ω=106 rad/s), for medium frequency we set ¯ω=1010 rad/s and for high frequency phenomena ¯ω=1012 rad/s. Then, concerning the characteristic electric conductivity it seems to be reasonable to take for ¯σ the value of the effective electric conductivity of the composite material. Yet this choice implies to compute a coarse estimate of this effective conductivity at this level.
For this we take into account that the composite material is composed of carbon fibers and epoxy resin. The resin can be doped, which increases strongly its conductivity, or not. The tables below summarize the cases when the resin is doped and also when the resin is not doped. We also account for the fact there is not only one effective electric conductivity but a first one in the fiber direction : the effective longitudinal electric conductivity (in cases 1, 2, 5 and 6 of the tables below), and a second effective electric conductivity, in the direction transverse to the fibers (considered in cases 3, 4, 7 and 8). In this context, we consider the basic model which is based on the electrical analogy and the law of mixtures. It corresponds to the Wiener limits: the harmonic average and the arithmetic average. The effective values are the extreme limits of the conductivity of the composite introduced by Wiener in 1912 see S. Berthier p 76 [7].
The effective longitudinal electric conductivity corresponding of the upper Wiener limit is expressed by the equation:
|
¯σ=σlong=fc σc+(1−fc) σr,
|
(49)
|
where fc=πα24 is the volume fraction of the carbon fiber.
The effective transverse electric conductivity corresponding of the lower Wiener limit is expressed by
|
¯σ=σtrans=1fcσc+(1−fc)σr.
|
(50)
|
For the computation, we take values close to reality. We consider composite materials with similar proportions of carbon and resin, this means that α is close to 12. When the resin is not doped σr∼10−10 S.m−1 is much smaller than σc∼40000 S.m−1. Then, ¯σ=σlong is close to πα24 σc∼σc and ¯σ=σtrans is close to σr(1−πα24)∼σr.
Now, we express the electric conductivity of the air in terms of ¯σ, we consider two possibilities. The first one is relevant for a situation with a ionized channel. The second one of situation with a strong atmospheric electric field but without a ionized channel. In this situation air is not ionized and has a low conductivity. All possible situations are gathered in the tables below. Cases 5 to 8 are associated with the first situation with air conductivity σa being σlightning=4242 S.m−1 for an ionized lightning channel see [13]. Cases 1 to 4, to the second one, with σa=10−14 S.m−1.
All calculations of the different cases of the tables are detailed in Annex A. In our study we consider the case 6 for ω=106~rad.s−1, which corresponds to the air ionized, a resin doped and the effective longitudinal electric conductivity of the carbon fibers.
As it is well known the tables confirm that at high frequencies the thickness of the plate is much greater than the skin depth. This one depends on ¯σ and ¯ω and decreases strongly for high conductivity or high frequencies. For ¯ω=1010 rad.s−1 and ¯σ=4∗104 S.m−1, the effective conductivity in the direction of the carbon fibers, which the skin effect phenomenon appears. Indeed, for high frequencies ω=1012rad.s−1 and when ¯σ is the effective conductivity is in direction of the carbon fibers i.e. in high conductivity, ¯δ=10−4 m. In low frequencies and low conductivity δ is large so the electromagnetic wave can penetrate the composite material. The high conductivity limits the penetration of the electromagnetic wave to a boundary layer whose depth is about ¯δ.
Now, we will discuss on the values of ¯E and ¯ρ. It seems that the density of electrons in a ionized channel is about 1010 part.m−3. Hence we take ¯ρ=1010. When the air is not ionized, the charge density is much smaller, and we choose: ¯ρ=1.
For the boundary conditions, in the context of the case 6 and ¯ω=106 rad/s, we consider the peak of the current of the first return stroke. Then the magnetic field magnitude ¯H is ¯Hd given by (1).
|
∇×E(x,ω)×e2=−iω¯ωμ0¯L¯E¯HdHd(x,z)×e2,
|
(51)
|
where ¯HdHd(x,z)=~Hd(¯Lx,¯Lz) and where ¯ωμ0¯L¯E¯Hd being of order 1, with the characteristic electric field ¯E=20 kV/m.
From the physical spatial coordinates (˜x,˜y,˜z)∈˜Ω we define y=(ξ,ν,ζ) with ξ=˜xe,ν=˜ye,ζ=˜ze or equivalently ξ=xε,ν=yε,ζ=zε. And we now introduce Y, the basic cell. It is built from: Z=[−12,12]×[−1,0]×R and the set C=D×R with the disc D defined by:
|
D={(ξ,ν)∈R2 /ξ2+(ν+12)2<R2},
|
(52)
|
and R=α2. The set Ωc is then defined as:
|
Ωc={(i,j,0)+C,i∈Z,j∈Z−}.
|
(53)
|
We denote Yr as Yr=Z∖C and then the set
|
Ωr={(i,j,0)+Yr,i∈Z,j∈Z−}.
|
(54)
|
Then unit cell Y is defined as Y=(Yr,C). Finally, we define the domain Ωa:
|
Ωa={y=(ξ,ν,ζ) / ν>0}.
|
(55)
|
Using this, we will give a new expression of the sets in which the variables range in equations (46). We see the following:
|
(¯Lx,¯Ly,¯Lz)∈˜Ωr⇔{(¯Lx,¯Ly,¯Lz)∈˜P,(¯Lex,¯Ley,¯Lez)∈Ωr,
|
(56)
|
i.e.
|
(¯Lx,¯Ly,¯Lz)∈˜Ωr⇔{(¯Lx,¯Ly,¯Lz)∈˜P,(xε,yε,zε)∈Ωr.
|
(57)
|
In the same way:
|
(¯Lx,¯Ly,¯Lz)∈˜Ωc⇔{(¯Lx,¯Ly,¯Lz)∈˜P,(xε,yε,zε)∈Ωc,
|
(58)
|
and:
or
|
(¯Lx,¯Ly,¯Lz)∈˜Ωa⇔{¯Ly≤d(xε,yε,zε)∈Ωa.
|
(60)
|
We define:
|
Σε(y)=Σε(ξ,ν,ζ)={Σεain Ωa,Σεrin Ωr,Σεcin Ωc,
|
(61)
|
where Σεa=σa¯σ¯L2¯δ2,Σεr=σr¯σ¯L2¯δ2 and Σεc=σc¯σ¯L2¯δ2 have their expressions in term of ε given from Tables above depending on the case we are interested in. The detail of this expressions are in appendix B. The model that we present is the case ω=106~rad.s−1, η=5, Σεa=ε, Σεr=ε4 and Σεc=1.
Defining also mapping
|
ψε:R3→R3(x,y,z)↦(xε,yε,zε),
|
(62)
|
we can set Ωεa as ψ−1ε(Ωa)∩(R×[0,d¯L]×R), Ωεr as ψ−1ε(Ωr)∩˜P and Ωεc as ψ−1ε(Ωc)∩˜P. We also define the boundaries Γd={x∈R3, y=d¯L} and ΓL={x∈R3, y=−¯L} and interfaces Γra={x∈R3, y=0} and Γεcr=∂Ωc. Hence equation (46) reads:
|
∇×∇×Eε+(−ω2εηϵ⋆+i ω σε(x,y,z))Eε=0 in Ω,
|
(63)
|
where Ω=Ωεa∪Ωεr∪Ωεc={x∈R3,−1<y<d¯L} does not depend on ε. Only its partition in Ωεa, Ωεr and Ωεc is ε-dependent where
|
σε(x,y,z)=Σε(xε,yε,zε),
|
(64)
|
with Σε given by (61) and
with the value of η≥0 extracted from Tables, and where we replace E by Eε, to clearly state that it depends on ε.
Equation (63) is provided with the following boundary conditions:
|
∇×Eε×e2=−iωHd(x,z)×e2 on Γd,
|
(66)
|
coming from (51). And, coming from (47),
From (63) we can deduce the condition on the divergence of Eε which can be written in two ways. As previously in (34), (35) and (36) we obtain:
|
∇⋅[(−ω2εηϵ⋆+iωσε)Eε]=0 in Ω,
|
(68)
|
which will be preferentially used with (63) and its second one is
|
∇⋅Eε|Ωεa=0 in Ωεa, ∇⋅Eε|Ωεr=0 in Ωεr, ∇⋅Eε|Ωεc=0 in Ωεc,
|
(69)
|
with the transmission conditions on the interfaces Γra and Γεcr
|
(−ω2εη+iωΣεa) Eε|Ωεa⋅n|Ωεa=(−ω2εηϵr+iωΣεr) Eε|Ωεr⋅n|Ωεr on Γra,(−ω2εηϵr+iωΣεr) Eε|Ωεr⋅n|Ωεr=(−ω2εηϵc+iωΣεc) Eε|Ωεc⋅n|Ωεc on Γεcr.
|
(70)
|
Before treating mathematically the question we are interested in, we make a last simplification. Since it seems clear that physical relevant phenomena occur in the upper part of the plate. The boundary condition on the lower boundary of the plate has very little influence on the physics of what happens in the upper part, we consider that the lower boundary of Ω is located in y=−∞ in place of y=−1, making the second boundary condition useless. Besides, as ¯L and d are of the same order it seems reasonable to set Γd={x∈R3, y=1} and consequently
|
{Ω={x∈R3,y<1}=Ωεa∪Ωεr∪Ωεc, with,Ωεa=ψ−1ε(Ωa),Ωεr=ψ−1ε(Ωr),Ωεc=ψ−1ε(Ωc),
|
(71)
|
with ψε defined in (62). We have that the border of Ω is Γd. In the following section we will establish existence and uniqueness results.
3. Mathematical analysis of the models
3.1. Preliminaries
We are going to make precise the variational formulation. First of all, we need to introduce the following functional spaces. We have the standard function spaces L2(Ωε)=[L2(Ωε)]3
|
H(curl,Ω)={u∈L2(Ω): ∇×u∈L2(Ω)},H(div,Ω)={u∈L2(Ω): ∇⋅u∈L2(Ω)},
|
(72)
|
with the usual norms:
|
‖u‖2H(curl,Ω)=‖u‖2L2(Ω)+‖∇×u‖2L2(Ω),‖u‖2H(div,Ω)=‖u‖2L2(Ω)+‖∇⋅u‖2L2(Ω).
|
(73)
|
They are well known Hilbert spaces.
We use in this paper, the trace spaces H−12(curl,Γd) and H−12(div,Γd) defined by
|
H−12(curl,Γd)={u∈H−12(Γd,R3), (n⋅u)|Γd=0, curlΓdu∈H−12(Γd,R3)},
|
(74)
|
|
H−12(div,Γd)={u∈H−12(Γd,R3), (n⋅u)|Γd=0, divΓdu∈H−12(Γd,R3)}
|
(75)
|
where the surface divergence divΓdu and the surface rotation curlΓdu are defined by
|
(divΓdu,V)L2(Γd)=−(u,∇ΓdV)L2(Γd,R3), ∀ V∈C1(Γd)curlΓdu=n⋅(∇×u|Γd)
|
(76)
|
and the surface gradient ∇ΓdV is defined by the orthogonal projection of ∇ on Γd, n denotes the outward unit vector normal to Γd.
Finally we recall the trace theorems, see J.C Nédélec [19] for the demonstration, stating that the traces mappings
γT:H(curl,Ω)⟶H−12(curl,Γd), that assigns any u∈H(curl,Ω) its tangential components n×(u×n), is continuous and surjective, that is:
|
‖γT(u)‖H−12(curl,Γd)≤CγT‖u‖H(curl,Ω), ∀u∈H(curl,Ω)
|
γt:H(curl,Ω)⟶H−12(div,Γd), that assigns any u∈H(curl,Ω) its tangential components u×n, is continuous and surjective:
|
‖γt(u)‖H−12(div,Γd)≤Cγt‖u‖H(curl,Ω), ∀u∈H(curl,Ω).
|
Moreover, H−12(div,Γd) is the dual of H−12(curl,Γd) and one has the Green's formula:
|
∫Ω(∇×u⋅V−u⋅∇×V)dx=⟨u×n,VT⟩Γd ∀(u,V)∈H(curl,Ω).
|
(77)
|
We define the next space:
|
X(Ω)={u∈H(curl,Ω) | ∇⋅u|Ωεa∈L2(Ωεa),∇⋅u|Ωεr∈L2(Ωεr), ∇⋅u|Ωεc∈L2(Ωεc)}.
|
(78)
|
Our variational space is:
|
Xε(Ω)={u∈X(Ω) | (−ω2εη+iωσε|Ωεa)u|Ωεa⋅e2=(−ω2εηεr+iωσε|Ωεr)u|Ωεr⋅e2, (−ω2εηϵr+iωσε|Ωεr)u|Ωεr⋅nε|Ωεr=(−ω2εηεc+iωσε|Ωεc)u|Ωεc⋅nε|Ωεc.
|
(79)
|
Finally
|
Xε(Ω)={u∈X(Ω) | (−ω2εη+iωΣεa)u|Ωεa⋅e2=(−ω2εηεr+iωΣεr)u|Ωεr⋅e2, (−ω2εηϵr+iωΣεr)u|Ωεr⋅nε|Ωεr=(−ω2εηεc+iωΣεc)u|Ωεc⋅nε|Ωεc}.
|
(80)
|
This space is equipped with the norm
|
‖u‖2Xε(Ω)=‖u‖2L2(Ω)+‖∇⋅u|Ωεa‖2L2(Ωεa)+‖∇⋅u|Ωεr‖2L2(Ωεr)+‖∇⋅u|Ωεc‖2L2(Ωεc)+‖∇×u‖2L2(Ω).
|
3.2. Weak formulation
Now, we introduce the variational formulation of our problem (63), (66) and (67) for the electric field. Integrating (63) over Ω and using the Green's formula and (66) we obtain
|
∫Ω∇×Eε⋅∇ׯV dx+∫Ωεa(−ω2εη+iωΣεa)Eε⋅¯V dx+∫Ωεc(−ω2εηϵc+iωΣεc)Eε⋅¯V dx+∫Ωεr(−ω2εηϵr+iωΣεr)Eε⋅¯V dx=∫Γd(∇×Eε×e2)⋅¯VT dσ=∫Γd−iωHd×e2⋅¯VT dσ
|
(81)
|
where ¯V is the complex conjugate of V and VT=(e2×V)×e2. We introduce the sesquilinear form depending on parameters η and ε:
|
{For Eε,V∈Xε(Ω),aε,η(Eε,V)=∫Ω∇×Eε⋅∇ׯV dx+∑i=a,r,c∫Ωεi(−ω2εηϵi+iωΣεi) Eε⋅¯V dx.
|
(82)
|
Hence, the weak formulation of (63), (66) and (67) that we will use is the following:
|
{Find Eε∈Xε(Ω) such as ∀ V∈Xε(Ω) we have:aε,η(Eε,V)=−iω∫ΓdHd×e2⋅¯VT dσ.
|
(83)
|
Integrating by parts in the variational formulation (81), we find the following transmission problem:
|
{∇×∇×Eε+(−ω2εη+i ω Σεa)Eε=0 in Ωεa,∇×∇×Eε+(−ω2εηϵr+i ω Σεr)Eε=0 in Ωεr,∇×∇×Eε+(−ω2εηϵc+i ω Σεc)Eε=0 in Ωεc.Eε|Ωεa×e2=Eε|Ωεr×n|Ωεr on Γra,Eε|Ωεr×n|Ωεr=Eε|Ωεc×n|Ωεc on Γεcr,∇×Eε|Ωεa×e2=∇×Eε|Ωεr×n|Ωεr on Γra,∇×Eε|Ωεr×n|Ωεr=∇×Eε|Ωεc×n|Ωεc on Γεcr,
|
(84)
|
where e2 is the unit outward normal to Ωεa, n|Ωεr is the unit outward normal to Ωεr and n|Ωεc is the unit outward normal to Ωεc. We refer to Annex C for the proof that transmission problem (84) is equivalent to ((63), (66), (67), (69)).
3.3. Regularized Maxwell equations for the electric field
The sesquilinear form aε,η is not coercive on Xε(Ω), so we regularize it adding terms involving the divergence of Eε in Ωεa, Ωεr and Ωεc. Thanks to the additional terms, existence and uniqueness of the regularized variational formulation solution will be established by the Lax-Milgram theory. Let s be an arbitrary positive number, we define the regularized formulation of problem (83):
|
{Find Eε∈Xε(Ω) such that for any V∈Xε(Ω)aε,ηR(Eε,V)=aε,η(Eε,V)+s∫Ωεa∇⋅Eε∇⋅¯V dx+s∫Ωεr∇⋅Eε∇⋅¯V dx+s∫Ωεc∇⋅Eε∇⋅¯V dx=−iω∫ΓdHd×e2⋅¯VT dσ.
|
(85)
|
For any ε>0 and any η≥0, sesquilinear form aε,ηR(.,.) is continuous over Xε(Ω) thanks to the continuity conditions. We will show that it is also coercive. The following proposition was inspired by article [9] Lemma 1.1.
Proposition 3.1. For any ε>0, for any η≥0 and for any s>0, there exists a positive constant ω0 which does not depend on ε and such that for all ω∈(0,ω0), there exists a positive constant C0 depending on εr,εc,s,ω but not on ε such that:
|
∀ Eε∈Xε(Ω), ℜ[exp(−iπ4) aε,ηR(Eε,Eε)]≥C0‖Eε‖Xε(Ω)
|
(86)
|
Proof. We have:
|
ℜ[exp(−iπ4) aε,ηR(Eε,Eε)]=aεR(Eε,Eε)−∫Ωεaω2εη|Eε|2 dx−∫Ωεrω2εηϵr|Eε|2 dx−∫Ωεcω2εηϵc|Eε|2 dx.
|
(87)
|
with
|
aεR(Eε,Eε)=∫Ω|∇×Eε|2 dx+s∫Ωεa|∇⋅Eε|2 dx +s∫Ωεr|∇⋅Eε|2 dx+s∫Ωεc|∇⋅Eε|2 dx +∫ΩεaωΣεa|Eε|2 dx+∫ΩεrωΣεr|Eε|2 dx +∫ΩεcωΣεc|Eε|2 dx.
|
(88)
|
We have the following estimate:
|
|aεR(Eε,Eε)|≥min{1,ω,s}(‖∇×Eε‖2L2(Ω)+‖∇⋅Eε‖2L2(Ωεa)+‖∇⋅Eε‖2L2(Ωεr) +‖∇⋅Eε‖2L2(Ωεc)+‖Eε‖2L2(Ω)).
|
(89)
|
Then we have:
|
aεR(Eε,Eε)| ≥min{1,ω,s}‖Eε‖2Xε(Ω).
|
(90)
|
Returning to formulation (86), for η≥0, since max(Σεa,Σεr,Σεc)>εη, inequality (86) is valid with C0=min{1,ω,s} as soon as ω2min{1,εr,εc}<min{1,ω,s} or ω<√min{1,ω,s}min{1,εr,εc}. This ends the proof of Proposition 3.1.
Thanks to Proposition 3.1 we can state the existence and uniqueness of the solution to regularized problem (85).
Theorem 3.2. Under the assumptions of Proposition 3.1, there exists a unique solution Eε to regularized problem (85).
proof The sesquilinear form aε,ηR is continuous, bounded, coercive thanks to Proposition 3.1 and the right hand side is continuous on Xε(Ω), then problem (85) has a unique solution in Xε(Ω) thanks to the Lax-Milgram Lemma.
3.4. Existence, uniqueness and estimate
Theorem 3.3. For any ε>0, for any η≥0, there exists a positive constant ω0 which does not depend on ε and such that for all ω∈(0,ω0), there exists a unique solution of (84) or ((63), (66), (67), (69)).
proof We show that for an appropriate choice of s that Eε satisfies all equations (84) or ((63), (66), (67), (69)). It is obvious that any solution of (84) or of ((63), (66), (67), (69)) is also solution to (85). Indeed, since from (84) or from ((63), (66), (67), (69)) we have ∇Eε|Ωεa=0, ∇Eε|Ωεr=0, ∇Eε|Ωεc=0, the additional terms s∫Ωεa∇Eε∇¯V dx + s∫Ωεr∇Eε∇¯V dx + s∫Ωεc∇Eε∇¯V dx cancel in (85).
Uniqueness follows from that if Eε1 and Eε2 are two solutions to (63) with the boundary condition (67) their difference eε=Eε2−Eε1 satisfies the problem (63) with (67). Then it comes
|
∫Ω|∇×eε|2 dx+∫Ωεa(−ω2εη+iωΣεa)|eε|2 dx +∫Ωεc(−ω2εηϵc+iωΣεc)|eε|2 dx+∫Ωεr(−ω2εηϵr+iωΣεr)|eε|2 dx =0.
|
(91)
|
Taking the imaginary part of the expression we get ∫ΩεaωΣεa|eε|2 dx+∫ΩεcωΣεc|eε|2 dx+∫ΩεrωΣεr|eε|2 dx=0 and then eε=0.
Let us consider the reciprocal assertion, according to the same proof of S. Hassani, S. Nicaise, A. Maghnouji in [23], we define H10(Ωεc,Δ) the subspace of ψ∈H10(Ωεc) such that Δ(ψ)∈L2(Ωεc).
Let Eεs be the solution of the regularized formulation (85). In (85) we take a test function V=∇ψ where ψ∈H10(Ωεc,Δ), extended by zero outside Ωεc. We get:
|
∫Ωεcs∇⋅Eεs∇⋅(∇ψ) dx+∫Ωεc(−ω2εηϵc+iωΣεc)Eεs⋅∇ψ dx=0.
|
(92)
|
By Green's formula, ∀ψ∈H10(Ωεc,Δ), we obtain:
|
∫Ωεc∇⋅Eεs(Δψ+ω2εηϵc−iωΣεcs ψ) dx=0.
|
(93)
|
Thus, if we choose s such that ω2εηϵc−iωΣεcs is not an eigenvalue of (Δdir,Ωεc): the Laplacian operator in Ωεc with Dirichlet condition on its boundary, then for all φ∈L(Ωεc)2 there exists ψ∈H10(Ωεc,Δ) solution of
|
Δψ+ω2εηϵc−iωΣεcs ψ=φ.
|
(94)
|
Then, we conclude that
A similar argument in Ωεa yields ∇Eεs|Ωεa=0 for s such that ω2εη−iωΣεas is not an eigenvalue of (Δdir,Ωεa). In the same way, we obtain in Ωεr, ∇Eεs|Ωεr=0 with s such that ω2εηϵr−iωΣεrs is not an eigenvalue of (Δdir,Ωεr).
Hence ∇Eεs=0 in Ωεc, this cancels the additional term s∫Ωεc∇Eεs∇¯V dx in (85). In the same way, ∇Eεs=0 in Ωεr and ∇Eεs=0 in Ωεa cancel s∫Ωεr∇Eεs∇¯V dx and s∫Ωεa∇Eεs∇¯V dx in (85). So, (85) becomes (81). Applying Green's formula, we find (63).
Theorem 3.4. Under the assumptions of Theorem 3.2, Eε∈Xε(Ω) solution of (85) satisfies
with C=CγtCγTC0‖Hd‖H(curl,Ω)
Proof. The sesquilinear form aε,ηR(Eε,V) is coercive, weak formulation (85) becomes:
|
C0‖Eε‖2Xε(Ω)≤ℜ(exp(−iπ4)aε,ηR(Eε,Eε)) ≤ |exp(−iπ4)⋅aε,ηR(Eε,Eε)|=|aε,ηR(Eε,Eε)| ≤ |∫Γd−iωHd×e2⋅EεT dσ| ≤‖Hd×e2‖H−12(div,Γd)‖EεT‖H−12(curl,Γd) ≤CγtCγT‖Hd×e2‖H(curl,Ω)‖Eε‖H(curl,Ω)
|
(97)
|
where EεT=e2×(Eε×e2) and the continuous dependence of the trace norm with C=CγtCγTC0‖Hd‖H(curl,Ω) gives:
|
‖Eε‖2Xε(Ω)≤C‖Eε‖H(curl,Ω)≤C‖Eε‖Xε(Ω).
|
(98)
|
4. Homogenization
With the aim to obtain a convergence result for the problem (63), (66) and (67), we propose an approach based on two-scale convergence. This concept was introduced by G. Nguetseng [3, 4] and specified by G. Allaire [21, 22] which studied properties of the two-scale convergence. M. Neuss-Radu in [20] presented an extension of two-scale convergence method to the periodic surfaces. Many authors applied two-scale convergence approach D. Cionarescu and P. Donato [8]}, N. Crouseilles, E. Frénod, S. Hirstoaga and A. Mouton [10], Y. Amirat, K. Hamdache and A. Ziani [2] and also A. Back, E. Frénod [6]. This mathematical concept were applied to homogenize the time-harmonic Maxwell equations S. Ouchetto, O. Zouhdi and A. Bossavit [24], H.E. Pak [25].
In our model, the parallel carbon cylinders are periodically distributed in direction x and z, as the material is homogenous in the y direction, we can consider that the material is periodic with a three directional cell of periodicity. In other words, introducing Z=[−12,12]×[−1,0]2, function Σε given by (61) is naturally periodic with respect to (ξ,ζ) with period [−12,12]×[−1,0] but it is also periodic with respect to y with period Z.
Now, we review some basis definitions and results about two-scale convergence.
4.1. Two-scale convergence
We first define the function spaces
|
{H#(curl,Z)={u∈H(curl,R3): u is Z-periodic}H#(div,Z)={u∈H(div,R3): u is Z-periodic}
|
(99)
|
and where H(curl,R3) and H(div,R3) are defined by (72) with Ωε replaced by R3. We introduce
|
L2#(Z)={u∈L2(R3),u is Z-periodic},
|
(100)
|
and
|
H1#(Z)={u∈H1(R3),u is Z-periodic},
|
(101)
|
where H1(R3) is the usual Sobolev space on R3. First, denoting by C0#(Z) the space of functions in C0(R3) and Z-periodic, C00(R3) the space of continuous functions over R3 with compact support, we have the following definitions:
Definition 4.1. A sequence uε(x) in L2(Ω) two-scale converges to u0(x,y)∈ L2(Ω,L2#(Z)) if for every V(x,y)∈C00(Ω,C0#(Z))
|
limε→0∫Ωuε(x)⋅V(x,x/ε) dx=∫Ω∫Zu0(x,y)⋅V(x,y) dxdy.
|
(102)
|
Proposition 4.2. If uε(x) two-scale converges to u0(x,y)∈L2(Ω,L2#(Z)), we have for all v(x)∈C0(¯Ω) and all w(y)∈L2#(Z)
|
limε→0∫Ωuε(x)⋅v(x)w(xε) dx=∫Ω∫Zu0(x,y)⋅v(x)w(y) dxdy.
|
(103)
|
Theorem 4.3. (Nguetseng) Let uε(x)∈L2(Ω). Suppose there exists a constant c>0 such that for all ε
Then there exists a subsequence of ε (still denoted ε) and u0(x,y)∈L2(Ω,L2#(Z)) such that:
Proposition 4.4. Let be a sequence of functions in , which two-scale converges to a limit . Then converges also to in weakly. Furthermore, we have
Remark 4.5.:-For any smooth function , being -periodic in , the associated sequence two-scale converges to .
-Any sequence that converges strongly in to a limit , two-scale converges to the same limit .
-If admits an asymptotic expansion of the type , where the functions are smooth and -periodic in , two-scale convergence allows to identify the first term of the expansion with the two-scale limit of and the two-scale limit of with see (Frénod, Raviart and Sonnendrucker [11]).
Proposition 4.6. Let in . Suppose there exists a constant such that for all
Up to a subsequence, two-scale converges to such that:
where satisfies
and is a weak limit in .
Proof. is bounded in , then by application of Theorem 4.3, we get the first part of the proposition. Furthermore by defining as
we obtain the decomposition of .
Defining , , we have
Proposition 4.7. Let be bounded in . Then, up to a subsequence, there exists a function such that
where is given by Proposition 4.6.
Proof. From Theorem 4.3, since and are bounded in then, up to a subsequence, they two-scale converge to and . So we have for all :
Next, by integration by parts, we have:
If we choose a test function such that , passing to the limit in the left-hand side (111) we get
This means that with the difference between (111) and (113):
for all functions with . It follows that function is orthogonal to functions with zero rotational in . This implies that there exists a function such that
Thus
Proposition 4.8. Let be a bounded sequence in . Then a subsequence can be extrated from such that, letting
where is a scalar-valued function and where . And we have
where is given by Proposition 4.6.
proof. Proof of (117), for any , we have
Multiplying by we have
Taking the two-scale limit as we obtain
which implies that . Thus is a gradient with respect to the variable for some scalar function . And according to Proposition (4.6) can be written as , where for some scalar function .
Next, we choose a test function . Integration by parts yields:
These results are important properties of the two-scales convergence. We note that the usual concepts of convergence do not preserve information concerning the micro-scale of the function. However, the two-scale convergence preserves information on the micro-scale.
4.2. Homogenized problem
We will explore in this section the behavior of electromagnetic field using the two-scale convergence to determine the homogenized problem. We place in the context of the case 6 with and , then we have and , , which gives the following equation:
where for a given set , stands for the characteristic function of and where , hence and are the characteristic functions of the sets filled by carbon fibers and by resin. And where .
Remark 4.9. We recall that and are respectively the relative permittivity of the carbon fibers and the resin. You should not confused with the microscopic scale .
On this purpose, we have the following Theorem:
Theorem 4.10. Under assumptions of Theorem 4.3, sequence solution of (85) or (84) or ((63), (66), (67), (69)) converges to which is the unique solution of the homogenized problem:
with and .
And where the scalar function is the unique solution, up to an additive constant in the Hilbert space of periodic functions , of the following boundary value problem
where is the jump across the surface of , , is the projection on the axis of the normal of .
Proof. Step 1: Two-scale convergence. Due to the estimate (96), is bounded in . Hence, up to a subsequence, two-scale converges to belonging to . That means for any , we have:
Step 2: Deduction of the constraint equation. We multiply the equation (123) by oscillating test function where :
Integrating by parts, we get:
Now we multiply (128) by and we pass to the two-scale limit, applying Theorem 4.3 we obtain:
We deduce the constraint equation for the profile :
Step 3. Looking for the solutions to the constraint equation. Multiplying Equation (130) by and integrating by parts over leads to
We deduce that equation (131) is equivalent to
Moreover a solution of (132) is also solution of (130). So (130) and (132) are equivalent.
Hence, from Proposition (117) we conclude that can be decomposed as
Step 4. Equations for and . The divergence equation of (123) is multiplied with , where and . Theorem 4.3 and integration by parts yields for all and
from which it follows that
with given by the decomposition (117). So we obtain the local equation
The potential may be written on the form
From (133) and (137), we get:
Inserting in (136) we obtain
Now, we build oscillating test functions satisfying constraint (133) and use them in weak formulation (128). We define test function , and we inject in (128) test function , which gives:
with the restriction on which does not depend on . The term containing the constraint, the third one, disappears. Passing to the limit and replacing the expression of by the term , we have
Since , the term vanishes. Therefore, (140) becomes:
Now in (142) we replace expression giving by (138). We obtain
Taking in (143), we obtain
Integrating by parts
And since we obtain
which gives the cell problem
From (139) and (147), the scalar function is the unique solution, thanks to Lax-Milgram Lemma, up to an additive constant in the Hilbert space of periodic function of the following boundary value problem
where is the jump across the surface of and , is the projection on the axis of the normal of .
Remark 4.11. (148) can be seen as an electrostatic problem. Solving (139) and (147) reduces to look for a potential induced by surface density of charges. Then is this potential induced by the charges on the interface of carbon fiber.
Setting in (143) and integrating by parts, we get
which gives the following well posed problem for
with and .
This concludes the proof of Theorem (124).
5. Conclusion
We presented in this paper the homogenization of time harmonic Maxwell equation by the method of two-scale convergence. We started by studying the time harmonic Maxwell equations with coefficients depending of . We remind that is the wave length, is the skin length, is thickness of the medium and the size of the basic cell and then is the small parameter. We find for low frequencies the macroscopic homogenized Maxwell equations depending on the volume fraction of the carbon fibers and we find also the microscopic equation.
6. Annexes
A. Presentation of all cases of tables 1, 2, 3 and 4
Table 1. For .
|
case 1 |
case 2 |
case 3 |
case 4 |
case 5 |
case 6 |
case 7 |
case 8 |
| L(m) |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
| e(m) |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
| λ(m) |
106 |
106 |
106 |
106 |
106 |
106 |
106 |
106 |
| σ(S·m—1) |
40000 |
40000 |
10-10 |
10-3 |
40000 |
104 |
10-10 |
10-3 |
| σ(m) |
0, 1 |
0, 1 |
107 |
103 |
0, 1 |
0, 1 |
107 |
103 |
| σc(S·m-1) |
σ |
σ |
|
|
σ |
σ |
|
|
| σr(S·m-1) |
|
|
σ |
σ |
|
|
σ |
σ |
| σa(S·m-1) |
|
|
|
|
|
|
|
|
|
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
|
2 |
2 |
10 |
7 |
2 |
2 |
10 |
7 |
Table 2. For .
|
case 1 |
case 2 |
case 3 |
case 4 |
case 5 |
case 6 |
case 1 |
case 8 |
| L(m) |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
| e(m) |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
| λ(m) |
103 |
103 |
103 |
103 |
103 |
103 |
103 |
103 |
| σ(S.m-1) |
40000 |
40000 |
10-10 |
10-3 |
40000 |
40000 |
10-10 |
10-3 |
| δ(m) |
10-3 |
10-3 |
105 |
10 |
10-3 |
10-3 |
105 |
10 |
| σc(S·m-1) |
σ |
σ |
|
|
σ |
σ |
|
|
| σr(S·m-1) |
|
|
σ |
σ |
|
|
σ |
σ |
| σa(S·m-1) |
|
|
|
|
|
|
|
|
|
ε5 |
ε5 |
ε5 |
ε5 |
ε5 |
ε5 |
ε5 |
ε5 |
|
1 |
1 |
ε8 |
ε5 |
1 |
1 |
ε8 |
ε5 |
Table 3. For .
|
case 1 |
case 2 |
case 3 |
case 4 |
case 5 |
case 6 |
case 1 |
case 8 |
| L(m) |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
| e(m) |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
| λ(m) |
10-1 |
10-1 |
10-1 |
10-1 |
10-1 |
10-1 |
10-1 |
10-1 |
| σ(S.m-1) |
40000 |
40000 |
10-10 |
10-3 |
40000 |
40000 |
10-10 |
10-3 |
| δ(m) |
10-5 |
10-5 |
103 |
10-1/2 |
10-5 |
10-5 |
103 |
10-1/2 |
| σc(S·m-1) |
σ |
σ |
|
|
σ |
σ |
|
|
| σr(S·m-1) |
|
|
σ |
σ |
|
|
σ |
σ |
| σa(S·m-1) |
|
|
|
|
|
|
|
|
|
ε |
ε |
ε |
ε |
ε |
ε |
ε |
ε |
|
|
|
ε6 |
ε3 |
|
|
ε6 |
ε3 |
Table 4. For .
|
case 1 |
case 2 |
case 3 |
case 4 |
case 5 |
case 6 |
case 1 |
case 8 |
| L(m) |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
| e(m) |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
10-5 |
| λ(m) |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
10-3 |
| σ(S.m-1) |
40000 |
40000 |
10-10 |
10-3 |
40000 |
40000 |
10-10 |
10-3 |
| δ(m) |
10-6 |
10-6 |
1 |
10-3/2 |
10-6 |
10-6 |
1 |
10-3/2 |
| σc(S·m-1) |
σ |
σ |
|
|
σ |
σ |
|
|
| σr(S·m-1) |
|
|
σ |
σ |
|
|
σ |
σ |
| σa(S·m-1) |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
ε3 |
ε |
|
|
|
ε3 |
-The case 1 corresponds to the air not ionized, a resin not doped and is the effective electric conductivity in the direction of the carbon fibers. We have for the effective electric conductivity , the resin conductivity is about and the conductivity in the air is about . So when we want to calculate the ratio in (??)-(41) depending on we get: and .
-In case 2, the air is not ionized, the resin is doped and is the effective conductivity is in direction of carbon fibers. We have like the case 1 . The resin conductivity is about and the conductivity in the air is about . So and .
-In case 3, the air is not ionized, the resin is not doped and is the effective conductivity is orthogonal to the fibers. . The carbon fiber conductivity is about and the conductivity in the air is about . and .
-Case 4 corresponds to the air non ionized, the resin doped and is the effective conductivity orthogonal to the fibers. The effective electric conductivity is . The carbon fiber conductivity is about and the conductivity in the air is about . and .
-In case 5, the air is ionized, the resin is not doped and is the effective conductivity is in the direction of the carbon fibers. This one is equal , the resin conductivity is about and the conductivity in the air is now about . and .
-Case 6 corresponds to the air ionized, the resin doped and is the effective conductivity in direction of the carbon fibers. This one is equal , the resin conductivity is about and the conductivity in the air is now about . and .
-Case 7 corresponds to the air ionized, the resin not doped and is the effective conductivity orthogonal to the fibers. The effective conductivity is , the carbon fibers conductivity is about and the conductivity in the air is now about . and .
-Case 8 corresponds to the air ionized, the resin doped and is the effective conductivity orthogonal to the fibers. The effective conductivity is , the carbon fibers conductivity is about and the conductivity in the air is now about . and .
B. Structure of the equations depending of ε
For , we have
Case 1
Case 2
Case 3
Case 4
Case 5
Case 6
Case 7
Case 8
For
Case 1
Case 2
Case 3
Case 4
Case 5
Case 6
Case 7
Case 8
For
Case 1
Case 2
Case 3
Case 4
Case 5
Case 6
Case 7
Case 8
For
Case 1
Case 2
Case 3
Case 4
Case 5
Case 6
Case 7
Case 8
C. The transmission Maxwell problem
Taking a test function with compact support in , in weak formulation (83) associated with the problem ((63), (66), (67)). Since
we deduce the third equation in (84). Similarly, taking with compact support respectively in and , we obtain the first and the second equation in (84). Now, since and , let integrating by parts we get
Since on every point of the assumed continuity require
we obtain the fourth relation in (84). With the same argument on , we obtain the last relation in (84). This shows that (83) implies (84). And, if is solution to (84) following that for any regular set in the Stokes's formula gives, for more details see p 57, 58 of P. Monk's book [18]:
has the same definition as with replaced by and where , and is the unit outward normal of . For all , , and . Hence, fixing any according to the second equation in (84), we have then applying (186) in with and we get
Doing the same for , we have
Finally for , we have
Summing the relations above since in every point of and in every point of , it comes
According to (83) and the first, second and third equations in (84) we have
for all which causes the last two equalities in (84) and concludes the first part of the proof.
Reciprocally, integrating by parts (84) we have:
and
and
By adding these three integrals, we get the variational formulation (83) associated with the problem ((63), (66), (67)).
Taking the divergence of the first three equations of (84) we get (69).
Conflicts of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: