Dedicated to Antonio Giorgilli on his 70th birthday.
Foreword
It is a great pleasure to take part in the celebration of Antonio Giorgilli on the occasion of his retirement, albeit we are (egoistically) sorry he was leaving University life at this stage. So sorry we were about that, that our contribution is ready far too late for the occasion, and we ended up celebrating Antonio's 72th birthday rather than the 70th.
Antonio has always been ready to tackle any technically difficult problem, but also fond of finding the simplest way to solve these, avoiding unnecessary complications – or, in his words, to resort to the 'office for complication of simple affairs'. We are aware that our contribution is not at the level of clarity, deepness and at the same time simplicity that would be appropriate for the occasion; but we trust that the choice of the subject we decided to deal with in this occasion – if not our treatment – is indeed in this direction, as detuning allows to avoid a number of technical problems and yet provides an accurate picture of perturbed dynamics.
Antonio is fond not only of Mathematica and Physics, but of a number of other human activities – at the exception, as mentioned above, of bureaucratic complications. He is also passionate about poetry and dialectal poetry, as known to anybody who has visited his homepage. We will thus conclude this short foreword to our contribution – contribution in which we have tried to organise the classical and quantum approaches to detuning in a somewhat unified way – by a citation of Carlo Porta, actually from the same sonnet present in Antonio's homepage:
Ergo donca l'è cossa che la va,
Soeulia, soeulia, polid e del so pass,
Se droeuven i orghen per organizzà.
1.
Introduction
Despite the spectacular progresses of the theory of Nonlinear Integrable Systems, most nonlinear systems are beyond reach of exact analysis, and can only be studied through a perturbation approach.
Modern perturbation theory was created by H. Poincaré and has the transformation to normal form as one of its cornerstones [61]. As well known, this can be constructively characterized through solution of the homological equation at each perturbation level. The main problem met in solving this equation is the presence of small denominators, which are in turn related to near resonances in the unperturbed system. In practice, small denominators reduce the domain of analyticity of the normalizing transformation, and they can accumulate so to make this vanish. This is not surprising: as remarked by Moser, the normal form (at least for problems of interest in Physics and in Celestial Mechanics) has an additional symmetry and hence conserved quantity, so the transformation bringing the original system into normal form can be analytical only if the original system already had (at least in some neighborhood of the unperturbed solution) such an additional symmetry or conserved quantity. Note also, in this respect, that the most basic criteria for the convergence of the normalizing transformation (e.g., the condition that eigenvalues of the unperturbed linear operator lie in a Poincaré domain) are not satisfied in the case of resonant Hamiltonian systems.
It may seem paradoxical that, from this point of view, exactly resonant systems are easier to analyze that near-resonant ones. In fact, while for non-resonant system the normal form is linear, and thus all non-linear systems should be eliminated by solving the homological equation, for resonant system the normal form contains resonant terms, i.e., we (have to) accept that certain non-linear terms are not eliminated. This makes of course that the normal form dynamics is non-linear and thus at the same time richer and more difficult to analyze; but when we look at the reduction to normal form, the fact we accept to keep certain nonlinear terms makes of course things easier.
This trivial observation is at the basis of the method of detuning (also going under the name of frequency deviation in the Russian literature). In this, when we have a near-resonance, we treat an exactly resonant unperturbed system, and consider the detuning of the frequency as a perturbation, to be included in the perturbation analysis rather than in the analysis of the unperturbed system.
One of the consequences of this approach is that we aim at a resonant normal form, which will contain (nonlinear) resonant terms. These are exactly the terms which would call the small denominators into action were we attempting to eliminate them, and it is this not surprising that the method can give a much better outcome in terms of convergence of the normalizing transformation (and thus conjugation of the normal form dynamics with that of the full original system).
The aim of this paper is twofold: on the one hand we want to briefly review the detuning method in Classical Mechanics; on the other we want to stress a point which appears not to be usually made, i.e., that the detuning approach has a close relative in the (standard) approach to perturbation of near degenerate quantum systems.*
*We are not expert in the History of Mathematics, but it appears that these ideas have departed from perturbation of PDEs, made their way as a full theory in Quantum Mechanics in the thirties (of XX century), and then come back into Classical Mechanics; it would be interesting to have a discussion of the matter by historians of Science.
We will thus first review the detuning approach in Classical Mechanics, then review near-degenerate perturbation theory in Quantum Mechanics, and then consider some specific simple examples (perturbation of near-resonant oscillators) in both the Classical and the Quantum formulation. We will also give some (partial) parallel between the two formulations; hopefully we will be able to further progress in clarifying the connection among the two in the near future, but we trust that researchers in both Classical and Quantum Mechanics can profit from knowing that this kind of problems can be treated by essentially the same set of ideas in the other discipline, and techniques can be adapted from one to the other context.
2.
Classical detuning
Our main characters are resonance and detuning.
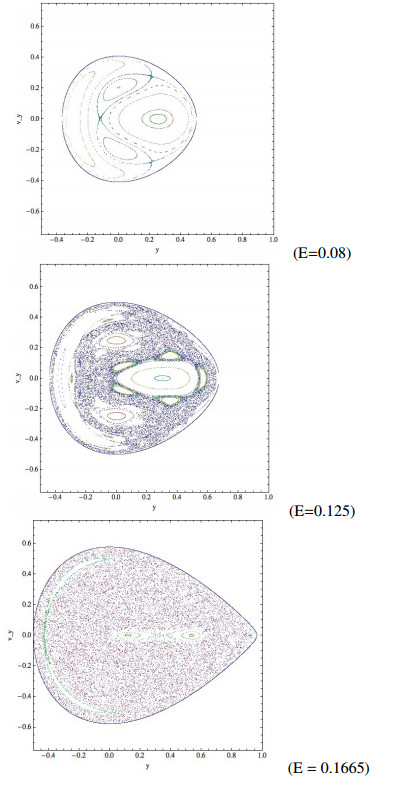
Resonance is the ubiquitous phenomenon [12] producing spectacular features of non-integrable Hamiltonian systems; see e.g., Figure 1.
Detuning is the simple device that, under certain hypotheses, allows us to explore the phase-space of a generic system undergoing resonant behaviour [35,71,78].
We will first focus on the classical setting, with an eye to the semi-classical and quantum applications. Bifurcations and stability/instability transitions are features common to all these frameworks. For systems close to resonance with nonlinear coupling terms, crossing an exact resonance is a general situation triggered by changes in some parameter, typically either the energy or some control parameter.
Let us consider a perturbed classical Hamiltonian model of the form
with p,q canonical coordinates in R2N and ε a book-keeping parameter – not necessarily small at this stage – playing the role of ordering the perturbation terms. The usual setting is provided by a system around an elliptic equilibrium for which
with ωa∈RN,a=1,…,N.
For non-degenerate systems, situations of effective equilibrium can be obtained by exploiting a symmetry through reduction or by expanding around some nominal (usually periodic) solutions.
We say that the frequency vector of the unperturbed system is resonant if
with resonant module provided by the vectors
Here M is the interaction number and j the associated label.
Suppose now that a given pair of components of the frequency vector (without loss of generality we can rearrange indices and take the first two components ω1,ω2) are "close" to a rational ratio k/ℓ, k,ℓ∈Z; then we can introduce the detuning parameter δ by defining
We can assume
where the power r is chosen according to the order of the first resonant term in the normal form. In principles, with N degrees of freedom, we can introduce N−1 detuning parameters.
2.1. Normalization
The most effective way to explore the backbone dynamics of a perturbed Hamiltonian system is to construct a suitable normal form [13,28,68]. Resonant normal forms are computed when a given exact resonance prevents standard normalization algorithms to work. However, the power of the detuning is just to exploit it even in strictly non-resonant cases, when, in principle, a standard Poincaré-Birkhoff normalization would perform flawlessly.
The idea is to proceed as in the case where the unperturbed part is exactly at the interesting resonance and hence leave in the normal form the associated resonant terms. The benefit is twofold: to eliminate several terms possessing small divisors and to get an effective tool to explore the phenomena associated with the resonance.
Let us then consider a sequence of polynomial functions in the phase-space
To each term of the sequence (2.7) is naturally associated the linear differential operator
whose action on a generic function F is given by the Poisson bracket:
Under the action of this operator, the original Hamiltonian system (2.1) undergoes a canonical transformation to new variables (Q,p) such that
and the new Hamiltonian is
where every function is assumed to be in the form of power series.
The process is recursive with first step given by G1 (we can start with the cubic term because a G0 would give only trivial linear transformations). The general relation (2.11) takes the form
By equating polynomials of the same degree in ε, we get the system:
and equations involving terms of higher degrees. The first equality simply states that the zero-order new Hamiltonian coincides with the zero-order old (unperturbed) one. The second equation has to be solved to find the first order term K1: to proceed we have to make some decision about the structure the new Hamiltonian must have, that is we have to chose a normal form for it.
We therefore select the new Hamiltonian in such a way that it admits a new integral of motion; that is we take a certain function, say F, and impose that {K,F}=0. The usual choice (but not the only possible one) is that of taking F=H0=K0 so that (2.2) plays the double role of determining the specific form of the transformation and assuming the status of the second integral of motion.
With this choice, the fundamental equation of the chain, that we can also write in the form
is solved by requiring that the action of the operator LH0 on any polynomial function which commutes with H0 (and therefore that has H0 as an integral of motion) is to "kill" it, whereas its action on any other polynomial gives a uniquely defined non-vanishing polynomial.
We can therefore split the polynomial H1 appearing in (2.13) as
where HK1 is the part belonging to the kernel of LH0,
and HR1 is the part belonging to the range of LH0,
where R1 is a non-vanishing cubic polynomial.
Since our new Hamiltonian, with the choice made, is in normal form if and only if it stays in the kernel of LH0, we can then solve (2.13) by applying the simple prescription:
We observe that the operation implied in the second expression is well defined and easily solved [6,28] to find the first Lie generating function G1: we can therefore use it in the subsequent equations of the system to compute the terms H(1)j with j>1 (which are still not in normal form), and go one step further by expanding Eq (2.11) at order two and applying the above recipe to compute G2 and the normal form at order 2
The procedure can then be iterated up to an arbitrary order. It is usually stopped before a threshold order N0 at which the remainder
ceases to decrease.
2.2. Quasi-resonant normalization
We have so far discussed the general normalization scheme; in this work, we are specially interested in the quasi-resonant case, and in this case the normalization algorithm may present some technical issue.
● The most natural way to construct a detuned resonant normal form is simply to exploit the standard method of recursive solution of the homological equation in which the linear operator is associated to the non-resonant linear part, but the choice of the resonant terms left in the normal form is dictated by the quasi-resonance of interest (Method 1).
● In alternative, terms proportional to the detuning (with a given book-keeping order) can be treated as perturbation terms and treated, at each step, by the resonant algorithm with exactly resonant homological operator (Method 2).
Each of these methods has pros and cons:
● Method 1 is straightforward since does not necessitate any adaptation but, in general, produces many terms with progressively smaller denominators. Moreover, it is computationally more demanding since the memory occupancy is larger than in the other approach. This can be a serious problem when the order of normalization is quite high.
● Method 2 requires to be adapted to manage terms of different algebraic order corresponding to the same perturbation order. By a proper adjustment of book-keeping orders in the algorithm, the treatment of terms of different degree at each step can be managed efficiently and so this method proves to be quite fast and accurate.
We remark that, in order to compare the results obtained in the two approaches, the simplest way is to perform, in the outcome of method 1, a series expansion in the detuning and a rearrangement of terms by means of powers of the book-keeping parameter.
2.3. Detuned resonant 2-DOF systems
The reference case, which can be considered with no loss of generality, is provided by a two degrees-of-freedom system around an elliptic equilibrium like (2.2) with perturbation given by a series of homogeneous polynomials
It is convenient to pass to action-angle variables (J,ϕ); with these, the Hamiltonian can be written in the form of the perturbed oscillator
Let us consider first the unperturbed system (ε=0). In the case where
only the solutions J1=0 and J2=0 are periodic. If
then all orbits are periodic. Solutions for J1=0 and for J2=0 are axial oscillations: they are called normal modes.
In phase-space the energy manifold is an ellipsoid diffeomorphic to the sphere S3:
When the oscillator is perturbed, the orbits will have different evolutions: let us still call normal modes the solutions, if they exist, corresponding to J1=0 and J2=0 (these are nonlinear normal modes in the sense of Moser & Weinstein [53,79]; see also [51,52]), and orbits in generic position those for which both J1 and J2 are nonzero.
Consider the detuned k:ℓ resonance defined by (2.5). It will be convenient to use complex coordinates
As the operator LH0 is linear, and hence so are also the homological equations, we can discuss the latter considering separately different monomials appearing in HN. Given a term
of a polynomial HN of degree N, the solutions of equations (2.17) are provided the vanishing of the scalar product
If (2.22) vanishes, the term belongs to the normal form; if not, it produces a term in the generating function GN−2. The resonant normal form therefore is [68]
with k,ℓ∈N, αj∈R,j=1,…,4. In action-angle variables
we have
2.4. Variables adapted to the k:ℓ resonance
Let (k∗,ℓ∗) such that (k,ℓ)⋅(k∗,ℓ∗)=ν≠0, with ν∈Z. We will now construct the variables adapted to the resonance k/ℓ. Define the matrix
and put
The coordinates adapted to the k/ℓ-resonance are {r1,r2,ψ1,ψ2} and are defined by
In these coordinates
with
The angle ψ2 is not present in (2.27), consistent with E being a conserved quantity for the resonant normal form.
The general analysis of the global structure of phase-space of each resonant normal form proceeds with the study of the bifurcations induced by changes in the internal "distinguished" parameter (E) and in the external or "control" parameters (δ,αj).
It can be approached by following two methods: (a) the analytical approach based on singularity theory considering (2.27) as a universal unfolding of a "catastrophe" germ [5,29,45]; (b) the geometric approach using the Poisson algebra of invariants of the harmonic oscillator and the corresponding reduced systems [15,62].
Clear and accurate references for these methods are given by [20,32].
3.
Quantum mechanics perturbation theory
Quantum mechanical perturbation theory has its roots in a venerable piece of Mathematics, i.e., the Rayleigh-Ritz method† for computing solutions to an eigenvalue–eigenvector problem
†So called after Lord Rayleigh, i.e., John William Strutt, third Baron Rayleigh (1842–1919), and Walther Heinrich Wilhelm Ritz (1878–1909). It should maybe be mentioned that both of these scientists were actually physicists.
where A:V→V is a linear operator in some vector space V=CN, and we look for eigenvalues λ and the corresponding eigenvectors x. Needless to say, in a Quantum Mechanics context we will most often deal with infinite dimensional Hilbert spaces.
In this section we will very sketchily discuss quantum-mechanical perturbation theory for what concerns determination of eigenstates, i.e., solutions to the stationary Schroedinger equation
where H is the Hamiltonian operator, ψ∈H (with H some Hilbert space) is the wave function describing the quantum state of the system, and λ are the eigenvalues of the Hamiltonian, i.e., the energy levels of the system. This material is of course quite standard [17,44,49,59], but is given here for completeness and to introduce notation.
For ease of discussion – and for the relevance in applications – we will just discuss the case where H is bounded from below (we will then assume, for ease of notation and with no loss of generality, that the potential is always non-negative; this guarantees that the energy levels are all positive) and an observable with pure point spectrum; this implies it is self-adjoint and admits, by definition, a set of eigenstates providing a basis for H.
We will denote these eigenstates as ψ0,ψ1,... and the corresponding energy levels as E0,E1,.... We will always order states and levels so that Ei≤Ei+1.
We will also discuss the situation only at first order in perturbations; albeit classical higher-order resonances will manifest their effect at higher order, discussing the first order case is sufficient to grasp the conceptual structure of near-degenerate perturbation theory and its relations with the method of detuning discussed in the previous Section.
We consider a Hamiltonian
and assume to know the solution to (3.2) for H0. We write this as
We will thus consider H0 as the "unperturbed" Hamiltonian and look at H1 as a perturbation.
The states ψ(0)k can be chosen to be of unit norm. We recall that states corresponding to distinct eigenvalues are always orthogonal to each other; in the case of one-dimensional systems all energy levels are always non-degenerate. In the vase of systems in higher dimension, degeneration is possible (and actually always present in case of symmetric systems, e.g., rotationally invariant ones); in this case the eigenspace corresponding to a degenerate eigenvalue λ(0)k has dimension nk but is orthogonal to eigenspaces corresponding to different eigenvalues, and within each eigenspace we can always choose nk mutually orthogonal unit vectors ψ(0). In other words, the vectors ψ(0)k are always – under our assumption that H0 is an observable – a complete orthonormal basis.
We will correspondingly look for the solutions to the Schroedinger problem (3.2) for H in the form
3.1. QM perturbations: the non-degenerate case
Let us first consider the case where H0 is non-degenerate, i.e., all the eigenspaces corresponding to the different eigenvalues are one-dimensional.
Plugging (3.5) and (3.3) into (3.2) we get, at first order in perturbations,
The terms of order zero give
which is satisfied by assumption.
Terms of order one yield
Note that as the ψ(0)k are a basis in H, we can express the ψ(1)k in terms of these, i.e., we can always write
where sum over the repeated index ℓ is understood, and c(1)kℓ are complex constants to be determined.
It is trivial – but relevant in the following – to observe that as states are defined up to a nonzero scalar factor, it would make no sense to consider corrections which are along the unperturbed state. In other words, we can and will always assume
With the notation (3.9), Eq (3.8) reads
recalling that ψ(0)k are eigenstates for (the linear operator) H0, this can also be rewritten as
By taking the scalar product of (both members of) this equation with ψ(0)k, and recalling (3.10), we get
Thus the first order correction to the energy levels is just the mean value of the perturbation H1 on the unperturbed states.
We have now to deal with perturbation of eigenstates, i.e., with determination of the coefficients c(1)kℓ. In order to do this, we consider the scalar product of (3.12) with ψ(0)m, with m≠k. We get
By orthonormality of the ψ(0)k and m≠k, this yields
and hence in conclusion we get
where in the second equality we have defined the matrix element
of the perturbation H1 between the unperturbed states ψ(0)m and ψ(0)k.
Remark 1. Note that our assumption about H0 being non-degenerate guarantees that λ(0)k≠λ(0)m for m≠k, so that the denominator in (3.16) is always non-vanishing (recall (3.10)); but of course these denominators
could be arbitrarily small. ⊙
Remark 2. Actually we have not discussed the conditions of validity for the formal expansion (3.5); this can be considered a posteriori, and our approach is justified provided on the one hand the correction λ(1)k to the k-th energy level is small not only in comparison with the unperturbed value λ(0)k, but also in comparison with the separations from nearby levels, i.e., provided
Again, an exceedingly small ηkm would cause the collapse of our approach. ⊙
Remark 3. Our computations were performed at first order in perturbations only; going at higher orders produces similar, albeit more complex, formulas. Thus, e.g., the second order correction to energy levels turns out to be
while the correction to eigenvectors is embodied in the coefficients
See e.g., [17,44,49,59] for details of computations. ⊙
3.2. QM perturbations: the degenerate case
As remarked above, the non-degeneration condition (λm≠λk for m≠k) guarantees the denominators in (3.16) do not vanish.
Albeit non-degeneration is guaranteed (by the non-degeneration theorem) for one-dimensional systems, not only this theorem does not apply in higher dimension, but many interesting quantum systems in two or three dimensions exhibit reflection or rotational invariance and are thus guaranteed to have a degenerate spectrum precisely due to their symmetry properties.
Needless to say, this degeneration will persist if the symmetry is preserved under perturbations, and in this sense (see also below) we have a trivial extension of the non-degenerate case, in that one can always choose arbitrarily the basis eigenstates belonging to a given degenerate eigenspace to be orthonormal.
But in many physically relevant cases (the most famous being perhaps that of the Hydrogen atom in a magnetic and/or electric field) one studies perturbations which break the symmetry of the unperturbed system, and in this case some extra care must be taken. As the method developed in the early days of QM [7,8,18] to deal with the degenerate case is also at the basis of the QM treatment of the near-degenerate case, we will discuss this in some detail.
It is quite clear that the problem resides within the degenerate eigenspace Em corresponding to an eigenvalue λ, of dimension d=nm; we will thus concentrate on this, so to get a simpler notation. This means we will only consider the eigenvectors and eigenvalues of H resulting from perturbation of states belonging to this degenerate eigenstates of H0; the formulas relating these to other unperturbed states – that is, the components of the perturbed degenerate states in the direction of the Hilbert space spanned by other unperturbed states – are obtained as before.
We choose arbitrarily an orthonormal basis
in Em=V; we have chosen a different symbol for these vectors to emphasize this is a "temporary" basis. That is, we will later on choose a more suitable basis, using the fact that any choice of a unitary matrix M and of vectors
will also yield an orthonormal basis in V; all of these are equivalent as far as H0 is concerned; but in general they are not equivalent when we also consider H1. (Note that in this case the degenerate eigenvalue λ will in general split into d distinct eigenvalues λi=λ+λ(1)i.)
In fact, let us choose an arbitrary state ψ=ψ(0)+ψ(1) of this form, which we write through
with a(i)k (i=0,1) constants to be determined. Let us now consider the Eq (3.14) at order one in perturbations for such states; recalling that the ϕk are all eigenvectors of H0 with eigenvalue λ and taking into account some trivial cancelations, this reads
We can now proceed as before, i.e., consider the scalar product of this with ϕm; recalling that the ϕ were chosen arbitrarily but to be orthonormal, we get
We can rephrase the problem in a slightly different way. Recalling the definition of the matrix elements Vmk of the perturbation H1 between states m and k, and letting V be the associated matrix, let us define the matrix Q and the vector a as Q=V−λ(1)I, a=(a(1)1,...,a(1)d). Then (3.23) reads
and this admits a solution if and only if Q has vanishing determinant.
This means that λ(1) must be one of the eigenvalues of the matrix V, and a the corresponding eigenvector. This a identifies in turn a state
In this way we get d solutions (in general different) for λ(1), and hence for
and correspondingly d eigenstates
belonging to the degenerate eigenspace V. Note that these will automatically be orthonormal if the eigenvalues are distinct, and can be chosen to be such (e.g., by the standard Gram-Schmidt method) if some degeneration is still present.
Remark 4. The relevant point is that our initial choice of the basis {ϕ} was completely arbitrary. If we change this choice, and choose exactly the basis of the {ψ(0)i}, we already have eigenfunctions of H=H0+H1 (at least at order one in perturbation) and thus we surely avoid any problem related to small denominators, simply because there is no correction to the states to be computed. This remark is at the basis of the treatment of near-degenerate cases, to be discussed in the next subsection. ⊙
3.3. QM perturbations: the near-degenerate case
We have seen above that near-resonances – associated to small denominators – can be dangerous, but exact resonances are actually harmless: in this case by making use of the degeneration we can actually arrange things (i.e., chose a suitable basis making use of the freedom left by the degeneration) so that no denominators are actually called into play.
This is not the case when we have really small but non vanishing denominators, i.e., when the energy levels are nearly degenerate. However, the experience built with fully degenerate systems suggests that we may consider instead a fully degenerate system as the unperturbed one, so to make use of the freedom of selecting the basis (as a basis of eigenvectors for the unperturbed operator) inherent to the degeneration. This is indeed at the basis of the QM approach to (perturbations of) near-degenerate systems, as we do now discuss following standard treatments [44,49,59], and in particular Davydov [17].
Let us then consider the case where some of the H0 eigenvalues are very near to each other‡; let us say these are {λ1,...,λn} and to fix ideas let these be within ε; we will denote by λ0 the "center of mass" of these,
‡In the same way as we did for the degenerate case, we will focus on these and disregard contributions to other ones, which are computed in the standard way.
and let us write
Thus the μi are of order ε.
We will assume, for the sake of simplicity, that there is no exact degeneration between these levels λi, so that to each of the levels λi is associated a normalized eigenstate ψi.
Thus the ψi form a basis for the space W=V1⊕...⊕Vn which is the direct sum of eigenspaces corresponding to the near degenerate levels. We are however free to use any other basis in W; in particular we can consider linear combinations
We stress that these states ϕi can be chosen to be orthonormal (if the ψi are orthonormal, the ϕi are automatically so provided the matrix A with elements aik is unitary) but in general they are not eigenstates for H0.
We will now look for eigenstates of H=H0+H1 belonging to this space W, and the associated eigenvalues. For a generic state of the form
this means looking for solutions to
By plugging (3.28) into this, we get
recalling that H0ψk=λkψk, this reads
We now write (here μk and η are of order ε)
In this way the previous Eq (3.31) reads
The terms of order zero cancel out, by construction; the equation simplifies then to
Let us consider, as by now customary, the scalar product of this with ψm; recalling that (ψm,ψk)=δmk, we get
We can write this as a matrix equation, defining matrices V and W with elements
we will also write
Now (3.35) reads simply
this admits solution if and only if M has vanishing determinant, i.e., if and only if η is one of the eigenvalues {η1,...,ηn} of W.
To each of these n eigenvalues ηi corresponds an eigenvector a(i) and hence a state
The point is that these are, by construction, eigenstates at order one. We have thus completely bypassed the computation described in Section 3.3 and the appearance of denominators.
Should be willing to consider the Hilbert space corresponding to the sum of the Hilbert spaces generated by eigenstates of different multiplets, the discussion would go along the same path with some more involved notation.
Remark 5. It is worth stressing the difference with the fully degenerate case considered in Section 3.2. In that case, the relevant matrix is V, i.e., the matrix encoding the matrix elements of the perturbation H1 between the (degenerate) states of the basis. In the present case, the relevant matrix is M; in this we have not only the matrix elements of the perturbation H1 between the (near degenerate) states of the basis, but also the differences μi of the eigenvalues λi with respect to the "center of mass" λ0. ⊙
Remark 6. The presence of the term ηI in the M matrix (3.38) has a very simple physical interpretation: the quadratic "detuning" term is now part of the perturbation w.r.t. the unperturbed degenerate case. In other words, quasi-degenerate quantum perturbation theory is the quantum version of the detuning approach according to Method 2 introduced in subsection 2.2; or conversely. ⊙
4.
Classical examples
We have so far described the general theory, both in the classical mechanics and in the quantum mechanics frameworks. It is time to discuss some specific examples in some detail, also to better understand the relationship between the classical and the quantum cases. We start by considering classical examples; in the next section we will consider some quantum ones.
In this section, we relate the bifurcations of the k/ℓ-resonances to their universal unfolding and catastrophe maps. Rather than providing a general formal treatment, we find more convenient to explicitly work out the most representative cases in 2 DOF.
4.1. The symmetric 1:1 resonance
The expression (2.23) cannot be directly applied to the k=ℓ=1 case because additional quadratic terms with many other free parameters should be included.
However, when enforcing typical symmetries of physical models, the normal form is simplified and belongs to the family (2.25). The standard case is that of the reflection symmetries with respect to one or both normal modes [77]. In this case it is simpler to assume k=ℓ=2 so that the normal form is
where an obvious rescaling has been applied but, for simplicity, we have kept the same symbols for the rescaled control parameters. In terms of variables adapted to the resonance we have, with the choice
and setting now ε=1, the function
where
Singularity theory is implemented by finding an unfolding of the central singularity with double reflection symmetry in the plane. By introducing coordinates in the plane defined by
so that
we get the function [10,45]
where
This is the standard form of the unfolding of the cusp catastrophe [5,29] giving pitchfork bifurcations. The bifurcation set is determined by finding the critical points of F inside the "limit circle"
We find four conditions corresponding to pairs of critical points colliding with either the origin or the limit circle:
Taking into account (4.8), we see that a non-vanishing detuning produces bifurcation thresholds for the distinguished parameter E (the "energy").
More precisely, at
the "loop" families (ψ=±π/2) bifurcate respectively from the J1,J2 normal modes; and at
the "inclined" families (ψ=0,π) bifurcate respectively from the J1,J2 normal modes.
A complementary view is offered by the geometric approach based on the invariants of the isotropic oscillator. It can be proven [15] that the Hilbert basis of the functions in R4 invariant under the action generated by the dynamics of the isotropic oscillator is given by
There is a relation among the invariants: the "syzygy" [36]
which can be interpreted as defining the reduced phase space.
In terms of the invariants the Hamiltonian is [62]
The reduced dynamics is now determined by the intersection of the two surfaces (4.11) and (4.12). Critical points of the reduced dynamics (periodic orbits of the original system) are given by the tangency conditions: they coincide with (4.9) and (4.10).
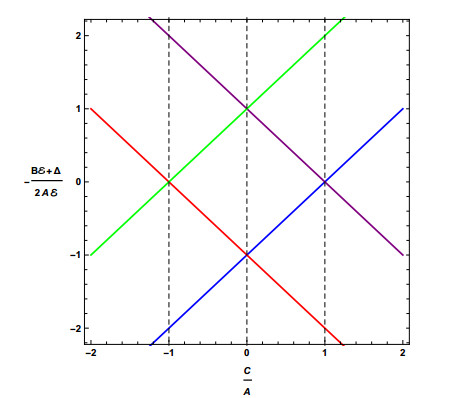
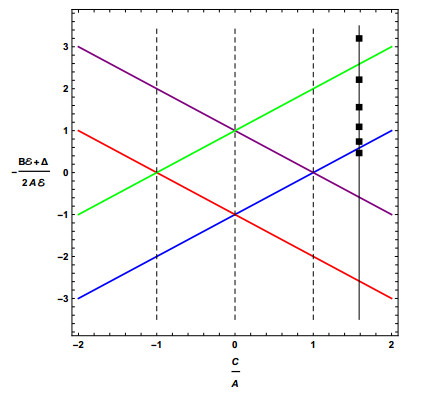
In the space of control parameter, the global bifurcation picture is obtained by introducing the combinations (see [63,76])
In terms of these, the bifurcation thresholds (4.9) and (4.10) become
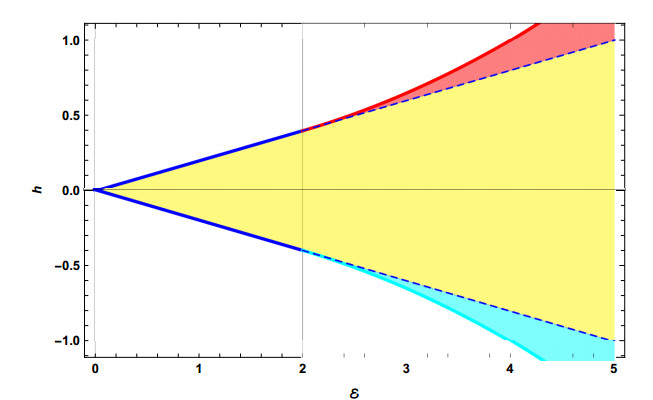
They are plotted in Figure 2 (taken from [62]), also known as "catastrophe map".
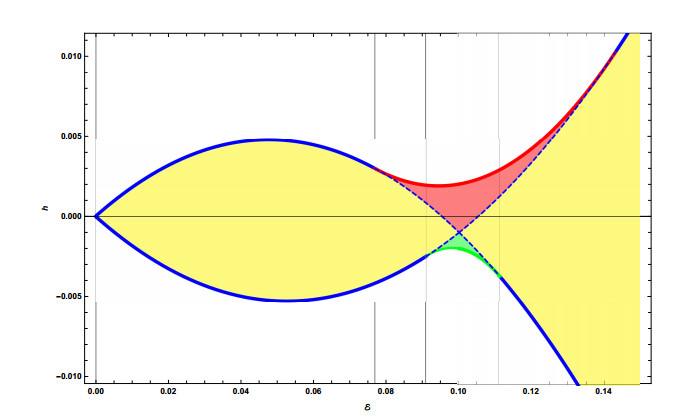
Figure 3 displays the energy-momentum-map [2,4,15,72] obtained by drawing, in the (E,h)-plane, the corresponding bifurcation curves in the case |Γ|>1.
4.2. The 2:1 resonance
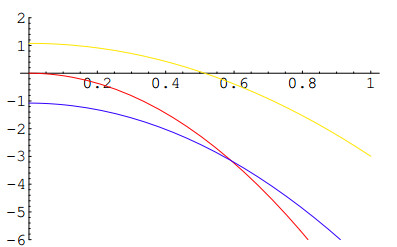
Even more basic than the synchronous resonance seen above, the 2:1 resonance plays an ubiquitous role in many areas spanning from galactic dynamics [14] to molecular physics [39,80], where is known as "Fermi resonance". In classical mechanics, the prototypical system is the spring-pendulum [10].
It can be described with a very simple first-order normal form, however its explicit treatment is slightly more involved algebraically.
The normal form is
The first normal mode becomes unstable at an energy level which depends quadratically on the detuning (see (4.20) below), when a "banana-shaped" resonant orbit appears in a period-doubling bifurcation. The second normal mode is always stable at first order. By using Kummer stereographic variables [43]
so that, as before, the "critical circle"
delimits the dynamics, we get the function
This is the standard form of the unfolding of the fold catastrophe [3,5,29]. The transcritical bifurcation is now determined by finding the critical points of F inside the limit circle. We find four solutions:
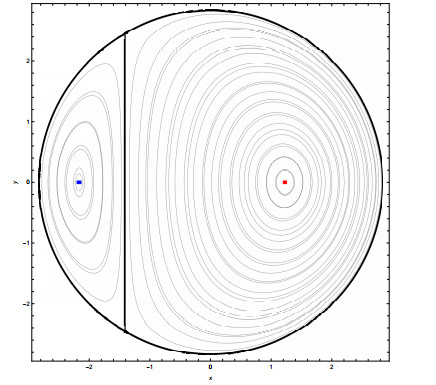
The point (x1,y1) represents the second normal mode and (x2,y2) gives the newly bifurcated orbit. It enters the limit circle when
At this critical energy, the two symmetric points (x3,y3) and (x4,y4) take real values and correspond to the intersection of the limit circle with its stable/unstable manifold; this is the vertical segment of Figure 4, which can also be interpreted as the Poincaré section in the (q1,p1)-phase plane.
5.
Quantum examples
We will now consider the quantum version of the examples considered above, in order to compare the classical and the quantum theory.
It is worth mentioning that a discussion of different approaches within the quantum theory would be quite instructive; but this would be too long in this context, and moreover it would risk to cause some confusion. So we will just work with the "right" procedure, i.e., within the framework of quasi-degenerate perturbation theory discussed in 3.3 above.
In particular we will consider – as in the Classical context of Section 4 – only two-dimensional systems, and more specifically perturbations of near-resonant oscillators. We will focus on concrete cases.
This choice, in view of the simplicity of the involved near-resonance, has some specific features which would get modified in considering generic m:(1+δ)n ones, but we prefer to keep to this simple case (again, as already done in the classical context) in order to focus on the essential features with no distraction from technical complexities.
Remark 7. One general remark is essential to our discussion: as we are in the quantum context, only states up to some – possibly variable – energy E∗ will be accessible and thus appear in our discussion. In other words, we should fix E∗ and consider only the finitely many states with energy E≤E∗. This leads to a considerable simplification in our discussion; in particular, all operators (in particular, observables) will be represented by (Hermitian) finite dimensional matrices. Moreover, as in our general discussion of Section 3, we will focus only on the "interesting" finite dimensional subspace spanned by eigenstates corresponding to the nearly degenerate eigenvalues. ⊙
5.1. Two dimensional quantum oscillators
The Hamiltonian for a generic two-dimensional quantum oscillator (with frequencies {ω1,ω2}) of mass m is
This Hamiltonian is obviously separable and its spectrum – as well as the associated complete system of eigenstates – can be fully described in terms of one-dimensional systems.
In particular, eigenstates are described by two quantum numbers n1,n2 (with ni=0,1,...) and hence denoted as |n1,n2⟩ in Dirac bra-ket notation. The energy of the state |n1,n2⟩ is
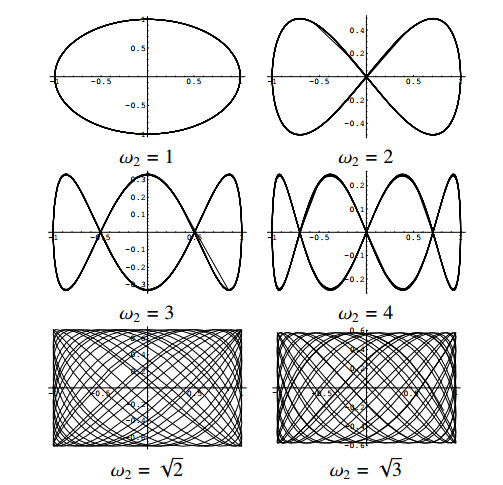
Remark 8. It is immediate to see that we have exactly degenerate levels if and only if the frequencies are in rational relation, ω1/ω2∈Q. This is analogous to the situation met in classical mechanics, where degeneration is replaced by exact resonance, and hence by the presence of closed orbits – also known in that context as Lissajous figures; see Figure 5 in this respect. ⊙
Remark 9. In the case of degenerate levels with ω1:ω2=k1:k2 (where ki are integers having no common factor), degenerate states are identified by the relation
we speak then of a multiplet (and identify it by the number N appearing in this relation).
In the simplest case of 1:1 resonances, the degenerate levels are all those with n1+n2=N; in this case the N multiplet has a degeneracy of order N+1.
In the general case the degeneracies are less simple but can still be explicitly determined. Thus e.g., for ω1:ω2=1:2 the N multiplet has degeneracy [N/2]+1 (the square brackets denoting integer part): the N=0 and N=1 multiplets are actually single states, the N=2 and N=3 are made of two states each (respectively, {|2,0⟩,|0,1⟩} and {|3,0⟩,|1,1⟩}), the N=4 and N=5 by three states each (respectively, {|4,0⟩,|2,1⟩,|0,2⟩} and {|5,0⟩,|3,1⟩,|1,2⟩}), and so on. ⊙
In the case of near-resonant frequencies, we will have near-degenerate states. We will then still speak of multiplets; note however that now states in a multiplet will not have the same energy, but very similar ones – albeit some care should be paid when we go to high quantum numbers.
Remark 10. The previous statement may need an explanation. Consider, for the sake of simplicity, a 1:1 (near) resonance; and write ω1=ω, ω2=(1+δ)ω. We also write, for ease of notation, E0=(ℏ/2)(ω1+ω2). The states in the N multiplet will have energies ranging from E0+Nω to E0+N(1+δ)ω=E0+Nω+Nδω. Thus, for N>1/δ the lowest level of the N+1 multiplet is actually lower than the highest level of the N multiplet; in other words the multiplet structure is well defined only for N≪1/δ. More generally, there will be some bound N∗ such that the multiplets are well defined only for N≪N∗. Our discussion will thus be valid only as long as we work at energies well below the corresponding limit energy E∗. On the other hand, when we work on any multiplet – or a finite union thereof – we are actually considering a finite dimensional Hilbert space, hence we are actually dealing with (finite-dimensional) matrices. See also Remark 7 in this respect. ⊙
Remark 11. It is interesting to consider such a system as the detuning δ is varied from δ=0 to some finite value δ=δ0. As seen in the previous remark for the simplest case of a 1:1 resonance (the discussion is promptly extended to the general case, with some slightly more involved notation), the arrangement of levels changes due to the presence of the detuning, and it is clear that when considering δ as a varying parameter, the "mixing" of multiplets will affect lower and lower ones as |δ| is larger and larger. This situation is also referred to as a quantum bifurcation (rearrangement of energy levels), see [82] and references therein, in particular [57].
We stress, to avoid any misunderstanding, that here we are just referring to the changes of the spectrum of the quadratic Hamiltonian as δ is changed. ⊙
5.2. Computational tools
In order to compute the corrections to the energy levels due to a perturbation H1 (to be considered in the following), we will have to compute the matrix elements Vab, see (3.17), of the perturbation H1 between the states a=|n1,n2⟩ and b=|m1,m2⟩. To this aim it is convenient to introduce, as usual in QM computations, the raising and lowering η+k and ηk operators [17,44,49,59], and recall that
Note that these expressions imply that if we consider terms involving squares or fourth powers of the qk and pk operators (i.e., perturbations which are symmetric under reflection across the axes, which are also the normal modes; see Section 4 above), that we have the selection rules δnk=0,±2,±4, the last possibility occurring only when considering q4k or p4k terms.
Remark 12. It should be stressed that the Hamiltonian H0 involves physical constants with the fundamental dimensions of mass, time, and length. We can choose the reference scale of mass and time so that m=1 and one of the frequencies, say ω1, or their average (ω1+ω2)/2, is unity. We can still use the length scale so that ℏ=1. Note that the perturbation to be considered later on, see in particular (5.6), involves at least a dimensional constant. In the case of (5.6), we have [α4]=1/([M][L]2): having used the length scale to set ℏ=1, we cannot eliminate α; alternatively, we can set α=1 but in this case we must keep track of the ℏk factors. ⊙
5.3. Resonant perturbations of two dimensional quantum oscillators
We have so far discussed the spectrum of two-dimensional (resonant and quasi-resonant) quantum oscillators. We want now to consider perturbations of such oscillators.
We will not consider general perturbations, but resonant perturbations. We have thus first of all to discuss – and justify – such a choice.
It could appear that the physically most natural choice would be that of a perturbation depending only on the q variables: we have an unperturbed Hamiltonian made of a kinetic part and a quadratic potential, and with this choice the perturbations would concern only the potential.
On the other hand, this choice would appear odd to readers with some familiarity with the Chemical Physics literature. In fact, chemists like to proceed by considering first the normalization of the (classical) Hamiltonian, and then the quantum version of the normal form, usually truncated at first nontrivial order. This procedure is quite successful, and actually successful beyond any reasonable limit; this in the sense that in many cases such a perturbation approach manages to correctly describe the energy levels not only near the minima of the potential (thus the lowest lying quantum states), but essentially up to the dissociation threshold [9,22,39,40,41,69,70].
Remark 13. Needless to say, a fully quantum approach would require to work in the quantum setting (thus dealing with operators in a Hilbert space, etc) from the beginning, i.e., also in the normalization step. We have no time here to discuss the relations between these two approaches, i.e., the problem of quantum normal forms, and we will just refer the reader to some classical papers in the field [1,11,19,30,31,56]. ⊙
Remark 14. Problems related to perturbations of near-resonant oscillators, like those we are considering in this paper, have been discussed in the Chemical Physics literature in relation to the spectra of certain simple molecules. For papers which are taking an approach related to our present one, we refer e.g., to [9,22,39,40,41,69,70]. The problem of quantum bifurcations was considered in this context by several groups, and we would like to mention in particular the work by Sadovskii, Zhilinskii and their collaborators [16,21,23,37,65,67,81,83]; see also [64] and [42]. ⊙
These considerations suggest to look at a perturbed near-resonant system for which the perturbation corresponds to terms appearing in the (resonant) normal form of the classical system.
5.4. Near 1:1 resonance
Our discussion of the near 1:1 classical case, see Section 4, suggests to consider a "minimal" perturbation H1 sufficient to generate (in the classical case) all the "interesting" dynamics. This is the term with the α4 coefficient in Eq (4.1), i.e., (in the p,q coordinates)
Remark 15. This choice is simple enough to allow a complete discussion and at the same time generates all the "interesting" dynamics (in the classical case) in the following sense: it contains the only term in the resonant normal form not expressible only in terms of the actions.
It should be stressed, however, that with the choices α1=α2=α3 in (4.1), the Eq (4.4) yield of course
this in turn yields, see (4.8), A=0. This means that Figure 2 does not exist in this setting.
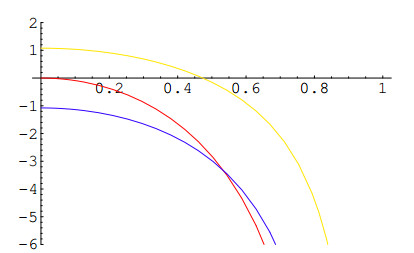
In any case the example is not trivial and contains the main aspect of the bifurcating dynamics. The energy-momentum map for the resonant part (5.6) is shown in Figure 6 with the choice α4=1/10,δ=−2/5. ⊙
One should take some care in choosing the quantum version of this H1, as its first term involves the product of non-commuting operators. We adopt the usual choice of the fully symmetrized version of the classical term; this produces 24 different terms (so each of them should get a weight 1/24), but using the fact that operators acting on different degrees of freedom commute we can reduce these to four not equivalent terms (each of them with a multiplicity 6, which together with the 4 factor cancels out the factor 1/24 introduced above):
Recalling that
where it follows from (5.4) and (5.5) that
it is clear that the perturbation is still satisfying the selection rules
(Note this follows from the fact that each degree of freedom is entering in H1 though two terms, independently of these being qi or pi.)
This implies that the states |1,0⟩ and |0,1⟩ – which in a way represent the quantum analogue of the classical normal modes – are not coupled by H1; so not only nothing interesting happens in the N=1 multiplet, but at first sight the phenomenology described in the classical case, see in particular Section 4.1, has no quantum analogue.
On the other hand, if we pass from the N=1 to the N=2 multiplet, we have that the states |2,0⟩ and |0,2⟩ are coupled by H1 (they are both not coupled to |1,1⟩). Now, each of these states still embodies excitation of only one degree of freedom; so they can in some sense be seen as the analogue of (larger amplitude) normal modes. One should pay attention to the fact that now the natural frequencies of these states are not ωk, but 2ωk, so that the correspondence with large amplitude classical normal modes motion is not complete.
Remark 16. Note that if we look at multiplets with N≥3, there is no analogue of this situation: now the state |N,0⟩ is coupled to |N−2,2⟩, and the state |0,N⟩ to |2,N−2⟩ (and more generally |N−k,k⟩ is coupled to |N−k−2,k+2⟩ and to |N−k+2,k−2⟩, provided respectively k≤N−2 and k≥2), but the states involving excitation of a single degree of freedom are not coupled to each other. This is a further reason, beside the desire to treat only simple cases, to limit our attention to the N=2 multiplet. ⊙
5.4.1. Action on the N multiplet
When restricting our attention to the action on a given N multiplet, only terms preserving N=n1+n2 are relevant§. In practice, this means that we should write pk and qk according to (5.8), but in the resulting expressions it suffices for our purposes to keep only terms in which there are as many raising operator η+ as lowering operators η (irrespective of their k=1,2 index). We will denote this by the ˆ= symbol.
§Note that as we will limit our attention to multiplets with N≤2, even considering all involved multiplets at once we would have only to add the coupling between the N=0 and N=2 ones.
With this convention, and writing for short
it results
We should still consider the last term in (5.7). Recalling again (5.8), writing for short
and with some simple computation we get – using again the ˆ= symbol and relation defined above – that
We are now ready to compute the matrix elements of H1 between states in the N multiplet, and in particular between states in the N=2 multiplet.¶
¶These formulas confirm once again that the action on the N=1 multiplet is trivial, in the sense that only diagonal matrix elements are nonzero.
We stress that here we are just considering H1, and not the detuning term. The latter, which causes the unperturbed system to be not exactly degenerate, will be taken care of through the general procedure for quasi-degenerate perturbation theory, see Section 3.3.
5.4.2. Action on the N=0 and N=1 multiplets
When acting on the N=0 and on the N=1 multiplets, as already remarked, H1 has only diagonal elements. This means that albeit the energy of the states is changed, the eigenstates are not modified nor mixed.
The new energy levels Es=E(0)s+E(2)s are easily computed via
where |s⟩ is the state under consideration.
Simple direct computations yield the results summarized in Table 1, where results are given in terms of two constants C and σ defined above, see Eqs (5.10) and (5.11). There and below we also write α:=α4/2.
We can thus easily compute the energy levels (at first order in perturbation theory) for the states belonging to the N=0 and N=1 multiplets; these are as follows:
These formulas hold for general ωi, albeit we have assumed ωi≈ω2 to have the multiplet structure. We would like to express our results in terms of the detuning. In order to do this we set
(note this is slightly different from the convention used in the classical examples of Section 4; this choice will produce more symmetric formulas). Writing moreover κ:=mω0 and working at first nontrivial order in δ, we get
and the energy levels computed above are (in the same approximation)
Note that the gap E(0,1)−E(1,0)=2ℏω0δ depends linearly on δ and on ω0, so no interesting phenomena take place as these parameters are varied.
5.4.3. Action on the N=2 multiplet
When we deal with the N=2 multiplet, the perturbation H1 has – beside diagonal terms – non zero matrix elements between the states |2,0⟩ and |0,2⟩. These are easily computed from the formulas given in Section 5.4.1 above (this also show that the state |1,1⟩ is not coupled to other states by H1). Moreover, we have in full generality ⟨2,0|H1|0,2⟩=(⟨0,2|H1|2,0⟩)∗, so it actually suffices to compute one matrix element.
To compute the matrix element of H1 between these two states, it is again convenient to consider separately the different terms making up H1. Now we have to compute both diagonal and off-diagonal elements; as for the latter ones, we know that the only coupling is between the |0,2⟩ and the |2,0⟩ states, so we need to compute only one off-diagonal term.
We start from computing this off-diagonal term. With simple computations we get
note that when we sum these, they cancel out. Moreover, with the notation introduced in Eq (5.11),
Thus, in conclusion,
Similar computations can be performed for the diagonal matrix elements; these are summarized in Table 2, where results are again given in terms of the two constants C,σ defined in (5.10) and (5.11).
Remark 17. The reader has surely noted that in all the cases considered here the contributions of the first four terms, i.e., of the term (p1p2q1q2+p1q1q2p2+p1q2q1p1+q1q2p1p2) in (5.7), cancel out. This could have been obtained by using the canonical commutation rules, but as this is unessential here we have preferred to go through direct computation. ⊙
Summarizing, the action of H1 on states belonging to the N=2 multiplet (ordered as {|2,0⟩,|1,1⟩,|0,2⟩}) is described by the matrix
In order to build the matrix W, see section 3.3, we need to consider the constants μk. To this aim, let us recall that the energy of the (unperturbed) state |n1,n2⟩ is given by Eq (5.2); setting ωi as in (5.13), we get
For the states in the N=0,1,2 multiplets, we get simply
In particular for the N=2 multiplet we have, in the notation of Section 3.3, λ0=3ℏω0 and the parameters μk are given by
This allows to write the matrix W as
Note that the detuning is now encoded into the coefficient
The eigenvalues of W/α are easily computed to be
setting ρ:=ξ/θ, the corresponding normalized eigenvectors are given by
As discussed in Sect.3.3, the energy levels of the perturbed system are
while the eigenvectors ai provide the eigenstates of the perturbed system through Eq (3.39). Note that the states ψ1=|2,0⟩ and ψ3=|0,2⟩ get mixed to form the eigenstates of the perturbed system, while the state ψ2=|1,1⟩ is not affected:
As for possible degeneracies in the perturbed system, these occur if and when η1=η2 or η1=η3 or η2=η3. Our explicit formulas (5.21) above allow to directly study these conditions.
In particular, it is obvious from (5.21) that η1=η3 if and only if ξ2+θ2=0, i.e., only for ξ=0 and θ=0; this is not relevant, as θ is always positive, see (5.11), and ξ=0 only for δ=0.
As for the other possible degenerations, we have that η1=η2 if
and η2=η3 if
obviously here we are taking the positive determination of the square root, so that solutions may exist depending on the sign of σ.
We would like to express these conditions in terms of the original physical constants appearing in the Hamiltonian. To this aim, we set
and insert the expressions for θ,σ,ξ, see (5.11) and (5.20), in the ηi. With the shorthand notation
these now read
These expressions can be simplified by conveniently choosing the units for mass and time (see Remark 12), so to have m=1 and ω=1, which also entails κ=1. Moreover, we can choose the unit of length so to have ℏ=1. In this way the expressions for the ηi are substantially simplified, and we get
These can be further simplified recalling that δ is a small parameter (and a pure number, so it is not affected by our choices of units); we can then expand in a power of δ around δ=0, which finally produces
here we have further simplified the writing by setting
Note that χ2≥1 is always a real parameter, finite for α≠0 (the case α=0 corresponds to no perturbation and is thus of no interest to us).
It is clear from (5.26) that η1=η2 admits no solution for real δ, whatever the value of α≠0; as for η2=η3 this has the solutions
These are always real since χ2≥1; in terms of the α perturbation parameter we get
Summarizing, we have that for |δ|<δ∗ the eigenvalues (and hence the energy levels) are ordered as
while for |δ|>δ∗ the ordering is modified into
Correspondingly, for |δ|<δ∗ the stable state in the N=2 multiplet is ϕ3, while for |δ|=δ∗ we have a quantum bifurcation and stable state for |δ|>δ∗ is ϕ2. The situation is illustrated in Figure 7. See also Figure 8.
When looking back at the classical case, see Section 4, one should note that ϕ3 is a deformation of the |0,2⟩ state, i.e., of one of the normal modes, while ϕ2 corresponds, loosely speaking, to the π/4 inclined mode.
It should be remarked, however, that the (quantum) bifurcation value δ∗ is rather large.
Remark 18. A final remark, at the end of this discussion, is in order. Even taking into account that we have preferred to give more details on the quantum computation than on the classical ones (supposing most readers from Mathematics and interested in Perturbation Theory are more familiar with classical than with quantum perturbation theory), it is rather clear that the quantum computations, albeit conceptually simpler, are technically more involved – at least at this level – for this simple model. It is thus not surprising that in many cases (see Section 6 below) one prefers to deal with a classical Hamiltonian and its normalization, and then study the quantization of the classical normal form; see in this respect Remark 13 and references mentioned there. This, however, introduces a number of issues: e.g., the new coordinates are in general not orthogonal (in the sense of the original cartesian metric in R2n), which makes the quantization problematic. These problem do not appear if one is working directly in terms of canonical quantum perturbation theory. ⊙
6.
Applications to simple molecules
We have discussed on the one hand the detuning approach in perturbation theory for (Hamiltonian) Classical Mechanics, and on the other Quantum Mechanics near-degenerate perturbation theory, claiming that the two approaches actually feed on the same set of ideas.
The usual realms of applications of classical and quantum perturbation theory are quite different: on the one hand, celestial mechanics and more generally macroscales; and on the other hand, atomic Physics and more generally microscales. As well known, there is however a field in which the two meet, and one uses depending on circumstances a classical or a quantum approach (or a semiclassical one); this is Molecular Physics.
In fact, this is not only the proper field for the meeting of classical and quantum Mechanics in general, and perturbation theory in particular; but this is also the field where the interrelation between detuning and near-degenerate perturbation theory has been more apparent – possibly unknown to scientists working in other fields.
Here we would like to focus in particular on a very simple system, which has also been the arena for the development on the kind of ideas discussed in this paper; that is, the dynamics of acetylene molecules. Acetylene is a simple molecule, made of two Carbon and two Hydrogen atoms, organized as follows in terms of chemical bonds
and in a one-dimensional array in geometrical terms, in its lowest energy state.
The molecule has several bending and rotational modes, which have been thoroughly studied not only experimentally, but also theoretically – and this precisely by means of perturbation theory, both classical, quantum, and semiclassical; see e.g., [38,46,48,63,76] and the review paper by Sibert and McCoy [75], focusing on the bending modes. Applications to other simple molecules (in particular HCN, SO2, H2CO, CO2, NO2) can be found e.g., in [23,39,40,46,47,48,57,58,60,66,67,69,70,82].
It should be said that the language used by chemists is sometimes not easy for a mathematician or a mathematical physicists, and possibly this hindered the communication between different communities. For our present purposes, it will suffice to say that in the case of molecules one speaks of polyads rather than multiplets; in both cases, however, one refers to a set of states (molecular or atomic) which are degenerate or nearly degenerate in Energy. Note that in the case of molecules, typically one has to do with multiple resonances [34,42] rather than with the single resonance we have been considering here. The mathematically oriented reader should also be warned that the near-degenerate quantum perturbation theory described here in Section 3 goes, in the Chemical literature, under the name of van Vleck (canonical) perturbation theory [73,74].
We will now briefly discuss the comparison between the classical and the quantum approach, focusing in particular on the simple acetylene molecule, and more specifically on the treatment of it provided in the foundational paper by Rose and Kellman [63].
First of all, we note that the normal form (4.3) is an integrable system, described in the R,ψ variables; this is parametrized by the Energy E and by the control parameters A,B,C,δ.
From the quantum point of view, E is determined by the quantum numbers ni, see (5.2). We will thus write
Let us fix the parameters A,B,C,δ, assuming for the sake of concreteness δ>0, and let us allow E to vary.
Looking back at Figure 2, this amounts to selecting a vertical line and move on it, say upward if E is increasing. Each crossing of a diagonal line corresponds to a bifurcation. See in this respect also Figure 2 in Rose and Kellman [63] (and several figures in Svitak et al. [76]); Figure 3 in Rose and Kellman [63] locates the quantum states, each point in there representing a polyad P, related in turn to n1,n2. Our computations reproduce the same situation, see Figure 9.
Let us now turn our attention to the energy-momentum map and to Figure 3; recall that here the coordinates correspond to the integrals of motion. This figure should be used by again fixing the value of E, and taking correspondingly a slice (that is, the corresponding vertical line) in the allowed region. Recall also that the vertical axis corresponds to the variable
Then the allowed states – corresponding to different possible values for the other parameters, in particular for K – will fall in regions of different colors, and their nature can be read from the color itself; needless to say if we follow the evolution of these states as E is varied, bifurcations are pointed out by the crossing of the boundaries between different regions.
One may try, in this context, to compare our results with those of Rose and Kellman [63]; note in this respect that the parameters appearing in the perturbation are hidden, in our Tables, within the constant C, defined in Eq (5.10).
The coefficients in the Rose and Kellman Hamiltonian (see Table I in their paper) become, when mapped into the notation (4.3),
We would then have E=n1+n2, which in Rose and Kellman notation becomes (with the same physical meaning) P=n4+n5; from now on we will pass to use the notation by Rose and Kellman, to ease the comparison with their results.
Using this, and the expression for the second integral of motion in terms of the quantum number, we have
We have then plotted, in Figure 9, the corresponding values – for 6≤P≤16 (only even values are allowed for P [63]) – on the "catastrophe map"; note that in order to compare this with Figure 3 in Rose and Kellman, one should take into account that their figure is vertically reflected with respect to our one (their vertical scale corresponds to −h).
We obtain that the Energy level for the first bifurcation (corresponding to crossing of the green line) is in between P=6 and P=8, while the Energy level for the second bifurcation (corresponding to crossing of the blue line) is in between P=14 and P=16; this is in full agreement with the results of Rose and Kellman.
It should be stressed that Rose and Kellman worked through a classical normalization and then quantization of the classical normal form, while our computations refer to the purely quantum computations given above.||
||Note that we are not providing an exact computation of their energy levels, in that we are not providing a computation of the contribution of the resonant term. This would require to extend the Tables given above, which deal with 0≤ni≤2, to the range 0≤ni≤6.
7.
Discussion & Conclusions
Classical perturbation theory in its modern form has been created by Poincaré through the theory of Normal Forms. Poincaré analyzed perturbations of non-degenerate linear systems, in which case the normal form is linear, while his pupil Dulac analyzed – along the same steps – degenerate ones, showing that one can proceed in essentially the same way but with a relevant difference in the outcome, i.e., the presence of resonant terms in the normal form; in this case one also speaks of a resonant normal form. The specific aspects of the theory for Hamiltonian systems – in which case one can deal directly with the Hamiltonian (a scalar function) rather than with the Hamiltonian vector field (2n components, i.e., 2n functions) – were studied by Birkhoff in the non-degenerate case and by Gustavsson in the degenerate one.
In all cases, the computations needed to reach the normal form are hindered by the presence of small denominators, which enter into play when we have to eliminate non-resonant (but nearly resonant) terms; their effect is to reduce the radius of convergence of the normalizing transformation, hence the region of phase space in which the normal form is properly approximating the full system.
In this sense, near-resonances are specially bad, leading to small denominators, while exact resonances are not so bad, as the corresponding terms do not have to be eliminated and hence the normalizing transformation does not have to face associated small denominators.
It is thus quite natural to approach systems with near-resonances by approximating them as fully resonant systems; correspondingly, one would aim at a resonant normal form. Albeit this is more complex than a linear normal form – in particular, it is nonlinear – it will be a valid approximation to the full dynamics in a wider region of phase space. In many situations, this will be preferable over a linear normal form which is simply analyzed but which describes the full dynamics only in an exceedingly small neighborhood of a stable (standard or relative) equilibrium.
The method of detuning (also called frequency deviation in the Russian literature, see e.g., Appendix 7.D to [2]) implements this idea: a near resonant nonlinear system is seen as a perturbation of a fully resonant one, which requires to see part of the linear terms as belonging themselves to the perturbation.
Here we have discussed the Hamiltonian framework, and actually considered for the sake of simplicity only the case of a neighborhood of an equilibrium position; but these ideas also extend to neighborhoods of periodic or quasi-periodic solutions and are also of use in the general Dynamical Systems and ODEs context; see e.g., [50].
Among other features, this detuning approach captures a very relevant qualitative feature: that is, while the dynamics of non-resonant systems (and hence their small enough perturbations) is described by invariant tori of maximal dimension, in resonant system we will have invariant tori of lower dimension, possibly closed orbits, and these may – suitably deformed – survive perturbations.
Another important feature of the detuning approach emerges when one has to deal with (slowly) varying parameters, in particular varying frequencies for the unperturbed system: through the detuning approach one can consider intervals of parameters, and in particular the case in which these go through a resonance [54,55]. In other words, the detuning approach is specially suit to analyze bifurcations, in particular those corresponding to crossing a resonance.
In this paper, we have reviewed the detuning approach to perturbations of near-resonant Hamiltonian systems, and remarked that this approach – or more precisely a conceptually equivalent one – is standard in Quantum Mechanics, were it goes under the name of nearly degenerate perturbation theory and as such is discussed in basic textbooks. It is remarkable that the same does not always hold for the detuning approach in Classical Mechanics (albeit of course some texts, such as the one by Arnold mentioned above [2], explain the need to consider a suspension of the system embedding it into a one parameter family, the parameter being just the detuning), so that a newcomer to the field could have the impression detuning was inspired by QM nearly degenerate perturbation theory. Even more remarkable (or regrettable) is the fact that a student could meet both the detuning approach in Classical Mechanics and near-degenerate perturbation theory in Quantum Mechanics without being told about the relations between the two.
The history of these ideas, and how they migrated from Classical Mechanics (and Linear Algebra) to Quantum Mechanics and back would deserve a study by scholars specialized in the History of Mathematics and Physics; we are not in this class, and our modest contribution here has been to stress this close relationship, also advocating a more ample diffusion of the detuning method among practitioners in classical perturbation theory – and the possibility to resort to the well developed quantum theory as a source of inspiration and of technical solutions.
The approach with varying parameters is rather common in Chemical Physics, see e.g., the references quoted above [9,23,34,38,39,40,41,42,46,47,48,57,58,60,63,66,67,69,70,75,76,82]; it has also been pursued in dealing with the Landau theory of phase transitions [24,25,26,27] (this is dealt with in a rather different mathematical context, dealing with gradient systems rather than Hamiltonian ones), and one could say with a little exaggeration that it is maybe more familiar to applied physicists than to mathematicians.
Here we have considered in full – and maybe excessive – detail the perturbation of a nearly resonant harmonic oscillator, both in the Classical and in the Quantum context, in order to display the seemingly different treatment of a simple case study in these two settings and how the same basic ideas which are behind the detuning approach and the nearly-degenerate quantum perturbation theory are embodied in different formalisms; and also how they, despite these formal differences and the obvious different features of Classical and Quantum Mechanics, lead to the same type of results.
If we may conclude on a personal note, we feel that the detuning approach has the merit of avoiding many technical intricacies of the standard approach leading to the same – or however comparable – results. We trust that this taste for simplicity without renouncing to mathematical rigor and technical exactness which is embodied in the detuning approach is also shared by Antonio Giorgilli and his many contributions to Dynamical Systems, Celestial Mechanics, and Perturbation Theory – in the past and we are sure also in the future.
Acknowledgements
We would like to thank the Editors of this Special Volume for giving us the opportunity to contribute to celebrating our friend Antonio Giorgilli on his retirement from non-mathematical activities, and for awaiting our contribution despite our delay. We also thank Ferdinand Verhulst for showing interest in this topic and thus pushing us (with no responsibilities on his side, of course) to write on the interrelations between classical and quantum perturbation theory with special emphasis on the detuning approach.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: