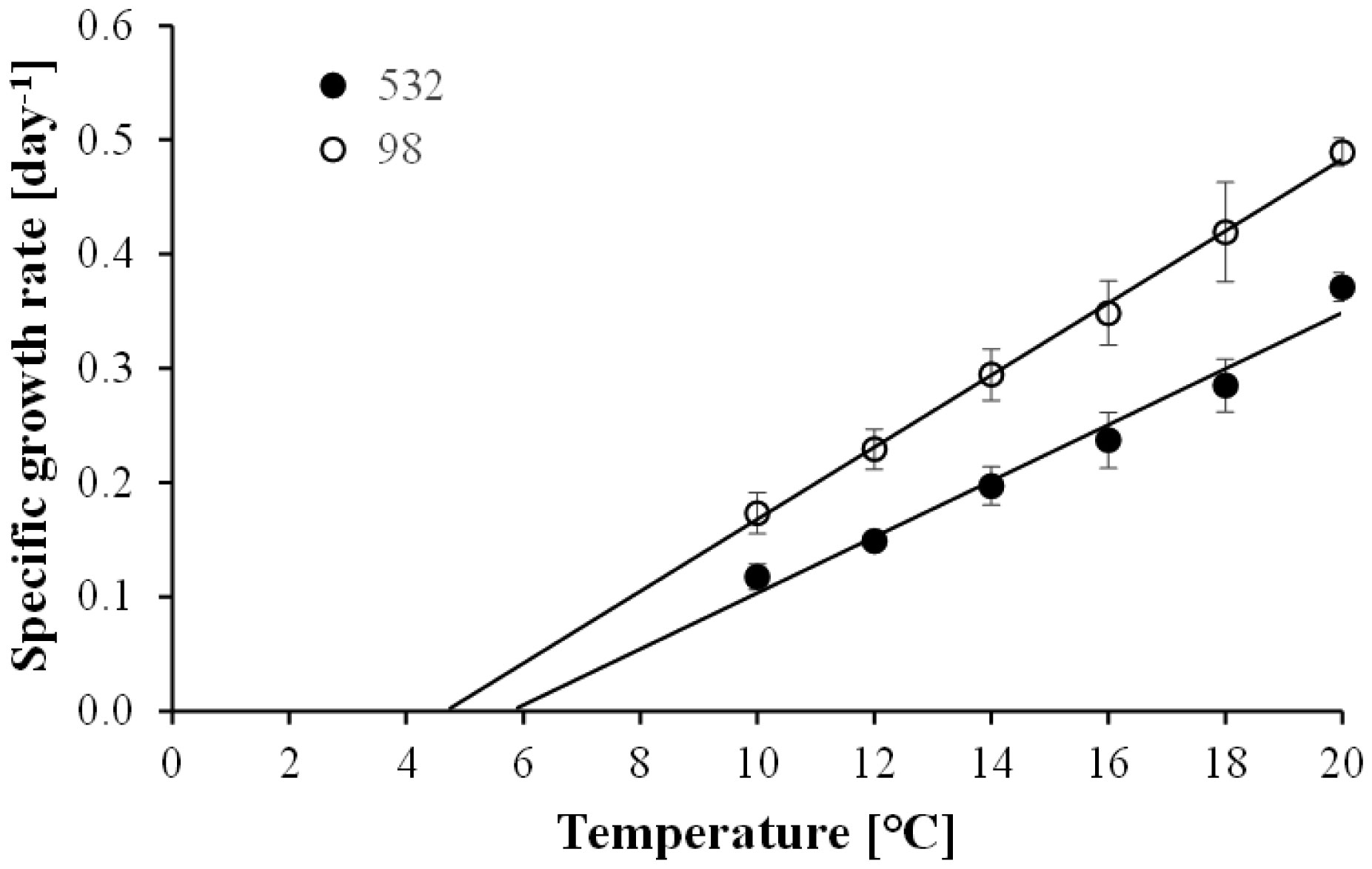
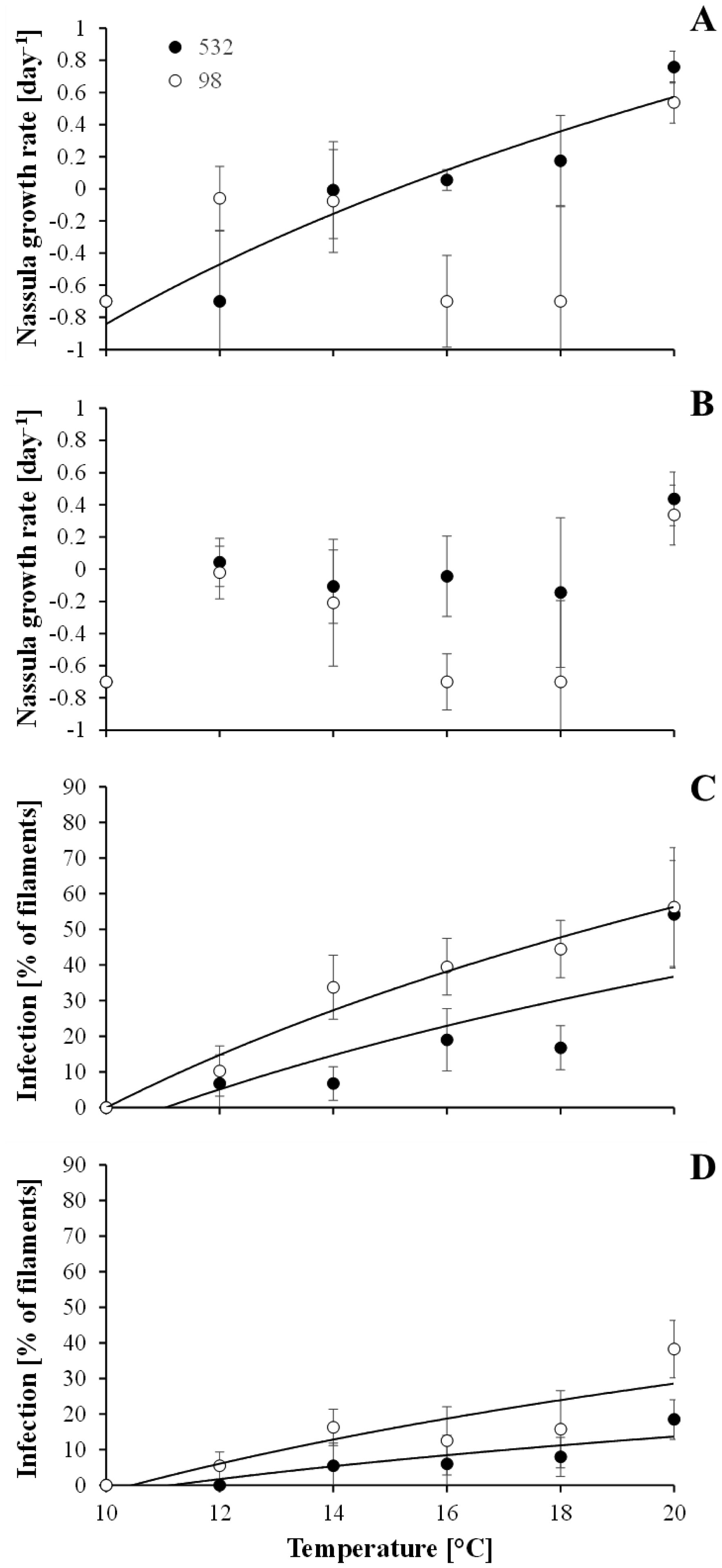
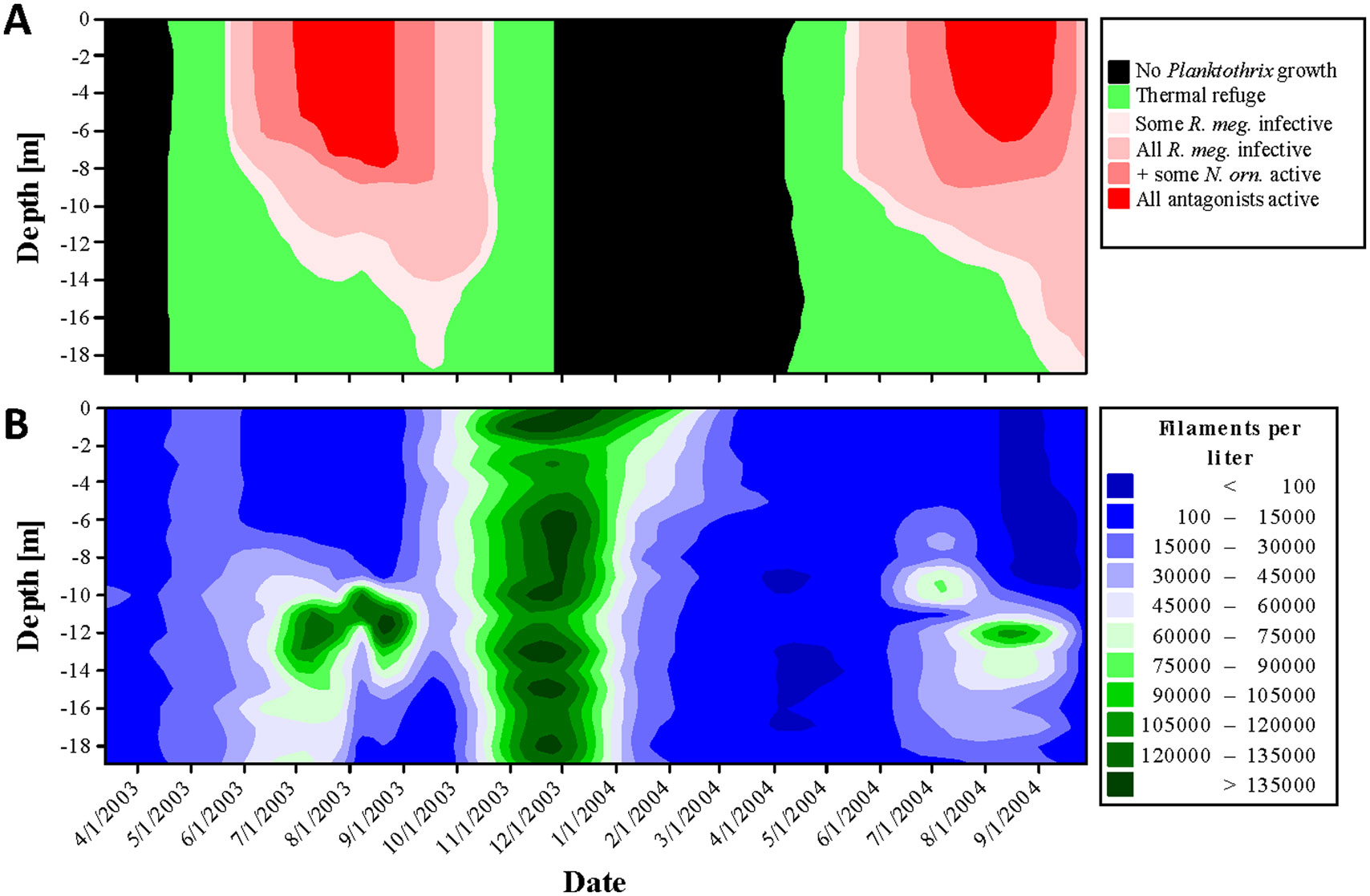
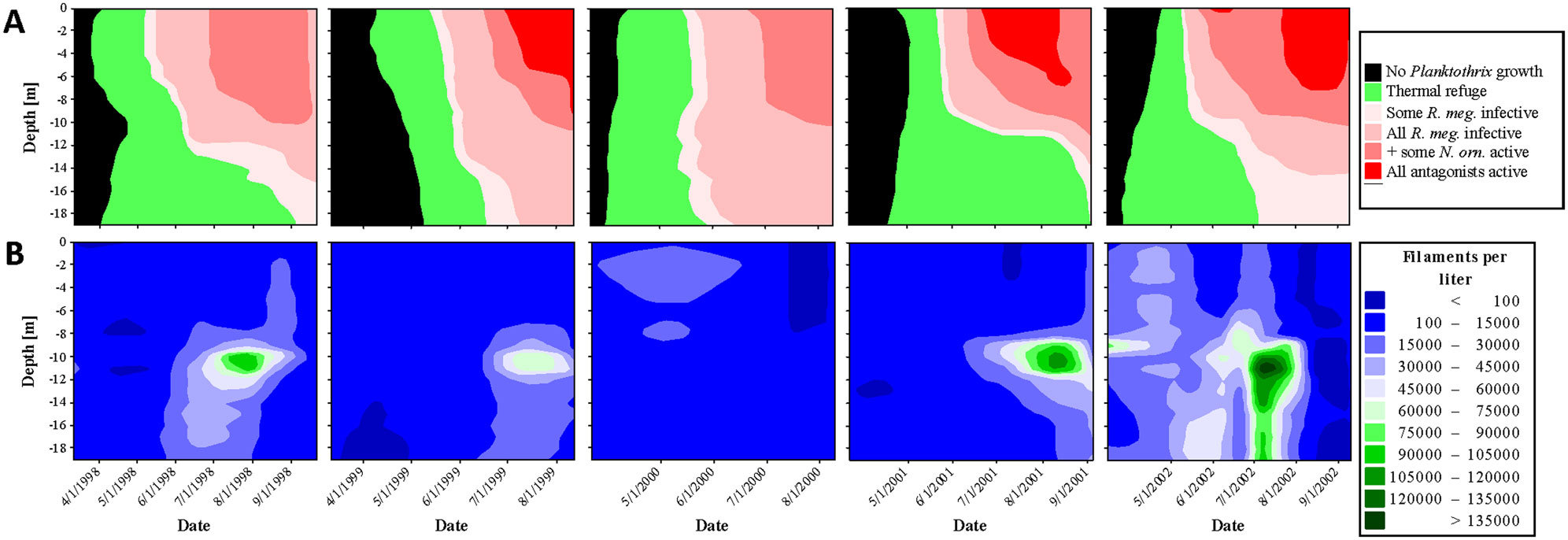
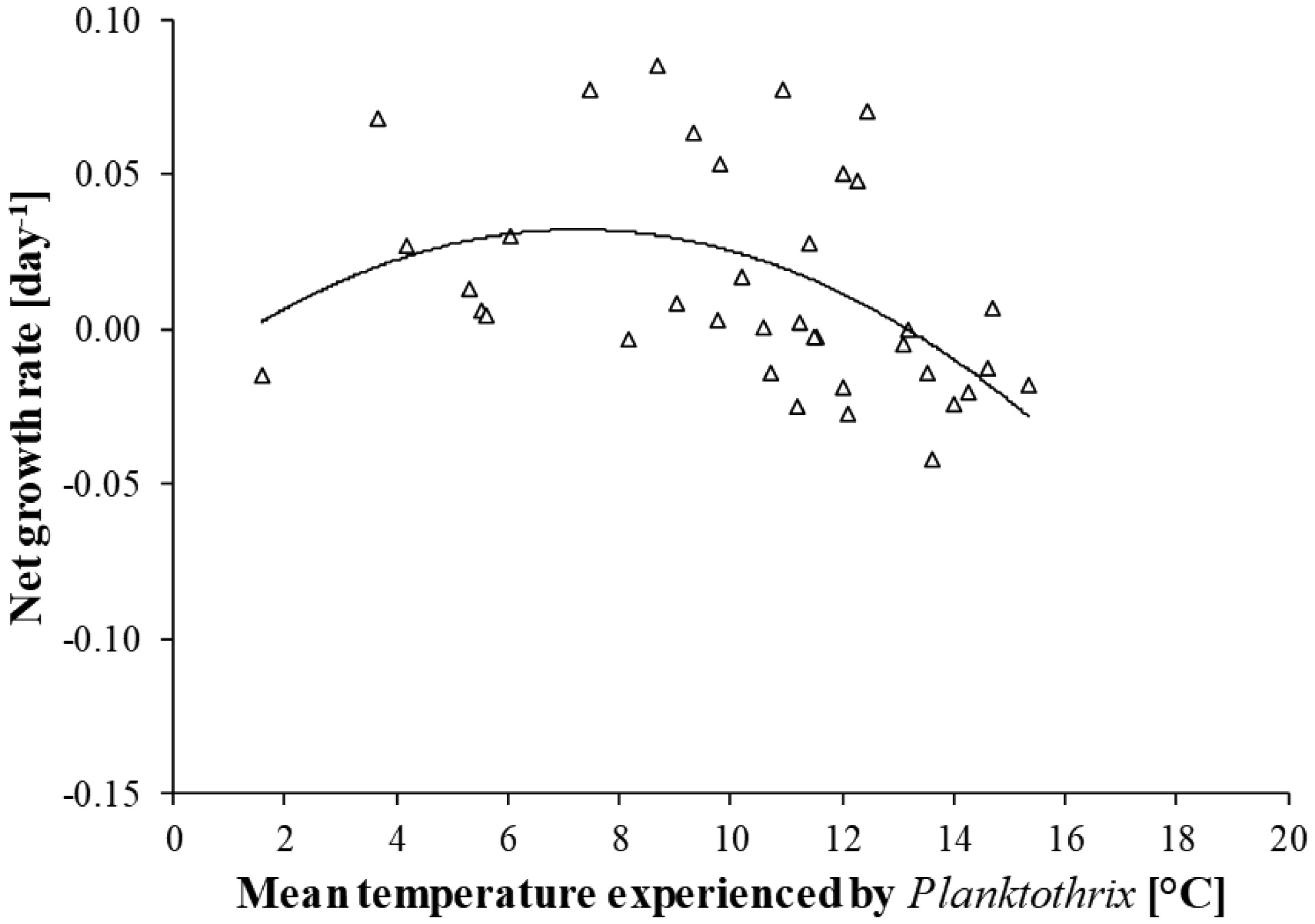
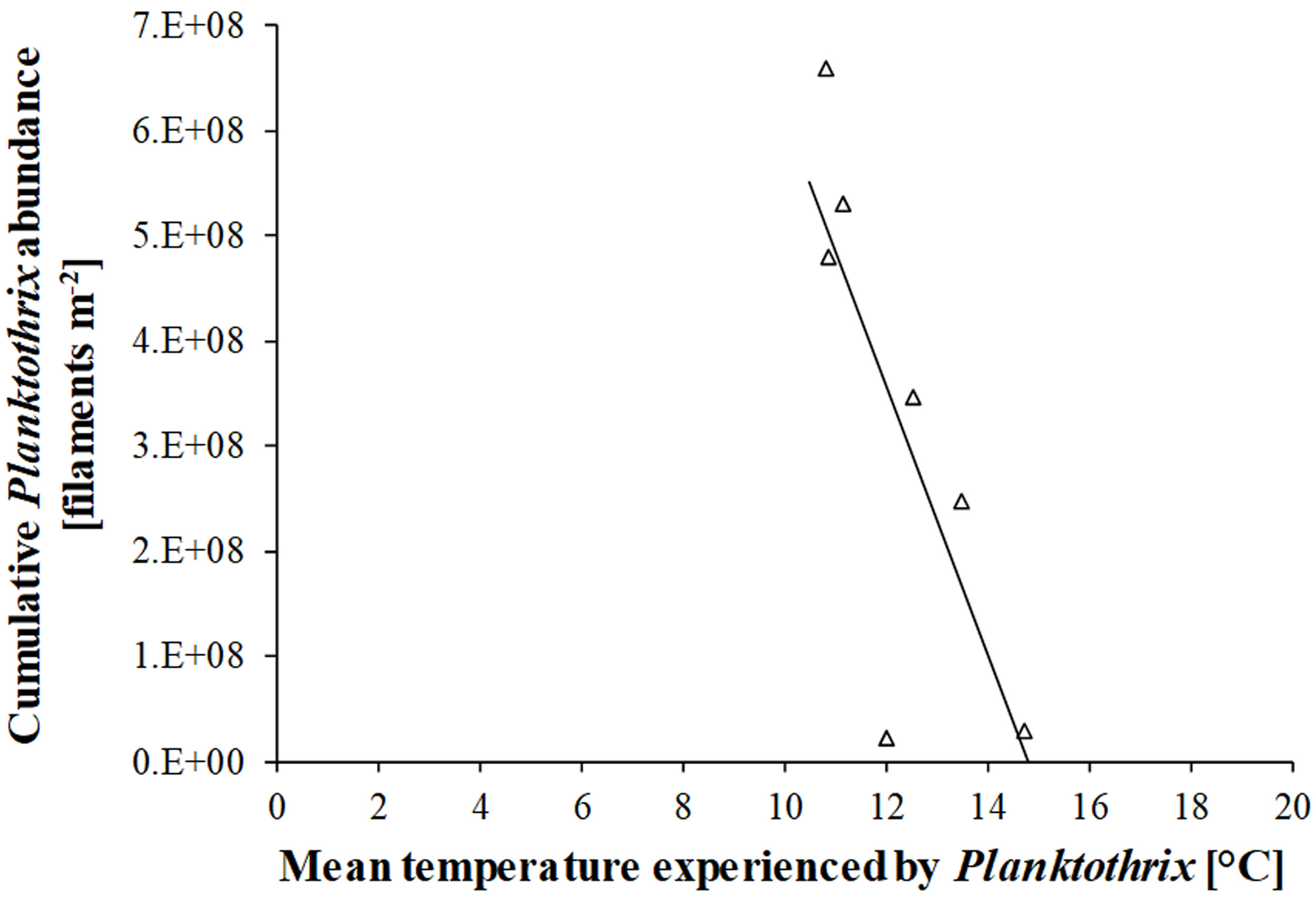
Freshwater cyanobacteria are prone to a wide range of highly potent microbial antagonists. Most of these exploit their prey in a frequency-dependent manner and are therefore particularly well suited to prevent any accumulation of cyanobacteria. Mass developments of cyanobacteria, the so-called blooms, should therefore be rare events, which is in striking contrast to what we actually see in nature. Laboratory experiments of the present study showed that the temperature range 5.8–10 °C forms a thermal refuge, inside which the cyanobacterium Planktothrix can grow without being exploited by two otherwise highly potent microbial antagonists. In nature, access of Planktothrix to this refuge was associated with positive net growth and a high probability of bloom formation, confirming that refuge temperatures indeed allow Planktothrix to grow with a minimum of biomass loss caused by microbial antagonists. Contact to higher temperatures, in contrast, was associated with decreases in net growth rate and in probability of bloom formation, with population collapses and with the occurrence of parasite infection. This is in agreement with the finding of laboratory experiments that above 10 °C exploitation of Planktothrix by multiple microbes increases in a temperature-dependent manner. Taken together, above findings suggest that temperature modulates the microbial control of natural Planktothrix populations. Low temperatures form a thermal refuge that may promote Planktothrix bloom formation by shielding the cyanobacterium from otherwise highly potent microbial antagonists.
1.
Introduction
The literature on epidemiological models incorporating behavioral aspects dates back, at least, to the pioneering works [13,40,41], in which the authors analyzed models with nonlinear incidence rates, which can be interpreted as behavioral changes due to awareness [24]. Since then, many authors have proposed epidemiological models that incorporated either the roles of awareness, information, or the influence of media reports in a more explicit way. We refer to the general reviews [7,24,57], where many references may be found, not only from mathematics, but also from economics, biology, and the social sciences. Even when looking specifically at the mathematical biology literature, the available works are still too numerous to mention. Therefore, besides the aforementioned reviews, we refer to the following works, which include useful summaries of existing works: [1,26,42,51,52,55,59,60].
In the context of susceptible-infected-recovered (SIR)/ susceptible-infectious-susceptible (SIS)-type (or mean-field) models, one can detect a general trend, namely that many existing works model awareness by introducing new 'aware' compartments for the susceptible or infected populations, respectively—see, for instance, [1,22,35,39,43,52,53] and especially the references cited in [60]. Other approaches include the use of a media function, which directly influences the incidence rate (although this approach is discouraged in [14]), or the use of an additional variable that models the cumulative number of media reports, thereby governing the transition from the unaware to the aware compartments [15,26,50,51,55]. For more in-depth reviews of the available literature, we point the reader to the aforementioned review papers, as well as the summary (up to 2015) compiled in [26].
Other models that incorporated awareness payed special attention to the contribution of spatial dynamics [23,59], introduced delays [2,3,26], explored the consequences of imposed lockdown or isolation measures [5,11,16,31,49,54,56], considered stochastic models [8], or detected information-induced oscillations [20], the effect of vaccinations [10,12,27], models with stage structure [38], hospitalization [11,44,58], and so on.
Notwithstanding these contributions, it would be desirable to have a more fine-grained description of the awareness states, instead of a simple aware/non-aware dicothomy. Additionally, it is reasonable to suppose that disease susceptibility can be similarly measured along a scale, and that awareness is an important factor to modulate the susceptibility: for instance, an individual who complies with preventive measures may be less likely to be infected.
With these aspects in mind, in this work, we introduce a model of epidemiological dynamics with heterogeneous susceptibility and disease awareness, which takes the form of a two-dimensional partial differential equation of transport type, a so-called structured model [47]. This will be the system (1.5) described below.
The model consists of a transport partial differential equation (PDE) acting on the healthy population. Moreover, in this work, we also focus on a system of ordinary differential equations (ODEs) (system (1.6) below), which are satisfied by integral quantities of the solutions of the PDE, in which the dynamical variables are the infected proportion, the mean susceptibility, and the mean awareness levels of the population. Besides providing an alternative viewpoint on infectious diseases modeling, we believe that the present approach has some advantages over more traditional ones found in the literature, which we discuss in more detail below.
An outline of the paper is as follows. In Section 1.1, we motivate and present our model, which, in its general form, consists of a two-dimensional transport equation, and deduce a $ 3\times 3 $ ODE system for its integral quantities. In Section 2, we provide an analysis of the transport equation, including the study of the characteristic curves and the definition of solution. In Section 3, we provide the theoretical results for the ODE system, including the threshold properties of the reproduction number $ R_0 $. In Section 4, we show an asymptotic result linking solutions of the structured model to the solutions of the ODE system. Finally, in Section 5, we provide some numerical experiments to illustrate the dynamics and our results, before some discussion and outlooks in Section 6.
1.1. Presentation of the model
As it turns out, even in epidemiology, the idea of using structured models (i.e., models in which the population is described by a density with respect to some property like age or size) dates back to the very first works on the subject [36,37], where the time since infection was taken as a structure variable. Since then, several works have considered epidemiological models with continuous structure variables. Among these, we can mention the books [6,17,34], where examples of various models and approaches can be found. Among the wider literature, we single out [32,46], where a structured model with virus evolution was studied. In those works, the number of cumulative virus aminoacid substitutions due to a mutation influenced the susceptibility rate. In [33], the models from [36,37] were revisited and given rigorous mathematical treatment. We also cite [28], where an age-structured model was considered. Then, [4] considered an infected population structured by a viral load, while [25] modeled within-host dynamics, with the infected structured by pathogen load and the level of immunity. Recently, [48] considered a model for malaria with age, time since infection, and immunity. As far as we know, no structured model in epidemiology has considered a disease awareness and a susceptibility structure (see, however, [45] for a related model). Finally, we mention the recent work [18], where a systematic approach to deduce models that took heterogeneity into account was developed, and where more references can be found.
Susceptibility and awareness structure
In this work, our proposal is to consider an epidemiological model where the susceptible (or healthy) part $ H $ of a population is structured by two attributes: the susceptibility to infection, $ s \in[0, 1] $, and a measure of the population's awareness of the disease, measured by the variable $ \lambda\in[0, 1]. $ Here, $ s $ ranges from no susceptibility to infection ($ s = 0 $) to maximum susceptibility ($ s = 1 $), while $ \lambda $ ranges from no awareness ($ \lambda = 0 $) to maximum awareness ($ \lambda = 1 $). In this way, for each time $ t $, $ H(t, s, \lambda) $ is the density of the susceptible population with respect to $ s, \lambda $, and $ \int_{s_1}^{s_2}\int_{a_1}^{a_2} H(t, s, \lambda) \, ds\, d\lambda $ represents the total population that has susceptibility in $ [s_1, s_2] $ and awareness in $ [a_1, a_2] $. For convenience, and since we do not consider deaths or other population dynamics in our model, we normalize the total population (susceptible and infected) to be one.
Awareness dinamics
As previously described, awareness may change according to many different factors [22]. In a structured model, these factors can be modeled by drift terms in a transport equation. Here, we will suppose that two main influences play a role: first, awareness may increase (i.e., the profile $ \lambda \mapsto H(t, s, \lambda) $ shifts to the right) proportionally to the total infected amount, with a saturation term $ (1-\lambda) $ preventing $ H(t, s, \cdot) $ from going beyond $ \lambda = 1 $. In our framework, this gives rise to the following term:
where $ I(t) = 1 - \iint H(t) \, ds\, d\lambda $ is the total amount of infected population.
Second, the disease awareness naturally decays to $ \lambda = 0 $ at a background rate $ \alpha_1 $, yielding the term $ \partial _\lambda(-\alpha_1\lambda H(t, s, \lambda)) $.
Susceptibility dynamics
Similarly, the susceptibility dynamics gives rise to the following drift terms:
where the quantity $ G_\lambda \ge 0 $ describes how the awareness of the population influences the speed at which susceptibility decreases. At this point, observe that we do not specify the form of $ G_\lambda $; reasonable choices include some explicit function of $ \lambda $ such as, $ G_\lambda (\lambda) = \lambda $, or nonlocal quantities of the healthy population distribution, such as the average awareness of the population. Thus, the first term models the natural growth of susceptibility towards the maximum $ s = 1 $, while the second term expresses that the susceptibility of the population decreases to zero with a speed governed by the awareness of the population, in a manner that we will make precise below.
Infection dynamics
The susceptible population can become infected by contact with the infected population $ I(t) $ through a mass-action law with a background transmission rate $ b > 0 $. Additionally, the infection probability should be influenced by the awareness and susceptibility of the population. In general, we can suppose that this influence takes the following form:
on the right hand side of the differential equation, for some quantities $ F_s, F_\lambda $ which describe the influence of susceptibility and awareness on the infection rate. As a general rule, $ F_s $ should increase with the susceptibility, and $ F_\lambda $ should decrease with the awareness, thus reflecting the assumption that individuals with a lower susceptibility and a greater awareness have a smaller chance of being infected. Again, we purposefully introduce these quantities here with a great degree of generality, noting that reasonable choices include functions of either $ s $ or $ \lambda $ (for instance, $ F_s(s) = s $ and $ F_\lambda(\lambda) = 1-\lambda $), or nonlocal, time-dependent functions of the population, such as the mean susceptibility and the mean awareness.
The infected population recovers with a mean infectious period $ 1/\gamma $, and this is modeled by a boundary term at $ s = 0 $, since we suppose that individuals recover with minimal susceptibility. Finally, when recovered individuals return to the susceptible pool at $ s = 0 $, we must specify what their distribution is according to awareness, which we do by considering a function $ f(\lambda) \ge 0 $. This gives a boundary term of the following form:
where $ \alpha_2 $ appears in order to ensure the proper units. Note that integrating the previous boundary condition in $ \lambda\in (0, 1) $ shows that it is natural to assume that $ \int_0^1 f(\lambda) \, d\lambda = 1 $ due to mass conservation, which we will do henceforth.
With the addition of the initial datum $ H_0(s, \lambda)\ge 0, $ these assumptions give rise to the following transport equation for $ H(t, s, \lambda) $:
for $ s, \lambda \in [0, 1], t\ge 0 $, with the following boundary and initial conditions:
and where $ I(t) = 1- \iint_{[0, 1]^2} H(t, s, \lambda) \, ds\, d\lambda $.
Since the specification of problem (1.2), (1.3) is, in fact, dependent on the choice of the response terms $ G_\lambda, F_s, F_\lambda $, it actually represents a family of models from which we hope particular and useful cases can be studied. Now, we present the particular choice for Eq (1.4), which we will focus on in this work.
A model depending on mean awareness and mean susceptibility
As mentioned, problem (1.2), (1.3) requires the specification of the quantities $ G_\lambda, F_s, F_\lambda $ which (we recall) represent the contribution of awareness on the decrease of susceptibility, the influence of susceptibility on the infection rate, and the influence of awareness on the infection rate, respectively.
It makes sense to choose some configuration which is tractable as a first object of study, but still nontrivial. In particular, it would be useful if at least some of the dynamics of the transport equation could be described by a system of ODEs through a reduction to certain integral quantities. It would be even more useful if the resulting system contained interesting and nontrivial dynamics related to the awareness and susceptibility, which are amenable to the analysis.
One simple way to achieve this is to assume that the dynamics are primarily determined by the mean values of the population's awareness and susceptibility distributions at each time, which we denote by $ \Lambda(t) $ and $ \Sigma(t) $, respectively, in such a way that the infection rate should increase with the susceptibility and decrease with the awareness. This leads to the following choice:
in Eq (1.2) above.
Remark 1.1. Other choices are possible in Eq (1.4), which would lead to models stressing different aspects of the dynamics. One natural possibility is to consider $ F_s = s $, $ F_\lambda = 1-\lambda $, $ G_\lambda = \lambda $, or other functions such as $ s^\alpha $, $ (1-\lambda)^\alpha $, for $ \alpha > 0 $. This type of choice would explicitly account for the fact that parts of the population with different levels of (say) susceptibility, in fact, should have a different disease transmission rate. In contrast, taking the average values within (1.4) means that we are approximating the transmission rate at each time with an "effective" transmission rate determined by the mean value of the relevant attribute of the population at that time. Despite this simplification, it is still true that different levels of awareness or susceptibility (but now seen as time-dependent averages) dictate the dynamics. Moreover, the choice Eq (1.4), as we shall see in the following, allows us to build a system of ODEs, which describe many of the aspects of the transport equation. In that system, the awareness and susceptibility dynamics play a major role, and that analysis is one of the main goals of this paper. To choose $ s, \lambda- $dependent functions in Eq (1.4) would require different techniques, which are more focused on the study of the transport equation (1.2) itself. That is an obvious next step which we leave for further works.
In view of the previous discussion, we now introduce the system under consideration in this paper:
and all integrals are taken in $ [0, 1]^2 $. Here, $ u(t) $ is the total susceptible proportion, $ I(t) $ is the infected proportion, $ \Sigma(t) $ is the mean susceptibility, $ \Lambda(t) $ is the mean awareness, and $ f(\lambda) $ is the awareness distribution of the population reentering the susceptible pool. The variables and parameters are described in Table 1 below.
1.2. Reduction to an ODE system
Despite the choice of time dependent averages for the response functions (cf. Eq (1.4) and Remark 1.1), the full transport equation model (1.5) is still challenging, from both analytical and numerical standpoints; see, for instance, Section 2.2, where some effort is required just to define the solution. However, the form of equations (1.5) and (1.4) allows us to deduce an ODE system from Eq (1.5), from which epidemiological results may be obtained. To this end, we now consider the integral quantities $ u(t) $, $ \Sigma(t), $ and $ \Lambda(t) $ of Eq (1.5), and check that they actually verify a $ 3\times 3 $ system of ODEs, which will be the object of the analysis in Section 3.
As previously mentioned, we assume that $ \int_0^1 f(\lambda) \, d\lambda = 1 $, and let $ \lambda_0 = \int_0^1\lambda f(\lambda) \, d\lambda $ be the mean awareness level of the recovered population. Then, from Eq (1.5), we can compute the time evolution of the quantities $ u(t), \Sigma(t), \Lambda(t) $. For instance,
where we have used integration by parts and the boundary condition. Similarly, denoting by
using the equation and with an integration by parts, we obtain the following:
After a little computation, this leads to the following:
Proceeding in a similar way to compute $ \Lambda'(t) $, we arrive at the following system for the healthy proportion $ u $, the mean susceptibility $ \Sigma $, and the mean awareness $ \Lambda $:
supplemented with initial data $ u(0), \Sigma(0), \Lambda(0) $. Note that the initial values can be computed from the initial susceptible density $ H_0(s, \lambda) $ according to the expressions in Eq (1.5). In Table 1, we summarize the variables and parameters that appear in systems (1.5) and (1.6).
In what follows, it will be useful to consider the variable $ I = 1-u $, yielding the following system:
Remark 1.2. We note that the reduction of the PDE (1.5) to the system (1.6) was possible only because of the choice Eq (1.4) for the response functions. In this way, solutions to the PDE with equal total initial masses and first moments will originate the same ODE solution. At least, when the conditions for the asymptotic results in Section 4 are verified, this determines the long time behavior of the solutions to the PDE (1.5). However, this does not preclude that different behaviors in the $ s $ and $ \lambda $ variables may occur, while maintaining the same evolution for the integral quantites present in the ODE system. This exploration, however, falls beyond the scope of the present work.
We have the following well-posedness theorem for Eq (1.6).
Theorem 1.3. Solutions of Eq (1.6) with an initial condition in $ (0, 1]\times [0, 1]^2 $ are unique and globally defined in the future, and the set $ (0, 1]\times [0, 1]^2 $ is positively invariant for the flow associated to Eq (1.6). An analogous result holds for system (1.7) when the initial condition lies in $ [0, 1)\times [0, 1]^2 $.
Proof. Uniqueness is guaranteed by the fact that the vector field is locally Lipschitz. As to the global existence, we will prove it for system (1.7) and hence the global existence for Eq (1.6) immediately follows. We prove this by ensuring that all the solutions with initial condition in $ [0, 1)\times [0, 1]^2 $ enter in the compact set
for some small $ \epsilon > 0 $ and stay there. First, observe that $ \Sigma, \Lambda \in [0, 1] $ for all $ t\ge 0 $, which is a consequence of the signs of $ \Sigma', \Lambda' $ when $ \Sigma, \Lambda \in \{0, 1\} $. Now, supposing that $ I\ge 1-\epsilon $, we find that $ I'(t) \le b\epsilon + \gamma (\epsilon -1) $. Thus, choosing
we find that $ I'(t) < -\gamma/2 $. Therefore, we can say that $ I(t) \in [1-\epsilon , 1) \Rightarrow I'(t) < -\gamma/2 $, from which the result follows. □
1.3. Relation with other models with disease awareness
Before proceeding to the more technical parts of this work, let us briefly comment on a few aspects of our model and results that highlight some points in our approach. First, we note that in earlier works, which divided the population into aware and unaware compartments in a binary way, two reproduction numbers appear, one for each compartment, thus leading to case-by-case analyses of their relative values (for example, in [22]); the same can be said for models with only two stages of susceptibility. Our approach only gives a single reproduction number $ R_0, $ which determines the dynamics and depends only on the transmission rate and the mean infectious period, just as in the traditional models. However, this does not mean that the awareness has no influence on the dynamics. Indeed, in Corollary 3.3 below, we show that the system parameters related to the awareness can have a large influence on the asymptotically-infected proportion.
Our model has a continuum of states for both the disease awareness and the susceptibility. For instance, works such as [9,29,30] only considered a finite number of susceptibility states, while [45] considered a continuum of states, although in a different approach.
Additionally, we note that our results can be compared to [19], where it was found that certain types of delayed memory models related to disease awareness could have a destabilizing effect, which generated a periodic behavior. Our approach also leads to the bifurcation phenomena and the appearance of limit cycles, as we show with numerical experiments below.
All in all, the present model exhibits a wide range of previously observed effects related to awareness dynamics, while being of a type not hitherto applied to these questions. Additionally, our methods provide new insights into the influence of awareness on epidemic outcomes, namely regarding the efficacy of sustained versus punctual awareness campaigns, as discussed in Section 5 below.
2.
Study of the transport equation
2.1. Characteristic curves and notations
In this section, we provide a basic theoretical study of the transport equation (1.5). To define its solutions, we first define the characteristic curves of the equation and explore their dynamics. We show that all characteristics eventually end up inside the unit square $ (s, \lambda) \in (0, 1)^2 $. This allows us to define an appropriate concept of solution in Definition 2.2.
Equation (1.5) has two families of characteristic curves, namely for $ t\ge0 $, $ t+r \ge 0 $,
They are obtained by integration of the following characteristic equations:
which are easily deduced from the equation (1.5). Here, $ \Lambda(t), I(t) $ are the solutions of the system (1.6) with the initial data computed from $ H_0(s, \lambda) $.
Therefore, the characteristic curve that passes by the point $ (s, \lambda) $ at time $ t $ is parametrised by $ r\mapsto (\phi_r(t; s, \lambda), \psi_r(t; s, \lambda)) $ in such a way that
In particular, the foot of the characteristic curve which reaches $ (s, \lambda) $ at time $ t $ is as follows:
Similarly, given $ (s_0, \lambda_0) $ at $ t = 0 $, then at time $ t > 0, $ the characteristic curve starting at $ (s_0, \lambda_0) $ is at the point $ (\phi_t(0;s_0, \lambda_0), \psi_t(0;s_0, \lambda_0)) $.
As long as $ I $ and $ \Lambda $ remain continuous and bounded functions of $ t $, then for each $ t > 0, $ $ t+r \ge0 $, the maps
define diffeomorphisms of $ \mathbb{R}^2 $.
Here, we record the following consequence of Eq (2.1), which we use throughout this work:
2.2. Definition of solution to the transport equation
With the characteristic curves in hand, we are able to define the solution by integrating along the characteristics. The domain of interest is the square $ (s, \lambda) \in [0, 1]^2 $. Therefore, our first task is to guarantee that the characteristics point into the interior of $ [0, 1]^2 $ along its boundary. However, this is immediate from the characteristic equations (2.2), as can be seen by setting in turn $ s = 0, 1, \lambda \in [0, 1], $ and $ s\in [0, 1], \lambda = 0, 1 $. From this, it follows that each characteristic crosses the boundary $ \partial \, [0, 1]^2 $ at most once.
Now, we prove that all characteristic curves must eventually end up inside $ (0, 1)^2 $:
Proposition 2.1. Let $ (s, \lambda) \in \mathbb{R}^2 $. Then, there exists $ t_* \ge 0 $ such that for all $ t > t_* $,
Proof. Let $ s\in \mathbb{R} $. Suppose that, for some time $ t > 0 $, we have that $ \phi_t(0;s, \lambda) = 0 $. From Eq (2.3), this is equivalent to the following:
so that necessarily $ s\le 0 $. Since the function $ t \mapsto -\alpha_2 \int_0^t e^{\alpha_2 r + \alpha_4 \int_0^r \Lambda(v) \, dv} \, dr $ is surjective over $ (-\infty, 0) $, we conclude that for any $ s\le 0, $ there exists $ t $ such that $ \phi_t(0;s, \lambda) = 0 $. Similarly, if $ \lambda\in \mathbb{R} $ and $ \psi_t(0;s, \lambda) = 0 $ for some $ t $, then from Eq (2.3) we must have the following:
and so $ \lambda \le 0 $ necessarily. As $ t \mapsto -\alpha_3 \int_0^t e^{\alpha_1 r + \alpha_3 \int_0^r I(v) \, dv} I(r) \, dr $ is surjective over $ (-\infty, 0) $, then for any $ \lambda\le 0, $ there exists $ t $ such that $ \psi_t(0;s, \lambda) = 0 $.
Suppose now that $ \psi_t(0;s, \lambda) = 1 $ for some $ t $. This is equivalent to the following:
First, note that $ h(0) = 1 $ and $ h'(t) = \alpha_1 e^{\alpha_1 t + \alpha_3 \int_0^t I(r) \, dr} > 0 $, so that $ h(t) > 0 $ for all $ t $. Therefore, it is necessary that $ \lambda\ge 1 $. Furthermore, we have that $ h"(t) = \alpha_1 (\alpha_1 + \alpha_3 I(t)) e^{\alpha_1 t + \alpha_3 \int_0^t I(r) \, dr} > 0, $ and so $ h(t) \to +\infty $ as $ t\to \infty $ and $ h(t) $ is surjective onto $ \mathbb{R}_+ $. Thus, every characteristic starting at some point with $ \lambda > 1 $ eventually reaches $ \lambda = 1 $. In a similar way, we find that every characteristic starting at some point with $ s > 1 $ eventually reaches $ s = 1 $. The situation is summarised in Figure 1. Thus, we see that from any starting point in the plane, the characteristic curve eventually reaches $ (0, 1)^2 $, where it remains for all subsequent times. □
Now, for a fixed $ t > 0 $, we see from Eq (2.3) that the image of the line segment (say) from $ (s, \lambda) = (0, 0) $ to $ (0, 1) $ under the action of the characteristics at time $ t $ is the following set:
in which (cf. Eq (2.3)) is linear in $ \lambda $, and is therefore a line segment. By the same reasoning applied to the four sides of the square $ \partial \, (0, 1)^2 $, and by the continuity of the characteristics, we conclude that for each $ t > 0 $, there exists a (filled) rectangle $ R_t \subset (0, 1)^2 $ such that $ (\phi_t(0;s, \lambda), \psi_t(0;s, \lambda)) \subset R_t $ for all $ (s, \lambda) \in (0, 1)^2 $ (see Figure 2). Equivalently, for any $ (s, \lambda) \in R_t $, the foot $ (\phi_{-t}(t; s, \lambda), \psi_{-t}(t; s, \lambda)) $ of the characteristic which passes through $ (s, \lambda) $ at time $ t $ lies in $ (0, 1)^2 $. Thus, we conclude that for each $ t, $ the map $ (s, \lambda) \mapsto (\phi_t(0;s, \lambda), \psi_t(0;s, \lambda)) $ is a bijection from $ (0, 1)^2 $ to $ R_t $. Therefore, for smooth solutions, at least, the solution $ H(t, s, \lambda) $ when $ (s, \lambda) \in R_t $ should be obtained by integrating along the characteristic using the initial data on $ (0, 1)^2 $:
Consider now that $ t > 0 $ and a point $ (s, \lambda) \in(0, 1)^2 \setminus R_t $. From what we have seen, $ (s_0, \lambda_0) \equiv(\phi_{-t}(t; s, \lambda), \psi_{-t}(t; s, \lambda)) $ must lie outside of $ (0, 1)^2 $. In that case, by Lemma 2.1, the characteristic curve emanating from $ (s_0, \lambda_0) $ crosses $ \partial \, (0, 1)^2 $ exactly once. This means that there exists a unique $ t_* > 0 $ such that
However, this point is exactly $ ((\phi_{-(t-t_*)}(t; s, \lambda), \psi_{-(t-t_*)}(t; s, \lambda)) $ by the semigroup property. Therefore, the solution $ H(t, s, \lambda) $ for $ (s, \lambda)\in (0, 1)^2\setminus R_t $ should be obtained by integrating the characteristic curve from $ t_* $ to $ t $ using the boundary data. Since the characteristics point towards the interior of $ (0, 1)^2 $ on all the boundaries, and a boundary condition is only active on the segment $ \{s = 0\} \times\{\lambda\in (0, 1)\} $, we can consider the function $ G: \mathbb{R}_+\times\partial \, (0, 1)^2 \to \mathbb{R} $ such that
and set
where, we recall, $ t_* > 0 $ is the unique time $ t_* < t $ (depending on $ t, s, \lambda $), at which the characteristic curve that passes through the point $ (t, s, \lambda) $ departs from the boundary $ \partial \, (0, 1)^2 $.
Collecting the previous considerations, we arrive at the following definition of solution.
Definition 2.2. For $ t > 0, $ define the open rectangle $ R_t\in (0, 1)^2 $ by the following:
see Figure 2. Let $ H_0(s, \lambda) \in C((0, 1)^2) $ with $ H_0 \ge 0 $, $ {\rm{supp}}\ H_0 \in (0, 1)^2, $ and $ \iint H_0 \, ds \, d\lambda > 0 $. A solution of Eq (1.5) is a function $ H(t, s, \lambda) \ge 0 $ such that
where $ G $ is defined in Eq (2.4), $ t_* $ is the unique time at which the characteristic curve that passes through the point $ (t, s, \lambda) $ departs from the boundary $ \partial \, (0, 1)^2 $, and
with all double integrals in $ (0, 1)^2 $.
With Definition 2.2 in hand, and due to the special structure of the system (1.5), it turns out that the existence of solution to the transport PDE (1.5) is a consequence of the well-posedness results obtained on the ODE system (1.6) in Theorem 1.3. Indeed, given an initial datum $ H_0(s, \lambda) $ for which the integral quantities $ \Sigma(0), \Lambda(0), $ and $ I(0) $ are well defined, we can consider the corresponding unique solution $ I(t), \Sigma(t), \Lambda(t) $ of system (1.6), defined for $ t\in[0, +\infty) $, and the expression (2.5) gives (by definition) a solution of the linear transport equation obtained by considering such a triplet in the coefficients and in the boundary conditions. Then, to show that such $ H $ actually solves the nonlocal transport equation (1.5), one only has to prove that the relations (2.6) hold.
This is done as follows: with $ H $ given by (2.5), we define $ \tilde u(t): = \iint_{Q} H(t, s, \lambda)\, dsd\lambda\, $ $ \, \tilde v(t): = \iint_{Q} s H(t, s, \lambda)\, ds d\lambda $ and $ \tilde w(t): = \iint_{Q} \lambda H(t, s, \lambda). $ Then, since $ Q: = [0, 1]^2 = R_t\cup (Q\setminus R_t), $ we compute the integrals on $ Q $ by means of the changes of variables
from $ Q $ to $ R_t $ (with inverse $ (\tilde s, \tilde\lambda) = (\phi_{-t}(t, s, \lambda), \psi_{-t}(t, s, \lambda))\, ) $ and
from $ [0, t_*]\times [0, 1]\to Q\setminus R_t $ (with inverse $ (s, \lambda) = (\phi_{-(t-t_*)}(t, s, \lambda), \psi_{-(t-t_*)}(t, s, \lambda))\, ) $
Computing $ \tilde u'(t), \tilde v'(t), \, w'(t), $ one sees that $ (\tilde u, \tilde\Sigma, \tilde\Lambda) $ and $ (u, \Sigma, \Lambda) $ satisfy the same ODE system with the same initial condition provided by $ H_0; $ therefore, by the uniqueness of solutions, we conclude that $ \tilde u = u, \tilde \Sigma = \Sigma, \tilde \Lambda = \Lambda. $ We omit the details of the computations.
3.
Dynamics of the ODE sytem
In this section, we will focus on the full ODE system (1.6) and analyze its properties. We begin by observing that the basic reproduction number is provided, in the case $ \gamma > 0 $, by $ R_0 = \frac{b}{\gamma} $, as can be found by linearizing the first equation around the disease-free equilibrium.
Theorem 3.1. Consider the system (1.6). Then,
1. If $ R_0 < 1 $ the disease-free equilibrium $ (u, \Sigma, \Lambda) = (1, 1, 0) $ is locally asymptotically stable and is the unique equilibrium of system (1.6) in $ [0, 1]^3 $.
If $ R_0 > 1 $, then:
2. The disease-free equilibrium is unstable, and there exists at least one endemic equilibrium $ (u_*, \Sigma_*, \Lambda_*) \in (0, 1)^3 $.
3. The endemic equilibrium is unique if either of the following conditions hold:
4. Under the conditions
an endemic equilibrium is locally asymptotically stable.
5. The system satisfies the following uniform persistence property: there exists a constant $ \eta > 0 $ (depending on $ R_0 $) such that for all $ (u_0, \Sigma_0, \Lambda_0) \in (0, 1] \times [0, 1]^2, $ the following holds:
Proof. At the disease-free equilibrium $ (u, \Sigma, \Lambda) = (1, 1, 0), $ it is easy to check that the characteristic equation for the Jacobian matrix is as follows:
with
The Routh-Hurwitz stability criterion reads as follows:
Then. it is trivial to verify that it is equivalent to the condition $ \gamma-b > 0 $, which is precisely $ R_0 < 1 $. This proves the stability property in Assertion 1, and also that the disease-free equilibrium is unstable if $ R_0 > 1 $. The uniqueness of the disease-free equilibrium is obtained from the equality $ \Sigma (1-\Lambda) = \frac{\gamma}{bu}, $ which cannot hold in $ [0, 1]^3 $ if $ R_0 < 1 $.
Suppose now that $ R_0 > 1 $, and let us sketch the proof that there exists at least one endemic equilibrium $ (u_*, \Sigma_*, \Lambda_*) $ in $ (0, 1)^3 $. Setting the right-hand side of Eq (1.6) equal to zero, we obtain after some computation that
Then, it is possible to check the following: (i) the denominators in the above expressions are never zero for $ u\in(0, 1) $; (ii) a lengthy but straightforward computation shows that $ \Sigma' = 0 \Leftrightarrow $
From this, we see that $ p(0) < 0 $ and $ p(1) > 0 $; thus, there exists at least one $ u_* \in (0, 1) $ such that $ p(u_*) = 0 $. Finally, (iii) one can check that, in fact, the expressions $ \Gamma_* $ and $ \Sigma_* $ resulting from setting $ u = u_* $ in Eq (3.3) are in $ (0, 1) $, though we omit the details for the sake of brevity.
To find a sufficient condition for uniqueness of $ u_* \in (0, 1) $ solving $ p(u) = 0 $, write Eq (3.4) as follows:
Then, since $ p(0) < 0 $ and $ p(1) > 0 $, we see that $ u_* $ will be unique in $ (0, 1) $ as long as $ a_3 < 0 $. Thus, the condition
is sufficient to ensure the uniqueness of $ u_* \in (0, 1) $. The stronger (but simpler) conditions
stated in the theorem easily imply Eq (3.6). This proves the first condition in Eq (3.1).
Now, let us check that the second condition in Eq (3.1) is also sufficient for the uniqueness of $ u_*\in(0, 1) $. As we already know, $ a_3 < 0 $ (cf. Eq (3.5)) is a sufficient condition for the uniqueness of $ u_* $; Now, suppose that $ a_3 > 0 $. Since $ p(0) < 0 $ and $ p(1) > 0 $ still hold, we can see that if there is more than one root of $ p(u) $ in $ (0, 1) $, then necessarily we must have $ p'(0) > 0 $ and $ p'(1) > 0 $. Therefore (always with $ a_3 > 0 $), if either $ p'(0) < 0 $ or $ p'(1) < 0, $ then there will be only one root of $ p(u) $ in $ (0, 1) $. Writing $ p'(0) < 0 $ gives $ a_1 < 0 $, which is precisely the second condition in Eq (3.1).
The stability conditions in Assertion 4 remain to be shown. Write $ (A_{ij}) $ as the Jacobian matrix at $ (u_*, \Sigma_*, \Lambda_*) $. We have the characteristic equation as follows:
where, since $ A_{32} = 0 $,
According to the Routh–Hurwitz criterion, linear stability is equivalent to the conditions
In the following, we again omit the subscripts in $ (u_*, \Sigma_*, \Lambda_*) $. First, we note that $ a_1 > 0 $ easily follows from the fact that the equilibrium is in $ (0, 1)^3 $.
Next, from Eq (3.7) write the term $ a_3 = A + B+C+D $, with obvious notations. We have that $ A, D > 0 $ simply by inspecting the signs in the expression of the Jacobian matrix (which we omit). On the other hand,
and
We see that a sufficient condition, which ensures that $ B, C > 0, $ is that $ \lambda_0 - \Lambda > 0 $. From Eq (3.3) we can easily find that this condition is ensured as long as
Therefore, under this condition, we have that $ a_3 > 0 $ in Eq (3.8).
Let us check the third condition in the Routh–Hurwitz criterion Eq (3.8). After some computation involving Eq (3.7), we find the following:
Supposing that Eq (3.9) holds, we have the following sign properties:
Using this, we see from Eq (3.10) that the only non-positive term is as follows:
Now, the idea is to find sufficient conditions on the coefficients of the problem, such that some of the positive terms in Eq (3.10) can compensate the negative contribution from this last term, enough to make $ a_1a_2-a_3 $ positive.
Putting this strategy into practice with the (negative) term $ -\alpha_3\alpha_4 \gamma (1-\Lambda)(1-u) $ and the (positive) term $ -2A_{11}A_{22}A_{33} $ in Eq (3.10), we get after some computations that $ 2R_0^2 \alpha_1 \alpha_2 < \alpha_3\alpha_4 $ implies that the total contribution of these two terms in Eq (3.10) is positive.
Now, only the term $ - \frac{\gamma^2}{u^2}\alpha_4(\lambda_0 - \Lambda) (1-u) $ remains to compensate with some positive term, which we do with the term $ A_{13}A_{31}A_{33} $. It turns out (again, we omit the details) that the condition $ \alpha_4 < \alpha_1 $ is sufficient, so that the contribution of these two terms to Eq (3.10) is positive, as announced in the Theorem.
Now, we prove the uniform persistence property in Assertion 5. For this, it will be more convenient to use the infected proportion $ I = 1-u, $ and hence consider Eq (1.7). By the proof of Theorem 1.3, we can restrict ourselves to the following compact set:
for a small $ \epsilon > 0 $.
Let $ S = X \cap \{I = 0\} $. We want to show that $ S $ is a uniform repeller by applying [21, Thm.1] with $ P(I, \Sigma, \Lambda) = I. $ Define the neighbourhood $ U_{\epsilon ^*} = \big\{ (I, \Sigma, \Lambda) \in X : I < \epsilon ^* \big\} $ of $ S $. We will show that it is possible to choose a sufficiently small $ \epsilon ilon^* $ in such a way that any solution for which $ I(0)\in U_{\epsilon ^*} $ satisfy $ I(t_1)\geq \epsilon ilon^* $ for a suitable $ t_1 > 0 $. Then, assume by contradiction that for any $ \epsilon ilon^* > 0 $ there exists $ (I, \Sigma, \Lambda) \in U_{\epsilon ^*} \setminus S $ with $ I(t) < \epsilon ^* $ for all $ t > 0 $. Then, from Eq (1.6), we find discarding some non-positive terms, and taking $ \epsilon ^* < 1/2 $,
This way, we have that $ \limsup_{t\to +\infty} \Lambda(t) \le \frac{\epsilon ^*}{\alpha_1}(\alpha_3 + 2\gamma\lambda_0). $ Thus, for all $ t $ sufficiently large, we have $ \Lambda(t) \le 2\frac{\epsilon ^*}{\alpha_1}(\alpha_3 + 2\gamma\lambda_0) \equiv C \epsilon ^* $.
Turning to the $ \Sigma $ equation, we find that for a large $ t $,
where here and in what follows $ C > 0 $ can change from line to line, but only depends on the parameters of the system. Therefore,
Accordingly, we can find $ \epsilon _1 > 0 $ (which goes to zero with $ \epsilon ^* $) and $ t_1 > 0 $ such that for all $ t > t_1 $ one has $ \Sigma > 1- \epsilon _1 $. From (1.7), we obtain the following:
Now, it suffices to choose a sufficiently small $ \epsilon ^* $ (and thus also $ \epsilon _1 $) so that $ b(1-\epsilon _1) (1-C\epsilon ^*)(1-\epsilon ^*) - \gamma > 0, $ which is possible since $ b-\gamma > 0 $. This way, we have that for all $ t $ large enough $ I'(t) \ge \partial ta I(t) $, for some $ \partial ta > 0 $, which is enough to conclude that eventually $ I(t) \ge \epsilon ^* $.
Therefore, $ S $ is a uniform repeller (cf. [21]). By using [21, Cor.1], we get that the remaining part of $ \partial X $ is also a uniform repeller. Consequently, the persistence property 5 holds. This concludes the proof of Theorem 3.1. □
Remark 3.2. After extensive numerical testing, the uniqueness property of $ u_* \in (0, 1), $ and hence of the endemic equilibrium, seems to hold only under the more natural condition $ R_0 > 1 $. However, we could not prove this fact analytically, since we are lead to expressions that quickly become unwieldy.
The following corollary asserts that, under meaningful conditions on the awareness decay, the infected proportion can be made as small as we wish for large times.
Corollary 3.3. Let $ R_0 = b/\gamma > 1 $, and suppose that the stability conditions (3.2) are verified. Moreover, suppose that
Then, the endemic equilibrium $ u_* $ of the susceptible proportion can be made unique, (locally) stable, and as close to one as desired – and thus the infected proportion as small as desired – as long as the natural decay rate of the mean awareness, $ \alpha_1 $, is small enough.
Proof. First, we observe that from the stability conditions (3.2), we can see that $ 1-\lambda_0 $ is small if, and only if, $ \alpha_1 $ is small, and that the smallness of $ \alpha_1 $ implies the smallness of $ \alpha_4 $. Therefore, with a small $ \alpha_1 $, we may suppose that all three parameters $ \alpha_1, \alpha_4, $ and $ 1-\lambda_0 $ are small.
From the analysis of the polynomial $ p(u) $ whose zeros give the equilibrium(s) $ u_* $ (cf. Eq (3.5)), we can see one situation in which $ u_* $ is unique in $ (0, 1) $ when $ a_3 > 0 $, $ p'(0) < 0 $ and $ p'(1) > 0 $. The condition $ a_3 > 0 $ reads as follows:
Thus, with a sufficiently small $ \alpha_1, \alpha_4, $ and $ 1-\lambda_0 $ (in fact, only $ 1-\lambda_0 $ is needed), we have that $ \alpha_2\alpha_3 > \gamma \alpha_3 \implies a_3 > 0 $. Therefore, we will suppose that $ \gamma < \alpha_2 $.
Next, we have that $ p'(0) < 0 \Leftrightarrow a_1 < 0, $ where $ a_1 $ is defined after Eq (3.5). As observed, $ a_1 < 0 $ gives $ 2\gamma < \alpha_1 + \alpha_2 +\alpha_3 +\lambda_0 \alpha_4 $, and so discarding the small terms again, we get that $ 2\gamma < \alpha_2 +\alpha_3 $ is enough to guarantee $ p'(0) < 0 $ under the present smallness conditions. This justifies the condition Eq (3.11).
Now, we look at the condition $ p'(1) > 0 $. From Eq (3.5), this is equivalent to $ 3a_3 + 2a_2 + a_1 > 0 $. This gives the following:
Since the terms on the left-hand side are positive, and the terms on the right-hand side can be made arbitrarily small, we conclude that $ p'(1) > 0 $ for $ \alpha_1, \alpha_4 $ and a sufficiently small $ 1-\lambda_0 $.
These properties of the cubic polynomial $ p(u) $ imply that it remains below the secant line from $ (0, p(0)) $ to $ (1, p(1)) $ in $ [0, 1] $. Additionally, Recall that, in any case, $ p(0) = -\gamma_2 < 0 $, and $ p(1) = \alpha_1\alpha_2 (R_0-1) > 0 $. Therefore, the (unique) root $ u_* $ of $ p(u) $ in $ [0, 1] $ lies in $ [u_1, 1] $, where $ u_1 $ is the root of the secant line from $ (0, p(0)) $ to $ (1, p(1)) $. An easy calculation gives the following:
which can be made arbitrarily close to one, by taking a sufficiently small $ \alpha_1 $. This completes the proof of Corollary 3.3. □
4.
Asymptotic behavior of the transport equation
In this section, we prove an asymptotic result characterizing the limit as $ t\to \infty $ of the solutions of the transport equation (1.5), whose initial data are in the basin of attraction of a stable endemic equilibrium. We recall that the conditions for the existence, uniqueness, and local asymptotic stability of the endemic equilibria are provided in Thm. 3.1.
We need the following technical lemma, whose elementary proof we only sketch.
Lemma 4.1. Let $ c_1\ge0, c_2\ge0, c_3, c_4 $ be constants with $ c_1^2+c_2^2 > 0 $, and suppose that $ w : (0, +\infty) \to \mathbb{R} $ is bounded and measurable with $ \lim\limits_{t\to \infty} w(t) = w_* > 0 $. Then,
If $ c_1 > 0 $, then the condition $ w_* > 0 $ can be relaxed to $ w_*\ge0 $.
Proof. Multiply and divide by $ e^{c_1t + c_2 w_* t} $ and apply l'Hôspital's rule. □
The following theorem gives the concentration of the characteristic curves associated to the transport equation (1.5) on a single point for any suitable initial data and large times, and a characterisation of $ \lim_{t\to\infty} H(t, s, \lambda). $
Theorem 4.2. Suppose that the initial datum $ H_0(s, \lambda) $ is such that $ (u_0, \Sigma_0, \Lambda_0) $ lies in the basin of attraction of an endemic equilibrium $ (u_*, \Sigma_*, \Lambda_*) $ of the system (1.6). Then:
1. The characteristic curves of the transport equation (1.5), defined in Eq (2.1), satisfy the following:
2. If $ H(t, s, \lambda) $ is the solution of the transport equation (1.5), defined in (2.5), we have $ \lim_{t\to\infty}H = H_\infty $ on the set
which is the (asymptotic) domain of influence of the boundary $ \{s = 0, \lambda\in[0, 1]\} $, where
with
and $ H_\infty = 0 $ on $ [0, 1]^2 \setminus \mathcal{A}_\infty $.
Proof. To show Eq (4.2), apply Lemma 4.1 to Eq (2.3) with the appropriate coefficients $ c_i $, and taking $ w = \Lambda $ and $ w = I $ in turn.
Now, we turn to the proof of $ \lim_{t\to \infty} H = H_\infty $. The key point is to observe that, if $ (s, \lambda) $ can be reached by a characteristic issuing from the boundary $ \{s = 0\} $, then in fact
where $ t_* $ is the time at which the characteristic that passes through $ (t, s, \lambda) $ departs from the boundary $ \{s = 0\} $ (cf. Definition 2.2). Let us prove Eq (4.7). From Eq (2.1) with $ r = t_*-t, $ we find that $ t_* $ is defined by the following identity:
Note that, formally substituting $ \Lambda(v) $ by its asymptotic value $ \Lambda_* $ and solving for $ t-t_* $ in the resulting identity immediately gives Eq (4.7), though we wish to make this more precise.
First, note that by implicitly differentiating Eq (4.8), we can see that $ \frac{\partial t_*}{\partial t} \ge C > 0, $ and so $ t_* $ goes to $ +\infty $ with $ t $. Now, since by assumption the equilibrium $ (u_*, \Sigma_*, \Lambda_*) $ is attractive, then for $ \epsilon ilon > 0 $ and a large $ t $ we have $ \Lambda(t)\in [\Lambda_*-\epsilon ilon, \Lambda_*+\epsilon ilon]. $ Then, a comparison with the flows $ \phi^+ $ and $ \phi^- $ of the equations, cf. Eq (2.2),
(for which the corresponding $ t-t_* $ are given by the same expression as Eq (4.7) but with $ \Lambda_* \pm \epsilon $ instead of only $ \Lambda_* $), gives the limit relation Eq (4.7) by taking $ \epsilon ilon\to 0 $.
With Eq (4.7) in hand, we can calculate the asymptotic domain of influence $ \mathcal{A}_\infty $ of the boundary $ \{s = 0, \lambda\in[0, 1]\} $. From the definition of the second characteristic field in Eq (2.1), we see that the points on the boundary $ \{s = 0, \lambda\in[0, 1]\} $ at time $ t_* $ are mapped by the flow to the points $ \psi_{t-t_*}(t_*, 0, \lambda) \in [\lambda^-(t, s), \lambda^+(t, s)] $, where
Therefore, when $ t\to \infty, $ we find the expressions (4.6) for $ \lambda_\infty^{\pm}(s) \equiv \lim_{t\to\infty}\lambda_{\pm}(t, s) $ using Eqs (2.1), (4.2) and (4.7), and consequently $ \mathcal{A}_\infty $. Then, for $ (s, \lambda)\in \mathcal{A}_\infty $ we find from Eqs (2.4) and (2.5), that
The expressions in Eqs (4.4) and (4.5) follow again from Eqs (2.1) and (4.10) and (4.7) after some computation.
Finally, the concentration of the characteristics on the point $ (s_*, \lambda_*) $ shows that $ H_\infty $ vanishes outside of $ \mathcal{A}_\infty $. However, this does not exclude the possibility that a dirac delta could form at that point. To discard this possibility, it is enough to show that $ \lim_{t\to\infty} \iint_{R_t} H(t, s, \lambda) \, ds \, d\lambda = 0 $. For this, we note that from the solution on $ R_t $ in Def. 2.2 and by the change of variables (2.7), we find the following
which tends to zero with $ t\to \infty $ since $ \Sigma (1-\Lambda) I \to \Sigma_* (1-\Lambda_*) I_* > 0 $. □
5.
Numerical examples
In this section, we provide some numerical experiments to illustrate the dynamical behavior of the solutions to the ODE system (1.6), as well as the theoretical results of the previous sections.
Example 1. As other authors have previously observed (see the details in the Introduction), awareness dynamics can have an important impact on epidemiological outcomes. Here, we present examples of some of that influence. First, we observe that according to the biological meaning of the parameters $ \alpha_i $, $ i = 1, 2, 3, 4 $, in Table 1, we can expect the following relations to occur:
● Lowering the background mean awareness decay rate $ \alpha_1 $ should give a positive epidemiological outcome, as measured by a lower cumulative infections number;
● Lowering the background mean susceptibility growth $ \alpha_2 $ should give a positive epidemiological outcome;
● Increasing the rate of awareness growth per infected, $ \alpha_3 $, should give a positive epidemiological outcome; and
● Increasing the rate of susceptibility decay per awareness, $ \alpha_4 $, should give a positive epidemiological outcome;
In Figure 3, we can check that these relations indeed hold. We plot the cumulative infections for a solution of Eq (1.7) in red. The curves in cyan correspond to larger values of the parameter being varied in each plot, and the curves in green correspond to smaller values of the parameter. The parameters used for the baseline red solution are as follows: $ I(0) = 0.95, \Sigma(0) = 0.85, \Lambda(0) = 0.05, R_0 = 2.5, \gamma = 0.3, \alpha_1 = 0.01, \alpha_2 = 0.01, \alpha_3 = 0.005, \alpha_4 = 0.2, $ and $ \lambda_0 = 0.5. $ In the case of $ \alpha_1 $ and $ \alpha_2 $, solutions with increased values of that parameter (in blue/cyan) have higher cumulative infection levels, while for $ \alpha_3 $ and $ \alpha_4, $ the opposite happens. Interestingly (for the parameter ranges tested), the value of the awareness growth per infected $ \alpha_3 $ has very little influence on the cumulative infections.
These results are in line with what has been observed in previous models, namely that a higher awareness response (in a broad sense) reduces the prevalence of the disease [1,23,26,50,52].
Example 2. The condition (3.2) only gives sufficient conditions for the asymptotic stability of the endemic equilibrium, which leaves the possibility of limit cycles and bifurcations. Indeed our numerical tests suggest that the system exhibits sustained oscillations for some parameter regimes.
For instance, increasing the background mean susceptibility growth $ \alpha_2 $ changes the behavior of the solution from periodic oscillations, separated by periods of very low prevalence, into convergence towards an endemic steady state, as shown in Figure 4. In this figure, the red line is plotted using values of the parameters giving periodic oscillations, and the blue lines have increased values of $ \alpha_2 $, which destroy the periodic behavior. Therefore, we can say that decreasing the background mean susceptibility growth $ \alpha_2 $ also contributes to the formation of isolated infection peaks separated by periods of near zero prevalence.
As shown in Figure 3, although our results are in line with other works and variations in the model parameters yield expected changes to epidemiological outcomes, our experiments reveal some counter-intuitive facts. In Figure 4, recall that the cyan lines correspond to larger values of the mean susceptibility growth. As mentioned, this is associated with a higher cumulative prevalence of the disease, which is to be expected. However, if one were to be given only the second from top plot in Figure 4, it would be natural to think that the cyan curves are associated with better epidemiological outcomes, since the population remains in a near-constant state of awareness, which is higher than that for the dark blue or red lines–and intuitively, more awareness is better. However, the opposite is true, and in this case higher (but near-constant) awareness levels produce worse outcomes in terms of cumulative infections.
In other words, a larger, but stable, mean awareness level leads to more stable susceptibility profiles, which can produce larger cumulative infection numbers; in contrast, periodic "scares" (as in the red line in Figure 4), where awareness and susceptibility vary more wildly in response to sharp, but localized in time, infection outbreaks, may in fact contribute to lower cumulative infections over time.
6.
Discussion and conclusions
We have presented and analyzed a model for epidemiology dynamics including disease awareness and susceptibility, where both of these aspects were allowed to assume any value in $ [0, 1] $. The base dynamics took the form of a transport equation (1.5), from which we deduced the ODE system (1.7) for integral quantities of the solution of the transport equation. This results in an SIS-type model where, in contrast to traditional models, the dynamical variables were the susceptible (or the infected) proportion, the mean awareness, and the mean susceptibility of the susceptible population.
In our model, the possible range of the awareness and susceptibility were not restricted to two (or even finitely many [45]) values. We showed that even when considering the awareness and susceptibility, a single, simply defined, reproduction number $ R_0, $ which depended only on the mean infectious period and the background transmission rate (that is, the transmission rate in a setting with full susceptibility and no awareness, which could therefore be estimated from contact rates and properties of the particular disease), determined the existence and properties of an endemic equilibrium. This is in contrast with previous works, where it was often necessary to consider two separate reproduction numbers, one for the aware, and one for the unaware population.
However, this result does not mean that awareness dynamics do not play a role in the epidemiological dynamics. On the contrary, we showed that even with an arbitrarily high reproduction number, it is possible (in appropriate parameter regimes) to ultimately reduce the infected proportion to arbitrarily small values, as long as the mean awareness decay rate of the susceptible population is small enough. This reinforces the results in the related literature in a precise way, which tends to agree that "more awareness" corresponds to better epidemiological outcomes.
However, in Section 5, we uncovered instances which showed that the relation between awareness and epidemiological outcomes was not so predictable due to the nonlinear nature of the model, and so must be analyzed with care. We found cases in our numerical experiments where a sustained high value of mean awareness originated worse outcomes (as measured by cumulative infections) as compared to lower levels of awareness interspersed with high peaks. This shows that care must be taken when using simulations of this nature to guide public policy: the temporal distribution of awareness campaigns may matter, and so it remains a delicate question whether sustained (but lower level) campaigns or intense campaigns in response to infection outbreaks are better.
We should remark about how it would be possible to estimate the parameters related to awareness dynamics, namely $ \alpha_{1, 3, 4} $ (see Table 1). In each of these parameters, a way must be found to distribute the population according to some measure of awareness in $ [0, 1] $, at least at $ t = 0 $. For instance, this could be acheived with surveys. Ideally, a survey can be used to create an (approximate) density function of the population supported on $ [0, 1] $. In that case, the precise meaning of an individual having a particular awareness value would depend on the particular survey and its analysis criteria. For practical purposes, it would also be necessary to map the possible susceptibility states of a population to the interval $ [0, 1] $, although that could be more easily relatable to existing epidemiological data. Then, a parameter such as $ \alpha_4 $ (the rate of susceptibility decay per unit of awareness per unit time) could be estimated by knowing the susceptibility of the population at given times through epidemiological data and assessing their disease awareness through surveys or other means. Needless to say, such a careful analysis falls beyond the scope of this work, where we attempted to show only a qualitative agreement between our model and epidemiological expectations.
Although our model does not account for demographic effects, these could be included. For instance, an extra equation for the demography of the infected population $ I(t) $ could model disease-related deaths. This would come at the cost of an extra equation in the ODE system (since the conservation of the total population would no longer hold); therefore, the analysis performed might not be straightforward to generalize.
Regarding the main ODE system under consideration, (1.6), a lot remains to be done. Namely, our results and numerical experiments suggested the possibility of periodic orbits, and so it would be interesting to check for the presence of (say) Hopf bifurcations. Similarly, we have only mentioned the most basic properties of the transport equation (1.5). At the very least, a numerical study is in order, which we leave for future work. Notice also that, despite the asymptotic result in Theorem 4.2, more interesting structures in the solutions of Eq (1.5) are not ruled out, in the case where the assumptions of the theorem are not met. For instance, it would be interesting to observe the segregation of the population into different sub-populations with either different dynamics, oscillatory behaviors, or to rule out such situations. These are questions which cannot be determined by the behavior of the ODE system alone and require a study of the PDE.
In the same vein, as noted in Remark 1.1, the right hand side of the transport equation (1.5) is, in some sense, the simplest possible within our setting: the integral quantities associated to any solution of the PDE verify the ODE system (1.6). More realistic coefficients in Eq (1.5), depending not just on the average quantities $ \Sigma, \Lambda $, but rather on the values of $ s, \lambda $ themselves, would make the analysis of the PDE more interesting, but would weaken the link with a system of ODEs in the way that is managed in this work. Still, the study of such more realistic models could shed more light on the dynamics of disease awareness beyond what is achieved in this work.
Finally, the presented methods are not restricted to the study of disease awareness. One may use similar ideas to consider other relevant traits in epidemiology, such as vaccination, immunity, treatment intensity, hospitalization, and so on. We hope that our methodology may be used to create new models in these, or other, topics.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgements
The authors would like to thank the anonymous referees for useful comments and suggestions. Paulo Amorim would like to thank CEMAT-Ciências, Universidade de Lisboa, for the warm hospitality during a visit where ideas for this work were developed. Paulo Amorim was partially supported by CNPq (Conselho Nacional de Pesquisa) grant no. 308101/2019-7 and by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. Alessandro Margheri was supported by FCT project UIDB/04561/2020. Carlota Rebelo was supported by FCT projects UIDB/04621/2020 and UIDP/04621/2020 of CEMAT at FC-Universidade de Lisboa.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: