Figure 1.
Block diagram of multi-slot RF energy harvesting system and time slot structure.
Citation: Lucy McMullen, Steven T Leach, Daniel A Lemberg, Andrew S Day. Current roles of specific bacteria in the pathogenesis of inflammatory bowel disease[J]. AIMS Microbiology, 2015, 1(1): 82-91. doi: 10.3934/microbiol.2015.1.82
| [1] | Nazanin Zaker, Christina A. Cobbold, Frithjof Lutscher . The effect of landscape fragmentation on Turing-pattern formation. Mathematical Biosciences and Engineering, 2022, 19(3): 2506-2537. doi: 10.3934/mbe.2022116 |
| [2] | Yue Xing, Weihua Jiang, Xun Cao . Multi-stable and spatiotemporal staggered patterns in a predator-prey model with predator-taxis and delay. Mathematical Biosciences and Engineering, 2023, 20(10): 18413-18444. doi: 10.3934/mbe.2023818 |
| [3] | S.A. Gourley, Yang Kuang . Two-Species Competition with High Dispersal: The Winning Strategy. Mathematical Biosciences and Engineering, 2005, 2(2): 345-362. doi: 10.3934/mbe.2005.2.345 |
| [4] | Minus van Baalen, Atsushi Yamauchi . Competition for resources may reinforce the evolution of altruism in spatially structured populations. Mathematical Biosciences and Engineering, 2019, 16(5): 3694-3717. doi: 10.3934/mbe.2019183 |
| [5] | Donald L. DeAngelis, Joel C. Trexler, Douglas D. Donalson . Food web dynamics in a seasonally varying wetland. Mathematical Biosciences and Engineering, 2008, 5(4): 877-887. doi: 10.3934/mbe.2008.5.877 |
| [6] | Pengfei Liu, Yantao Luo, Zhidong Teng . Role of media coverage in a SVEIR-I epidemic model with nonlinear incidence and spatial heterogeneous environment. Mathematical Biosciences and Engineering, 2023, 20(9): 15641-15671. doi: 10.3934/mbe.2023698 |
| [7] | Wanxiao Xu, Ping Jiang, Hongying Shu, Shanshan Tong . Modeling the fear effect in the predator-prey dynamics with an age structure in the predators. Mathematical Biosciences and Engineering, 2023, 20(7): 12625-12648. doi: 10.3934/mbe.2023562 |
| [8] | Fiona R. Macfarlane, Mark A. J. Chaplain, Tommaso Lorenzi . A hybrid discrete-continuum approach to model Turing pattern formation. Mathematical Biosciences and Engineering, 2020, 17(6): 7442-7479. doi: 10.3934/mbe.2020381 |
| [9] | Jinyu Wei, Bin Liu . Coexistence in a competition-diffusion-advection system with equal amount of total resources. Mathematical Biosciences and Engineering, 2021, 18(4): 3543-3558. doi: 10.3934/mbe.2021178 |
| [10] | Yongli Cai, Yun Kang, Weiming Wang . Global stability of the steady states of an epidemic model incorporating intervention strategies. Mathematical Biosciences and Engineering, 2017, 14(5&6): 1071-1089. doi: 10.3934/mbe.2017056 |
With the unprecedented increase in the usage of portable and small wireless devices, the demand for energy is increasing, which leads to the problem of battery energy depletion becoming one of the bottlenecks restricting the application of wireless devices in some occasions. Recent advances in energy acquisition technology have attracted a lot of attention from academic and industrial research fields, focusing on using more renewable energy in the next generation wireless communication and network [1]. To achieve this goal, energy harvesting (EH) technology has been proposed as a feasible solution, which enables wireless devices to harvest energy from natural or artificial phenomena by physical or chemical means, such as vibration, pressure, temperature difference, sun and electromagnetic radiation, etc. Electromagnetic radiation, one of them, is characterized by wide existence of Radio frequency (RF) energy and easy harvesting. Therefore, RF EH technology has attracted much attention and has broad application prospects [2,3,4]. RF energy can be electromagnetic radiation from surrounding devices, such as portable communication devices, WIFI access points, TV broadcasting stations, AM/FM radio transmitters and cellular base stations, or directional beam signals transmitted by special RF base stations or transmitters [5,6]. At present, RF EH technology has been preliminarily studied and applied in sensor network, cooperative relay, cognitive radio, Internet of things (IoT), multi-user and cellular network [7,8,9,10]. For example, a base station with tens of watts of power can provide radio frequency energy to remote sensor nodes and even smart phones [11].
RF EH schemes are mainly divided into two categories. One is that the base station transmits radio frequency energy to remote devices or nodes through downlink, and then the remote devices harvest the energy and transmit data to the base station through uplink by using the harvested energy, thus realizing the cross transmission of wireless power and information. The other is to set up a special electromagnetic energy transmitting antenna to transmit electromagnetic energy in the form of broadcasting, so that the radio frequency power covers the mobile devices or nodes in the whole network, and then the remote nodes can realize uninterrupted EH and information transmission [12,13,14]. In a low-power wireless transmission system such as a sensor network, in order to harvest as much energy as possible, remote nodes can install multiple antennas, occupying multiple frequency bands or multiple time slots to accumulate energy in time, space or spectrum domain respectively. Different schemes have obvious advantages and disadvantages. For example, installing multiple antennas on a device requires adding additional antennas, which not only increases the size and volume of equipment, but also increases energy consumption. When using multiple frequency bands, it is necessary to consider transmitting energy in a wider frequency range and occupy extra bandwidth. Considering these unfavorable factors, using multiple time slots is a better choice. For multi-slot EH, the remote device first harvests and stores the RF energy sent by the base station in multiple time slots. If a fixed transmission power is used for data transmission and a fixed rate service is provided after sufficient energy is accumulated, it is called "harvest-store-use" multi-slot EH scheme. The advantage of this scheme is that it requires a rechargeable battery with large capacity and low leakage. If the number of time slots for harvesting energy is fixed and information is transmitted immediately after the energy harvesting process is completed, it is called "harvest-use" multi-slot EH scheme [15,16,17,18]. The advantage of this scheme is that cheap supercapacitor with low capacity can be used to save storage costs and simplify energy management strategy. The disadvantage of this scheme is that the transmission power used for communication has random characteristics because EH device exhausts harvested energy every time [19,20].
Because of the broadcast characteristics of wireless communication, RF signals from other base stations or wireless communication devices working in the same frequency band are called co-channel interference, which will inevitably affect EH efficiency and data communication performance. Therefore, the research on CCI in EH communication is a new subject direction. In the EH process, the interference signals mixed in when sending RF signals can enhance energy harvesting, but such interference signals will also affect the signals that use the same frequency band for information transmission, which needs theoretical analysis and experimental verification for EH communication effects. Related literatures have studied the influence of CCI on the communication performance of EH communication. In [21], the effect of CCI was studied on the EH communication performance of wireless powered communications (WPC), the average signal-to-interference-plus-noise ratio, the outage probability and the average throughput are examined. In [22,23], the EH communication performance of the amplify-and-forward (AF) and the decode-and-forward (DF) relaying were analyzed by deriving the outage probability and the throughput in Nakagami-m fading channels, when both the relay and the destination suffer from CCI. In [24,25], the EH communication performance was studied when CCI signal was treated as a new source of EH rather than a waste energy in cooperative network and cognitive relay network. In the above researches, two commonly used EH schemes, namely "power splitting" and "time switching", and similar EH schemes were used as different network structures for harvesting energy. These works have not studied the mechanism and effect of CCI on the multi-slot "harvest-store-use" and "harvest-use" EH communication schemes.
The main contributions of this paper can be summarized as follows: Firstly, to the best of our knowledge, this is the first time to investigate the communication performance of "harvest-store-use" and "harvest-use" multi-slot EH schemes with Rayleigh fading and CCI scenario. Secondly, the exact closed-form expressions of the effective throughput index of the above EH scheme are derived theoretically. These expressions are accurate and universal enough to be used as important parameters in the design of EH wireless communication system. Finally, based on the simulation analysis of these expressions, useful and reliable conclusions are drawn on the operating conditions of the above schemes in Rayleigh fading and CCI EH communication, which can provide reference for practice. In particular, the key problem of how to optimize EH communication performance is discussed in detail when CCI is beneficial to EH, but also deteriorates information transmission.
The rest of the paper is organized as follows. Section 2 introduces the EH communication system model. Section 3 and Section 4 deduce the theoretical formulas of EH communication effective throughput of "harvest-store-use" scheme and "harvest-use" scheme respectively. In Section 5, the simulation examples are given to analyze and verify the conclusion. A summary of the full text is given in Section 6.
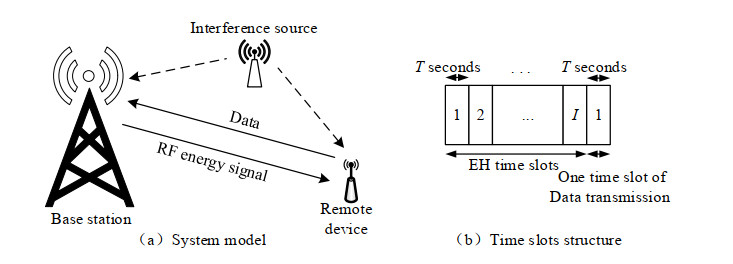
A multi-slot EH wireless communication system is presented in this section, the block diagram of which is shown in figure 1(a). The system includes a base station, a remote information sending device or node and an interference source. The base station sends RF energy to the remote device or node in the downlink, and the remote device or node harvests energy, and sends local information to the base station via the uplink by using the harvested energy. The main feature of this system is that energy and information are transmitted in half duplex mode. In the "harvest-store-use" scheme, the remote node first stores the harvested energy, and only provides fixed-rate data transmission service after the accumulated energy exceeds a given value. In the "harvest-use" scheme, energy is used immediately after harvest. No matter which scheme, in order to harvest as much energy as possible, multiple time slots are needed to harvest energy, which increases delay and reduces throughput. Due to the broadcast characteristics of wireless communication, CCI from other base stations or wireless communication devices operating in the same frequency band is ubiquitous. In Figure 1(a), CCI from the same CCI interference source affects both base station and remote equipment. The wireless channel satisfies Rayleigh fading, and the signals involved in the analysis process include radio frequency energy signals, information data and CCI.
The multi-slot EH communication scheme based on the above EH communication model assumes that a time slot unit is $ T $ seconds, the RF power transmitted by the base station is $ {P_B} $, and the power transmission from the base station to the remote node for EH communication lasts for $ I $ time slots, with a total duration of $ IT $ seconds in Figure 1(b). The data transmission from the remote device to the base station lasts for one time slot. In the multi-slot EH communication scheme, the transmitting antenna of the base station transmits RF energy or power to the remote device on the downlink for EH, and other factors affecting the energy harvesting of the remote device, including channel fading, CCI and noise. CCI can be a superimposed signal of multiple signals with different strengths and the same frequency. For simplicity, they are combined into one CCI, which affects the EH of remote node and the information reception of base stations at the same time. The signal received by the remote device in the $ I{\rm{th}} $ time slot is expressed as
| ${y_i} = {h_i}\sqrt {{P_B}} {x_i} + {w_i}\sqrt {{W_i}} {z_i} + {n_i}, $ | (1) |
where $ {h_i} $ is the channel fading coefficient of the downlink in the $ i{\rm{th}} $ time slot, which satisfies the Rayleigh fading and the quasi-static distribution in one time slot. $ {P_B} $ is the transmission power of the base station. $ {x_i} $ is the RF power signal sent by the base station, which has unit power $ \operatorname{E} \left\{ {{{\left| {{x_i}} \right|}^2}} \right\} = 1 $. $ {\rm{E}}\left[{\, \cdot \, } \right] $ is the expectation operator. $ {w_i} $ is the fading coefficient from the interference source to the remote device in the $ i{\rm{th}} $ time slot, satisfies the Rayleigh fading and the quasi-static distribution in one time slot. $ {z_i} $ is the CCI with unit power $ \operatorname{E} \left\{ {{{\left| {{z_i}} \right|}^2}} \right\} = 1 $. $ {W_i} $ is the transmission power of the interference source in the $ i{\rm{th}} $ time slot. $ {n_i} $ is a complex additive white Gaussian noise(AWGN)with a mean value of zero and a variance of $ 2{\beta ^2} $. If the RF signal in formula (1) is used for EH of remote device, the harvested energy is [17]
| ${E_h} = T\sum\limits_{i = 1}^I {{\eta _i}{{\left| {{h_i}\sqrt {{P_B}} {x_i} + {w_i}\sqrt {{W_i}} {z_i} + {n_i}} \right|}^2}} , $ | (2) |
where $ {\eta _i} $ is the conversion efficiency of EH converter, if the same converter is used, then $ {\eta _i}{\rm{ = }}\eta, \; i = 1, 2, \cdots, I $. In the second stage, the remote device uses the harvested energy to send data or information to the base station. If CCI also exists, the signal received by the base station can be expressed as
| $y = g\sqrt {{P_E}} x + q\sqrt Q z + n, $ | (3) |
where $ g $ is the channel fading coefficient, satisfies the Rayleigh fading and the quasi-static distribution in one time slot. $ {P_E} $ is the transmission power of remote device, and $ x $ is the transmission signal with unit power, $ {\rm{E}}\left\{ {{{\left| x \right|}^2}} \right\} = 1 $. The transmit power of CCI is $ {Q_0} $. $ q $ is the fading coefficient from the interference source to the remote device, which satisfies the Rayleigh fading and the quasi-static distribution in one time slot. $ z $ is the CCI with unit power $ \operatorname{E} \left\{ {{{\left| z \right|}^2}} \right\} = 1 $. $ n $ is the complex AWGN with zero mean and variance $ 2{\beta ^2} $. The transmission power of remote device for information comes from the EH process in the first stage, and the harvested power $ {P_E} $ is
| ${P_E} = \frac{{{E_h}}}{T} = \eta {\sigma ^2}S, $ | (4) |
where $ S = \left({{1 \mathord{\left/ {\vphantom {1 {{\sigma ^2}}}} \right. } {{\sigma ^2}}}} \right)\sum\nolimits_{i = 1}^I {{{\left| {{h_i}\sqrt {{P_B}} {x_i} + {w_i}\sqrt {{W_i}} {z_i} + {n_i}} \right|}^2}} $ and $ 2{\sigma ^2} = 2\alpha _h^2{P_B} + 2\alpha _w^2{W_0} + 2{\beta ^2} $. $ S $ is a random variable related to the RF transmission power $ {P_B} $ sent by the base station and the existing CCI power $ {W_i} $. Therefore, the information transmission power in the above formula must be a random variable, which also shows the main difference between EH communication and traditional communication. The performance of EH communication system is affected not only by radio frequency power of base station and channel fading, but also by CCI and noise.
In the scheme of multi-slot "harvest-store-use" in EH communication, the remote equipment must harvest enough energy before sending data in the next time slot, so that the base station can receive strong enough signals and resist the influence of CCI and noise. Therefore, the power that the remote device can use for information transmission in EH communication must be $ {P_{TH}} $ or higher, that is, the required power must be greater than the threshold $ {P_{TH}} $. Therefore, the probability of communication without interruption is
| ${P_T} = 1 - \Pr \left\{ {{P_E} < {P_{TH}}} \right\} = \Pr \left\{ {{P_E} \geqslant {P_{TH}}} \right\}.$ | (5) |
For this reason, the remote device must wait for time slots to harvest energy. Due to the waiting time during one transmission, the actual throughput is $ {1 \mathord{\left/ {\vphantom {1 {\left({I + 1} \right)}}} \right. } {\left({I + 1} \right)}} $ times. Let the required transmission rate be $ R = 1bits/\left({s \cdot Hz} \right) $, Define the effective throughput for successful transmission of EH communication as follows [17,23]
| $\tau = \frac{{{P_T}}}{{I + 1}}.$ | (6) |
Next, we need to calculate the transmission probability. The PDF and CDF of random variable are required. PDF and CDF are probability density function and cumulative distribution function respectively. When signal and CCI exist simultaneously, Rayleigh fading satisfies quasi-static distribution in one time slot, which can be expressed as a complex Gaussian random variable. Therefore, $ {h_i} $ and $ {w_i} $ can be expressed as a complex Gaussian random variable with a mean value of zero and a variance of $ 2\alpha _h^2 $ and $ 2\alpha _w^2 $ respectively. Because the energy harvesting lasts for $ I $ time slots in the whole EH process, $ S $ becomes the square sum of independent Gaussian random variables with zero mean and unit variance, and satisfies the condition of central Chi-square distribution [26]. Therefore, PDF and CDF of $ S $ are respectively.
| ${f_S}\left( x \right) = \frac{1}{{{2^I}\Gamma \left( I \right)}}{x^{I - 1}}{e^{ - \frac{x}{2}}}, $ | (7) |
| ${F_S}\left( x \right) = \frac{1}{{\Gamma \left( I \right)}}\gamma \left( {I, \frac{x}{2}} \right), $ | (8) |
where $ \Gamma \left(\cdot \right) $ is the Gamma function[27, eq.(8.310.1)]. $ \gamma \left(\cdot, \cdot \right) $ is the lower incomplete Gamma function [27, eq.(8.350.1)]. Due to $ {P_E} = \eta {\sigma ^2}S $, according to variable substitution, the PDF and CDF obtained are
| ${f_{{P_E}}}\left( y \right) = {\left( {\frac{1}{{2\eta {\sigma ^2}}}} \right)^I}\frac{{{y^{I - 1}}}}{{\Gamma \left( I \right)}}{e^{ - \frac{y}{{2\eta {\sigma ^2}}}}}, $ | (9) |
| ${F_{{P_E}}}\left( y \right) = \frac{1}{{\Gamma \left( I \right)}}\gamma \left( {I, \frac{y}{{2\eta {\sigma ^2}}}} \right).$ | (10) |
Finally, according to formulas (6) and (10), the effective throughput of EH wireless communication with Rayleigh fading and CCI is obtained as follows
| $\tau {\rm{ = }}\frac{1}{{I + 1}}\left[ {1 - \frac{1}{{\Gamma \left( I \right)}}} \right.\gamma \left( {I, } \right.\left. {{{\frac{{{P_{TH}}}}{\eta }} \mathord{\left/ {\vphantom {{\frac{{{P_{TH}}}}{\eta }} {\left( {2\alpha _h^2{P_B} + 2\alpha _w^2{W_0} + 2{\beta ^2}} \right)}}} \right. } {\left( {2\alpha _h^2{P_B} + 2\alpha _w^2{W_0} + 2{\beta ^2}} \right)}}} \right).$ | (11) |
It is assumed that the same interference affects both the reception of base station signals and the energy harvesting of remote node, and the signal received by the base station is interference limited (ignore the influence of noise), then $ {Q_0}{\rm{ = }}{W_0} $, and define the signal-to-interference ratio $ \omega = {{2\alpha _h^2{P_B}} \mathord{\left/ {\vphantom {{2\alpha _h^2{P_B}} {2\alpha _q^2{Q_0}}}} \right. } {2\alpha _q^2{Q_0}}} $ and the threshold of the signal-to-interference ratio $ {\lambda _T} = {{{P_{TH}}} \mathord{\left/ {\vphantom {{{P_{TH}}} {2\alpha _q^2{Q_0}}}} \right. } {2\alpha _q^2{Q_0}}} $. The effective throughput can be obtained by formula (11)
| $\tau {\rm{ = }}\frac{1}{{I + 1}}\left[ {1 - \frac{1}{{\Gamma \left( I \right)}}\gamma \left( {I, \frac{{{\lambda _T}}}{{\eta \left( {\omega + 1} \right)}}} \right)} \right].$ | (12) |
It is noted from the formula (11) that the interference power and the base station transmission power are in the same position in the formula, that is to say, the RF signal of the base station and the interference RF signal both promote the energy harvesting of the remote device. It is noted from the formula (11) or (12) that $ \tau $ decreases when $ I + 1 $ increases, but $ \tau $ increases when $ I $ increases while the other conditions of lower incomplete Gamma function remain unchanged. Therefore, there may be an optimal value $ I $ that maximizes $ \tau $, which will be further analyzed by simulation method later. Next, we continue to deduce the effective throughput of EH communication using the "harvest-use" scheme.
In the "harvest-use" scheme, energy is used immediately after the end of EH process. In this scheme, cheap low-capacity supercapacitors can be used to save storage costs and simplify energy management strategy. However, since the remote device will run out of energy every EH, the power used for information transmission will also change randomly.
When analyzing the influence of CCI and noise on EH communication system, comparing CCI power and noise power, it is usually divided into two situations, interference limited and noise limited. Since the main purpose of this paper is to analyze the influence of wireless communication environment with CCI on EH performance, it focuses on limited CCI without losing generality. Then, according to the definition of throughput of interruption probability in the "harvest-use" scheme, it is found that the analysis of the influence of CCI on EH communication performance is complicated, because it is necessary to obtain the exact expressions of PDF and CDF functions of the signal-to-interference ratio received by the base station. The signal-to-interference ratio of information received by base station can be expressed as
| $U = \frac{{P{P_E}}}{{{P_c}}}{\rm{ = }}V{P_E}, $ | (13) |
where $ {P_E} $ is a random variable, and its PDF and CDF are expressed by formula (9) and formula (10), respectively. $ {P_c} $ is the interfering power of CCI, which is also a random variable. Then the signal-to-interference ratio (ratio of signal to CCI) $ V = {P \mathord{\left/ {\vphantom {P {{P_c}}}} \right. } {{P_c}}} $ at the base station is also a random variable. According to formula (3), $ P $ is the fading signal power received by the base station, which satisfies exponential distribution under Rayleigh channel fading conditions, and the PDF can be expressed as
| $f\left( p \right) = \frac{1}{{2\alpha _g^2}}{e^{ - \frac{p}{{2\alpha _g^2}}}}.$ | (14) |
The information received by the base station is interfered by CCI. According to formula (3), the interference satisfies Rayleigh fading, and its interference power satisfies exponential distribution. The PDF of CCI can be expressed as
| ${f_{{P_c}}}\left( p \right) = \frac{1}{{2\alpha _q^2{Q_0}}}{e^{ - \frac{p}{{2\alpha _q^2{Q_0}}}}}, $ | (15) |
where $ 2\alpha _q^2{Q_0} $ is the average power of CCI. Using the relationship between the ratio of two random variables, $ f\left(v \right) $ is obtained
|
$fV(x)=∫∞0yfP(xy)f(y)dy=14α2gα2qQ0∫∞0yexp(−xy2α2g−y2α2qQ0)dy=14α2gα2qQ0(x2α2g+12α2qQ0)−1 .$
|
(16) |
The expression [27, eq.(3.381.4)] is used in the derivation of formula (16). Next, calculate PDF and CDF of $ U $. Because $ U $ is the ratio of $ V $ to CCI, according to the relationship of random variable product $ U = V{P_E} $, the PDF of $ U $ is
|
$fU(u)=∫∞01vfV,PE(uv,y)dy=1Γ(I)(2ησ2)Iα2gα2qQ0uI−1×∫∞0y−I(y+α2gα2qQ0)−2exp(−u2ησ2y)dy=uI2−1I(α2qQ02ησ2α2g)I2exp(α2qQ04ησ2α2gu)W−I2−1,I2−12(α2qQ02ησ2α2gu) , $
|
(17) |
where the $ {W_{ \cdot, \cdot }}(\cdot) $ is Whittaker function [27, eq. (9.222.1)]. The above integration process adopts variable substitution and uses formula [27, eq. (6.643.3)]. It is also difficult to get CDF by directly integrating the formula (17), and the CDF is calculated as follows
|
$FU(u)=P{VPE<u}=P{V<uPE}=1Γ(I)(2ησ2)I[∫∞0yI−1exp(−y2ησ2)dy−∫∞0yI+N−1exp(−y2ησ2)(α2qQ0α2gu+y)−Ndy]=1−I(α2qQ02ησ2α2gu)I2−12exp(α2qQ04ησ2α2gu)W12−I2−1,I2(α2qQ02ησ2α2gu) .$
|
(18) |
The derivation process of the above formula mainly uses integral transformation and formulas [27, eq.(3.381.4)] and [27, eq.(3.471.7)]. According to the definition formula (6) of effective throughput, in "harvest-use" EH communication, the total signal-to-interference ratio is greater than a certain threshold of the signal-to-interference ratio $ {\lambda _T} $ in order to ensure resistance to limited CCI and guarantee a certain quality of service. Combined with formula (18), the effective throughput calculation formula is
| $\tau = \frac{I}{{I + 1}}{\left( {\frac{{\alpha _q^2{Q_0}}}{{2\eta {\sigma ^2}\alpha _g^2}}{\lambda _T}} \right)^{\frac{I}{2} - }}^{\frac{1}{2}}\exp \left( {\frac{{\alpha _q^2{Q_0}}}{{4\eta {\sigma ^2}\alpha _g^2}}{\lambda _T}} \right){W_{\frac{1}{2} - \frac{I}{2} - 1, \frac{I}{2}}}\left( {\frac{{\alpha _q^2{Q_0}}}{{2\eta {\sigma ^2}\alpha _g^2}}{\lambda _T}} \right), $ | (19) |
where $ 2{\sigma ^2} = 2\alpha _h^2{P_B} + 2\alpha _w^2{W_0}{\rm{ + }}2{\beta ^2} $. It is noted that the interference power and the base station transmission power are in the same position in the formula (19), that is to say, the RF signal of the base station and the interference RF signal both promote the energy harvesting of the remote device. If the remote device and the base station work in the same interference environment and suffer from the same CCI, then CCI experiences the same Rayleigh fading and CCI has the same interference power $ {Q_0}{\rm{ = }}{W_0} $, and defines the signal-to-interference ratio $ \omega = {{2\alpha _h^2{P_B}} \mathord{\left/ {\vphantom {{2\alpha _h^2{P_B}} {2\alpha _w^2{W_0}}}} \right. } {2\alpha _w^2{W_0}}} $. Further considering that the signal received by the base station is interference limited (ignore the influence of noise), then
| $\tau = \frac{I}{{I + 1}}{\left( {\frac{{{\lambda _T}}}{{2\eta \alpha _g^2\left( {\omega + 1} \right)}}} \right)^{\frac{I}{2} - }}^{\frac{1}{2}}\exp \left( {\frac{{{\lambda _T}}}{{4\eta \alpha _g^2\left( {\omega + 1} \right)}}} \right){W_{\frac{1}{2} - \frac{I}{2} - 1, \frac{I}{2}}}\left( {\frac{{{\lambda _T}}}{{2\eta \alpha _g^2\left( {\omega + 1} \right)}}} \right).$ | (20) |
It is noted from formula and formula that the effective throughput of the "harvest-use" scheme is closely related to the number of EH time slots and the power of CCI. Increasing the number of time slots can increase the power of EH, but at the same time increase the delay. Similarly, the appearance of CCI increases the harvesting efficiency of EH energy, but it also leads to the interruption of information transmission, which will be given in detail in the following simulation analysis.
In this section, combined with the theoretical closed-form expressions of effective throughput of multi-slot "harvest-store-use" and "harvest-use" EH communication schemes, some simulation examples under specific conditions are given, and the design problems mentioned in the introduction are verified and some valuable conclusions are obtained. At the same time, Monte Carlo, MC) simulation ($ {\rm{1}}{{\rm{0}}^5} $ times) is carried out for EH communication performance of multi-slot "harvest-store-use" and "harvest-use" schemes, which are mutually verified with numerical simulation. In these examples, unless otherwise specified, EH conversion efficiency $ \eta {\rm{ = }}0.5 $ and Rayleigh channel fading parameters $ 2\alpha _h^2{\rm{ = }}1 $, $ 2\alpha _w^2{\rm{ = }}1 $, $ 2\alpha _g^2{\rm{ = }}1 $ are set.
According to the formulas (12), the "harvest-store-use" scheme of the EH communication, which is an accurate and theoretical closed-form expression of the effective throughput. Figures 2 to 5 shows the relationship between EH communication effective throughput $ \tau $ and parameters such as $ I $, $ \omega $, $ \eta \; \; {\rm{and}}\; \; {\lambda _T} $ in CCI environment with Rayleigh channel fading, respectively. Figure 2 simulates the relationship between effective throughput and the number of time slots. In the following simulation, the number of slots varies from 1 to 20, and the interval is 1, and the threshold of the signal-to-interference ratio $ {\lambda _T}{\rm{ = }}5{\rm{dB}} $. First of all, we can see from Figure 2 that the effective throughput first increases with $ I $ and then decreases with the increase of $ I $ for different signal-to-interference ratio of the base station. These curves in the figure show that there are optimal values of time slot $ I $, which make the effective throughputs reach the maximum values, which is consistent with our discussion of "harvest-store-use" scheme in the introduction. The larger the number of time slots, the more energy is obtained, and the higher the probability of successful transmission is, but at the same time, the longer the delay will be, and the effective throughput will decrease continuously. In these examples, in order to balance the maximum effective throughput and delay, when $ \omega {\rm{ = - }}15\operatorname{dB} $, the optimal number of time slots $ I = 9 $; when $ \omega {\rm{ = - }}5\operatorname{dB} $, the optimal number of time slots $ I = 7 $; when $ \omega {\rm{ = }}0\operatorname{dB} $, the optimal number of time slots $ I = 5 $; when $ \omega {\rm{ = }}5\operatorname{dB} $, the optimal number of time slots $ I = 3 $; when $ \omega {\rm{ = }}10\operatorname{dB} $, the optimal number of time slots $ I = 2 $; when $ \omega {\rm{ = }}20\operatorname{dB} $, the optimal number of time slots $ I = 1 $. Secondly, the maximum effective throughput increases with the increase of signal-to-interference ratio, which indicates that increasing the transmission power of the base station under the above conditions can improve the performance of EH system. Finally, we find that with the increase of the number of time slots, the simulation curves coincide, which is due to $ I \to \infty $, the effective throughput $ \tau \sim \frac{1}{\left(I+1\right)} $.
Figure 3 shows the relationship between effective throughput $ \tau $ and signal-to-interference ratio $ \omega $. In the figure, the signal-to-interference ratio is set from 0dB to 40dB with an interval of 2dB. Number of time slots $ I{\rm{ = }}1 $ or 2. Since the signal-to-interference ratio $ \omega $ is closely related to the transmission power $ {P_B} $ of the base station, it is generally considered that a larger $ {P_B} $ can send more energy to the remote device if the interference power is constant. First of all, when $ \omega $ is small, $ \tau $ is also small. With the increase of $ \omega $, $ \tau $ also increases, but when $ \omega $ exceeds a certain threshold, $ \tau $ increases sharply, and then with the increase of $ \omega $, $ \tau $ remains unchanged. Secondly, the threshold values under different conditions are not the same. For example, when $ {\lambda _T}{\rm{ = }}10{\rm{dB}} $, $ I{\rm{ = }}1 $, and $ \omega $ is greater than 2dB, $ \tau $ begins to increase sharply, until $ \omega $ is greater than 20dB, $ \tau $ reaches its peak and remains unchanged; when $ {\lambda _T}{\rm{ = }}10{\rm{dB}} $, $ I{\rm{ = }}2 $, and $ \omega $ is greater than 2dB, $ \tau $ begins to increase sharply, until $ \omega $ is greater than 10dB, $ \tau $ reaches its peak and remains unchanged. When $ {\lambda _T}{\rm{ = }}20{\rm{dB}} $, $ I{\rm{ = }}1 $, and $ \omega $ is greater than 8dB, $ \tau $ begins to increase sharply, until $ \omega $ is greater than 30dB, $ \tau $ reaches its peak and remains unchanged; when $ {\lambda _T}{\rm{ = }}20{\rm{dB}} $, $ I{\rm{ = }}2 $, and $ \omega $ is greater than 6dB, $ \tau $ begins to increase sharply, until $ \omega $ is greater than 20dB, $ \tau $ reaches its peak and remains unchanged. When $ {\lambda _T}{\rm{ = }}30{\rm{dB}} $, $ I{\rm{ = }}1 $, and $ \omega $ is greater than 14dB, $ \tau $ begins to increase sharply, until $ \omega $ is greater than 40dB, $ \tau $ reaches its peak and remains unchanged; when $ {\lambda _T}{\rm{ = }}30{\rm{dB}} $, $ I{\rm{ = }}2 $, and $ \omega $ is greater than 12dB, $ \tau $ begins to increase sharply, until $ \omega $ is greater than 28dB, $ \tau $ reaches its peak and remains unchanged. That is to say, when the interference signal power is constant, it is necessary to increase the base station RF power to maintain a certain throughput, but continuously increasing the base station RF power cannot continuously improve the effectively throughput. The maximum effective throughput is determined by the number of time slots. Finally, in theory $ \omega \to \infty $, effective throughput $ \tau \sim \frac{1}{\left(I+1\right)} $. This means that in EH communication with the "harvest-store-use" scheme, the traditional method of increasing the effective throughput by increasing the transmission power is no longer effective. The threshold of the signal-to-interference ratio and the appropriate number of time slots should be combined to maximize the effective throughput of EH communication, otherwise it will cause energy waste.
Figure 4 shows the relationship between effective throughput $ \tau $ and the threshold of the signal-to-interference ratio $ {\lambda _T} $. The threshold of the signal-to-interference ratio $ {\lambda _T} $ is set ranging from -10dB to 20dB, with an interval of 2dB and the number of time slots $ I = 2 $ or 3. The figure shows that with the increase of $ {\lambda _T} $, the effective throughput $ \tau $ starts to decrease from the maximum value, but after $ {\lambda _T} $ exceeding a certain threshold value, $ \tau $ decreases sharply until it reaches 0, and the communication is completely interrupted. The threshold value of $ {\lambda _T} $ is about 2dB for the signal-to-interference ratio $ \omega {\rm{ = }}15{\rm{dB}} $. The threshold value of $ {\lambda _T} $ is about 4dB for the signal-to-interference ratio $ \omega {\rm{ = }}20{\rm{dB}} $. The threshold value of $ {\lambda _T} $ is about 8dB for the signal-to-interference ratio $ \omega {\rm{ = }}30{\rm{dB}} $. Under the condition of a certain effective throughput, the threshold value corresponds to the uplink channel quality from the remote device to the base station in the "harvest-store-use" scheme EH communication. The large threshold value indicates that the uplink channel quality is relatively poor, so the RF power sent by the base station needs to be increased accordingly.
Figure 5 shows the relationship between the effective throughput $ \tau $ of the "harvest-store-use" scheme and the conversion efficiency of energy harvester $ \eta $. In the simulation, conversion efficiency of energy harvester $ \eta $ is set from 0 to 1, and the interval size is 0.1. The threshold SNR value is set $ {\lambda _T}{\rm{ = }}10{\rm{dB}} $.The figure shows that with the improvement of the conversion efficiency of the energy harvester, the throughput increases, indicating that the energy harvesting converter with higher efficiency should be selected as much as possible in practice, and if the RF power of the base station is large enough, the influence of the energy conversion efficiency of the energy harvester on the throughput tends to be flat. These conclusions are consistent with our practical experience.
Figures 6 to 8 show the relationship between the effective throughput $ \tau $ of the "harvest-use" scheme of the EH communication and the parameters of time slot, conversion efficiency of energy harvester $ \eta $, signal-to-interference ratio $ \omega $ and threshold of the signal-to-interference ratio $ {\lambda _T} $. Figure 6 shows the relationship between the effective throughput $ \tau $ of the "harvest-use" scheme and the EH time slot $ I $ according to formula (20). In the simulation, the number of time slots ranges from 1 to 20, and the interval number is 1. The threshold of the signal-to-interference ratio $ {\lambda _T}{\rm{ = }}5{\rm{dB}} $. From the figure, we can see that there is a similar change pattern in all curves, that is, the effective throughput $ \tau $ decreases gradually with the increase of $ I $ in general. At this time, the optimal number of time slots $ I{\rm{ = }}1 $. In other cases, the optimal number of time slots $ I{\rm{ = }}2 $.These curves also show that there is an optimal value of time slot, which makes the effective throughput $ \tau $ reach the maximum. The number of time slots is preferably 1 or 2. Although the more time slots, the more energy is harvested, and the higher the probability of successful information transmission, it will also lead to the longer delay and the decreasing of effective throughput. Comparing Figure 5 with Figure 1, we can see that under the above simulation conditions, the "harvest-use" scheme should adopt a smaller number of time slots than the "harvest-store-use" scheme to achieve optimal communication. Actually, supercapacitors can be used as energy storage devices in the RF energy harvesting of the "harvest-use" scheme, so as to avoid the problem that the larger the $ I $ value, the more energy leakage may occur.
Figure 7 shows the relationship between effective throughput $ \tau $ of the "harvest-use" scheme and the signal-to-interference ratio $ \omega $. In the figure, the signal-to-interference ratio is set from -20dB to 50dB with an interval of 2dB. Since the signal-to-interference ratio $ \omega $ is closely related to the transmission power $ {P_B} $ of the base station, it is generally considered that a larger $ {P_B} $ can send more energy to the remote device if the interference power is constant. It can be seen from the figure that the effective throughput $ \tau $ increases with the increase of $ \omega $, but when the effective throughput $ \tau $ reaches the maximum $ {1 \mathord{\left/ {\vphantom {1 {\left({I + 1} \right)}}} \right. } {\left({I + 1} \right)}} $, it is meaningless to increase the RF power of the base station. Therefore, after ensuring the required performance, there is no need to continuously increase the power supply $ {P_B} $ of the base station to reduce the RF energy loss of the base station. Obviously different from the "harvest-store-use" scheme, the throughput of the "harvest-use" scheme decreases to a small value when the signal-to-interference ratio tends to 0dB. Different from the working mechanism of the "harvest-store-use" scheme, the "harvest-use" scheme will send information immediately even after harvesting tiny energy, including RF energy sent by the base station and interference from the surrounding environment, resulting in non-zero throughput. If interference exists all the time, even if the RF power transmitted by the base station is zero, the remote node can still harvest a certain amount of energy, which reasonably explains why the throughput of some curves in the following figure is not zero.
Figure 8 shows the relationship between effective throughput $ \tau $ of the "harvest-use" scheme and the threshold of signal-to-interference ratio $ {\lambda _T} $. Set the threshold of signal-to-interference ratio from -10dB to 20dB with an interval of 2dB. The setting of the threshold of signal-to-interference ratio $ {\lambda _T} $ corresponds to the different quality of service requirements of EH communication, and the higher value of $ {\lambda _T} $ requires higher quality of service. The figure shows that with the increase of $ {\lambda _T} $, the effective throughput decreases from the maximum value.
Figure 9 shows the relationship between the effective throughput $ \tau $ of the "harvest- use" scheme and the conversion efficiency $ \eta $ of energy harvester. In the simulation, conversion efficiency $ \eta $ of energy harvester is set from 0.05 to 1, and the interval size is 0.05. The threshold SNR value is set $ {\lambda _T}{\rm{ = }}5{\rm{dB}} $.The figure shows that with the improvement of the conversion efficiency of the energy harvester, the throughput increases, indicating that the energy harvesting converter with higher efficiency should be selected as much as possible in practice, and if the RF power of the base station is large enough, the influence of the energy conversion efficiency of the energy harvester on the throughput tends to be flat. These conclusions are consistent with our practical experience.
Table 1 compares the influence of different parameters of "harvest-store-use" and "harvest-use" EH communication modes on communication performance, and summarizes the advantages and disadvantages of the two communication schemes.
| Performance | Harvest-Store-Use | Harvest-Use |
| Energy storage device | Rechargeable battery with large capacity and low leakage | Cheap supercapacitor with low capacity |
| Transmission power used for communication | No random characteristics | Have random characteristics |
| Optimal time slot | Exist, the value is larger | Exist, the value is small |
| Maximum effective throughput | Restricted by the number of time slots | Restricted by the number of time slots |
| Minimum effective throughput | zero | Exists and is not zero |
| Threshold of signal-to-interference ratio | Severe impact | Gentle impact |
| CCI at the remote device | Conducive to energy harvesting | Conducive to energy harvesting |
| CCI at the base station | Not conducive to information transmission | Not conducive to information transmission |
| Conversion efficiency of the energy harvester | Improve effective throughput | Improve effective throughput |
| Transmission power of the base station | Continuous increase cannot improve system performance | Continuous increase cannot improve system performance |
DownLoad:
CSV
In this paper, the EH wireless communication performance of CCI multi-slot "harvest-store-use" and "store-use" schemes in the wireless communication environment of Rayleigh fading coexistence CCI is studied, and the exact theoretical closed expression of effective throughput is derived theoretically. Simulation and analysis results show that CCI at the remote device can make up for the shortage of RF energy EH in Rayleigh fading environment, and the interference of CCI at the base station greatly reduces the communication performance. Whether EH wireless communication adopts "harvest-store-use" scheme or "harvest-use" scheme, the optimal time slot should be selected for EH to balance the transmission probability and delay, and minimize the interference of CCI at the base station to the desired signal. In a word, these two EH wireless communication schemes are suitable for different application purposes and scenarios and have different performances. The possible future work and suggestions of this paper is given for interested researchers to explore new research directions. For multi-slot energy harvesting wireless communication in interference environment, further research can consider various influencing factors, such as the attenuation of transmitted RF energy and signal power with the increase of transmission distance, and the fading of various complex channels, such as Nakagami-m, Rician, shadow fading and so on. CCI interference may come from many different interference sources with different powers, etc. Introducing these more complicated factors into multi-slot EH communication makes the research more extensive and in-depth.
This paper is supported by the science and technology key project of Shaanxi science and technology department, China (No.2020NY-172, 2020JQ-732, 2020NY-023, 2020GY-091), doctoral scientific research foundation of Shaanxi university of science & technology, China (No.2019BJ-03, 2018J-01), and key industrial project of Xianyang science and technology bureau, Shaanxi province, China (No.2019K02-17).
The authors have no conflict of interest.
| [1] |
Rigsbee L, Agans R, Shankar V, et al. (2012) Quantitative profiling of gut microbiota of children with diarrhea-predominant irritable bowel syndrome. Am J Gastroenterol 107: 1740-1751. doi: 10.1038/ajg.2012.287
|
| [2] |
Brown K, DeCoffe D, Molcan E, et al. (2012) Diet-induced dysbiosis of the intestinal microbiota and the effects on immunity and disease. Nutrients 4: 1095-1119. doi: 10.3390/nu4081095
|
| [3] |
Scaldaferri F, Pizzoferrato M, Pecere S, et al. (2012) Bacterial flora as a cause or treatment of chronic diarrhea. Gastroenterol Clin North Am 41: 581-602. doi: 10.1016/j.gtc.2012.06.002
|
| [4] |
Geier MS, Butler RN, Howarth GS (2007) Inflammatory bowel disease: current insights into pathogenesis and new therapeutic options; probiotics, prebiotics and synbiotics. Int J Food Microbiol 115: 1-11. doi: 10.1016/j.ijfoodmicro.2006.10.006
|
| [5] | Aster JC, Robbins SL, Kumar V, et al. (2013) Robbins Basic Pathology: Elsevier/Saunders. |
| [6] | Fujita H, Eishi Y, Ishige I, et al. (2002) Quantitative analysis of bacterial DNA from Mycobacteria spp., Bacteroides vulgatus, and Escherichia coli in tissue samples from patients with inflammatory bowel diseases. J Gastroenterol 37: 509-516. |
| [7] |
De Cruz P, Prideaux L, Wagner J, et al. (2012) Characterization of the gastrointestinal microbiota in health and inflammatory bowel disease. Inflamm Bowel Dis 18: 372-390. doi: 10.1002/ibd.21751
|
| [8] |
Sartor RB (2008) Microbial influences in inflammatory bowel diseases. Gastroenterology 134: 577-594. doi: 10.1053/j.gastro.2007.11.059
|
| [9] |
Eckburg PB, Relman DA (2007) The role of microbes in Crohn's disease. Clin Infect Dis 44: 256-262. doi: 10.1086/510385
|
| [10] |
Bibiloni R, Mangold M, Madsen KL (2006) The bacteriology of biopsies differs between newly diagnosed, untreated, Crohn's disease and ulcerative colitis patients. J Med Microbiol 55: 1141-1149. doi: 10.1099/jmm.0.46498-0
|
| [11] |
Darfeuille-Michaud A, Neut C, Barnich N (1998) Presence of adherent Escherichia coli strains in ileal mucosa of patients with Crohn's disease. Gastroenterology 115: 1405-1413. doi: 10.1016/S0016-5085(98)70019-8
|
| [12] |
Swidsinski A, Ladhoff A, Pernthaler A (2002) Mucosal flora in inflammatory bowel disease. Gastroenterology 122: 44-54. doi: 10.1053/gast.2002.30294
|
| [13] |
Rolhion N, Darfeuille-Michaud A (2007) Adherent-invasive Escherichia coli in inflammatory bowel disease. Inflamm Bowel Dis 13: 1277-1283. doi: 10.1002/ibd.20176
|
| [14] | Barnich N, Carvalho FA, Glasser AL, et al. (2007) CEACAM6 acts as a receptor for adherent-invasive E. coli, supporting ileal mucosa colonization in Crohn disease. J Clin Invest 117: 1566-1574. |
| [15] |
Pineton de Chambrun G, Colombel JF, Poulain D, et al. (2008) Pathogenic agents in inflammatory bowel diseases. Curr Opin Gastroenterol 24: 440-447. doi: 10.1097/MOG.0b013e3283023be5
|
| [16] |
Giaffer M, Holdsworth C, Duerden B (1992) Virulence properties of Escherichia coli starins isolated from patients with inflammatory bowel disease. Gut 33: 646-650. doi: 10.1136/gut.33.5.646
|
| [17] |
Chiba M, Komatsu M, Iizuka M, et al. (1998) Microbiology of the intestinal lymph follicle: a clue to elucidate causative microbial agent(s) in Crohn's disease. Med Hypotheses 51: 421-427. doi: 10.1016/S0306-9877(98)90039-1
|
| [18] |
Neut C, Bulois P, Desreumaux P, et al. (2002) Changes in the bacterial flora of the neoterminal ileum after ileocolonic resection for Crohn's disease. Am J Gastroenterol 97: 939-946. doi: 10.1111/j.1572-0241.2002.05613.x
|
| [19] |
Darfeuille-Michaud A, Boudeau J, Bulois P, et al. (2004) High prevalence of adherent-invasive Escherichia coli associated with ileal mucosa in Crohn's disease. Gastroenterology 127: 412-421. doi: 10.1053/j.gastro.2004.04.061
|
| [20] | Kallinowski F, Wassmer A, Hofmann MA, et al. (1998) Prevalence of enteropathogenic bacteria in surgically treated chronic inflammatory bowel disease. Hepato-Gastroenterology 45: 1552-1558. |
| [21] |
Fava F, Danese S (2011) Intestinal microbiota in inflammatory bowel disease: friend of foe? World J Gastroenterol 17: 557-566. doi: 10.3748/wjg.v17.i5.557
|
| [22] |
Abubakar I, Myhill D, Aliyu SH, et al. (2008) Detection of Mycobacterium avium subspecies paratuberculosis from patients with Crohn's disease using nucleic acid-based techniques: a systematic review and meta-analysis. Inflamm Bowel Dis 14: 401-410. doi: 10.1002/ibd.20276
|
| [23] |
Sartor RB (2005) Does Mycobacterium avium subspecies paratuberculosis cause Crohn's disease? Gut 54: 896-898. doi: 10.1136/gut.2004.055889
|
| [24] |
Behr M, Schurr E (2006) Mycobacteria in Crohn's disease: a persistent hypothesis. Inflamm Bowel Dis 12: 1000-1004. doi: 10.1097/01.mib.0000228183.70197.dd
|
| [25] |
Autschbach F, Eisold S, Hinz U, et al. (2005) High prevalence of Mycobacterium avium subspecies paratuberculosis IS900 DNA in gut tissues from individuals with Crohn's disease. Gut 54: 944-949. doi: 10.1136/gut.2004.045526
|
| [26] |
Kirkwood CD, Wagner J, Boniface K, et al. (2009) Mycobacterium avium subspecies paratuberculosis in children with early-onset Crohn's disease. Inflamm Bowel Dis 15: 1643-1655. doi: 10.1002/ibd.20967
|
| [27] |
Sechi LA, Scanu AM, Molicotti P, et al. (2005) Detection and Isolation of Mycobacterium avium subspecies paratuberculosis from intestinal mucosal biopsies of patients with and without Crohn's disease in Sardinia. Am J Gastroenterol 100: 1529-1536. doi: 10.1111/j.1572-0241.2005.41415.x
|
| [28] | Sechi LA, Gazouli M, Ikonomopoulos J, et al. (2005) Mycobacterium avium subsp. paratuberculosis, genetic susceptibility to Crohn's disease, and Sardinians: the way ahead. J Clin Microbiol 43: 5275-5277. |
| [29] |
Naser SA, Ghobrial G, Romero C (2004) Culture of Mycobacterium avium subspecies paratuberculosis from the blood of patients with Crohn's disease. Lancet 364: 1039-1044. doi: 10.1016/S0140-6736(04)17058-X
|
| [30] |
Selby W, Pavli P, Crotty B (2007) Two-year combination antibiotic therapy with clarithromycin, rifabutin and clofazimine for Crohn's disease. Gastroenterology 132: 2313-2319. doi: 10.1053/j.gastro.2007.03.031
|
| [31] |
Kuehbacher T, Rehman A, Lepage P, et al. (2008) Intestinal TM7 bacterial phylogenies in active inflammatory bowel disease. J Med Microbiol 57: 1569-1576. doi: 10.1099/jmm.0.47719-0
|
| [32] |
Brinig MM, Lepp PW, Ouverney CC, et al. (2003) Prevalence of bacteria of division TM7 in human subgingival plaque and their association with disease. Appl Environ Microbiol 69: 1687-1694. doi: 10.1128/AEM.69.3.1687-1694.2003
|
| [33] |
Kumar PS, Griffen AL, Barton JA, et al. (2003) New bacterial species associated with chronic periodontitis. J Dental Res 82: 338-344. doi: 10.1177/154405910308200503
|
| [34] |
Ouverney CC, Armitage GC, Relman DA (2003) Single-cell enumeration of an uncultivated TM7 subgroup in the human subgingival crevice. Appl Environ Microbiol 69: 6294-6298. doi: 10.1128/AEM.69.10.6294-6298.2003
|
| [35] | Newman A, Lambert J (1980) Campylobacter jejuni causing flare-up in inflammatoty bowel disease. Lancet 2: 919-919. |
| [36] | Zhang L, Man SM, Day AS, et al. (2009) Detection and isolation of Campylobacter species other than C. jejuni from children with Crohn's disease. J Clin Microbiol 47: 453-455. |
| [37] |
Man SM, Zhang L, Day AS, et al. (2010) Campylobacter concisus and other Campylobacter species in children with newly diagnosed Crohn's disease. Inflamm Bowel Dis 16: 1008-1016. doi: 10.1002/ibd.21157
|
| [38] |
Mukhopadhya I, Thomson JM, Hansen R, et al. (2011) Detection of Campylobacter concisus and other Campylobacter species in colonic biopsies from adults with ulcerative colitis. PLoS One 6: e21490. doi: 10.1371/journal.pone.0021490
|
| [39] |
Deshpande NP, Kaakoush NO, Mitchell H, et al. (2011) Sequencing and validation of the genome of a Campylobacter concisus reveals intra-species diversity. PLoS One 6: e22170. doi: 10.1371/journal.pone.0022170
|
| [40] |
Kovach Z, Kaakoush NO, Lamb S, et al. (2011) Immunoreactive proteins of Campylobacter concisus, an emergent intestinal pathogen. FEMS Immunol Med Microbiol 63: 387-396. doi: 10.1111/j.1574-695X.2011.00864.x
|
| [41] |
Man SM (2011) The clinical importance of emerging Campylobacter species. Nat Rev Gastroenterol Hepatol 8: 669-685. doi: 10.1038/nrgastro.2011.191
|
| [42] |
Setoyama H, Imaoka A, Ishikawa H, et al. (2003) Prevention of gut inflammation by Bifidobacterium in dextran sulfate-treated gnotobiotic mice associated with Bacteroides strains isolated from ulcerative colitis patients. Microb Infect 5: 115-122. doi: 10.1016/S1286-4579(02)00080-1
|
| [43] | Onderdonk BW (2000) Intestinal microflora and inflammatory bowel disease; Krisner JB, editor. Philadelphia, USA: Saunders. |
| [44] |
Rath HC, Herfath HH, Ikeda JS, et al. (1996) Normal luminal bacteria, especially Bacteroides species, mediate chronic colitis, gastritis, and arthritis in HLA-B27/human β2 microglobulin transgenic rats. J Clin Invest 98: 945-953. doi: 10.1172/JCI118878
|
| [45] |
Lamps LW, Madhusudhan KT, Havens JM, et al. (2003) Pathogenic Yersinia DNA is detected in bowel and mesenteric lymph nodes from patients with Crohn's disease. Am J Surg Pathol 27: 220-227. doi: 10.1097/00000478-200302000-00011
|
| [46] |
Saebo A, Vik E, Lange OJ, et al. (2005) Inflammatory bowel disease associated with Yersinia enterocolitica O:3 infection. Eur J Inter Med 16: 176-182. doi: 10.1016/j.ejim.2004.11.008
|
| [47] |
Knosel T, Schewe C, Petersen N, et al. (2009) Prevalence of infectious pathogens in Crohn's disease. Pathol Res Pract 205: 223-230. doi: 10.1016/j.prp.2008.04.018
|
| [48] |
Farrell RJ, LaMont JT (2002) Microbial factors in inflammatory bowel disease. Gastroenterol Clin North Am 31: 41-62. doi: 10.1016/S0889-8553(01)00004-8
|
| [49] |
Liu Y, Van Kruinigen HJ, West AB, et al. (1995) Immunocytochemical evidence of Listeria, Eschericha coli, and Streptococcus antigen in Crohn's disease. Gastroenterology 108: 1396-1404. doi: 10.1016/0016-5085(95)90687-8
|
| [50] |
Chen W, Dong L, Paulus B, et al. (2000) Detection of Listeria monocytogenes by polymerase chain reaction in intestinal mucosal biopsies from patients with inflammatory bowel disease and controls. J Gastroenterol Hepatol 15: 1145-1150. doi: 10.1046/j.1440-1746.2000.02331.x
|
| [51] |
Chow J, Tang H, Mazmanian SK (2011) Pathobionts of the gastrointestinal microbiota and inflammatory disease. Curr Opin Immunol 23: 473-480. doi: 10.1016/j.coi.2011.07.010
|
| [52] | Cahill RJ, Foltz CJ, Fox JG, et al. (1997) Inflammatory bowel disease: An immunity-mediated condition triggered by bacterial infection with Helicobacter hepaticus.Infect Immun 65: 3126-3131. |
| [53] | Chin EY, Dangler CA, Fox JG, et al. (2000) Helicobacter hepaticus infection triggers inflammatory bowel disease in T cell receptor alpha/beta mutant mice. Compar Med 50: 586-594. |
| [54] |
Dieleman LA, Arends A, Tonkonogy SL (2000) Helicobacter hepaticus does not induce or potentiate colitis in interleukin-10-deficient mice. Infect Immun 68: 5107-5113. doi: 10.1128/IAI.68.9.5107-5113.2000
|
| [55] | Calza L, Manfredi R, Chiodo F (2003) Stenotrophomonas (Xanthomas) maltophilia as an emerging oppurtunistic pathogen in association with HIV infection: a 10-year surveillance study. Infection: 155-161. |
| [56] | Denton M, Kerr KG (1998) Microbilogical and clinical aspects of infection associated with Stenotrophomonas maltophilia. Clin Microbiol Rev: 57-80. |
| [57] |
Thompson-Chagoyan OC, Maldonado J, Gil A (2005) Aetiology of inflammatory bowel disease (IBD): role of intestinal microbiota and gut-associated lymphoid tissue immune response. Clin Nutr 24: 339-352. doi: 10.1016/j.clnu.2005.02.009
|
| 1. | Linhao Xu, Donald L. DeAngelis, Anatomy of the last days of a long transient spatial pattern: The ecological mechanism by which a traveling wave spatial patterns may end, 2025, 505, 03043800, 111101, 10.1016/j.ecolmodel.2025.111101 |
Lucy McMullen, Steven T Leach, Daniel A Lemberg, Andrew S Day. Current roles of specific bacteria in the pathogenesis of inflammatory bowel disease[J]. AIMS Microbiology, 2015, 1(1): 82-91. doi: 10.3934/microbiol.2015.1.82
| Performance | Harvest-Store-Use | Harvest-Use |
| Energy storage device | Rechargeable battery with large capacity and low leakage | Cheap supercapacitor with low capacity |
| Transmission power used for communication | No random characteristics | Have random characteristics |
| Optimal time slot | Exist, the value is larger | Exist, the value is small |
| Maximum effective throughput | Restricted by the number of time slots | Restricted by the number of time slots |
| Minimum effective throughput | zero | Exists and is not zero |
| Threshold of signal-to-interference ratio | Severe impact | Gentle impact |
| CCI at the remote device | Conducive to energy harvesting | Conducive to energy harvesting |
| CCI at the base station | Not conducive to information transmission | Not conducive to information transmission |
| Conversion efficiency of the energy harvester | Improve effective throughput | Improve effective throughput |
| Transmission power of the base station | Continuous increase cannot improve system performance | Continuous increase cannot improve system performance |
DownLoad:
CSV
| Performance | Harvest-Store-Use | Harvest-Use |
| Energy storage device | Rechargeable battery with large capacity and low leakage | Cheap supercapacitor with low capacity |
| Transmission power used for communication | No random characteristics | Have random characteristics |
| Optimal time slot | Exist, the value is larger | Exist, the value is small |
| Maximum effective throughput | Restricted by the number of time slots | Restricted by the number of time slots |
| Minimum effective throughput | zero | Exists and is not zero |
| Threshold of signal-to-interference ratio | Severe impact | Gentle impact |
| CCI at the remote device | Conducive to energy harvesting | Conducive to energy harvesting |
| CCI at the base station | Not conducive to information transmission | Not conducive to information transmission |
| Conversion efficiency of the energy harvester | Improve effective throughput | Improve effective throughput |
| Transmission power of the base station | Continuous increase cannot improve system performance | Continuous increase cannot improve system performance |
