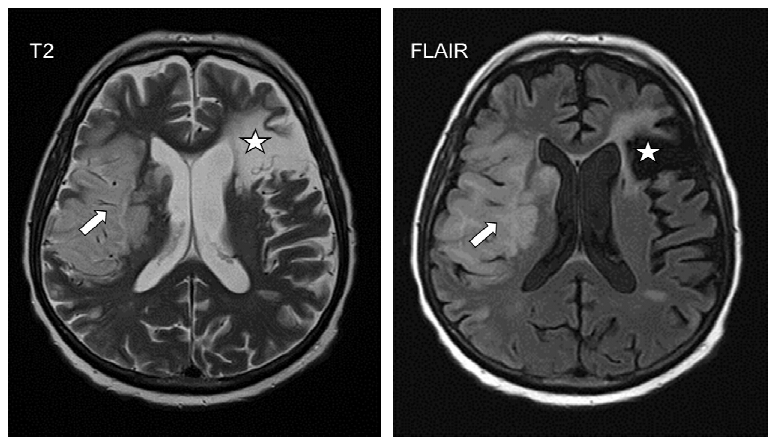
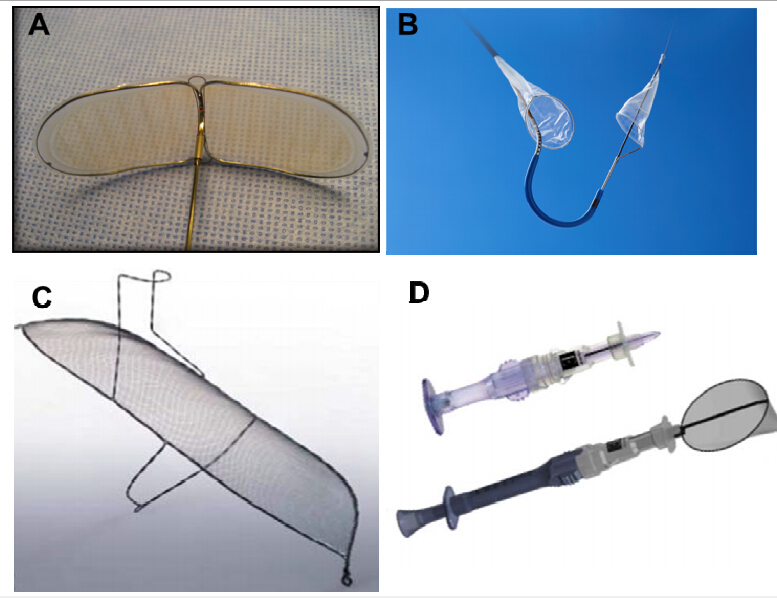
Transcatheter aortic valve implantation (TAVI) is now a widely adopted option for many inoperable and high risk patients with severe aortic valve stenosis, and clinical trials continue to show great benefit with regards to mortality and major cardiovascular endpoints. As the technology continues to expand and possibly grow to include intermediate and low risk populations, investigators have remained focused on efforts to reduce the risk of peri-procedural complications, of which neurologic events remain some of the most feared. Fortunately, contemporary studies have shown a significant decline in the risk of stroke with TAVI as compared to early clinical trials, and no difference when compared to surgical aortic valve replacement in the most recent trials. This review will focus on current methods for diagnosing, defining, and quantifying the effect of stroke after TAVI, explore the evidence with regards to stroke risk in various populations undergoing these procedures, discuss possible mechanisms for both early and late neurologic events after TAVI, and discuss strategies for both pharmacologic and device based embolic protection during these procedures.
1.
Introduction
In this paper, let $ H $ denote a real Hilbert space with inner product $ \langle \cdot, \cdot\rangle $ and norm $ \|\cdot\| $. Let $ M $, $ \mathbb{R} $, and $ \mathbb{N} $ stand for the nonempty closed convex subset of $ H $, set of real numbers and set of positive integers, respectively. Let $ G:H\to H $ be a mapping. The variational inequality problem (VIP) is concerned with the problem of finding a point $ u^\star\in M $ such that
We denote the solution set of VIP (1.1) by $ VI(M, G) $. The VIP, which Fichera [12] and Stampacchia [38] independently examined, is a crucial tool in both the applied and pure sciences. It has attracted the attention of many authors in recent years due to its wide range of applications to issues arising from partial differential equations, optimal control problems, saddle point problems, minimization problems, economics, engineering, and mathematical programming.
On the other hand, an element $ u\in M $ is said to be the fixed point of a mapping $ S:M\to M $, if $ Su = u $. The set of all the fixed points of $ S $ is denoted by $ F(S) = \{u\in M:Su = u\} $. The study of the fixed point theory of nonexpansive mappings has been applied in several fields such as game theory, differential equations, signal processing, integral equations, convex optimization, and control theory [19]. There are several recent results in the literature on approximation of fixed points of nonexpansive mappings (see, for example, [8,9,26,27,28,29,34,35,36] and the references therein).
It is well-known that the VIP (1.1) can be reformulated as a fixed point problem as follows:
where $ P_M:H\to M $ is the metric projection and $ \eta > 0 $. The extragradient method is a prominent method that has been used by many authors over the years to solve VIP. This method was first introduced by Korpelevich [21] in 1976. Given an initial point $ u_0\in M $, the sequence $ \{u_m\} $ generated by the extragradient method is as follows:
where $ \eta\in (0, \frac{1}{L}) $, and $ G $ is an operator that is $ L $-Lipschitz continuous and monotone. For $ VI(M, G)\neq \emptyset $, the author showed that the sequence $ \{u_m\} $ defined by (1.3) converges weakly to an element in $ VI(M, G) $.
The extragradient method's main flaw is its iterative requirement to compute two projections on the feasible set M. In fact, if M has a complex structure, this might have an impact on how efficiently the method computes. In recent years, several authors have paid a great deal of attention to overcoming this restriction (see, for example [6,7,11,16,48]). In order to address the drawback of the extragragient method, in 1997, He [16] introduced a method that requires only a single projection per each iteration. This method is known as the projection and contraction method and it is given as follows:
where $ \sigma \in (0, 2) $, $ \eta\in (0, \frac{1}{L}) $ and $ \varpi_m $ is defined as
The author showed that the sequence $ \{u_m\} $ generated by (1.4) converges weakly to a unique solution of VIP (1.1). The subgradient extragradient method, which was developed by Censor et al. [6,7,11], is another effective strategy for addressing the limitation of the extragradient method and it is defined as follows:
where $ \eta\in (0, \frac{1}{L}) $, and $ G $ is a $ L $-Lipschitz continuous and monotone operator. The main idea in this method is that a projection onto a special contractible half-space is used to replace the second projection onto $ M $ of the extragradient method, and this significantly reduces the difficulty of calculation. The authors showed that if $ VI(M, G)\neq \emptyset $, the sequence $ \{u_m\} $ defined by (1.5) weakly converges to a point in $ VI(M, G) $.
Furthermore, the notion of the inertial extrapolation technique is based upon a discrete analogue of a second order dissipative dynamical system and it is known as an acceleration process of iterative methods. It was first developed in [37] to solve smooth convex minimization problems. For some years now, the inertial techniques have been widely adopted by many authors to improve the convergence rate of various iterative algorithms for solving several kinds of optimization problems (see, for example, [1,17,30,31,32,41,44,45,46,55]).
It is worthy to note that the study of the problem involving the approximation of the common solution of the fixed point problem (FPP) and VIP plays a significant role in mathematical models whose constraints can be expressed as FPP and VIP. This happens in real-world applications such as image recovery, signal processing, network resource allocation, and composite site reduction (see, for example, [2,14,18,22,24,25,33,51] and the references therein).
Very recently, Thong and Hieu [43] introduced two modified subgradient extragradient methods with line search process for solving the VIP with $ L $-Lipschitz continuous and monotone operator $ G $ and FPP involving quasi-nonexpansive mapping $ S $, such that $ I-S $ is demiclosed at zero. Under appropriate assumptions, the authors showed that the sequences generated by their algorithms weakly converge some points in $ F(S)\cap VI(M, G) $.
We note that Thong and Hieu [43] only proved weak convergence results for their algorithms. According to Bauschke and Combettes [3], for the solution of optimization problems, the strong convergence of iterative methods are more desirable than their weak convergence counterparts. Furthermore, we observe that Thong and Hieu [43] employed the Armijo-type line search rule step size to their algorithms in order to enable them to operate without requiring prior knowledge of the Lipschitz constant of the operators. However, the use of Armijo-type step sizes may cause the considered methods to perform multiple calculations of the projection values per iteration on the feasible set. To overcome this limitation, Liu and Yang [23] developed an adaptive step size criterion, which only needs the use of some previously given information to complete the step size calculation.
As far as we know, there is no result in the literature involving the subgradient extragradient method with double inertial extrapolations for finding the common solution of VIP and FPP in real Hilbert spaces. Due to the importance of common solutions of VIP and FPP to some real-world problems, it is natural to ask the following question:
Is it possible to construct a double inertial subgradient extragradient-type algorithms with a new step size for finding the common solution of VIP and FPP?
One of the purposes of this article is to give an affirmative answer to the above question. Motivated by the ongoing research in these directions, we propose some modified subgradient extragradient methods with a new step size. These proposed methods are derived from the combinations of the original subgradient extragradient method, viscosity method, projection and contraction method. We prove that our new methods converge strongly to the common solutions of VIP involving pseudo-monotone mappings and FPP involving quasi-nonexpansive mappings that are demiclosed at zero in real Hilbert spaces. The following are more contributions made in this research:
● Our algorithms do not need any Armijo-type line search techniques. Rather, they use a new self-adaptive step size technique, which generates a non-monotonic sequence of step sizes. This step size is formulated such that it reduces the dependence of the algorithms on the initial step size. Conducted numerical experiments proved that the proposed step size is more efficient and ensures that our methods require less computation time than many methods in the literature that work with Armijo-type line search technique.
● Our step size properly includes those in [23,41,50].
● Our algorithms are constructed to approximate the common solution of VIP involving pseudo-monotone mappings and FPP involving quasi-nonexpansive mappings. Since the class of Pseudo-monotone mappings is more general than the class of monotone mappings, it means that our results improve and generalize several results in the literature for finding common solution VIP involving monotone mappings and quasi-nonexpansive mappings. Hence, our results are improvements of the results in [22,43,47] and several others.
● Our algorithms are embedded with double inertial terms to accelerate their convergence speed. Numerical tests showed that the proposed algorithms converge faster than the compared existing methods with single inertial term.
● We prove our strong convergence result under mild conditions imposed on the parameters. Our results are improvements on the weak convergence results in [43,47].
● To show the computational advantage of the suggested methods over some well-known methods in the literature, several numerical experiments are provided.
● We utilize our methods to solve some real-world problems, such as optimal control and signal processing problems.
● The proofs of our strong convergence results do not require the conventional "two cases" approach that have been employed by several authors in the literature to establish strong convergence results; see, for example, [5,30].
The article is organized as follows: In Section 2, some useful definitions and lemmas are recalled. The proposed algorithms and their convergence results are presented in Section 3. In Section 4, we conduct some numerical experiments to show the efficiency of our proposed algorithms over several well known methods. In Section 5, we consider the application of our algorithms to the solution of optimal control problem. In Section 6, we apply our methods to image recovery problem and in Section 7, we give summary of the basic contributions in this work.
2.
Preliminaries
In what follows, we denote the weak convergence of the sequence $ \{u_m\} $ to $ u $ by $ u_m\rightharpoonup u $ as $ m\to\infty $ and the strong convergence of the sequences $ \{u_m\} $ is denoted by $ u_m\to u $ as $ m\to\infty $.
Next, the following definitions and lemmas will be recalled. Let $ G:H\to H $ be an operator, then $ G $ is called:
$(a_1)$ contraction if there exists a constant $ k\in [0, 1) $ such that
$ (a_2)$ $ L $-Lipschitz continuous, if $ L > 0 $ exists with
If $ L = 1 $, then $ G $ becomes a nonexpansive mapping;
$(a_3)$ Quasi-nonexpansive, if $ F(G)\neq\emptyset $ such that
$ (a_4) $ $ \alpha $-strongly monotone, if there exists a constant $ \alpha > 0 $ such that
$ (a_5) $ Monotone, if
$ (a_6) $ Pseudo-monotone, if
$ (a_7) $ Sequentially weakly continuous, if for any sequence $ \{u_m\} $ which converges weakly to $ u $, then the sequence $ \{Gu_m\} $ weakly converges to $ Gu $.
Lemma 2.1. [15] Let $ H $ be a real Hilbert space and $ M $ a nonempty closed convex subset of $ H $. Suppose $ u\in H $ and $ v\in M $, then $ v = P_M u $ $ \iff $ $ \langle u-v, v-w\rangle\geq 0 $, $ \forall w\in M $.
Lemma 2.2. [15] Let $ M $ be a closed convex subset of a real Hilbert space $ H $. If $ u\in H $, then
(i) $ \|P_M u-P_M v\|^2\leq \langle P_M u-P_M v, u-v\rangle, \, \, \forall v\in H $;
(ii) $ \langle (I-P_M)u-(I-P_M)v, u-v\rangle \geq\|(I-P_M)u-(I-P_M)v\|^2, \, \, \forall v\in H $;
(iii)$ \|P_M u-v\|^2\leq \|u-v\|^2-\|u-P_M u\|^2, \, \, \forall v\in H $.
Lemma 2.3. For each $ u, v, w\in H $ and where $ \alpha, \beta, \delta \in [0, 1] $ with $ \alpha+\beta+\delta = 1 $, the followings hold in Hilbert spaces:
(a)
(b)
(c)
Lemma 2.4. [15] Let $ G:H\to H $ be a nonlinear operator such that $ F(G)\neq \emptyset $. Then $ I -G $ is called demiclosed at zero if for any $ {u_m} \in H $, the following implication holds:
Lemma 2.5. [52] Let $ \{a_m\} $ be a sequence of nonnegative real numbers such that
where $ \{\nu_m\}\subset (0, 1) $ with $ \sum_{m = 0}^{\infty}\nu_m = \infty $. If $ \limsup\limits_{k\to\infty}b_{m_k}\leq 0 $ for every subsequence $ \{a_{m_k}\} $ of $ \{a_{m}\} $, the following inequality holds:
Then $ \lim\limits_{m\to\infty}a_m = 0 $.
3.
Main results
In this section, we introduce three new double inertial subgradient extragradient algorithm-types for solving VIP and FPP. In order to establish our main results, we assume that the following conditions are fulfilled:
($ C_1 $) The feasible set $ M $ is nonempty, closed and convex.
($ C_2 $) The mapping $ G:H\to H $ is pseudo-monotone and $ L $-Lipschitz continuous.
($ C_3 $) The solution set $ F(S)\cap VI(M, G)\neq \emptyset $.
($ C_4 $) The mapping $ G $ is sequentially weak continuous on $ M $.
($ C_5 $) The mappings $ K, J:H\to H $ are non-expansive.
($ C_6 $) The mapping $ S:H\to H $ is quasi-nonexpansive such that $ I-S $ is demiclosed at zero.
($ C_7 $) The mapping $ f:H\to H $ is a contraction with constant $ k \in [0, 1) $.
($ C_8 $) Let $ \{\alpha_m\}\subset(0, 1) $, $ \{\beta_m\} $, $ \{\gamma_m\}\subset[a, b]\subset (0, 1) $ such that $ \alpha_m+\beta_m+\gamma_m = 1 $, $ \lim\limits_{m\to \infty}\alpha_m = 0 $, $ \sum\limits_{m = }^{\infty}\alpha_m = \infty $ and $ \lim\limits_{m\to\infty}\frac{\epsilon_m}{\alpha_m} = 0 = \lim\limits_{m\to\infty}\frac{\xi_m}{\alpha_m} $, where $ \{\epsilon_m\} $ and $ \{\xi_m\} $ are positive real sequences.
($ C_9 $) Let $ \{p_m\}, \{q_m\}\subset [0, \infty) $ and $ \{h_m\}\subset [1, \infty) $ such that $ \sum\limits_{m = 0}^{\infty}p_m < \infty $, $ \lim\limits_{m\to \infty}q_m = 0 $, and $ \lim\limits_{m\to \infty}h_m = 1 $.
Remark 3.1. We note the following in Algorithm 3.1:
(i) It is not hard to see from (3.1), (3.2), and condition $ (C_8) $ that
and
(ii) In order to get larger step sizes, we introduce the sequence $ \{q_m\} $ and $ \{h_m\} $ in (3.11) to relax the the parameter $ \mu $. The relaxation parameters can often improve the numerical performances of algorithms, see [10]. If $ q_m = 0 $ in (3.11), then $ \{\eta_m\} $ becomes the step size in [41]. If $ h_m = 1 $ in (3.11), then $ \{\eta_m\} $ becomes that in [50]. If $ q_m = 0 $ and $ h_m = 1 $ in (3.11), then the step size $ \{\eta_m\} $ reduces to that in [23]. Lastly, if $ q_m = p_m = 0 $ and $ h_m = 1 $, $ \{\eta_m\} $ reduces to the step sizes used by many authors in the literature (see, for example, [13,42,53,54]).
We now establish the following lemmas that will be useful in proving our strong convergence theorems.
Lemma 3.1. If conditions $ (C_3) $ and $ (C_4) $ are fulfilled and $ \{\eta_m\} $ is the sequence generated by (3.11). Then, $ \{\eta_m\} $ is well-defined and $ \lim\limits_{m\to\infty}\eta_m = \eta\in \left[\min \left\{\frac{\mu}{L}, \eta_1\right\}, \eta_1+\sum\limits_{m = 1}^{\infty}p_m\right] $.
Proof. Since $ G $ is Lipschitz continuous with $ L > 0 $, $ q_m\geq 0 $ and $ h_m\geq 1 $, by (3.11), if $ Gs_m\neq Gw_m $, we have
We omit the remaining part of the proof to avoid repetitive expressions of the proof of Lemma 3.1 in [50]. □
Lemma 3.2. Let $ \{s_m\} $ and $ \{w_m\} $ be two sequences generated by Algorithm 3.1. Suppose that conditions $ (C_1) $–$ (C_4) $ are fulfilled and if a subsequence $ \{s_{m_k}\} $ of $ \{s_m\} $ exists, such that $ s_{m_k}\rightharpoonup v^\star\in H $ and $ \lim\limits_{k\to \infty}\|s_{m_k}-w_{m_k}\| = 0 $, then $ v^\star\in VI(M, G) $.
Proof. Since $ w_{m_k} = P_M(s_{m_k}-\eta_{m_k}Gs_{m_k}) $, then by applying Lemma 2.1, we have
Equivalently, we have
It follows that
Since $ s_{m_k}\rightharpoonup v^\star $, we know that $ \{s_{m_k}\} $ is bounded and $ G $ is $ L $-Lipschitz continuous on $ H $, this means that $ \{Gs_{m_k}\} $ is also bounded. Again, since $ \lim\limits_{k\to \infty}\|s_{m_k}-w_{m_k}\| = 0 $, then $ \{w_{m_k}\} $ is also bounded and $ \{\eta_{m_k}\} \geq \left\{\frac{\mu}{L}, \eta_1\right\} $. From (3.12), we have
On the other hand, we have
Since $ \lim\limits_{k\to \infty}\|s_{m_k}-w_{m_k}\| = 0 $ and $ G $ is $ L $-Lpischitz continuous on $ H $, we have
By $ \lim\limits_{k\to \infty}\|s_{m_k}-w_{m_k}\| = 0 $, (3.13) and (3.15), (3.14) reduces to
Next, we show that $ v^\star\in VI(M, G) $. To show this, we choose a decreasing sequence $ \{\xi_k\} $ of positive numbers which approaches zero. For each $ k $, let $ N_k $ stand for the smallest positive integer fulfilling the following inequality:
It is not hard to see that the sequence $ \{N_k\} $ increases as $ \{\xi_k\} $ decreases. Moreover, since $ w_{N_k}\subset M $, for each $ k $, we can assume that $ Gw_{N_k}\neq 0 $ (otherwise, $ w_{N_k} $ is a solution). Putting
we get $ \langle Gw_{N_k}, g_{N_k}\rangle = 1 $, for each $ k $. We can infer from (3.17) that for each $ k $
Now, owing to the pseudo-monotonicity of $ G $ on $ H $, we have
This means that
We now have to show that $ \lim\limits_{k\to \infty}\xi_kg_{N_k} = 0 $. Indeed, by the fact that $ s_{m_k}\rightharpoonup v^\star $ and $ \lim\limits_{k\to \infty}\|s_{m_k}-w_{m_k}\| = 0 $, we have $ w_{N_k}\rightharpoonup v^\star $ as $ k\to \infty $. Since the norm mapping is sequentially weakly lower semicontinuous, we have
Since $ w_{N_k}\subset w_{m_k} $ and $ \xi_k \to 0 $ as $ k\to\infty $, we have
which implies that $ \lim\limits_{k\to \infty}\xi_kg_{N_k} = 0 $. Now, owing to the fact that $ G $ is Lipschitz continuous, $ \{w_{m_k}\} $, $ \{g_{N_k}\} $ are bounded, and $ \lim\limits_{k\to \infty}\xi_kg_{N_k} = 0 $, then letting $ k\to\infty $ in (3.18), we obtain
Thus, for all $ u\in M $, we have
□
Lemma 3.3. Assume that conditions $ (C_1) $–$ (C_3) $ hold and $ \{z_m\} $ is a sequence generated by Algorithm 3.1, then, for all $ u^\star\in VI(M, G) $, and for $ m_0 > 0 $, we have
Proof. From Lemma 3.1 and (3.9), we have
By Lemma 3.1, we know that $ \lim\limits_{m\to \infty}\eta_m $ exists, which together with $ \lim\limits_{m\to\infty}q_m = 0 $ and $ \lim\limits_{m\to\infty}h_m = 1 $ gives
Thus, there exists $ m_0\in \mathbb{N} $ such that
By (3.22), for all $ m\geq m_0 $, we have
Since $ u^\star \in VI(M, C)\subset M\subset T_m $, then by Lemmas 2.2 and 2.3,
This implies that
Since $ w_m\in M $ and $ u^\star\in VI(M, G) $, we have $ \langle Gu^\star, w_m-u^\star\rangle\geq 0 $. From the pseudo-monotonicity of $ G $, we know that $ \langle Gw_m, w_m-u^\star\rangle\geq 0. $ This implies that
Thus,
On the other hand, from $ z_m\in T_m $, we have
It follows that
Thus,
Therefore,
Moreover, we have
Recalling (3.23), we have know that $ v_m\neq 0 $, for all $ m\geq m_0 $. This implies that $ \delta_m = \frac{\langle s_m-w_m, v_m\rangle}{\|v_m\|^2} $. Thus, we have
On the other hand,
Putting (3.28) and (3.29) into (3.27), then for all $ m\geq m_0 $, we get
Using (3.26) and (3.30), we get
Also, from the combination of (3.25) and (3.31), we have
□
Putting (3.32) into (3.24), we obtain
Now, by Lemma 3.1 and (3.9), we have
Thus,
or equivalently
Again, from (3.9), we have
Therefore, for all $ m\geq m_0 $, we have
and
Combining (3.34) and (3.35), we have
Putting (3.36) into (3.33), we have
Next, the strong convergence theorem of Algorithm 3.1 is established as follows:
Theorem 3.1. Suppose the conditions $ (C_1) $–$ (C_8) $ are performed and $ \{u_m\} $ is the sequence generated by Algorithm 3.1, then $ \{u_m\} $ converges strongly to an element $ u^\star\in F(S)\cap VI(M, G) $, where $ u^\star = P_{F(S)\cap VI(M, G)}\circ f(u^\star) $.
Proof. We divide the proof into four parts as follows:
Claim 1. We show that $ \{u_m\} $ is bounded.
Indeed, due to (3.21), we have
From (3.3), we have
From Remark 1, $ \lim\limits_{m\to \infty}\frac{\phi_m}{\alpha_m}\|u_m-u_{m-1}\| = 0 $. Therefore, $ \{\frac{\phi_m}{\alpha_m}||u_m-u_{m-1}\|\} $ is bounded, so, a constant $ \Gamma_1 > 0 $ exists such that
Combining (3.37)–(3.39), we have
Also, from (3.4), we have
From Remark 3.1, we see that $ \lim\limits_{m\to \infty}\frac{\theta_m}{\alpha_m}\|u_m-u_{m-1}\| = 0 $. Thus, a constant $ \Gamma_2 > 0 $ exists such that
Combining (3.41) and (3.42), we have
Using (3.10) and condition $ (C_7) $, we have
Putting (3.40) and (3.43) into (3.44), we have
where $ \Gamma_3 = \Gamma_1+\Gamma_2 $. This means that $ \{u_m\} $ is bounded. It follows that $ \{z_m\} $, $ \{s_m\} $, $ \{w_m\} $, $ \{f(r_m)\} $ and $ \{f(z_m)\} $ are bounded.
Claim 2.
for some $ \Gamma_7 > 0 $.
Indeed, from (3.40), we have
Since $ \{u_m\} $ is a bounded sequence, it therefore implies that a constant $ \Gamma_4 > 0 $ exists, such that $ 2\Gamma_1\|u_m-u^\star\|+\alpha_m\Gamma^2_1\leq \Gamma_4 $. Hence, (3.46) becomes
Also, from (3.43), we get
Since $ \{u_m\} $ is a bounded sequence, it therefore implies that a constant $ \Gamma_5 > 0 $ exists, such that $ 2\Gamma_2\|u_m-u^\star\|+\alpha_m\Gamma^2_2\leq \Gamma_5 $. Hence, (3.47) becomes
Now, from (3.10) and Lemma 2.3, we have
Due to the boundedness of $ \{r_m\} $, we know that a constant $ \Gamma_6 > 0 $ exists, such that $ 2\|r_m-u^\star\|\|f(u^\star)-u^\star\|+\|f(u^\star)-u^\star\|^2\leq \Gamma_6 $. Therefore, (3.48) becomes
Putting (3.21) into (3.49), we get
Substituting (3.40) and (3.43) into (3.50), we have
it follows from (3.51) that
where $ \Gamma_7 = \Gamma_1+\Gamma_2+\Gamma_6 > 0 $.
Claim 3.
for some $ \Gamma_8 > 0 $ and $ \Gamma_9 > 0 $.
Indeed, using (3.3), we have
Also, from (3.4), we get
Using (3.10) and Lemma 2.3, we have
Substituting (3.53) and (3.54) into (3.55), we obtain
where $ \Gamma_8 = \sup\limits_{m\in \mathbb{N}}\{\|u_m-u^\star\|, \theta\|u_m-u_{m-1}\|\} $ and $ \Gamma_9 = \sup\limits_{m\in \mathbb{N}}\{\|u_m-u^\star\|, \phi\|u_m-u_{m-1}\|\} $.
Claim 4. The sequence $ \{\|u_m-u^\star\|^2\} $ converges to zero. Indeed, from (3.52), Remark 3.1 and Lemma 2.5, it is enough to show that $ \limsup\limits_{k\to \infty}\langle f(u^\star)-u^\star, u_{m_k+1}-u^\star\rangle\leq 0 $ for any subsequence of $ \{\|u_{m_k}-u^\star\|^2\} $ of $ \{\|u_m-u^\star\|^2\} $ fulfilling
Now, we assume that $ \|u_{m_k}-u^\star\|^2 $ is a subsequence of $ \|u_{m}-u^\star\|^2 $ such that (3.56) holds, then
By Claim 2 and condition $ (C_8) $, we get
which implies that
On the other hand,
By (3.8) and (3.23), we know that
Putting (3.59) into (3.58) and using the Cauchy Schwartz inequality, we have
Recalling (3.57), we have
Also, from (3.3), we have
By Remark 3.1, condition $ (C_8) $ and (3.61), we have
Using (3.60) and (3.62), we have
Again, from (3.10), we have
From condition $ (C_8) $, (3.57) and (3.64), we obtain
Next, we have that
Combing (3.60), (3.62), (3.65), and (3.66), we have
Since the sequence $ \{u_{m_k}\} $ is bounded, then we know that a subsequence $ \{u_{m_{k_j}}\} $ of $ \{u_{m_k}\} $ exists such that $ u_{m_{k_j}}\rightharpoonup q^\star $. Furthermore,
Thus, we have $ s_{m_{k_j}}\rightharpoonup q^\star $ since $ \lim\limits_{k\to \infty} \| s_{m_k}-u_{m_k}\| = 0. $ Since $ \lim\limits_{k\to \infty} \| s_{m_k}-w_{m_k}\| = 0 $, it follows from Lemma 3.2 that $ q^\star\in VI(M, G) $. From (3.63), it follows that $ z_{m_{k_j}}\rightharpoonup q^\star $. Following the demiclosedness of $ I-S $ at zero as defined in Lemma 2.4, we know that $ q^\star\in F(S) $. Thus, $ q^\star\in F(S)\cap VI(M, G) $. By combining (3.68), $ q^\star\in F(S) $ and $ u^\star = P_{F(S)\cap VI(M, G)}\circ f(u^\star) $, we get
Using (3.67) and (3.69), we have
By Claim 3, Remark 1, (3.70), and Lemma 2.5, we obtain that $ \lim\limits_{m\to\infty}\|u_m-u^\star\| = 0 $, and this completes the proof of Theorem 3.1. □
Next, we propose our second and third algorithms as in Algorithms 3.2 and 3.3, which differ slightly from Algorithm 3.1.
Remark 3.2. In Algorithm 3.2, we replace the term $ f(z_m) $ in (3.10) of Algorithm 3.1 with $ f(u_m) $. Also, in Algorithm 3.3, we replace the term $ f(z_m) $ in (3.10) of Algorithm 3.1 with $ f(s_m) $. Now, the strong convergence theorems of Algorithms 3.2 and 3.3 will be stated without proofs. Their proofs are very similar to that of Theorem 3.1. Hence, we leave the proofs for the reader to verify.
Theorem 3.2. Suppose the conditions $ (C_1) $–$ (C_8) $ are performed and $ \{u_m\} $ is the sequence generated by Algorithm 3.2, then $ \{u_m\} $ converges strongly to an element $ u^\star\in F(S)\cap VI(M, G) $, where $ u^\star = P_{F(T)\cap VI(M, G)}\circ f(u^\star) $.
Theorem 3.3. Suppose the conditions $ (C_1) $–$ (C_8) $ are performed and $ \{u_m\} $ is the sequence generated by Algorithm 3.3, then $ \{u_m\} $ converges strongly to an element $ u^\star\in F(S)\cap VI(M, G) $, where $ u^\star = P_{F(T)\cap VI(M, G)}\circ f(u^\star) $.
4.
Number experiments
In this part of the work, we consider two numerical examples to demonstrate the computational efficiency of our Algorithms 3.1–3.3 (shortly, OAUAN Algs. 3.1, 3.7 and 3.8) over some existing modified algorithms, namely, Algorithms 1 and 2 of Thong and Hieu [43] (shortly, TH Alg. 1 and TH Alg. 2), Algorithm 2 of Tian and Tong [47] (shortly, TT Alg. 2), Algorithm 3.1 of Ogwo et al. [33] (shortly, OAM Alg. 3.1), Algorithm 3.1 of Godwin et al. [14] (shortly, GAMY Alg 3.1), and Algorithm 3.1 of Maluleka et al. [24] (shortly, MUA Alg 3.1). We perform all numerical simulations using MATLAB R2020b and carried out on PC Desktop Intel$ ^{Ⓡ} $ Core$ ^{ TM} $ i7-3540M CPU @ 3.00GHz $ \times $ 4 memory 400.00GB.
Example 4.1. Suppose that $ G:\mathbb{R}^k\to \mathbb{R}^k \; (k = 30, 50, 80,110) $ is defined by $ G(u) = Qu+q $, where $ q\in \mathbb{R}^k $ and $ Q = AA^T+B+C $, $ C $ is a $ k\times k $ diagonal matrix whose diagonal terms are nonnegative (hence $ Q $ is positive symmetric definite), $ B $ is a $ k\times k $ skew-symmetric, and $ A $ is a $ k\times k $ matrix. We define the feasible set $ M $ by
It is not hard to see that the mapping $ G $ is monotone and $ L $-Lipschitz continuous with $ L = \|Q\| $ (hence, $ G $ is pseudo-monotone). For $ q = 0 $, the solution set $ VI(M, G) = \{0\} $. On the other hand, let $ Su $$ = \frac{3}{4}u\sin \|u\| $. Clearly, the only fixed point of $ S $ is 0, i.e., $ F(S) = \{0\} $. The mapping $ S $ is quasi-nonexpansive but not nonexpansive. Indeed, for $ k = 1 $, we have
Hence, $ S $ is quasi-nonexpansive. Moreover, if we take $ u = 2\pi $ and $ v = \frac{3\pi}{2} $, then we have
Therefore, $ S $ is not quasinonexpansive. Notice that $ I-S $ is demiclosed at 0 and $ F(S)\cap VI(M, G) = \{0\}\neq\emptyset $. Furthermore, we take $ Ku = \sin u $, where for $ k > 1 $, $ \sin u = (\sin u_1, \sin u_2, \; \ldots\; , \sin u_k)^T $ and $ Ju = \frac{u}{2} $.
The parameters for all the algorithms are taken as follows:
● For Algorithms 3.1–3.3, we take $ \eta_1 = 0.9 $, $ \mu = 0.4 $, $ \alpha_m = \frac{1}{2m+20} $, $ \beta_m = \gamma_m = \frac{m}{2m+20} $, $ p_m = \frac{1}{(m+100)^{1.1}} $, $ q_m = \frac{m+1}{m} $, $ h_m = \frac{1}{m+100} $, $ \phi = 0.6 $, $ \theta = 0.9 $, $ \rho = 0.0001 $ and $ \epsilon_m = \frac{1}{(2m+1)^3} $.
● For TH Algs. 1 and 2 $ \gamma = 2, \; l = 0.5, \; \tau_1 = 0.8, \; \alpha_m = 0.5 $, $ \beta_m = 0.5 $, $ \mu = 0.6 $.
● For Algorithm 2 of Tian and Tong [47] (TT Alg.), we take $ \alpha_m = 0.5 $, $ \beta_m = 0.5 $, $ \mu = 0.4 $ and $ \lambda_1 = \frac{1}{7} $.
● For Algorithm 3.1 of Godwin et al. [14] (GAMY Alg. 3.1), we take $ \alpha = 4 $, $ \lambda_1 = 0.5, \; \theta_m = \bar{\theta}_m $ $ \delta = 0.4 $ $ c'(x) = 2x $, $ \phi_m = \frac{2m+1}{5m+2} $, $ \beta_m = \frac{2m}{3m+2} $, $ \gamma = 1 $, $ \gamma_m = \Big(\frac{2}{3m+1}\Big)^2 $, $ \alpha_m = (\frac{2}{3m+1} $, $ \mu = 0.8 $, $ Dx = Tx = 0.5x $ and $ f(x) = \frac{1}{3}x $.
● For Algorithm 3.1 of Maluleka et al. [24] (MUA Alg. 3.1), we take $ \theta = 0.9 $, $ \lambda_1 = 3.1, \; \mu_m = \frac{1}{(m+1)^2} $ $ \alpha_m = \frac{1}{m+1} $, $ \beta_m = 0.5 $ and $ \rho = 0.5 $.
● For Algorithm 3.2 of Ogwo et al. [33] (OAM Alg. 3.1), we take $ \alpha = 3 $, $ \lambda_1 = 0.5, \; \alpha_m = \bar{\alpha}_m $ $ \mu = 0.4 $, $ \beta_m = \frac{m}{m+10} $, $ \gamma_1 = 0.01 $, $ \tau_m = (\frac{1}{(m+1)^2} $, $ \theta_m = \frac{1}{m+10} $, $ Dx = 0.01x $ and $ f(x) = 0.01x $.
In this example, all entries $ A $, $ B $ and $ C $ are taken randomly from [1, 100]. We consider 4 different dimensions for $ k $, Case I: $ k = 50 $, Case II: $ k = 100 $, Case III: $ k = 300 $, Case IV: $ k = 500 $. The initial values $ u_1 = u_2 $ are chosen at random using $ randn(k, 1) $ in MATLAB and stopping criterion is taken as $ \|u_{m+1}-u_m\|\leq 10^{-8} $. The results of the numerical simulations are presented in Table 1 and Figures 1 and 2.
Example 4.2. Let $ {H} = \ell^2 $, i.e., $ {H} = \{u = (u_1, u_2, u_3, \cdots, u_i, \cdots):\sum\limits_{i = 1}^{\infty}|u_i|^2 < +\infty\} $. Let $ e, d\in\mathbb{R} $ be such that $ d > e > \frac{d}{2} > 0 $. Let $ {M} = \{u\in \ell^2:\|u\|\leq e\} $ and $ {G}u = (d-\|u\|)u $. Obviously, the solution set $ {VI(M, G)} = \{0\} $. Now, we show that $ {G} $ is $ L $-Lipschitz continuous on $ {H} $ and pseudo-monotone on $ {M} $. Indeed, for any $ u, v\in {H} $, we have
Hence, $ {G} $ is Lipschitz continuous with $ L = d+2e $. Now, let $ u, v\in {M} $ be such that $ \langle {G}u, v-u\rangle > 0 $, then we have $ (d-\|u\|)\langle u, v-u\rangle > 0 $. Since $ \|u\|\leq e\leq d $, we have $ \langle u, v-u\rangle > 0 $. Hence,
This shows that $ {G} $ is a pseudo-monotone mapping. If we set $ e = 3 $ and $ d = 5 $, the projection formula is defined by
Now, let $ Su = \frac{u}{2}. $ It is not hard to show that the mapping $ S $ is nonexpansive (hence, quasi-nonexpansive). We see that $ F(S) = \{0\}\neq \emptyset $. Thus, $ F(S)\cap VI(M, G) $. We take the stopping criterion as $ \|u_{m+1}-u_m\| \leq 10^{-8} $. Furthermore more, we maintain the same control parameters as in Example 4.1. Since we cannot sum to infinity in MATLAB, we considered the subspace of $ \ell_0^2 $ consisting of finite nonzero terms defined by
The first $ i $ points of the initial points are generated randomly considering the following cases for $ i $: Case I: $ i = 100 $, Case II: $ i = 1,000 $, Case III: $ i = 10,000 $, Case IV: $ i = 100,000 $. We use the same control parameters used in the previous example for all the algorithms. The results of the numerical simulations are presented in Table 2 and Figures 3 and 4.
Remark 4.1. After conducting numerical simulations in Examples 4.1 and 4.2 our proposed Algorithms 3.1–3.3 have exhibited a competitive nature and potential when compared to existing algorithms. They outperformed Algorithms 1 and 2 of Thong and Hieu [43], Algorithm 2 of Tian and Tong [47], Algorithm 3.1 of Ogwo et al. [33], Algorithm 3.1 of Godwin et al. [14], and Algorithm 3.1 of Maluleka et al. [24] in terms of computational time and the number of iterations required to meet the specified stopping criteria, highlighting their superior performance.
5.
Application to optimal control problems
In this section, the solution of variational inequality problem arising from optimal control problem is approximated by our Algorithm 3.1. Let $ 0 < T\in \mathbb{R} $, then we denote the Hilbert space of the square integrable by $ L_2([0, 1], \mathbb{R}^k) $, measurable vector function $ s:[0, T]\to \mathbb{R}^m $ induced with the inner product
and norm
Now, the following optimal control problem will be considered on [0, T]:
supposing such control exists. Note that $ S $ denotes the set of admissible controls, which takes the form an $ k $-dimensional box and is made up of a piecewise continuous function:
Particularly, the control can be piecewise constant function (bang-bang).
The terminal objective can be expressed as:
where $ \theta $ is a differentiable and convex function defined on the attainability set. If the trajectory $ u(z)\in L_2([0, 1]) $ fulfills constrains in the form of a linear differential equation system:
where $ D(g)\in \mathbb{R}^{m\times m} $ and $ B(g)\in \mathbb{R}^{m\times k} $ are matrices which are continuous for all $ z\in [0, T] $. Using the Pontryagin maximum principle, we know that a function $ x^*\in L_2([0, 1]) $ exists with the triple $ (u^*, x^*, s^*) $ solving the following system for a.e. $ z\in [0, T] $:
where $ N_S(s) $ is the normal cone to $ S $ at $ s $ defined by
Letting $ Fs(g) = B(z)^Tx(g) $, where $ Fs $ is shown by Khoroshilova [20] to be the gradient of objective cost function $ \zeta $. The express (5.4) can be expressed as a variational inequality problem as follows:
Next, we discretize the continuous function and also take a natural number $ N $ with the mesh size $ h = \frac{T}{N} $. Furthermore, we identify any discretized control $ s^N = (s_0, s_1, \cdots, s_{N}) $ with its piecewise constant extension:
Again, any discretized state $ u^N = (u_0, u_1, \cdots, u_{N}) $ is identified with its piecewise linear interpolation
The same approach can be used to identify the co-state variable $ x^N = (x_0, x_1, \cdots, x_{N}) $.
The system of ordinary differential equations (ODEs) (5.3) and (5.4) will be solved by the Euler method [49]
Next, we solve use Algorithm 3.1 to solve the problem in the following example:
Example 5.1. (see [4])
The exact solution of the problem in Example 5.1 is
The initial controls $ s_0(t) = s_1(t) $ are randomly taken in [-1, 1]. For this, we use the same parameters defined in Example 4.1 and set $ Su = \frac{u}{2} $. The stopping criterion for this section is $ \|u_{m+1}-u_m\|\leq 10^{-7} $. The approximate optimal control and the corresponding trajectories of Algorithm 3.1 are shown in Figure 5.
6.
Application to restoration problem
It is noticed that images are, in most cases distorted by the process of acquisition. The purpose of the restoration technique for distorted images is to restore the original image from the noisy observation of it. The image restoration problem can be modeled as the following undetermined system of the linear equation:
where $ F:\mathbb{R}^N\to \mathbb{R}^M (M < N) $ is a bounded linear operator, $ u\in \mathbb{R}^N $ is an original image and $ v\in \mathbb{R}^M $ is the observed image with noise $ w $. It is well-known that the solution of the model (6.1) is equivalent the solution of the (LASSO) problem as follows [39]:
where $ k > 0 $. It is worthy to know that according [40], one can reconstruct the LASSO problem (6.2) as a variational inequality problem by letting $ {G}u = F^T(Fu-v) $. For this, $ {G} $ is monotone (hence $ {G} $ is pseudomonotone) and Lipschitz continuous with $ L = \|F^TF\| $.
Now, we compare the restoration efficiency of our suggested Algorithms 3.1–3.3 (shortly, OAUAN Algs. 3.1, 3.7 and 3.8) with Algorithms 1 and 2 of Thong and Hieu [43] (shortly, TH Alg. 1 and TH Alg. 2), and Algorithm 2 of Tian and Tong [47] (shortly, TT Alg. 2), Algorithm 3.1 of Ogwo et al. [33] (shortly, OAM Alg. 3.1), Algorithm 3.1 of Godwin et al. [14] (shortly, GAMY Alg. 3.1), and Algorithm 3.1 of Maluleka et al. [24], (shortly, MUA Alg. 3.1). The test images are Austine and Peacock of sizes $ 289\times 350 $ and $ 245\times 245 $, respectively. The images went through a Gaussian blur of size $ 9\times 9 $ and standard deviation of $ \sigma = 4 $. The performances of the algorithms are measured via signal-to-noise ratio (SNR) defined by
where $ u^* $ is the restored image and $ u $ is the original image. In this experiment, we maintain the same parameters used for all the algorithms in Example 4.1 with stopping criterion $ E_m = \|u_{m+1}-u_m\|\leq 10^{-5} $. The numerical results for this experiment are shown in Figures 6–9 and Tables 3–6.
It is well-known that the higher the SNR value of an algorithm, the better the quality of the image it restores. From Figures 6–9 and Tables 3–6, it is evident that our Algorithms 3.1–3.3 restored the blurred images better than Algorithms 1 and 2 of Thong and Hieu [43], and Algorithm 2 of Tian and Tong [47], Algorithm 3.1 of Ogwo et al. [33], Algorithm 3.1 of Godwin et al. [14], and Algorithm 3.1 of Maluleka et al. [24]. Hence, our algorithms are more effective and applicable than many existing methods.
7.
Conclusions
In this work, we have introduced three novel iterative algorithms for finding the common solution of quasi-nonexpansive FPP and pseudo-monotone variational inequality problems. Our algorithms embed double inertial steps which accelerate their convergence rates. Numerical experiments have shown that our algorithms outperformed several existing algorithms with single or no inertial terms. Further, we a considered a new self-adaptive step size technique that produces a non-monotonic sequence of step sizes while also correctly incorporating a number of well-known step sizes. The step size is designed to lessen the algorithms' reliance on the initial step size. Numerical tests were performed, and the results showed that our step size is more effective and that it guarantees that our methods require less execution time. Our convergence results were obtained without the imposition of stringent conditions on the control parameters. The class of pseudo-monotone operators, which has been studied in the work, is more general than the class of monotone operators which has been studied in [43,47] and several other articles. To test the applicability and efficiencies of our methods in solving real-world problems, we utilized the methods to solve optimal control and image restorations problems.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this work through the projection number (PSAU/2023/01/8980).
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: