Hyperideal-based zero-divisor graph of the general hyperring $\mathbb{Z}_{n}$

1.   Introduction

Connecting different theories from different perspectives is a powerful tool to reveal remarkable properties and results in one theory through the elements of the other theory, by identifying previously unnoticed aspects or hidden structures. This can lead to a deeper understanding of the original theory and its limitations. This is also the case of the connections between different algebraic structures theories (such as group theory, ring theory, hypercompositional algebra, etc.) and graph theory. On one side, many properties of the algebraic structures have been better visualized and easily described using the properties of the associated graphs ^[23,25,28]. On the other side, new algebraic properties of graphs have been derived from the properties of the algebraic structures, and this is the aim of the algebraic graph theory. The interconnection between the two theories- very nicely called "conversation" by Peter Cameron in his recently published paper ^[6] with the significant title "What can graphs and algebraic structures say to each other?"- dates back in 1878 to the fundamental work of Cayley ^[5], where he defined the Cayley graphs. One hundred years later, in 1988, Beck ^[4] introduced the concept of the zero-divisor graph of a commutative ring (extended to the non-commutative case in 2002 by Redmond ^[31]) in order to solve problems related to the colorings of rings. Let $R$ be a unitary ring, and $Z(R)$ denote the set of the zero-divisors of $R$. Then, the zero-divisor graph of $R$, defined by Beck and denoted by $\Gamma_0(R)$, has the vertex set $R$, and two distinct vertices $x$ and $y$ are joined by an edge if and only if $xy = 0$. It is then clear that the vertex $0$ in $\Gamma_0(R)$ is connected with any other vertex, while non-zero-divisors are connected only with $0$. This definition was slightly changed in 1999 by Anderson and Livingston ^[2], considering the graph $\Gamma(R)$ as an undirected graph with the vertex set $Z(R)^* = Z(R)\setminus\{0\}$ (the set of non-zero zero-divisors of $R$) and where two distinct vertices $x$ and $y$ are connected by an edge if and only if $xy = 0$. This is the definition that was further explored by Levy and Shapiro ^[22] and later on extended to semirings ^[12,13], nearrings ^[7], semigroups ^[11], etc.

A generalization of the zero-divisor graph was proposed in 2003 by Redmond ^[32], who changed the definition of the edges in this graph, by considering two vertices connected if their product lies in a fixed ideal of the ring. He called the new graph $\Gamma_I(R)$ the ideal-based zero-divisor graph of a commutative ring $R$. If the fixed ideal $I$ is the trivial one, i.e., $I = \{0\}$, then the ideal-based zero-divisor graph coincides with the zero-divisor graph. In this paper, we will extend this construction to the case of general hyperrings. The first definition of a hyperring was given by Marc Krasner, after defining hyperfields, and this notion has remained in the literature with the name of Krasner hyperring ^[21]. It is a hypercompositional structure $(R, +, \cdot)$, having the additive part a canonical hypergroup, the multiplicative one being a semigroup with a bilaterally absorbing element $0$, and satisfying the distributive axiom. Hypergroups appeared in 1934 as a natural generalization of groups, when F. Marty noticed the importance of this structure in the study of the cosets determined by non-normal subgroups. A hypergroup is a non-empty set $H$ endowed with a hyperoperation $\circ: H\times H\longrightarrow \mathcal{P}(H)\setminus\{\emptyset\}$ (where $\mathcal{P}(H)$ denotes the power set of $H$) that is associative and reproductive (see the detailed definitions in Section 2). A commutative hypergroup $(H, +, 0)$, where each element has a unique inverse (for any $x\in H$, there exists $-x\in H$ such that $0\in -x+x = x+(-x)$) and the reversibility axiom holds ($z\in x+y$ implies $x\in z+(-y)$, for any $x, y, z\in H$), was called canonical by Mittas ^[29]. A general hyperring is an algebraic structure $(R, +, \cdot)$, where $(R, +)$ is a hypergroup, $(R, \cdot)$ is a semihypergroup and the multiplication inclussively distributes on both sides over addition: $(x+y)\cdot z\subseteq x\cdot z+y\cdot z$ and $x\cdot (y+z)\subseteq x\cdot y+x\cdot z$, for any $x, y, z\in R$. This structure was first defined by Vougiouklis ^[34] and then studied by Spartalis ^[33], Cristea ^[9], Jančic-Rašovic ^[18]. Several non-trivial constructions of general hyperrings have been recently proposed by Hamidi et al. ^[3]. One of them refers to the general hyperring $(\mathbb{Z}_n, \oplus, \odot)$ of the integers modulo $n$, where $n$ is an even number (see Example 2.1). In the same paper, the authors also determined the hyperideals of this general hyperring (see Proposition 2.3), which will be used in Section 4.

In this manuscript, we introduce and study the hyperideal-based zero-divisor graph of a general hyperring. This is a simple graph $\Gamma^{(I)}(R)$ associated with a general hyperring $R$ with respect to a hyperideal $I\neq R$. Its vertex set is $Z^{(I)}(R) = \{x\in R\setminus I\mid \exists y\in R\setminus I: x\cdot y\cap y\cdot x\subseteq I\}$ and two distinct vertices $x$ and $y$ are adjacent, so connected by an edge, if $(x\cdot y)\cap (y\cdot x)\cap I\neq\emptyset$. First, we present some general aspects of this graph associated to an $\mathcal{O}_R$-general commutative hyperring, i.e., to a general hyperring $R$ satisfying the property $x\cdot y = y\cdot x = \mathcal{O}_R$, for any $x, y\in R$, where $\mathcal{O}_R$ denotes the set of all absorbing elements of $R$. Properties and examples related to the absorbing elements are covered in Section 3. The second part of the paper is dedicated to the particular case of the general hyperring $R = (\mathbb{Z}_n, \oplus, \odot)$. If $n\in\mathbb{N}$ is an even number, then there exists $\overline{a}\in\mathbb{Z}_n$, $\overline{a}\neq\overline{0}$, such that $\overline{2a} = \overline{0}$ and $I = \{\overline{0}, \overline{a}\}$ is a hyperideal of $R$. We investigate the properties of the $I$-based zero-divisor graph $\Gamma^{(I)}(R)$, taking the hyperideal $I = \{\overline{0}, \overline{a}\}$ and different particular values of $n = 2p^mq$, with $m\in\mathbb{N}$, $p$ and $q$ different odd primes. The paper ends with some conclusive ideas and proposals for a continuation of this study.

2.   Preliminaries

In this section, we briefly recall the definitions and main properties of the fundamental notions related to the theory of general hyperrings, fixing also the used notation and terminology. For more details, the reader is referred to the original manuscripts where general hyperrings were introduced and studied ^[3,26,33,34], as well as to the fundamental book ^[10].

Let $R$ be a nonempty set; $\mathcal{P}(R)$ denotes the power set of $R$, i.e., the set of all subsets of $R$, while $\mathcal{P}^*(R) = \mathcal{P}(R)\setminus \{\emptyset\}$. A hyperoperation or a hypercomposition defined on $R$ is a function $\circ: R\times R\longrightarrow \mathcal{P}^*(R)$, that can be denoted also additively or multiplicatively, which associates with any pair of elements $x, y$ in $R$ a nonempty subset $x\circ y$ of $R$. For two nonempty subsets $A$ and $B$ of $R$, we write $A\circ B = { }\bigcup_{\substack{x\in A, y\in B}} x\circ y$, $A\circ y = A\circ \{y\}$, and $x\circ B = \{x\}\circ B$. The pair $(R, \circ)$ is called a hypergroupoid which becomes a semihypergroup if the associativity holds, i.e., $(x\circ y)\circ z = x\circ (y\circ z)$, for any $x, y, z$ in $R$. If a semihypergroup $(R, \circ)$ satisfies the reproduction axiom, i.e., $R\circ x = x\circ R = R$, for any element $x$ in $R$, then it is called a hypergroup.

Endow now a nonempty set $R$ with two hyperoperations: one is written in the additive form with respect to which $(R, +)$ is a hypergroup, while the second one is given in the multiplicative form such that $(R, \cdot)$ is a semihypergroup. Moreover, if the multiplication inclussively distributes over the addition, i.e., $(x+y)\cdot z\subseteq x\cdot z+y\cdot z$ and $x\cdot (y+z)\subseteq x\cdot y+x\cdot z$, for any $x, y, z$ in $R$, then the hypercompositional structure $(R, +, \cdot)$ is called a general hyperring. A general hyperring $(R, +, \cdot)$ is called commutative, if the multiplication commutes, i.e., $x\cdot y = y\cdot x$, for any $x, y$ in $R$, while it is a $\Delta$-general hyperring, if $x\cdot y = y\cdot x = \Delta$, for any $x, y$ in $R$ and $\Delta$ a nonempty subset of $R$. We say that a general hyperring $(R, +, \cdot)$ satisfies the strongly distributivity property, if $x\cdot(y + z) = x\cdot y + x\cdot z$ and $(x + y)\cdot z = x\cdot z +y\cdot z,$ for any $x, y, z\in R$, briefly being called an S.D.-general hyperring.

A nonempty subset $I$ of $R$ is called a right (respectively a left) hyperideal of $R$, if $(I, +)$ is a hypergroup and $R\cdot I\subseteq I$ (respectively $I\cdot R \subseteq I$). A hyperideal $I$ is both a left and a right hyperideal of $R$ and it is called prime hyperideal if $P\neq R$ and $(x\cdot y)\cap (y\cdot x)\subseteq P$ implies that $x\in P$ or $y\in P$.

As an example of a general hyperring, we recall here the construction proposed in ^[3] related to the cyclic group $\mathbb{Z}_n$ of the integers modulo $n$, with $n\in \mathbb{N}$.

Example 2.1. Let $n\in\mathbb{N}$ be an even natural number. Endow the set $\mathbb{Z}_n$ with two binary hyperoperations, denoted $\oplus$ and $\odot$, as follows: for a fixed $\overline{a}\in\mathbb{Z}_n$, $\overline{a}\neq \overline{0}$ such that $\overline{2a} = \overline{0}$, define $\overline{x}\oplus\overline{y} = \overline{x}+_ {\overline{a}}\overline{y} = \{\overline{x+y}, \overline{x+y+a}\}$ and $\overline{x}\odot\overline{y} = \overline{x}\cdot_ {\overline{a}}\overline{y} = \{\overline{xy}, \overline{xy+a}\}$, for any $\overline{x}, \overline{y}\in \mathbb{Z}_n$.

According to Theorem 3.7 ^[3], $(\mathbb{Z}_n, \oplus, \odot)$ is a general hyperring. Besides, notice that if $n$ is an odd number, then $(\mathbb{Z}_n, \odot)$ is not a semihypergroup. Indeed, in the particular case of $n = 3$, $\overline{a} = \overline{2}\neq\overline{0}$, we get $(\overline{0}\odot \overline{a})\odot \overline{2} = \{\overline{0}, \overline{1}, \overline{2}\}$, while $\overline{0}\odot (\overline{1}\odot \overline{2}) = \{\overline{0}, \overline{2}\}$.

As a consequence, we get the following properties of the general hyperring $(\mathbb{Z}_{2^n}, \oplus, \odot)$.

Corollary 2.2. ^[3] Let $n$ be a natural number, $n\geq 2$, and $\overline{a}$ be an arbitrary element in $\mathbb{Z}_{2^n}$ such that $\overline{2a} = \overline{0}$. Then, for all $k\in \mathbb{N}$, we have $k\overline{a} = \overline{a}^k = \{\overline{0}, \overline{a}\}$.

In ^[3], the authors have determined all the hyperideals of the general hyperring $R$ defined in Example 2.1. They are hyperideals generated by one element, where for any $\overline{x}\in \mathbb{Z}_n$, the hyperideal generated by $\overline{x}$ is $\langle \overline{x}\rangle = \bigcup_{k\in\mathbb{N}}k\overline{x}$. More details follow in the next result.

Proposition 2.3. ^[3] Let $R = (\mathbb{Z}_n, \oplus, \odot)$ be the genenal hyperring defined in Example 2.1, where $\overline{a}\in\mathbb{Z}_n$, such that $\overline{2a} = \overline{0}$. Then the following statements are true:

1) $\langle \overline{a}\rangle = \{\overline{0}, \overline{a}\}$.

2) If $x\neq a$ and $\gcd\{x, a\} = d$, then $\langle \overline{x}\rangle = \langle \overline{d}\rangle$.

3) $I$ is a hyperideal of $R$ if and only if there exists $\overline{x}\in \mathbb{Z}_n$ such that $I = \langle \overline{x}\rangle$.

3.   Absorbing elements in general hyperrings

In a groupoid $(G, \ast)$, an element $x$ is called an absorbing element if it satisfies the equalities $x\ast g = g\ast x = x$, for all elements $g\in G$. If such an element exists, then it is unique, and if a group has an absorbing element, then it is a trivial group. Thus, the absorbing elements have a significant role in rings, where $0$ (the neutral element with respect to the addition) is a multiplicative absorbing element, i.e., $r\cdot 0 = 0\cdot r = 0$, for any element $r$ of the ring.

In this section we study the concept of an absorbing element in a general hyperring. First, we recall that, unlike a group, a hypergroup can have one or more bilateral identities, or even have no bilateral identity at all.

Definition 3.1. ^[14] Let $(R, +, \cdot)$ be a general hyperring.

$(i)$ An element $x\in R$ is a multiplicative absorbing element or $(\cdot)$-absorbing element of $R$ if, for all $r\in R$, $x\in x\cdot r\cap r\cdot x$.

$(ii)$ A bilateral identity of $(R, +)$ is called an absorbing element of $R$, if it is a $(\cdot)$-absorbing element of $R$.

We denote by $\mathcal{O}^{(\cdot)}_R$ the set of all $(\cdot)$-absorbing elements of $R$, while $\mathcal{O}_R$ is the set of all absorbing elements of the general hyperring $R$.

Example 3.2. ^[14] $i)$ On the set $R = \{a, b, c, d\}$ define the structure of the general hyperring as follows:

It is clear that $a$ is a bilateral identity of $(R, +)$ and the only $(\cdot)$-absorbing element in $R$, thus $\mathcal{O}^{(\cdot)}_R = \mathcal{O}_R = \{a\}$.

$ii)$ The set $R = \{a, b, c\}$ endowed with the addition and multiplication defined by the following Cayley's tables

is a general hyperring, having $a$ as its unique bilateral identity. But $\mathcal{O}^{(\cdot)}_R = \emptyset$ and thus $\mathcal{O}_R = \emptyset$.

$iii)$ The set $R = \{a, b, c, d, e\}$ with the following addition and multiplication becomes a commutative general hyperring:

Immediately one notices that every element is a bilateral unit and $\mathcal{O}^{(\cdot)}_R = \{a, b\}$, meaning that $\mathcal{O}_R = \{a, b\}$ and moreover $R$ is an $\mathcal{O}_R$-general hyperring, i.e., $x\cdot y = y\cdot x = \mathcal{O}_R$, for any $x, y\in R$.

Proposition 3.2. Let $(R, +, \cdot)$ be an S.D.- general hyperring. Then the following assertions are valid:

$(i)$ $\mathcal{O}^{(\cdot)}_R$ is a subsemihypergroup of $(R, \cdot)$.

$(ii)$ For any $x, y\in\mathcal{O}^{(\cdot)}_R$, the inclusion $x+y\subseteq\mathcal{O}^{(\cdot)}_R$ holds.

$(iii)$ If $R$ is commutative, then $\mathcal{O}^{(\cdot)}_R$ and $\mathcal{O}_R$ are hyperideals of $R$. Besides, any hyperideal $I$ of $R$ contains $\mathcal{O}_R$.

Proof. $(i)$ Let $x, y \in \mathcal{O}^{(\cdot)}_R$. Then, for any $r\in R$, we have $x\cdot y\subseteq (r\cdot x)\cdot y = r\cdot(x\cdot y)$, and similarly, $x\cdot y\subseteq x\cdot (y\cdot r) = (x\cdot y)\cdot r$, meaning that $x\cdot y\subseteq \mathcal{O}^{(\cdot)}_R.$ Thus, $\mathcal{O}^{(\cdot)}_R$ is a subsemihypergroup of $(R, \cdot)$. Notice that here, strong distributivity is not necessary.

$(ii)$ Let $x, y \in \mathcal{O}^{(\cdot)}_R$. Then, for any $r\in R$, we have $x+y\subseteq r\cdot x+r\cdot y = r\cdot(x+y)$ and similarly, $x+y\subseteq x\cdot r+y\cdot r = (x+y)\cdot r$, meaning that $x+y\subseteq \mathcal{O}^{(\cdot)}_R.$

$(iii)$ Accordingly with $(ii)$, $(\mathcal{O}^{(\cdot)}_R, +)$ is a subhypergroup of $(R, +)$. Let $x$ be an arbitrary element in $\mathcal{O}^{(\cdot)}_R$. Then, for any $r, s\in R$, we get $r\cdot x\subseteq r\cdot(x\cdot s) = (r\cdot x)\cdot s$ and $x\cdot r\subseteq (s\cdot x)\cdot r = s\cdot(x \cdot r)$. Since $(R, \cdot)$ is commutative, we also get $r\cdot x\subseteq s\cdot (r\cdot x)$ and $x\cdot r\subseteq (x \cdot r)\cdot s$, therefore $r\cdot x\cup x\cdot r \subseteq\mathcal{O}^{(\cdot)}_R$.

Since the set of all bilateral identities with respect to the addition is a hyperideal of $R$, it follows that $\mathcal{O}_R$ is a hyperideal of $R$, too. Besides, for any $x\in\mathcal{O}_R$ and $r\in I$, we have $x\in x\cdot r\subseteq I$, so $\mathcal{O}_R\subseteq I$. □

Theorem 3.4. Let $(R, +, \cdot)$ be a $\Delta$-general hyperring.

$(i)$ If $\Delta$ is a subhypergroup of $(R, +)$, then $(R, +, \cdot)$ is a commutative S.D.-general hyperring.

$(ii)$ If $\Delta = \mathcal{O}^{(\cdot)}_R$, then $\Delta$ and $\mathcal{O}_R$ are hyperideals of $R$.

Proof. $(i)$ Take arbitrary three elements $x, y, z \in R$. Then $x\cdot(y+z) = { }\bigcup_{w\in y+z}x\cdot w = { }\bigcup\Delta = \Delta = \Delta+\Delta = x\cdot y+ x\cdot z$. Similarly, one proves that $(x+y)\cdot z = x\cdot y+ x\cdot z$ and $x\cdot y = \Delta = y\cdot x$, so $(R, +, \cdot)$ is a commutative S.D.-general hyperring.

$(ii)$ Since $\mathcal{O}^{(\cdot)}_R$ is a subhypergroup of $(R, +)$ it follows that $R$ is a commutative S.D.-general hyperring, and according with Proposition 3.3, we know that $\mathcal{O}^{(\cdot)}_R$ and $\mathcal{O}^{(\cdot)}_R$ are hyperideals of $R$.

□

4.   Hyperideal-based zero-divisor graph of a general hyperring

In this section, we introduce the concept of a zero-divisor graph based on nontrivial hyperideals of general hyperrings and investigate its algebraic properties with respect to the $(\cdot)$-absorbing elements and absorbing elements.

First, we fix some notations related to graph theory. In this paper, we consider simple graphs, i.e., undirected graphs without loops and multiple edges. A simple graph is called connected, if there is a path connecting any two distinct vertices in the graph. A graph $\Gamma$ is called complete if any two distinct vertices are adjacent, so there is an edge between them. $K_n$ denotes the complete graph on $n$ vertices. A complete bipartite graph is a graph whose vertex set may be partitioned into two subsets such that no edge has both endpoints in the same subset, and every possible edge that could connect vertices in different subsets is part of the graph. A complete bipartite graph with partitions of the size $m$ and $n$ is denoted by $K_{m, n}$. For two vertices $x$ and $y$ of a graph $\Gamma$, we define $d(x, y)$ to be the length of a shortest path connecting $x$ and $y$ in $\Gamma$. In particular, $d(x, x) = 0$ and $d(x, y) = \infty$ if there is no such path. The diameter of $\Gamma$ is $diam(\Gamma) = sup\{d(x, y)\mid \mbox{ $x$ and $y$ are vertices in $\Gamma$ }\}$. The girth of $\Gamma$, denoted by $gr(\Gamma)$, is the length of a shortest cycle in $\Gamma$, where by cycle we mean a path starting and ending at the same point. We make the convention that $gr(\Gamma) = \infty$ if $\Gamma$ contains no cycles.

With an arbitrary general hyperring $(R, +, \cdot)$, let us associate a simple graph related to one hyperideal of $R$. Let $\mathcal{I}(R)$ denote the set of all hyperideals of $R$. For any $I\in\mathcal{I}(R)\setminus R$, define the set $Z^{(I)}(R) = \{x\in R\setminus I\mid \exists y\in R\setminus I \mbox{such that }\; x\cdot y\cap y\cdot x\subseteq I\}$.

Definition 4.1. The hyperideal-based zero-divisor graph $\Gamma^{(I)}(R)$ associated with a general hyperring $R$ and a hyperideal $I\neq R$ of $R$ is the simple graph having $Z^{(I)}(R)$ as its vertex set, where two distinct vertices $x, y$ are adjacent if $(x\cdot y)\cap (y\cdot x)\cap I\neq \emptyset$.

We better illustrate this definition in the following two examples.

Example 4.2. ^[14] $(i)$ Endow the set $R = \{a, b, c, d, e\}$ with the structure of a general hyperring, as in Example 3.2 $iii)$. The set of its hyperideals is the following:

For any hyperideal $I\in \mathcal{I}(R)$, we first determine the vertex set of the associated $I$-based divisor graph $\Gamma^{(I)}(R)$, and we obtain:

, and similarly $Z^{(I_2)}(R) = \{c, e\}$, $Z^{(I_3)}(R) = \{d, c\}$. Since all three hyperideals $I_1, I_2$, and $I_3$ contain the set $\{a, b\}$, it follows that the three associated $I$-based zero-divisor graphs $\Gamma^{(I_1)}(R)$, $\Gamma^{(I_2)}(R)$, and $\Gamma^{(I_3)}(R)$ are isomorphic with the path graph $P_2$, which is isomorphic with the complete bipartite graph $K_{1, 1}$.

Since $Z^{(I_4)}(R) = \{e\}$, $Z^{(I_5)}(R) = \{d\}$ and $Z^{(I_6)}(R) = \{c\}$ and all hyperideals $I_4, I_5$, and $I_6$ contain the set $\{a, b\}$, it follows that the associated $I$-based zero-divisor graphs $\Gamma^{(I_j)}(R)$, $j\in\{4, 5, 6\}$, are isomorphic with the complete graph $K_1$ (the graph with one vertex and no edges). Finally, we get that $Z^{(I_7)}(R) = \{c, d, e\}$, where any pair of vertices is connected, meaning that the associated $I_7$-based zero-divisor graph $\Gamma^{(I_7)}(R)$ is isomorphic with the complete graph $K_3$.

$(ii)$ Endow the set $R = \{a, b, c, d, e, f\}$ with a general hyperring structure, where the two hyperoperations are defined by the following Cayley tables:

and

The set $J = \{a, d\}$ is a hyperideal of $(R, +, \cdot)$ and $Z^{(J)}(R) = \{b, c, e, f\}$, but no pair of vertices is connected, so $\Gamma^{(J)}(R)\cong N_4$, the graph with $4$ vertices and no edge.

Let $(R, +, \cdot)$ be a general commutative hyperring and $\mathcal{O}_R$ the set of its absorbing elements. $R$ is an $\mathcal{O}_R$-general hyperring if $x\cdot y = y\cdot x = \mathcal{O}_R$, for any $x, y\in\mathcal{O}_R$. The next result summarizes the main properties of the hyperideal-based zero-divisor graph $\Gamma^{(I)}(R)$ of an $\mathcal{O}_R$-general hyperring.

Theorem 4.3. Let $(R, +, \cdot)$ be an $\mathcal{O}_R$-general commutative hyperring. For an arbitrary hyperideal $I\neq R$ of $R$, the associated hyperideal-based zero-divisor graph $\Gamma^{(I)}(R)$ has the following properties:

$(i)$ $Z^{(I)}(R) = R\setminus I\subseteq R\setminus\mathcal{O}_R$,

$(ii)$ $\Gamma^{(I)}(R)$ is a complete graph, so $diam(\Gamma^{(I)}(R)) = 1$ and $gr(\Gamma^{(I)}(R)) = 3$.

Proof. $(i)$ According to Theorem 3.3, $(R, +, \cdot)$ is a commutative $S.D.$- general hyperring, and thus, $\mathcal{O}_R$ is a hyperideal of $(R, +, \cdot)$. By hypothesis, for any $x, y\in R$, it holds $x\cdot y = y\cdot x = \mathcal{O}_R$, implying that

$(ii)$ Since $(R, +, \cdot)$ is an $\mathcal{O}_R$-general hyperring, any two vertices of the graph $\Gamma^{(I)}(R)$ are connected, since $x\cdot y\cup y\cdot x\cup I\neq\emptyset$, therefore the graph $\Gamma^{(I)}(R)$ is complete; thus, $diam(\Gamma^{(I)}(R)) = 1$ and $gr(\Gamma^{(I)}(R)) = 3$. □

Theorem 4.4. Let $(R, +, \cdot)$ be a general hyperring and $I$ a hyperideal of $R$, such that $I\neq R$. Then the following statements hold:

$(i)$ $I\cap Z^{(I)}(R) = \emptyset$.

$(ii)$ If $R$ has the unit element $1$, then $1\not\in Z^{(I)}(R)$.

$(iii)$ If $P$ is a prime hyperideal of $R$, then $Z^{(P)}(R) = \emptyset$.

Proof. $(i)$ This is an obvious observation.

$(ii)$ Suppose that $1\in Z^{(I)}(R)$. Then there exists $y\in R\setminus I$ such that $y\in (1\cdot y)\cap(y\cdot 1)\subseteq I$, which is a contradiction.

$(iii)$ Suppose that $Z^{(P)}(R)\neq \emptyset$ and take an arbitrary $x\in Z^{(P)}(R)$. Then $x\in R\setminus P$ and there exists $y\in R\setminus P$ such that $(x\cdot y)\cap (y\cdot x)\subseteq P$. Since $P$ is a prime hyperideal, we get that $x\in P$ or $y\in P$, which is a contradiction. Thus, $Z^{(P)}(R) = \emptyset$. □

5.   The particular case of the general hyperring $(\mathbb{Z}_{2p^mq}, \oplus, \odot)$

In this section, we consider the finite general hyperring $(\mathbb{Z}_{n}, \oplus, \odot)$, with $n\in \mathbb{N}$ an even integer, considered in Example 2.1, where there exists $\overline{a}\in \mathbb{Z}_n$, $\overline{a}\neq\overline{0}$, such that $\overline{2a} = \overline{0}$. We investigate the properties of the hyperideal-based zero-divisor graph $\Gamma^{(I)}(R)$, taking the hyperideal $I = \{\overline{0}, \overline{a}\}$ and the different particular values of $n = 2p^mq$, with $p$ and $q$ different odd primes and $m\in \mathbb{N}$.

We first start with a general property of the vertex set $Z^{(I)}(R)$ of the hyperideal-based zero-divisor graph $\Gamma^{(I)}(R)$, determining it then for the basic case when $m = 0$, so $n = 2p$, with $p$ an odd prime.

Theorem 5.1. Let $R = (\mathbb{Z}_n, \oplus, \odot)$ be the general hyperring in Example 2.1, and consider the hyperideal $I = \{\overline{0}, \overline{a}\}$.

$(i)$ If $\overline{x} \in Z^{(I)}(R)$, then $\overline{x} \in\mathbb{Z}_n\setminus\{\overline{0}, \overline{1}, \overline{a}\}$ and $\gcd(x, n)\neq 1$.

$(ii)$ $Z^{(I)}(R) = \emptyset$ if and only if $n = 2p$, with $p$ being an odd prime.

Proof. $(i)$ If $\overline{x}\in Z^{(I)}(R)$, by Theorem 4.3, we immediately have $\overline{x}\in R\setminus \{\overline{0}, \overline{1}, \overline{a}\}$ and there exists $\overline{y}\in R\setminus I$ such that $\overline{x}\odot \overline{y} = \{\overline{xy}, \overline{xy+a}\}\subseteq \{\overline{0}, \overline{a}\}$, meaning that $\overline{xy} = \overline{0}$ or $\overline{xy} = \overline{a}$.

Suppose now, by absurdity, that $\gcd(x, n) = 1$. If $\overline{xy} = \overline{0}$, then $n\lvert y$, which is a contradiction with the fact that $\overline{y}\neq\overline{0}$. If $\overline{xy} = \overline{a}$, then $xy\equiv a\pmod{n}$, implying that $2xy\equiv 2a\pmod{n}\equiv 0\pmod{n}$. Thus $n\lvert 2xy$, so $n\lvert y$, which is again a contradiction. Therefore, $\gcd(x, n)\neq1$.

$(ii)$ Suppose that $Z^{(I)}(\mathbb{Z}_n, \oplus, \odot) = \emptyset$, where $n = 2m, m\in \mathbb{N}$, and then $I = \{\overline{0}, \overline{m}\}$. It follows that, for any $\overline{x}, \overline{y}\in \mathbb{Z}_n\setminus\{\overline{0}, \overline{m}\}$, we have $xy \not\equiv 0 \pmod{2m}$ or $xy \not\equiv m \pmod{2m}$. Thus, $2m\not\lvert xy$ or $2m\not\lvert xy-m$, both lead to the conclusion that $m\not\lvert xy$. Thereby, for any $\overline{x}, \overline{y}\in\mathbb{Z}_{2m}$ such that $m\not\lvert x$ and $m\not\lvert y$, it follows that $m\not\lvert xy$, meaning that $m$ is a prime number.

Conversely, consider $n = 2p$, with $p$ an odd prime number, and then $I = \{\overline{0}, \overline{p}\}$. If there exists $\overline{x}\in Z^{(I)}(\mathbb{Z}_{2p})$, then $\overline{x}\in\mathbb{Z}_{2p}\setminus\{\overline{0}, \overline{1}, \overline{p}\}$ and there exists $\overline{y}\in\mathbb{Z}_{2p}\setminus\{\overline{0}, \overline{p}\}$ such that $\overline{x}\odot \overline{y} = \{\overline{xy}, \overline{xy+p}\}\subseteq \{\overline{0}, \overline{p}\}$, equivalently with $\overline{xy}\in \{\overline{0}, \overline{p}\}$. On one side, if $\overline{xy} = \overline{0}$, then $xy\equiv 0\pmod{2p}$, and thus $p\lvert xy$, with $p$ a prime, leads to $p\lvert x$ or $p\lvert y$. Both conclusions are in contradiction with the hypothesis $\overline{x}\neq \overline{p}$ and $\overline{y}\neq \overline{p}$. On the other side, if $\overline{xy} = \overline{p}$, then $xy\equiv p \pmod{2p}$, and thus $\gcd(x, 2p)\lvert p$, meaning that $\gcd(x, 2p) = 1$ or $\gcd(x, 2p) = p$. The first case is excluded by item $(i)$ of this theorem, while in the second case we get $p\lvert x$, which is again a contradiction of the fact that $\overline{x}\neq\overline{p}$. Concluding, if $n = 2p$, with $p$ an odd prime, then it follows that $Z^{(I)}(\mathbb{Z}_{2p}) = \emptyset$, and the proof is now complete.

□

The aim of the next result is to show that the hyperideal-based zero-divisor graph $\Gamma^{(I)}(R)$ associated to the general hyperring $R = (\mathbb{Z}_{2pq}, \oplus, \odot)$, is a bipartite complete graph.

Theorem 5.2. Let $R = (\mathbb{Z}_n, \oplus, \odot)$ be the general hyperring in Example 2.1, where $n = 2pq$, with $p\neq q$ two distinct odd primes, and $I = \{\overline{0}, \overline{pq}\}$. Then the following statements are true:

$(i)$ $Z^{(I)}(R) = \{\overline{x} \in \mathbb{Z}_n\setminus\{\overline{0}, \overline{1}, \overline{pq}\}\mid p\lvert x\; \mathit{\mbox{or}}\; q\lvert x\}$.

$(ii)$ $\lvert Z^{(I)}(R)\rvert = \lfloor{ }\frac{n-1}{p}\rfloor+\lfloor{ }\frac{n-1}{q}\rfloor-2$.

$(iii)$ $E(\Gamma^{(I)}(R)) = V_1\times V_2$, where $V_1 = \{kp\mid 1\leq k\leq { }\lfloor\frac{n-1}{p}\rfloor, k\neq q\}$ and $V_2 = \{k'q\mid 1\leq k'\leq { }\lfloor\frac{n-1}{q}\rfloor, k'\neq p\}$.

$(iv)$ $\Gamma^{(I)}(R) = K_{\alpha, \beta}$, with $\alpha = \lfloor{ }\frac{n-1}{p}\rfloor-1$ and $\beta = \lfloor{ }\frac{n-1}{q}\rfloor-1$.

Proof. $(i)$ Let $\overline{x}\in Z^{(I)}(R)$. According to Theorem 5.1 and Definition 4.1, we know that $\overline{x}\not \in \{\overline{0}, \overline{1}, \overline{pq}\}$ and there exists at least one $\overline{y}\in \mathbb{Z}_n\setminus\{\overline{0}, \overline{pq}\}$ such that $\overline{x}\odot \overline{y}\subseteq I$, equivalently with $xy \equiv 0 \pmod{2pq}$ or $xy \equiv pq \pmod{2pq}$. In both cases, it follows that $pq\lvert xy$. Since $p$ and $q$ are distinct odd primes and $\gcd(x, 2pq)\neq 1$, by Theorem 5.1, we get that $\gcd(x, 2pq)\in\{2, p, q, 2p, 2q\}$. It is enough to prove that $\gcd(x, n)\neq 2$, meaning that $p\lvert x$ or $q\lvert x$. Indeed, if $\gcd(x, 2pq) = 2$, since $pq\lvert xy$, it follows immediately that $pq\lvert y$, which is a contradiction with the condition $\overline{y}\neq\overline{pq}$.

$(ii)$ For any $\overline{x} \in Z^{(I)}(R)$, we know that $p\lvert x$ and $q\lvert x$ and there exists at least one $\overline{y}\in \mathbb{Z}_n\setminus\{\overline{0}, \overline{pq}\}$ such that $xy \equiv 0 \pmod{2pq}$ or $xy \equiv pq \pmod{2pq}$. Let us consider first that $p\lvert x$.

● If $xy \equiv 0 \pmod{2pq}$, then $y\equiv 0 \pmod{2q}$, and thus $y\in\{2q, 2\cdot (2q), 3\cdot (2q), \ldots, (p-1)\cdot (2q)\} = A_1$, with $\lvert A_1\rvert = p-1$.

● If $xy \equiv pq \pmod{2pq}$, then $y\equiv q \pmod{2q}$, and so $y\in\{q, 2q+q, 2\cdot (2q)+q, \ldots, (p-1)\cdot (2q)+q\} = A_2$, with $\lvert A_2\rvert = p$. Since $\overline{y}\neq \overline{pq}$, from the set $A_2$, we must exclude the value $pq = (\frac{p-1}{2})(2q)+q$.

Consider now the case when $q\lvert x$. Again we have to discuss the following two cases:

● If $xy \equiv 0 \pmod{2pq}$, then $y\equiv 0 \pmod{2p}$, and thus $y\in\{2p, 2\cdot (2p), 3\cdot (2p), \ldots, (q-1)\cdot (2p)\} = B_1$, with $\lvert B_1\rvert = q-1$.

● If $xy \equiv pq \pmod{2pq}$, then $y\equiv p \pmod{2q}$, and so $y\in\{p, 2p+p, 2\cdot (2p)+p, \ldots, (q-1)\cdot (2p)+p\} = B_2$, with $\lvert B_2\rvert = p$. But again, from the set $B_2$, we must exclude the value $pq = (\frac{q-1}{2})(2p)+p$.

Since the sets $A_1, A_2\setminus\{pq\}, B_1$, and $B_2\setminus\{pq\}$ are mutually disjoint, we conclude that

$(iii)$ Let $\overline{x}, \overline{y}\in Z^{(I)}(R)$. Then $\overline{x}$ and $\overline{y}$ are adjacent if and only if $\overline{x}\odot \overline{y}\cap \{\overline{0}, \overline{pq}\}\neq\emptyset$, so if and only if $x, y\in \mathcal{A}$, where $\mathcal{A} = A_1\cup(A_2\setminus\{pq\})\cup B_1\cup (B_2\setminus\{pq\})$. This is equivalently with $(x, y) = (kp, k'q)$, with $1\leq k\leq { }\lfloor\frac{n-1}{p}\rfloor$, $k\neq q$ and $1\leq k'\leq { }\lfloor\frac{n-1}{q}\rfloor$, $k'\neq p$.

Indeed, if $(x, y) = (kp, k'p)$, which $1\leq k, k'\leq { }\lfloor\frac{n-1}{p}\rfloor$, $k\neq q$, $k'\neq q$, then $xy = kk'p^2$ and since $pq\lvert xy$, it follows that $q\mid p$, which is a contradiction. A similar contradiction is obtained if $(x, y) = (kq, k'q)$, with $1\leq k, k'\leq { }\lfloor\frac{n-1}{q}\rfloor$, $k\neq p$, $k'\neq p$.

$(iv)$ Since $V_1\cap V_2 = \emptyset$, it follows clearly that $\Gamma^{(I)}(R) = K_{\alpha, \beta}$, with $\alpha = \lfloor{ }\frac{n-1}{p}\rfloor-1$ and $\beta = \lfloor{ }\frac{n-1}{q}\rfloor-1$. □

Theorem 5.3. Let $R = (\mathbb{Z}_n, \oplus, \odot)$ be the general hyperring in Example 2.1, where $n = 2p^m$, with $p$ an odd prime number, $m\geq 2$, and the hyperideal $I = \{\overline{0}, \overline{p^m}\}$. Then the following statements are true:

$(i)$ $Z^{(I)}(R) = \{\overline{x} \in \mathbb{Z}_n\setminus\{\overline{0}, \overline{1}, \overline{{p^m}}\}\; \mathit{\mbox{such that}}\; p\lvert x\}$.

$(ii)$ $\lvert Z^{(I)}(R)\rvert = \lfloor{ }\frac{n-1}{p}\rfloor-1$.

$(iii)$ $E(\Gamma^{(I)}(R)) = Z^{(I)}(R)\times Z^{(I)}(R)$.

$(iv)$ $\lvert E(\Gamma^{(I)}(R))\rvert = { }\frac{1}{2}\big({ }\sum_{i = 1}^{m-1}({ }\lfloor\frac{n-1}{p^i}\rfloor-1)(p^i-1+\theta_i)\big)$, where we denote

$\theta_i = \begin{cases} { }\lfloor\frac{2p^i-1}{2}\rfloor, & \; \mathit{\mbox{if}}\; 1\leq i\leq \lfloor{ }\frac{m}{2}\rfloor, \\ { }\lfloor\frac{2p^i-1}{2}\rfloor-1, & \; \mathit{\mbox{if}}\; \lfloor{ }\frac{m}{2}\rfloor < i\leq m-1. \end{cases}$

$(v)$ $\Gamma^{(I)}(R) = K_{\lfloor\frac{n-1}{p}\rfloor-1}$.

Proof. $(i)$ Let $\overline{x} \in Z^{(I)}(R)$. Then $\overline{x}\not\in \{\overline{0}, \overline{1}, \overline{p^m}\}$ and there exists at least one $\overline{y}\in \mathbb{Z}_n\setminus\{\overline{0}, \overline{p^m}\}$ such that $xy\equiv 0\pmod{2p^m}$ or $xy\equiv p^m\pmod{2p^m}$. Thus, in any case, $p^m\lvert xy$. Since $x\notin\{ p^m, 2p^m\}$, it follows that $\gcd (x, 2p^m)\in\{2, p, p^2, \ldots, p^{m-1}, 2p, 2p^2, \ldots, 2p^{m-1}\}$. If $\gcd(x, 2p^m) = 2$, since $\gcd(2, p) = 1$ and $p^m\lvert xy$, it follows that $p^m\lvert y$, which is in contradiction with the fact that $\overline{y}\neq\overline{p^m}$. Therefore, it is clear that $p\lvert x$. Moreover, $\gcd (x, 2p^m) = p^i$, because otherwise, if $\gcd (x, 2p^m) = 2p^j\not\lvert p^m$, $1\leq j\leq m-1$, we get $xy\not\equiv p^m\pmod{2p^m}$, which is not possible.

$(ii)$ From the previous item, it follows that the cardinality of $Z^{(I)}(R)$ is the number of multiplies of $p$, except $p^m$ and less than $n = 2p^m$. Hence $\lvert Z^{(I)}(R)\rvert = \lfloor{ }\frac{n-1}{p}\rfloor-1$.

$(iii)$ It is clear that any two elements $\overline{x}, \overline{y}\in Z^{(I)}(R)$ are adjacent, so $E(\Gamma^{(I)}(R)) = Z^{(I)}(R)\times Z^{(I)}(R)$.

$(iv)$ Let $\overline{x}, \overline{y}\in Z^{(I)}(R)$. Then $\gcd(x, 2p^m) = p^i$, $1\leq i\leq m-1$ and $\overline{y}\notin \{\overline{0}, \overline{p^m}, \overline{p^i}\}$ (since $\overline{x}\neq \overline{y}$). On one side, if $xy \equiv 0 \pmod{2p^m}$, then $({ }\frac{x}{p^i})y\equiv 0 \pmod{2p^{m-i}}$ and so $y\in \{2p^{m-i}, 2(2p^{m-i}), \ldots, (p^i-1)2p^{m-i})\} = W_i$. Since, for any $i, 1\leq i\leq m-1$, $p^{m}\not\in W_i,$ we get that $\lvert W_i\rvert = p^i-1$.

On the other side, for any $i, 1\leq i\leq m-1$, if $xy \equiv p^{m} \pmod{2p^m}$, then $({ }\frac{x}{p^i})y\equiv p^{m-i} \pmod{2p^{m-i}}$ and so $y\in \{p^{m-i}, 2p^{m-i}+p^{m-i}, \ldots, ({ }\lfloor\frac{2p^{i}-1}{2}\rfloor)2p^{m-i}+p^{m-i})\} = W_i$. Since, for any $i, 1\leq i\leq \lfloor\frac{n}{2}\rfloor-1, p^m\in W_i$, we get that $\lvert W_i\rvert = { }\lfloor\frac{2p^{i}-1}{2}\rfloor$ and for any $i, { }\lfloor\frac{m}{2}\rfloor < i\leq m-1$, $\{p^m, p^i\}\subseteq W_i$, we get that $\lvert W_i\rvert = { }\lfloor\frac{2p^{i}-1}{2}\rfloor-1$. (Indeed, $p^i\in W_i$ if and only if there exists $k, 1\leq k\leq { }\lfloor\frac{2p^{i}-1}{2}\rfloor$ such that $k(2p^{m-i})+p^{m-i} = p^i$, equivalently with $k = { }\frac{p^{2i-m}-1}{2}$. Thus, $k$ is well defined if $2i-m\geq 1$, i.e., $i\geq { }\lfloor\frac{m+1}{2}\rfloor > { }\lfloor\frac{m}{2}\rfloor$.)

Thereby $\lvert E(\Gamma^{(I)}(R))\rvert = { }\frac{1}{2}\big({ }\sum_{i = 1}^{m-1}({ }\lfloor\frac{n-1}{p^i}\rfloor-1)(p^i-1+\theta_i)\big)$, where we denote

$\theta_i = \begin{cases} { }\lfloor\frac{2p^i-1}{2}\rfloor, & \; \mbox{if}\; 1\leq i\leq \lfloor{ }\frac{m}{2}\rfloor, \\ { }\lfloor\frac{2p^i-1}{2}\rfloor-1, & \; \mbox{if}\; \lfloor{ }\frac{m}{2}\rfloor < i\leq m-1. \end{cases}$

$(v)$ $\Gamma^{(I)}(R)$ is the complete graph on $(\lfloor\frac{n-1}{p}\rfloor-1)$ elements. □

We consider now the case when $n = 2p^mq$, $m\geq 1$, with $p$ and $q$ distinct odd primes. Since the computations are more complex, we will find the properties of the associated hyperideal-based zero-divisor graph $\Gamma^{(I)}(R)$ associated with the general hyperring $R = (\mathbb{Z}_{2p^mq}, \oplus, \odot)$ in the next three theorems.

Theorem 5.4. Let $R = (\mathbb{Z}_{2p^mq}, \oplus, \odot)$ be the general hyperring defined in Example 2.1 and the hyperideal $I = \{\overline{0}, \overline{p^nq}\}$. Then there exists a partition $V = \{V_i\}_{i = 1}^{2n}$ of $Z^{(I)}(R)$ such that $\lvert { }\bigcup\limits_{i = 1}^{2n}V_i\rvert = \lvert Z^{(I)}(R)\rvert = \lfloor{ }\frac{n-1}{p}\rfloor+\lfloor{ }\frac{n-1}{q}\rfloor-\lfloor{ }\frac{n-1}{pq}\rfloor-1$.

Proof. Let $\overline{x} \in Z^{(I)}(R)$. Then there exists at least one $\overline{y}\in \mathbb{Z}_n\setminus I$ such that $xy \equiv 0 \pmod{2p^mq}$ or $xy\equiv p^mq\pmod{2p^mq}$. Similarly to the previous cases, it follows that $\gcd(x, n)\in\{2, p^i, q, p^jq\mid 1\leq i\leq m, 1\leq j\leq m-1\}$. The following possibilities appear.

$1)$ If $\gcd(x, n) = 2$ and $xy\equiv 0\pmod{2p^mq}$, then $y\equiv p^mq\pmod{2p^mq}$, which is a contradiction. Besides, since $\gcd(2, p^mq) = 1$, it follows that $xy\not\equiv p^mq\pmod{2p^mq}$. Thus $\gcd(x, n)\neq 2$.

$2)$ Consider that $\gcd(x, n) = p^i, 1\leq i\leq m$.

● If $xy\equiv 0\pmod{2p^mq}$, then $\frac{x}{p^i}y\equiv 0\pmod{2p^{m-i}q}$, with $\gcd(\frac{x}{p^i}, 2p^{m-i}q) = 1$. Thus

because $k(2p^{m-i}q)+2p^{m-i}q = 2p^mq\Leftrightarrow (k+1)2p^{m-i}q = 2p^mq\Leftrightarrow k+1 = p^i\Leftrightarrow k = p^i-1.$

● If $xy\equiv p^mq\pmod{2p^mq}$, then $\frac{x}{p^i}y\equiv p^{m-i}q\pmod{2p^{m-i}q}$, with $\gcd(\frac{x}{p^i}, 2p^{m-i}q) = 1$. Thus

because $k(2p^{m-i}q)+p^{m-i}q\leq 2p^mq\Leftrightarrow (2k+1)p^{m-i}q\leq 2p^mq\Leftrightarrow 2k+1 < 2p^i\Leftrightarrow k\leq \lfloor\frac{2p^i-1}{2}\rfloor,$ so we have to consider the multiplies of $2p^{m-i}q$ till $(k-1)(2p^{m-i}q)$.

$3)$ If $\gcd(x, n) = q$ and $xy\equiv 0\pmod{2p^mq}$, then $\frac{x}{q}y\equiv 0\pmod{2p^m}$, with $\gcd(\frac{x}{q}, 2p^m) = 1.$ Thus,

because $k(2p^m)+2p^m = 2p^mq\Leftrightarrow k+1 = q$.

If $xy\equiv p^mq\pmod{2p^mq}$, then $\frac{x}{q}y\equiv p^m\pmod{2p^m}$ and therefore

$4)$ Consider that $\gcd(x, n) = p^jq, 1\leq j\leq m-1$.

● If $xy\equiv 0\pmod{2p^mq}$, then $\frac{x}{p^jq}y\equiv 0\pmod{2p^{m-j}}$, and thus

● If $xy\equiv p^mq\pmod{2p^mq}$, then $\frac{x}{p^j}qy\equiv p^{m-j}\pmod{2p^{m-j}}$, and thus

Concluding, $\gcd(x, n)\in\{p^i, q, p^jq\mid 1\leq i\leq m, 1\leq j\leq m-1\}$. It follows that

and thus

Moreover, considering the sets

and denoting $V_{m+1} = V'_1, V_{m+2} = V'_2, \ldots, D = V_{2m}$, we get $Z^{(I)}(R) = \bigcup\limits_{i = 1}^{2m}V_i$, where for any $r, s\; , 1\leq r\neq s\leq 2m$, $V_r\cap V_s = \emptyset$, so the family $\{V_i\}_{1\leq i\leq 2m}$ is a partition of the set $Z^{(I)}(R)$. □

Based on Theorem 5.4, there exists a partition $\{V_i\}_{i = 1}^{2m}$ for $Z^{(I)}(R)$, meaning that we can define an equivalence relation $\sim$ on $(\mathbb{Z}_{2p^mq}, \oplus, \odot)$ as follows:

For any $\overline{y}\in \mathbb{Z}_{2p^mq}$, we denote by $\widehat{\overline{y}} = \{\overline{y'}\in \mathbb{Z}_{2p^mq}\mid \overline{y}\sim \overline{y'}\}$ the equivalence class of $\overline{y}$ with respect to the equivalence $\sim$.

In addition, for any $j$, $1\leq j\leq m-1$, we will take

From now on, in the $I$-based zero-divisor graph $\Gamma^{(I)}(R)$, for any vertex $\overline{y}\in Z^{(I)}(R)$, we denote $deg(\widehat{\overline{y}}) = \{deg(x)\mid x\in \widehat{\overline{y}}\} = deg(\overline{y})$ as the degree of equivalence class of $\overline{y}$. We recall that, the degree $deg(x)$ of a vertex $x$ of a graph is the number of edges that are incident to the vertex.

Theorem 5.5. Let $m$ be an even number. In the same hypothesis of Theorem 5.4, we get

Proof. Let $\overline{x}, \overline{y}\in Z^{(I)}(R)$. Then $\overline{x}\notin\{ \overline{0}, \overline{1}, \overline{p^mq}\}$ and there exists at least one $\overline{y}\in R\setminus\{\overline{0}, \overline{p^mq}\}$ such that $xy\equiv 0\pmod{2p^mq}$ or $xy\equiv p^mq\pmod{2p^mq}$.

Based on Theorem 5.4 case $2)$ (when $\gcd (x, n) = p^i$), for any $i, 1\leq i\leq m$, we have $\overline{y}\in \{\overline{y}\mid p^iy\equiv 0\pmod{2p^mq}\}\cup \{\overline{y}\mid p^iy\equiv p^mq\pmod{2p^mq}\}$ if and only if

where $\lvert W_1\rvert = p^i-1$ and $\lvert W_2\rvert = \lfloor{ }\frac{2p^i-1}{2}\rfloor$ (we must exclude from the set $W_2$ the element $({ }\frac{p^i-1}{2})(2p^{m-i}q+p^{m-i}q) = p^mq$), $W_1$ and $W_2$ being disjoint. This means that, for any $\overline{y}\in \widehat{\overline{p^i}}$, $deg(\overline{y}) = p^i-1+ \lfloor{ }\frac{2p^i-1}{2}\rfloor$.

Considering now case $4)$ of Theorem 5.4 (when $\gcd (x, n) = p^jq, 1\leq j\leq m-1$), we have $\overline{y}\in \{\overline{y}\mid p^jqy\equiv 0\pmod{2p^mq}\}\cup \{\overline{y}\mid p^jqy\equiv p^mq\pmod{2p^mq}\}$ if and only if

Since, for any $j, 1\leq j < { }\lfloor{ }\frac{m}{2}\rfloor,$ we must exclude from the set $W'_2$ the element $p^mq = ({ }\frac{p^jq-1}{2})(2p^{m-j})+p^{m-j},$ we get that, $deg(\widehat{\overline{p^jq}}) = p^jq-1+\lfloor{ }\frac{2p^jq-1}{2}\rfloor$ and for any $j, { }\lfloor{ }\frac{m}{2}\rfloor\leq j\leq m-1$, we must exclude the elements $p^mq = ({ }\frac{p^jq-1}{2})(2p^{m-j})+p^{m-j}$ and $p^jq = ({ }\frac{p^{2j}q-p^m}{2p^m})(2p^{m-j})+p^{m-j}$, we conclude that $deg(\widehat{\overline{p^jq}}) = p^jq-1+\lfloor{ }\frac{2p^jq-1}{2}\rfloor-1$. In other words, $deg(\widehat{\overline{p^jq}}) = p^jq-1+\beta_j$.

Finally, in case $3)$ of Theorem 5.4 (when $\gcd (x, n) = q$), we have $\overline{y}\in \{\overline{y}\mid qy\equiv 0\pmod{2p^mq}\}\cup \{\overline{y}\mid qy\equiv p^mq\pmod{2p^mq}\}$ if and only if

Excluding from the set $W''_2$ the element $({ }\frac{q-1}{2})(2p^{m})+p^m = p^mq$, we get $deg(\widehat{\overline{q}}) = q-1+ \lfloor{ }\frac{2q-1}{2}\rfloor$. Hence

$\lvert E(\Gamma^{(I)}(R))\rvert = { }\frac{1}{2}\big({ }\sum_{i = 1}^m\lvert \widehat{\overline{p^i}}\rvert (p^i-1+ \lfloor{ }\frac{2p^i-1}{2}\rfloor)+{ }\sum_{j = 1}^{m-1}\lvert \widehat{\overline{ p^jq}}\rvert (p^jq-1+\beta_j)+\lvert \widehat{\overline{q}}\rvert (q-1+ \lfloor{ }\frac{2q-1}{2}\rfloor)\big),$ where, based on Theorem 5.4, we compute

□

Moreover, for any $j, 1\leq j\leq m-1$, let's introduce the following notation:

Theorem 5.6. Let $m$ be an odd number. In the same hypothesis of Theorem 5.4, we get

Proof. The proof is similar to the one of Theorem 5.5. □

We will conclude our study with the case when $n = 2^m$, with $m\leq 2$. Also here, we must divide the study into two subcases: when $m$ is an even natural number and when it is an odd one.

Theorem 5.7. Let $R = (\mathbb{Z}_{2^m}, \oplus, \odot)$, with $m\geq 2$ an even number, be the general hyperring defined in Example 2.1, with the hyperideal $I = \{\overline{0}, \overline{2^{m-1}}\}$. The following assertions hold:

$(i)$ $Z^{(I)}(R) = \{\overline{x} \in \mathbb{Z}_{2^m}\setminus\{\overline{0}, \overline{1}, \overline{2^{m-1}} \}\mid 2\lvert x\}$.

$(ii)$ $\lvert Z^{(I)}(R)\rvert = 2^{m-1}-2$.

$(iii)$ $\lvert E(\Gamma^{(I)}(R))\rvert = { }\frac{1}{2}({ }\sum_{i = 1}^{m-1}\lvert \widehat{\overline{2^i}}\rvert (\gamma_i+\lfloor{ }\frac{2^{i+1}-1}{2}\rfloor -1))$, where $\gamma_i = \begin{cases} 2^i-2, & \mathit{\mbox{if}}\; 1\leq i < { }\frac{m}{2}, \\ 2^i-3, & \mathit{\mbox{if}}\; { }\frac{m}{2}\leq i\leq m-2. \end{cases}$

Proof. $(i)$ The proof is similar to the one in Theorem 5.2.

$(ii)$ Let $\overline{x} \in Z^{(I)}(R)$. Since, by item $(i)$, we know that $2\mid x$, and moreover that $x\notin \{2^{m-1}, 2^m\}$, it follows immediately that $\lvert Z^{(I)}(R)\rvert = { }\frac{2^m}{2}-2 = 2^{m-1}-2$.

$(iii)$ Let $\overline{x}, \overline{y}\in Z^{(I)}(R)$. Then $\gcd(x, n)\in \{1, 2, 2^2, 2^3, \ldots, 2^{m-1}\}$. Clearly, $\gcd(x, 2^m)\neq 1$. Let $\gcd(x, n) = 2^i$, with $1\leq i\leq m-1$. As in the previous theorems, if $xy \equiv 0 \pmod{2^m}$, then $({ }\frac{x}{2^i})y\equiv 0 \pmod{2^{m-i}}$ and so $y\in \{2^{m-i}, 2(2^{m-i}), \ldots, (2^i-1)2^{m-i}\} = W_i$. Since $m$ is an even number, for any $i, { }\frac{m}{2}\leq i\leq m-2$, the inclusion $\{2^{m-i}, 2^{m-1}\} \subseteq W_i$ holds, so we get that $\lvert W_i\rvert = 2^i-3$. For any $i, 1\leq i < { }\frac{m}{2}$, we have $2^{m-1}\in W_i$, therefore $\lvert W_i\rvert = 2^i-2$.

In addition, for any $i, 1\leq i\leq m-1$, the relation $xy \equiv 2^{m} \pmod{2^m}$ leads to $({ }\frac{x}{2^i})y\equiv 2^{m-1-i} \pmod{2^{m-i}}$ and thus $y\in \{2^{m-i-1}, 2^{m-i}+2^{m-i-1}, \ldots, ({ }\lfloor\frac{2^{i+1}-1}{2}\rfloor)2^{m-i}+2^{m-i-1})\} = W_i$. Since, for any $i, 1\leq i\leq m-1$, $y$ must be different by $2^{m-1}, 2^{m-i-1}$, we get that $\lvert W_i\rvert = { }\lfloor\frac{2^{i+1}-1}{2}\rfloor-1$.

Thus $\lvert E(\Gamma^{(I)}(R))\rvert = { }\frac{1}{2}({ }\sum\limits_{i = 1}^{m-1}\lvert \widehat{\overline{2^i}}\rvert (\gamma_i+\lfloor{ }\frac{2^{i+1}-1}{2}\rfloor -1))$, where $\gamma_i = \begin{cases} 2^i-2, & \mbox{if}\; 1\leq i < { }\frac{m}{2}, \\ 2^i-3, & \mbox{if}\; { }\frac{m}{2}\leq i\leq m-2. \end{cases}$ □

Theorem 5.8. In the same hypothesis as Theorem 5.7, but with $m\geq 2$ an odd number, the following statements hold:

$(i)$ $Z^{(I)}(R) = \{\overline{x} \in \mathbb{Z}_{2^m}\setminus\{\overline{0}, \overline{1}, \overline{2^{m-1}} \}\mid 2\lvert x\}$

$(ii)$ $\lvert Z^{(I)}(R)\rvert = 2^{m-1}-2$,

$(iii)$ $\lvert E(\Gamma^{(I)}(R))\rvert = { }\frac{1}{2}({ }\sum_{i = 1}^{m-1}\lvert \widehat{\overline{2^i}}\rvert(\gamma_i+\delta_i))$, where we have $\gamma_i = \begin{cases} 2^i-2, & \mathit{\mbox{if}}\; 1\leq i\leq { }\lfloor{ }\frac{m}{2}\rfloor, \\ 2^i-3, & \mathit{\mbox{if}}\; { }\lfloor{ }\frac{m}{2}\rfloor < i\leq m-2 \end{cases}$ and $\delta_i = \begin{cases} \lfloor{ }\frac{2^{i+1}-1}{2}\rfloor, & \mathit{\mbox{if}}\; i = \lfloor{ }\frac{m}{2}\rfloor, \\\\ \lfloor{ }\frac{2^{i+1}-1}{2}\rfloor+1, & \mathit{\mbox{if}}\; i\neq\lfloor{ }\frac{m}{2}\rfloor. \end{cases}$

Proof. $(i), (ii)$ The proof of these two assertions is similar to the one in Theorem 5.7.

$(iii)$ Let $m$ be an odd number and $\overline{x}, \overline{y}\in Z^{(I)}(R)$. Then $\gcd(x, 2^m)\in \{1, 2, 2^2, 2^3, \ldots, 2^{m-1}\}$. Clearly, $\gcd(x, 2^m)\neq 1$. Let $\gcd(x, 2^m) = 2^i$, with $1\leq i\leq m-1$. If $xy \equiv 0 \pmod{2^m}$, then $({ }\frac{x}{2^i})y\equiv 0 \pmod{2^{m-i}}$ and therefore $y\in \{2^{m-i}, 2(2^{m-i}), \ldots, (2^i-1)2^{m-i}\} = W_i$. Since $m$ is an odd number, for any $i, { }\lfloor{ }\frac{m}{2}\rfloor < i\leq m-2$, the inclusion $\{2^i, 2^{m-1}\} \subseteq W_i$ holds, and therefore we calculate that $\lvert W_i\rvert = 2^i-3$, while for any $i, 1\leq i\leq { }\lfloor{ }\frac{m}{2}\rfloor$, we have that $2^{m-1}\in W_i$, leading to $\lvert W_i\rvert = 2^i-2$.

Besides, for any $i, 1\leq i\leq m-1$, the congruence $xy \equiv 2^{m} \pmod{2^m}$ leads to $({ }\frac{x}{2^i})y\equiv 2^{m-1-i} \pmod{2^{m-i}}$ and thus $y\in \{2^{m-i-1}, 2^{m-i}+2^{m-i-1}, \ldots, ({ }\lfloor\frac{2^{i+1}-1}{2}\rfloor)2^{m-i}+2^{m-i-1})\} = W_i$. Since $m$ is odd, it follows that, for any $i = \lfloor{ }\frac{m}{2}\rfloor, 2^{i}\in W_i$, so we get that $\lvert W_i\rvert = { }\lfloor\frac{2^{i+1}-1}{2}\rfloor$ while for any $i\neq\lfloor{ }\frac{m}{2}\rfloor, 2^{i}\not\in W_i$, so in this case, we get that $\lvert W_i\rvert = { }\lfloor\frac{2^{i+1}-1}{2}\rfloor+1$.

Hence $\lvert E(\Gamma^{(I)}(R))\rvert = { }\frac{1}{2}({ }\sum_{i = 1}^{m-1}\lvert \widehat{\overline{2^i}}\rvert(\gamma_i+\delta_i))$, where $\gamma_i = \begin{cases} 2^i-2, & \mbox{if}\; 1\leq i\leq { }\lfloor{ }\frac{m}{2}\rfloor, \\ 2^i-3, & \mbox{if}\; { }\lfloor{ }\frac{m}{2}\rfloor < i\leq m-2 \end{cases}$ and $\delta_i = \begin{cases} \lfloor{ }\frac{2^{i+1}-1}{2}\rfloor, & \mbox{if}\; i = \lfloor{ }\frac{m}{2}\rfloor, \\\\ \lfloor{ }\frac{2^{i+1}-1}{2}\rfloor+1, & \mbox{if}\; i\neq\lfloor{ }\frac{m}{2}\rfloor. \end{cases}$ □

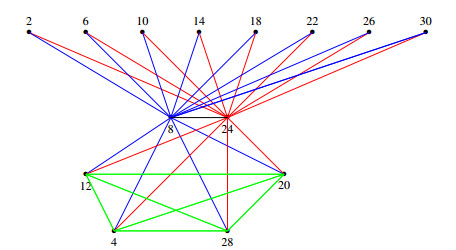
We will now illustrate this result in one particular case, when $n = 32 = 2^5$.

Example 5.9. Consider the general hyperring $(\mathbb{Z}_{32}, \oplus, \odot)$ with its hyperideal $I = \{\overline{0}, \overline{16}\}$. Then, based on Theorem 5.8, it is easy to calculate the following data:

$\widehat{\overline{2^3}} = \{\overline{8}, \overline{24}\}, \widehat{\overline{2^2}} = \{\overline{4}, \overline{12}, \overline{20}, \overline{28}\}, \widehat{\overline{2^1}} = \{\overline{2}, \overline{6}, \overline{10}, \overline{14}, \overline{18}, \overline{22}, \overline{26}, \overline{30}\},$ and therefore

We may now verify formula for the cardinality of each equivalence class:

while the degree of each vertex is

and therefore

Thus, we get that the $I$-based zero-divisor graph $\Gamma^{(I)}(R)$ is the one shown in Figure 1.

6.   Conclusions

One remarkable line of research in hypercompositional algebra is represented by the study of the connections between hypercompositional structures and graphs. On one side, several types of graphs have been associated with hypergroups ^[8,17], while on the other, different hypercompositions (very often called path hypercompositions) have been defined using the elements of a given graph or hypergraph ^{[1,19,20,24,27,30]}. Applications in the automata theory of this association have been recalled in ^[23,25]. In the last few years, works related to graphs associated with rings have inspired several studies on hyperrings ^[3,14,15,16], and the aim of this article goes in the same direction.

In this manuscript, the hyperideal-based zero-divisor graph associated with a general hyperring has been introduced. Several properties related to prime hyperideals and absorbing elements have been emphasized, but the main part of the manuscript is dedicated to the study of this graph associated with the general hyperring $\mathbb{Z}_{n}$, for the special case when $n = 2^m$ or $n = 2p^mq$, with $m\in \mathbb{N},$ and $p$ and $q$ two distinct odd primes. We have noticed that the computations of the number of the vertices and edges of this particular graph are complex, although the considered hyperideal has only two elements. That is why, in order to extend this study to a more general case, we will try to construct an algorithm that determines the needed parameters. Based on this study, similar results could be obtained related to the hyperideal-based zero-divisor graph associated with a multiring, a general multiring, or even the related fuzzy hypercompositional structures.

Author contributions

Conceptualization: M.H., Methodology: M.H., I. C., Investigation: M.H., I. C., Writing -original draft: M.H., Writing- review & editing: I.C., Funding acquisition: I.C.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The second author acknowledges the financial support from the Slovenian Research and Innovation Agency (research core funding No. P1-0285).

Irina Cristea is the Guest Editor of special issue "New trends of Group theory and its applications" for AIMS Mathematics. Irina Cristea was not involved in the editorial review and the decision to publish this article.

Conflict of interest

All authors declare no conflicts of interest in this paper.