Determination of medical emergency via new intuitionistic fuzzy correlation measures based on Spearman's correlation coefficient

1.   Introduction

Ethiopia is a country located in the East of Africa lies between 3° to 15°N latitude and 33° to 48°E longitudes, as shown in Figure 1, with land area of about 1.097 million km^{2 [1]}. According to World population review report, currently Ethiopia has the population of about 105 million (2019) ^[2,3] of which 83% lives in rural areas. Ethiopia is endowed with various and diversified renewable energy resources, namely hydro, wind, solar, geothermal, and biomass ^[4]. The estimated exploitable potential for hydropower is 45 GW, wind is 10 GW, geothermal is 5 GW, and solar irradiation ranges from 4.5 kWh/m²/day to 7.5 kWh/m²/day ^[5]. The reserve of fossil fuels is also significant. For instance, the natural gas reserve is about 4 trillion cubic feet and the reserve of coal is over 300 million tons ^[6]. Despite the abundance of available potentials, access to clean energy in the country is one of the lowest in the world ^[7]. Country depends heavily on biomass as an energy source, which accounted about 45.8 out of 49.9 million tonnes of oil equivalent (Mtoe) of total primary energy supply in 2015 ^[8]. According to Ethiopia ministry of water, irrigation and electricity in 2017, access to the electric grid is about 56% and household connectivity is only about 25% ^[9]. Country estimated electricity consumption per capita was 70 kWh by 2014 ^[2] and increased to about 100 kWh by 2017 ^[9]. However, this level is significantly lower than the average level of per capita energy consumption across all African countries (500 kWh per capita) ^[5,6]. Therefore, to solve this problem the government of Ethiopia gave strategic priorities in the energy sector i.es: universal electrification access, energy efficiency improvement, developing decentralized off-grid power generation, and exporting electricity to neighboring countries. Nowadays a number of grand projects i.es. Koysha and Great Ethiopian Renaissance Dam (GERD) are under construction to increase the country’s energy production ^[10] and strength a country to be a major producer and exporter of renewable energy to eastern Africa.

2.   Methodology

This Article is based on review of latest scientific literature presented in journals, books related on renewable energy, Internet sources and country data obtained from various ministries of the governments of Ethiopia to collect qualitative and quantitative information. Based on data collected a comprehensive literature review is carried out on Ethiopia renewable energy potentials and current state. The article is divided in to five sections: in section 1 introduction and literature review of renewable energy potential is carried out and in section 2 methodology parts is discussed. Section 3 discusses energy potentials and consumption status of Ethiopia in brief and section 4 review energy policy of the country with important recommendations. Finally, section 5 summarizes this article with intensive conclusion.

3.   Energy potential and consumption status of Ethiopia

Ethiopia is one of the countries in Africa in which energy resources are underexploited, as evident from the past, significant energy demands are still met from traditional resources. Currently final energy consumption of country was around 40,000 GWh, in which about 92% are consumed by domestic appliances, 4% by transport sector and 3% by industry. However, energy supply thereby is covered by bio-energy which accounts about 90% of final energy consumption ^[11]. While a transport sector is predominantly run by imported petroleum; which account about 4.5% and the modern energy contributes only about 6% of the overall energy consumption ^[12]. Nowadays Ethiopia total installed capacity of electric generation is about 4.5 GW (2019) mainly generated by hydro (90%) and followed by wind energy (7.6%) ^[13]. Table 1 shows country exploitable energy potential and currently exploited amount. According to Ethiopia country report in 2019, only about 45% of the country population has access to electricity. From this urban population has 97% access to electricity, while in rural areas electricity access remains extremely low at about 31% ^[14]. However, only few researches were conducted in Ethiopia to solve problem in rural energy access and empower the development of alternative energy technology. Therefore, this article presents the review of Ethiopia renewable energy potential with current state in a more comprehensive way and provides valuable information for researchers, industrial companies and decision makers to promote investment in renewable energy technology development.

3.1.   Hydropower potential

Hydropower has been one of the main role players in many African power systems and is the most used renewable energy source. Hydropower is attractive because of the large scale of potential development, environmentally friendly nature and the low average costs of electricity generated than any other energy generation technology. The technical hydropower potential in Africa is estimated to be about 283 GW and is able to generate close to 1200 TWh per year, which will account 8% of the global technical potential. This amount of electricity is more than three times the current electricity consumption in sub-Saharan Africa. However, only less than 10% of the technical energy potential has so far been tapped ^[16].

Due to this reason, about 620 million People in Sub-Saharan Africa have the least energy access as they are dependent on unreliable energy grid, which doesn’t satisfy their day to day energy requirement. The average energy access, in most of the countries in this region, is below 20% ^[4].

Ethiopia is one of the countries in sub Saharan Africa and endowed with numerous rivers, lakes and ample water resources which, constitutes 20% of the total technically feasible potential in Africa. With this potential Ethiopia is usually referred as the power house of Africa. However, the country has utilized less than 10% of its potential so far ^[17]. The country’s annual surface runoff is close to 122 billion cubic meters of water. The Ethiopian highlands are the origin of many North African rivers, and rivers i.es. Abbay (Blue Nile) River, Atbara River, Sobat River, Shebele River, and Juba River, radiate in all directions ^[18].

Out of eleven major river basins found in Ethiopia eight of them are identified for their hydroelectric power production potentials. In those eight river basins around 300 hydropower plant sites with a total technical power potential of 159,300 GWh/year have been identified. Out of those potential sites, 102 are large scale (more than 60 MW) and the rest are small scale (less than 40 MW) ^[19].

In 2018, the bulk of Ethiopia 4.5 GW of power generating capacity came from Fourteen (14) hydropower plants, which account about 85% (3.8 GW) of the country’s total capacity, making it the main energy source ^[18]. In Table 2 data on catchment area, elevation and the respective energy potential of hydropower plants in the country by 2020 is presented. The annual theoretical hydro energy potential of the country was estimated at 954TWh, out of which its geographic potential is 286 TWh ^[1].

The country has initiated to construct a number of large hydroelectric projects which includes 2,160 MW Gilgel Gibe Ⅳ (Koysha) hydropower project and also the massive 6,500 MW Great Ethiopian Renaissance Dam (GERD) being built on the Abbay (Blue Nile) River, which will be the largest dam in Africa and the sixth largest in the world upon completion ^[20].

Hydropower is the main renewable energy source that can serve the country transition to more sustainable sources of energy. Considering this, government of Ethiopia has recognized hydropower as economically feasible and environmentally friendly option ^[21]. However, hydropower plant is less reliable as droughts intensify, hence; to solve this problem the country should diversify its power mix and support by intermittent sources such as wind and solar to be able to deal with peak demand.

3.2.   Wind energy potential

In Africa wind power deployment has been very limited when compared to hydropower, with about 5.5 GW installed capacity by 2018 ^[22]. Sub-Saharan Africa’s wind potential is estimated at around 1300 GW, which would produce several times the current level of total African electricity consumption ^[16,23].

Most wind resources are found close to coastal locations, mountain ranges and other natural channels in the eastern and northern regions of the continent. Algeria, Egypt, Somalia, South Africa and Sudan are among the countries with the highest wind energy potentials ^[16].

Ethiopia being located near the equator, its wind resource potential is very much limited. There are few promising windy areas in Ethiopia located along side the main east African rift valley, the north eastern escarpment of the country near Tigray regional state and the eastern part of the country ^[24]. In those areas the wind velocities are in the range of 7 to 9 m/s which is very good for wind energy generation. According to Ethiopia electric power report, the total exploitable wind energy potential of the country is around 1,350 GW ^[17].

However, despite a tremendous potential of this energy system, the development of wind farm is in its early stages in Ethiopia. For technical and economic reasons appropriate wind regions for grid based electricity generation are those with wind density of 300 W/m², wind speed of 6.5 m/s and above. Ayisha in the eastern part of the country has good potential with an average wind speed exceeding 8 m/s. Currently, Ashegoda, Adama Ⅰ and Adama Ⅱ wind farms have been completed and connected to the grid with 324 MW total installed capacities ^[19]. Ethiopia exploited and upcoming wind energy power plants with their power generation capacity are shown in Table 3. In the context of the Ethiopian power system, wind power will play a vital complementary role with hydroelectric power due to the natural cycle of high wind energy availability in the dry season during hydropower reservoirs are low in water, and it decreases in the wet seasons when the reservoirs are rapidly filling up with water. This will make wind power a crucial ingredient of the grid energy mix by improving the reliability of the system even in dry seasons ^[25]. Although, in behind mega projects planned to achieve energy mix; the government of Ethiopia should also plan offgrid and microgrid wind farm to cover isolated rural areas as well as for the village level rural electrification; microgrid wind and solar hybrid system with the subsidize tariff is also better if introduced.

3.3.   Solar energy potential

Africa is rich in solar energy potential, with which most parts of the continent getting annually average irradiance levels of more than 2 000 kWh/m^{2 [27]}. Africa’s estimated theoretical potential of solar PV could provide the continent with more than 660,000 TWh of electricity a year, far above its projected needs. But, has only installed capacity of 5 GW solar photovoltaic (PV), which account less than 1% of global capacity. If planned to install well with the right policies, solar could become one of the Africa’s top energy sources ^[22].

From the part of Africa, east Africa was identified as having the highest theoretical potential more than 200,000 TWh/year. Ethiopia one of the country in east of Africa has abundant solar energy resources. The national annual average irradiance of the country is estimated to be about 5.2 kWh/m²/day ^[9,22]. The solar resource is relatively lower in the most populous northern, central and western highlands of the country while the rift valley regions and western and eastern lowlands of the country receive higher annual average irradiance (above 6 kWh/m²/day) ^[28]. Even though, abundant solar energy resources was available in the country; only about 14 MW solar PV have been used for telecom service, lighting, powering water pump in rural areas and for water heating in major cities ^[18]. Currently, Ethiopia has launched the first tender to build, own and operate three 100 MW solar PV projects and ENEL Green Power (EGP) was selected as the preferred bidder for one of the projects, located near Metehara while; the remaining sites located near Mekele and Humera, were not awarded ^[2]. In addition to this, country has intended to construct 125 MW solar power plants, which are the Scaling Solar Gad Phase Ⅰ in the Somali region and the Scaling Solar Dicheto Phase Ⅰ in the Afar region ^[29]. However, until the recent times country’s use of PV for meeting off-grid power needs was confined to projects funded by donors that use PV based technologies (distance-education radios and vaccine fridges) in remote rural areas ^[6]. Thus, for rural households those needs low electricity consumption, off-grid solar solutions should be prioritized by the government as an immediate solution for un-electrified rural households that are far from electric grid and not covered by the densification program in the short term.

3.4.   Geothermal energy potential

Geothermal resources are generally concentrated in the eastern part of Africa; which is considered as the most excited prospects, with potential equivalent to more than 15 GW. This potential is more than east Africa’s total existing power generation capacity and a large share of which is concentrated in Ethiopia and Kenya. The cost of generation is competitive with fossil fuels and geothermal power is not characterized by the variability issues associated with some renewable energy, so that it can serve as base load generation. However, only Kenya has tapped its geothermal potential and installed capacity of about 700 MW ^[19,22]. Ethiopia has estimated exploitable geothermal potential of around 5000 MW. However, this potential is largely untapped at present time and only a pilot project of 7.5 MW has been installed at Aluto Langano and 10 MW pilot project is under construction at Tendaho Dubti ^[2]. Further, with the help of Japanese overseas development assistance, feasibility study for the expansion of the Aluto Langano geothermal power has been done. The Ethiopian government is currently working on the enhancement of the Aluto Langano geothermal field to up to 70 MW. Additionally, Corbetti, Abaya, Dofan Fantale and Tulu Moye areas are surface explored for future geothermal prospects ^[4].

3.5.   Biomass energy potential

In sub-Saharan Africa, solid biomass is the largest energy source and accounts about 70% of total energy consumption of the continent. About 280 million tons of oil equivalents of solid biomass was currently used in sub-Saharan Africa, which accounts 90% of energy used by households, almost all being fuel wood, straw, charcoal or dried animal and human waste, mostly used as cooking fuel. Among the population of around 915 million in sub-Saharan Africa in 2012, an estimated 730 million people do not have access to clean cooking facilities ^[16]. Even though biomass has great advantage for global renewable energy mix, in most of sub-Saharan African countries it is used in an inefficient manner and resulted in high depletion of the forest resources which leads to a host of adverse implications on environment, human health, and social wellbeing. Therefore, the utilization of biomass in a clean and efficient manner to deliver modern energy services to the world's poor remains an imperative for the development of community ^[30,31].

Ethiopia is one of the developing countries in the sub-Saharan Africa with a high level of household energy consumption. This consumption is primarily satisfied through excessive burning of biomass ^[30,32].

According to 2010 World Bank data, the majority of the Ethiopian population about 83.2% are lives in rural areas, where modern energy services are rarely available and largely rely on traditional biomass energy sources, such as wood, cow dung and agricultural residues; for cooking and heating. Even if electricity accessibility is vast in urban areas, most of application is run by traditional biomass energy input. Half of the urban households rely on traditional biomass for cooking, and virtually all do in rural areas (except for 0.2% households use kerosene, and 1.2% is charcoal) ^[33].

Ethiopia estimated exploitable biomass potential and currently exploited potential is separately presented in Table 4. Country’s energy demand is forecasted with the model and indicates that demand can be expected to grow from 194 TWh in 2000 to more than 527 TWh by 2030, a growth rate of 3.5% per year ^[24]. According to World Bank report, it is expected that a rapid growth of renewable energy power plants installations will be carried out and about 500 MW of biomass capacity is also expected to be brought in the power mix by 2025 ^[41].

3.5.1.   Largescale biomass energy

In Ethiopia large-scale biomass power plants currently producing electricity are from biomass sources like bagasse in sugar factory and dry waste to energy from municipality.

Large-scale biomass utilization in the sugar factory is carried out by heat cogeneration, using bagasse as fuel stock and the production of ethanol as a substitute for petroleum fuel. The potential for electricity generation in sugar factory from bagasse is high since; cogeneration equipment is almost uniformly an integral component of sugar factory designs ^[34]. Until 2018, Ethiopia has a capacity to produce 317.5 MW of power by cogeneration in five sugar factories where, 225 MW of additional power will be expected to be produced at the end 2020 by four sugar factories under construction ^[2].

Additionally, Ethiopia was constructed first waste to energy power plant in Africa that called Reppie waste to energy power plant, with the capacity to generate 25 MW of electricity ^[28]. The plant has two 25 MW turbine generators, however; currently it is only capable of operating at 25 MW because; the boiler is only sufficient of delivering steam to power one of the two generating units. The plant uses dry waste to generate electricity and currently processes over 1000 tons of municipal waste per day ^[2]. Ethiopian installed and ongoing biomass power plants with their power generating capacities and commercial operation dates are presented in Table 5.

3.5.2.   Bio-fuel

In behind electric power generation, the production of ethanol is carried out with in sugar factories. Ethiopia has the expected potential of producing one billion liters of ethanol per year. Currently, the country annual ethanol production capacity is around 20 million liters in the two of the sugar factories; Fincha and Metehara ^[35].

3.6.   Biogas energy potential

The main renewable based alternatives to solid biomass for cooking are biogas and solar cookers. Domestic biogas digesters enable more efficient use of animal manure and human waste, converting it into methane that can be used as a cooking fuel ^[16]. Biogas has a dual advantage of providing critically needed energy for rural households such as energy for lighting and cooking, while; at the same time providing high quality organic fertilizer from the slurry produced after the gas is extracted ^[36]. Based on Africa energy outlook new bottom-up assessment, today in Africa there is sustainable technical potential available to produce around 50 Mtoe of biogas. The potential doubles by 2040 to almost 100 Mtoe at an average cost of just over $10 per million British thermal units (MBtu), which would represent around one-third of the projected natural gas demand in the region in the Stated Policies Scenario. The biggest contribution to the potential comes from rural areas with strong agricultural sectors. Crop residues, especially cereals, account for almost 60% of the total potential, animal manure for close to 25%, and municipal solid waste for most of the remainder ^[22]. Biogas technology was introduced in Ethiopia since 1957, when the first batch type floating digester was constructed in Ambo University to generate energy required for the purpose of welding agricultural tools. In 1970s food and agriculture organization (FAO) introduced two biogas digester plants to promote the technology ^[37].

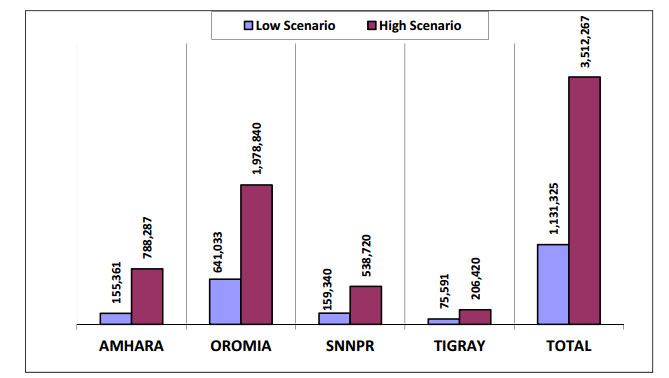
Country has a high potential for biogas production with its sufficient resources of crop residues and animal manures. Ethiopia’s livestock population according to 2009/10 central statistical agency survey is about 150 million. The effort to generate biogas from cattle dung started in early 1970s in Ethiopia. Over these past four decades, the progress of biogas digester construction has remained very low ^[37]. Since 2000, a local NGO called LEM-Ethiopia gave awareness and promotion programme on biogas digester ^[32] and installed about, 22 and 25 digesters in schools and households, respectively ^[39]. A feasibility study undertaken by the Ethiopian Rural Energy Development and Promotion Centre (EREDPC) and SNV-Ethiopia in 2006 assessed two scenarios of biogas production potential in Ethiopia, with the options to benefit about 1.1 million to 3.5 million households in four regions of Ethiopia ^[38,39]. Figure 2 shows biogas potentials in four regions of Ethiopia. Based on this study, about 7,000 digesters were constructed in between 2008 and 2013. However, there was no local capacity to neither up-scale the technology nor sustains it. Hence, just only about 40% of the aforementioned bio-digesters are now operational ^[39].

4.   Energy policy

Policy is an essential tool in guiding a country towards the efficient utilization of its energy resources for socio-economic development. Therefore, it is must to be stressed that the existence of an energy policy is crucial. However, only the existence of policy does not guarantee the prudent responsibility management of a country's energy resources ^[40].

4.1.   The national energy policy, 1994

The National Energy Policy of 1994 was implemented with the goal of addressing the problem of energy supply and its utilization ^[41]. This policy prioritized to enhance hydrological energy resource development for the power sector, energy efficiency, and transition to modern energy services for the household sector. However, this policy stayed about two decades without any revision and it doesn’t address rural area electrification, as well as energy supply was not based on detailed need analysis. The following gaps were identified by researchers, in the national energy policy issued in 1994 to be updated ^{[41,42,43,44]}:

■ The 1994 energy policy was silent on development and marketing of modern fuel such as bio-fuels to save foreign exchange.

■ Moreover, it did not address new technologies such as: electric rail, electric cars, hybrid cars and flexifuel vehicles to reduce dependence of country on imported fuel and improve the country’s carbon footprint.

■ The policy also needs to be aligned with the recently launched Climate Resilient Green Economy (CRGE) strategy to protect the country against the adverse effect of climate change and to build green economy.

■ To address InterRegional electric power interconnection to create source of foreign currency and also to play a critical role for geopolitical stability.

Therefore, to fill those gaps Ethiopian ministry of water, irrigation and energy prepare a draft of national energy policy in 2013, to give emphasis in the development and utilization of all renewable energy sources. Consider current technological levels, bottle-necks in the energy development including crosscutting issues.

4.2.   The national energy policy (2^nd draft), 2013

Ethiopian ministry of water, irrigation and energy is now the power holding institution in the new energy policy outlined a plan to diversify its energy sector and pursue all exploitable renewable energy resources. The key goal in the updated national energy policy is to ensure the availability, accessibility, affordability, safety and reliability of energy services to support accelerated and sustainable social and economic development and transformation of the country. The Energy policy seeks to meet the following broad objectives ^[36,41]:

■ Improve the security and reliability of energy supply and be a regional hub for renewable energy.

■ Increase access to affordable modern energy.

■ Promote efficient, cleaner, and appropriate energy technologies and conservation measure.

■ Strengthen energy sector governance and build strong energy institution.

■ Ensure environmental and social safety and sustainability of energy supply and utilization.

■ Strengthen energy sector financing.

Therefore, setting guidelines for the utilization of energy resources and developing recommendations on the exploitation of new sources of energy. The drafted policy emphasizes Renewable Energy (RE) as one of role player for the future energy development of the country. The key elements in the national energy policy on the development and utilization of RE and its technologies are as follows:

■ To develop, promote and harness RE resources of Ethiopia and diversify energy generation mix.

■ To promote decentralized energy supply for the rural areas, based on available RE resources.

■ To encourage and build the skills in domestic production of RE technologies, accessories, and appliances.

■ To encourage the participation of the private sector and enhance investment for exploiting RE resources ^[36].

Following are the recommendations:

■ Establishment of off grid energy generation and distribution should be encouraged by the government to solve energy problems in rural areas.

■ Policy makers could target appropriate measures in order to improve household wealth, education and awareness to successfully promote energy technology use by rural household and institutions.

■ The development and dissemination of mini and micro wind, hydro and PV power system should be made for rural community.

■ There should be authority and organ responsible for introducing rural energy initiatives other than grid electricity and petroleum products.

5.   Conclusions

Majority of the Ethiopian people is living in rural areas where electricity access is limited. Mostly the rural communities run their daily life without electricity access, as the national grids location was quite far from rural communities’ residents (considering dispersed distribution of population on the country’s vast land area). They largely rely on traditional biomass energy sources (by burning wood, dung and agricultural residues) for cooking and heating even a significant proportion for lighting. The energy consumption demand is increasing while observed with energy source elaboration and power generation rate for supply. Ethiopia has abundant renewable energy resources even left extra for foreign countries and will makes huge income for country but, presently given least consideration concerning with the existing potential and exploitability rate. This paper explains the country’s current energy type dependency with its capacity and supporting being in favor of using renewable energy resources to minimize the gap between energy demand and supply and make rural communities’ life healthy. Basically, the country has the various renewable energy potentials such as hydropower, solar, wind, geothermal; biogas and biomass energy. Currently, Ethiopia total 4.5 GW energy capacity consumed in the country’s households, industrial sectors and all, shared in amongst about 3.8 GW of hydropower excluding recently inaugurated Genale Dawa Ⅲ power plant, 324 MW of wind power, 7.5 MW of Geothermal, 317 MW of biomass and others. The exploitable and exploited potentials of Ethiopia renewable energy resources have been addressed in this paper to raise awareness for researchers as well as the government officials to find the better renewable energy technology to meet rural community energy demand. Also, the implementation of renewable energy technologies certainly lead usage and profitable allocation of energy sources throughout the country’s un-electrified rural households even in specifically grid-connected areas as an alternative.

Conflict of interest

The authors declare that there are no conflicts of interest related to this study.