Coordinate-free Lie-group-based modeling and simulation of a submersible vehicle

1.   Introduction

A numerical sequence is an ordered set of numbers ^[1,2,3,4,5]. A famous example is the sequence of Fibonacci numbers ^[1,2,3,4,5]. A sequence can be created from an explicit formula (such as an arithmetic progression) or by taking into consideration specific properties of their elements (such as the sequence of prime numbers) ^[1,2,3,4,5].

In this article, $\{x\}$ represents an increasing list of positive integer numbers. A positive integer number $x$ with $d$ divisors may be called $d$-prime ^[6]. Hence, according to this definition, the number 1 is the single 1-prime and the usual prime numbers correspond to the particular case $d = 2$.

Consider the sequence of divisors $\{x, D(x)\}$, in which $D(x) = d$ is the number of divisors of $x$. The divisor function $D(x)$ appears in the literature with distinct names and notations ^[1,2,3,4,5]. For $\{x\} = \{n\}$, in which $n$ is a natural number, the sequence of divisors of natural numbers $\{n, D(n)\}_{n \in \mathbb{N}}$ starts as follows:

For instance, $D(6) = 4$, because 6 has four divisors: the numbers 6, 3, 2, and 1; therefore, 6 is a 4-prime. The list $\{D(n)\}_{n \in \mathbb{N}}$ has the code A000005 in the On-Line Encyclopedia of Integer Sequences (OEIS) ^[7].

Any positive integer number $x$ can be written as $x = \sum_{p = 0}^{\infty} \delta_p 10^p$, with $\delta_p \in \{0, 1, 2, ..., 9\}$. Now, replace this number by the sum of the square of its digits; that is, by $\sum_{p = 0}^{\infty} (\delta_p)^2$. Repeat this process. If the number 1 is eventually reached, then $x$ is called happy number in Number Theory ^[8,9]. For instance, 23 is happy because $2^2+3^2 = 13$, $1^2+ 3^2 = 10$, and $1^2+0^2 = 1$. Let a happy number be denoted by $h$ and the set of happy numbers by $\mathbb{H}$. In the online database OEIS, the code of the list $\{h\}_{h \in \mathbb{H}}$ is A007770 ^[7]. For $\{x\} = \{h\}$, the beginning of the sequence of divisors of happy numbers $\{h, D(h)\}_{h \in \mathbb{H}}$ is:

Consider also the sequence here called sequence of trajectories $\{x, T(x)\}$. For $x > 1$, each pair $(x, T(x))$ is obtained from $D(d_i) = d_{i+1}$ with $i = 0, 1, 2, ..., T$, in which $d_0 = x$ and $d_T = 2$. Since $D(1) = 1$ and $D(2) = 2$, then 1 and 2 are fixed points of the map $D(d_i) = d_{i+1}$; however, the fixed point 2 is globally attracting for $x > 1$. Hence, the value of $T$ specifies the amount of steps required to arrive at this attracting fixed point from any $x > 1$. For instance, take $x = 60$, in order to illustrate how this sequence is formed. Observe that $D(60) = 12$, $D(12) = 6$, $D(6) = 4$, $D(4) = 3$, and $D(3) = 2$. As the fixed point 2 was reached after 5 steps from $x = 60$, then $T(60) = 5$. For the natural numbers $\{n\}$, the code of the list $\{T(n)\}_{n \in \mathbb{N}}$ in the online database OEIS is A036459 ^[7]. The sequence of trajectories of natural numbers $\{n, T(n)\}_{n \in \mathbb{N}}$ is given by:

The sequence of trajectories of happy numbers $\{h, T(h)\}_{h \in \mathbb{H}}$ is written as:

Graphs have been used to examine the relations among prime numbers and natural numbers ^[10], prime numbers and even numbers ^[11], integer numbers and their divisors ^[12,13], Fibonacci numbers ^[14], rational numbers ^[15], the gaps between successive $d$-primes for $d \in \{2, 3, ..., 11\}$ ^[6]. Informational entropy has been computed in studies on the distribution of primes ^[16,17,18] and $d$-primes ^[6]. In this manuscript, the sequences $\{x, D(x)\}$ and $\{x, T(x)\}$ are numerically investigated for $\{x\} = \{n\}$ and $\{x\} = \{h\}$. This investigation is based on visibility graphs and informational entropy, which is the approach that we used to study $d$-primes ^[6]. Notice that, in Eqs (1.1)–(1.4), $\{n\}$ and $\{h\}$ are increasing lists, but $\{D(n)\}$, $\{D(h)\}$, $\{T(n)\}$, and $\{T(h)\}$ are non-monotonic lists.

The aim of this article is to investigate the properties of numerical sequences that are not obtained from an explicit recurrence relation. The remainder of this article is organized as follows. In Section 2, in order to evaluate the variability of the sequences given by Eqs (1.1)–(1.4), their informational entropy ^[19] is calculated in function of the sequence length. In Section 3, the four mentioned sequences are transformed into undirected graphs by using two visibility algorithms ^[20,21]. Thus, eight graphs are built and numerically characterized. For each graph, the average degree $\langle k \rangle$, the average shortest-path length $\langle l \rangle$, the average clustering coefficient $\langle c \rangle$, and the values of $A$, $\gamma$, and $\delta$ of the degree distribution $P(k) = A k^{-\gamma} e^{- \delta k}$ are computed. Observe that the degree distribution is supposed to be fitted by a power law multiplied by an exponential term ^{[22,23,24,25,26]}. The percentages of links between even numbers, between odd numbers, and between an even number and an odd number are also determined for these eight graphs. In Section 4, the results for $\{n\}$ and $\{h\}$ are compared and discussed.

2.   Informational entropy

Let a numerical sequence be written as $\{x, F(x)\}$ with $\{F(x)\} = \{y\}$. The variability of the list $\{y\} = (y_1, y_2, ..., y_N)$ with $N$ elements can be evaluated by computing its normalized informational entropy $\Delta$ defined as:

in which $q_j$ is the relative frequency of the distinct number $y_j$ and $J$ is the amount of distinct numbers $y_j$. Since repetitions in $\{y\}$ can occur, then $J \leq N$. In Eq (2.1), $H_{max}$ is the maximum value of the informational entropy $H$ ^[19]; thus, $0 \leq \Delta \leq 1$.

Notice that $\Delta = 0$ for a sequence in which $q_j = 1$ for $j = j^*$ and $q_j = 0$ for $j \neq j^*$ (which implies $H = 0$); that is, a sequence formed by a single $y_j$; and $\Delta = 1$ for a sequence in which $q_j = 1/J$ for any $j$ (which implies $H = H_{max} = \log J$); that is, a sequence derived from an equiprobable distribution. Therefore, $\Delta$ expresses the level of intrinsic uncertainty in $\{y\}$. It increases with the variability in $\{y\}$, ranging from 0 for a constant sequence (in which all numbers are the same) to 1 for an equiprobable sequence (in which the numbers occur with the same relative frequency). The complexity of numerical sequences (or time series) has been related to its variability. In fact, there are complexity measures based on informational entropy ^[27,28], which have been used, for instance, in analyzes of economic crises ^[29] and texture of images ^[30].

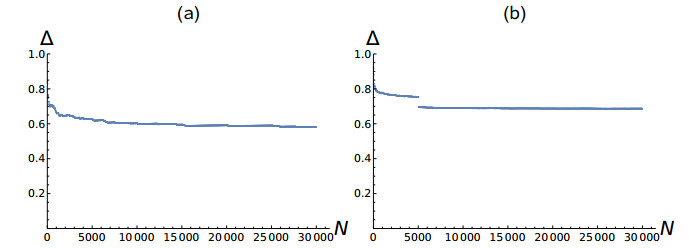
Figure 1 shows how $\Delta$ for $\{D(n)\}$ and $\{T(n)\}$ varies with the length $N$; Figure 2 is for $\{D(h)\}$ and $\{T(h)\}$. In these figures, $N$ goes up to 30000. The choice of this upper bound was influenced by the computer processing power required to map these sequences into graphs (see the next section). Figures 1 and 2 show that the dependence of $\Delta$ on $N$ is non-trivial. Two factors account for the oscillations and jumps observed in these figures. The first factor is the variation of the values of $q_j$ (the relative frequency of $y_j$), as the sequence length increases. In fact, the proportions of the numbers $y_j$ vary with $N$. The second factor is the introduction of new numbers $y_j$ as $N$ increases; thus, $J$ (the amount of distinct $y_j$) increases with $N$. The normalized entropy $\Delta$ given by Eq (2.1) depends on $q_j$ and $J$. Since $q_j$ and $J$ vary with $N$, then $\Delta$ also varies with $N$. For instance, the jump observed in Figure 1(b) occurs for $n = 5040$, because $T(5040) = 6$ and, for $n < 5040$, the maximum value of $\{T(n)\}$ is 5. The introduction of the number 6 causes the jump.

Figure 1.  The normalized informational entropy $\Delta = H/H_{max}$ for $\{D(n)\}$ (a) and $\{T(n)\}$ (b) in function of the sequence length $N$. For $N = 30000$, $\Delta = 0.582$ for $\{D(n)\}$ and $\Delta = 0.687$ for $\{T(n)\}$.

DownLoad: Full-Size Img PowerPoint

Figure 2.  The normalized informational entropy $\Delta = H/H_{max}$ for $\{D(h)\}$ (a) and $\{T(h)\}$ (b) in function of the sequence length $N$. For $N = 30000$, $\Delta = 0.575$ for $\{D(h)\}$ and $\Delta = 0.692$ for $\{T(h)\}$.

DownLoad: Full-Size Img PowerPoint

For $N = 30000$, the maximum values in $\{D\}$ and $\{T\}$ are: $\max(\{D(n)\}) = 96$, $\max(\{D(h)\}) = 160$, and $\max(\{T(n)\}) = \max(\{T(h)\}) = 6$. The minimum values in these sets are: $\min(\{D (n)\}) = \min(\{D(h)\}) = 1$ and $\min(\{T(n)\}) = \min(\{T(h)\}) = 0$. Therefore, the sets $\{T(n)\}$ and $\{T(h)\}$ are within the same range and the sets $\{D(n)\}$ and $\{D(h)\}$ belong to different ranges. For $N = 30000$, $\Delta = 0.582$ for $\{D(n)\}$, $\Delta = 0.575$ for $\{D(h)\}$, $\Delta = 0.687$ for $\{T(n)\}$, and $\Delta = 0.692$ for $\{T(h)\}$. Thus, for $N = 30000$, $\Delta \simeq 0.6$ for $\{D(n)\}$ and $\{D(h)\}$, and $\Delta \simeq 0.7$ for $\{T(n)\}$ and $\{T(h)\}$.

3.   Graphs from sequences

There are several ways of converting a numerical sequence into a graph ^[31]. Here, two visibility algorithms are employed for transforming the sequence $\{x, F(x) \}$ into undirected graphs, because these graphs inherit some properties of the converted sequences ^[20,21]. Visibility algorithms have been used in studies, for instance, on infection spread ^[32] and precipitation records ^[33].

Assume that each node of the visibility graphs corresponds to a distinct value of $x$. Assume also that $x_a < x_i < x_b$. In the natural visibility (NV) graph ^[20], the nodes $x_a$ and $x_b$ are linked if:

Therefore, these nodes are linked if any intermediate point $(x_i, F(x_i))$ is below the straight line connecting $(x_a, F(x_a))$ and $(x_b, F(x_b))$ in the plot $x \times F(x)$.

In the horizontal visibility (HV) graph ^[21], the nodes $x_a$ and $x_b$ are linked if:

Hence, these nodes are linked if any intermediate point $(x_i, F(x_i))$ is below the horizontal line connecting $(x_a, F(x_a))$ and $(x_b, F(x_b))$ in the plot $x \times F(x)$. If two nodes are connected in the HV graph, then they are connected in the corresponding NV graph; however, the reverse is not true. Figure 3 illustrates this statement.

Figure 3.  The sequence $\{(a, F(a)), (i, F(i)), (b, F(b))\}$ in the plot $x \times F(x)$ can be converted into graphs by using visibility algorithms. In the NV graph (the graph with red links), the nodes $a$ and $b$ are connected, since $F(i)$ is below the (red dashed) straight line connecting $(a, F(a))$ and $(b, F(b))$. In the HV graph (the graph with black links), the nodes $a$ and $b$ are not connected, because $F(i) > F(a)$; that is, the (black dashed) horizontal line passing through $(a, F(a))$ can not reach $(b, F(b))$ without crossing the bar representing $(i, F(i))$. In both graphs, $a$ is connected to $i$ and $i$ is connected to $b$.

DownLoad: Full-Size Img PowerPoint

Figures 4 and 5 respectively exhibit the partial graphs and the degree distributions $P(k)$ obtained from $\{n, D(n)\}$ and $\{n, T(n)\}$ by using the NV algorithm; in Figures 6 and 7, the HV algorithm is employed. Figures 8 and 9 are for $\{h, D(h)\}$ and $\{h, T(h)\}$ with the NV algorithm; in Figures 10 and 11, the HV algorithm is used.

Figure 4.  The first 100 links in the graphs built from $\{n, D(n)\}$ (a) and $\{n, T(n)\}$ (b) by employing the NV algorithm.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Degree distribution $P(k)$ for $\{n, D(n)\}$ (a) and $\{n, T(n)\}$ (b) for the graphs obtained from the NV algorithm by considering the first 30000 natural numbers. The solid line is the fitted curve $P(k) = A k^{-\gamma} e^{- \delta k}$.

DownLoad: Full-Size Img PowerPoint

Figure 6.  The first 100 links in the graphs built from $\{n, D(n)\}$ (a) and $\{n, T(n)\}$ (b) by employing the HV algorithm.

DownLoad: Full-Size Img PowerPoint

Figure 7.  Degree distribution $P(k)$ for $\{n, D(n)\}$ (a) and $\{n, T(n)\}$ (b) for the graphs obtained from the HV algorithm by considering the first 30000 natural numbers. The solid line is the fitted curve $P(k) = A k^{-\gamma} e^{- \delta k}$.

DownLoad: Full-Size Img PowerPoint

Figure 8.  The first 100 links in the graphs built from $\{h, D(h)\}$ (a) and $\{h, T(h)\}$ (b) by employing the NV algorithm.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Degree distribution $P(k)$ for $\{h, D(h)\}$ (a) and $\{h, T(h)\}$ (b) for the graphs obtained from the NV algorithm by considering the first 30000 happy numbers. The solid line is the fitted curve $P(k) = A k^{-\gamma} e^{- \delta k}$.

DownLoad: Full-Size Img PowerPoint

Figure 10.  The first 100 links in the graphs built from $\{h, D(h)\}$ (a) and $\{h, T(h)\}$ (b) by employing the HV algorithm.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Degree distribution $P(k)$ for $\{h, D(h)\}$ (a) and $\{h, T(h)\}$ (b) for the graphs obtained from the HV algorithm by considering the first 30000 happy numbers. The solid line is the fitted curve $P(k) = A k^{-\gamma} e^{- \delta k}$.

DownLoad: Full-Size Img PowerPoint

In the partial graphs (Figures 4, 6, 8, and 10), only the first 100 links are shown, in order to better visualize their structure. Observe the small-world characteristic ^[34] of these graphs; that is, the existence of long-range links that shorten the path between any pair of nodes. This characteristic is also present in biological, social, and technological networks that were investigated in classic papers on complex networks ^[34,35,36].

The plots of $P(k)$ (Figures 5, 7, 9, and 11) and the calculations of the network properties shown in Tables 1 and 2 were made by taking the first 30000 natural numbers and the first 30000 happy numbers.

Table 1.  Values of average degree $\langle k \rangle$, average shortest-path length $\langle l \rangle$, average clustering coefficient $\langle c \rangle$, and $A$, $\gamma$, and $\delta$ of the degree distribution $P(k) = A k^{-\gamma} e^{- \delta k}$ (and the mean squared error (MSE) of this fitted function) of the graphs obtained from the algorithms of natural visibility (NV) and horizontal visibility (HV). These algorithms were applied on the sequences of divisors ($\{D(x)\}$) and trajectories ($\{T(x)\}$) of natural ($\{x\} = \{n\}$) and happy ($\{x\} = \{h\}$) numbers. The corresponding figure numbers are given in the first column.

Figs.	sequence	algorithm	$\langle k \rangle$	$\langle l \rangle$	$\langle c \rangle$	$A$	$\gamma$	$\delta$	MSE
4, 5	$\{D(n)\}$	NV	5.78	7.92	0.33	0.17	$-2.27$	0.78	$1.6 \times 10^{-5}$
4, 5	$\{T(n)\}$	NV	5.04	28.3	0.06	0.38	$-0.76$	0.48	$2.4 \times 10^{-5}$
6, 7	$\{D(n)\}$	HV	3.58	16.3	0.27	1.68	1.53	0.14	$3.3 \times 10^{-5}$
6, 7	$\{T(n)\}$	HV	2.98	257	0.26	1.87	0.60	0.46	$1.6 \times 10^{-4}$
8, 9	$\{D(h)\}$	NV	6.61	7.39	0.35	0.10	$-2.25$	0.66	$9.6 \times 10^{-6}$
8, 9	$\{T(h)\}$	NV	5.33	100	0.14	0.19	$-2.19$	0.77	$7.2 \times 10^{-6}$
10, 11	$\{D(h)\}$	HV	3.51	15.4	0.27	1.34	0.71	0.33	$9.8 \times 10^{-6}$
10, 11	$\{T(h)\}$	HV	2.92	157	0.26	1.71	$-0.39$	0.77	$1.4 \times 10^{-4}$

---

 | Show Table

DownLoad: CSV

Table 2.  Percentages of odd nodes ($\chi_1$), even nodes ($\chi_2$), links between odd nodes ($m_{11}$), links from an odd node to an even node ($m_{12}$), links from an even node to an odd node ($m_{21}$), and links between even nodes ($m_{22}$) in the eight graphs. The total number of links ($M$) is given in the last column.

sequence	algorithm	$\chi_1$	$\chi_2$	$m_{11}$	$m_{12}$	$m_{21}$	$m_{22}$	$M$
$\{D(n)\}$	NV	50.0	50.0	3.4	26.7	26.7	43.2	86645
$\{T(n)\}$	NV	50.0	50.0	3.7	28.7	28.4	39.2	75579
$\{D(n)\}$	HV	50.0	50.0	1.0	31.8	31.8	35.4	53723
$\{T(n)\}$	HV	50.0	50.0	1.3	37.2	37.2	24.3	44655
$\{D(h)\}$	NV	49.6	50.4	11.1	23.6	22.6	42.7	99143
$\{T(h)\}$	NV	49.6	50.4	13.2	23.0	23.1	40.7	79940
$\{D(h)\}$	HV	49.6	50.4	14.6	23.3	22.7	39.4	52626
$\{T(h)\}$	HV	49.6	50.4	17.4	25.8	25.6	31.2	43755

---

 | Show Table

DownLoad: CSV

Table 1 presents the values of $\langle k \rangle$, $\langle l \rangle$, $\langle c \rangle$, $A$, $\gamma$, and $\delta$. Recall that the node degree $k$ is the number of edges linked to the node, the path length $l$ is the shortest distance between two nodes, and the node clustering coefficient $c$ is percentage of neighbors that are linked together ^[35,36]. The average values $\langle k \rangle$, $\langle l \rangle$, and $\langle c \rangle$ are calculated by considering all nodes in the graph. Also, $P(k)$ is the percentage of nodes with degree $k$ ^[35,36]. The values of $A$, $\gamma$, $\delta$, and the mean squared error (MSE) of fitted function $P(k) = A k^{-\gamma} e^{- \delta k}$ were determined from the least square fitting method ^[37].

Table 2 presents $\chi_1$ and $\chi_2$, which respectively are the percentages of odd nodes and even nodes in each graph. Obviously, $\chi_1 + \chi_2 = 1$. For $N = 30000$, there are $49.6\%$ of odd happy numbers and $50.4\%$ of even happy numbers, and, obviously, $50\%$ of odd natural numbers and $50\%$ of even natural numbers. Table 2 also presents $m_{11}$, $m_{22}$, $m_{12}$, and $m_{21}$, which respectively denote the percentages of links between odd nodes, links between even nodes, links from an odd node to an even node, and links from an even node to an odd node. Notice that, despite the visibility algorithms generating undirected graphs, $m_{12}$ and $m_{21}$ express properties of nodes of directed graphs. This can be done by associating the horizontal axis $x$ in Figure 3 to the direction of time of $\{x, F(x)\}$ ^[21]. As time $x$ passes, links start from the current node to arrive at nodes in the future (for instance, in Figure 3, links start from $x = a$ and arrive at $x = i$ and $x = b$, in the NV graph). Obviously, $m_{11}+m_{12}+m_{21}+m_{22} = 1$ and $m_{12}+m_{21}$ represent the percentage of links between nodes with distinct parity, if the presumed orientation of the links is ignored. Table 2 also shows $M$, which is the total number of links in each graph. Recall that $\langle k \rangle = 2M/N$^[35,36].

4.   Discussion and conclusions

As far as we know, this is the first analysis of the sequences $\{n, D(n)\}$, $\{h, D(h)\}$, $\{n, T(n)\}$, and $\{h, T(h)\}$ based on the computation of informational entropy and on the construction of visibility graphs. These mathematical tools were selected for the following reasons. Since these four sequences do not exhibit any evident pattern, it is relevant to estimate their variability by calculating their informational entropy. Since visibility graphs inherit some properties of the associated sequences, the study of these graphs may provide hints about the underlying process generating such sequences.

Evidently, the set of the happy numbers $\{h\}$ is a subset of the set of the natural numbers $\{n\}$. Table 2 shows that the percentage of odd (even) happy numbers is similar to the percentage of odd (even) natural numbers for $N = 30000$. Figure 1 reveals that, for $N = 30000$, $\Delta \simeq 0.6$ for $\{D(n)\}$ and $\{D(h)\}$. Notice that, despite the similarity in this value of the normalized entropy, which implies comparable variability, and despite the similar proportion of odd and even numbers in $\{n\}$ and $\{h\}$, the sequences given by Eqs (1.1) and (1.2) are mapped into graphs with distinct topological measures. This statement is also true for the sequences given by Eqs (1.3) and (1.4). Observe that $\Delta \simeq 0.7$ for $\{T(n)\}$ and $\{T(h)\}$, as can be seen in Figure 2; however, these sequences are transformed into graphs with different features.

For $N = 30000$, $1 \leq D(n) \leq 96$, $1 \leq D(h) \leq 160$, and $0 \leq T(n), T(h) \leq 6$. Thus, the number of distinct values in the $\{D\}$-sequences is much higher than in the $\{T\}$-sequences. Surprisingly, the normalized entropy $\Delta$ is higher for the $\{T\}$-sequences than for the $\{D\}$-sequences.

The HV graph is subgraph of the corresponding NV graph ^[20,21,31]; hence, as expected, Table 2 shows that $M$ is higher in NV graphs than in HV graphs and Table 1 shows that $\langle k \rangle$ is higher in NV graphs than in HV graphs and $\langle l \rangle$ is lower in NV graphs than in HV graphs. For instance, for $\{D(n)\}$, $M_{NV} = 86645 > M_{HV} = 53723$, $\langle k \rangle_{NV} = 5.78 > \langle k \rangle_{HV} = 3.58$, $\langle l \rangle_{NV} = 7.92 < \langle l \rangle_{HV} = 16.3$. However, the highest amount of edges in the NV graphs does not imply higher $\langle c \rangle$. For instance, $\langle c \rangle_{NV} = 0.33 > \langle c \rangle_{HV} = 0.27$ for $\{D(n)\}$, but $\langle c \rangle_{NV} = 0.06 < \langle c \rangle_{HV} = 0.26$ for $\{T(n)\}$.

By employing the NV algorithm, the graphs built from the sequence of divisors $\{D\}$ present greater $\langle k \rangle$, lower $\langle l \rangle$, and greater $\langle c \rangle$ than the respective graphs built from the sequence of trajectories $\{T\}$, for natural and happy numbers. For instance, for the NV-graphs, $\langle k \rangle_{\{D(h)\}} = 6.61 > \langle k \rangle_{\{T(h)\}} = 5.33$, $\langle l \rangle_{\{D(h)\}} = 7.39 < \langle l \rangle_{\{T(h)\}} = 100$, and $\langle c \rangle_{\{D(h)\}} = 0.35 > \langle c \rangle_{\{T(h)\}} = 0.14$. By using the HV algorithm, the $\{D\}$-graphs present greater $\langle k \rangle$ and lower $\langle l \rangle$ than the respective $\{T\}$-graphs, but $\langle c \rangle$ is similar in both graphs.

The expression $\langle l \rangle_{random} = \log N/\log\langle k \rangle$, usually employed to estimate the average shortest path length in purely random graphs, gives lower values than those shown in Table 1. For instance, for the NV graph for $\{D(h)\}$, $\langle l \rangle = 7.39 > \langle l \rangle_{random} = 5.49$; for the HV graph for $\{D(h)\}$, $\langle l \rangle = 15.4 > \langle l \rangle_{random} = 8.21$. In fact, the graphs obtained from visibility algorithms are not purely random; hence, $\langle l \rangle$ in Table 1 is higher than $\langle l \rangle_{random}$. However, the plots of $P(k)$ suggest that the four sequences can be viewed as quasi-random.

The fitted function $P(k)$ qualitatively changes from the NV plot to the HV plot, for the natural and happy numbers considered here. Loosely speaking, the NV algorithm creates random/small-world networks ^[35,36] and the HV algorithm creates scale-free networks ^[35,36]; that is, $P(k)$ in the NV graphs is a Poisson-like distribution (Figures 5 and 9) and $P(k)$ in the HV graphs is a scale-free distribution with an exponential cutoff (Figures 7 and 11). Since a random sequence is mapped by the NV algorithm into a graph with a Poisson degree distribution ^[20] and by the HV algorithm into a graph with an exponential degree distribution ^[21], the plots of $P(k)$ suggest that the four analyzed sequences behave like quasi-random sequences. However, these sequences are not generated by a purely random process, because such a process would present $\Delta = 1$ and these sequences have $\Delta \simeq 0.6-0.7$. The MSE of the fitted function in these plots could be decreased by increasing the sequence length used in the numerical experiments. Thus, the discrepancies between the data and the fitted function usually found for $k$ above a critical number could be reduced.

Table 2 reveals that, in all graphs, the least frequent type of connection is that between odd numbers (that is, $m_{11} < m_{12}, m_{21}, m_{22}$); however, this type of connection is more prevalent in the graphs derived from happy numbers than those derived from natural numbers. For instance, by considering the NV algorithm, $m_{11, \{D(h)\}} = 0.111 > m_{11, \{D(n)\}} = 0.034$. This table also reveals that connections from odd number to even number and connections from even number to odd number appear in similar percentages (that is, $m_{12} \simeq m_{21}$) in all graphs. Notice that links between odd numbers and links between even numbers connect non-consecutive nodes in the graphs for $\{n\}$; however, this is not true in the graphs for $\{h\}$.

In short, in this manuscript, four sequences of purely mathematical nature were mapped into graphs with $\langle l \rangle \gtrsim \langle l \rangle_{random}$ and $0 \ll \langle c \rangle < 1$, which are connectivity features usually found in real-world networks ^[34,35,36]. Thus, from a topological perspective, mathematical networks can be similar to networks representing biological, social, and technological systems. Also, the monotonically decreasing degree distributions obtained from the HV-algorithm and the bell-type degree distributions obtained from the NV-algorithm may be a consequence of mapping quasi-random sequences. This study also showed that $\{D\}$-graphs are more connected than the corresponding $\{T\}$-graphs; and even numbers are more connected than odd numbers. These conclusions were drawn for the four sequences of natural and happy numbers taken into account in this manuscript and they can be useful in the proposition of a theoretical model for these graphs.

Data Availability

The data used to support the findings of this study are available from the first author (bleemayer@gmail.com) upon request.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

Acknowledgements

BLM thanks to Instituto Presbiteriano Mackenzie for the scholarship. LHAM is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under the grant #302946/2022-5. This study was financed in part by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - finance code 001.