Some dynamic Hardy-type inequalities with negative parameters on time scales nabla calculus

1.   Introduction

In 1941, Hopf ^[1] put forward the concept of both algebraic structure and coalgebra structure in the study of cohomology algebra $H^*(G, K)$ of Lie group $G$. In 1965, Milnor and Moore ^[2] formally called them Hopf algebras, then Sweedler ^[3] and Artamonov ^[4] also studied it. Especially in recent two decades, the rise of quantum groups, the successful solution of Kaplansky's conjectures ^[5] and the development of Hopf algebra theory make it a new scientific system. Hopf algebras are widely used in various fields, for example, universal enveloping algebras in Lie theory and free Lie algebras ^[6,7], nonlinear control theory ^[8], geometry algebras ^[9], degenerate versions of Drinfeld-Jimbo quantum groups ^[10], generalized Clifford algebras in aforementioned categories ^[11] and even the genetic inheritance in biology ^[12].

In 1984, Michel Van den Bergh ^[13], Blattner and Montgomery ^[14] introduced the duality of Hopf algebras. It is proved that the group ring is a classical special case of Hopf algebra. But the dual space of a general Hopf algebra is only an algebra, not a Hopf algebra. Only when a Hopf algebra is graded, its graded dual space has a corresponding graded Hopf algebra structure.

Because the rigidity of Hopf algebra structure often reveals the deep nature and connection in combinatorics, Hopf algebra has gradually become one of the important research contents in algebraic combinatorics. In 1979, Joni and Rota ^[15] found that the discrete structures in combinatorics have natural Hopf algebraic structures. In 2006, Aguiar, Bergeron and Sottle ^[16] proposed the concept of combinatorial Hopf algebras and studied the category of them. More and more combinatorial Hopf algebras have been discovered and studied. In 2009, Bergeron and Li ^[17] gave the axioms on a tower of algebras to guarantee that its Grothendieck groups are dual graded Hopf algebras. Later, Bergeron, Lam and Li ^[18] analyzed the relationship between combinatorial Hopf algebras and dual graded graphs. The Hopf algebra of symmetric functions is a self-dual Hopf algebra, which plays an important role in algebraic combinatorics. In 2016, using the duality Li, Morse and Shields ^[19] provided a dual approach to the structure constants for $K$-theory of Grassmannians. It is well-known that symmetric functions are closed related to symmetric groups. They can be applied to algebraic number theory ^[20] and substochastic matrices ^{[21,22,23,24]}.

In combinatorics, a permutation of degree $n$ is an arrangement of $n$ elements. The symmetric group of degree $n$, denoted by $S_n$, contains all permutations of $[n] = \{1, 2, \ldots , n\}$. Let $KS_n$ be the vector space spanned by $S_n$ over field $K$. Define $KS: = \bigoplus_{n\geq0}KS_n$, the direct sum of $KS_n$, where $S_0 = \{\epsilon\}$ and $\epsilon$ is the empty permutation. Then $KS$ is graded and its $n$th component is $KS_n$. In 1958, Ree ^[25] studied an algebra associated with shuffles, then the study of shuffles is further promoted ^[26,27]. In 1995, Malvenuto and Reutenauer ^[28] constructed the product $*$ according to ^[29]. In fact, the product $*$ is the shuffle product ${\rm{III}}$ (Eq 2.2 in Section 2). However, this product $*$ is not commutative on permutations.

In 2005, Aguiar and Sottile ^[30] introduced global descents of permutations in symmetric group $S_n$. It plays a crucial role in this paper. In 2018, Bergeron, Ceballos and Pilaud ^[31] introduced the concept of gaps on permutations of $S_n$. Then Bergeron et al. linked the global descents and the shuffle product ${\rm{III}}$ together and defined a new shuffle product on permutations. The new shuffle product is based on the global descents of permutations, which requires that from a standard factorization to the original permutation we renumber the numbers in the atoms from right to left. This ensures the new shuffle product is commutative on permutations. We denote such a shuffle by ${\rm{III}}_G$ and define a coproduct $\Delta$ on $KS$ such that ($KS, {\rm{III}}_G, \mu, \Delta, \nu$) is a Hopf algebra ^[32]. There must be a graded Hopf algebra dual to the shuffle Hopf algebra ($KS, {\rm{III}}_G, \mu, \Delta, \nu$), which could be seen from the definition of dual graded Hopf algebras.

The main result of this paper is to find the duality ($KS, {\rm{III}}_G^*, \mu, \Delta^*, \nu$). In Section 2, we introduce the dual Hopf algebras of Malvenuto and Reutenauer in details. In Section 3, we first introduce the shuffle product ${\rm{III}}_G$ and deconcatenation coproduct $\Delta$, then define a new product ${\rm{III}}_G^*$ and a new coproduct $\Delta^*$ on $KS$. In Section 4, we prove that the product ${\rm{III}}_G^*$ and the coproduct $\Delta^*$ are compatible so ($KS, {\rm{III}}_G^*, \mu, \Delta^*, \nu$) becomes a bialgebra. Since the bialgebra is graded and connected, it is a graded Hopf algebra. Then, we give a closed-formula of its antipode and prove it. In Section 5, we prove that graded Hopf algebras ($KS, {\rm{III}}_G, \mu, \Delta, \nu$) and ($KS, {\rm{III}}_G^*, \mu, \Delta^*, \nu$) are dual to each. In Section 6, we apply products ${\rm{III}}_G$, ${\rm{III}}_G^*$ and coproduct $\Delta$, $\Delta^*$ on different objects and get some other pairs of dual graded Hopf algebras and link some of them to dual graded graphs. Furthermore, we post some open questions on ungraded bialgebras.

2.   A classic example of dual Hopf algebras on $KS$

One of the classic examples of dual graded Hopf algebras were introduced by Malvenuto and Reutenauer, who defined two products $*$ and $*'$, and two coproducts $\Delta$ and $\Delta'$ on $KS$. More details can be found in ^[28]. Here, we only briefly introduce these two graded Hopf algebras.

A bialgebra ($H$, $\psi$, $\mu$, $\Delta$, $\nu$) over a field $K$, where $\psi$ is a product, $\mu$ is a unit map, $\Delta$ is a coproduct and $\nu$ is a counit map, is a Hopf algebra if it admits a unique antipode $\theta$ satisfying the following identity

A graded connected bialgebra ($H$, $\psi$, $\mu$, $\Delta$, $\nu$) admits a unique antipode $\theta$ so is a graded Hopf algebra.

Let $A$ be a set called an alphabet and the elements in it are called letters. A word $f$ over alphabet $A$ is composed of finite letters, i.e., $f = f_1f_2\cdots f_n$ with $f_i\in A$ for all $i$. A word without any letters is called the empty word, denoted by $\epsilon$.

The shuffle product ${\rm{III}}$ on words is defined by

where $f = f_1f_2\cdots f_n$, $g = g_1g_2\cdots g_m$ and $f {\rm{III}} \epsilon = \epsilon {\rm{III}} f = f$.

For example, if $f = ab$ and $g = ac$, then

For any permutation $\alpha\in S_n$, it can be written in the one-line notation as $\alpha = \alpha_1\alpha_2\cdots\alpha_n$, where $\alpha_i = \alpha(i)\in[n]$.

For $\alpha \in S_n$ and $\beta \in S_m$, define the product $*$ on permutations by

where ${\rm{III}}$ is the shuffle product above.

For example, $12*21 = 12{\rm{III}}43 = 1243+1423+1432+4123+4132+4312.$ The empty permutation $\epsilon$ serves as the unit, and $\alpha * \epsilon = \epsilon * \alpha = \alpha$.

The unit map is defined by $\mu$: $K \rightarrow$ $KS$, $\mu(1) = \epsilon$.

A sequence on $[n]$ is obtained by selecting finite different elements from the set $[n]$, denoted by $\beta = \beta_1\beta_2\cdots\beta_m$ $(1\leq m\leq n)$ where $\beta_i \in[n]$. When no element is selected, we have the empty sequence, also denoted by $\epsilon$. Let ${\rm alph}(\beta)$ be the set that consists of all elements in $\beta$.

The standard form ^[33,34] of a sequence $\beta = \beta_1\cdots\beta_m$ on $[n]$ $(1\leq m\leq n)$ is a unique permutation in $S_m$, denoted by st$(\beta)$, satisfying that

where $1\leq i < j\leq n$.

For instance, st$(4769) = 1324$. And the standard form of the empty sequence is the empty permutation, i.e., st$(\epsilon) = \epsilon$.

The coproduct $\Delta$ on $KS$ is defined by

for $\alpha = \alpha_1\alpha_2\cdots\alpha_n$ in $S_n$.

For example,

The counit is defined by $\nu$: $KS \rightarrow K$, $\nu(\epsilon) = 1$ and $\nu(\alpha) = 0$ for any $\alpha \in S_n$, $n\geq 1$.

Malvenuto and Reutenauer also defined product $*'$ and coproduct $\Delta'$ as follows.

For $\alpha \in S_n$ and $\beta \in S_m$, define the product $*'$ by

where the sum is over all sequences $u$, $v$ satisfying the following conditions:

1) $uv$ is the concatenation of $u$ and $v$;

2) ${\rm alph}(u)\bigcup {\rm alph}(v) = [n+m]$;

3) $uv \in S_{n+m}$.

For example, $12 *' 21 = 1243+1342+1432+2341+2431+3421.$

Here neither product $*$ nor product $*'$ is commutative.

For a permutation $\alpha\in S_n$ and $0\leq i \leq n$, let $\alpha_{[i]}$ consist of all elements of $[i]$ in the one-line notation of $\alpha$. Then $\alpha_{[i]}$ is a permutation over $[i]$, which is obtained by removing all digits greater than $i$ in permutation $\alpha$. For the permutation $\alpha = 3642751$ we have $\alpha_{[5]} = 34251$ and $\alpha_{[0]} = \epsilon$ because $[0] = \emptyset$.

For any permutation $\alpha \in S_n$, define the coproduct $\Delta'$ by

For example, $\Delta'(2413) = \epsilon\otimes2413+1\otimes {\rm st}(243)+21\otimes {\rm st}(43)+213\otimes {\rm st}(4)+2413\otimes\epsilon = \epsilon\otimes2413+1\otimes 132+21\otimes 21+213\otimes 1+2413\otimes\epsilon$.

Then ($KS, *, \mu, \Delta, \nu$) and ($KS, *', \mu, \Delta', \nu$) are both graded connected bialgebras, and so they are both Hopf algebras. In 2005, Aguiar and Sottile gave a detailed description of their antipodes [30, Theorem 5.4].

If there is a bilinear pairing $<, > : H\otimes H^{*gr}\rightarrow K$ satisfying the following identities:

for any $P$, $Q$ $\in$ $H$, $M$, $N$ $\in$ $H^{*gr}$, then $H$ and $H^{*gr}$ are graded dual to each other.

Define a bilinear pairing $<, >$ on $KS\otimes KS$ by

for any permutations $\alpha$ and $\beta$.

For $x, y, z\in KS$,

Thus the graded Hopf algebras ($KS, *, \mu, \Delta, \nu$) and ($KS, *', \mu, \Delta', \nu$) are dual to each.

3.   Concatenation product and draw coproduct

For a permutation $\alpha$ in $S_n$ in one-line notation, from left to right the positions in front of the first number, between two adjacent numbers and behind the last number indexed by $\{0, \ldots, n\}$ are called the $gaps$ of $\alpha$.

For example, consider permutation 78645312

where each $_{\bigcirc}$ represents a position of 78645312 and corresponds to a gap. Thus, the gaps of 78645312 are 0, 1, 2, 3, 4, 5, 6, 7 and 8.

If a gap $\gamma$ of $\alpha$ satisfies $\alpha ([\gamma]) = [n] \backslash [n-\gamma]$, then $\gamma$ is a global descent, where gaps $0$ and $n$ are always globe descents. An atom is a permutation that has no other global descent except 0 and $n$. For example, permutations 1, 12, 132 and 1432 are all atoms.

Consequently, for $\alpha$ in $S_n$ putting a bullet $\bullet$ at each global descent except $0$ and $n$ we get the factorization of $\alpha = \alpha_1 \bullet \alpha_2 \bullet \cdots \bullet \alpha_s$. Denote the length of $\alpha$ by $|\alpha| = s$, which is always less than or equal to its degree $n$. It is obvious that all ${\rm st}(\alpha_i)$'s are atoms. Replacing all $\alpha_i$'s in the factorization of $\alpha$ by their standard form ${\rm st}(\alpha_i)$'s, we get the standard factorization of $\alpha$, i.e., $\alpha = \alpha_1 \bullet \alpha_2 \bullet \cdots \bullet \alpha_s = {\rm st}(\alpha_1) \bullet {\rm st}(\alpha_2) \bullet \cdots \bullet {\rm st}(\alpha_s)$. From the standard factorization to the original permutation, we renumber all the numbers in the standard factorization from right to left then eliminate all bullets.

For example, $321 = 3 \bullet 2 \bullet 1 = {\rm st}(3) \bullet {\rm st}(2) \bullet {\rm st}(1) = 1 \bullet 1 \bullet 1$ and $312 = 3 \bullet 12 = {\rm st}(3) \bullet {\rm st}(12) = 1\bullet 12$.

From now on, all factorizations are standard.

Define the shuffle product ${\rm{III}}_G$ on $KS$ recursively by

and

where $\alpha = \alpha_1 \bullet\cdots\bullet \alpha_i \bullet\cdots\bullet \alpha_s \in S_n$ and $\beta = \beta_1 \bullet\cdots\bullet \beta_j \bullet\cdots\bullet \beta_t \in S_m$, $\alpha_i$ ($0\leq i \leq s\leq n$) and $\beta_j$ ($0\leq j \leq t\leq n$) are atoms.

Obviously, the shuffle product ${\rm{III}}_G$ is commutative and $\alpha\, {\rm{III}}_G \, \beta$ $\in$ $KS_{n+m}$. Thus, ($KS, {\rm{III}}_G, \mu$) is a graded algebra.

Example 1.

From the example above, if we color the atoms of $\alpha$ blue and the atoms of $\beta$ red then atoms 1 and 1 are different and we can consider all permutations in the shuffle product distinct even them are same, for example, 654312, 654312, 654312 and 654312 are distinct. In this paper, we color the atoms of different permutations in different colors.

For any permutaion $\alpha = \alpha_1\bullet\alpha_2\bullet\cdots\bullet\alpha_s$, let $I$ be a subset of $[s]$. Define $\alpha_{I}$ be a permutation consisting of atoms index by $I$ and keeping their relative positions in the factorization of $\alpha$. Therefore, $\alpha_{\emptyset} = \epsilon$ and $\alpha_{[s]} = \alpha$.

Define the deconcatenation coproduct $\Delta$ on $KS$ by

where $\alpha = \alpha_1 \bullet \alpha_2 \bullet \cdot\cdot\cdot \bullet \alpha_s$ is its factorization with length $|\alpha| = s$ and $\Delta(\epsilon) = \epsilon \otimes \epsilon$.

From (3.2), each term in the deconcatenation coproduct of a permutation is putting a tensor sign at one of its global descents.

Example 2.

The following lemma was first mentioned in ^[31] without a proof. Zhao and Li proved it and the result is published in a journal in Chinese ^[32]. Here we give a sketch of the proof.

Lemma 1. The shuffle product ${\rm{III}}_G$ and the deconcatenation coproduct $\Delta$ are compatible, i.e.,

where $\alpha$ and $\beta$ are permutations and $\Delta(\alpha{\rm{III}}_G \beta) = \sum(\alpha_{[i]}{\rm{III}}_G\beta_{[j]}) \otimes(\alpha_{[s]\backslash [i]}{\rm{III}}_G\beta_{[t]\backslash [j]})$, if $\Delta(\alpha) = \sum\alpha_{[i]}\otimes\alpha_{[s]\backslash [i]}$ and $\Delta(\beta) = \sum\beta_{[j]}\otimes\alpha_{[t]\backslash [j]}$.

Proof. Let $\alpha = \alpha_1\bullet\cdots\bullet\alpha_s$ and $\beta = \beta_1\bullet\cdots\bullet\beta_t$. Denote $\Delta(\alpha {\rm{III}}_G \beta)|_{j = k}$ to be the sum of terms in $\Delta(\alpha {\rm{III}}_G \beta)$ with the number of atoms of $\beta$ on the left side of the tensor sign is $k$, $0\leq k\leq t$.

Then

Hence

From Lemma 1 the deconcatenation coproduct $\Delta$ is an algebra homomorphism, thus ($KS, {\rm{III}}_G, \mu, \Delta, \nu)$ is a bialgebra, where the unit $\mu$ and counit $\nu$ are the same in Section 2. A graded connected bialgebra is a Hopf algebra so the bialgebra ($KS, {\rm{III}}_G, \mu, \Delta, \nu)$ is a Hopf algebra.

Next, we would introduce another product and coproduct on $KS$.

Definition 1. Defined the concatenation product $\diamond$ on $KS$ by

where $\alpha = \alpha_1\bullet\alpha_2\bullet\cdots\bullet\alpha_s$, $\beta = \beta_1\bullet\beta_2\bullet\cdots\bullet\beta_t$ are their standard factorizations, and $\alpha \diamond \epsilon = \alpha = \epsilon \diamond \alpha$.

The renumbering of the product is still from right to left and we notice that the concatenation product $\diamond$ does not satisfy commutativity.

Example 3. Take $\alpha = 312 = 1 \bullet 12 \in S_3, \beta = 4213 = 1 \bullet 213 \in S_4$, then

It is easy to check that $\mu$ is also a unit for the concatenation product $\diamond$.

In ($KS, \diamond, \mu$), the product of any two permutations of degrees $p$ and $q$ is a permutation of degree $p+q$. So ($KS, \diamond, \mu$) is a graded algebra.

Definition 2. The draw coproduct $\Delta^*$ on $KS$ is defined by

for $\alpha = \alpha_1\bullet\alpha_2\bullet\cdots\bullet\alpha_s$, where the sum is over all subsets $I$ in $[s]$.

Example 4. Take $\alpha = 564312 \in S_6$. It has global descents at positions 0, 2, 3, 4 and 6. Then its factorization is $\alpha = {56}\bullet{4}\bullet{3}\bullet{12} = {12}\bullet{1}\bullet{1}\bullet{12}$. Thus,

Since $\Delta^*(KS_n)\subseteq\bigoplus_{k = 0}^n(KS_k\otimes KS_{n-k})$ and $\nu$ is also a counit for the draw coproduct $\Delta^*$, ($KS, \Delta^*, \nu$) is a graded coalgebra. We will prove that ($KS, \diamond, \mu, \Delta^*, \nu$) is a graded bialgebra in Section 4.

4.   A Hopf algebra on permutations

From Section 3, we have a graded algebra ($KS, \diamond, \mu$) and a graded coalgebra ($KS, \Delta^*, \nu$). In this section, we would prove ($KS, \diamond, \mu, \Delta^*, \nu$) is a Hopf algebra and give a closed-formula of its antipode.

Theorem 1. ($KS, \diamond, \mu, \Delta^*, \nu)$ is a bialgebra.

To prove this we need to prove the following properties:

(1) $\nu(\mu(1)) = 1$,

(2) $\nu(\alpha\beta) = \nu(\alpha)\nu(\beta)$, for any $\alpha, \beta$ in $KS$,

(3) $\Delta^*(\mu(1)) = \mu(1)\otimes\mu(1),$

(4) $\Delta^*(\alpha\diamond\beta) = \sum(\alpha_i\diamond\beta_j)\otimes(\alpha'_i\diamond\beta'_j)$, if $\Delta^*(\alpha) = \sum\alpha_i\otimes\alpha'_i$ and $\Delta^*(\beta) = \sum\beta_j\otimes\beta'_j$, for any $\alpha, \beta$ in $KS$.

Conditions (1)–(3) are obvious, so here we only prove Condition (4) which is equivalent to

for any two permutations $\alpha$ and $\beta$, i.e., the coproduct $\Delta^*$ is an algebra homomorphism.

Proof. Let $\alpha = \alpha_1\bullet\alpha_2\bullet\cdots\bullet\alpha_s$ and $\beta = \beta_1\bullet\beta_2\bullet\cdots\bullet\beta_t$ in standard factorization form. Then $\alpha \diamond\beta = \alpha_1\bullet\alpha_2\bullet\cdots\bullet\alpha_s\bullet\beta_1\bullet\beta_2\bullet\cdots\bullet\beta_t$.

Denote $\Delta^*(\alpha \diamond \beta)|_{y = k}$ to be the sum of terms in $\Delta^*(\alpha \diamond \beta)$ with the number of atoms of $\beta$ on the left side of the tensor sign is $k$, $0\leq k\leq t$.

Therefore,

where $X$ is a subset of $[s]$ and the sum is over all subsets $X$ of $[s]$.

And

Similarly,

Then

where the sums are over all subsets $X$ of $[s]$ and $Y$ of $[t]$ respectively.

Corollary 1. The bialgebra (K$S, \diamond, \mu, \Delta^*, \nu)$ is a Hopf algebra.

Proof. The bialgebra ($KS, \diamond, \mu, \Delta^*, \nu)$ is graded and connected, so it is a Hopf algebra.

Because the bialgebra ($KS, \diamond, \mu, \Delta^*, \nu)$ is a Hopf algebra, it possesses an antipode $\theta$. The antipode of ($KS, \diamond, \mu, \Delta^*, \nu)$ is given by the following proposition.

Proposition 1. The antipode $\theta$ of Hopf algebra ($KS, \diamond, \mu, \Delta^*, \nu)$ is given by

for any permutation $\alpha = \alpha_1\bullet\alpha_2\bullet\cdots\bullet\alpha_{t-1}\bullet\alpha_t$ and $\theta(\epsilon) = \epsilon$.

Proof. According to the definition of the antipode, we are supposed to verify that all elements of the Hopf algebra ($KS, \diamond, \mu, \Delta^*, \nu)$ are all satisfy Eq (2.1).

Since the both sides of the equal signs in Eq (2.1) are symmetric and the coproduct $\Delta^*$ is cocommutative, we just need to prove one side of the formula

First, for a permutation $\alpha$ and $|\alpha| = t$, then

where the sum is over all subsets $I$ of $[t]$.

It is easy to check that $\diamond\circ(\theta\otimes {\rm{id}})\circ\Delta^*(\epsilon) = \epsilon = \nu\circ\mu(\epsilon)$.

Assume $\alpha \neq \epsilon$. From the definition of coproduct $\Delta^*$, we have

Denote

where $I_k$ is a subset of $[t]$ consist of $k$ elements of $[t]$ and $\alpha_{I_k}$ are permutations consisting of all atoms indexed by $I_k$.

For convenience, we denote $(\alpha) ^{-1} =\alpha_t \bullet \alpha_{t-1}\bullet...\bullet \alpha_2 \bullet \alpha_1$ for $\alpha= \alpha_1 \bullet \alpha_2\bullet ... \bullet \alpha_{t-1} \bullet \alpha_t$. Obviously, $(\epsilon) ^{-1}= \epsilon$. Then

Hence

From Eq (4.12), when $x = k-1$, we have

When $x = k+1$, we have

It is easy to see that $\diamond\circ(\theta\otimes {\rm{id}})\circ\Delta^*(\alpha)|_{\mathop{}_{x = k}}$ would be cancelled by part of $\diamond\circ(\theta\otimes {\rm{id}})\circ\Delta^*(\alpha)|_{\mathop{}_{x = k-1}}$ and part of $\diamond\circ(\theta\otimes {\rm{id}})\circ\Delta^*(\alpha)|_{\mathop{}_{x = k+1}}$.

When $x = 0$, we have

When $x = 1$, we have

When $x = t-1$, we have

When $x = t$, we have

From the results above (4.12–4.18)

We notice that the closed-formula of the antipode is similar to the antipode in [7, Proposition 1.10], because for a graded connected Hopf algebra we always can compute its antipode recursively.

5.   Duality of the shuffle Hopf algebra

A sub-permutation of a permutation $\alpha$ is a subsequence composed of some atoms of $\alpha$ with the same relative positions.

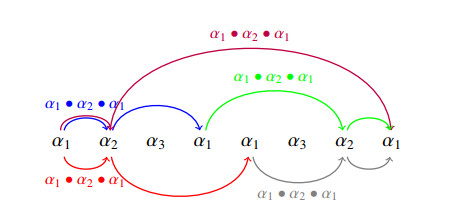
We can see the sub-permutations of any permutation from its contact map. Let $\alpha_1 = 1, \alpha_2 = 12, \alpha_3 = 123$ and $\alpha = \alpha_1\bullet\alpha_2\bullet\alpha_3\bullet\alpha_1\bullet\alpha_1\bullet\alpha_3\bullet\alpha_2\bullet\alpha_1\in S_{14}$. See Figure 1 for an illustration. In order to see the sub-permutations of a permutation clearly, we omit bullets $\bullet$ of the standardization factorization in the figures.

Given two permutations $\alpha$, $\beta$, the number of sub-permutations equal to $\beta$ in $\alpha$ is called the binomial coefficient ^[15,27] of $\beta$ in $\alpha$, denoted by $\left (\begin{array}{c} \alpha \\ \beta \end{array} \right).$ Notice that $\left (\begin{array}{c} \alpha \\ \epsilon \end{array} \right) = 1$ and $\left (\begin{array}{c} \alpha \\ \alpha \end{array} \right) = 1.$

Example 5. (1) Permutation $7564231 = {\rm st}(7) \bullet {\rm st}(56) \bullet {\rm st}(4) \bullet {\rm st}(23) \bullet {\rm st}(1) = 1 \bullet 12 \bullet 1 \bullet 12 \bullet 1$. Let $a_1 = 1$, $a_2 = 12$, then $7564231 = a_1 \bullet a_2 \bullet a_1\bullet a_2\bullet a_1$.

(2) The binomial coefficients also work on subwords of a word. For example,

From the above examples, for any permutations $\alpha$ and $\beta$, $\left (\begin{array}{c} \alpha \\ \beta \end{array} \right)$ is also a useful tool for determining whether $\beta$ is a sub-permutation of $\alpha$. If $\beta$ is not sub-permutation of $\alpha$, then $\left (\begin{array}{c} \alpha \\ \beta \end{array} \right) = 0$.

For a sub-permutation $\alpha$ of $\omega$, the remaining atoms of $\omega$ compose another sub-permutation $\beta$ (keeping the relative positions), denoted by $\beta = \omega\backslash\alpha$. Obviously, $|\alpha|+|\beta| = |\omega|$.

Thus, we define that $\left [\begin{array}{c} \omega \\ \alpha, \beta \end{array} \right]$ is the number of ways to chose $\alpha$ as a sub-permutation in $\omega$ with $\beta = \omega\backslash\alpha$. Then $\left [\begin{array}{c} \omega \\ \epsilon, \omega \end{array} \right]$ = $\left [\begin{array}{c} \omega \\ \omega, \epsilon \end{array} \right]$ = 1. Therefore, if $\omega\backslash\alpha\neq\beta$ or $|\alpha|+|\beta|\neq|\omega|$ then $\left [\begin{array}{c} \omega \\ \alpha, \beta \end{array} \right] = 0$.

Example 6. Let a permutation $\omega = a_1\bullet a_2\bullet a_2\bullet a_3\bullet a_2\bullet a_3$.

Hence, the draw coproduct $\Delta^*$ can be written as follows

Here $\left[\begin{array}{c} \omega \\ \alpha, \beta \\ \end{array} \right]$ is the coefficient of $\alpha \otimes \beta$ in $\Delta^*(\omega)$.

Example 7. We also can define draw coproduct $\Delta^*$ on words by binomial coefficients. For example,

From the definition of $\left [\begin{array}{c} \omega \\ \alpha, \beta \\ \end{array} \right]$, we can think it as a top-down calculation, that is, it counts the number of ways that the upper permutation $\omega$ can be divided into the lower two sub-permutations $\alpha$ and $\beta$ with $\beta = \omega\backslash\alpha$. We can also think it as a bottom-up calculation, that is, it counts the number of ways that the lower permutations $\alpha$ and $\beta$ compose the upper permutation $\omega$ with with $\beta = \omega\backslash\alpha$.

Therefore, the shuffle product ${\rm{III}}_G$ can be written as

for any permutations $\alpha$ and $\beta$ in $S$.

Similarly, for a subword $f$ of $\eta$, the remaining letters of $\eta$ compose another subword $g$ (keeping the relative positions), denoted by $g = \eta\backslash f$. Thus, we define that $\left[\begin{array}{c} \eta \\ f, g \\ \end{array} \right]$ is the number of ways to chose $f$ as a subword in $\eta$ with $g = \eta\backslash f$.

Then, Eq (2.2) can be rewritten as

Theorem 2. Hopf algebras $(KS, {\rm{III}}_G, \mu, \Delta, \nu)$ and $(KS, \diamond, \mu, \Delta^*, \nu)$ are dual to each.

Proof. According to the definition of dual Hopf algebras, we first prove the three conditions:

$1)\ < P\otimes Q, M\otimes N > = < P, M > < Q, N >$,

$2)\ < \mu(1), M > = \nu(M)$,

$3)\ < P, \mu(1) > = \nu(P)$.

Let $P$, $Q$ $\in$ $(KS, {\rm{III}}_G, \mu, \Delta, \nu)$, $M$, $N$ $\in$ $(KS, \diamond, \mu, \Delta^*, \nu)$. If $P = M$, $Q = N$, then $< P\otimes Q, M\otimes N > = < P, M > < Q, N > = 1$; if $P\neq Q$ or $Q\neq N$, then $< P\otimes Q, M\otimes N > = < P, M > < Q, N > = 0$.

If $M = \epsilon$, then $< \mu(1), \epsilon > = < \epsilon, \epsilon > = 1 = \nu(\epsilon)$; if $M\neq \epsilon$, then $< \epsilon, M > = 0 = \nu(M)$. Similarly, $< P, \mu(1) > = \nu(P)$.

Then we prove Conditions 4) and 5):

$4) < {\rm{III}}_G(P\otimes Q), M > = < P\otimes Q, \Delta^*(M) >$,

$5) < \Delta(P), M\otimes N > = < P, \diamond(M\otimes N) >$.

By Eqs (5.1) and (5.2), we have

When $M = W, \alpha = P, \beta = Q$, then

Thus Condition $4)$ is proved.

From Eq (3.2) and Example 2 we can notice that in the result of $\Delta(P)$ each term is different. That is to say the coefficient of each term of $\Delta(P)$ all is 1. Thus, when $P = M\bullet N$, we have $< \Delta (P), M\otimes N > = 1$; meanwhile, since $M\diamond N = P$, so $< P, \diamond(M\otimes N) > = 1$. That proves the Condition $5)$.

Here, we verified Conditions 4) and 5) by the example following.

Example 8. For permutations $P = 231$, $Q = 231$, $M = 564231$, then

Because

and

hence

And

then

6.   Conclusions

Let $A$ be a set called an alphabet and the elements in it are called letters. A finite sequence consisting of several letters is called a word over $A$. Denoted $A^*$ as the set of all such words with the empty word $\epsilon$. Thus, if we replace all atoms by letters in $A$ or all standard factorizations by words in $A^*$, then $(KA^*, {\rm{III}}_G, \mu, \Delta, \nu)$ and $(KA^*, \diamond, \mu, \Delta^*, \nu)$ are also dual graded Hopf algebras.

Furthermore, let $X = \{x_1, x_2, \ldots\}$. The set of polynomials on noncommutative variables $X$ equipped shuffle product ${\rm{III}}_G$ and deconcatenation coprodcut $\Delta$, concatenation product $\diamond$ and draw coprodcut $\Delta^*$, respectively, is a pair of dual graded Hopf algebras. In particular, when $X = \{x\}$, the corresponding dual graded graphs ^[18] are the chain and weighed chain ^[35]. When $X = \{x_1, x_2\}$, the corresponding dual graded graphs are the binary tree and the weighed binary tree ^[35]. Similarly, when $X = \{x_1, x_2, \ldots, x_n\}$, the corresponding dual graded graphs are the $n$-ary tree and weighted $n$-ary tree.

Similarly, if we use global ascents ^[36] instead of global descents of permutations and renumber atoms from left to right, then we obtain dual graded Hopf algebras $(KS, {\rm{III}}_G, \mu, \Delta, \nu)$ and $(KS, \diamond, \mu, \Delta^*, \nu)$.

In this paper we consider a pair of dual graded Hopf algebras. A graded Hopf algebra $H$ has a direct sum decomposition $H = \bigoplus_{i = 0}H_i$, where the degree of elements in $H_i$ is $i$, satisfying that the product of two elements of degree $p$ and degree $q$ is an element of degree $p+q$. If a bialgebra has a direct sum decomposition $H = \bigoplus_{i = 0}H_i$ but the product of two elements of degree $p$ and degree $q$ is not an element of degree $p+q$, then this biagebra is not graded. If we have a such bialgebra, we can study the following problems:

1. How to verify that a such bialgebra is a Hopf algebra or not?

2. If it is a Hopf algebra, how to figure out its antipode?

3. What is the duality of the bialgebra or Hopf algebra?

Acknowledgments

The authors would like to express sincere thanks to the reviewers for careful reading and suggestions which helped us to improve the paper. This work was supported by National Natural Science Foundation of China (Nos. 11701339, 12071265 and 11771256).

Conflict of interest

The authors declare there is no conflict of interests.