Crafting optimal cardiovascular treatment strategy in Pythagorean fuzzy dynamic settings

1.   Introduction

It is known to us all that tumor growth has attracted considerable attention over the past few decades. In order to study the importance of tumor growth and better understand the disease itself, it is critical to find a model that may help to treat the tumor. For this purpose, some basic relations between mathematical modeling and tumor model have been presented in ^[1]. With the diffusion process about cell and nutrient proliferation as a basis, many mathematical models ^{[2,3,4,5,6,7,8]} have been used to discuss these growth phenomena, such as the fractional mathematical model of tumor invasion and metastasis ^[2], tumor spheroid models ^[3,4], the androgen-deprivation prostate cancer treatment model ^[5], the foundations of cancer modeling ^[6] and hepatitis C evolution models ^[7,8].

In this paper, we will discuss the following reaction-diffusion model for cancer invasion ^[9,10]:

where $u(x, t), v(x, t)$ and $w(x, t)$ stand for dimensionless and rescaled versions of healthy tissue, tumor tissue and excess $H^+$ ions, respectively. The subscripts represent the partial derivatives relative to the corresponding variables. $a, b, c$ and $d$ are all constant functions. $a$ indicates the destructive effect of $H^+$ ions on the healthy tissue, $b$ is the productivity of neoplastic tissue which pumps $H^+$ ions at a rate $c$ and $d$ is displayed in the form $d = D_2/D_3$ where $D_2$ and $D_3$ are the diffusion coefficients of malignant tissue and $H^+$ ions, respectively. The phenomenon in many instances of tumor propagation of an interstitial gap has been discussed in ^[9]. Some wave propagation dynamics were considered in ^[11].

As everyone knows, the Lie group method plays an important role in studying the exact significant solutions of nonlinear partial differential equations ^{[12,13,14,15]}. The main aims of the symmetry method are to construct invariance conditions and obtain reductions to differential equations ^[16,17,18]. Once the reduced equations are given, a large number of corresponding exact solutions can be obtained. Utilizing Lie group analysis, we are going to get some fascinating special solutions of Eq (1.1) and identify the analysis stability behaviors of the model.

The remainder of the paper is arranged as follows. Symmetries of the acid-mediated cancer invasion model are analyzed in Section 2; Section 3 considers the symmetry reductions through the use of similar variables; in Section 4, some new explicit solutions are provided with help of the power-series method, and the convergence of the solutions of the power-series is presented; also, we will investigate the properties of different solutions via imaging analysis; the last section summarizes the results of the study.

2.   Lie point symmetry

In this paper, we demonstrate the Lie symmetry technique for Eq (1.1). First of all, let us think about a vector field of infinitesimal transformations of Eq (1.1) with the form

where $\xi, \tau, \phi, \varphi$ and $\eta$ are functions of $x, t, u, v, w$ respectively and are called infinitesimals of the symmetry group.

Based on the transformation (2.1), applying the invariance conditions to Eq (1.1), we get ^[16,19]

where $\mbox{pr}^{(i)}X, \; i = 1, 2$ is the $i$th-order prolongation of $X$ ^[16,19]. For Eq (1.1),

where

and $D_x$ and $D_t$ represent the total differential operators; for example,

Next, we get an overdetermined system of equations for $\xi, \tau, \phi, \varphi$ and $\eta$

Solving the above equations, one gets

where $c_1$ and $c_2$ are arbitrary constants. Therefore, Lie algebra $L_2$ of the transformations of Eq (1.1) is spanned by the following vector fields

To obtain the symmetry groups, we solve the initial problems of the following ordinary differential equations

then we get the one-parameter symmetry groups $G_i:(x, t, u, v, w)\rightarrow (\tilde{x}, \tilde{t}, \tilde{u}, \tilde{v}, \tilde{w})$ of the infinitesimal generators $X_i(i = 1, 2)$ as follows:

Based on the above discussion, we obtain the following theorem.

Theorem 2.1. If $u = f(x, t), \; v = g(x, t)$ and $w = h(x, t),$ constitute a solution of Eq (1.1), then by applying the above-mentioned groups $G_i(i = 1, 2)$, the corresponding new solutions $u_i, \; v_i, \; w_i\; (i = 1, 2)$ can be presented respectively as follows:

3.   Similarity reductions

In this section, we are going to cope with the similarity reductions of Eq (1.1).

Case 3.1. For the generator $X_1+X_2$, the invariants are $z = x-t, \; u = f(z), \; v = g(z)$ and $w = h(z)$, Eq (1.1) becomes

where $f' = \frac{df}{dz}, \; g' = \frac{dg}{dz}$ and $h' = \frac{dh}{dz}$.

Case 3.2. For the generator $X_1$, the invariants are $z = t, \; u = f(z), \; v = g(z)$ and $w = h(z)$, Eq (1.1) can be reduced to

where $f' = \frac{df}{dz}, \; g' = \frac{dg}{dz}$ and $h' = \frac{dh}{dz}$. The invariant solution of Eq (1.1) is as follows: $u(x, t) = f(t), \; v(x, t) = g(t), \; w(x, t) = h(t)$. Obviously, in this case, the variable $x$ has no effect on the solution of Eq (1.1).

Case 3.3. For the generator $X_2$, analogously, we have $z = x, \; u = f(z), \; v = g(z)$ and $w = h(z)$. The reduction of Eq (1.1) is

where $f' = \frac{df}{dz}, \; g' = \frac{dg}{dz}$ and $h' = \frac{dh}{dz}$. The invariant solution of Eq (1.1) is as follows: $u(x, t) = f(x), \; v(x, t) = g(x), \; w(x, t) = h(x)$. In this case, the variable $t$ has no effect on the solution of Eq (1.1).

4.   Power-series solutions

Next, by way of the power-series method which is a very useful technique for treating partial differential equations ^[20], we will discuss cases 3.1–3.3.

4.1.   Power-series solutions of Eq (3.1)

For Case $3.1$, we assume that the power-series solution to Eq (3.1) is as follows

where the coefficients $p_n, \; q_n$ and $l_n$ are constants to be resolved.

Putting Eq (4.1) into Eq (3.1), we obtain

Comparing the coefficients for Eq (4.2), we get

Generally, for $n\geq 1$, we have

Given Eq (4.4), the coefficients $p_i(i\geq2), q_j$ and $l_j(j\geq3)$ of (4.1) can be obtained, i.e.,

Therefore, for the arbitrary constants $p_0\neq1, q_0, l_0, q_1$ and $l_1$, the other terms of the sequences $\{p_n, q_n, l_n\}_{n = 0}^\infty$, according to Eqs (4.3) and (4.4), can be determined. This implies that there is a power-series solution, i.e., Eq (4.1) which has coefficients that are composed of Eqs (4.3) and (4.4).

Furthermore, for Eq (3.1), we confirm the convergence of Eq (4.1). In fact, from Eq (4.4), we get

where $M = \mbox{max}\{1, a\}, \; N = \mbox{max}\{|\frac{dp_1-1}{d(1-p_0)}|, |\frac{b}{d(1-p_0)}|, |\frac{1}{1-p_0}|\}$ and $L = \mbox{max}\{1, c\}$.

Next, we construct three power-series $R = R(z) = \sum_{n = 0}^\infty r_nz^n,$ $S = S(z) = \sum_{n = 0}^\infty s_nz^n$ and $T = T(z) = \sum_{n = 0}^\infty t_nz^n$ by using

and

where $n = 1, 2, \cdots.$ It is easily seen that

Therefore, $R = R(z) = \sum_{n = 0}^\infty r_nz^n,$ $S = S(z) = \sum_{n = 0}^\infty s_nz^n$ and $T = T(z) = \sum_{n = 0}^\infty t_nz^n$ are majorant series of Eq (4.1) respectively. Next, we prove that $R = R(z), \; S = S(z)$ and $T = T(z)$ have a positive radius of convergence.

and

Then, we discuss the implicit functional system with the independent variable $z$:

Based on the implicit function theorem ^[21], because $F_1, F_2$ and $F_3$ are analytic in the neighborhood of $(0, r_0, s_0, t_0)$ and $F_1(0, r_0, s_0, t_0) = F_2(0, r_0, s_0, t_0) = F_3(0, r_0, s_0, t_0) = 0$, and given the Jacobian determinant

we reach that $R = R(z), \; S = S(z)$ and $T = T(z)$ are analytic in a neighborhood of the point $(0, r_0, s_0, t_0)$ and have a positive radius. This shows that Eq (4.1) converges in a neighborhood of the point $(0, r_0, s_0, t_0)$. The proof is completed.

Thus the power-series solution given by Eq (4.1) for Eq (3.1) is analytic and can be described as

Moreover, the power-series solution of Eq (1.1) is

where $p_0\neq1, q_0, l_0, q_1$ and $l_1$ are arbitrary constants; the other terms $p_n, q_n$ and $l_n\; (n\geq2)$ can be provided according to Eqs (4.3) and (4.4).

4.2.   Numerical simulation of power-series solutions of Eq (3.1)

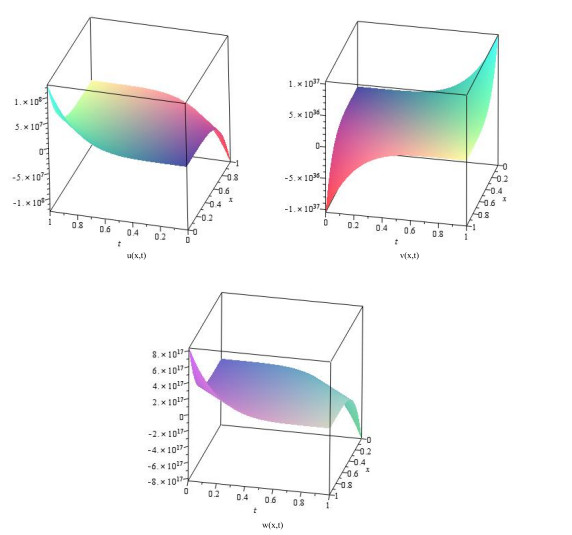
We take the first six terms of Eq (4.5) as approximate to $u, v$ and $w$ for $a = 1.5, \; b = 1, \; c = 2, \; d = 4\times10^{-10}, \; p_0 = 0.5, \; q_0 = 3, \; l_0 = 5, \; q_1 = 4$ and $l_1 = 6$. Then the approximation is depicted in Figure 1.

Figure 1 shows that the values of $u, v$ and $w$ tend to be stable when $x\in(0, 1)$ and $t\in(0, 1)$. However, when $x\rightarrow0$ and $t\rightarrow1$ or $x\rightarrow1$ and $t\rightarrow0$, $u$ and $w$ change suddenly in one direction and $v$ changes sharply in the other direction. The rate of change of $v$ is faster than that of $u$, and that of $w$ is between them. This shows that healthy tissue may be destroyed before malignant cells arrive. Tumor progression is mediated by the acidification of surrounding tissues. Due to anaerobic glycolysis and metabolism, tumor cells produce excessive $H^+$ ions. This leads to local acidification, which then destroys the surrounding healthy tissue and promotes tumor invasion.

4.3.   Power-series solutions of Eq (3.2)

For Case $3.2$, similarly, we can also obtain the following power-series solution to Eq (1.1):

where $p_0, q_0$ and $l_0$ are arbitrary constants.

4.4.   Numerical simulation of Power-series solutions of Eq (3.2)

We get the first six terms of the power-series solutions of (4.6) as approximate to $u, v$ and $w$ for $a = 1.5, \; b = 1, \; c = 2, \; d = 4\times10^{-10}, \; p_0 = 0.5, \; q_0 = 3$ and $l_0 = 5$ respectively, then, the approximations of $u, v$ and $w$ are illustrated in Figure 2.

Figure 2 illustrates that, when $t\in(0, 1)$, the values of $u, v$ and $w$ are stable first and mutate over time. When $u$ and $v$ decrease at the same time, $w$ increases. The rate of change of $u$ is the same as that of $v$, and the rate of change of $w$ is slightly slower than them. This indicates that when healthy cells and cancer cells decrease at the same time, $H^+$ ions will increase. We find that $H^+$ ions are sensitive to changes in healthy cells and cancer cells.

4.5.   Power-series solutions of Eq (3.3)

For Case $3.3$, the power-series solution to Eq (1.1) is described as follows:

where $p_0, l_0, q_0, q_1$ and $l_1$ are arbitrary constants and that satisfy $1-2p_0-al_0\neq0$ and $1-p_0\neq0$.

4.6.   Numerical simulation of power-series solutions of Eq (3.3)

We acquire the first six terms of the power-series solutions of Eq (4.7) as approximate to $u, v$ and $w$ for $a = 0.1, \; b = 1, \; c = 2, \; d = 4\times10^{-10}, \; p_0 = 0.5, \; q_0 = 3, \; l_0 = 5, \; q_1 = 4$ and $l_1 = 6$ respectively; then, the approximations of $u, v$ and $w$ are portrayed in Figure 3.

Figure 3 shows that, when $x\in(0, 1)$, the values of $u, v$ and $w$ are initially stable and mutate in the same direction. The rate of change of $v$ is the fastest, and the rates of change of $u$ and $w$ are basically the same. It describes that cancer cells decline faster than healthy cells. This shows a process of complete destruction of healthy tissue after tumor tissue invasion.

Remark 4.1. For Case $3.2$ and Case $3.3$, the proofs of convergence of the power series solutions are similar to that for Case $3.1$. The details have been omitted here.

5.   Conclusions

In this study, we applied the Lie group analysis method to an acid-mediated cancer invasion model. An important feature of this model is that tumor progression is mediated by acidification of the surrounding tissue. Especially, the model presumes that an excess of $H^+$ ions is produced by tumor cells as a consequence of their anaerobic, glycolytic metabolism. Based on this method, the symmetries and reduced equations of Eq (1.1) were derived. Furthermore, explicit solutions of the reduced equations were obtained using the power-series method. Finally, this paper also demonstrates the stability behavior of the model for different parameters as achieved through the use of graphical analysis. In this way, we have found that $H^+$ is decreased ahead of the advancing tumor front. Moreover, for certain parameter values, healthy tissue could be destroyed prior to the arrival of malignant cells. In the future, we can use this method to solve more tumor-related mathematical problems.

Acknowledgments

This research was supported by the Natural Science Foundation of Shanxi (No. 202103021224068).

Conflict of interest

The authors declare that they have no competing interests.