1.
Introduction
Singularity theory (ST) is commonly discussed in physics and mathematics for analyzing curves and surfaces. Differential geometry locates curves and surfaces using functions with one and two parameters, respectively. Recently, ST has been widely used in fields such as medical imaging and computer vision (see, e.g., [1,2,3,4]).
A swept surface SS is constructed by moving a planar curve (generatrix) through space with the movement of the plane orthogonal to it. Sweeping along a line is an accurate method in geometric modeling, often involving sweeping over a spine curve (SC) (path). The significance of this evolution, which depends on the movement through space and the intrinsic deformation of shape, lies in the concept of a swept theme. The type of swept surface is determined by the choice of the generatrix and the path. For example, rotating one curve over another creates a swept surface. Various types of swept surfaces include tubular surfaces, pipe surfaces, strings, and canal surfaces [5,6]. The geometry of SS can be described employing the Serret-Frenet frame (SFF) of space curves, an orthonormal frame that is related in some studies to eigenvalue problems [7,8]. Xu et al. [9] identified the geometric attributes required for canal surfaces as a type of SS. They also derived conditions to avoid local self-intersection in canal surfaces and formulated expressions for their area and Gaussian curvature. Izumiya et al. [10] studied conformable circular surfaces along with traditional ruled surfaces. Ro and Yoon [11] studied tubes in Euclidean 3-space, deriving expressions for Gaussian curvature, mean curvature, and second Gaussian curvature. Cui et al. [12] explored the kinematic geometry of circular surfaces with fixed radii based on Euclidean invariants.
However, the SFF is not applicable to every point on a curve. A novel frame is needed for certain types of mathematical analyses, particularly those done via computer graphics. Bishop et al. [13] developed a novel moving frame along a space curve, allowing for movement along the curve using parallel vector fields. This is known as the Bishop frame (BF) or rotation minimizing frame (RMF). The BF has been successfully applied in fields such as biology, where it can model the shape of DNA sequences by employing curves defined by the BF. The BF can also be employed to track to the positioning of cameras in computer animations [14,15]. Recently, numerous descriptions of SS and developable surfaces have been acquired using the BF [16,17,18,19]. Various methods have been used to generate new curves in different spaces, as described in [20,21,22,23,24,25,26].
However, to the best of our knowledge, no existing literature discusses the singularities of SS with a conjugate mate curve using the Type-2 BF. Then, utilizing the BF, we classify generic models and introduce a novel invariant associated with the singularities of the SS. The main generic singularities of these SS are the well-known cuspidal edge and swallowtail, which are illustrated by this novel invariant. We use traditional and established outcomes in ST to demonstrate our major outcomes in this paper. In addition, this paper establishes the necessary and adequate situations for when the SS with conjugate mate curve is a developable ruled surface (DRS) and discusses further epilogues. Regarding the DRS, we inspected the ST of the DRS. Finally, to highlight the major outcomes, two examples are presented and analyzed in detail. It is worth noting that Mathematica was used to generate figures in this study.
2.
Preliminaries
The ambient space considered in this article is the Euclidean 3-space E3, with generic references taken from [5,6]. Let γ(s) be a unit speed curve with the SF systems denoted as {κ(s), τ(s), t(s), p(s), b(s)} in E3. Then, γ(s) is termed an SF curve if κ>0, and τ≠0. So, we obtain
where t=γ′(s), p(s)=γ′′(s)/‖γ′′(s)‖, and b(s)=t×p are the unit tangent vector, the principal normal vector, and the binormal vector, respectively.
Lemma 2.1. Given the above notation, there exists a unit speed conjugate mate curve β(s)=∫b(s)ds. The pair {γ(s), β(s)} is referred to as a conjugate couple [27].
The Type-2 BF of γ(s) is defined as [18]:
where
We find that {b,ξ1, ξ2} is a Type-2 BF. The relation matrix can be expressed as:
The frame {b,ξ1, ξ2} has a Darboux vector ω(s)=−ϵ2(s)ξ1(s)+ϵ1(s)ξ2(s). The Bishop spherical Darboux indicatrix is:
Thus, we introduce a new geometric invariant σ(s)=ϵ1ϵ′2−ϵ2ϵ′1.
A surface M can be expressed as follows:
The unit vector normal is defined by ζ(s,u)=ys×yu‖ys×yu‖−1, where yi=yy∂i. A RS in E3 is given by:
where α(s) is the base (directrix) curve, and ξ(s) is the director curve. The straight lines s→α(s)+uξ(s) are called rulings. It is well known that D(s,u) is a DRS iff det(α′,ξ,ξ′)=0.
3.
Swept surfaces due to Type-2 BF
This section presents the representation of SS using the Type-2 BF along the spine curve β(s) as follows: The SS related with β(s) corresponds to a one-parameter set of unit spheres centered at β(s). It is simple to find that the intersection between the spheres from the set and the SS forms a great circle on the unit sphere within the subspace Sp{ξ1, ξ2}, of β(s). Let y be the location connecting a point on the curve β(s) with a point on the surface. Then,
where the unit vector r∈Sp{ξ1, ξ2}. Let the angle u be the angle from r to ζ1. Thus, we write:
which is the distinctive circles of SS. By combining the last two equations, we obtain the parameterization of the SS,
This representation of M excludes SS with a constant vector ζ, as its geometric assets are not particularly remarkable and are relatively easy to examine.
Remark 3.1. Perspicuously, if β(s) is a line, then the SS is a circular cylinder with β(s) as the symmetry axis. However, if β(s) is a circle, then SS forms a torus.
We now examine the relationship between the regularity of β(s) and the associated SS. Then,
Then,
It can be seen from Eq (3.3) that ζ(s,u) lies in the osculating plane of the curve γ(s), where <ζ,b>=0. Thus, the normal of the profile curve q(u)=(0, cosu sinu)T and the surface normal ζ(s,u) are identical.
Proposition 3.1. Let q be a point in the osculating plane of the SC γ(s). The tangent vector of its trajectory γ(s)+A(s)q(u), created by the Type-2 BF, is permanently parallel to t.
The main aim of this article is to establish the following theorem: Note that (LD) refers to locally diffeomorphic.
Theorem 3.1. Under the above conditions, with ϵ21+ϵ22≠0. We have:
A- (1) d(s) is LD to a line {0}×R at s0 iff σ(s0)≠0;
(2) d(s) is LD to the cusp C×R at s0 iff σ(s0)=0, and σ′(s0)≠0.
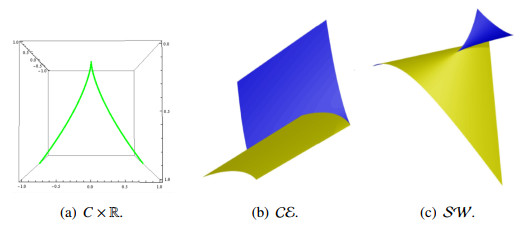
B- (1) M is LD to the cuspidal edge (CE) at (s0,u0) iff x=±d(s0), and σ(s0)≠0;
(2) M is LD to the swallowtail (SW) at (s0,u0) iff x=±d(s0), σ(s0)=0, and σ′(s0)=0.
Here, C×R={(x1,x2)∣x21=x32}×R, CE={(x1,x2,x3)∣x1 = u, x2 = v2, x3 = v3}, and SW={(x1,x2,x3)∣x1=u, x2=3v2+uv2, x3=4v3+2uv} (See Figure 1).
3.1. Bishop height functions
Now, we will identify two families of Bishop height functions that will be useful in characterizing the singularities of M as follows [1,2,3]: χ:I×S2→R, by χ(s,x)=<β(s),x>. We refer to this as the Bishop height function. We denote χx(s)=χ(s,x) for any stationary unit vector x∈S2. Additionally, we define ˜χ:I×S2×R→R, by ˜χ(s,x,w)=<β,d>−w. This is called the extended Bishop height function of β(s). We denote ˜χx(s)=˜χ(s,x,w).
Proposition 3.2. Let β(s) be a conjugate mate curve with ϵ21+ϵ22≠0. Then:
(A)
(1)- χ′x(s)=0 iff x=a1ξ1+a2ξ2, and a21+a22=1;
(2)- χ′x(s)=χ′′x(s)=0 iff x=±d(s);
(3)- χ′x(s)=χ′′x(s)=χ′′′x(s)=0 iff x=±d(s), and σ(s)=0;
(4)- χ′x(s)=χ′′x(s)=χ′′′x(s)=χ(4)x(s)=0 iff x=±d(s), and σ(s)=σ′(s)=0;
(5)- χ′x(s)=χ′′x(s)=χ′′′x(s)=χ(4)x(s)=χ(5)x(s)=0 iff x=±d(s), and σ(s)=σ′(s)=σ′′(s)=0.
(B)
(1)- ˜χx(s)=0 iff there exist <β,x>=w;
(2)- ˜χx(s)=˜χ′x(s)=0 iff there exist a1, a2∈R such that x=cosuξ1+sinuβ2, and <β,x>=w;
(3)- ˜χx(s)=˜χ′x(s)=˜χ′′x(s)=˜χ′′x(s)=0 iff x=±d(s), <β,x>=w, and σ(s)=0;
(4)- ˜χx(s)=˜χ′x(s)=˜χ′′x(s)=˜χ′′x(s)=˜χ′′′x(s)=0 iff x=±d(s), <β,x>=w, and σ(s)=σ′(s)=0;
(5)- ˜χx(s)=˜χ′x(s)=˜χ′′x(s)=˜χ′′x(s)=˜χ′′′x(s)=˜χ(4)x(s)=0 iff x=±d(s), <β,x>=w and σ(s)=σ′(s)=σ′′(s)=0;
(6)- ˜χx(s)=˜χ′x(s)=˜χ′′x(s)=˜χ′′x(s)=˜χ′′′x(s)=˜χ(4)x(s)=˜χ(5)x(s)=0 iff x=±d(s), <β,x>=w, and σ(s)=σ′(s)=σ′′(s)=σ′′′(s)=0.
Proof. From Eq (2.2), we have ‖b′‖2≠0 iff ϵ21+ϵ22≠0.
(A). (1)- Since χ′x(s)=<b,x>=0, and {b,ξ1, ξ2} is an orthonormal frame along β(s), there exist a1, a2∈R such that x=a1ξ1+a2ξ2. Given that x∈S2, we get a21+a22=1. The converse is also holds.
(2)- Since χ′′x(s)=<b′,x>=<ϵ1ξ1−ϵ2ξ2,x>=0, we have a1ϵ1−a2ϵ2=0. Given that a21+a22=1 that a1=±ϵ2/√ϵ21+ϵ22, and a2=∓ϵ1/√ϵ21+ϵ22.
Therefore, we have:
Therefore, χ′x(s)=χ′′x(s)=0 iff x=±d(s).
(3)- Since χ′′′x(s)=<b′′,x>=<−(ϵ21+ϵ22)b+ϵ′1ξ1−ϵ′2ξ2,x>=0
Thus, χ′x(s)=χ′′x(s)=χ′′′x(s)=0 iff x=±d(s), and σ(s)=0.
(4)- Since
by the conditions in (3), we have:
Thus, χ′x(s)=χ′′x(s)=χ′′′x(s)=χ(4)x(s)=0 iff x=±d(s), and σ(s)=σ′(s)=0.
(5)- Since χ(5)x(s)=<b(4),x>0, we have:
By using the conditions in (4), we have:
Therefore, χ′x(s)=χ′′x(s)=χ′′′x(s)=χ(4)x(s)=χ(5)x=0 iff x=±d(s), and σ(s)=σ′(s)=σ′′(s)=0.
(B). Using a similar calculation as in the proof of (A), we can get (B) (1). □
From now on, we shall often omit the parameter s.
Proposition 3.3. Let β(s) be a conjugate mate curve with ϵ1(s)≠0. Then, we have σ(s)=0 iff
is a constant vector.
Proof. Suppose that ϵ1≠0. Then, we have:
Thus, d′(s)=0 iff σ(s)=0. □
We can also state the following propositions.
Proposition 3.4. Let β(s) be a conjugate mate curve with ϵ1(s)≠0, and σ(s)=(ϵ2/ϵ1)′=0. Then,
(a) ξ1 lies on a circle on S2 centered at the constant vector d0.
(b) ξ2 lies on a circle on S2 centered at the constant vector d0.
Proof. (a) Suppose that ϵ1≠0, and σ(s)=(ϵ2/ϵ1)′=0. Since
we find that
This shows that ξ2 lies on a circle on S2 centered at the constant vector d0.
(b) Suppose that ϵ1>0. By a similar computation, we find that
is constant. This means that the second Bishop spherical indicatrix, lies on a circle on S2 centered at the constant vector d0. □
3.2. Unfolding of functions by one-variable
We employed significant results from the singularity theory for families of function germs [1,2,3]. Let G: (R×Rr,(s0,x0))→R be a differentiable function, and let g(s)=Gx0(s,x0). Then, G is called an r-parameter unfolding of g(s). We say that g(s) has Ak-singularity at s0 if g(p)(s0)=0 for all 1≤p≤k, and g(k+1)(s0)≠0. We also consider that g has A⩾- \sin gularity ( \mathfrak{k}\geqslant 1 ) at \mathfrak{s}_{0} . Let the \left(\mathfrak{k}-1\right) -jet of the partial derivative \frac{\partial \mathcal{F}}{\partial x_{i}} at \mathfrak{s}_{0} be \mathfrak{j}^{\left(\mathfrak{k}-1\right) }\left(\frac{\partial \mathcal{G}}{\partial x_{i}}\left(\mathfrak{s}, {\mathbf{x}} _{0}\right) \right) \left(\mathfrak{s}_{0}\right) = \Sigma _{\mathfrak{j} = 0}^{\mathfrak{k}-1}\mathcal{L}_{ji}\left(\mathfrak{s}-\mathfrak{s} _{0}\right) ^{\mathfrak{j}} (excluding the constant term), for \mathfrak{i} = 1, ..., \mathfrak{r} . Then \mathcal{G}(\mathfrak{s}) is called an \mathfrak{p} -versal unfolding ( {VU} ) if the \mathfrak{k} \times \mathfrak{r} matrix of coefficients \left(\mathcal{L}_{ji}\right) has rank \mathfrak{k} \left(\mathfrak{k}\leq \mathfrak{r}\right) . Next, we define useful sets related to the unfolding with the above notations. The discriminant set of \mathcal{G} is the set
The bifurcation set of \mathcal{G} is the set
Then, similar to the results of [1,2,3], we state the following theorem.
Theorem 3.2. Let \mathcal{G} : \left(\mathbb{R}\times { \mathbb{R} ^{\mathfrak{r}}}, (\mathfrak{s}_{0}, {\mathbf{x}}_{0})\right) \rightarrow \mathbb{R} be an \mathfrak{r} -parameter unfolding of \mathcal{G}(\mathfrak{s}) , which has the \mathcal{A}_{\mathfrak{k}} singularity at \mathfrak{s}_{0} .
Suppose that \mathcal{G} is a \mathfrak{p} -versal unfolding.
(a) If \mathfrak{k} = 1 , then \mathfrak{D}_{\mathcal{G}} is {LD} to \{{{\mathbf 0}\}\times }\mathbb{R}^{\mathfrak{r}-1} , and \mathfrak{B}_{ \mathcal{G}} = \varnothing ;
(b) If \mathfrak{k} = 2 , then \mathfrak{D}_{\mathcal{G}} is {LD} to C{ \times }\mathbb{R}^{\mathfrak{r}-2} , and \mathfrak{B}_{ \mathcal{G}} is \mathcal{D} to \{{{\mathbf 0}\}\times }\mathbb{R}^{ \mathfrak{r}-1} ;
(c) If \mathfrak{k} = 3 , then \mathfrak{D}_{\mathcal{G}} is {LD} to {SW}{ \times }\mathbb{R}^{\mathfrak{r}-3} , and \mathfrak{ B}_{\mathcal{G}} is \mathcal{D} to C{ \times }\mathbb{R}^{ \mathfrak{r}-2} .
Hence, we have the following main proposition.
Proposition 3.5. Let {\mathbf{\beta }}(\mathfrak{s}) be a conjugate mate curve with \epsilon _{1}^{2}+\epsilon _{2}^{2}\neq 0 . (1). If \chi _{ {\mathbf{x}}}(\mathfrak{s}) = \chi (\mathfrak{s}, {\mathbf{x}}) has an \mathcal{A} _{\mathfrak{k}} -singularity ( \mathfrak{k} = 2, \ 3) at \mathfrak{s} _{0}\in \mathbb{ \mathbb{R} } , then \chi is a \mathfrak{p}-{VU} of \chi _{{\mathbf{x}}_{0}}(\mathfrak{s}_{0}) . (2). If \widetilde{\chi }_{{\mathbf{x}}}(\mathfrak{s}) = \widetilde{\chi }(\mathfrak{s}, {\mathbf{x}}, w) has an \mathcal{A}_{\mathfrak{ k}} -singularity ( \mathfrak{k} = 2, 3) at \mathfrak{s}_{0}\in \mathbb{ \mathbb{R} } , then \widetilde{\chi } is a \mathfrak{p}-{VU} of \widetilde{ \chi }_{{\mathbf{x}}_{0}}(\mathfrak{s}_{0})
Proof. (1) Since {\mathbf{x = }}\left(x_{0}{\mathbf, } x_{1}, x_{2}\right) \in \mathcal{S}^{2} , x_{0}^{2}+x_{1}^{2}+x_{2}^{2} = 1, \ x_{0}{\mathbf, } x_{1}, and x_{2} cannot be all zero. Suppose that x_{2}\neq 0 . Then, by x_{2} = \pm \sqrt{1-x_{0}^{2}-x_{1}^{2}} , we have that
Thus, we have:
Therefore, the 2-jets of \frac{\partial \chi }{\partial x_{i}} at \mathfrak{s}_{0} (i = 0, 1) are as follows: Let {\mathbf{x}}_{0}{\mathbf = }\left(x_{00} {\mathbf, }x_{10}, x_{20}\right) \in \mathcal{S}^{2} , and assume that x_{20}\neq 0 , then
and
(ⅰ) If \chi _{{\mathbf{x}}_{0}}(\mathfrak{s}_{0}) has the \mathcal{A}_{2} -singularity at \mathfrak{s}_{0} , then \chi _{{\mathbf{x}}_{0}}^{^{\prime }}(\mathfrak{s}_{0}) = 0 . So, the 1\times 2 matrix of coefficients \left(\mathcal{L}_{ji}\right) is:
Suppose that rank( \mathcal{A} ) = 0, then we have:
Since \left\Vert {\mathbf{\beta }}^{^{\prime }}(\mathfrak{s}_{0})\right\Vert = \left\Vert {\mathbf{b}}(\mathfrak{s}_{0})\right\Vert = 1 , we have \beta _{2}^{^{\prime }}(\mathfrak{s}_{0})\neq 0 , leading to the following contradiction:
Therefor, rank( \mathcal{A}) = 1 , and \chi is the ( \mathfrak{p} ) { VU} of \chi _{{\mathbf{x}}_{0}} at s_{0} .
(ⅱ) If \chi _{{\mathbf{x}}_{0}}(\mathfrak{s}_{0}) has the \mathcal{A}_{3} -singularity at \mathfrak{s}_{0}\in \mathbb{ \mathbb{R} } , then \chi _{{\mathbf{x}}_{0}}^{^{\prime }}(\mathfrak{s}_{0}) = \chi _{ {\mathbf{x}}_{0}}^{^{\prime \prime }}(\mathfrak{s}_{0}) = 0 , and by Proposition 3.2:
where \epsilon _{1} > 0 , \sigma ^{^{\prime }}(\mathfrak{s}_{0}) = 0 , and \sigma ^{^{\prime \prime }}(\mathfrak{s}_{0})\neq 0 . Note that x_{20} = \pm \sqrt{1-x_{0}^{2}-x_{1}^{2}} \ It is sufficient to have rank( \mathcal{B} ) = 2, where
Then, the determinant of this matrix at \mathfrak{s}_{0} is
Since {\mathbf{\beta }}^{^{\prime }} = {\mathbf{b}} , we have {\mathbf{\beta }} ^{^{\prime \prime }} = \epsilon _{1}{\mathbf{\xi }}_{1}{\mathbf -}\epsilon _{2} {\mathbf{\xi }}_{2} . Substituting these into the equations, we get
This means that rank (\mathcal{B}) = 2 .
(2) Under the same notations as in (1), we have
We require the 2\times 3 matrix \mathcal{D} to have the maximal rank, where
By case (1) in Eq. (3.10), the second row of \mathcal{D} does not vanish, so rank (\mathcal{D}) = 2 . □
Proof of Theorem 3.1. (1) By Proposition 3.2, the bifurcation set of \chi (\mathfrak{s}, {\mathbf{x}}) is
The assertion (1) of Theorem 3.1 follows from Propositions 3.2 and 3.5, and Theorem 3.2.
The discriminant set of \widetilde{\chi }(\mathfrak{s}, {\mathbf{x}}) is specified as follows:
The assertion (2) of Theorem 3.1 follows from Propositions 3.2 and 3.5, and Theorem 3.2. □
Example 3.1. Let {\mathbf \gamma }(\mathfrak{s}) be
Then,
From \kappa (\mathfrak{s}) = \frac{1}{2} , we find \psi (\mathfrak{s}) = \frac{ \mathfrak{s}}{2} . The transformation matrix is:
Hence, we have
Hence, the geometric invariant \sigma (\mathfrak{s}) = \frac{1}{8}\neq 0 . The swept surface is (Figure 2)
The Bishop spherical Darboux indicatrix is (Figure 3)
3.3. Developable surfaces
In the following, we resolve the issue where {\mathbf q(}u) disintegrates into a line. Then, we have the following:
which defines a {DRS} . Similarly, another {DRS} can be defined as:
It is clear that {\mathbf P}(\mathfrak{s}, 0) = {\mathbf{\beta }}(\mathfrak{s}) (resp. {\mathbf P}^{\bot }(\mathfrak{s}, 0) = {\mathbf{\beta }}(\mathfrak{s}) ), 0\leq \mathfrak{s}\leq L , meaning that the surface \mathbb{D} (resp. \mathbb{ D}^{\bot } ) intersects the curve {\mathbf{\beta }}(\mathfrak{s}) . We can effortlessly have:
and
Thus, \mathbb{D} (resp. \mathbb{D}^{\bot } ) is non-singular at (\mathfrak{s}_{0}, u_{0}) if and only if 1+u_{0}\epsilon _{2}(\mathfrak{ s}_{0})\neq 0 (resp. \left(1-u_{0}\epsilon _{1}(s_{0})\neq 0\right) . Under these conditions, the singularities of the {DRS } \mathbb{D} (resp. \mathbb{D}^{\bot } ) can be identified by employing \epsilon _{2} (resp. \epsilon _{1} ).
Theorem 3.3. Let \mathbb{D} be the {DRS} defined by Eq (3.14). Then:
(1) \mathbb{D} is {LD} to {CE} at (\mathfrak{s} _{0}, u_{0}) iff \epsilon _{2}(\mathfrak{s}_{0}) = 0 , and \epsilon _{2}^{^{\prime }}(\mathfrak{s}_{0})\neq 0 ;
(2) \mathbb{D} is {LD} to {SW} at (\mathfrak{s} _{0}, u_{0}) iff \epsilon _{2}(\mathfrak{s}_{0})\neq 0 , and \frac{ \epsilon _{2}^{^{\prime }}(\mathfrak{s}_{0})}{\epsilon _{2}^{2}(\mathfrak{s} _{0})}\neq 0 .
Proof. If there exists a parameter \mathfrak{s}_{0} such that \epsilon _{2}(\mathfrak{s}_{0}) = 0 , and u_{0}^{^{\prime }} = \frac{\epsilon _{2}^{^{\prime }}(\mathfrak{s}_{0})}{\epsilon _{2}^{2}(\mathfrak{s}_{0})} \neq 0 ( \epsilon _{2}^{^{\prime }}(\mathfrak{s}_{0})\neq 0 ), then \mathbb{D} is {LD} to {CE} at (\mathfrak{s}_{0}, u_{0}) Thus, assertion (1) holds. Also, if there exists a parameter \mathfrak{s} _{0} such that u_{0} = -\frac{1}{\epsilon _{2}(\mathfrak{s}_{0})}\neq 0 , u_{0}^{^{\prime }} = \frac{\epsilon _{2}^{^{\prime }}(\mathfrak{s}_{0})}{ \epsilon _{2}^{2}(\mathfrak{s}_{0})} = 0 , and \left(\frac{1}{\epsilon _{2}(\mathfrak{s}_{0})}\right) ^{^{^{\prime \prime }}}\neq 0 , then \mathbb{D} is LD to {SW} at (\mathfrak{s}_{0}, u_{0}) . Assertion (2) holds. □
Example 3.2. Using the data from Example 3.1, we have the following:
(1). The equation of \ \mathbb{D} and its singular locus \mathfrak{C}(\mathfrak{s}) are:
and
(2). The equation of \mathbb{D}^{\bot } and its singular locus \mathfrak{C }^{\bot }(\mathfrak{s}) , respectively, are:
and
We address a local part of {\mathbf{\beta }}(\mathfrak{s}) as follows: We see that \epsilon _{1}^{^{\prime }}(\mathfrak{s}) = -\frac{1}{2}\sin \frac{ \mathfrak{s}}{2}\neq 0 for \mathfrak{s} = \pm \pi . This shows that the {DRS} \mathbb{D} is {LD} to a {CE} , and its singular locus \mathfrak{C}(\mathfrak{s}) is {LD} to a line (the red lines); see Figure 4. Moreover, the equation \epsilon _{2}^{^{\prime }}(\mathfrak{s}) = \frac{1}{2}\cos \frac{s}{2} = 0 gives two roots \mathfrak{s} = \pm \pi . We can also get that \epsilon _{2}^{^{^{\prime \prime }}}(\pm \pi /2) = \mp \frac{1}{4}\neq 0 . This shows that the {DRS} \mathbb{ D}^{\bot } is {LD} to an {SW} and its singular locus \mathfrak{C}^{\bot }(\mathfrak{s}) is {LD} to a line (the red lines) at \mathfrak{s} = \pm \pi ; see Figure 5. Notice that \mathbb{D} and \mathbb{D}^{\bot } intersect along the curve {\mathbf{\beta }}(\mathfrak{s}) at \pi /2 , as shown in Figure 6.
4.
Conclusions
This study focused on researching a special type of tube surface, known as the swept surface, in Euclidean 3-space. It was created by a plane curve moving through a conjugate curve of a spatial curve such that the motion of any point on the surface remained orthogonal to the plane. We then attained the adequate and essential situations for this swept surface to be a {DRS} . Afterwards, the issue of singularity in a DRS was inspected. We also interpreted our main outcomes by giving some representative examples.
Author contributions
Fatemah Mofarreh: Conceptualization, investigation, methodology, and writing—original draft. Rashad A. Abdel-Baky: Investigation, methodology, writing—review, and editing. All authors have read and approved the final version of the manuscript for publication.
Acknowledgments
The authors thank the anonymous reviewers for their careful reading of the manuscript and their many insightful comments and suggestions.
Funding
This research was funded by the Princess Nourah bint Abdulrahman University Researchers Supporting Project (PNURSP2024R27), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of interest
The author declares that there is no conflict of interest.









 DownLoad:
DownLoad:








