1.
Background
Controlled blasting has been used (1) as ground improvement technique to densify loose, saturated granular soils (e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14]), (2) to physically model liquefaction for large full-scale testing (e.g., [6,15,16,17,18,19,20,21,22]), and (3) to evaluate the effects of liquefaction on deep foundation performance (e.g., [23,24,25,26,27]). Controlled blasting can be performed on the ground surface and/or underground. For underground blasting, the energy generated from the explosion is typically considered as the key parameter that is required to induce liquefaction. Specifically, explosive charges create a blast wave that propagates through the soil, and generate enough excess porewater pressure to liquefy the target soil material. The dissipation of the generated blast-induced porewater pressures causes the liquefied soil material to compress or consolidate following blasting. As reported by Narin van Court and Mitchell [7], for liquefaction to occur, the amount of energy generated from blasting must exceed the amount of energy required to resist soil liquefaction. This amount of required energy is not only a function of explosive weight, but also a function of the blasting geometry, the type of explosive, used the charge spacing, the detonation time, the soil characteristics, and the wave attenuation from the blasts.
Several laboratory and in-situ techniques have been previously performed, and various empirical models have been developed to evaluate soil liquefaction potential based on the blast-induced porewater pressure responses [13,15,16,18,19,21,25,27,28,29,30,31,32,33,34]. However, many of the methods that have been developed are only applicable for relatively loose sands at shallow depth, and do not take into account the in-situ soil properties such as: relative density, grain size distribution, permeability, and overburden effective stress. In addition, some of these methods are only applicable for certain types of soils (e.g., clean sands and silty sands).
1.1. Predicting excess porewater pressure ratio
The standard of practice that is currently used for controlled blasting testing relies upon using existing empirical models. Several empirical models have been developed from single and/or multiple denotations to predict the excess pore water pressure (Ru) as a function of peak particle velocity (PPV), peak compression strain (εp), scaled distance (SD), and in-situ soil properties [17,25,32,35,36,37,38,39,40]. These empirical equations are summarized in Table 1. The Studer and Kok [36] approach (Eq 2 in Table 1) has been commonly used to develop most of the existing empirical methods to predict the amount of excess porewater pressure. The Studer and Kok [36] relationship was originally developed by considering a single blast in saturated sandy soils. By using this approach, the excess porewater pressure ratio values are predicted using scaled distance (SD), and in-situ soil properties are not taken into consideration.
The SD term, shown in Table 1, is defined as the distance between the explosive charge location and the piezometer (in meters) divided by squared or cubed root of the charge weight (in kilograms of TNT explosives). As reported by Kumar et al. [41], the cubic-root and square-root scaling methods can be used to determine SD in the case of spherical charges and cylindrical charges, respectively. Ru is typically obtained by diving the change in the porewater pressure by the initial vertical effective stress. The Ru values have commonly been used as a threshold to evaluate the blast-induced liquefaction potential. For instance, Studer and Kok [36] reported that Ru values that were less than 0.10 represented a safe zone for liquefaction, Ru values that were between 0.80 and 1.0 represented a dangerous zone, and Ru values that were greater than or equal to 1.0 represented full soil liquefaction. In addition, The Studer and Kok [36] method, and other existing empirical models that have been used to predict porewater pressure responses (e.g., [17,42,43,44,45]), were based only on the blasting layout (SD), and not on the in-situ soil conditions.
To minimize the uncertainties and limitations that were associated with not considering the in-situ soil properties, several researchers [32,37,38,39,40] developed empirical models to predict the residual porewater pressure ratio and the initiation of liquefaction as a function of peak particle velocity, peak compressive strain, relative density (Dr) and initial vertical effective stress (σvo'), as presented in Table 1. The peak compressive strain, presented in Table 1, is defined as the ratio of the peak particle velocity divided by the compression wave velocity (Vp). As previously discussed, the Studer and Kok [36] approach, and other empirical equations (e.g., [17,23,32]), were developed from a single detonation. Due to this shortcoming, Eller [39] established the following empirical relationship for multiple detonations (Eq 10), that is a modified version of cubic-root scaling method.
within Eq 10, R is the distance between the explosive charge location and the monitoring piezometer, W is the TNT-equivalent weight of the charge in kg, and N is the number of blasts.
A large number of theoretical and empirical methods have been presented to determine blast-induced peak particle velocities [4,7,17,32,40,43,44,45,46,47,48]. A summary of these developed empirical equations are presented in Table 2. It should be noted that the aforementioned empirical equations, and other equations presented in the literature, are site-specific equations. For PPV determination, only Kumar et al. [41] provided an empirical model (Eq 25) that considers the variation in soil properties including, unit weight (γ), degree of saturation (S), and Young's modulus (E). Kumar et al. [41] also stated that the results obtained using the latter model are reasonable for fully saturated soils irrespective of soil type, and the model predicts high values for partially saturated soils. In addition, Charlie and Doehring [21] reported that the approach provided by Drake and Little [46] predicts a reasonably accurate value of PPV for most of the testing sites.
1.2. Existing threshold values of PPV, p and SD required for liquefaction
Besides Ru being commonly used as a threshold to assess the liquefaction potential, various researchers [2,4,13,17,35,36,37,38,39,40,42,49,50,51,52,53,54,55,56] provided other blasting parameters (PPV, εp and SD) to be used as threshold limits for liquefaction. For a very loose saturated cohesionless soil, Lyakhov [42] reported that liquefaction occurred at the PPV values exceeding 0.11 m/s. A study conducted by Puchkov [49] reported liquefaction at the SD values less than 5 m/kg1/3 with PPV exceeding 0.08 m/s. According to Ivanov [2], a very loose saturated sand experienced liquefaction at the SD values ranging from 6 to 8 m/kg1/3. Charlie et al. [17] observed liquefaction of dense alluvial sand at PPV values exceeding 0.16 m/s with SD less than 3 m/kg1/3 and peak strain exceeding 0.01 percent. Charlie and Doehring [21] performed an analysis of single underground explosions using chemicals explosives, and reported that liquefaction can be induced with SD values of 3 m/kg1/3, when the estimated measured peak compressive strain exceeded 0.07 percent and peak particle velocity exceeded 1.1 m/sec. Charlie and Doehring [21] also identified the SD of 1 m/kg1/3 as the upper bound maximum for liquefaction induced by surface explosives. These threshold values of PPV, εp and SD and other values presented in the literature are summarized in Table 3. In addition, the presented threshold values have been proven to be as a function of the soil properties including soil density, effective stress and number of strain cycles, and lithification [21,23,32].
1.3. Controlled blasting tests as ground improvement method
Ground improvement and the effects of blast-induced liquefaction on the in-situ soil properties have been evaluated by measuring the ground surface settlements and by investigating the pre- and post-blast CPT measurement. Several researchers [3,10,22,57,58,59,60,61,62] have assessed pre-and post-blast CPT data. Despite soil densification measured after the dissipation the porewater pressure, no increase or decrease of tip resistance have been observed from the aforementioned research studies.
The topic of using penetration tests, including CPT and standard penetration tests (SPT), to verify ground improvement or the effect of liquefaction on the soil resistances is a topic of ongoing discussion. Several research studies [3,11,57,60,62,63,64,65] have been conducted to confirm why there is a little or no increase of penetration resistance after blasting. Finno et al. [62] performed an extensive research study to investigate the effect of free gas released from explosives on penetration resistance test results. Based on the post-blast field testing results, Finno et al. [62] concluded that the gas released during blasting affect the mechanical behavior of soil. A detailed discussion of this theory and other proposed theories can be found in Finno et al. [62]. In contrast, Liao and Mayne [59] conducted CPT soundings within the NMSZ, and concluded that the post-blast CPT measurements might be significantly affected by blast-induced liquefaction and time effects. A review of CPT profiles provided by Liao and Mayne [59] showed a decrease of cone tip resistance, sleeve friction, and shear wave velocity values at the testing site. These results were consistent with the observations presented in Camp et al. [60].
A controlled blast test was conducted at the Turrell Arkansas Testing Site (TATS) to (1) evaluate the effect of in-situ conditions on blast-induced excess porewater pressure responses and (2) predict liquefaction at the testing site located within the NMSZ. A review of the existing empirical models used to predict blast-induced porewater pressure responses and liquefaction is presented herein. A comparison of pre- and post-blast CPT data is also presented. Based on the results obtained from the TATS, a new empirical model was developed to predict Ru and PPV. For the new empirical model, for determination of Ru, the contribution of PPV and σvo', were taken into consideration for a certain range of Dr values.
2.
Geotechnical site characteristics
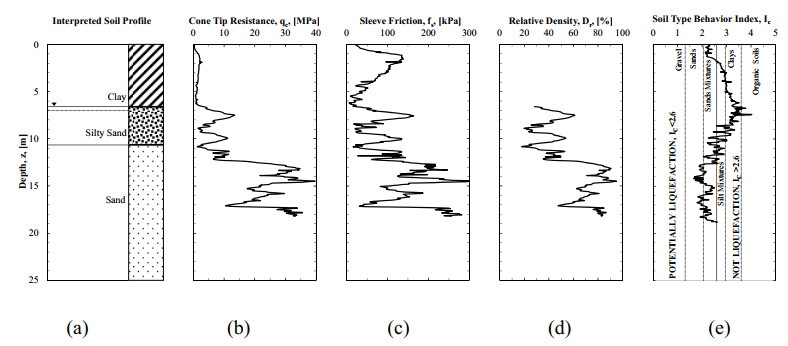
The TATS is located in Northeast Arkansas within the New Madrid Seismic Zone (NMSZ), and within the Mississippi Embayment. The generalized soil profile, average cone tip resistance (qc), average sleeve friction (fs), average relative density (Dr) and soil type behavior index (Ic), are presented in Figure 1. The Dr and Ic values were correlated from the CPT soundings data using Kulhawy and Mayne [66] and Robertson and Cabal [67], respectively. The soil profile consists of high plasticity clay, from the ground surface to a depth of 6.60 m, underlain by a potentially liquefiable sand deposit. As illustrated in Figure 1, the liquefiable sand deposit consists of a silty sand layer (6.60 to 10.65 m), and a loose sand layer (10.65 to 25 m). The plasticity index (PI) within the clay layer ranged from 40 to 55 percent, with an average fines content (FC) of approximately 97.67 percent. Although the groundwater table fluctuates with the river level of the Mississippi River, the groundwater table was encountered at an approximate depth of 7.01 m below the ground surface before blasting.
Based on the liquefaction susceptibility chart that was developed from the Ic criteria (Figure 1e), as proposed by Robertson and Wride [68], the soil types with calculated Ic values less than 2.6, were thought to be susceptible to liquefaction. At this site, the soil materials with Ic values less than 2.6 were observed below an approximate depth of 8 m. The values of Ic, PI, and FC observed at the depths above 8 m indicated that no liquefaction should occur within the upper soil layer. The liquefaction susceptibility at the TATS was first investigated by Race and Coffman [69] following the procedures proposed by Idriss and Boulanger [70]. Using the results obtained from in-situ and laboratory tests, liquefaction was predicted to occur within the silty sand and the sand layers for the design mean magnitude of 7.5 and a peak ground acceleration of 0.64g that might be produced within the NMSZ [69].
3.
Blast-induced liquefaction tests
3.1. Explosive charge weight for liquefaction
As previously indicated, several researchers, including Charlie et al. [17], Al-Qasimi et al. [32], Charlie et al. [40], Charlie and Doehring [21] provided guidance regarding the conditions required for the development of liquefaction (Table 3). At the TATS, charge weight values of 1.0 kg and 0.82 kg per deck were estimated for inner and outer ring; respectively, by using the Drake and Little [46], Eller [39], and Studer and Kok [36] equations to estimate PPV, SD and Ru required for liquefaction. The amount of explosive charge were also determined by considering (1) a SD value of 3 m/kg3 as the upper bound, (2) a PPV value of 1.1 m/s and a εp value of 0.07 percent as lower boundaries, and (3) an Ru value equal to the unity for liquefaction to occur. These threshold values were selected based on the results obtained from the existing empirical models summarized in Table 3. To prevent possible damage to the adjacent infrastructure, an average of 0.91 kg (2 lbs) per deck was detonated to induce liquefaction at the testing site.
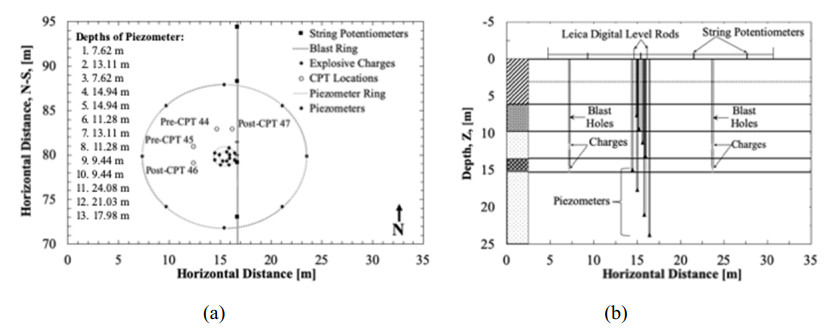
A plan view and a cross-sectional layout of the testing site are shown in Figure 2. Prior to blasting, thirteen (13) porewater pressure transducers (piezometers) were installed at different depths around two circular arrays (inner and outer rings), as shown in Figure 2b. These piezometers were used to monitor the generation and dissipation of the excess porewater pressure responses as a function of time and depth during, and after blasting. The inner and outer rings of the piezometers were installed at a distance of 0.53 and 1.07 m from the center of blast ring, respectively. The piezometers were installed following the procedures provided in Rollins et al. [71]. The PPV values were measured using seismographs located at the ground surface. Four string potentiometers were installed inside the blast ring to monitor the ground surface movement associated with the excess porewater pressure dissipation following blasting. This blasting geometry design was similar to blasting layouts used by various researchers [23,24,25,26,27] to induce liquefaction around deep foundation elements.
Two decks of explosives charges were detonated to liquefy the soil material within the target layer (8 to 13 m). The explosive charges were placed in a circular array that consisted of the eight, pre-drilled and cased blast holes (Figure 2). The blast holes were drilled at a radial distance of 8.10 m from the center of the blast ring. As illustrated in Figure 2, the explosive charges were placed in two decks within each blast hole. The first deck contained 0.91 kg of explosive charge at a depth of 14.60 m. The second deck also contained 0.91 kg of explosive charge at a depth of 11.60 m below the ground surface. A total of 14.56 kg (1.82 per blast hole) of charge was detonated to liquefy the sand deposit between 8 and 13 m. The explosive charges that were installed, consisted of a mixture of ammonium nitrate, sodium nitrate, and aluminum. The charges were detonated one at a time, proceeding around the ring at the deepest deck (14.60 m) and then around the ring at the shallowest deck (11.60 m) to (1) minimize vibrations, and (2) to generate multiple blast pulses. The charges were sequentially detonated in counterclockwise fashion around the blasting ring with a 500ms delay between the detonations of each individual charge.
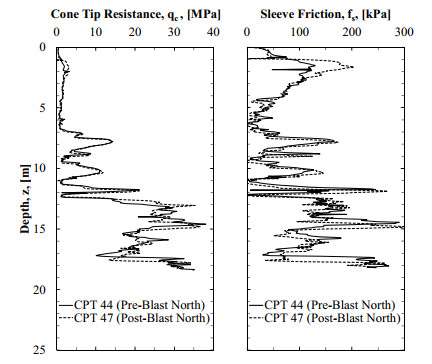
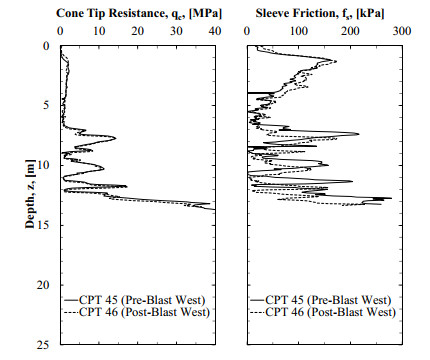
Four CPT tests were performed to investigate the effects of blast-induced liquefaction on in-situ soil properties. Two series of CPT tests, referred as Pre-CPT 44 and Pre-CPT 45, were performed prior to blasting. These pre-blast CPT tests were also used to characterize the subsurface stratigraphy and to evaluate the soil liquefaction susceptibility. Two other CPT tests, referred as Post-CPT 46 and Post-CPT 47, were performed after blasting. A comparison of the cone tip resistance (qc) and sleeve friction (fs) measurements that were collected before and after blasting are presented and discussed in subsequent sections. As shown in Figure 2a, the pre-and post-blast CPT tests were performed inside the blast ring.
4.
Results and discussion
4.1. Excess porewater pressure ratio results
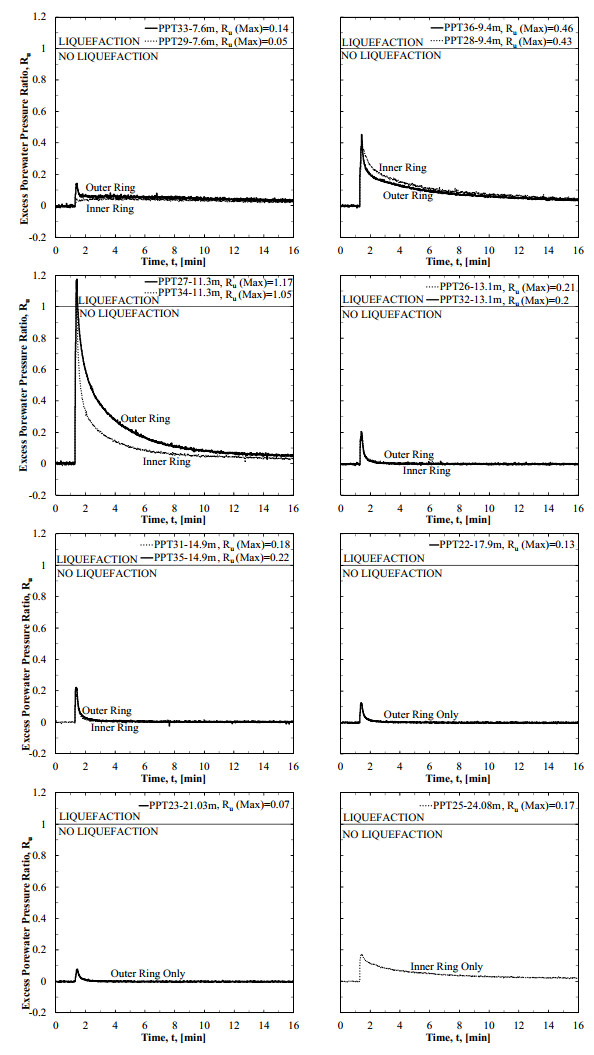
The excess porewater pressure ratio time histories and the maximum Ru values recorded from the installed piezometers are presented in Figure 3. Although the blast charge weights used in this study were similar to the charges used to produce liquefaction at testing site in Vancouver, Canada [72] and Christchurch, New Zealand [73], the piezometers showed Ru values much smaller than required for liquefaction. A shown in Figure 3, the porewater pressures were instantaneously elevated immediately after blasting, and then gradually dissipated over a period of approximately 10 minutes. Maximum Ru values of 1.17 and 1.05, indicating liquefaction, were observed in the piezometers located at a depth of 11.30 m in the outer and inner ring piezometers, respectively. Ru values of 0.46 and 0.43 were measured at a depth of 9.4 m for the piezometer located in the outer and inner ring, respectively.
The low Ru values that were observed from piezometers located at the depths of 7.60 m, 13.10 m, 14.90 m, 17.90 m, 21.03 m and 24.08 m were attributed to: (1) the generated vibrations and shock waves that were not large enough to induce complete liquefaction, (2) the presence of the impermeable soil materials (clay and silty sand) that were observed at the depth of 7.60 m, (3) the higher relative density values that were observed at the depths of 13.10 m, 14.90 m, and 17.90 m, and (4) the piezometer devices located at 21.03 and 24.08 m being located farther away from explosive charges.
Based on video recordings and seismometer records, only 12 of the 16 individual 0.91 kg charges that were set to detonate (eight blast holes, two decks with 0.91 kg of charge per deck per blast hole), were detonated properly. Four of the charges completed a low-order detonation due to dynamic shock when the blasting cap fired. Based on discussions with the blasting contractor, lack of stemming and water hammer that developed following detonation of the lower deck of charges may have prevented the upper charges from detonating properly. It was believed that this low-order detonation may have also contributed to the low Ru measurements.
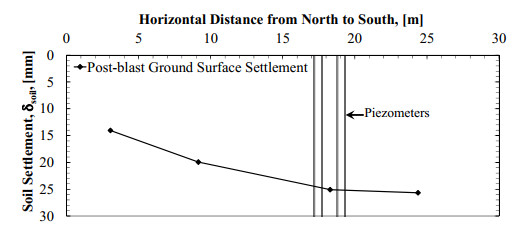
The post-blast ground surface settlements are presented in Figure 4. A total ground settlement of 25.67 mm was measured inside of the blast ring. Due to the presence of impervious soil overlying the liquefied layer, sand boils and flowing of groundwater were not observed at the ground surface following blasting.
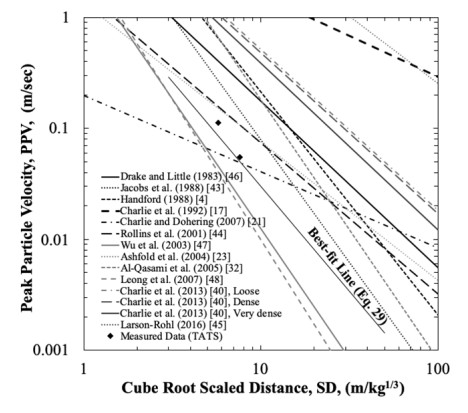
Predicted PPV values obtained using existing empirical models and measured PPV values, as a function of the cubic-root-scaled distances are presented in Figure 5. The best-fit empirical equation developed from the TATS for PPV is provided as Eq 29:
Like with the lower than predicted excess porewater pressure ratio measurements, lower than expected peak particle velocity values were also measured at the TATS. As shown in Figure 5, the measured PPV values were also lower than most of the predicted PPV values, except the values obtained using Leong et al. [48], and Wu et al. [47]. This difference can be attributed to (1) the presence of cohesive materials within the upper layer of the profile at the TATS, (2) a different blasting layout, and (3) variation of site conditions.
4.2. Pre-and post-blast CPT measurements
Results from the pre- and post-CPT tests, that were obtained from the northern and western locations, are shown in Figures 6 and 7, respectively. A slight decrease of tip resistance and sleeve friction was observed within the target layer. This decrease was observed within the silty sand layer in the northern CPT soundings, and within silty sand and sand in the western CPT soundings. Some zones within the post-blast CPT profiles also showed a slight increase of both tip resistance and sleeve friction values. These slight increases were not consistent within the entire soil profile. Therefore, it is reasonable to attribute the decrease and/or increase of cone-penetration test results to (1) the soil variability and (2) CPT measurement errors for this specific site.
Based on the piezometer measurements (as previously presented in Figure 3), the measured excess porewater pressure ratio values were elevated for a period of 10 minutes. The post-CPT soundings were performed one hour after blasting. It is very possible that the porewater pressures were completely dissipated when the post-CPT soundings were acquired. The delay in the collection of the CPT data may have prevented capturing the complete decrease of tip resistance and sleeve friction values. As can been seen in Figures 6 and 7, despite the dissipation of excess porewater pressure and the post-blast settlement measurements, there was no evidence of the increase of tip resistance and sleeve friction data, as a result of excess porewater dissipation. This was consistent with the observations obtained within the NMSZ by Liao and Mayne [59], and also discussed by other researchers [3,10,22,57,58,60,61,62,65]. As discussed in Finno et al. [62], due to the soil conditions at the TATS (higher fines content), the release of nitrogen gas may have also prevented the increase of tip resistance measurements at the TATS.
5.
Proposed empirical model
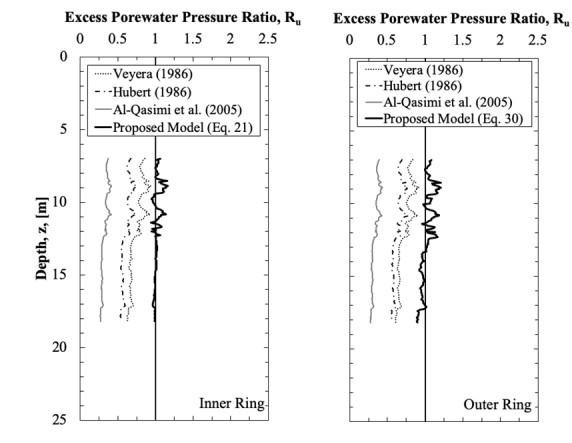
Liquefaction occurred at the testing site, as was evident from the observed excess porewater pressure ratio measurements and ground surface settlement measurements. However, the required amount of the explosive charges, that was predicted using existing equations (Eqs 2, 10, and 11, for determination of Ru, SD, and PPV, respectively) did not produced enough energy to liquefy the entire target layer. This was mostly attributed to (1) not all of the explosive charges being detonated, and (2) in-situ soil properties not being considered into Eqs 2, 10 and 11. Therefore, a site-specific, empirical model, that includes vertical effective stress and relative density was developed. The measured and predicted excess porewater pressure ratio values, determined using the existing empirical models that consider the soil conditions [32,37,38,40] are presented in Figure 8. In general, the values estimated using the Al-Qasimi et al. [32] method (Eq 7) were the most comparable to the measured results, within and below the target layer, except for the liquefied soil. The other methods over-predicted the Ru values. Therefore, the Al-Qasimi et al. [32] was modified to incorporate the pre-blast in-situ soil properties that were acquired at this site. Specifically, the Al-Qasimi et al. [32] model was modified by changing the leading coefficient (CDr) to fit the measured and predicted Ru values into a linear equation. As previously shown in Table 1, within the Al-Qasimi et al. [32] empirical model (Eq 7), the CDr equaled 1.13 for the entire soil profile. For the proposed model, CDr = 3 for Dr > 55% and CDr = 12.5 for Dr < 55%. The modified Al-Qasimi et al. [32] equations that is expressed in terms of PPV, vertical effective stress (in kPa) and relative density (in percentage) is expressed as Eq 30:
The development of a proper empirical equation, for the testing site described herein, allowed for the calculation of the explosive charge weight that should have been used to liquefy the entire target layer (8 to 13 m). As shown in Figure 9, liquefaction was predicted to occur within the silty sand and sand layers by using explosive charge weights of 3.77 or 3.37 kg per borehole for the inner and outer ring, respectively. These explosive charge weights were determined using (1) the Eller [39] equation (Eq 10) to calculate the SD values for multiple detonations, (2) the proposed PPV equation (Eq 29) to calculate the appropriate PPV values for the site, (3) the relative density and effective stress values from CPT correlations, and (4) the proposed empirical equation (Eq 30) to determine Ru, and (5) the Ru values being greater than or equals to unity for liquefaction to occur. Therefore, at least 3.77 kg of explosive charges per borehole were recommended for future blast testing at this site.
6.
Conclusions
A proper empirical equation for predicting the excess porewater pressure ratio at the TATS was developed. CPT tests were not able to verify the effect of blasting on penetration resistances of the soil at the testing site. Although blast-induced liquefaction may contribute to the changes of both tip resistance and sleeve friction, a review of the post-CPT profiles showed no evidence of increase of tip resistance and sleeve friction due densification. The changes of tip resistance and sleeve friction values that were observed in post-blast CPT data were associated to the soil variability and CPT measurement errors. Therefore, in the case of verifying ground improvement or post-blast densification, it is recommended to measure pre-and post-blast ground settlements instead of penetration test results.
For the future blasting tests, it is recommended that the blast boreholes contain one deck of explosives rather than multiple decks of explosives to avoid improper detonations. In addition, because the in-situ properties (vertical effective stress, particle size distribution, relative density, permeability and drainage) affected the amount of excess pore pressure responses, these parameters should be accounted for in the blasting design. For the sites within the NMSZ and other sites with similar soil conditions, it is recommended to use the threshold values provided in herein and Eqs 29 and 30 to estimate the PPV and the Ru values, respectively.
Acknowledgements
The authors thank the Arkansas State Highway and Transportation Department, the Missouri Department of Transportation, Duane Houkom, Inc., and Loadtest, Inc., for financial and/or in kind contributions to the scope work described herein.
Conflicts of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: