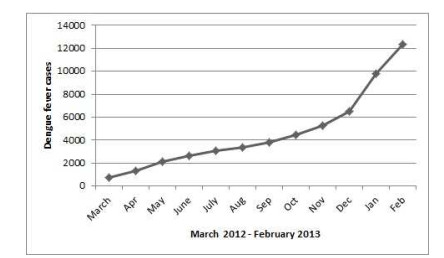
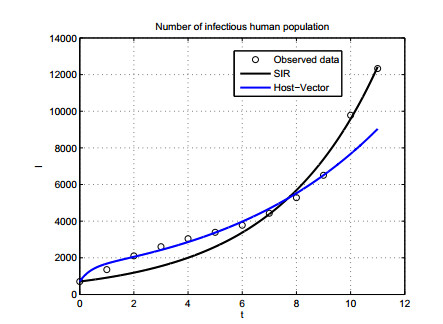
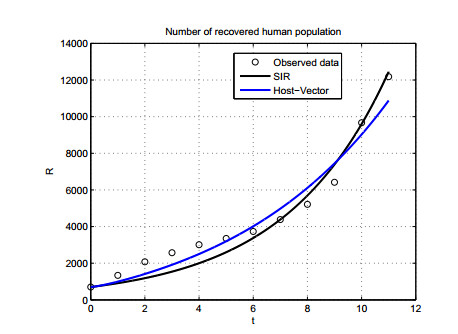
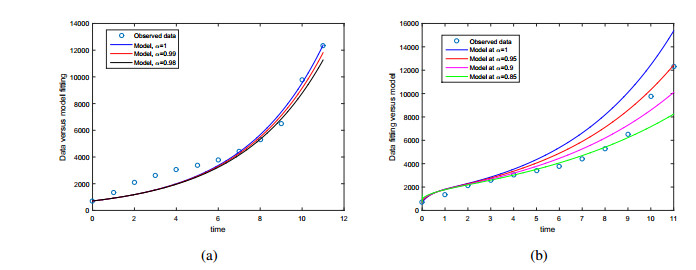
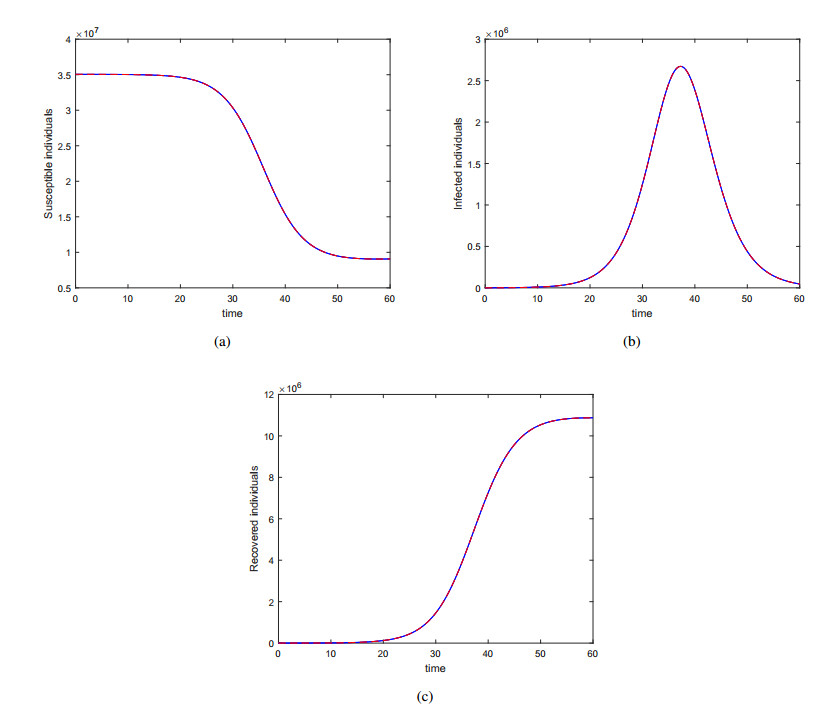
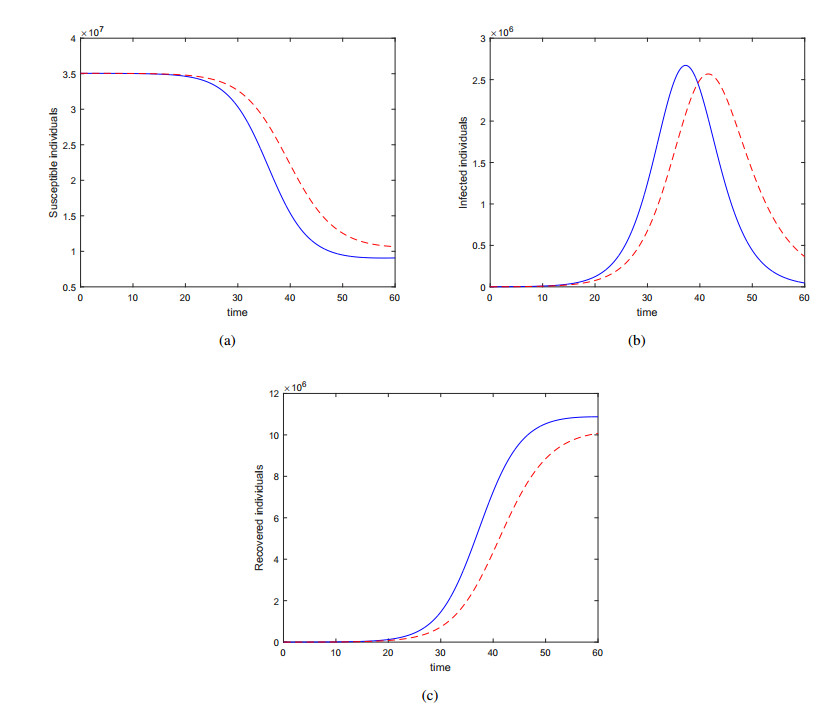
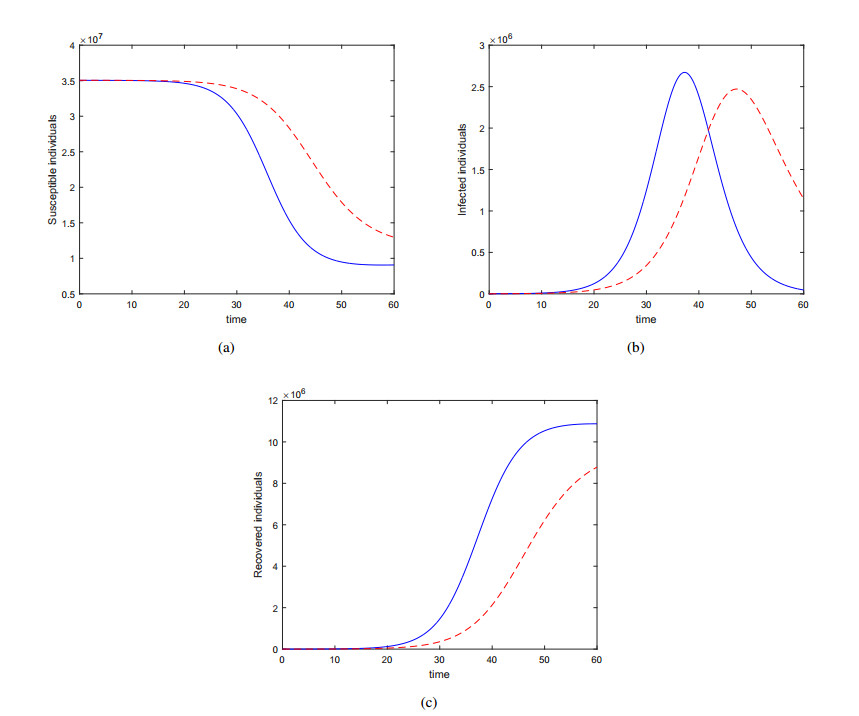
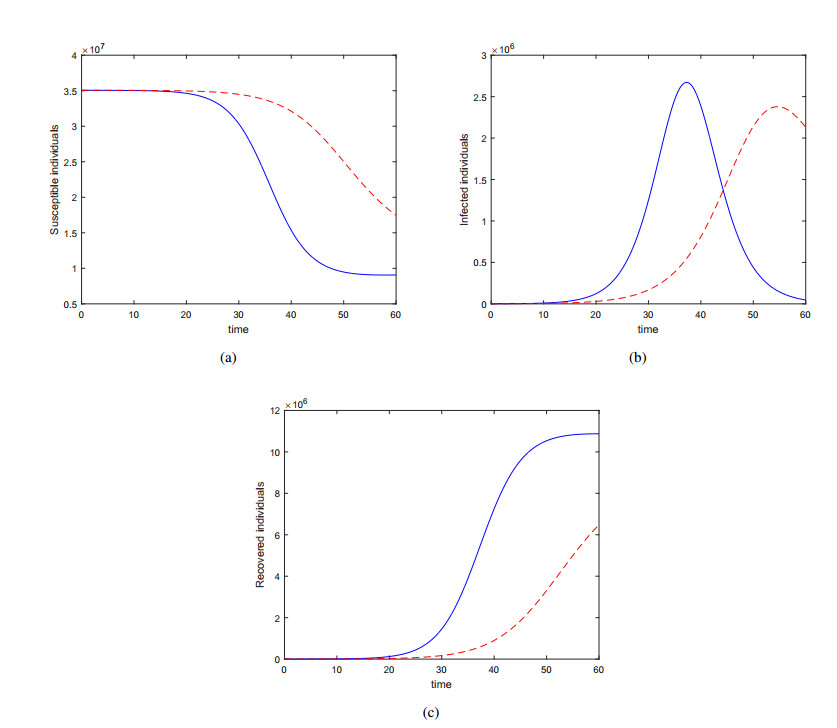
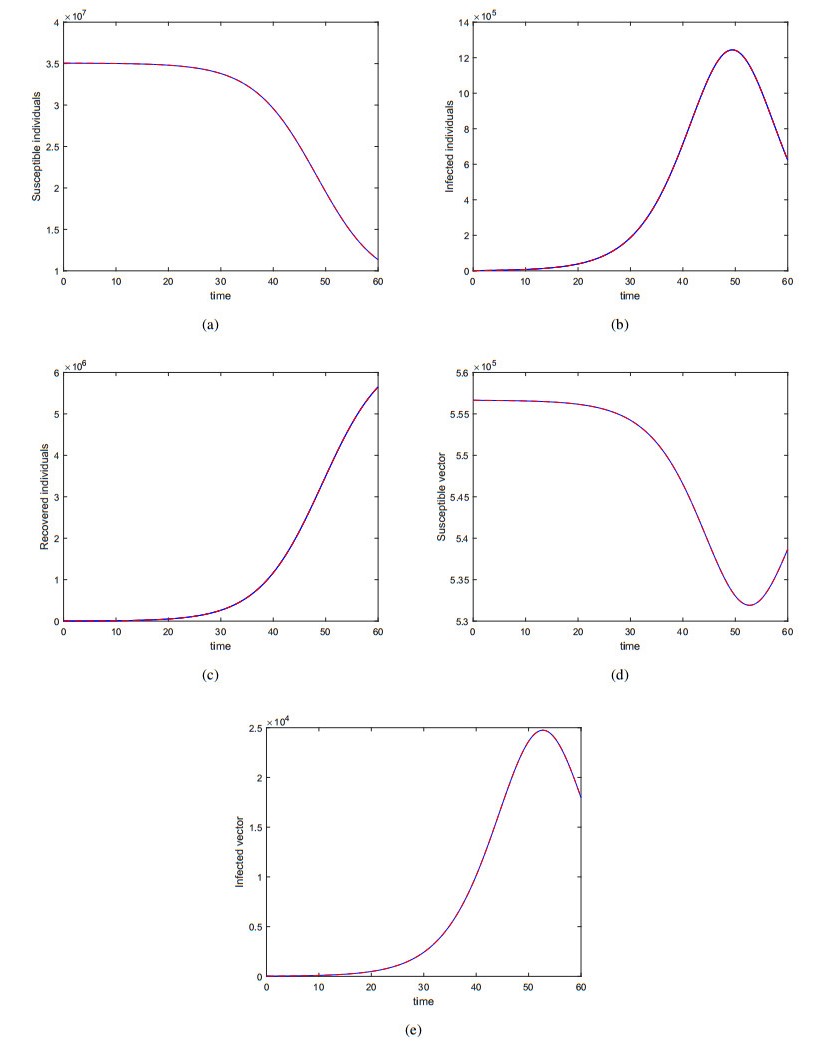
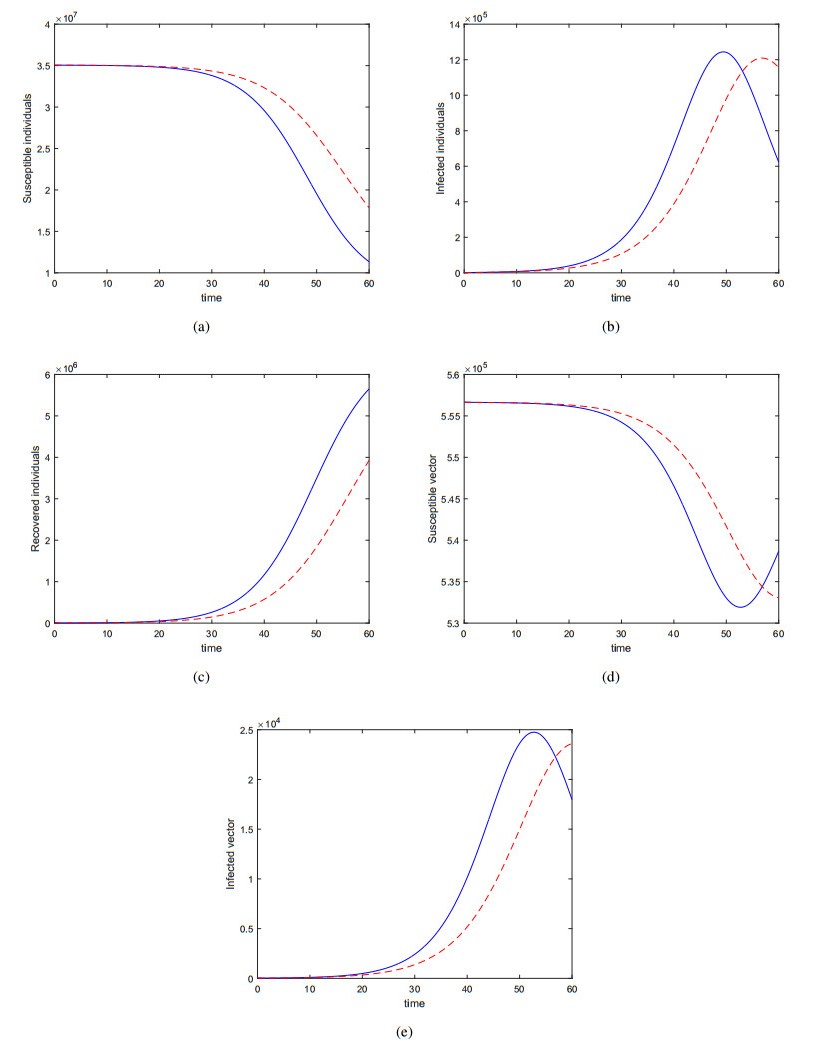
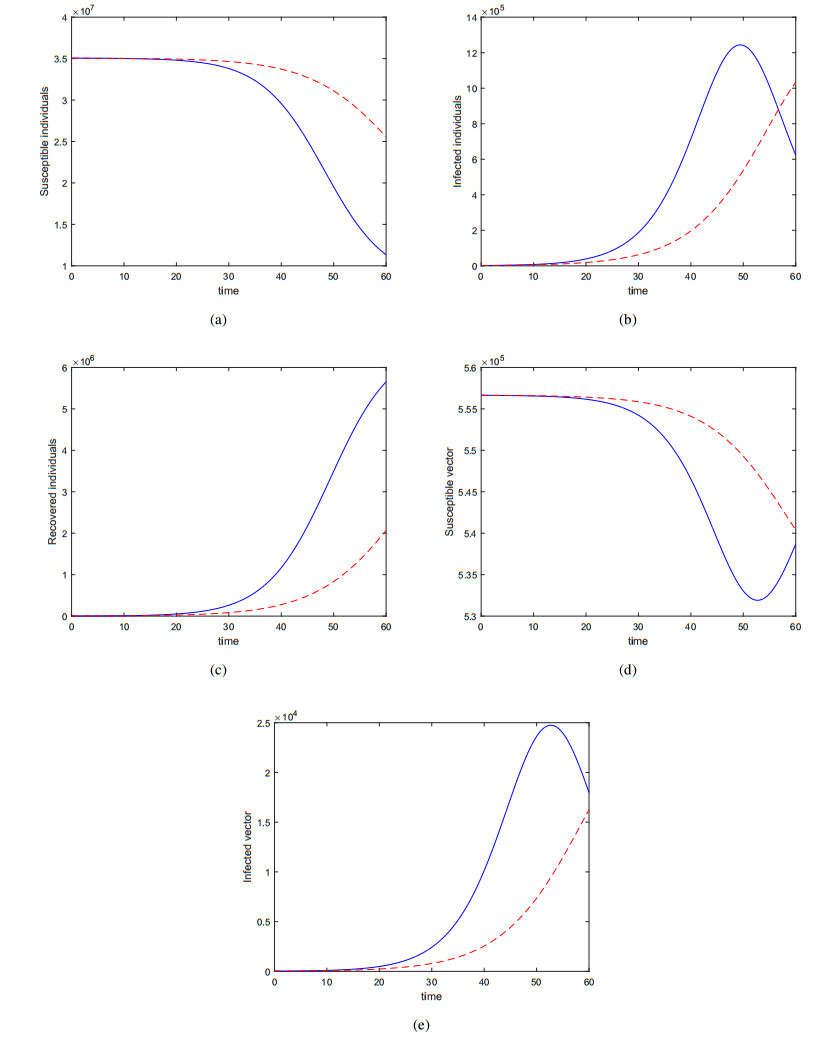
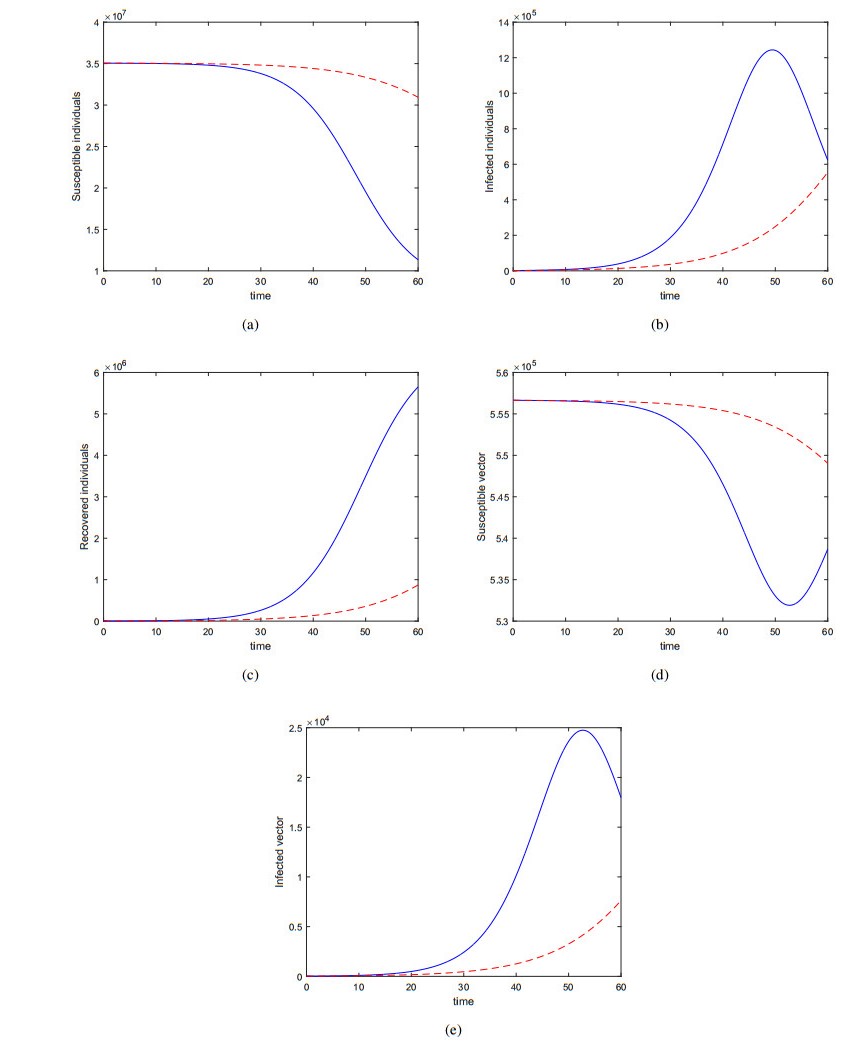
In this paper, we propose a parameter estimation of dengue fever transmission model using a particle swarm optimization method. This method is applied to estimate the parameters of the host-vector and SIR type dengue transmission models by using cumulative data of dengue patient in East Java province, Indonesia. Based on the parameter values, the basic reproduction number of both models are greater than one and obtained their value for SIR is R0=1.4159 and for vector host is R0=1.1474. We then formulate the models in fractional Atangana-Baleanu derivative that possess the property of nonlocal and nonsingular kernel that has been remained effective to many real-life problems. A numerical procedure for the solution of the model SIR model is shown. Some specific numerical values are considered to obtain the graphical results for both the SIR and Vector Host model. We show that the model vector host provide good results for data fitting than that of the SIR model.
1.
Introduction
The Sylvester equation
appears frequently in many areas of applied mathematics. We refer readers to the elegant survey by Bhatia and Rosenthal [1] and the references therein for the history of the Sylvester equation and many interesting and important theoretical results. The Sylvester equation is important in a number of applications such as matrix eigenvalue decompositions [2,3], control theory [3,4,5], model reduction [6,7,8,9], physics mathematics to construct exact solutions of nonlinear integrable equations [10], feature problemss of slice semi-regular functions [11] and the numerical solution of the matrix differential Riccati equations [12,13,14]. There are several numerical algorithms to compute the solution of the Sylvester equation. The standard ones are the Bartels Stewart algorithm [15] and the Hessenberg Schur method first described by Enright [14], but more often attributed to Golub, Nash and Van Loan [16]. Other computationally efficient approaches for the case that both A and B are stable, i.e., both A and B have all their eigenvalues in the open left half plane, are the sign function method [17], Smith method [18] and ADI iteration methods [19,20,21,22]. All these methods are efficient for the small size of the dense matrices A and B.
The recent interest is directed more towards the large and sparse matrices A and B, and C with low rank. For the dense A and B, the approach based on the sign function method is suggested in [23] that exploits the low rank structure of C. This approach is further used in [24] in order to solve the large scale Sylvester equation with sparse A and B, i.e., the matrices A and B can be represented by O(nlog(n)) data. Problems for the sensitivity of the solution of the Sylvester equation are also widely studied. There are several books that contain the results for these problems [25,26,27].
In this paper, we focus our attention on the multiple constrained least squares solution of the Sylvester equation, that is, the following multiple constrained least squares problem:
where A,B,C,L and U are given n×n real matrices, X is a n×n real symmetric matrix which we wish to find, λmin(X) represents the smallest eigenvalue of the symmetric matrix X, and ε is a given positive constant. The inequality X≥Y, for any two real matrices, means that Xij≥Yij, here Xij and Yij denote the ijth entries of the matrices X and Y, respectively.
Multiple constrained conditions least squares estimations of matrices are widely used in mathematical economics, statistical data analysis, image reconstruction, recommendation problems and so on. They differ from the ordinary least squares problems, and the estimated matrices are usually required to be symmetric positive definite, bounded and, sometimes, to have some special construction patterns. For example, in the dynamic equilibrium model of economy [28], one needs to estimate an aggregate demand function derived from second order analysis of the utility function of individuals. The formulation of this problem is to find the least squares solution of the matrix equation AX=B, where A and B are given, the fitting matrix X is a symmetric and bounded matrix, and the smallest eigenvalue is no less than a specified positive number since, in the neighborhood of equilibrium, the approximate of the utility function is a quadratic and strictly concave with Hessian matrix. Other examples discussed in [29,30] are respectively to find a symmetric positive definite patterned matrix closest to a sample covariance matrix and to find a symmetric and diagonally dominant matrices with positive diagonal matrix closest to a given matrix. Based on the above analysis, we have a strong motivation to study the multiple constrained least squares problem (1.2).
In this paper, we first transform the multiple constrained least squares (1.2) into an equivalent constrained optimization problem. Then, we give the necessary and sufficient conditions for the existence of a solution to the equivalent constrained optimization problem. Noting that the alternating direction method of multipliers (ADMM) is one-step iterative method, we propose a multi-step alternating direction method of multipliers (MSADMM) to the multiple constrained least squares (1.2), and analyze the global convergence of the proposed algorithm. We will give some numerical examples to illustrate the effectiveness of the proposed algorithm to the multiple constrained least squares (1.2) and list some problems that should be studied in the near future. We also give some numerical comparisons between MSADMM, ADMM and ADMM with Anderson acceleration (ACADMM).
Throughout this paper, Rm×n, SRn×n and SRn×n0 denote the set of m×n real matrices, n×n symmetric matrices and n×n symmetric positive semidefinite matrices, respectively. In stands for the n×n identity matrix. A+ denotes a matrix with ijth entry equal to max{0,Aij}. The inner product in space Rm×n defined as ⟨A,B⟩=tr(ATB)=∑ijAijBij for all A,B∈Rm×n, and the associated norm is Frobenius norm denoted by ‖A‖. PΩ(X) denotes the projection of the matrix X onto the constrained matrix set Ω, that is PΩ(X)=argminZ∈Ω‖Z−X‖.
2.
Preliminaries
In this section, we give an existence theorem for a solution of the multiple constrained least squares problem (1.2) and some theoretical results for the optimization problems which are useful for discussions in the next sections.
Theorem 2.1. The matrix ˜X is a solution of the multiple constrained least squares problem (1.2) if and only if there exist matrices ˜Λ1,˜Λ2 and ˜Λ3 such that the following conditions (2.1)–(2.4) are satisfied.
Proof. Obviously, the multiple constrained least squares problem (1.2) can be rewritten as
Then, if ˜X is a solution to the constrained optimization problem (2.5), ˜X certainly satisfies KKT conditions of the constrained optimization problem (2.5), and hence of the multiple constrained least squares problem (1.2). That is, there exist matrices ˜Λ1,˜Λ2 and ˜Λ3 such that conditions (2.1)–(2.4) are satisfied.
Conversely, assume that there exist matrices ˜Λ1,˜Λ2 and ˜Λ3 such that conditions (2.1)–(2.4) are satisfied. Let
then, for any matrix W∈SRn×n, we have
This implies that ˜X is a global minimizer of the function ˉF(X) with X∈SRn×n. Since
and ˉF(X)≥ˉF(˜X) holds for all X∈SRn×n, we have
Noting that ˜Λ1≥0,˜Λ2≥0 and ˜Λ3+˜ΛT3∈SRn×n0, then F(X)≥F(˜X) holds for all X with X−L≥0, U−X≥0 and X−εIn∈SRn×n0. Hence, ˜X is a solution of the constrained optimization problem (2.5), that is, ˜X a solution of the multiple constrained least squares problem (1.2). □
Lemma 2.1. [31] Assume that ˜x is a solution of the optimization problem
where f(x) is a continuously differentiable function, Ω is a closed convex set, then
Lemma 2.2. [31] Assume that (˜x1,˜x2,...,˜xn) is a solution of the optimization problem
where fi(xi)(i=1,2,...,n) are continuously differentiable functions, Ωi(i=1,2,...,n) are closed convex sets, then
where ˜λ is a solution to the dual problem of (2.6).
Lemma 2.3. Assume that Ω={X∈Rn×n:L≤X≤U}, then, for any matrix M∈Rn×n, if Y=PΩ(Y−M), we have
Proof. Let
and noting that the optimization problem
is equivalent to the optimization problem
then ˜Z satisfies the KKT conditions for the optimization problem (2.7). That is, there exist matrices ˜Λ1≥0 and ˜Λ2≥0 such that
Since
then
So we have from the above conditions that (˜Λ1)ij(˜Λ2)ij=0 when Lij≠Uij, and (˜Λ1)ij and (˜Λ2)ij can be arbitrarily selected as (˜Λ1)ij≥0 and (˜Λ2)ij≥0 when Lij=Uij. Noting that M=˜Λ1−˜Λ2, ˜Λ1 and ˜Λ2 can be selected as ˜Λ1=(M)+ and ˜Λ2=(−M)+. Hence, the results hold. □
Lemma 2.4. Assume that Ω={X∈Rn×n:XT=X,λmin(X)≥ε>0}, then, for any matrix M∈Rn×n, if Y=PΩ(Y−M), we have
Proof. Let
and noting that the optimization problem
is equivalent to the optimization problem
then ˜Z satisfies the KKT conditions for the optimization problem (2.8). That is, there exists a matrix ˜Λ∈SRn×n0 such that
Since
then
Hence, the results hold. □
3.
Accelerated ADMM
In this section we give a multi-step alternating direction method of multipliers (MSADM) tothe multiple constrained least squares problem (1.2). Obviously, the multiple constrained least squares problem (1.2) is equivalent to the following constrained optimization problem
The Lagrange function, augmented Lagrangian function and dual problem to the constrained optimization problem (3.1) are, respectively,
where M and N are Lagrangian multipliers and α is penalty parameter.
The alternating direction method of multipliers [32,33] to the constrained optimization problem (3.1) can be described as the following Algorithm 3.1.
Alternating direction method of multipliers (ADMM) has been well studied in the context of the linearly constrained convex optimization. In the last few years, we have witnessed a number of novel applications arising from image processing, compressive sensing and statistics, etc. ADMM is a splitting version of the augmented Lagrange method (ALM) where the ALM subproblem is decomposed into multiple subproblems at each iteration, and thus the variables can be solved separably in alternating order. ADMM, in fact, is one-step iterative method, that is, the current iterates is obtained by the information only from the previous step, and the convergence rate of ADMM is only linear, which was proved in [33]. In this paper we propose a multi-step alternating direction method of multipliers (MSADMM), which is more effective than ADMM, to the constrained optimization problem (3.1). The iterative pattern of MSADMM can be described as the following Algorithm 3.2.
Compared to ADMM, MSADMM yields the new iterate in the order X→M→N→Y→Z with the difference in the order of X→Y→Z→M→N. Despite this difference, MSADMM and ADMM are equally effective to exploit the separable structure of (3.1) and equally easy to implement. In fact, the resulting subproblems of these two methods are of the same degree of decomposition and they are of the same difficulty. We shall verify by numerical experiments that these two methods are also equally competitive in numerical senses, and that, if we choose the correction factor γ suitably, MSADMM is more efficient than ADMM.
4.
Convergence analysis
In this section, we prove the global convergence and the O(1/t) convergence rate for the proposed Algorithm 3.2. We start the proof with some lemmas which are useful for the analysis of coming theorems.
To simplify our analysis, we use the following notations throughout this section.
Lemma 4.1. Assume that (X∗,Y∗,Z∗) is a solution of problem (3.1), (M∗,N∗) is a solution of the dual problem (3.4) to the constrained optimization problem (3.1), and that the sequences {Vk} and {˜Wk} are generated by Algorithm 3.2, then we have
Proof. By (3.6)–(3.10) and Lemma 2.1, we have, for any (X,Y,Z,M,N)∈Ω, that
or compactly,
Choosing W as W∗=(X∗V∗), then (4.3) can be rewritten as
Noting that the monotonicity of the gradients of the convex functions, we have by Lemma 2.2 that
Therefore, the above two inequalities imply that
from which the assertion (4.1) is immediately derived. □
Noting that the matrix Q is a symmetric and positive semi-definite matrix, we use, for convenience, the notation
Then, the assertion (4.1) can be rewritten as
Lemma 4.2. Assume that (X∗,Y∗,Z∗) is a solution of the constrained optimization problem (3.1), (M∗,N∗) is a solution of the dual problem (3.4) to the constrained optimization problem (3.1), and that the sequences {Vk},{˜Vk} are generated by Algorithm 3.2. Then, we have
Proof. By elementary manipulation, we obtain
where the inequality follows from (4.1) and (4.4). □
Lemma 4.3. The sequences {Vk} and {˜Wk} generated by Algorithm 3.2 satisfy
for any (X,Y,Z,M,N)∈Ω.
Proof. By (4.2) or its compact form (4.3), we have, for any (X,Y,Z,M,N)∈Ω, that
Thus, it suffices to show that
By using the formula 2⟨a,Qb⟩=‖a‖2Q+‖b‖2Q−‖a−b‖2Q, we derive that
Moreover, since (3.11)–(3.14) can be rewritten as (Vk−Vk+1)=γ(Vk−˜Vk), we have
Combining (4.9) and (4.10), we obtain
On the other hand, we have by using (3.11)–(3.14) that
By adding (4.11) and (4.12), and again using the fact that (Vk−Vk+1)=γ(Vk−˜Vk), we obtain that
which is equivalent to (4.8). Hence, the lemma is proved. □
Theorem 4.1. The sequences {Vk} and {˜Wk} generated by Algorithm 3.2 are bounded, and furthermore, any accumulation point ˜X of the sequence {˜Xk} is a solution of problem (1.2).
Proof. The inequality (4.5) with the restriction γ∈(0,2) implies that
(ⅰ) limk→∞‖Vk−˜Vk‖Q=0;
(ⅱ) ‖Vk−V∗‖Q is bounded upper.
Recall that the matrix Q is symmetric and positive semi-definite. Thus, we have by the assertion (ⅰ) that Q(Vk−˜Vk)=0 (k→∞) which, together with (3.7) and (3.8), imply that ˜Yk=˜Xk=˜Zk (k→∞). The assertion (ⅱ) implies that the sequences {Yk}, {Zk}, {Mk} and {Nk} are bounded. Equations (3.11)–(3.14) hold, and the sequences {Yk}, {Zk}, {Mk} and {Nk} are bounded imply the sequence {˜Yk}, {˜Zk}, {˜Mk} and {˜Nk} are also bounded. Hence, by the clustering theorem and together with (3.11)–(3.14), there exist subsequences {˜Xk}K, {˜Yk}K, {˜Zk}K, {˜Mk}K, {˜Nk}K, {Yk}K, {Zk}K, {Mk}K and {Nk}K such that
Furthermore, we have by (3.7) and (3.8) that
By (3.6)–(3.8), we have
So we have
Let k→∞,k∈K, we have by (3.9), (3.10) and (4.13) that
Noting that α>0, we have by (4.15), Lemma 2.3 and Lemma 2.4 that
and
Let
we have by (4.14) and (4.16)–(4.18) that
Hence, we have by Theorem 2.1 that ˜X is a solution of problem (1.2). □
Theorem 4.2. Let the sequences {˜Wk} be generated by Algorithm 3.2. For an integer t>0, let
then 1t+1∑tk=0(˜Xk,˜Yk,˜Zk,˜Mk,˜Nk)∈Ω and the inequality
holds for any (X,Y,Z,M,N)∈Ω.
Proof. First, for any integer t>0, we have (˜Xk,˜Yk,˜Zk,˜Mk,˜Nk)∈Ω for k=0,1,2,⋯,t. Since 1t+1∑tk=0˜Wk can be viewed as a convex combination of ˜W′ks, we obtain
Second, since γ∈(0,2), it follows from Lemma 4.3 that
By combining the monotonicity of G(W) with the inequality (4.22), we have
Summing the above inequality over k=0,1,⋯,t, we derive that
By dropping the minus term, we have
which is equivalent to
The proof is completed. □
Noting that problem (3.1) is equivalent to find (X∗,Y∗,Z∗,M∗,N∗)∈Ω such that the following inequality
holds for any (X,Y,Z,M,N)∈Ω. Theorem 4.2 means that, for any initial matrices Y0,Z0,M0,N0∈Rn×n, the point ˜Wt defined in (4.20) satisfies
which means the point ˜Wt is an approximate solution of (4.23) with the accuracy O(1/t). That is, the convergence rate O(1/t) of the Algorithm 3.2 is established in an ergodic sense.
5.
Numerical experiments
In this section, we present some numerical examples to illustrate the convergence of MSADMM to the constrained least squares problem (1.2). All tests were performed by Matlab 7 with 64-bit Windows 7 operating system. In all tests, the constant ε=0.1, matrices L with all elements are −1 and U with all elements are 3. The matrices A,B and C are randomly generated, i.e., generated in Matlab style as A=randn(n,n), B=randn(n,n), C=randn(n,n). In all algorithms, the initial matrices are chosen as the null matrices. The maximum number of inner iterations and out iterations are restricted to 5000. The error tolerance εout=εin=10−9 in Algorithms 3.1 and 3.2. The computational methods of the projection PΩi(X)(i=1,2) are as follows[38].
where
and W is such that X+XT2=WΔWT is spectral decomposition, i.e., WTW=I and Δ=diag(λ1(X+XT2),λ2(X+XT2),⋯,λn(X+XT2)). We use LSQR algorithm described in [34] with necessary modifications to solve the subproblems (3.5) in Algorithm 3.1, (3.6) in Algorithm 3.2 and (6.1) in Algorithm 6.2.
The LSQR algorithm is an effective method to solve consistent linear matrix equation or least square problem of inconsistent linear matrix equation. Using this iterative algorithm, for any initial matrix, a solution can be obtained within finite iteration steps if exact arithmetic is used. In addition, using this iterative algorithm, a solution with minimum Frobenius norm can be obtained by choosing a special kind of initial matrix, and a solution which is nearest to given matrix in Frobenius norm can be obtained by first finding minimum Frobenius norm solution of a new consistent matrix equation. The LSQR algorithm to solve the subproblems (3.5), (3.6) and (6.1) can be described as follows:
Table 1 reports the average computing time (CPU) of 10 tests of Algorithm 3.1 (ADMM) and Algorithm 3.2 (MSADMM) with penalty parameter α=n. Figures 1–4 report the computing time of ADMM with the same size of problem and different penalty parameters α. Figures 5–8 report the computing time of MSADMM with the same size of problem and different correction factor γ. Figure 9 reports the computing time curve of Algorithm 3.1 (ADMM) and Algorithm 3.2 (MSADMM) with different matrix size.
Based on the tests reported in Table 1, Figures 1–9 and many other performed unreported tests which show similar patterns, we have the following results:
Remark 5.1. The convergence speed of ADMM is directly related to the penalty parameter \alpha . In general, the penalty parameter \alpha in this paper can be chosen as \alpha\approx n (see Figures 1–4). However, how to select the best penalty parameter \alpha is an important problem should be studied future time.
Remark 5.2. The convergence speed of MSADMM is direct relation to the penalty parameter \alpha and the correction factor \gamma . The selection of the penalty parameter \alpha is similar to ADMM since MSADMM is a direct extension of ADMM. For the correction factor \gamma , as showed in Table 1 and Figures 5–8, aggressive values such as \gamma\approx 1.5 are often preferred. However, how to select the best correction factor \gamma is also an important problem should be studied future time.
Remark 5.3. As showed in Table 1 and Figure 9, MSADMM, with the correction factor \gamma\approx 1.5 and the penalty parameter \alpha be chosen as the same as ADMM, is more effective than ADMM.
6.
Algorithm 3.1 with Anderson acceleration
Anderson acceleration, or Anderson mixing, was initially developed in 1965 by Donald Anderson [35] as an iterative procedure to solve some nonlinear integral equations arising in physics. It turns out that the Anderson acceleration is very efficient to solve other types of nonlinear equations as well, see [36,37,38], and the literature cited therein. When Anderson acceleration is applied to the equation f(x) = g(x)-x = 0 , the iterative pattern can be described as the following Algorithm 6.1.
In this we define the following matrix functions
where g(Y_k, Z_k, M_k, N_k) = (Y_{k+1}, Z_{k+1}, M_{k+1}, N_{k+1}) with Y_{k+1}, Z_{k+1}, M_{k+1} and N_{k+1} are computed by (b)–(e) in Algorithm 3.1, and let f_k = f(Y_k, Z_k, M_k, N_k), g_k = g(Y_k, Z_k, M_k, N_k) , then Algorithm 3.1 with Anderson acceleration can be described as the following Algorithm 6.2.
Algorithm 6.2 (ACADMM) is m -step iterative method, that is, the current iterates is obtained by the linear combination of the previous m steps. Furthermore, the combination coefficients of the linear combination are modified at each iteration steps. Compared to ACADMM, Algorithm 3.2 (MSADMM) is two-step iterative method and the combination coefficients of the linear combination are fixed at each iteration steps. The convergence speed of ACADMM is directly related to the penalty parameter \alpha and the backtracking step m . The selection of the penalty parameter \alpha is the same as ADMM since ACADMM's iterates are corrected by ADMM's iterates. For the backtracking step m , as showed in Table 2 (the average computing time of 10 tests) and Figure 10, aggressive values such as m = 10 are often preferred (in this case, ACADMM is more efficient than MSADMM). However, how to select the best backtracking step m is an important problem which should be studied in near future.
7.
Conclusions
In this paper, the multiple constraint least squares solution of the Sylvester equation AX+XB = C is discussed. The necessary and sufficient conditions for the existence of solutions to the considered problem are given (Theorem 2.1). MSADMM to solve the considered problem is proposed and some convergence results of the proposed algorithm are proved (Theorem 4.1 and Theorem 4.2). Problems which should be studied in the near future are listed. Numerical experiments show that MSADMM with a suitable correction factor \gamma is more effective than ADMM (See Table 1 and Figure 10), and ACADMM with a suitable backtracdking step m is the most effective of ADMM, MSADMM and ACADMM (See Table 2 and Figure 10).
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by National Natural Science Foundation of China (grant number 11961012) and Special Research Project for Guangxi Young Innovative Talents (grant number AD20297063).
Conflict of interest
The authors declare no competing interests.









 DownLoad:
DownLoad: