1.
Introduction
Fractional calculus is a notably attractive subject owing to having wide-ranging application areas of theoretical and applied sciences. Despite the fact that there are a large number of worthwhile mathematical works on the fractional differential calculus, there is no noteworthy parallel improvement of fractional difference calculus up to lately. This statement has shown that discrete fractional calculus has certain unforeseen hardship.
Fractional sums and differences were obtained firstly in Diaz-Osler [1], Miller-Ross [2] and Gray and Zhang [3] and they found discrete types of fractional integrals and derivatives. Later, several authors began to touch upon discrete fractional calculus; Goodrich-Peterson [4], Baleanu et al. [5], Ahrendt et al. [6]. Nevertheless, discrete fractional calculus is a rather novel area. The first studies have been done by Atıcı et al. [7,8,9,10,11], Abdeljawad et al. [12,13,14], Mozyrska et al. [15,16,17], Anastassiou [18,19], Hein et al. [20] and Cheng et al. [21] and so forth [22,23,24,25,26].
Self-adjoint operators have an important place in differential operators. Levitan and Sargsian [27] studied self-adjoint Sturm-Liouville differential operators and they obtained spectral properties based on self-adjointness. Also, they found representation of solutions and hence they obtained asymptotic formulas of eigenfunctions and eigenvalues. Similarly, Dehghan and Mingarelli [28,29] obtained for the first time representation of solution of fractional Sturm-Liouville problem and they obtained asymptotic formulas of eigenfunctions and eigenvalues of the problem. In this study, firstly we obtain self-adjointness of DFSL operator within nabla fractional Riemann-Liouville and delta fractional Grünwald-Letnikov operators. From this point of view, we obtain orthogonality of distinct eigenfunctions, reality of eigenvalues. In addition, we open a new gate by obtaining representation of solution of DFSL problem for researchers study in this area.
Self-adjointness of fractional Sturm-Liouville differential operators have been proven by Bas et al. [30,31], Klimek et al. [32,33]. Variational properties of fractional Sturm-Liouville problem has been studied in [34,35]. However, self-adjointness of conformable Sturm-Liouville and DFSL with Caputo-Fabrizio operator has been proven by [36,37]. Nowadays, several studies related to Atangana-Baleanu fractional derivative and its discrete version are done [38,39,40,41,42,43,44,45].
In this study, we consider DFSL operators within Riemann-Liouville and Grünwald-Letnikov sense, and we prove the self-adjointness, orthogonality of distinct eigenfunctions, reality of eigenvalues of DFSL operator. However, we get sum representation of solutions for DFSL equation by means Laplace transform for nabla fractional difference equations. Finally, we compare the results for the solution of DFSL problem, discrete Sturm-Liouville (DSL) problem with the second order, fractional Sturm-Liouville (FSL) problem and classical Sturm-Liouville (CSL) problem with the second order. The aim of this paper is to contribute to the theory of DFSL operator.
We discuss DFSL equations in three different ways with;
i) Self-adjoint (nabla left and right) Riemann-Liouville (R-L) fractional operator,
ii) Self-adjoint (delta left and right) Grünwald-Letnikov (G-L) fractional operator,
iii)(nabla left) DFSL operator is defined by R-L fractional operator,
2.
Preliminaries
Definition 2.1. [4] Delta and nabla difference operators are defined by respectively
Definition 2.2. [46] Falling function is defined by, α∈R
where Γ is Euler gamma function.
Definition 2.3. [46] Rising function is defined by, α∈R,
Remark 1. Delta and nabla operators have the following properties
Definition 2.4. [2,7] Fractional sum operators are defined by,
(i) The left defined nabla fractional sum with order μ>0 is defined by
(ii) The right defined nabla fractional sum with order μ>0 is defined by
where ρ(t)=t−1 is called backward jump operators, Na={a,a+1,...}, bN={b,b−1,...}.
Definition 2.5. [47] Fractional difference operators are defined by,
(i) The nabla left fractional difference of order μ>0 is defined
(ii) The nabla right fractional difference of order μ>0 is defined
Fractional differences in (7−8) are called the Riemann-Liouville (R-L) definition of the μ-th order nabla fractional difference.
Definition 2.6. [1,21,48] Fractional difference operators are defined by,
(i) The left defined delta fractional difference of order μ, 0<μ≤1, is defined by
(ii) The right defined delta fractional difference of order μ, 0<μ≤1, is defined by
Fractional differences in (9−10) are called the Grünwald-Letnikov (G-L) definition of the μ-th order delta fractional difference.
Theorem 2.7. [47] We define the summation by parts formula for R-L fractional nabla difference operator, u is defined on bN and v is defined on Na, then
Theorem 2.8. [26,48] We define the summation by parts formula for G-L delta fractional difference operator, u, v is defined on {0,1,...,n}, then
Definition 2.9. [20] f:Na→R, s∈ℜ, Laplace transform is defined as follows,
where ℜ=C∖{1} and ℜ is called the set of regressive (complex) functions.
Definition 2.10. [20] Let f,g:Na→R, all t∈Na+1, convolution property of f and g is given by
where ρ(s) is the backward jump function defined in [46] as
Theorem 2.11. [20] f,g:Na→R, convolution theorem is expressed as follows,
Lemma 2.12. [20] f:Na→R, the following property is valid,
Theorem 2.13. [20] f:Na→R, 0<μ<1, Laplace transform of nabla fractional difference
Definition 2.14. [20] For |p|<1, α>0, β∈R and t∈Na, discrete Mittag-Leffler function is defined by
where t¯n={t(t+1)⋯(t+n−1),n∈ZΓ(t+n)Γ(t),n∈R is rising factorial function.
Theorem 2.15. [20] For |p|<1, α>0, β∈R, |1−s|<1, and |s|α>p, Laplace transform of discrete Mittag-Leffler function is as follows,
Definition 2.16. Laplace transform of f(t)∈R+, t≥0 is defined as follows,
Theorem 2.17. For z, θ∈C,Re(δ)>0, Mittag-Leffler function with two parameters is defined as follows
Theorem 2.18. Laplace transform of Mittag-Leffler function is as follows
Property 2.19. [28] f:Na→R, 0<μ<1, Laplace transform of fractional derivative in Caputo sense is as follows, 0<α<1,
Property 2.20. [28] f:Na→R, 0<μ<1, Laplace transform of left fractional derivative in Riemann-Liouville sense is as follows, 0<α<1,
here Iα0+ is left fractional integral in Riemann-Liouville sense.
3.
Main results
3.1. Discrete fractional Sturm-Liouville equations
We consider discrete fractional Sturm-Liouville equations in three different ways as follows:
First Case: Self-adjoint L1 DFSL operator is defined by (nabla right and left) R-L fractional operator,
where p(t)>0, r(t)>0, q(t) is a real valued function on [a+1,b−1] and real valued, λ is the spectral parameter, t∈[a+1,b−1], x(t)∈l2[a+1,b−1]. In ℓ2(a+1,b−1), the Hilbert space of sequences of complex numbers u(a+1),...,u(b−1) with the inner product is given by,
for every u∈DL1, let's define as follows
Second Case: Self-adjoint L2 DFSL operator is defined by(delta left and right) G-L fractional operator,
where p,r,λ is as defined above, q(t) is a real valued function on [0,n], t∈[0,n], x(t)∈l2[0,n]. In ℓ2(0,n), the Hilbert space of sequences of complex numbers u(0),...,u(n) with the inner product is given by, n is a finite integer,
for every u∈DL2, let's define as follows
Third Case:L3 DFSL operator is defined by (nabla left) R-L fractional operator,
p,r,λ is as defined above, q(t) is a real valued function on [a+1,b−1], t∈[a+1,b−1].
Firstly, we consider the first case and give the following theorems and proofs;
Theorem 3.1. DFSL operator L1 is self-adjoint.
Proof.
If (16−17) is subtracted from each other
and sum operator from a+1 to b−1 to both side of the last equality is applied, we get
If we apply the summation by parts formula in (11) to right hand side of (18), we have
Hence, the proof completes.
Theorem 3.2. Two eigenfunctions, u(t,λα) and v(t,λβ), of the equation (13) are orthogonal as λα≠λβ.
Proof. Let λα and λβ are two different eigenvalues corresponds to eigenfunctions u(t) and v(t) respectively for the the equation (13),
If we multiply last two equations by v(t) and u(t) respectively, subtract from each other and apply definite sum operator, owing to the self-adjointness of the operator L1, we have
since λα≠λβ,
Hence, the proof completes.
Theorem 3.3. All eigenvalues of the equation (13) are real.
Proof. Let λ=α+iβ, owing to the self-adjointness of the operator L1, we can write
Since ⟨u(t),u(t)⟩r≠0,
and hence β=0. The proof completes.
Secondly, we consider the second case and give the following theorems and proofs;
Theorem 3.4. DFSL operator L2 is self-adjoint.
Proof.
If (19−20) is subtracted from each other
and definite sum operator from 0 to t to both side of the last equality is applied, we have
If we apply the summation by parts formula in (12) to r.h.s. of (21), we get
Hence, the proof completes.
Theorem 3.5. Two eigenfunctions, u(t,λα) and v(t,λβ), of the equation (14) are orthogonal as λα≠λβ. orthogonal.
Proof. Let λα and λβ are two different eigenvalues corresponds to eigenfunctions u(t) and v(t) respectively for the the equation (14),
If we multiply last two equations to v(t) and u(t) respectively, subtract from each other and apply definite sum operator, owing to the self-adjointness of the operator L2, we get
since λα≠λβ,
So, the eigenfunctions are orthogonal. The proof completes.
Theorem 3.6. All eigenvalues of the equation (14) are real.
Proof. Let λ=α+iβ, owing to the self-adjointness of the operator L2
Since ⟨u,u⟩r≠0,
and hence β=0. The proof completes.
3.2. Sum representation of solution of discrete fractional Sturm-Liouville problem
Now, we consider the third case and give the following theorem and proof;
Theorem 3.7.
where p(t)>0, r(t)>0, q(t) is defined and real valued, λ is the spectral parameter. The sum representation of solution of the problem (22)−(23) is found as follows,
where |λ|<1, |1−s|<1, and |s|α>λ from Theorem 2.15.
Proof. Let's use the Laplace transform of both side of the equation (22) by Theorem 2.13, and let q(t)x(t)=g(t),
from Lemma 2.12, we get
Applying inverse Laplace transform to the equation (25), then we get representation of solution of the problem (22)−(23),
4.
General discussions
Now, let us consider comparatively discrete fractional Sturm-Liouville (DFSL) problem, discrete Sturm-Liouville (DSL) problem, fractional Sturm-Liouville (FSL) problem and classical Sturm-Liouville (CSL) problem respectively as follows by taking q(t)=0,
DFSL problem:
and its analytic solution is as follows by the help of Laplace transform in Lemma 2.12
DSL problem:
and its analytic solution is as follows
FSL problem:
and its analytic solution is as follows by the help of Laplace transform in Property 2.19 and 2.20
CSL problem:
and its analytic solution is as follows
where the domain and range of function x(t) and Mittag-Leffler functions must be well defined. Note that we may show the solution of CSL problem can be obtained by taking μ→1 in the solution of FSL problem and similarly, the solution of DSL problem can be obtained by taking μ→1 in the solution of DFSL problem.
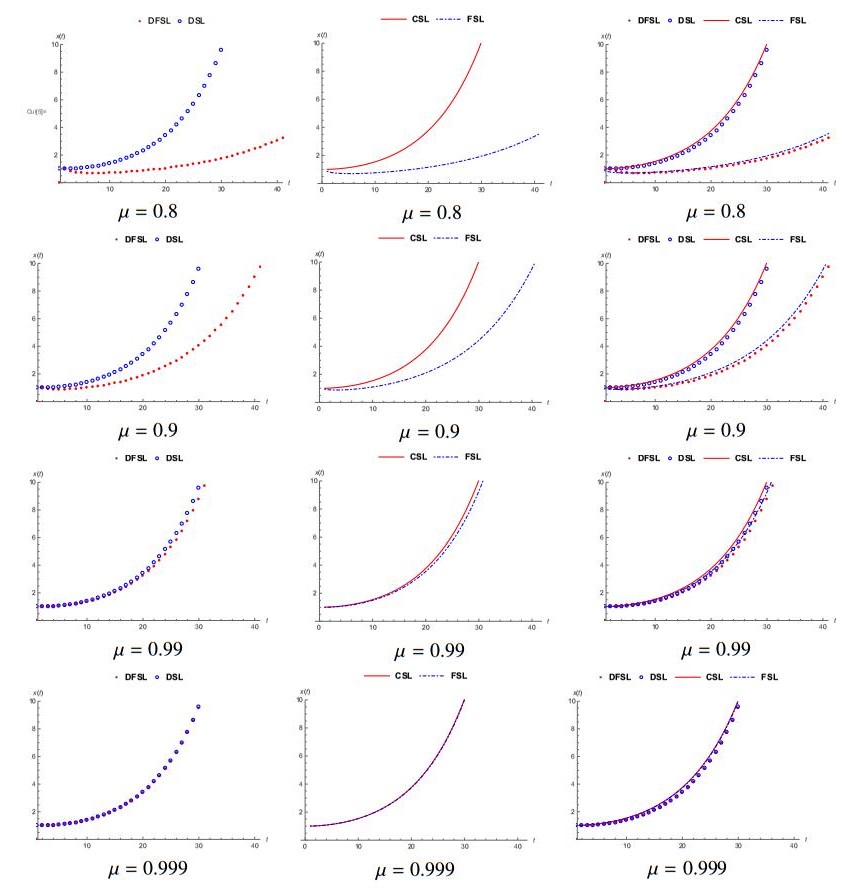
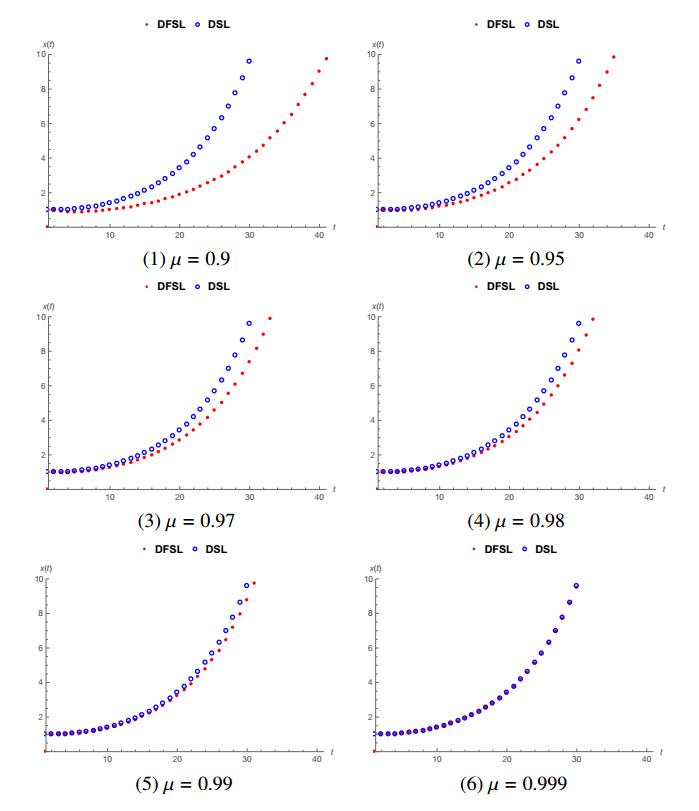
Firstly, we compare the solutions of DFSL and DSL problems and from here we show that the solutions of DFSL problem converge to the solutions of DSL problem as μ→1 in Figure 1 for discrete Mittag-Leffler function Ep,α,β(t,a)=1000∑k=0pk(t−a)¯αk+βΓ(αk+β+1); let λ=0.01,
Secondly, we compare the solutions of DFSL, DSL, FSL and CSL problems for discrete Mittag-Leffler function Ep,α,β(t,a)=1000∑k=0pk(t−a)¯αk+βΓ(αk+β+1). At first view, we observe the solution of DSL and CSL problems almost coincide in any order μ, and we observe the solutions of DFSL and FSL problem almost coincide in any order μ. However, we observe that all of the solutions of DFSL, DSL, FSL and CSL problems almost coincide to each other as μ→1 in Figure 2. Let λ=0.01,
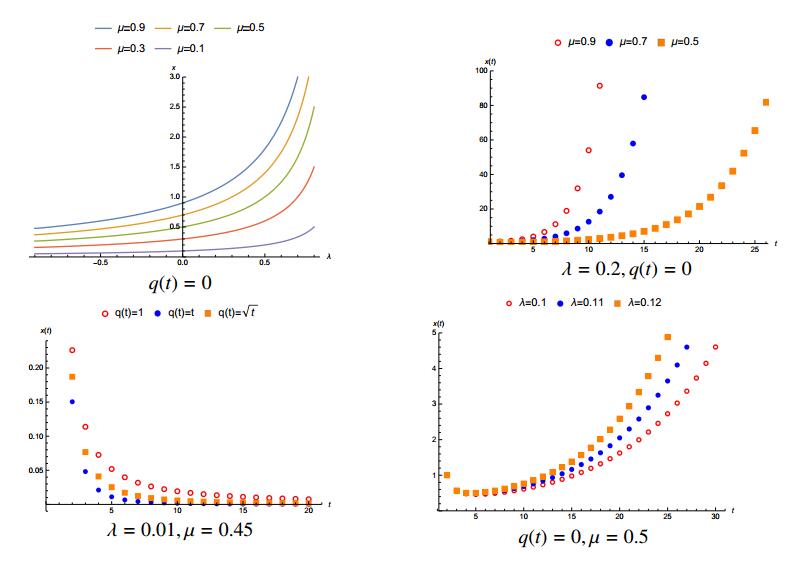
Thirdly, we compare the solutions of DFSL problem (22−23) with different orders, different potential functions and different eigenvalues for discrete Mittag-Leffler function Ep,α,β(t,a)=1000∑k=0pk(t−a)¯αk+βΓ(αk+β+1) in the Figure 3;
Eigenvalues of DFSL problem (22−23), correspond to some specific eigenfunctions for numerical values of discrete Mittag-Leffler function Ep,α,β(t,a)=i∑k=0pk(t−a)¯αk+βΓ(αk+β+1), is given with different orders while q(t)=0 in Table 1;
Finally, we give the solutions of DFSL problem (22−23) with different orders, different potential functions and different eigenvalues for discrete Mittag-Leffler function Ep,α,β(t,a)=100∑k=0pk(t−a)¯αk+βΓ(αk+β+1) in Tables 2–4;
4.1. Discussions on eigenvalues and eigenfunctions of DFSL, DSL, FSL, CSL problems
Now, let's consider the problems together DFSL (26)−(27), DSL (29)−(30), FSL (32)−(33) and CSL (35)−(36). Eigenvalues of these problems are the roots of the following equation
Thus, if we apply the solutions (28), (31), (34) and (37) of these four problems to the equation above respectively, we can find the eigenvalues of these problems for the orders μ=0.9 and μ=0.99 respectively in Table 5, and Table 6,
In here, we observe that these four problems have real eigenvalues under different orders μ=0.9 and μ=0.99, hence we can find eigenfunctions putting these eigenvalues into the four solutions. Furthermore, as the order changes, we can see that eigenvalues change for DFSL problems.
5.
Conclusion
We consider firstly discrete fractional Sturm-Liouville (DFSL) operators with nabla Riemann-Liouville and delta Grünwald-Letnikov fractional operators and we prove self-adjointness of the DFSL operator and fundamental spectral properties. However, we analyze DFSL problem, discrete Sturm-Liouville (DSL) problem, fractional Sturm-Liouville (FSL) problem and classical Sturm-Liouville (CSL) problem by taking q(t)=0 in applications. Firstly, we compare the solutions of DFSL and DSL problems and we observe that the solutions of DFSL problem converge to the solutions of DSL problem when μ→1 in Fig. 1. Secondly, we compare the solutions of DFSL, DSL, FSL and CSL problems in Fig. 2. At first view, we observe the solutions of DSL and CSL problems almost coincide with any order μ, and we observe the solutions of DFSL and FSL problem almost coincide with any order μ. However, we observe that all of solutions of DFSL, DSL, FSL and CSL problems almost coincide with each other as μ→1. Thirdly, we compare the solutions of DFSL problem (22−23) with different orders, different potential functions and different eigenvalues in Fig. 3.
Eigenvalues of DFSL problem (22−23) corresponded to some specific eigenfunctions is given with different orders in Table 1. We give the eigenfunctions of DFSL problem (22−23) with different orders, different potential functions and different eigenvalues in Table 2, Table 3 and Table 4.
In Section 4.1, we consider DFSL, DSL, FSL and CSL problems together and thus, we can compare the eigenvalues of these four problems in Table 5 and Table 6 for different values of μ. We observe that these four problems have real eigenvalues under different values of μ, from here we can find eigenfunctions corresponding eigenvalues. Moreover, when the order change, eigenvalues change for DFSL problems.
Consequently, important results in spectral theory are given for discrete Sturm-Liouville problems. These results will lead to open gates for the researchers studied in this area. Especially, representation of solution will be practicable for future studies. It worths noting that visual results both will enable to be understood clearly by readers and verify the results to the integer order discrete case while the order approaches to one.
Acknowledgment
This paper includes a part of Ph.D. thesis data of Ramazan OZARSLAN.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: