Performance evaluation of hybrid biodegradable oils as a lubricant during cylindrical turning of AISI 304 austenitic stainless steel

1.   Introduction

In the last two decades years, applied mathematics and physics nonlinear phenomena play an important role in soliton theory, the calculation of analytical and numerical solutions, especially the travelling wave solutions of nonlinear equations in mathematical physics ^[1]. Thus, deeper investigation of the analytical solutions to the nonlinear evolution equations with the help of newly developed and improved approaches have been considered as one of the important study area in nonlinear sciences such as engineering, chemistry, biology, dynamics, plasma physics, electrodynamics, applied physics and others. In this regard, many powerful models with high nonlinearity such as the nonlinear (3+1)-dimensional B-type Kadomtsev-Petviashvili-Boussinesq equation ^[2], modified α and modified Vakhnenko-Parkes equations ^[3], the perturbed nonlinear Schrödinger equation ^[4], Davey-Stewartson equation ^[5], KDV equation ^[6], the Calogero-Bogoyavlenskii-Schiff and KPH equations ^[7] some conformable nonlinear model ^[8], the Hirota Maccari system ^[9], Bogoyavlenskii equation ^[10], conformable space-time fractional Fokas-Lenells equation ^[11], the (2+1)-dimensional Boussinesq equation with fourth order ^[12], the (3+1) dimensional conformable fractional Zakharov-Kuznetsov equation with power law nonlinearity ^[13], the conformable Ablowitz-Kaup-Newell-Segur equation ^[14], nonlinear Phi-4 equation ^[15] and many others ^{[16,17,18,19,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75]} have been suggested to investigate deeper physical properties such as complex, dark, bright and soliton solutions.

In the organization of this paper, in section 2, the brief description of considered methods such as sine-Gordon Expansion method (SGEM) and improved Bernoulli sub-equation method (IBSEFM) are given. In section 3, these projected methods are successfully applied to the nonlinear conformable Date-Jimbo-Kashiwara-Miwa equation (CDJKM) defined as ^[20]

where $\alpha$ and $\beta$ are non-zero and $u = u\left( {x, y, t} \right)$ is the wave-amplitude function, which describes long water waves. In case of $\theta = 1$, Eq (1) turns DJKM equation. DJKM equation was firstly presented by Kadomtsev and Petviashvili so as to study the stability of the KdV soliton ^[21]. Later, some important properties of DJKM have been investigated in ^{[22,23,24,25]}. In 2020, Wazwaz have observed the Painlevé integrability and multiple soliton solutions by getting variable coefficient in ^[26].

Some important discussions and physical meanings of figures are also presented in section 4. After the graphical simulations, a conclusion completes the paper in section 5.

2.   Projected methods

2.1.   The Sine-Gordon expansion method

We will give general structure of the SGEM in this section. Let's consider the sine-Gordon equation given by ^[28];

where $u = u(x, t)$, $\eta$ is a real constant. Using the wave transform

into Eq (2), we find the corresponding ordinary differential equation (ODE) as following,

where $U = U\left( \xi \right).$ If we integrate Eq (3), we obtain

where $\kappa$ is the integration constant. Substituting $\kappa = 0, w\left( \xi \right) = \frac{U}{2}$ and ${b^2} = \frac{{{\eta ^2}}}{{1 - {c^2}}}$ in Eq (4), gives

Setting $b = 1$ in Eq (5), gives

Solving Eq (6) via separation of variables, we obtain

Suppose that the nonlinear fractional differential equations given in the more general form;

where and $\theta \in \left( {0, 1} \right]$ is the order of the conformable derivative. By using wave transformation given as

we find the following nonlinear ordinary differential equation (NODE)

where $U = U\left( \xi \right), \, \, U' = \frac{{dU}}{{d\xi }}, \cdots .$ To obtain the solutions of this equation, we suppose the following equation as trial solution

Applying the homogeneous balance principle between the highest power nonlinear term and highest derivative in the nonlinear ordinary differential equation (NODE), we determine the value of $n$. Putting Eq (11) and its consecutive derivatives into the NODE, we obtain a polynomial equation with ${\sin ^i}\left( w \right){\cos ^j}\left( w \right).$ Using some trigonometric properties to the polynomial equation, it is obtained an algebraic equation system by equating to zero the same power summation of coefficients. With aid of the computation programme, we solve the equation system to obtain the ${A_i}, {B_i}, c, k$ values. Substituting the ${A_i}, {B_i}, c, k$ values into Eq (10), we get the new travelling wave solutions to the Eq (9).

2.2.   The structure of IBSEFM

In this subsection of the paper, we will mention about general structures of the IBSEFM ^[29,30].

Step 1: Suppose that the following fractional differential equation,

where $u = u(x, t)$ and $\alpha \in \left( {0, 1} \right]$ is the order of the conformable. The wave transformation is

where $\sigma , \mu$ are real constants and can be determined later. This transformation reduces Eq (12) into NODE as following;

Step 2: Let consider the trial solution form of Eq (14) as following

We can determine the general form of Bernoulli differential equation for $F'$ according to Bernoulli theory as

where $F = F\left( \zeta \right)$ is Bernoulli differential polynomial function. Eq (16) put into Eq (14), it gives polynomial equation $\Omega \left( F \right)$ which depends on $F$ as the following equality.

We put account the homogeneous balance principle to determine the relation between $n, m \ {\rm{ and }} \ M$ constants.

Step 3: Equating all the coefficients of $\Omega \left( F \right)$ yields an algebraic equation system;

Once we have solved this system, we can determine the values of ${a_0}, {a_1}, ..., {a_n}$ and ${b_0}, {b_1}, ..., {b_m}$.

Step 4: We have two situations depend on $b \ {\rm{ and }} \ d$ according to solution of Eq (16).

We get the analytical solutions to Eq (14) via software program by using complete discrimination system for polynomial of $F\left( \zeta \right)$.

3.   Applications of approaches

3.1.   Application of SGEM

In this section of the paper, we apply SGEM to the Eq (1) to investigate some analytical solutions such as exponential and complex.

First of all, we transform Eq (1) into a NODE by the following wave transformation

where $k, m, c$ are non-zero, $\theta$ is conformable derivative order. Putting Eq (20) into Eq (1) and after some simple calculating, we reach the following NODE

where $V = U',$ and also both integral constants are zero.

With the help of balance principle for Eq (10), we find $n = 2$. For this value, Eq (10) can be written as

and its second derivation

Putting Eq (22) and its second derivation into Eq (21), we find a trigonometric algebraic equation. When we take all coefficients of trigonometric functions as zero, we obtain a system of coefficients. Via some computational programs, we reach the some of coefficients as follows:

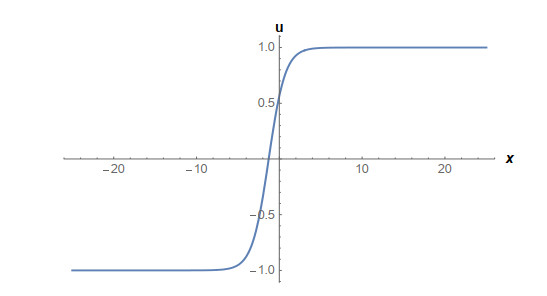
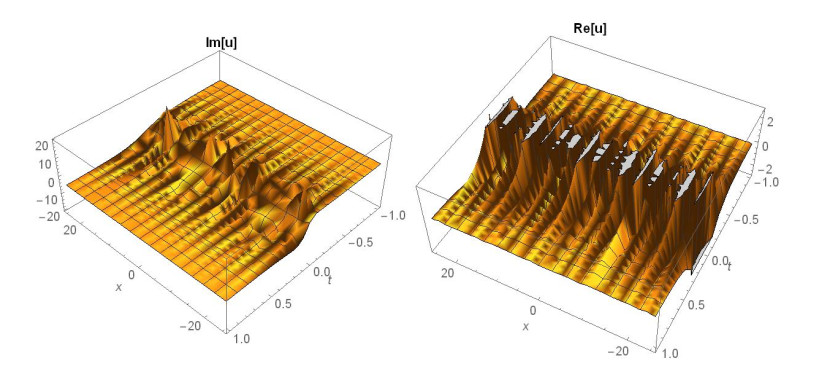
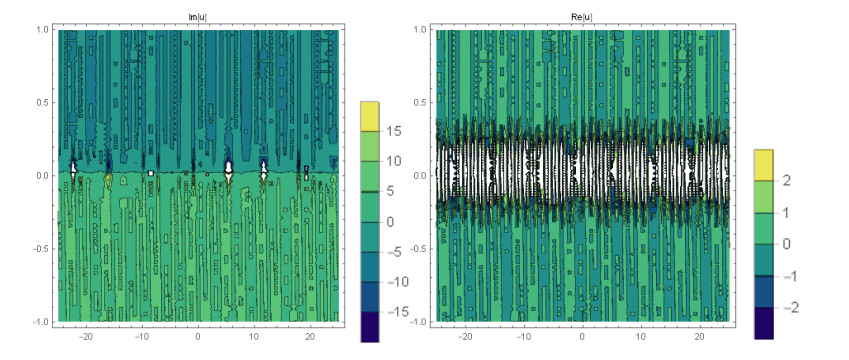
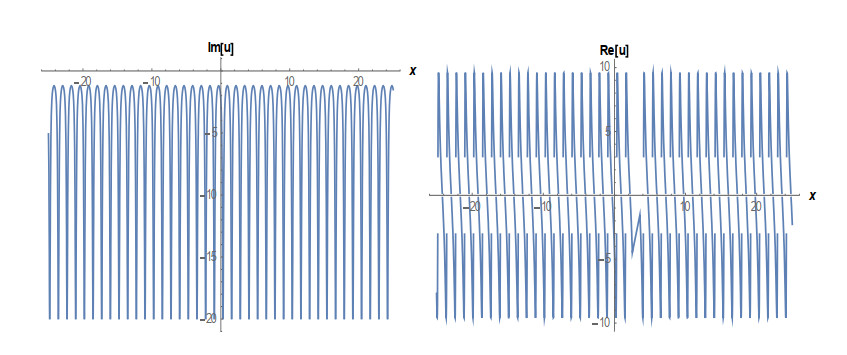
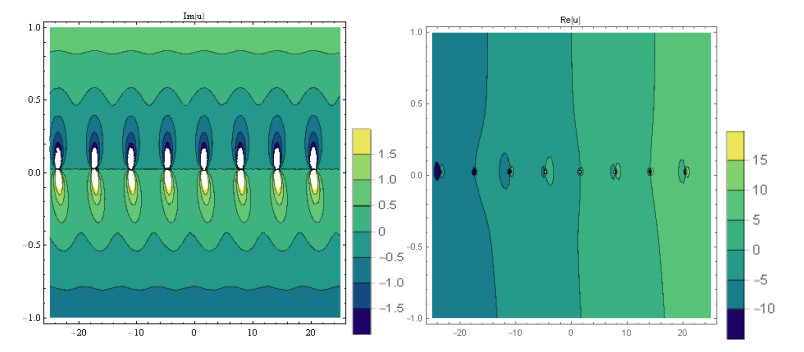
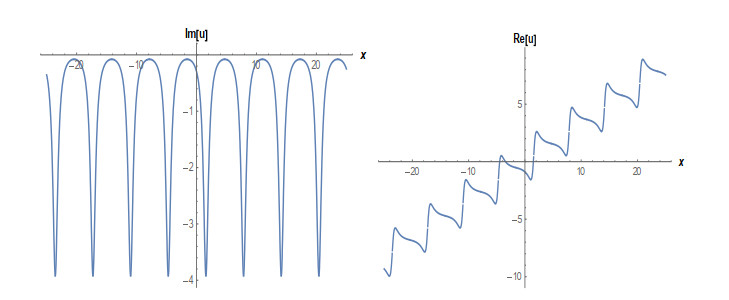
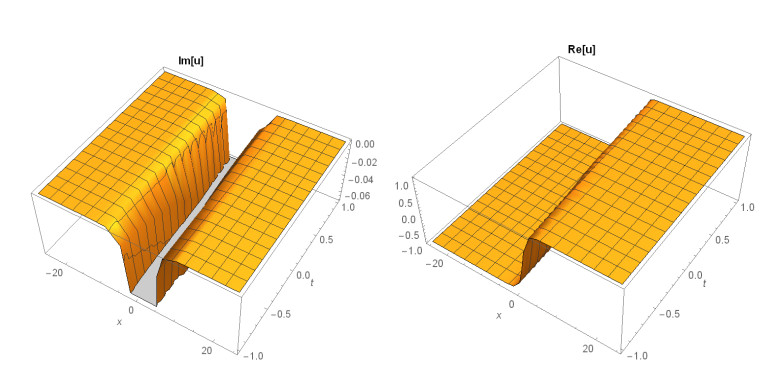
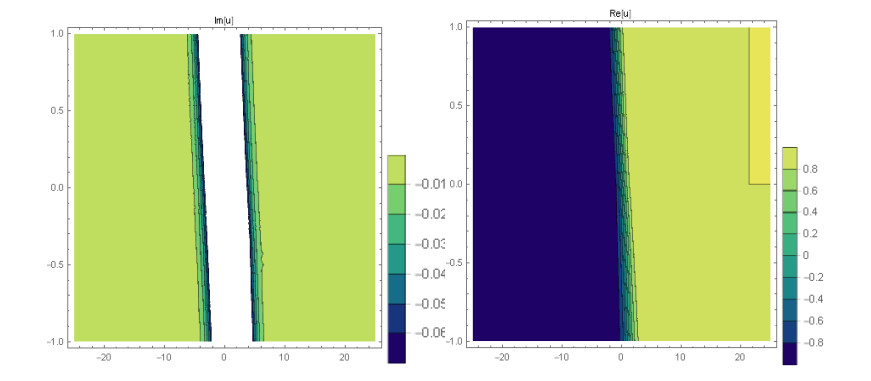
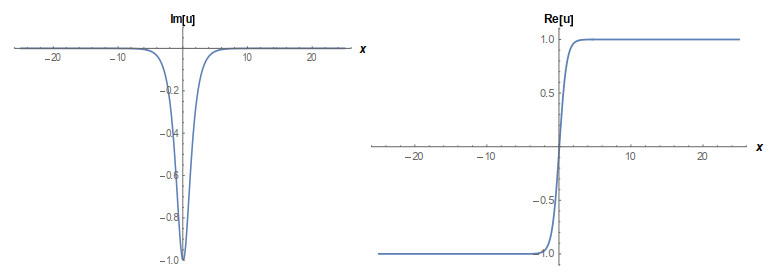
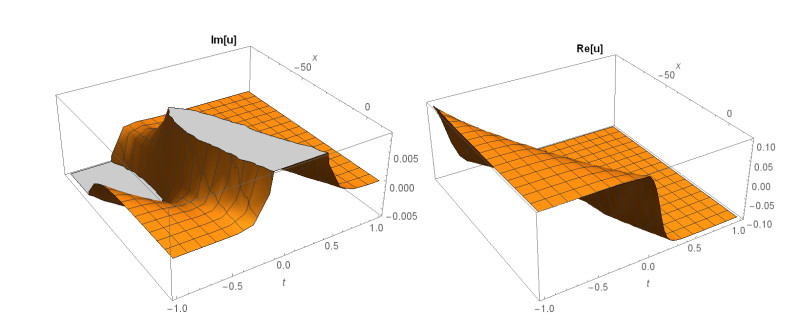
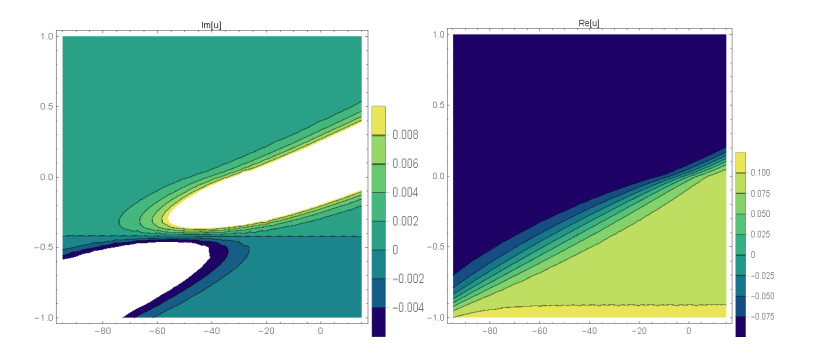
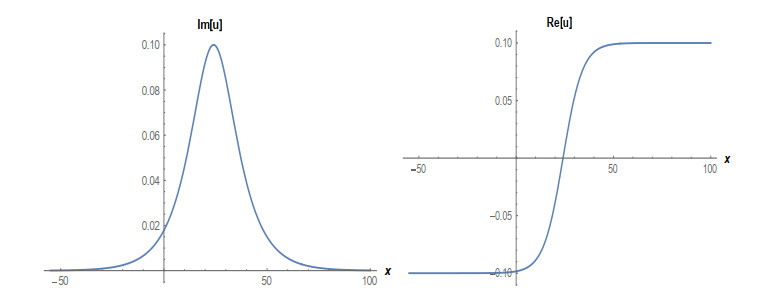
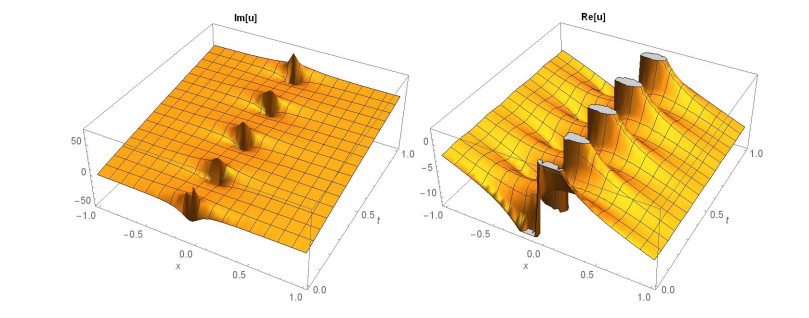
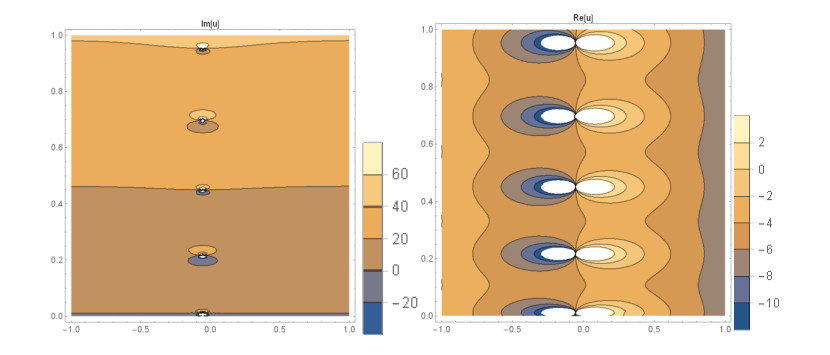
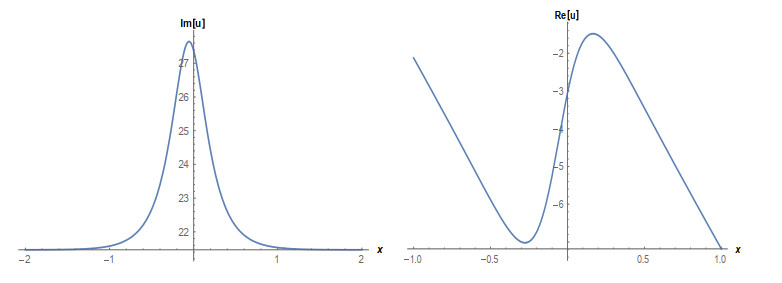
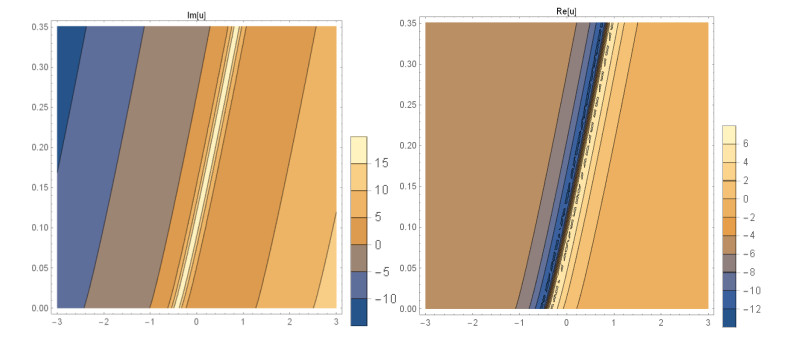
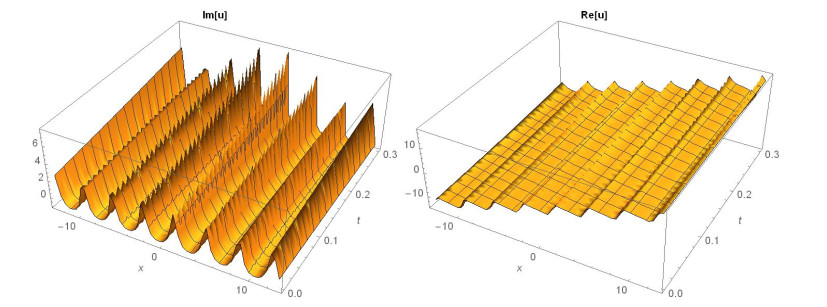
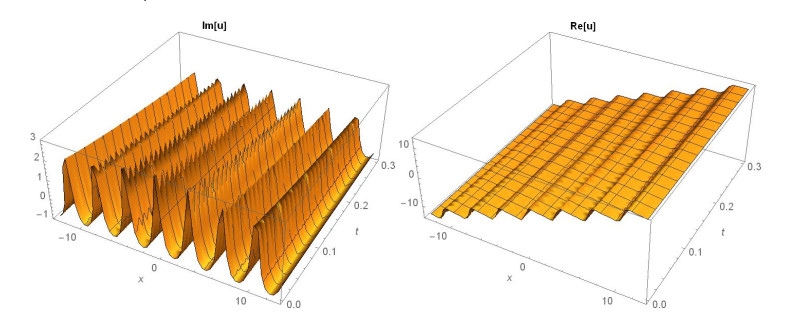
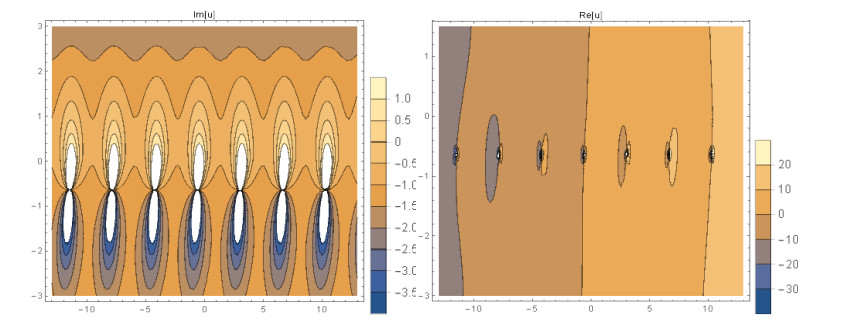
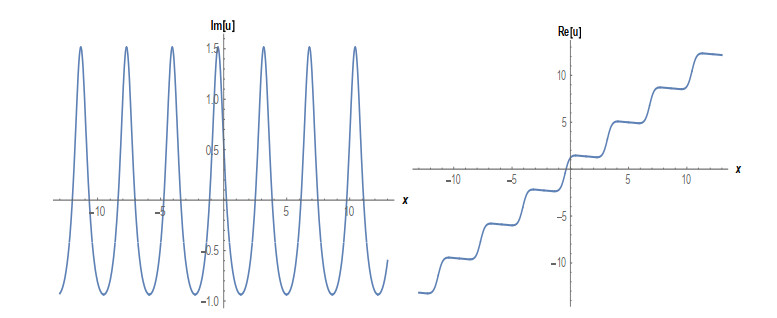
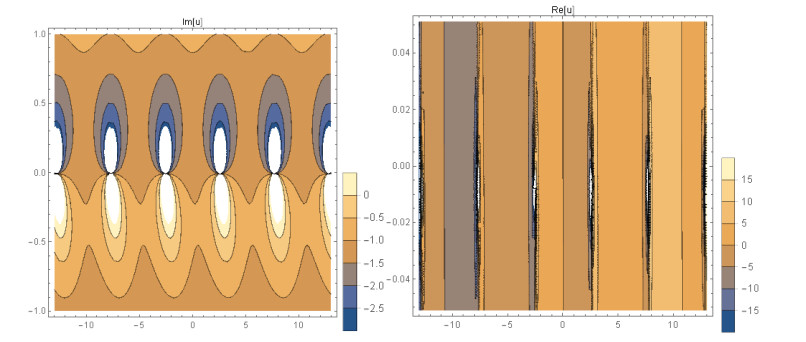
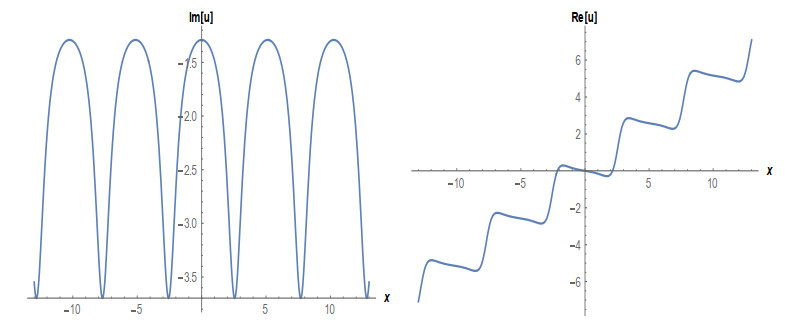
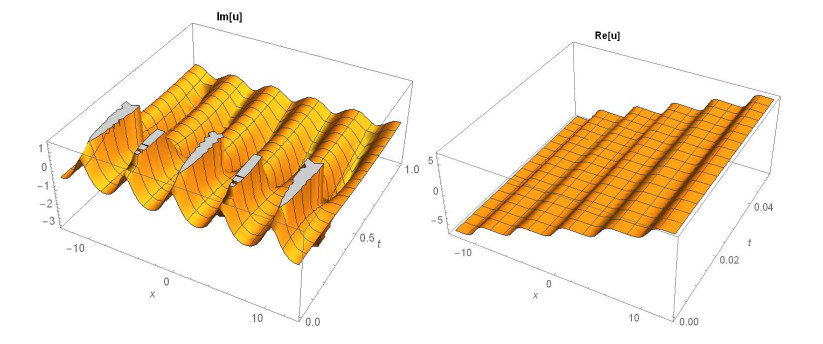
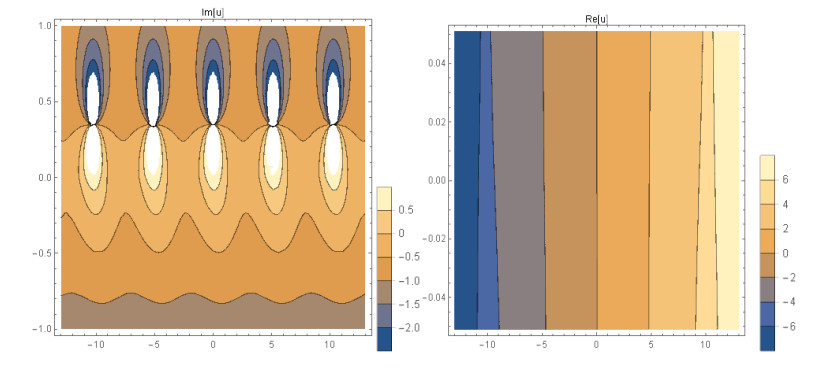
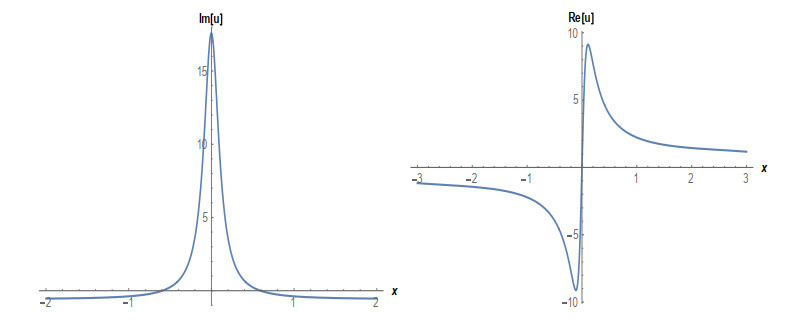
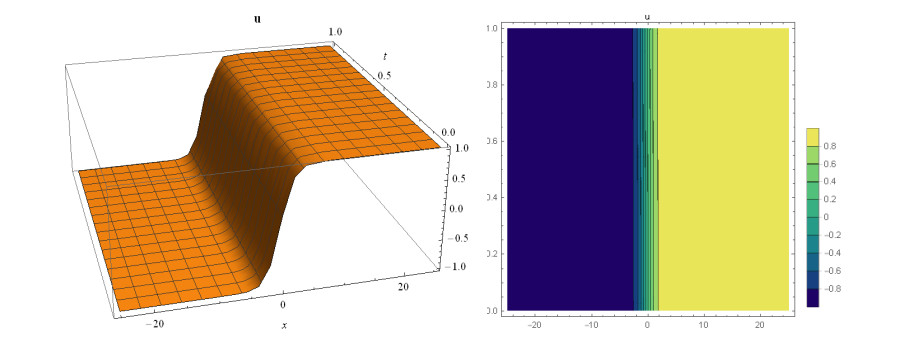
Case 1: (Figures 1 and 2) When ${A_0} = - {A_2}, {A_1} = {B_1} = {B_2} = 0, k = - \frac{{{A_2}}}{2}, \lambda = - \frac{{m\left( { - 4{m^2}\alpha + A_2^4} \right)}}{{2\beta A_2^2}},$ gives the solution in the form,

where ${A_2}, m, \alpha , \beta$ are real constants with non zero.

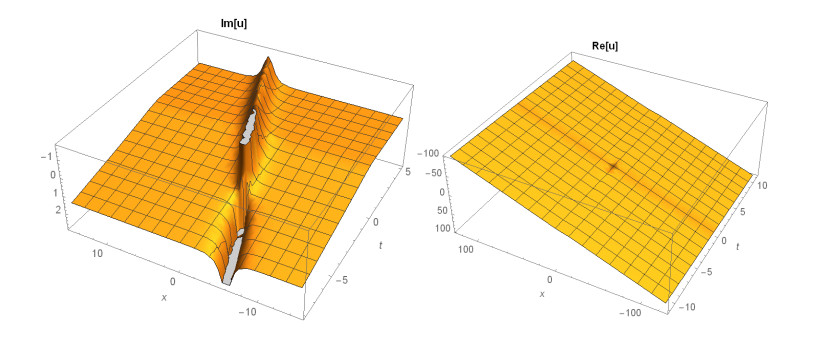
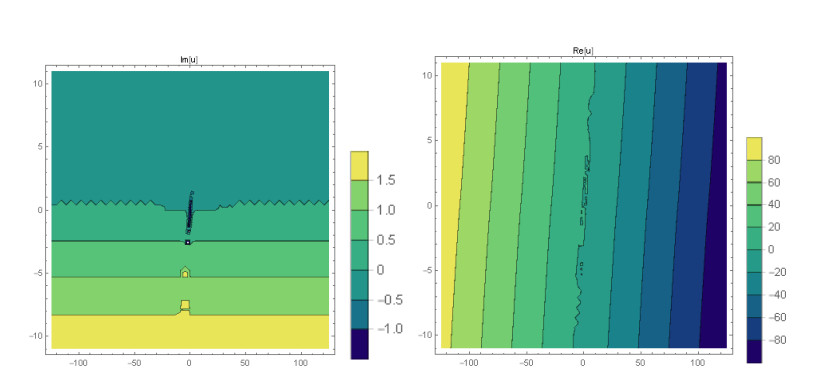
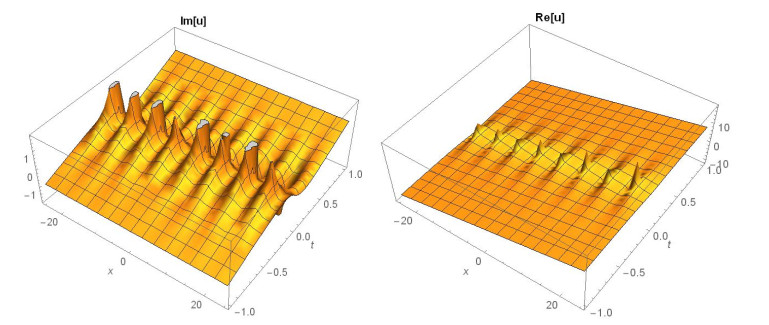
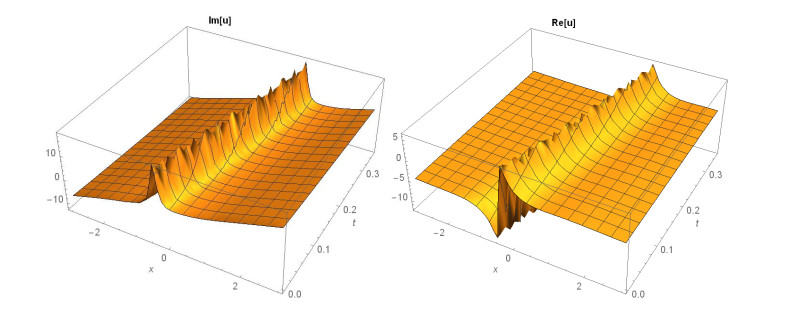
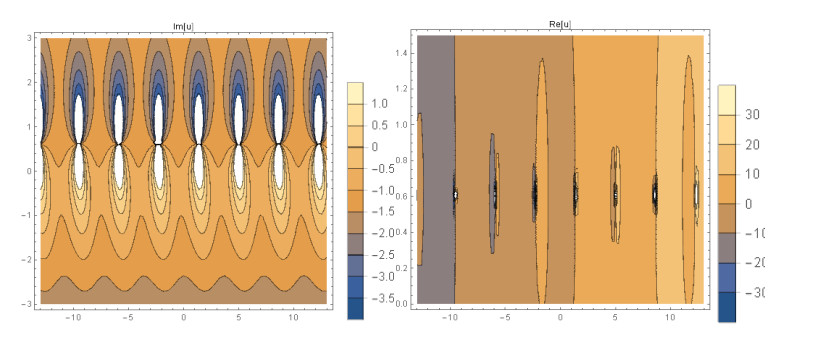
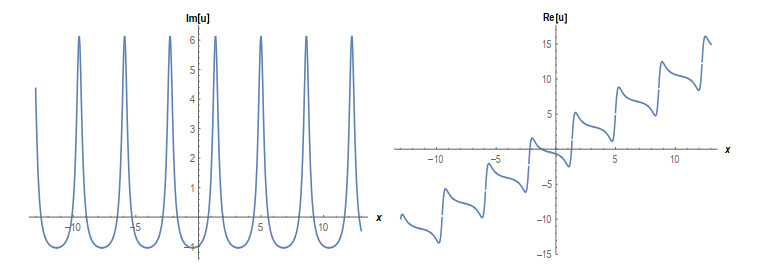
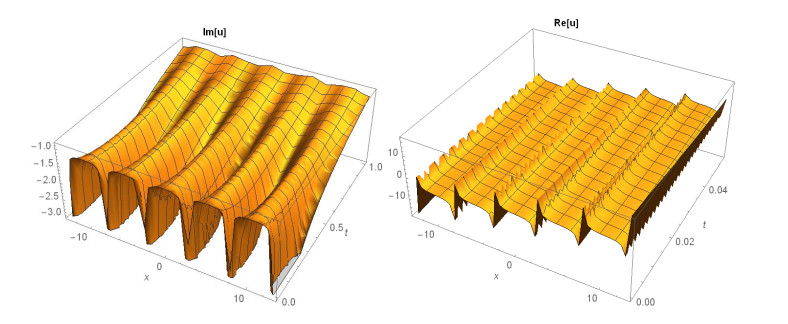
Case 2. (Figures 3-5) If ${A_1} = 0, {A_2} = - \frac{{3{A_0}}}{2}, {B_1} = 0, {B_2} = - \frac{{3i{A_0}}}{2}, k = \frac{{3{A_0}}}{2}, \beta = \frac{{16{m^3}\alpha + 81mA_0^4}}{{72\lambda A_0^2}},$ produces

where ${A_0}, m, \lambda$ are real constants with non zero.

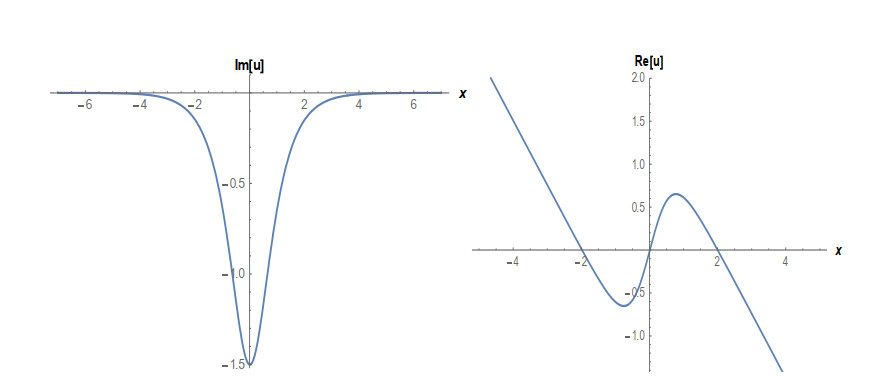
Case 3. (Figures 6-8) Selecting as ${A_0} = i{B_2}, {A_1} = {B_1} = 0, {A_2} = - i{B_2}, \beta = \frac{{m\left( { - {m^2}\alpha + B_2^4} \right)}}{{2\lambda B_2^2}}, k = i{B_2},$ gives

where ${B_2}, m, \lambda$ are real constants and non zero.

Case 4. (Figures 9-11) Choosing ${A_0} = \frac{{i{B_2}}}{2}, {A_1} = {B_1} = 0, {A_2} = - i{B_2}, k = i{B_2}, \alpha = - \frac{{2\beta B_2^2 + mB_2^4}}{{{m^3}}},$ gives

where ${B_2}, m, \lambda$ are real constants and non zero.

Case 5. (Figures 12-14) When we select another coefficients for obtaining analytical solution as following, ${A_0} = k, {A_1} = {B_1} = 0, {A_2} = - k, {B_2} = - ik, \beta = \frac{{ - {k^4}m + \alpha {m^3}}}{{2{k^2}\lambda }},$ gives

in which $k, m, \lambda ,$ are real constants and non zero.

Case 6. (Figures 15-17) Once ${A_0} = - {A_2}, {A_1} = {B_1} = 0, {B_2} = - i{A_2}, k = - {A_2}, \lambda = \frac{{\alpha {m^3} - mA_2^4}}{{2\beta A_2^2}},$ it is formed as

in which $k, m, \lambda ,$ are real constants and non zero.

3.2.   Application of IBSEFM

This section applies IBSEFM to the governing model Eq (1) for obtaining some new complex analytical solutions. Let's consider the following wave transformation into Eq (1)

being $k, m, c$ are non-zero, $\theta$ is conformable derivative. Putting Eq (30) into Eq (1) and after some simple calculations, we find

where $V = U',$ and also both integral constants are zero. With the aid of homogeneous balance principle between $V''$ and V², we get relationship for $n, m$ and $M$ according to IBSEFM properties

Using this relationship, we can find many new complex solutions for governing model as following cases.

Case 1: When we take $M = 3, m = 1$ and $n = 5$, then we can obtain follows,

where $F' = wF + d{F^3}, \, \, {a_5} \ne 0, \, \, \, {b_1} \ne 0$. If we put Eqs (33, 35) into Eq (31), we get a system of algebraic equations of $F$. Solving these models yields different coefficients as follows

Case 1.1. (Figures 18-20) For $b \ne d$, we select follows

These coefficients presents following solution for governing model

where $f\left({x, y, t} \right) = \frac{{4d\sqrt 3 }}{{\sqrt {{a_5}} }}\left({x + iy - i\frac{{\left({48{d^2} - \alpha {a_5}} \right)}}{{2\beta \theta {a_5}}}{t^\theta }} \right).$

Case 1.2. (Figures 21-23) Taking as $b \ne d$, and selecting follows

finds

where $\alpha , \beta , \lambda , \varepsilon$ are real constants and non-zero.

Case 1.3. (Figures 24-26) Gaining as $b \ne d$, and selecting follows

gives the following complex solution to the governing model

where $\alpha , \beta , \lambda , \varepsilon$ are real constants and non-zero.

Case 1.4. (Figures 27-29) With $b \ne d$, considering into account as

gives the following complex solution to the governing model

where $f\left( {x, y, t} \right) = \frac{{i\sqrt 6 }}{{\sqrt {{b_1}} }}\left( {x + iy + \frac{{i\left( {6 + \alpha {b_1}} \right)}}{{2\beta \theta {b_1}}}{t^\theta }} \right)$ and ${b_1}, \alpha , \beta , \theta , \varepsilon , {a_4}$ are real constants and non-zero.

Case 1.5. (Figures 30-32) When we consider as

we gain

where $\alpha , \beta , d, \varepsilon$ are real constants and non-zero.

Case 1.6. (Figures 33-35) When we consider as

we gain

where $\alpha , \beta , d, \varepsilon$ are real constants and non-zero.

4.   Discussion, comparision and physical explanations

This paper finds entirely new complex analytical solutions for governing model with the help of two powerful approaches such as SGEM and IBSEFM. These solutions have some more important physical features. The hyperbolic secant (bright soliton) arises in the profile of a laminar jet, the hyperbolic tangent (dark soliton) arises in the calculation of magnetic moment, the hyperbolic sine (periodic wave solution) arises in the gravitational potential, and the hyperbolic cotangent (singular soliton) arises in the Langevin function for magnetic polarization ^[76]. In this sense, Eq (24) is a dark soliton solution. Eqs (25-29) are used to explain the combined dark-bright soliton solutions. It is estimated that these solutions may be related to such physical meanings. When we compare these solutions in ^[21], one can see that these solutions entirely new complex dark, mixed dark-bright and dark soliton solutions to the governing model.

In IBSEFM, if we consider more values of $M = 3, m = 2$ as $n = 6$, we obtain another new solution for the governing model as

where $F' = wF + d{F^3}, \, \, {a_6} \ne 0, \, \, \, {b_2} \ne 0$. In this regards, this projected technique is a powerful tool for obtaining new analytical solutions for the nonlinear models.

5.   Conclusions

This paper studies on the nonlinear Date-Jimbo-Kashiwara-Miwa equation with conformable which defines to explain wave propagation. By using SGEM and IBSEFM, we reach the some new dark, bright, singular solitons and complex wave solutions. All the found wave solutions in this study are entirely new and they have satisfied the nonlinear Date-Jimbo-Kashiwara-Miwa equation with conformable. Under the suitable chosen of the values of parameters, we plotted 2D, 3D and contour simulations of the wave solutions. From these Figures (1-35), it may be observed that wave solutions to the studied nonlinear model show the estimated wave propagations.

Acknowledgments

We would like to thank you for reviewers for their valuable comments on developing this paper.

This paper was supported by University of Messina (Italy) and National Groups of Mathematical Physic GNFN-INdAM (Italy). Moreover, This projected work was partially (not financial) supported by Harran University with the project HUBAP ID:20124.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.