1.
Introduction
The report released by the American Heart Association states that cardiovascular disease maintains its status as the primary global cause of death, claiming over 17.6 million lives annually, with forecasts suggesting this figure will rise to exceed 23.6 million by 2030 [1]. The coronary artery, the vascular system dedicated to providing nutrients and energy to the heart, has been the main research focus in recent years.
The lumped parameter model, also known as the 0D model, was first developed by Otto Frank in 1898. It is the simplest mathematical model to describe the cardiovascular system and it is frequently employed to simulate the systemic characteristics of the cardiovascular system. The 0D model is known for its simple structure, easy-to-understand features, low computational cost, and efficient computing power. It has a wide range of simulations and can cover many fields and application scenarios. Compared with the coronary artery multi-scale model, its accuracy is relatively low and difficult to handle in the simulation of some complex physiological conditions, but it is still an effective modeling method in many fields [2]. Rideout et al. simulated the human pulmonary circulation system [3], accounting for the interactive effects of left atrial and right ventricular contractions on pressures in the pulmonary veins. They also developed an analog computer model to research the human cardiovascular system[4,5], with a particular emphasis on pressure and flow dynamics within veins, encompassing gravitational effects, respiration, venous collapse, and valve function. Liang et al. [6] developed a human cardiovascular system lumped parameter model featuring a detailed compartmental representation of both the main vascular circulations and the heart.
Wang et al. [7] employed a closed-loop circuit model to simulate the left coronary arterial system and studied the impacts of stenosis, heart rate, and other factors on coronary hemodynamics. Mantero et al. [8] studied the role of the coronary artery bed in the cardiovascular system. Pietrabissa et al. [9] improved the cardiovascular system closed-loop circuit model, incorporating a more intricate depiction of the left coronary artery, which was also utilized to assess the coronary artery hemodynamics of surgical reconstruction. Duanmu et al. [10] established a new closed-loop lumped parameter model for the whole coronary network (including the right coronary artery). They first proposed the head loss model, which describes the physiological phenomenon of a sudden pressure drop at the coronary artery's entrance.
Since considering the entire coronary artery becomes prohibitively expensive computationally, the model needs an outflow boundary condition to simulate the truncated tree. The three-element Windkessel model, put forth by Westerhof et al. [11], is the most classical lumped parameter model and is widely employed as the outflow boundary condition. At present, there is no strict theoretical support for the selection of parameters in the Windkessel model, which is usually obtained through experiments. Olufsen et al. [12,13,14] proposed the structured tree model that can also serve as a boundary condition, with its evaluation based on the root radius of each blood vessel.
Arterial system stenosis can cause a variety of cardiovascular diseases. Zhang et al. [15] studied carotid artery stenosis. Pagiatakis et al. [16,17] studied the influence of stenosis eccentricity and stenosis severity on coronary bifurcation lesions. The fractional flow reserve (FFR), a nondimensional index, can combine the physiological effects of the coronary artery with the severity of stenosis to evaluate the hemodynamic significance of the coronary artery disease noninvasively. FFR is referred to as the ratio of the maximum hyperemic blood flow in the coronary artery with stenosis to the maximum hyperemic blood flow that occurs in the same coronary artery under normal conditions [18,19,20]. Clinical research has demonstrated that FFR between 0.75 and 0.8 (that is, under maximum congestion conditions, when the pressure of the distal coronary artery is 75–80% of the proximal) is usually considered to be the threshold for ischemic attacks. Lesions below this threshold are considered to be the cause of ischemia [21,22].
Our purpose is to establish a coronary artery lumped parameter model that can effectively simulate its blood supply capacity. The aortic valve fluid-structure interaction (AV FSI) simulator can simulate the interaction between the heart and the arterial system and provide an in-depth understanding of the function of the cardiovascular system. The 0D model simplifies the description of the cardiovascular system and provides a series of algebraic equations to simulate changes in blood flow and pressure. In this paper, combining the AV FSI simulator and the 0D model can make full use of the advantages of both to achieve more accurate simulation and prediction. The head loss model is incorporated at the entrance of the coronary artery. The outlet connects with the symmetric structured tree model proposed by Olufsen et al. The resistance-inductance-capacitance (RLC) parameters in the 0D coronary artery model are optimized in a special way. In addition, the coronary artery stenosis model is established by changing the local RLC parameters, and the blood supply capacity of the coronary artery under different degrees of stenosis is analyzed using FFR and relative flow.
2.
Models
2.1. AV FSI simulator
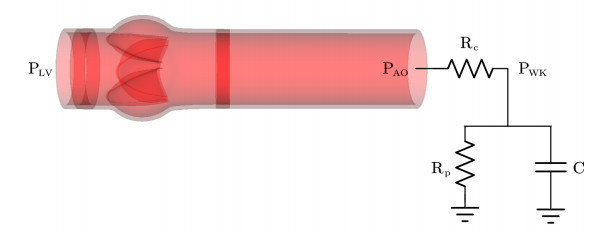
The AV FSI simulator is built using a porcine pericardial valve, as demonstrated in our previous research [23,24]. The thickness of the valve leaflet is 0.04 cm, and the outer wall connecting with it has a thickness of about 0.15 cm and an inner diameter of 1.3 cm. The length of the whole blood vessel is 13 cm. The three-element Windkessel model, frequently used to simulate the afterload [25], is coupled in the outlet. Figure 1 shows the schematic illustration of the AV FSI simulator.
Aortic valve leaflets are considered to be nonlinear, incompressible, anisotropic, and hyperelastic. Specifically, the strain energy function of aortic valve leaflets [26] is
in which k1, k2, C10, and C01 are material parameters; k1, k2 are the material constants related to the stress and the dimensionless parameter, respectively; C10, C01 are utilized to characterize the properties of the matrix material. There are two strain invariants, I1=tr(C) and I4=f0⋅(Cf0), along with the reference fiber direction (f0). C is the right Cauchy-Green deformation tensor. These parameter values are presented in Table 1.
The Windkessel model [28] is
in which C represents the vascular compliance, PWK represents the pressure stored within the Windkessel model, Rp represents the peripheral resistance, and Rc represents the characteristic resistance. These parameter values are presented in Table 1.
In the Immersion Boundary/Finite Element (IB/FE) method [29], the fluid domain (Ωf(0)) uses the Eulerian grids and finite difference discretization, while the structure domain (Ωs(0)) employs the Lagrangian grids and finite element discretization [23,30]. The influence of the structure on the fluid is represented by incorporating a force source term into the Navier-Stokes equation [31]. The Dirac delta function δ(x) is utilized to establish the coupling between the structure described in Lagrangian form and the fluid represented in Eulerian form. The IB/FE method can be described as follows [31,32]:
where x=(x1,x2,x3)∈Ω represents the Euler coordinate system, and Ω represents the physiil region occupied by the aortic valve model. X=(X1,X2,X3)∈Ωs(0) represents the Lagrange coordinate system. χ(X,t)∈Ω represents the Eulerian coordinate of the position that a Lagrangian coordinate point X occupies at time t. u(x,t) represents the Eulerian velocity, and p(x,t) represents the Eulerian pressure. fe(x,t) and Fe(X,t) are the Eulerian elastic force and the Lagrangian elastic force, respectively. Pe(X,t) represents the first Piola-Kirchhoff stress tensor, which can be derived from the strain energy function. In general, the density of blood (ρ) and its dynamic viscosity (μ) are assumed to remain constant, e.g., ρ=1.0 g/cm3 and μ=4.0×10−3 kg/m⋅s. For more details of the AV FSI simulator and the IB/FE method, see [24,29,30].
2.2. Coronary artery lumped parameter model
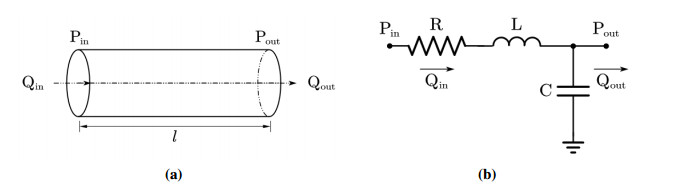
The blood regarded as a continuous, incompressible Newtonian fluid, and the blood vessel has a cylindrical wall that is rigid [33,34]. According to the analogy between the hemodynamic system and the circuit system, we can establish an equivalent circuit model of a blood vessel; see Figure 2. The blood flow satisfies the Newton equation and the continuity equation for any minuscule artery length [7]. The governing equations [7,35] for flow rate and pressure of each blood vessel is
in which Pin and Pout are the average inlet and outlet pressures that vary with time. Similarly, Qin and Qout represent the average inlet and outlet flow rates changing with time, respectively. R, L, and C are the blood flow viscous resistance, blood flow inertia, and vascular compliance, respectively, analogous to the resistance, inductance, and capacitance in the circuit system.
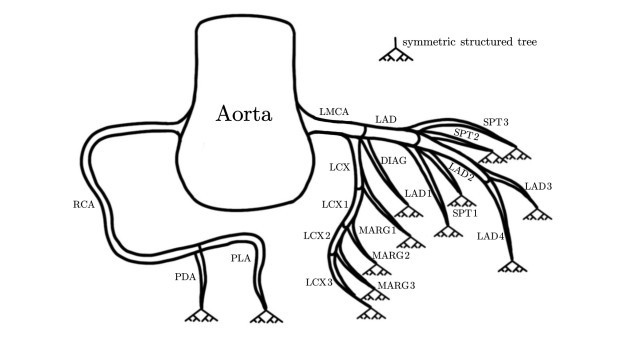
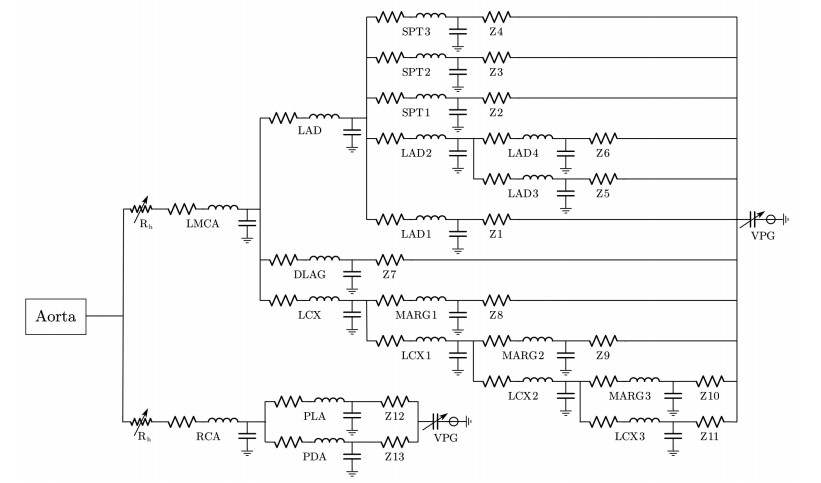
The coronary artery emerges from the aortic sinus at the root of the aorta and is divided into the left and right branches that contain many vascular branches. Based on the CT of a patient-specific coronary [10] and literature [9], we consider a coronary artery model composed of 20 segments: 17 segments attributed to the left coronary artery (three additional septal branch (SPT) vascular segments are added) and 3 segments pertaining to the right coronary artery. The schematic diagram of the coronary artery simplified structure model is shown in Figure 3, and the 0D model of the whole coronary artery is detailed in Figure 4. Each segment of the coronary artery can be modeled with Eq (2.4). The complete system can be mathematically modeled by the ordinary differential equations (ODEs) as
In this system, y denotes the vector consisting of unknown vessel flow rates and pressures, A represents a square matrix composed of parameter values, and b represents a column vector derived from the specified boundary conditions.
Initial conditions, inlet and outlet boundary conditions, bifurcation boundary conditions, and so on are needed to solve the hemodynamics of the coronary artery described by Eq (2.5). In this study, we give the following conditions:
(1) After several numerical simulations, it is observed that the initial conditions mainly have a significant effect on the speed of reaching the stable solution but have a small effect on the final numerical results of the steady state. According to the Wiggers diagram [36], the initial pressure and flow rate at each segment can be set to 80 mmHg and 0 ml/s.
(2) In order to obtain the physiologically realistic blood pressure and flow rate in the coronary artery, the aortic root pressure calculated by the AV FSI simulator (see Section 2.1) is selected as the inlet boundary condition.
(3) At the entrance of LMCA and RCA, the sudden decrease in blood vessel radius will lead to an abrupt decrease in blood pressure. The pressure drop can be described by the following empirical formula:
where ζ=2.88 is the local energy loss coefficient [37] and v is the average velocity. Therefore, the flow resistance Rh can be calculated using the following Eq [10]:
in which A represents the cross-sectional area of the blood vessel. It can be seen that Rh is a variable flow resistance proportional to the flow rate.
(4) Each vessel's terminal is connected to the capillaries downstream, making it challenging to assess the boundary conditions at the outlet. An outflow boundary condition, the structured tree model presented by Olufsen et al. [12], has been used in literature, in which each vessel is modeled as a compliant linear segment, and the root impedance (Z) depends largely on the minimum vessel diameter at the end truncation (rmin). The structured tree has nothing to do with the actual geometry of the vessel but a topological structure based on the literature data [14]. In order to simplify the model, we choose the symmetric structured tree model and set rmin = 0.01 mm, indicating that the structured tree terminates when the vessel radius is less than 0.01 mm. The root impedance calculation formula [13] of the N-generation symmetric structured tree model is
in which λ=50 defines the ratio of vessel length to radius [38], r0 represents the root radius of the initial vessel, and the ratio of the radius of the daughter vessel (rd) to the radius of the parent vessel (rp) is α=0.778. The terminal impedance of each coronary artery outlet is shown in Table 2.
(5) Blood flow in the coronary artery is distinct from that in other parts of the arterial system, as it is significantly affected by the relaxation and contraction of the heart. In order to simulate coronary blood flow veritably, it is necessary to include the cardiac pressure acting on the coronary artery vessel (i.e., ventricular pressure) [39]. At the end of the model, the VPG is connected to simulate the intramyocardial pressure, which selected left ventricular pressure according to the location of the coronary artery.
(6) The principles of flow conservation and pressure continuity are ensured at the points where blood vessels bifurcate. Specifically, the blood flow in the parent vessel is equivalent to the aggregate sum of the flows in all its daughter vessels, and the blood pressure of the parent vessel is equal to the blood pressure of each daughter vessel.
In this paper, a fourth-order Runge-Kutta method [40] is employed for the solution of the ODEs describing the hemodynamics of the coronary artery. In order to obtain stable numerical results, each simulation performs three cycles.
2.3. RLC parameters optimization
Generally, there are two methods to determine the RLC parameter values in the 0D coronary artery model. One is the manual estimate method, which depends on experimental measurements, empirical data, or iterative adjustment of parameters. This method takes a lot of time. The other is calculated through the lumped parameter modeling formula, but the formula is not unique, there is [7],
in which the Young's modulus of blood vessel G=2×105 Pa [41], l is the length of the blood vessel, D represents the diameter of the blood vessel, and the thickness of the blood vessel wall h=0.08D [42]. These parameter values related to the anatomical structure of the patient's coronary artery can be obtained through a series of medical examinations, such as coronary angiography and echocardiography.
In order to obtain realistic coronary artery blood pressure and flow rate, the value range of RLC parameters in the 0D coronary artery model is preliminarily estimated by Eq (2.9), and then optimized by the intelligent optimization algorithm, common artificial intelligence [43], genetic algorithm [44], and particle swarm optimization (PSO) algorithm [45]. The PSO algorithm was first developed by Russell Eberhart and James Kennedy in 1995, inspired by the foraging mode of birds (the birds allow groups to find optimal purposes through information sharing). In the PSO algorithm, each optimization solution is simulated as a 'particle'. Each particle navigates through the search space, continually updating its position and velocity information to iteratively converge toward the optimal solution. The algorithm is simple, easy to understand, and easy to program. It has fast convergence speed and can find the approximate optimal solution to the problem in a short time. The number of parameters is small, and the adjustment of parameters is relatively simple [46]. It is suitable for solving high-dimensional optimization problems. The summary of the PSO algorithm can be seen in Appendix A.
The optimization objective function is defined as the root mean square error between the reference solution (yn) and the numerical result (y′n), expressed as:
in which K represents the number of sample points. The optimal results are obtained when the objective function attains its minimum value. The termination condition is to reach the maximum number of iterations or obtain an acceptable satisfactory solution.
2.4. Coronary artery stenosis model
Coronary stenosis leads to diminished blood flow reaching the heart, causing myocardial ischemia, which in turn leads to various cardiovascular diseases. It is necessary to research the influence of coronary artery stenosis on local blood flow. To establish the lumped parameter model of coronary artery stenosis, we adjust the RLC parameter values of the corresponding vascular segments in our 0D coronary artery model. The reduction rate of the vascular cross-sectional area (β) is defined as the ratio between the stenosed vessel's cross-sectional area (As) and the healthy cross-sectional area (A0), namely,
According to the Eq (2.9), the relationship [47] between the RLC parameter values in the stenosis state and the healthy state can be derived as follows:
where Rs, Ls, and Cs represent the resistance, inductance, and capacitance in the stenosis state, respectively. R0, L0, and C0 represent the ones in the healthy state. The value (1−β) represents the vascular stenosis rate, usually expressed as a percentage. It is assumed that other parameters remain constant in the stenosis state.
FFR quantifies the percentage of normal, hyperemic myocardial blood flow retained when the supplying artery has stenosis [17], has become an important clinical indicator for judging the degree of arterial stenosis that prevents blood flow from reaching the myocardium [20], and is also the gold standard for evaluating whether coronary artery stenosis causes ischemia [48]. In clinical practice, FFR can be expressed as the ratio between the time-averaged proximal pressure Pp and the time-averaged distal pressure Pd in coronary artery stenosis (under conditions of maximal myocardial hyperemia) [20], i.e.,
For the flow rates predicted by the 0D model, the average flow is calculated by integrating the flow rate waveform over one heartbeat. This average flow is subsequently normalized by dividing it with the average flow rate that would occur in the absence of stenosis, thus obtaining the relative flow [7]. Relative flow represents the change of flow under different stenosis degrees based on normal conditions. It can be employed to compare the blood flow under different conditions and is an effective index for gauging the coronary artery's ability to supply blood to the myocardium.
The cross-sectional area of the coronary artery is decreased by 20%, 40%, 60%, and 80% to simulate different degrees of stenosis. The pressure-related FFR and flow rate-related relative flow are analyzed to study the blood supply capacity under coronary artery stenosis.
3.
Results
3.1. Numerical results of the AV FSI simulator
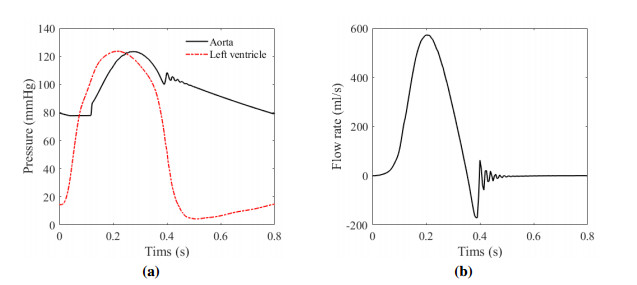
In all numerical simulations, the heart rate is set to 75 beats/min, so one cardiac cycle is 60/75 = 0.8 s. Using the IBAMR open source software platform (http://github.com/IBAMR/IBAMR) to implement the AV FSI simulator introduced in Section 2.1, the aortic root pressure and the flow rate through the aortic valve are in line with the real physiological conditions, as shown in Figure 5. The systolic/diastolic blood pressure of the aorta is maintained within the normal physiological range (120/80 mmHg). With the aortic valve opening, blood flows into the aorta, and the flow rate increases to a peak of 572.43 ml/s. When the aortic valve closes, regurgitation occurrs and the backflow rate can reach up to 170.70 ml/s. Over the course of a single cardiac cycle, the volume of blood that flows into the aorta is 89.73 ml. The numerical results align well with the experimental data reported in articles [49] and [50].
It should be noted that there are oscillations in the pressure and flow rate curves in Figure 5, which are mainly caused by numerical effects and also involve physiological effects. The oscillations occur at about 0.4 s. This period is the stage when the aortic valve is about to close completely, and the hemodynamic behavior is particularly complex. The AV FSI simulator cannot accurately simulate this phenomenon.
3.2. Parameter optimization results
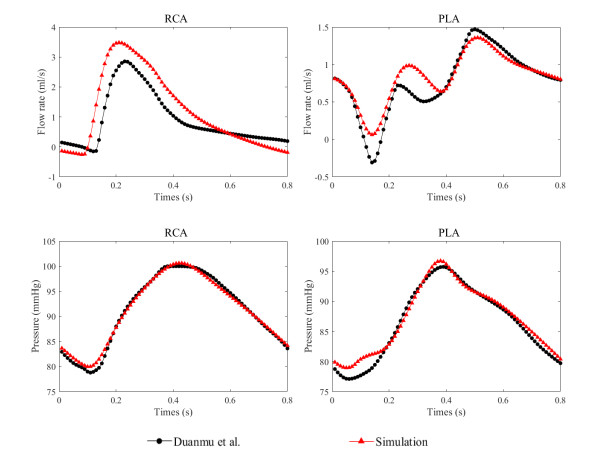
In order to obtain the parameters that can better describe the properties, the RLC parameters in the coronary artery lumped parameter model are optimized as introduced in Section 2.3. For the right coronary artery model, the numerical results of Duanmu et al. [10] (the flow rate and pressure of RCA and PLA) are selected as the reference solution, and their left ventricular pressure and aortic pressure are used as the boundary conditions to complete the parameter optimization. The comparison results are shown in Figure 6. The black circular data are the results of Duanmu et al. [10], and the red triangle data are numerical results after parameter optimization. It can be seen that the numerical results of the flow rate and pressure after parameter optimization are in good agreement with the reference solution. The fitness values of pressure and flow rate waveforms are calculated separately. Specifically, the pressure-related fitness value is 0.195, while the flow rate-related fitness value is 0.239. Therefore, the optimization result of the pressure waveform seems to be more ideal than that of the flow rate waveform.
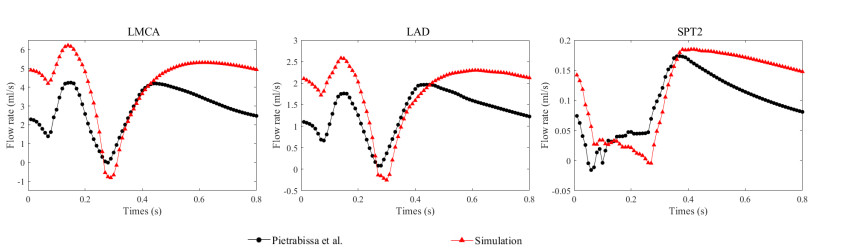
For the left coronary artery model, the numerical results of Pietrabissa et al. [9] (the flow rate of LMCA, LAD, and SPT2) are selected as the reference solution, and their left ventricular pressure and aortic pressure are used as the boundary conditions to obtain the parameter optimization values. Figure 7 presents the comparison of the flow rate numerical results with those obtained by Pietrabissa et al. [9]. It can be seen that the numerical results of the flow rate after parameter optimization are similar to the waveforms of the reference solution. After parameter optimization, the objective function values of the left and right coronary arteries calculated by Eq (2.10) are 0.526 and 0.209, respectively. This shows that optimizing the right coronary artery model is easier than optimizing the left coronary artery model. On the one hand, the complexity of the structure of the left and right coronary arteries is different; the left coronary artery has more branches, its structure is more complex, and the parameter optimization is more difficult. On the other hand, the choice of the reference solution is different. The left coronary artery lacks the pressure reference solution, and the number of reference solutions is relatively scarce. To address this issue, we employed two strategies. First, the RLC parameters with an ideal optimization effect are fixed, reducing the number of variables while dynamically adjusting them based on optimization outcomes. Second, the numerical results with an ideal optimization effect can be approximated as a reference solution, increasing the available data. Table 2 lists the optimized parameter values of the 0D coronary artery model.
3.3. Healthy condition
We first set the aortic root pressure calculated by the AV FSI simulator as the inlet boundary condition, and the corresponding flow rate of each segment of the left coronary artery is shown in Figure 8. The blood flow dynamics in the coronary artery differ from those in other sections of the arterial system. During the systolic period (the time is 0–0.39 s), the left ventricle contracts, the intramyocardial pressure increases, the extravascular pressure of the left coronary artery increases, and the blood flow is restricted, resulting in a decrease in the flow rate, which is not synchronized with aortic flow. Then, it increases with the decrease in intramyocardial pressure until entering the diastolic period (the time is 0.39–0.8 s). The trend is well-captured in Figure 8. The relative position of the coronary artery in the heart also has an effect on the flow rate. For example, the flow rate of the epicardial coronary artery (e.g., LMCA, LAD, and LCX) in the systolic period is not as pronounced as that of the endocardial coronary artery (e.g., SPT2). Specifically, the flow rate of the endocardial coronary artery decreases rapidly at the beginning of the systolic period and maintains a low level for a period of time. The flow rate of the epicardial coronary artery decreases slowly during systole, and there is a slight increase. During diastole, the flow rate of the endocardial coronary artery and epicardial coronary artery increases rapidly.
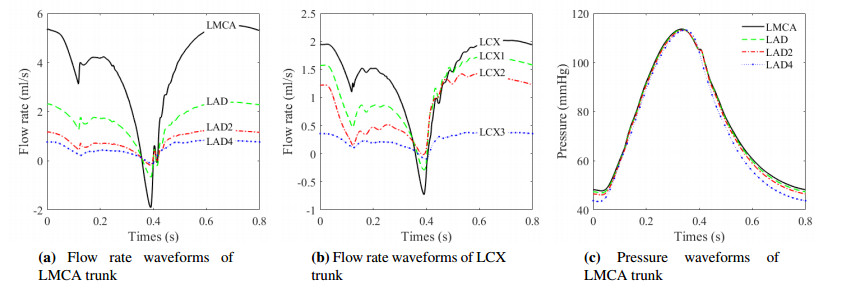
Figure 9(a) depicts the flow rate waveforms at various spatial locations along the main trunk, starting from the entrance of the LMCA trunk (LMCA, LAD, LAD2, and LAD4). It can be observed that the magnitude of the flow rate wave decreases significantly, but the waveforms remain basically unchanged. The flow rate waveforms in the LCX trunk (LCX, LCX1, LCX2, LCX3) shown in Figure 9(b) also present the same trend. In contrast, the pressure waveforms change little at different positions in the same trunk, as illustrated in Figure 9(c).
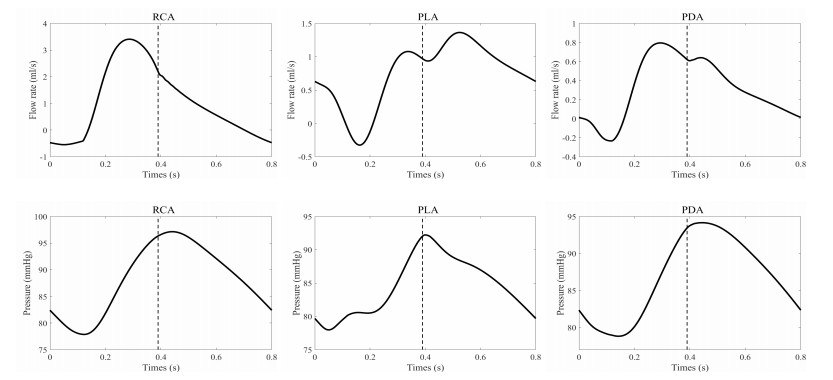
Figure 10 shows the flow rate and pressure of each segment of the right coronary artery. In the systolic period, the flow rate in the right coronary artery does not significantly decrease compared with the left coronary artery. This is mainly due to the lower pressure environment in which the right ventricle functions, with its peak pressure being only about one-fifth of the mean aortic pressure [51]. Based on the numerical results obtained from the 0D coronary artery model, it is estimated that during a single cardiac cycle, the blood flow entering the coronary artery distributes as follows: 3.96 ml into the overall coronary artery, with 3.11 ml flowing to the left coronary artery and 0.85 ml directed toward the right coronary artery. In total, the coronary artery blood flow accounted for about 4.41% of the cardiac output.
3.4. Stenosis conditions
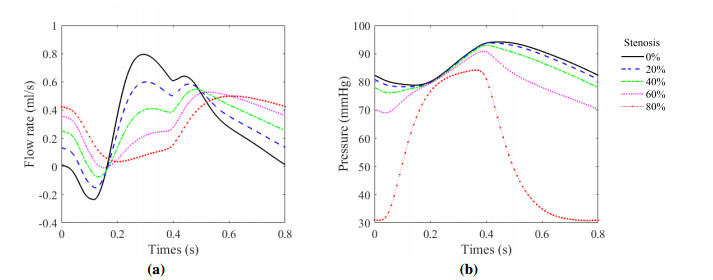
Coronary artery stenosis is very important for the study of coronary artery blood supply capacity, which leads to a decrease in the cross-sectional area of blood vessels, hindering blood flow. In severe cases, it can cause myocardial ischemia. The coronary artery stenosis model is established by changing the RLC parameters of a specific segment; see Eqs (2.11) and (2.12). In these simulations, we observe the changes in flow rate and pressure at different degrees of stenosis (20%, 40%, 60%, and 80%) to study how the stenosis rate affects flow rate and pressure. Figure 11 illustrates the relationship between flow rate, pressure, and stenosis rate in the PDA of the right coronary artery. We find that when the stenosis rate rises, the flow rate and the pressure decrease, and when the stenosis rate is higher than 60%, the blood pressure decreases significantly.
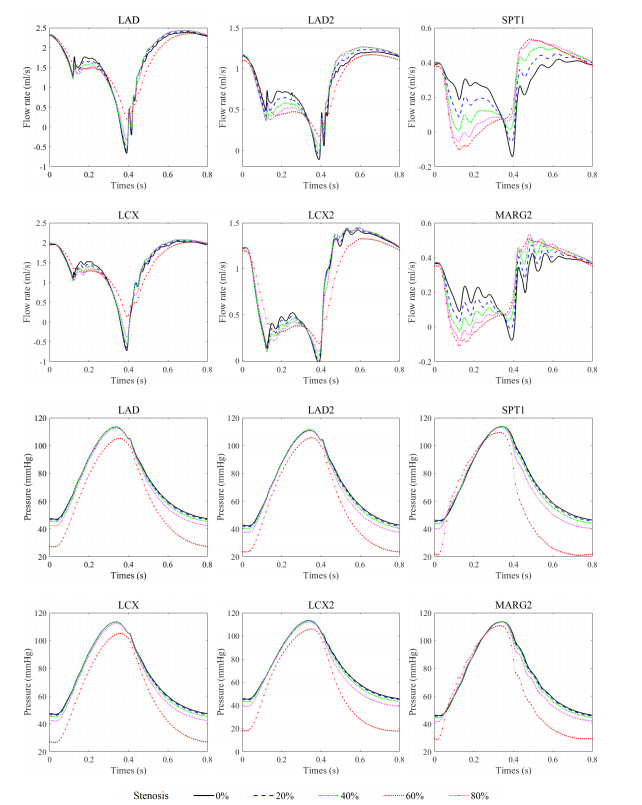
In the left coronary artery, six typical blood vessels (LAD, LAD2, SPT1, LCX, LCX2, and MARG2) are selected for stenosis simulation according to different locations (different branches and different generations). The relationship between flow rate, pressure, and stenosis rate of the left coronary artery is similar to that of the right coronary artery. Figure 12 displays the variations in flow rate and pressure across six different segments at varying stenosis rates. The relationship between flow rate, pressure, and stenosis rate in the left coronary artery is analogous to that in the right coronary artery. Compared with flow rate, pressure decreases gradually with an increase in stenosis rate, which indicates that blood pressure is a more stable diagnostic criterion than flow rate in clinical medicine.
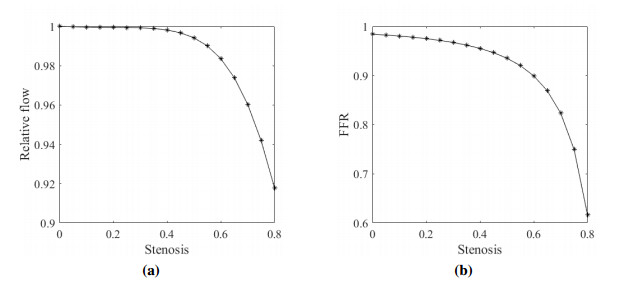
According to the flow rate and pressure at different stenosis rates, the relative flow and FFR can be calculated. Figure 13(a) shows the relative flow of the right coronary artery PDA when PDA is stenosed, and its FFR is shown in Figure 13(b), which is calculated by Eq (2.13). The FFR of PDA in healthy state is 0.98. With the increase in stenosis rate, the relative flow and FFR both decrease. The rate of change in relative flow and FFR increases significantly when the stenosis rate exceeds 60%, consistent with Figure 11. When the stenosis rate is higher than 72%, the FFR is lower than 0.8, reaching the threshold of myocardial ischemia.
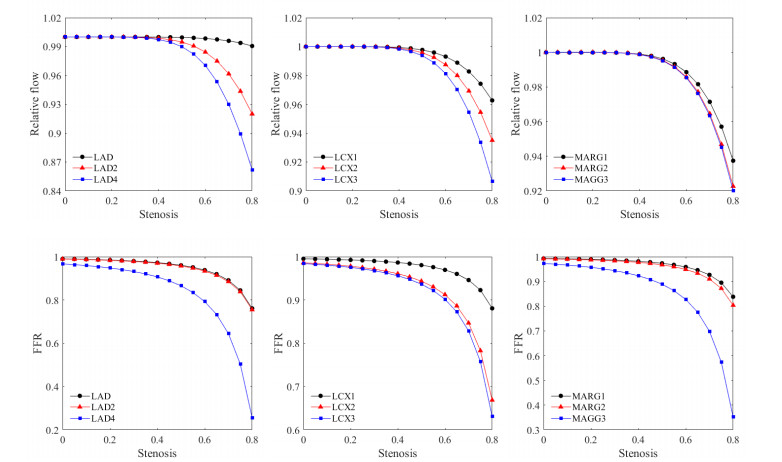
In the left coronary artery, the relative flow and FFR of LMCA trunk (LAD, LAD2, and LAD4), LCX trunk (LCX1, LCX2, and LCX3), and MARGs at different locations (MARG1, MARG2, and MARG3) are calculated and shown in Figure 14. Similar to PDA, the relative flow and FFR of the left coronary artery decrease with increased stenosis. The FFR of each vessel segment of the LMCA trunk in the healthy state is 0.990, 0.989, and 0.967, respectively. The FFR of the LCX trunk and MARGs are also above 0.97. When the stenosis rate is between 50% and 60%, the relative flow and FFR begin to decrease significantly. In addition, for the LMCA trunk, LCX trunk, and MARGs, the decrease in relative flow and FFR becomes more and more significant with the increase in generation.
4.
Discussion
In a cardiac cycle, the movement of the aortic valve occurs mainly in the systolic period. The strong contraction of the ventricular myocardium leads to a dramatic rise in the intraventricular pressure. Once the left ventricular pressure surpasses the aortic pressure, the aortic valve opens, and the blood starts to flow into the aorta. When the left ventricular pressure reaches its peak, the aortic valve is completely opened, and blood rushes into the aorta. The maximum flow rate was 572.43 ml/s. As the left ventricular pressure decreases below that of the aorta, the aortic valve begins to close. The AV FSI simulator can well simulate the hemodynamics of the aortic valve in a cardiac cycle and is consistent with clinical measurement data and published literature results [49,50]. Therefore, the AV FSI simulator can provide the boundary condition in a healthy state for the 0D model to achieve a more realistic simulation. In the future, we plan to introduce more boundary conditions in different states to simulate the performance of the cardiovascular system in various complex situations.
Taking the results of the coronary artery published by Pietrabissa et al. [9] and Duanmu et al. [10] as the reference solution, the PSO algorithm is utilized to optimize the RLC parameters in the 0D model. Because the right coronary artery has a simple structure (including only three vessels) and gives more reference solution, its optimization outcome has superior performance compared to that of the left coronary artery. Table 2 presents the RLC parameter values for each segment of the coronary artery. These optimized parameters are then implemented in subsequent studies.
The 0D coronary artery model established in this paper can simulate the flow rate and pressure of all vessel segments in a cardiac cycle and evaluate the blood supply capacity of the coronary artery. The predictions align well with previous research findings and clinical experimental data. However, there is oscillation in the numerical result, which may be due to the influence of discretization error, mesh accuracy, boundary condition processing, and other factors. The flow rate in the coronary artery is highly correlated with the heart and arterial system. During the systolic period, the driving force for perfusing the left myocardial is the difference between the intramyocardial pressure and the aortic pressure, and the flow rate decreases with myocardial contraction [10,17,51] and then increases with the reduction of intramyocardial pressure until the beginning of diastole. However, the flow rate in the right coronary artery does not significantly decrease during the systolic period because the lower pressure environment within the right ventricle is compared to the left ventricle [9,39]. In addition, we also studied the flow rate and pressure waveforms along the different spatial positions of the trunk. Since the different cross-sectional areas of vessels along the trunk, the flow rate shows different amplitudes. Concretely, the flow rate waveforms tend to scale (normalized relative to their average) into a curve except for a small phase difference, and the pressure waveforms change little. Huo et al. [52] discovered that the attenuation of the pressure waveforms' amplitude is particularly pronounced in blood vessels with a diameter less than 10 μm. Under normal circumstances, the average coronary blood flow constitutes 4% to 5% of the total cardiac output [51], and our numerical result is 4.41%.
To investigate the impact of coronary artery stenosis on both flow rate and pressure dynamics and evaluate the blood supply capacity of the stenotic coronary artery, the stenosis model is established to simulate the flow rate and pressure of each segment of the coronary artery when the stenosis rate varied between 20% and 80%. As the stenosis rate increases, the flow rate and pressure decrease to varying degrees. In clinical medicine, pressure is a very stable diagnostic criterion because the reduction of pressure is more regular [10]. The flow rate-related relative flow and pressure-related FFR show good concurrence with the previously published experimental data [7,53]. With the increase in stenosis rate, the relative flow and FFR have the same trend, which is decreasing. Hamilos et al. [54] showed that the FFR value of the stenosis rate between 60% and 70% is between 0.68 and 0.97. Koo et al. [55] found that when the stenosis rate is 79 ± 11%, the average FFR is 0.81 ± 0.12, and only one-third of lesions exhibit an FFR value below 0.75. For intermediate blood vessel segments, the FFR in healthy status is not less than 0.97, while for the terminal vessels, the range is between 0.9 and 0.97 [16].
However, the coronary artery model still has some limitations. This model ignored the interplay between the heart, the arterial system, and the coronary artery, and it could not predict wave propagation. We assume that the RLC parameters are always constant, which is approximately true in the diastolic period, but in the systolic period, the parameters will change due to ventricular contraction [7]. For a solitary lesion, the occurrence of ischemia is affected by many factors, such as the shape and location of the lesion, the size and function of the myocardium being perfused, and the degree of collateral circulation [56,57,58]. These factors are not taken into account in the coronary artery stenosis model.
5.
Conclusions
In this paper, we establish a complete coronary artery lumped parameter model based on the similarity between the circuit system and the cardiovascular system, including the left and right coronary arteries. The model uses RLC parameters to describe each vessel segment and introduces the AV FSI simulator to calculate the inlet boundary condition. It can predict the pressure and flow rate distribution throughout the coronary artery tree up to the terminal blood vessel and evaluate the blood supply capacity under health status and different degrees of stenosis. The relative flow and FFR align well with the published literature. The model can effectively simulate the common characteristics of coronary artery hemodynamics and be easily transformed into clinical practice for real-time clinical diagnosis.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work is supported by National Natural Science Foundation of China (Grant No. 12271440), which are gratefully acknowledged.
Conflict of interest
The authors declare there is no conflict of interest.
Appendix A.
The PSO algorithm
The PSO algorithm is programmed on the MATLAB platform without relying on any ready-made libraries or toolkits. It is constructed according to the core idea of the PSO algorithm. Its pseudocode is as follows:
where N is the particle swarm size set to 200. k is the current number of iterations and cannot exceed the maximum number of iterations of 400. d represents the particle dimension, that is, the number of independent variables, and there are 60 RLC parameters to be optimized in this paper. The inertia weight ω = 0.7, the individual learning factor (c1), and group learning factor (c2) are set to 0.5. rand1 and rand2 are two random numbers over [0, 1] intervals.









 DownLoad:
DownLoad: