1. Introduction

Carbon nanostructures of low dimensions like fullerenes (C60), carbon nanotubes (CNT) and single layer graphene (SLG) have attracted great research interest due to their novel physical properties ^[1]. Graphene is a mono atomic (2D) sheet of carbon. It is a promising material for advanced technological applications. C60 is a soccer ball shaped carbon allotrope with sixty sp2-hybridized carbon atoms. It is also employed in a broad range of applications such as solar cells, superconductors, photosensitizer and molecular electronics ^[2]. Porphyrins are micro cyclic compounds with four modified pyrrole rings linked through a methine bridge ^[3]. Metals can be inserted into the central region of a macrocyclic ring. This gives the derivative of porphyrin called Metallo-porphyrin. These are more stable and significant natural compounds that play an important role in respiration, electron transfer and photosynthesis ^[4]. These porphyrins and their derivatives with C60 are considered as potential materials for photovoltaic devices ^[5,6,7,8,9].

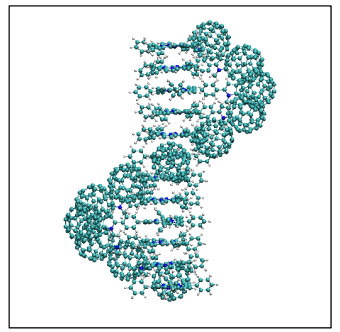
Recently, we showed that novel fullerene-porphyrin supramolecular nanowires are very promising structures to be used in organic photovoltaics ^[10]. It was demonstrated that two well-defined fullerene-porphyrin nanowires have clear channels for charge transport by electrons and holes. These two interesting nanowires have zigzag or helical chains of C60 molecules around a π-stacked porphyrin core. The helical fullerene-porphyrin nanowire is presented in figure 1. The nanowires also have frontier electronic states that are spatially extended along the axes of the nanowires. Ballistic electronic transport is shown to be possible for ultrafast transfer of electrons along C60 chains. Meanwhile, transparent conducting electrodes such as graphene are necessary for the charge collection in solar cells.

Here, we present our theoretical investigations on fullerene-porphyrin dyad-graphene interactions for organic photovoltaics. Models of C60, porphyrin and their dyad on graphene were created. Classical molecular mechanics and quantum ab-initio molecular orbital calculations were carried out. The total energy and geometry optimization calculations were performed. We employed density functional theory (DFT) in quantum calculations to find the interactions between C60, porphyrin and their dyad with graphene. It was found that fullerene-porphyrin dyad was interacting more strongly with graphene. It is also found that C60ZnTPP-graphene combined structure has metallic character. The fullerene-porphyrin nanowire-graphene contacts can be engineered to possess particular electronic properties appropriate for photovoltaic or electronic devices.

---

2. Models

Three different molecule-graphene models were created. The first model contained a fullerene (C60) and a single layer graphene. The second model had zinc-tetraphenylporphyrin (ZnTPP) and graphene, and the third model had the combined structure of C60-ZnTPP dyad and the graphene. In the fullerene-graphene model, the graphene sheet contained 240 atoms and C60 was placed at the middle of graphene. A single atom at the bottom of C60 was placed above a carbon atom of graphene.

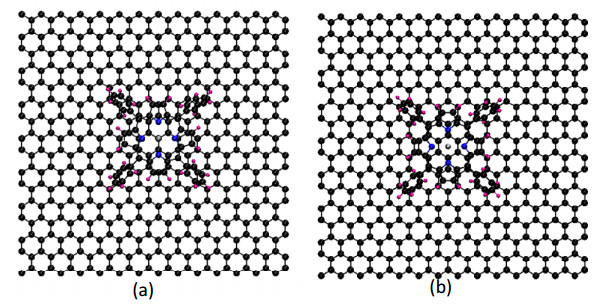
We have created and studied two different ZnTPP-graphene atomic models. In one of the models, the zinc atom of ZnTPP was placed at the top of an atom of the underlying graphene (top site). In the other model, the zinc atom was facing the center of a hexagonal ring of carbon atoms in graphene (hollow site). Both of these models are shown in figure 2.

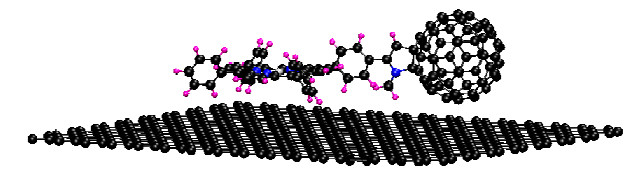
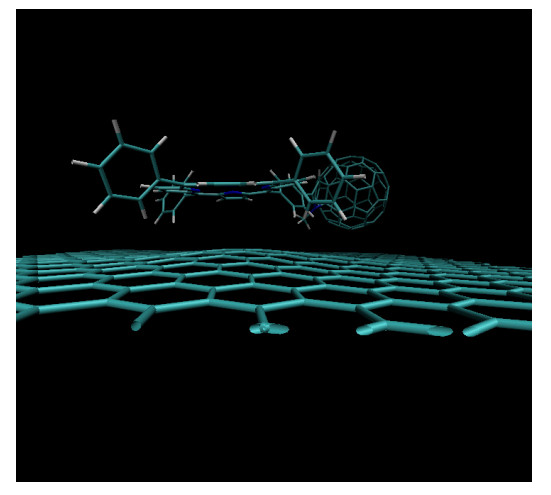
In the last model a fullerene-porphyrin dyad (C60ZnTPP) was placed on top of the graphene sheet. The graphene sheet contained 540 atoms C60ZnTPP had 144 atoms. Figure 3 presents a side view of C60ZnTPP-graphene model. The separations were taken between the zinc atom of C60ZnTPP and the graphene. The super cell sizes were 24.60 × 25.56 × 35.00 Å in the C60-graphene model, 34.43 × 34.08 × 35.00 Å in the ZnTPP-graphene models and 36.89 × 38.34 × 40.00 Å C60ZnTPP-graphene model. Periodic boundary conditions were used in all three directions in all of these models.

---

3. Molecular Mechanics Calculations

In order to study the model structures and determine their equilibrium geometries, classical molecular mechanics calculations were performed using Material Studio 4.0 Software ^[11]. Universal Force Field (UFF) was used for the interactions between the atoms ^[12]. The variation of total energy as a function of molecule-graphene separation was obtained for all the model structures. Equilibrium heights of the molecules above the graphene were determined. Geometry optimizations based on smart algorithm of materials studio were also performed.

In the fullerene-graphene model, the fullerene was placed at different heights and total energy of the combined model is calculated. After the minimum C60-graphene separation is determined, geometry optimizations were performed. We found that the fullerene is 3.1 Å above the graphene in the equilibrium configuration.

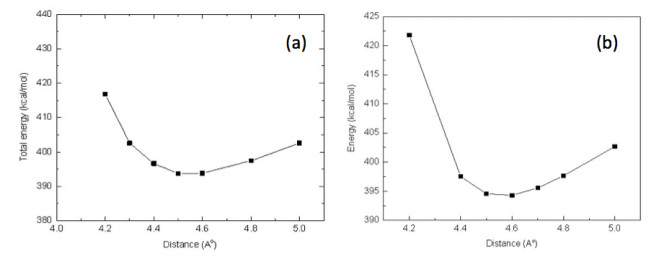
Next, molecular mechanics calculations of porphyrin-graphene model were performed. The variation of total energy as a function of the ZnTPP-graphene separation is shown in figure 4. We studied two different models as presented in section 2. The equilibrium height in the first model (top site model) was 4.5 Å. In the second model (hollow site model) the equilibrium height was 4.6 Å. The energy of the first model was 393.713 kcal/mol and the second model was 394.547 kcal/mol. Thus, the top site model has relatively lower energy and it has relatively closer porphyrin-graphene separation.

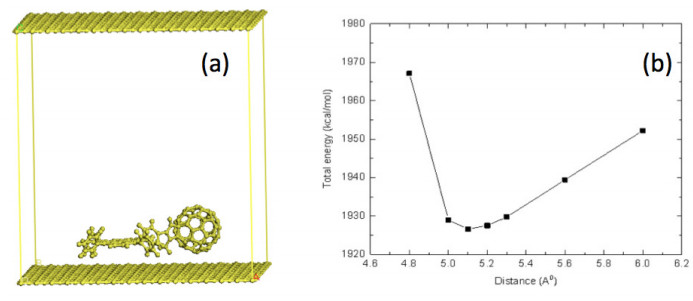
The molecular mechanics calculation results of the fullerene-porphyrin dyad-graphene model are presented in figure 5. The geometry optimized structure is shown in figure 5(a) and the total energy versus molecule-graphene separation graph is presented in figure 5(b). The separation used in the graph is the distance between the Zn atom of the C60ZnTPP dyad and the graphene. The equilibrium separation is calculated as 5.1 Å.

---

4. Ab-initio Density Functional Theory Calculations

Our total energy, electronic structure and geometrical optimization calculations were based on the Density Functional Theory (DFT) method. The Quickstep module ^[13] in the CP2K package was used. Periodic structures can be investigated using this module, but only Γ-point calculations can be performed. The exchange-correlation term in the Kohn-Sham equation was approximated by Perdew-Burke-Erznerhof (PBE) ^[14] generalized gradient approximation (GGA). The basis set DZVP-MOLOPT ^[15] and Goedecker-teter-Hutter (GTH) pseudopotentials were used. The van der Waals interactions were described by using the semi-empirical DFT+D3 dispersion correction term ^[16].

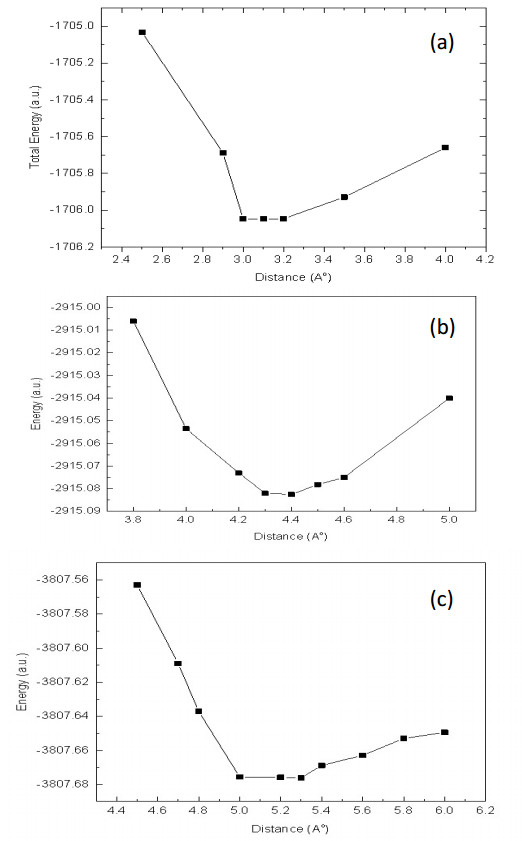
We calculated the total energies of fullerene-graphene model for different C60-graphene separations ranging from 2.5 to 4 Å. We found that the equilibrium separation was 3.1 Å. The total energy vs. C60-graphene separation curve is presented in figure 6(a). After geometry optimization the equilibrium separation changed to 3.12 Å. The total energy vs molecule-graphene separation of the ZnTPP-graphene model is presented in figure 6(b). This model structure had minimum energy at the equilibrium separation of 4.3 Å. By keeping the C60ZnTPP dyad at various separations from graphene, we found a minimum energy structure at a separation of 5.3 Å. The total energy as a function of the separation is shown in figure 6(c). The minimum energy was −3807.6760 a.u.

After the equilibrium separation between C60ZnTPP and graphene was found, geometry optimization calculations were performed. LBFGS algorithm within the quickstep module of cp2k was employed to determine the atomic structure of the combined system corresponding to minimum total energy. It appeared that the planar structures (ZnTPP part of the dyad and the graphene) interact more strongly and try to come more closer to each other. The minimum energy structure is presented in figure 7. As it can be seen in the figure the portion of the graphene just under center of ZnTPP was deformed and that part of graphene moved towards the ZnTPP by 0.97 Å. ZnTPP was also slightly curved to decrease the separation between the center of it and the graphene. After the relaxation, the ZnTPP graphene separation was reduced to 3.84 Å.

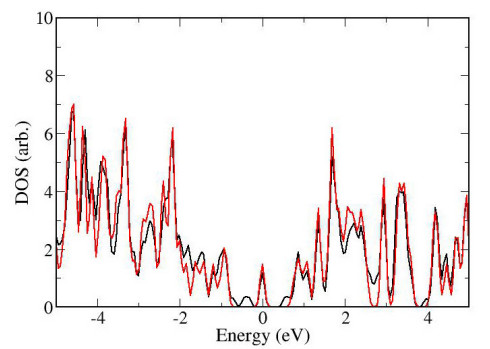
We also found that the interaction between C60ZnTPP and the graphene is not purely van der Waals attraction but there is an electronic interaction between them. An investigation of the electronic structure of the combined system showed that the molecular orbitals of the dyad and the electronic states of graphene were mixed especially at and around the Fermi level. The density of states (DOS) of a system is the number of available states for electrons at a particular energy level, i.e., the number of electronic states per unit volume per unit energy. A low DOS at a particular energy level means that there are only a few states available for occupation. Figure 8(a) and 8(b) present density of states of graphene and C60ZnTPP-graphene models, respectively. Fermi energy is shifted to zero in both plots for comparison. Both structures have finite density of states at the Fermi level due to four half filled electronic states.

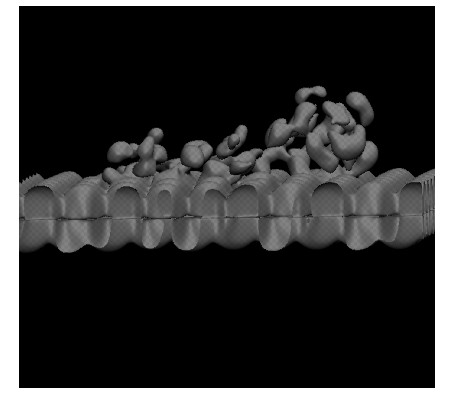
This is due to the Dirac point of graphene and there four half filled electronic states in graphene and also in the fullerene-porphyrin dyad-graphene combined structure at the Fermi level. In the graphene structure these states are pure graphene pi-orbital type states. We found that in the C60ZnTPP-graphene combined structure, these states are mixed between graphene states and C60ZnTPP's molecular orbitals. One of the four half filled mixed state is presented in figure 9. Please note that these four states have more contribution from graphene electronic states.

There are two other mixed states (fully occupied) just below which have more C60ZnTPP contribution and two mixed states (completely empty) with more C60 contribution just above the Fermi level. This electronic interaction and presence of mixed states show that there can be electron transfer with significant rates between C60ZnTPP and graphene.

---

5. Conclusions

In order to study fullerene-porphyrin dyad-graphene interactions for organic photovoltaics and molecular electronics, three different atomic models were created and studied using classical molecular mechanics and quantum ab initio density functional theory calculations. These models contained fullerene-graphene and ZnTPP-graphene, C60ZnTPP dyad-graphene structures. The variation of total energy as a function of molecule-graphene separation was obtained for all the model structures. Equilibrium heights of the molecules above the graphene were determined. Geometry optimizations were also performed. We found that the C60ZnTPP dyad and graphene interact more strongly than the individual C60 or ZNTPP molecules with graphene. It appeared that the planar structures (ZnTPP part of the dyad and the graphene) try to come more closer to each other resulting with graphene deformation under ZnTPP. It is also found that the interaction between C60ZnTPP and the graphene is not purely van der Waals attraction but there is an electronic interaction between them. There were four half filled electronic states that are mixed between graphene states and C60ZnTPP's molecular orbitals at the Fermi level. There were also two mixed states below the Fermi level and two other mixed states above the Fermi level. This electronic interaction and presence of mixed states show that there can be electron transfer with significant rates between C60ZnTPP and graphene. Thus, graphene can be an electrode to collect or emit electrons from or to the C60ZnTPP structures including their nanowires.

---

Acknowledgments

We would like to thank Ohio Supercomputing Center for their support.

---

Conflict of Interest

All authors declare no conflicts of interest in this paper.

---