TCN-Attention-BIGRU: Building energy modelling based on attention mechanisms and temporal convolutional networks

1.   Introduction

Dengue is one of the deadliest and most dangerous infections. According to the World Health Organization (WHO), 50–100 million viruses cause illness each year, resulting in 500,000 emergency room visits and approximately 12,500 deaths ^[1]. Recently, dengue has come to be presumed as a tropical illness, but it has propagated the zone of infection to maintain or restore zones, owing mainly to global climate change ^[2]. Dengue is spread to individuals through the mouth of contaminated Aedes aegypti and Aedes albopictus mosquitoes. It is believed that four highly associated DENV adenoviruses occur, namely DENV-1, DENV-2, DENV-3 and DENV-4 ^[3], so these serotypes lead to illnesses of varying severities in individuals. The contaminated person typically suffers from an intense bacteraemia known as dengue fever that is checked by a highly complicated immune reaction within seven days of disease initiation. Dengue hemorrhagic fever (DHF) and dengue shock syndrome (DSS) are more drastic representations of this illness (DSS). DHF/DSS can be potentially lethal if not cured appropriately and properly. The WHO previously suggested a new dengue classification predicated on infection intensity ^[4]. We should notice that, despite significant initiatives to create an efficacious vaccine against dengue pathogens, advertising for dengue immunization is still not accessible ^[5]. From this perspective, it is critical to comprehend the biochemical practices and dynamic system procedures at work all throughout the infection ^[6,7]. These intricate nonlinear natural mechanisms also produce a model structure with diverse and significant complexities. The incidence rate of dengue in various demographics has been investigated previously or in gradually expanded editions of the fundamental SIR mathematical formulation ^[8]. Moreover, we should mention that only a handful of micro-epidemiological experiments on dengue viruses, including one new analysis focusing on the T-cell immune reaction, provide a comprehensive and vibrant model that encompasses a specific antibody immune reaction ^[9,10].

Furthermore, secondary infection occurs when a person who has had a systemic virus is subjected to dengue virus with a high degree of specificity. It is common for certain sick people to develop intricate and potentially lethal DSS/DHF environments. Because the new DENV serotype is similar in composition to the old one, it stimulates the development of lymphocytes that enhance the old serotype (i.e., cross immunity) as well as the most recent immune responses that counteract the different pathogenicity. Consequently, there are primarily two pertinent immunoglobulins presently: one generated by the viral illness that is heterologous to the unique subtype and one generated by the antibiotic treatment that is homologous. Both of these immune cells have the ability to attach to and incapacitate viral genomes. After neutralization, the specific antibody are transported to phagocytes. However, owing to their low attachment to this fresh serotype, the heterologous immune cells are primed to extract the pathogen when it enters the leukocytes. This leaves a portion of the virions exposed and willing to inoculate the phagocyte. Hence, reactions are catalyzed against the latest serotype that both safeguard and transport the pathogen to their priorities, contingent on the attachment of the immune response receptor. This is known as antibody reliant augmentation (ARA) of infection ^[11]. For generations, the most prevalent speculation that could describe the increased heinousness of potential pathogens has been ARA ^[12]. As a result, we can conclude that the immune system is mainly accountable for both influencing the virus and supplying protection, while also boosting responses within the bloodstream that cause extreme manifestations such as DHF/DSS. Lastly, a framework for reinfection should incorporate the similar phenomenon of ARA of viruses and increased lymphocyte proliferation.

Researchers in numerous classifications and scientific disciplines have gravitated toward using fractional systems of differential equations (DEs) in the majority of their novel evidence and investigations as a consequence of the emergence of fractional derivatives ^[13]. In addition, to see this realistically, we can resort to numerical techniques for the proliferation and evolution of numerous infections and communicable conditions, which have emerged as an intriguing issue for scholars in past centuries; they employ fractional frameworks of initial value problems ^[14,15]. While reviewing the articles, we discovered that various scholars have proposed kernels that can be employed to create fractional differential formulations ^[16]. The major motivation behind this is that serious challenges exhibit signs of mechanisms that are similar to the behaviors of precise scientific expressions. Fractional calculus incorporating a power law kernel has been led by the contributions of Riemann, Liouville, Cauchy, and Abel. Caputo later improved their approach, and this form has been employed in several scientific disciplines owing to its capacity to enable classical initial conditions (ICs) ^[17]. Prabhakar proposed an appropriate kernel containing three components as a combination of index laws and the generalized Mittag-Leffler (GML) kernel. This form has likewise piqued the interest of numerous scholars and investigations into both concepts and implementations have been conducted.

Furthermore, the various kernels have distinctive features; for instance an index kernel only aids in the replication of systems that indicate index kernel tendencies. GML, the combination of the index kernel, exponential kernel and GML kernel. The generalized three distinct have their own domain of applicability ^[18,19]. Because the phenomenon is multifaceted, Caputo and Fabrizio developed a novel kernel with a particular exponential kernel exhibiting Delta Dirac characteristics. A differential formulation that is becoming increasingly popular due to memory. Furthermore, the notion of a fractional derivative having a nonsingular kernel was pioneered by this kernel, marking the inauguration of a revolutionary era in fractional calculus ^[20]. A scientist's observation regarding the kernel's non-fractionality resulted in the creation of a novel kernel, i.e., the GML function, which includes one component. Atangana and Baleanu ^[21] proposed this formulation, which represents another advancement in the discipline of fractional calculus. The formulations have been employed successfully in a variety of fields of study. Glancing at reality and its intricacies, it is clear that these proposed kernels are insufficient to forecast all of our universe's complicated characteristics. Following the remark, one will look for a different kernel or modified kernel, or a set of procedures that will be used to add novel differential formulations. Sabatier has proposed various kernel variants that will additionally lead to novel avenues of inquiry ^[22]. In addition to these remarkable breakthroughs, numerous additional notions were proposed, such as the conception of short memory and the definition of a fractional derivative in the Caputo interpretation for distinct characteristics of fractional orders. Notwithstanding the well-known formulation, which takes a fractional order to be time-dependent, the goal was to achieve a different form of variable order derivative. Wu et al. ^[23] proposed and implemented this scenario in chaotic theory. However, researchers have discovered that some real-world phenomena demonstrate mechanisms exhibiting varying behaviors as a factor of space and time. A transition from deterministic to stochastic, either from index-law to exponential decay, is an example. Because conventional differential formulations may be incapable of accounting for these tendencies, piecewise differential/integral formulations were devised to cope with issues manifesting crossover phenomena ^[24]. The primary goal of this article is to present a detailed evaluation, potential implementations, strengths and shortcomings of these two notions.

Moreover, there are multiple fractional operators that identify dengue evolution in the research ^[25,26] and the reference materials therein. All of the additional implications above depict the complexities of dengue viruses from various perspectives, including nonlinear dynamic analysis, vaccination and stochastic optimization analysis. El-Sayed et al. ^[27] lists several notable survey reports that mentioned dengue disease by using actual information.

The purpose of this research is to investigate the dynamic behavior of a deterministic-stochastic secondary dengue viral infection (SDVI) model with multiple target cells via the piecewise fractional differential operators approach, which aids in the identification of mechanisms with crossover patterns. Thus, it is more pragmatic to investigate frameworks with both white noise and deterministic noise rather than just white noise. Even so, there are no studies on the stationary distribution of the stochastic SDVI model under regime switching in the existing literature. In this manuscript, we demonstrate the ergodicity stationary distribution (ESD) of an SDVI model under regime switching by effectively preparing Lyapunov candidates and an invariant region. Piecewise modeling via the well-noted fractional derivative operators is highlighted with descriptions of chaos concerns. Taking into account the computed findings, we procure a critical value for the extinction of SDVI, which is presented by $\mathbb{R}_{0}^{s} < 1$. As a result, the intermittent nature of untreated specific receptors has a significant impact on virus infection elimination. We contend that, while the GML kernel, exponential decay and power law have been revealed to be capable of depicting several crossover behaviors, their strengths to accomplish this may be restricted due to the enormity of nature.

The structure of the article is organized as follows, Section 2 describes preliminary ideas related to stochastic processes and fractional calculus. Also, the model formulation is predicted herein. Section 3 examines the qualitative characteristics of the deterministic and stochastic states. By formulating a certain adequate Lyapunov mapping, we demonstrate the existence of a unique ESD of the solution. In Section 4, theoretical findings are analyzed by utilizing the crossover effects with varying kernels. Section 5 exhibits the results and discussion of the suggested model. Finally, Section 6 contends with some epilogue and future perspectives.

2.   Model formulation

The secondary infectious disease framework presented by ^[28] is an extended version of the acute infection system depicted in ^[9]. A sixth component, which also characterized the threshold of immune response constituted during the preceding reinfection but is heterologous to the active viral serotype, has been incorporated into the main framework. The homologous recombination immune cells can connect to the virus particles in this scenario, but the severity of complexation is determined not only by the substitutability between the pathogen and immunoglobulin but also by the densities of the heterologous immune cells. It has been discovered that various pathogen serovars in both dominant and supplementary pathogens share immunologic similarities in their enzyme shell. Tanvi et al. ^[28] developed the SDVI model for neutralizing antibody:

with ICs $\mathbf{s}_{1}(0) = {\mathbf{s}_{1}}_{0}, \mathbf{x}_{1}(0) = {\mathbf{x}_{1}}_{0}, \mathbf{u}_{1}(0) = {\mathbf{u}_{1}}_{0}, \mathbf{r}_{1}(0) = {\mathbf{r}_{1}}_{0}, \mathbf{v}_{1}(0) = {\mathbf{v}_{1}}_{0}, \mathbf{m}_{1}(0) = {\mathbf{m}_{1}}_{0}, \mathbf{j}_{1}(0) = {\mathbf{j}_{1}}_{0}.$ At a time step $\mathbf{t}$, the intensities of the heterologous immune response interacting on the initial infection and homologous specific antibody against the deadly pathogen serogroup of the serious infection are denoted by $\mathbf{m}_{1} = \mathbf{m}_{1}(\mathbf{t})$ and $\mathbf{j}_{1} = \mathbf{j}_{1}(\mathbf{t})$, respectively. The descriptor $\omega_{2}\mathbf{v}_{1}\mathbf{j}_{1}$ refers to the yield of dengue virus neutralization by immune responses $\mathbf{j}_{1}$. The phrase $\rho_{2}\mathbf{j}_{1}$ refers to the mortality speed of specific antibody $\mathbf{j}_{1}$. B-cells produce specific antibody $\mathbf{m}_{1}$ and $\mathbf{j}_{1}$ at rates of $\rho_{1}\mathbf{m}_{1}$ and $\rho_{2}\mathbf{j}_{1}$, respectively. The immune response pathogen compound has an effect on the antibody development at rates of $\mathbf{s}_{1}\mathbf{v}_{1}\mathbf{m}_{1}$ and $\mathbf{x}_{1}\mathbf{v}_{1}\mathbf{m}_{1}.$ Researchers ^[29] have incorporated immunity and CTL immunity into their framework of supplementary reinfection. Rashid et al. ^[30] presented the numerical investigation of a fractional-order cholera epidemic model with transmission dynamics via fractal–fractional operator technique. Atangana and Rashid ^[31] contemplated the novel view of a deterministic-stochastic oncolytic M1 model involving immune response through the use of a crossover behavior. Rashid and Jarad ^[32] expounded upon the stochastic dynamics of the fractal-fractional ebola epidemic model by combining a fear and environmental spreading mechanism. Al-Qureshi et al. ^[33] established the dynamical behavior of a stochastic highly pathogenic avian influenza A (HPAI) epidemic model via piecewise fractional differential technique. Boisov et al. ^[34] evaluated a SDVI model with contagious and systemic infections of viral diseases, trying to take secretory and CTL prerogatives into consideration. Bonyah et al. ^[35] contemplated the fractional order dengue fever model in the frame of reference of secured travellers. Fatmawati et al. ^[36] expounded a new framework for dengue fever in the context of fractional calculus. Khan and Fatmawati ^[37] examined the modeling and simulation consequences of a fractional dengue system.

In fact, there is unpredictability and stochasticity. As a result of the impact of Browinian motion on modeling techniques, the stochastic framework is more accurate than the other modeling techniques ^[38,39,40]. We assume that stochastic disturbances to individuals are influenced by random intensities and are proportional to each state $\mathbf{s}_{1}(\mathbf{t}), \; \mathbf{x}_{1}(\mathbf{t}), \; \mathbf{u}_{1}(\mathbf{t}), \; \mathbf{r}_{1}(\mathbf{t}), \; \mathbf{v}_{1}(\mathbf{t}), \; \mathbf{m}_{1}(\mathbf{t})$ and $\mathbf{j}_{1}(\mathbf{t}),$ respectively.

In light of the preceding discussion conducted in ^[38], we advocate for the stochastic SDVI framework via logistic growth as follows:

where the concentrations of the standard Gaussian white noises are $\wp_{\mathbf{p}}, \mathbf{p} = 1, ..., 7$ and $\mathcal{B}_{\mathbf{p}}(\mathbf{t}), \; \mathbf{p} = \; 1, ..., 7$ are independent standard Wiener mechanisms.

Throughout this investigation, it is assumed that the scheme (2.2) is identified on a complete probability space $(\beth, \mathfrak{F}, \{\mathfrak{F}_{\mathbf{t}}\}_{\mathbf{t} > 0}, \mathbf{P})$ with a right continuous filtration $\{\mathfrak{F}_{\mathbf{t}}\}_{\mathbf{t} > 0}$ and an $\{\mathfrak{F}_{0}\}$ comprising all of the components with measure zero.

The stochastic DE in $\mathfrak{d}$-dimensions is described as follows:

where $\mathbf{f}:\mathbb{R}^{\mathfrak{d}}\times[\mathbf{t}_{0}, \mathbf{T}]\mapsto\mathbb{R}^{\mathfrak{d}}$ and $g_{1}:\mathbb{R}^{\mathfrak{d}}\times[\mathbf{t}_{0}, \mathbf{T}]\mapsto\mathbb{R}^{\mathfrak{d}\times m_{1}}$ are Borel measurable, $\mathcal{B} = \{\mathcal{B}(\mathbf{t})\}_{\mathbf{t}\geq \mathbf{t}_{0}}$ is an $\mathbb{R}^{m_{1}}$-valued Wiener technique, and $\mathbf{u}_{0}$ is an $\mathbb{R}^{\mathfrak{d}}$-valued random variable stated on $\Theta.$

Furthermore, $\mathbb{C}^{2, 1}(\mathbb{R}^{\mathfrak{d}}\times[\mathbf{t}_{0}, \infty); \mathbb{R}_{+})$ is regarded as the collection of all positive mappings $\mathcal{V}(\mathbf{u}, \mathbf{t})$ on $\mathbb{R}^{\mathfrak{d}}\times[\mathbf{t}_{0}, \infty)$ that are continuously twice differentiable in $\mathbf{u}\in\mathbb{R}^{\mathfrak{d}}$ and once in $\mathbf{t}\in[\mathbf{t}_{0}, \infty)$. The differential operator $\mathbb{L}$ for the stochastic DE (2.3) is provided by

Define the mapping $\mathcal{V}\in\mathbb{C}^{2, 1}(\mathbb{R}^{\mathfrak{d}}\times[\mathbf{t}_{0}, \infty)$; then,

where $\mathcal{V}_{\mathbf{t}}: = \frac{\partial\mathcal{V}}{\partial \mathbf{t}}, \; \mathcal{V}_{\mathbf{s}_{1}} = (\mathcal{V}_{\mathbf{u}_{\mathbf{p}}}, ..., \mathcal{V}_{\mathbf{u}_{\mathfrak{d}}})\; and\; \mathcal{V}_{\mathbf{u}\mathbf{u}} = (\mathcal{V}_{\mathbf{u}_{\mathbf{p}}}, \mathcal{V}_{\mathbf{u}_{\mathbf{p}}})_{\mathfrak{d}\times \mathfrak{d}}.$

For $\mathbf{u}(\mathbf{t})\in\mathbb{R}^{\mathfrak{d}},$ Ito's approach is defined as

Here, we provide the accompanying description to help readers who are acquainted with fractional calculus^[17,20,21].

where $\mathcal{M}(\beta)$ is defined as a normalized function with $\mathcal{M}(0) = \mathcal{M}(1) = 1.$

The formulation of the Atangana-Baleanu derivative is represented below:

where $ABC(\beta) = 1-\beta+\frac{\beta}{\Gamma(\beta)}$ signifies the normalization function.

3.   Qualitative analysis of SDVI model

3.1.   Deterministic state

To verify that our framework is reproductively adequate, we define a region for the densities of the system's cohorts. Intensities should not be negative or undefined on specific terms.

Generate the compact set $\Delta = \big\{({\mathbf{s}_{1}}$, $..., {\mathbf{s}}_{\mathfrak{n}}, {\mathbf{u}}_{1}, ..., {\mathbf{u}}_{\mathfrak{n}}, \mathbf{v}_{1}$, $\mathbf{m}_{1}, \mathbf{j}_{1})\in\mathbb{R}_{+}^{2\mathfrak{n}+3}:{\mathbf{s}}_{\mathbf{p}}$, ${\mathbf{u}}_{\mathbf{p}}\in[0, \mathcal{L}_{\mathbf{p}}]$, $\mathbf{v}_{1}\in[0, \mathcal{K}_{1}]$, $\mathbf{m}_{1}\in[0, \mathcal{K}_{2}], \mathbf{j}_{1}\in[0, \mathcal{K}_{3}], \; \mathbf{p} = 1$, $..., \mathfrak{n}\big\}.$

Lemma 3.1. The domain $\Delta$ of the model (2.1) is positively invariant.

Proof. Equating the system Eq (2.1) to zero, we have

Therefore, $({\mathbf{s}}_{1}, ..., {\mathbf{s}}_{\mathfrak{n}}, {\mathbf{u}}_{1}, ..., {\mathbf{u}}_{\mathfrak{n}}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathbb{R}_{+}^{2\mathfrak{n}+3}$ for all $\mathbf{t}\geq0.$

Taking $\mathbf{T}_{\mathbf{p}} = {\mathbf{s}_{1}}_{\mathbf{p}}+{\mathbf{u}_{1}}_{\mathbf{p}};$ then,

where $\sigma_{\mathbf{p}} = \min\big\{\xi_{\mathbf{p}}, \varsigma_{\mathbf{p}}\big\}, \mathbf{p} = 1, ..., \mathfrak{n}.$ Thus, $\mathbf{T}_{\mathbf{p}}\leq\mathcal{L}_{\mathbf{p}},$ if $\mathbf{T}_{\mathbf{p}}(0)\leq\mathcal{L}_{\mathbf{p}},$ where $\mathcal{L}_{\mathbf{p}} = \frac{\vartheta_{\mathbf{p}}}{\sigma_{\mathbf{p}}}.$ The positivity of the system's parameters implies that ${\mathbf{s}_{1}}_{\mathbf{p}}, {\mathbf{u}_{1}}_{\mathbf{p}}\in\mathcal{L}_{\mathbf{p}}.$ Moreover, we describe $\mathcal{G} = \mathbf{v}_{1}+\frac{\omega_{1}}{\chi_{1}}\mathbf{m}_{1}+\frac{\omega_{2}}{\chi_{2}}\mathbf{j}_{1}$; then,

where $\varpi = \min\{\varphi, \rho_{1}, \rho_{2}\}.$ Thus $\mathcal{G}(\mathbf{t})\leq \mathcal{K}_{1},$ if $\mathcal{G}(0)\leq \mathcal{K}_{1},$ where $\mathcal{K}_{1} = \frac{1}{\varpi}\sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\zeta_{\mathbf{p}}\mathcal{L}_{\mathbf{p}}.$ Since $\mathbf{v}_{1}(\mathbf{t}), \mathbf{m}_{1}(\mathbf{t})\geq0$ and $\mathbf{j}_{1}(\mathbf{t})\geq0;$ then, $\mathbf{v}_{1}(\mathbf{t})\in[0, \mathcal{K}_{1}], \; \mathbf{m}_{1}(\mathbf{t})\in[0, \mathcal{K}_{2}]\; and\; \mathbf{j}_{1}(\mathbf{t})\in[0, \mathcal{K}_{3}].$ Also, $\mathcal{K}_{2} = \frac{\chi_{1}}{\omega_{1}}\mathcal{K}_{1}$ and $\mathcal{K}_{3} = \frac{\chi_{2}}{\omega_{2}}\mathcal{K}_{1}.$

Next, we established the equilibria and basic reproduction numbers of the system (2.1).

Theorem 3.1. Assume that there are three thresholds parameters $\mathbb{R}_{0}, \; \mathbb{R}_{1}$ and $\mathbb{R}_{2}$ with $\mathbb{R}_{1} < \mathbb{R}_{0}$ and $\mathbb{R}_{2} < \mathbb{R}_{0}$ such that

(a) if $\mathbb{R}_{0}\leq1;$ then, (2.1) has one equilibrium point $\mathcal{E}_{0}\in\Delta,$

(b) if $\mathbb{R}_{1}\leq1 < \mathbb{R}_{0}$ and $\mathbb{R}_{2}\leq1 < \mathbb{R}_{0}$ then (2.1) has two equilibria points $\mathcal{E}_{0}\in\Delta$ and $\mathcal{E}_{1}\in\Delta^{\circ}$, where $\Delta^{\circ}$ is the interior point of $\Delta,$

(c) if $\mathbb{R}_{1} > 1$ and $\mathbb{R}_{2} < 1$ then (2.1) has three equilibria points $\mathcal{E}_{0}\in\Delta, \; \mathcal{E}_{1}\in\Delta^{\circ}$ and $\mathcal{E}_{2}\in\Delta^{\circ}$,

(d) if $\mathbb{R}_{2} > 1$ and $\mathbb{R}_{1} < 1$ then (2.1) has three equilibria points $\mathcal{E}_{0}\in\Delta, \; \mathcal{E}_{1}\in\Delta^{\circ}$ and $\mathcal{E}_{3}\in\Delta^{\circ}$,

(e) if $\mathbb{R}_{2} > 1$ and $\mathbb{R}_{1} > 1$ then (2.1) has three equilibria points $\mathcal{E}_{0}\in\Delta, \; \mathcal{E}_{1}\in\Delta^{\circ}, \mathcal{E}_{2}\in\Delta^{\circ}$ and $\mathcal{E}_{3}\in\Delta^{\circ}$.

Proof. Equating the left side of the model (2.1) to zero, we have

Utilizing last two equations of (3.1), we have three scenarios, as follows:

Case (a) For $\mathbf{m}_{1} = \mathbf{j}_{1} = 0;$ then, the first and second equations of (3.1) can reduces to

In view of the third equation of (3.1), we find

Then, (3.3) has one of two configurations $\mathbf{v}_{1} = 0$ or $\sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\frac{\zeta_{\mathbf{p}}\delta_{\mathbf{p}}x_{\mathbf{p}}}{\varphi\varsigma_{\mathbf{p}}}-1 = 0.$

Further, if $\mathbf{v}_{1} = 0;$ then, inserting it into (3.2) yields the infection-free equilibrium $\mathcal{E}_{0}\Big({\mathbf{s}}^{0}, ..., {\mathbf{s}}_{\mathfrak{n}}^{0}, \overbrace{0, ..., 0, 0}^{\mathfrak{n}+3}\Big)$ with ${\mathbf{s}_{1}}_{\mathbf{p}}^{0} = \frac{\vartheta_{\mathbf{p}}}{\xi_{\mathbf{p}}}.$ If $\mathbf{v}_{1}\neq0,$ we have

Inserting the first equation of (3.1) into (3.4), we have

As ${\mathbf{s}_{1}}_{\mathbf{p}}$ depends on $\mathbf{v}_{1};$ then, from (3.5), we present a mapping $\Upsilon_{1}(\mathbf{v}_{1})$ as

We must demonstrate that there exists $\tilde{\mathbf{v}_{1}} > 0$ such that $\Upsilon_{1}(\tilde{\mathbf{v}_{1}}) = 0.$ Note that, if $\mathbf{v}_{1} = 0$ then ${\mathbf{s}_{1}}_{\mathbf{p}} = {\mathbf{s}_{1}}_{\mathbf{p}}^{0}$ and $\Upsilon_{1}(0) = 0$ and when $\mathbf{v}_{1} = \mathbf{v}_{1}^{\ast} = \sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\frac{\zeta_{\mathbf{p}}\xi_{\mathbf{p}}{\mathbf{s}_{1}}_{\mathbf{p}}^{\ast}}{\varphi\varsigma_{\mathbf{p}}} > 0,$ we have ${\mathbf{s}_{1}}_{\mathbf{p}}^{\ast} = {\mathbf{s}_{1}}_{\mathbf{p}}(\mathbf{v}_{1}^{\ast})$ and

Therefore, we have

Thus, $\Upsilon_{1}^{\prime}(0) > 0$ if

This implies that if the criterion (3.7) is fulfilled, then there exists $\tilde{\mathbf{v}_{1}}\in(0, \mathbf{v}_{1}^{\ast})$ fulfilling $\Upsilon_{1}(\tilde{\mathbf{v}_{1}}) = 0.$ Again, from (3.2), we have that $\tilde{\mathbf{s}_{1}}_{\mathbf{p}}, \tilde{\mathbf{u}_{1}}_{\mathbf{p}}, \tilde{\mathbf{v}_{1}} > 0.$ Therefore, a persistent infection to a deactivated immunologic antibody reaction $\mathcal{E}_{1}(\tilde{\mathbf{s}}_{1}, ..., \tilde{\mathbf{s}}_{\mathfrak{n}}, \tilde{\mathbf{u}}_{1}, ..., \tilde{\mathbf{u}}_{\mathfrak{n}}, \tilde{\mathbf{v}}_{1}, 0, 0)$ holds when $\sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\frac{\zeta_{\mathbf{p}}\delta_{\mathbf{p}}\vartheta_{\mathbf{p}}}{\varphi\xi_{\mathbf{p}}\varsigma_{\mathbf{p}}} > 1.$

Then, we can establish

In this case, $\mathbb{R}_{0}$ represents the basic reproduction number, which also represents the number of productive specific receptors produced by a single afflicted cell over the course of its existence. The next-generation matrix approach ^[41] or the local stability of the infection equilibrium point $\mathcal{E}_{0}$ can furthermore be applied to determine $\mathbb{R}_{0}$.

Case (b) If $\mathbf{m}_{1}\neq0\; and\; \mathbf{j}_{1} = 0,$ we achieve a contaminated equilibrium point by using only the effective heterologous immune response $\mathcal{E}_{2}(\bar{\mathbf{s}}, ..., \bar{\mathbf{s}}_{\mathfrak{n}}, \bar{\mathbf{u}}, ..., \bar{\mathbf{u}}_{\mathfrak{n}}, \bar{\mathbf{v}_{1}}, \bar{\mathbf{m}_{1}}, 0),$ where $\bar{\mathbf{s}_{1}}_{\mathbf{p}} = \frac{\vartheta_{\mathbf{p}}}{\xi_{\mathbf{p}}+\frac{\delta_{\mathbf{p}}\rho_{1}}{\chi_{1}}}, \; \bar{\mathbf{u}_{1}}_{\mathbf{p}} = \frac{\delta_{\mathbf{p}}\vartheta_{\mathbf{p}}\rho_{1}}{\varsigma_{\mathbf{p}}(\chi_{1}\xi_{\mathbf{p}}+\delta_{\mathbf{p}}\rho_{1})}, \; \bar{\mathbf{v}_{1}} = \frac{\rho_{1}}{\chi_{1}}, \bar{\mathbf{m}_{1}} = \frac{\varphi}{\omega_{1}}(\mathbb{R}_{1}-1)\; and\; \mathbb{R}_{1} = \sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\frac{\chi_{1}\zeta_{\mathbf{p}}\delta_{\mathbf{p}}\vartheta_{\mathbf{p}}}{\varphi\varsigma_{\mathbf{p}}(\chi_{1}\xi_{\mathbf{p}}+\delta_{\mathbf{p}}\rho_{1})}.$

Case (c) If $\mathbf{m}_{1} = 0\; and\; \mathbf{j}_{1}\neq0,$ we achieve an afflicted steady state by using only the effective homologous immune response $\mathcal{E}_{3}(\hat{\mathbf{s}}, ..., \hat{\mathbf{s}}_{\mathfrak{n}}, \hat{\mathbf{u}}, ..., \hat{\mathbf{u}}_{\mathfrak{n}}, \hat{\mathbf{v}_{1}}, 0, \hat{\mathbf{j}_{1}}),$ where $\hat{\mathbf{s}}_{\mathbf{p}} = \frac{\vartheta_{\mathbf{p}}}{\xi_{\mathbf{p}}+\frac{\delta_{\mathbf{p}}\rho_{2}}{\chi_{2}}}, \; \hat{\mathbf{u}_{1}}_{\mathbf{p}} = \frac{\delta_{\mathbf{p}}\vartheta_{\mathbf{p}}\rho_{2}}{\varsigma_{\mathbf{p}}(\chi_{2}\xi_{\mathbf{p}}+\delta_{\mathbf{p}}\rho_{2})}, \; \hat{\mathbf{v}_{1}} = \frac{\rho_{2}}{\chi_{2}}, \hat{\mathbf{j}_{1}} = \frac{\varphi}{\omega_{2}}(\mathbb{R}_{2}-1)\; and\; \mathbb{R}_{2} = \sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\frac{\chi_{2}\zeta_{\mathbf{p}}\delta_{\mathbf{p}}\vartheta_{\mathbf{p}}}{\varphi\varsigma_{\mathbf{p}}(\chi_{2}\xi_{\mathbf{p}}+\delta_{\mathbf{p}}\rho_{2})}.$

Obviously $\mathbb{R}_{1} < \mathbb{R}_{0}$ and $\mathbb{R}_{2} < \mathbb{R}_{0}.$

Assertions (b) and (c) show that if $\mathbb{R}_{1} > 1$ and $\mathbb{R}_{2} > 1$ then $\mathcal{E}_{0}, \; \mathcal{E}_{1}, \; \mathcal{E}_{2}$ and $\mathcal{E}_{3}$ all occur.

Here, $\mathbb{R}_{1}$ is the heterologous specific antibody immune system stimulation quantity and $\mathbb{R}_{2}$ is the handful of homologous specific antibody immune reaction stimulation.

We presently demonstrate that $\mathcal{E}_{0}\in\Delta$ and $\mathcal{E}_{1}, \mathcal{E}_{2}, \mathcal{E}_{3}\in\Delta^{\circ}.$ It is obvious that $\mathcal{E}_{0}\in\Delta.$ Suppose that that $\mathbb{R}_{0} > 1;$ then, $\mathcal{E}_{1}$ holds and $\vartheta_{\mathbf{p}} = \xi_{\mathbf{p}}\tilde{\mathbf{s}}_{\mathbf{p}}+\varsigma_{\mathbf{p}}\tilde{\mathbf{u}}_{\mathbf{p}}.$ As a result of this,

Also, we have that $\varphi\tilde{\mathbf{v}_{1}} = \sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\zeta_{\mathbf{p}}\tilde{\mathbf{u}}_{\mathbf{p}};$ then,

We obtain $\tilde{\mathbf{m}_{1}} = \tilde{\mathbf{j}_{1}};$ then, $\mathcal{E}_{1}\in\Delta^{\circ}.$ Obvious that $\bar{\mathbf{s}}_{\mathbf{p}}, \bar{\mathbf{u}}_{\mathbf{p}}\in(0, \mathcal{L}_{\mathbf{p}}).$

Following that, we define that $0 < \bar{\mathbf{v}_{1}} < \mathcal{K}_{1}$ and $0 < \bar{\mathbf{m}_{1}} < \mathcal{K}_{2}$ when $\mathbb{R}_{1} > 1$. The equilibrium condition of $\mathcal{M}_{2}$ yields

Thus, if $\mathbb{R}_{1} > 1,$ we have that $\varphi\bar{\mathbf{v}_{1}} < \sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\zeta_{\mathbf{p}}\bar{\mathbf{u}}_{\mathbf{p}}\implies0 < \bar{\mathbf{v}_{1}} < \frac{1}{\varphi}\sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\zeta_{\mathbf{p}}\mathcal{L}_{\mathbf{p}}\leq\frac{1}{\varpi}\sum\limits_{\mathbf{p} = 1}^{\mathfrak{n}}\zeta_{\mathbf{p}}\mathcal{L}_{\mathbf{p}} = \mathcal{K}_{1}.$

Eventually, we get

Thus, $\mathcal{E}_{2}\in\Delta^{\circ}.$ Analogously, we can easily prove that $\mathcal{E}_{3}\in\Delta^{\circ}.$

3.2.   Stochastic state

The first consideration when researching the dynamic characteristics of an outbreak framework is determining whether the configuration is global and non-negative. In this segment, we will demonstrate that the Scheme (2.2) has a unique global non-negative solution with any initial settings by using the Lyapunov mechanism technique referenced in ^[42]. We demonstrate the subsequent formalism.

Theorem 3.2. Assume that a system (2.2) $(\mathbf{s}_{1}(\mathbf{t}), \mathbf{x}_{1}(\mathbf{t}), \mathbf{u}_{1}(\mathbf{t}), \mathbf{r}_{1}(\mathbf{t}), \mathbf{v}_{1}(\mathbf{t}), \mathbf{m}_{1}(\mathbf{t}), \mathbf{j}_{1}(\mathbf{t}))$ on $\mathbf{t}\geq0$ by the ICs $(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0))\in\mathbb{R}_{+}^{7}$ and the solution $(\mathbf{s}_{1}(\mathbf{t}), \mathbf{x}_{1}(\mathbf{t}), \mathbf{u}_{1}(\mathbf{t}), \mathbf{r}_{1}(\mathbf{t}), \mathbf{v}_{1}(\mathbf{t}), \mathbf{m}_{1}(\mathbf{t}), \mathbf{j}_{1}(\mathbf{t}))\in\mathbb{R}_{+}^{7}, \; \forall \mathbf{t}\geq0$ almost surely (a.s.).

Proof. Because the system (2.2) indices fulfill the local Lipschitz requirement, for any ICs $(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0))\in\mathbb{R}_{+}^{7}$, there exists only one local solution $(\mathbf{s}_{1}(\mathbf{t}), \mathbf{x}_{1}(\mathbf{t}), \mathbf{u}_{1}(\mathbf{t}), \mathbf{r}_{1}(\mathbf{t}), \mathbf{v}_{1}(\mathbf{t}), \mathbf{m}_{1}(\mathbf{t}), \mathbf{j}_{1}(\mathbf{t}))$ on $\mathbf{t}\in[0, \lambda _{\epsilon}),$ where $\lambda _{\epsilon}$ indicates the moment of explosion ^[43]. In order to prove the global solution, we need $\lambda _{\epsilon} = \infty.$ To that point, let $\Bbbk_{0} > 1$ be large enough that $(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0))\in\mathbb{R}_{+}^{7}$ is defined on $[1/\Bbbk_{0}, \Bbbk_{0}].$ Identify the stopping time for every integer $\Bbbk\geq\Bbbk_{0}$ as shown:

For the sake of simplicity, we take $\inf\emptyset = \infty$ ($\emptyset$ signifies the empty set). Evidently, $\lambda _{\Bbbk}$ is nondecreasing as $\Bbbk\mapsto\infty.$ Assume that $\lambda _{\infty} = \lim\limits_{\Bbbk\mapsto\infty}\lambda _{\Bbbk},$ where $\lambda _{\infty}\leq\lambda _{\epsilon}$ (a.s). When $\lambda _{\infty} = \infty$ holds (a.s), then $\lambda _{\epsilon} = \infty$ (a.s) and $(\mathbf{s}_{1}(\mathbf{t}), \mathbf{x}_{1}(\mathbf{t}), \mathbf{u}_{1}(\mathbf{t}), \mathbf{r}_{1}(\mathbf{t}), \mathbf{v}_{1}(\mathbf{t}), \mathbf{m}_{1}(\mathbf{t}), \mathbf{j}_{1}(\mathbf{t}))\in\mathbb{R}_{+}^{7}, \; \forall\; \mathbf{t}\geq0$ (a.s). That is, we only need to demonstrate $\lambda _{\infty} = \infty\; (a.s)$ to obtain the evidence. If this assumption is factually inaccurate, then a couple of constants exist $\mathbf{T} > 0$ and $\epsilon\in(0, 1)$ such that

As a result, there is an integer $\Bbbk_{1}\geq\Bbbk_{0}$ such that

We introduce a $\mathbb{C}^{2}$-function ${\Phi}:\mathbb{R}_{+}^{7}\mapsto\mathbb{R}_{+}$ as follows:

The positivity of (3.9) is evident from $\rho_{1}-\ln\rho_{1}-1\geq0$ for every $\rho_{1} > 0.$

Using Ito's strategy ^[44], we get

where $\mathbb{L}\Phi:\mathbb{R}_{+}^{7}\mapsto\mathbb{R}$ is stated as

Since $a_{1} = \chi_{1}+\varphi+\chi_{2}-\delta_{1}-\delta_{2}$, it follows that

Additionally, $\digamma$ is non-negative constant. Therefore, we have

For every $\Bbbk > \Bbbk_{0},$ integrating (3.11) on both sides from $0$ to $\lambda_{\Bbbk}\wedge\mathbf{T}$ and then applying the expectation gives

For $\Bbbk\geq\Bbbk_{0},$ $\Lambda_{\Bbbk} = \big\{\omega\in\Lambda:\lambda _{\Bbbk} = \lambda _{\Bbbk}(\omega)\leq\mathbf{T}\big\}.$ Thus, we get $\mathbf{P}(\Lambda_{\Bbbk})\geq\tilde{\epsilon}.$ Obviously, for each $\omega\in\Lambda_{\Bbbk}$ there exists $\mathbf{s}_{1}(\lambda _{\Bbbk}, \omega), \mathbf{x}_{1}(\lambda _{\Bbbk}, \omega)$, $\mathbf{u}_{1}(\lambda _{\Bbbk}, \omega)$, $\mathbf{r}_{1}(\lambda _{\Bbbk}, \omega), \mathbf{v}_{1}(\lambda _{\Bbbk}, \omega), \mathbf{m}_{1}(\lambda _{\Bbbk}, \omega)\; and\; \mathbf{j}_{1}(\lambda _{\Bbbk}, \omega)$ equating to either $\Bbbk$ or $\frac{1}{\Bbbk}.$ Therefore, $\Phi\big(\mathbf{s}_{1}(\lambda _{\Bbbk}, \omega), \mathbf{x}_{1}(\lambda _{\Bbbk}, \omega)$, $\mathbf{u}_{1}(\lambda _{\Bbbk}, \omega), \mathbf{r}_{1}(\lambda _{\Bbbk}, \omega), \mathbf{v}_{1}(\lambda _{\Bbbk}, \omega)$, $\mathbf{m}_{1}(\lambda _{\Bbbk}, \omega)$, $\mathbf{j}_{1}(\lambda _{\Bbbk}, \omega))$ is not less than either $\Bbbk-a_{1}-a_{1}\ln\frac{\Bbbk}{a_{1}}\; or\; \frac{1}{\Bbbk}-a_{1}-a_{1}\ln\frac{1}{a_{1}\Bbbk}$ = $\frac{1}{\Bbbk}-a_{1}+a_{1}\ln(a_{1}\Bbbk)$, $\Bbbk-1-\ln\Bbbk$, $\frac{1}{\Bbbk}-1-\ln\frac{1}{\Bbbk} = \frac{1}{\Bbbk}-1+\ln\Bbbk.$

As a result, we have

Finally, we have

where $\mathcal{I}_{\Lambda_{\Bbbk}}$ presents the indicator function of $\Lambda_{\Bbbk}.$ Taking $\Bbbk\mapsto\infty$ leads to the contradiction

This completes the proof.

3.3.   ESD

In disease transmission, it is important to determine when an illness will persist in the community. We demonstrate that the endemic equilibrium exists and is globally asymptotically stable in the deterministic model (2.1). However, the highly prevalent stabilization does not exist in the stochastic model (2.2) of the infected individual. According to Has'minskii's theory ^[45], there exists an ESD that reveals that the illness will endure.

Besides that, we reveal several hypotheses about the ESD (see Has'minskii ^[45]). Suppose that there is a homogeneous Markov procedure $\mathbf{u}(\mathbf{t})$ in $\mathbb{R}_{+}^{7}$ that is characterized by the stochastic DE presented as

The diffusion matrix of the system $\mathbf{u}(\mathbf{t})$ is presented as follows:

Lemma 3.2. ^[45] Suppose that $\mathbf{u}(\mathbf{t})$ is the Markov process with a unique ESD $\pi(.)$ if there exists a bounded region $\mathcal{Q}\in\mathbb{R}^{\mathfrak{n}}$ has a regular boundary $\mathcal{O}$ and

(i) $\exists$ a positive $S_{1}$ such that $\sum\limits_{\mathbf{i}, \mathbf{p} = 1}^{\mathfrak{d}}a_{\mathbf{i}\mathbf{p}}(\mathbf{y})\xi_{\mathbf{i}}\xi_{\mathbf{p}}\geq S_{1}\vert\xi\vert^{2}, \; \; \forall\; \mathbf{y}\in\mathcal{Q}, \forall\xi\in\mathbb{R}^{\mathfrak{n}},$

(ii) $\exists$ a positive $\mathbb{C}^{2}$-mapping $\Phi$ such that $\mathbb{L}\Phi$ is non-positive for every $\mathbb{R}^{\mathfrak{n}}\setminus\mathcal{Q},$ where $\mathbb{L}$ presents the differential operator described by

Then

where $\mathbf{f}(.)$ is an integrable mapping regarding to the measure $\pi.$

Define a parameter

Theorem 3.3. Suppose that system (2.2) $\big(\mathbf{s}_{1}(\mathbf{t}), \mathbf{x}_{1}(\mathbf{t}), \mathbf{u}_{1}(\mathbf{t}), \mathbf{r}_{1}(\mathbf{t}), _{1}(\mathbf{t}), \mathbf{v}_{1}(\mathbf{t}), \mathbf{m}_{1}(\mathbf{t}), \mathbf{j}_{1}(\mathbf{t})\big)$ is ergodic and admits a unique stationary distribution $\pi(.)$.

Proof. To test the assertion (ii) of Lemma 3.2, we must classify a non-negative $\mathbb{C}^{2}$-mapping $\Phi:\mathbb{R}_{+}^{7}\mapsto\mathbb{R}_{+},$ which must be categorized

where $\mathbf{q}_{1}, \mathbf{q}_{2}, \mathbf{q}_{3}, \mathbf{q}_{4}$ and $\mathbf{q}_{5}$ are the constants to be determined later. Using Ito's methodology and the proposed framework, we produce the mentioned findings (2.2).

It follows that

Now, we have

The preceding signifies that

Assume that

Accordingly, we have

As a result, we get

Furthermore, we obtain

Note that $\mathbf{q}_{6} > 0$ is a constant which will be determined later. It is effective to demonstrate that

where $\mathcal{H}_{\ell} = (1/\ell, \ell)\times(1/\ell, \ell)\times(1/\ell, \ell)\times(1/\ell, \ell)\times(1/\ell, \ell).$ The next process is to demonstrate that $\Phi_{2}(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})$ has only specified minimum value $\Phi_{2}({\mathbf{s}_{1}}_{0}, {\mathbf{x}_{1}}_{0}, {\mathbf{u}_{1}}_{0}, {\mathbf{r}_{1}}_{0}, {\mathbf{v}_{1}}_{0}, {\mathbf{m}_{1}}_{0}, {\mathbf{j}_{1}}_{0})$.

The partial derivatives of $\Phi_{2}(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})$ corresponding to $\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}\; and\; \mathbf{j}_{1}$ is as follows:

It is not difficult to determine that $\Phi_{2}$ has a distinct stagnation point.

Also, the Hessian matrix $\Phi_{2}(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})$ at $(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0))$ is

The aforesaid matrix seems to be positive definite. As a result, $\Phi_{2}(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})$ has the lowest value of $\Phi_{2}(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0)).$

In view of (3.19) and the continuity of $\Phi_{2}(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1}),$ observe that $\Phi_{2}(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})$ has at least one value $\Phi_{2}(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0))\in\mathbb{R}_{+}^{7}.$

After that, we shall define a positive $\mathbb{C}^{2}$-mapping $\Phi:\mathbb{R}_{+}^{7}\mapsto\mathbb{R}_{+}$ as follows

In view of Ito's formula and the suggested model, we have

As a result of this, the following supposition can be constituted:

where $\mathbf{q}_{7} = 7(\vartheta_{1}+\vartheta_{2})\Big[(\mathbb{R}_{0}^{s})^{1/7}-1\Big] > 0.$

The next stage is to produce the set

where $\epsilon_{\mathbf{p}} > 0, \; \mathbf{p} = 1, 2$ is a very small arbitrary constant. For the sake of clarification, we will split up the whole $\mathbb{R}_{+}^{7}\setminus\mathcal{Q}$ into the aforementioned domains.

Here we will demonstrate that $\mathbb{L}\Phi(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})$ on $\mathbb{R}_{+}^{7}\setminus\mathcal{Q}$, which is equivalent to conveying it on the ten previously specified domains.

Case I. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{1},$ Eq (3.25), yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{1}.$

Case II. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{2},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{2}.$

Case III. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{3},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{3}.$

Case IV. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{4},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{4}.$

Case V. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{5},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{5}.$

Case VI. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{6},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{6}.$

Case VII. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{7},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{7}.$

Case VIII. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{8},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{8}.$

Case IX. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{9},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{9}.$

Case X. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{10},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{10}.$

Case XI. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{11},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{11}.$

Case XII. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{12},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{12}.$

Case XIII. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{13},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{13}.$

Case XIV. For $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{14},$ Eq (3.25) yields

where

Thus, we conclude that $\mathbb{L}\Phi\leq-1$ for each $(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\mathcal{Q}_{14}.$

Evidently, we can deduce from (3.27)–(3.40) that for a sufficiently small $\epsilon$,

As a result, we develop that a constant $\mathcal{U} > 0$ is such that it ensures

Finally,

Suppose that $(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0)) = (r_{1}, r_{2}, r_{3}, r_{4}, r_{5}, r_{6}, r_{7}) = \bar{r}\in\mathbb{R}_{+}^{7}\setminus\mathcal{Q},$ and that $\delta^{\bar{r}}$ is the time span from an initial point $\bar{r}$ to reach a domain $\mathcal{Q};$ then

By integrating both sides of the variant (3.41) from zero to $\lambda ^{(\mathfrak{n})}(\mathbf{t})$, contemplating the expectation and using Dynkin's computation, one can obtain the following:

Since $\Phi(\bar{r})$ is positive,

This indicates that $\mathbf{P}\big\{\lambda _{\epsilon} < \infty\big\} = 1$ as a consequence of proof of Theorem 3.3. Conversely, the model (2.2) can be stated as regular. Thus, if $\mathfrak{n}, \mathbf{t}\mapsto\infty,$ we almost surely find $\lambda ^{(\mathfrak{n})}(\mathbf{t})\mapsto\lambda ^{\bar{r}}, \; (a.s).$

Applying Fatou's lemma, we have

Obviously, $\sup_{\bar{r}\in\ell}\mathbb{U}\lambda ^{\bar{r}}$, where $\ell$ is a compact subset of $\mathbb{R}_{+}^{7}$. It validates the Lemma 3.2 assertion (ii).

Also, the diffusion matrix of the model (2.2) is

Selecting $V_{1} = \min\limits_{(\mathbf{s}_{1}, \mathbf{x}_{1}, \mathbf{u}_{1}, \mathbf{r}_{1}, \mathbf{v}_{1}, \mathbf{m}_{1}, \mathbf{j}_{1})\in\bar{\mathcal{Q}}\in\mathbb{R}_{+}^{7}}\big\{\wp_{1}^{2}\mathbf{s}_{1}^{2}, \wp_{2}^{2}\mathbf{x}_{1}^{2}, \wp_{3}^{2}\mathbf{u}_{1}^{2}, \wp_{4}^{2}\mathbf{r}_{1}^{2}, \wp_{5}^{2}\mathbf{v}_{1}^{2}, \wp_{6}^{2}\mathbf{m}_{1}^{2}, \wp_{7}^{2}\mathbf{j}_{1}^{2}\big\},$ we find that

where $\Im = (\Im_{1}, \Im_{2}, \Im_{3}, \Im_{4}, \Im_{5}, \Im_{6}, \Im_{7})\in\mathbb{R}_{+}^{7}.$ This shows that the assertion (i) of Lemma 3.2 is satisfied. Based on the foregoing discussion, Lemma 3.2 illustrates that the framework (2.2) is ergodic and has only one stationary distribution.

4.   Numerical experiments for fractional SDVI system

4.1.   Caputo fractional derivative operator

In this part, we will investigate the dynamical behavior of SDVI models (2.1) and (2.2) that incorporate the multi-target cells and involve classical, index-law and eventually, stochastic processes. In this scenario, if we define $\mathbb{T}$ as the final time of transmission, that is, the penultimate time when a secondary outbreak occurs, then the mathematical framework will be developed by using the classical derivative formulation in the first round, then the index-law kernel in the second step and finally the stochastic environment in the later phases. Following that, the mathematical formalism that explains this phenomenon is offered as follows:

Here, we apply the technique described in ^[24] for the scenario of Caputo's derivative to analyze quantitatively the piecewise structure described by (4.1)–(4.3). We commence the technique as follows:

It follows that

where

and

4.2.   Caputo-Fabrizio fractional derivative operator

In this subsection, we will examine the system dynamics of SDVI propagation involving multiple-target cells comprising classical, exponential decay law and stochastic mechanisms. If we describe $\mathbb{T}$ as the concluding time of transmission, that is, the final time when a secondary epidemic appears, then the mathematical structure will be formed in the first round by using the classical derivative implementation, then the exponential decay kernel in the second step and eventually the stochastic environment in the subsequent periods. Regarding that, the mathematical approach used to illustrate this occurrence is presented as follows:

Here, we apply the technique described in ^[24] for the scenario of the Caputo-Fabrizio derivative to analyze quantitatively the piecewise structuredescribed by (4.7)–(4.9). We commence the technique as follows:

It follows that

4.3.   Atangana-Baleanu fractional derivative operator

Here, we will concentrate on the dynamic behavior of SDVI spreading, which demonstrates three main phases for a certain region, including the classical, GML law and lastly, stochastic causes. If we define $\mathbb{T}$ as the final time when a secondary epidemic appears, the mathematical configuration will be constituted in the first round employing the classical derivative application, followed by the Mittag-Leffler kernel in the second step and finally the stochastic environment in subsequent periods. In this regard, the mathematical model utilized to describe this phenomenon is as follows:

Here, we apply the technique described in ^[24] for the scenario of the Atanagan-Baleanu-Caputo derivative to analyze quantitatively the piecewise structure described by (4.12)–(4.14). We commence the technique as follows:

It follows that

where $\Xi_{1}, \Xi_{2}$ and $\Xi_{3}$ are stated as before in (4.4)–(4.6).

5.   Results and discussion

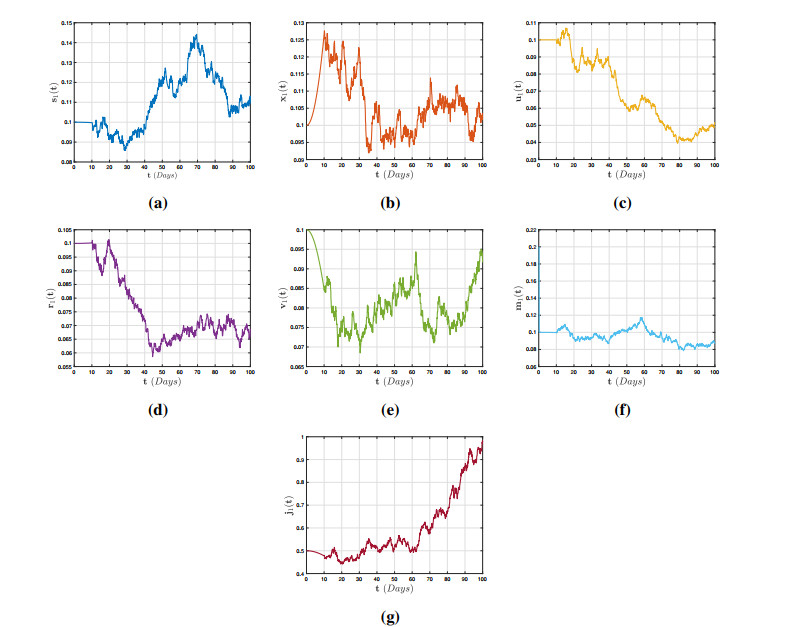
This part comprises numerical computations that demonstrate the simulated predictions via the notable technique proposed by Atangana and Araz ^[24]. We utilize the stochastic piecewise fractional DE method to obtain the stochastic version of the designed system by employing the power-kernel described by (4.1)–(4.3), exponential decay kernel described by (4.7) and (4.8) and GML kernel described by (4.12)–(4.14) for simulation analysis, as shown below. Suppose that $\vartheta_{1} = 10, \; \vartheta_{2} = 6, \; \gamma_{1} = 0.01$, $\; \gamma_{2} = 0.01$, $\; \varsigma_{1} = 0.5$, $\; \varsigma_{2} = 0.3, \; \zeta_{1} = 10$, $\; \zeta_{2} = 5, \; \varphi = 3$, $\; \omega_{1} = 0.3$, $\; \omega_{2} = 0.1$, $\; \rho_{1} = 0.1$, $\; \rho_{2} = 0.1$, $\; \delta_{1} = \delta_{2} = 0.00005$, $\; \chi_{1} = 0.0005$ and $\chi_{2} = 0.001$ with random intensities $\wp_{1} = \wp_{2} = \wp_{3} = \wp_{4} = \wp_{5} = \wp_{6} = \wp_{7} = 0.01.$ Moreover, we assumed the ICs as $\mathbf{s}_{1}(0) = 0.1$, $\; \mathbf{x}_{1}(0) = 0.1, \; \mathbf{u}_{1}(0) = 0.1$, $\; \mathbf{r}_{1}(0) = 0.1$, $\; \mathbf{v}_{1}(0) = 0.1$, $\; \mathbf{m}_{1}(0) = 0.2\; and\; \mathbf{j}_{1}(0) = 0.5.$ We can instantly compute the threshold parameter $\mathbb{R}_{0}^{s} = 0.258 < 1$ and the solution of the model (2.2) must comply with Theorem 3.3.

Depending on the above discussion, we took into account the model parameters and accompanying noise concentrations of the dynamical system (4.1)–(4.9) for Figure 1 by utilizing the deterministic-stochastic approach with crossover impacts. The estimate illustrates and validates eradication, and it demonstrates that the stochastic framework (2.2) is stochastically asymptotically stable in the prescribed environments. Figure 1 demonstrates that the simulation of Theorem 3.2 and its deterministic counterpart have analogous features. Both model solutions congregate at the disease-free equilibrium point of (2.1). This means that the illness becomes exterminated when such a prescribed requirement is satisfied, i.e., the number of affected patients will decrease tremendously, whereas susceptible individuals will remain.

Analogously, in Figure 2, we presume another case for the system's parameters to fix intensities of white noise (stated above) through the use of the exponential decay kernel, which also reveals an irreversible or steady dispersion and quantitatively appeases the theorem's "stationary distribution" declaration. According to modeling, the deterministic-stochastic model (4.7)–(4.9) will oscillate for a long time around the correlating deterministic model's specific regional steady state given by (2.1). Because the low noise concentration of the virus will persist, the mean volatility all around the outbreak steady state is minimal. In the long term, both frameworks result in similarities and differences between the stochastic model (2.2) and its deterministic counterpart described by (2.1).

Figure 3 represents the deterministic-stochastic dynamics of the SDVI described by (4.12)–(4.14) considering the piecewise fractional DEs with the system parameters and low random intensities. The dynamics of the Atanagana-Baleanu Caputo fractional derivative can predict the dynamics in a better way than the power-kernel and exponential decay kernel. Thus, we furthermore illustrate that the stochastic approach described by (2.2) has a unique stationary distribution only when the random intensities are small enough and the threshold parameter $\mathbb{R}_{0}^{s} > 1.$

Figures 4–6 shows the phase portrait of the deterministic-stochastic behavior utilizing the GML kernel influence by the crossover effects with varying random intensities $\wp_{1} = 0.01, \; \wp_{2} = 0.02, \; \wp_{3} = 0.03, \; \wp_{4} = 0.04, \; \wp_{5} = 0.05, \; \wp_{6} = 0.06\; and\; \wp_{7} = 0.07.$ Nonetheless, while the crossover qualities of the Mittag-Leffler kernel have been recognized as potent analytical techniques for depicting major difficulties, it is important to recognize that only underlying complications continuing to pursue the crossover residences of this kernel can be modeled with certain restrictions, as is present in legitimate challenges; this kernel will not be capable of demonstrating the time where the crossover occurred. Admittedly, serious concerns exemplifying multiple procedures mean that the GML cannot be recreated by using the Atangana-Baleanu derivative. The investigation is not constricted to the conceptual scheme for the SDVI model, as it can be extended to several other vector-borne diseases, including Rift Valley fever, yellow fever and Zika, to discuss the piecewise deterministic-stochastic behavior related to dynamical systems.

6.   Conclusions

Many real-world phenomena are not deterministic but include stochastic consequences, which allows for a more precise prediction of their highly infectious evolution. In this research, we developed a viral model to describe the deterministic-stochastic effects of secondary dengue viral infection through the use of multiple target cells. In the framework, we have used both heterologous and homologous immune cells. We tested the fundamental features of solutions, such as the feasibility and invariant region. We determined the threshold parameters for both deterministic and stochastic simulations, respectively. More accurately, we have verified the following result:

Then, for any initial setting $(\mathbf{s}_{1}(0), \mathbf{x}_{1}(0), \mathbf{u}_{1}(0), \mathbf{r}_{1}(0), \mathbf{v}_{1}(0), \mathbf{m}_{1}(0), \mathbf{j}_{1}(0))\in\mathbb{R}_{+}^{7},$ the scheme (2.2) has a unique ESD $\pi(.).$ We clearly see the adverse effect of noise concentration on virus transmission. The extermination of dengue virus infection in people grows in tandem with the extent of the noise in the vulnerable community. Accordingly, the persistence of the virus declines as the noise level increases. We contend that, while the GML kernel, exponential-decay kernel and power kernel have been revealed to be capable of depicting several crossover behaviors, their strengths to do so may be curtailed due to the intricacy of existence. Furthermore, numerous serious concerns exist about crossover behaviors that have yet to be illustrated by the Mittag-Leffler, the exponential or the power law kernel, so any mathematical formula based on these derivatives will be unable to exemplify such behavior. Some key features of piecewise concepts are described in the proposed model, and a numerical mechanism has been proposed. We are convinced that this theory will lead to opportunities for additional exploration of biological impacts, including time delay ^[46] and reaction-diffusion ^[47].

Conflict of interest

The authors declare that they have no competing interests.