1.
Introduction
Fuzzy models established themselves many years ago as a globally recognized standard in technical control systems and form the basis for numerous systems in this area that are referred to as “intelligent” – the spectrum ranges from image stabilization and scene recognition in digital cameras to production automation and robot control [1]. What is far less well-known, however, is the fact that the underlying concepts of fuzzy-set theory established by Zadeh [2] can also be used, according to an approach developed by Rommelfanger [3], to develop models to support advisory and diagnostic tasks [1,4], such as those required in strategic asset allocation (on this and on the issues subsequently described, see [5]). This is a matter of deciding in which proportions an investor should invest in which investment forms – such as shares, real estate and fixed-interest securities – during the planned investment period [6,7].
So far, there has been no satisfactory support for this in the form of a viable algorithm, as is also reflected in the often divergent proposals of investment advisors [7,8]. This also results in the poor ratings given by the consumer protection organization “Stiftung Warentest”, which has already examined the advisory quality of financial service providers on numerous occasions; see for example Stiftung Warentest [9,10].
Financial experts are nevertheless in a position to attain good solutions, and according to Rommelfanger’s concepts, in which the basic principle of technical fuzzy controls is transferred and extended to non-technical problems, the intelligent problem-solving behavior of such an expert can be adequately depicted in a fuzzy model (on this and the descriptions of this approach in the following sections see [1,4,11].
A fuzzy model based on this approach can form the basis of a robo-advisor. This is consulting software in which – after entering the market expectations, the features of an investment project and of an investor profile – the user can call up the proposals that are recommendable from the point of view of the expert depicted in the model.
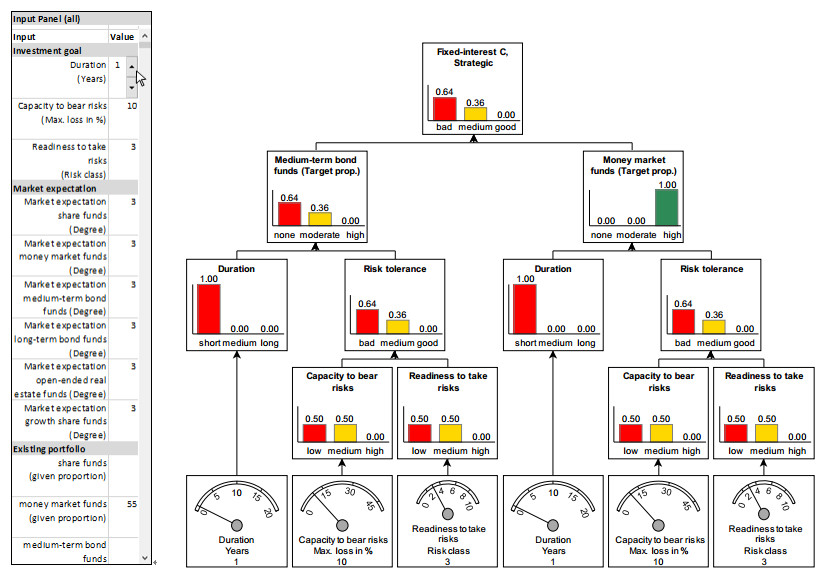
Such a fuzzy model was developed in North [5]. The expert whose problem-solving behavior it depicts is one of the directors of a major bank which is globally active in asset management. He has extensive knowledge of asset allocation. Following Rommelfanger’s approach, the model is hierarchically structured and compacts the features of the investment project and the investor profile via rules for valuations of predefined investment strategies, cf. Figure 1. The structure of the model and its advantages and disadvantages are presented in detail in [5].
In order for such a model – which is also referred to as a “fuzzy expert system“ – to be accepted in expert circles, two further problems need to be solved in addition to the depiction of human problem-solving behavior (on this and on the further explanations, see [5,12]).
The first additional problem that arises is how to adapt the model to new knowledge and the ideas of experts from other financial institutions, as otherwise one would have to adopt the ideas of the expert depicted in the model for one’s own financial institution. This problem is addressed in [12]. There it is shown how the model can be adapted to other ideas, input parameters, asset classes and investment strategies.
The second problem is how to comprehensively examine the extent to which the model achieves good results and reacts plausibly to changes in the input parameters. This paper deals with this problem.
A practical application of a fuzzy advisory system requires a comprehensive validation, since one-off decisions are made, which are intended to be correct in all constellations (on this and the following see [3,13]). In technical control processes a complex validation is not necessary because the control decisions are repeated at short intervals and calculated manipulated variables, which only tend to be correct, are corrected in the subsequent run. In contrast, an erroneous asset allocation can only be changed by accepting transaction costs and, in addition, book losses may already have occurred due to temporary fluctuations in value, which would have to be realized in the event of a correction [14].
Validation standards that explicitly include fuzzy expert systems were developed by the “Deutsche Vereinigung für Finanzanalyse und Asset Management” (German Association for Financial Analysis and Asset Management) [15]. According to these guidelines, a fuzzy logic-based model is valid if both the validity of the results and the validity of the procedure are fulfilled (on this and on the following explanations see [15]). Validity of the results means that the model provides accurate results for all supported constellations of the input parameters as far as possible. Validity of the procedure means that the results are determined on the basis of professionally correct assumptions and rules. For example, a Strategic Asset Allocation system is only valid if, on the one hand, the recommended asset allocations are suitable for achieving the investor’s objectives and, on the other hand, the right partial conclusions are reached, for example on the investor’s risk tolerance.
A valid procedure is also characterized by the fact that the conclusions react realistically to changes in the input parameters, something which is investigated with the aid of a sensitivity validation (on this and on the following comments on this method see [16,17,18]). This is regarded as one of the most powerful validation methods. In this examination, it is expected that the conclusions of the system will change only slightly with small changes in the input parameters, or possibly not at all if, in the opinion of the expert, small changes in individual parameters have no influence on the results in some constellations. On the other hand, major changes should result in significantly different recommendations. According to [19], such behavior is an essential prerequisite for having confidence in the results of an asset allocation model.
However, the question arises as to how it can be recognized in a simple and complete way to what extent all interim and final evaluations of a model change if the input parameters are varied consistently in their value ranges.
Therefore, several validation tools were developed together with the asset allocation model: a factor variation with animation of the changes of all interim and final evaluations, an “expert comparison”, in which different depictions of a decision behavior can be compared with each other, and progression analyses, with which changes can be graphically represented. Chapter 2 presents these tools and examples of outcomes resulting from their application using the fuzzy logic-based asset allocation model which was developed in [5] on the basis of the concepts of Zadeh and Rommelfanger.
2.
Instruments of sensitivity validation
In order to be able to perform a comprehensive validation, several validation tools were developed in addition to the model. They are part of the development environment “Visual Fuzzy” constructed by the author, which is aimed at the development of models for consulting and diagnostic tasks (on this and on the following descriptions of Visual Fuzzy see [5,12]). In these areas, a comprehensible and understandable approach to finding a solution is an essential prerequisite for the acceptance of the recommendations, as for example it is also necessary to explain a proposal to an investor so that he can agree to it [3,19]. Therefore, all model components and calculation steps can be visualized in Visual Fuzzy. As is usual with hierarchical processes, flowcharts are used for the representation, which also allow all variables and relationships of a model to be created and changed interactively, cf. Figure 1.
On the flowchart objects the structure of a variable together with the calculation results can be displayed in different ways. For example, in the flowchart shown in Figure 1, membership values and degrees of fulfillment are represented in the form of bar charts; on this form of representation see [20].
The flowchart shows on the basis of which features and via which analysis fields the expert evaluates the extent to which the investment strategy “Fixed Interest C” is suitable for the realization of an investment project (see [5] on this and on the following remarks relating to the structure of the model). With this investment strategy, an investor invests 50% in money market funds and 50% in medium-term bond funds. It is one of the 15 model investment strategies of the financial institution depicted in the model, from which an investment advisor can select one which is suitable. All strategies are valued according to the same scheme.
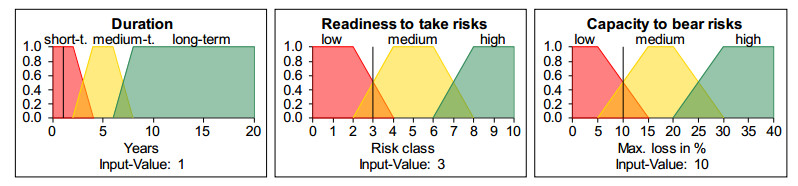
The lowest level of the flowchart shows the input features of the model: the investor’s readiness to take risks, his capacity to bear risks and the planned duration of the investment (for a variant that also takes into account current market expectations for the asset classes, see [5]).
Figure 2 shows how these features are displayed in the flowchart when the display is selected for them which shows the structure of the variable. The black bars shown represent the input values.
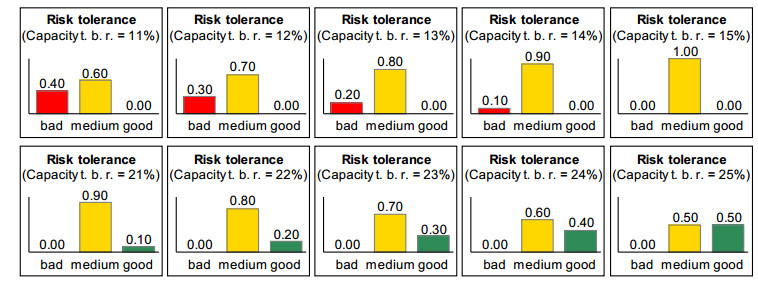
At analysis level 1, following the expert’s approach, the readiness to take risks and the capacity to bear risks are compacted into the risk tolerance, which represents an interim summary judgement on the risk that can be tolerated in an investment [14,21]. On the associated rules cf. Figure 8.
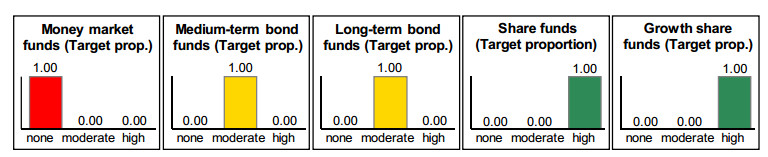
At analysis level 2, the target proportions are determined for the asset classes contained in the strategy. The judgement class “none” means “no proportion”,
“moderate” means a share of up to 45% and “high” a share of between 45% and 100%. The rules for the example of the asset class “Share funds” are displayed in Table 2. For example, Rule 6 states that a high proportion of shares should be included when there is a long duration and a good risk tolerance. On the other hand, in the opinion of the expert depicted, no investments should be made in shares when there is a short duration, as there is no time to “sit out” temporary fluctuations in share prices. Since this is independent of the investor’s risk tolerance, it is sufficient to set up only one rule for a short-term duration without further differentiating according to the risk tolerance, cf. Rule 4. For each rule, an explanatory text can also be stored describing the professional background of the rule from the expert’s point of view. In the example of rule 4, the stored text reflects the facts described above.
At analysis level 3, it is evaluated how advantageous the investment strategy is for the investment project. For this purpose, the valuations of the asset classes contained in the investment strategy are considered. A comparison is made how well the target proportions for the asset classes determined at analysis level 2 match the proportions contained in the investment strategy, cf. the corresponding rules for a strategy with an asset class ratio of 75% to 25% in Table 1.
For example, Rule 6 states that if the ratio of shares is the same, the strategy is rated good, while Rule 3 states that if the ratio is exactly the opposite, the strategy is rated bad. If one of the asset classes making up the strategy is not to be included in the strategy, the strategy is also rated as poor, see Rules 1 and 2. In all other constellations, the strategy is rated as medium.
In the development environment used it is possible to create any number of flowcharts. All components of a model can be displayed on them in any combination, regardless of which flowcharts they were originally created on or which analysis levels they are assigned to. If changes are made to the model using a flowchart, all other flowcharts are updated so that they always show the current status of the model components they contain.
These properties allow a complex model with many variables to be split across multiple flowcharts for easier editing and reviewing. For example, as Figure 1 shows, a separate flowchart can be created for each investment strategy, which contains its complete analysis tree, so that the calculation steps for strategy evaluation can be traced across all subordinate elements involved. In addition, a further flowchart can be created which presents the evaluations of all investment strategies side by side without their subordinate analysis trees, so that the user can see at a glance which strategies for an investment project are evaluated as advantageous and disadvantageous to what extent, see Figure 14. All the sensitivity validation instruments described below build on these possibilities.
2.1. Factor variations with animation sequences
To test a model, its input values can be changed in several interactive ways in the development environment used. This is done via a so-called “input panel”, which displays all input variables with their currently assigned values.
Through the visualization options it is possible to recognize the resulting changes at all levels of analysis; such a check, in which the conclusion process is visualized while parameters are changed interactively, is also referred to as “visual interaction” following [16], see [22]. In addition, it is also possible to display the changes in the form of an animation.
Figure 1 shows the input panel on the left area of the section of the user interface shown. The values of the input variables can be entered directly in the panel or changed via control elements. As soon as a value is changed, the model is recalculated and all flowcharts are updated. Using “Spin buttons”, as shown in the figure for the example of “Duration”, the value of an input parameter can also be continuously increased or decreased in small steps. Since the displayed flowchart is constantly updated during this time, the changes resulting from the variation are displayed as an animation sequence in this way.
Figure 1 shows the initial situation of a factor variation in which the model behavior for a test case of Stiftung Warentest is investigated. This consumer protection organization continuously – with updates every few years – examines the advisory quality of financial service providers in Germany on the basis of typical,
“timeless” investment projects with which investment advisors are confronted on a daily basis; see for example [9,10].
In the test case shown here, a student, shortly before graduating and still without a job, would like to invest 5000 euros (see [23]). Stiftung Warentest gave a positive assessment to a financial institution’s proposal to invest first in the short term and securely and to consider a longer-term investment only after employment. The recommendation of the financial institution, which was rated positively, was to invest in money market or bond funds.
However, the expert depicted in the model evaluates more cautiously than Stiftung Warentest (on this and the rules and evaluations of the expert described below see [5,12]). Given the initial constellation – what he sees as a clearly short-term duration, clearly low capacity to bear risks and clearly low readiness to take risks – he advises against bond funds, as they have at least a low price risk and a fluctuation cannot be “sat out” due to the short duration, which is not compatible with a clearly poor risk tolerance.
The expert in principle evaluates strategies with risky investment forms – such as bond funds or the far more riskier share funds – only positive when better conditions are available, i.e. a higher risk tolerance and a longer investment period. This more cautious evaluation is also correctly reflected in the model, as proven by the factor variation in the example of the strategic evaluation of the investment strategy “Fixed interest C”, which is made up of 50% money market funds and 50% medium-term bond funds. In the initial situation of the variation, the investment project was already represented with a slightly higher readiness to take risks (risk class 3) and a slightly higher capacity to bear risks (10%), resulting in a bad to medium risk tolerance at analysis level 1 (cf. Figure 1). However, the duration is still clearly short-term.
According to the expert, all three incoming features must have reached a sufficient level before he recommends investing a moderate proportion in bond funds. As this is not the case here due to the duration, he predominantly advises against this asset class. Accordingly, the investment strategy is evaluated as “predominantly bad to moderately suitable”.
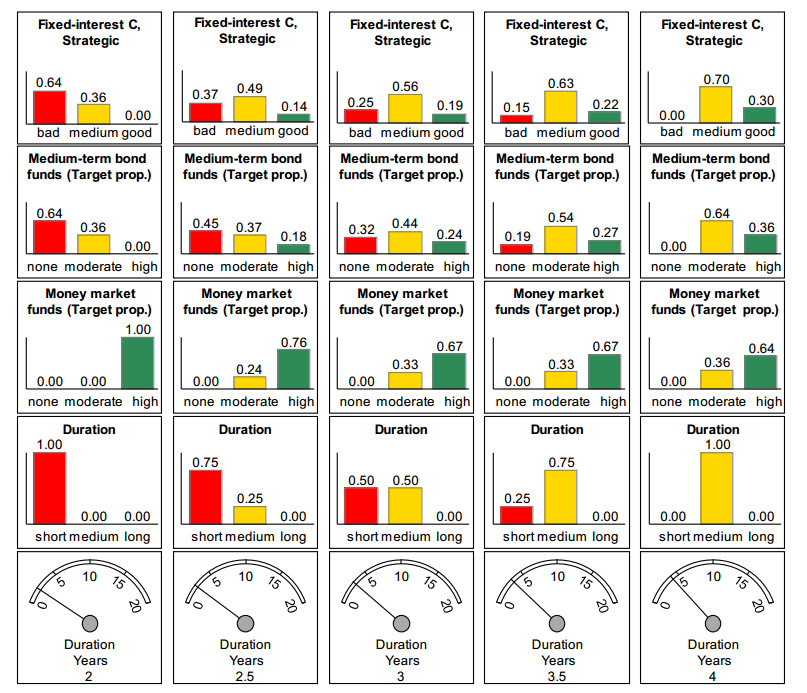
On the basis of this constellation, the duration was increased from one year to four years in steps of 0.1 years. Figure 3 shows in compact form, using several examples, which degrees of fulfillment occur with this factor variation and are shown in the analysis tree of Figure 1. The evaluation of the risk tolerance does not change with this variation.
If, as the graph proves, the duration changes slightly, the evaluations change at all analysis levels, but only to a small extent. Significant changes, on the other hand, also lead to significant evaluation changes. This corresponds to the views of the expert depicted.
Medium-term bond funds are successively better evaluated with increasing duration, while money market funds are evaluated increasingly worse, but they remain in the range “predominantly high”. Given the investor’s specified risk profile, an investment of a high proportion in money market funds is seen somewhat less favorably with increasing duration, as these have a lower profitability than bond funds. For the latter, a moderate proportion is increasingly recommended.
With duration of four years, all features have sufficiently good conditions for a somewhat risky investment with a limited price risk. A “predominantly moderate” proportion of the portfolio is now recommended for bond funds. However, money market funds should still predominate in the portfolio, so that the strategy, which is composed of equal parts of both asset classes, is not evaluated as clearly good, but as “medium to good”.
Only if the conditions are even better – i.e. if not only the duration is clearly medium-term, but also a clearly medium readiness to take risks (risk class 4) and a clearly medium capacity to bear risks (15%) are present, resulting in a clearly medium risk tolerance – is a high proportion clearly recommended for medium-term bond funds, while only a moderate proportion is recommended for money market funds, cf. Figure 4. Thus, as this figure also shows, two other strategies, “Fixed Interest A” and “Fixed Interest B” are clearly evaluated as good because they consist exclusively or predominantly of medium-term bond funds. The strategy “Fixed Interest C”, on the other hand, is no longer evaluated as “medium to good”, but only as “medium” because its proportion of money market funds is now too high.
As Flach and Rommelfanger show, such a relationship as that between the three input variables and the evaluation of the strategy “Fixed Interest C” – with increasingly better conditions, the evaluation of the strategy improves, but worsens again at a certain level – could not be modelled using most mathematical-statistical agammaegation methods, as these require a proportional relationship between the sub-objectives and the overall objective [5,11,20].
In contrast, in a rule-based fuzzy model a nonlinear relationship can be reproduced realistically – even in the area in which the evaluation of the strategy deteriorates again [11,20]. As is proven by the example in Figure 5, with a medium-term duration (4 years) and a medium readiness to take risks (risk class 4), the strategy’s evaluation (only) successively decreases with increasing capacity to bear risks, from “medium to good” to “medium”.
Using comparable factor variations, each analysis field of a fuzzy model can be checked – not only technically, but also professionally, by looking at the explanatory texts, which are deposited with the rules with a positive degree of fulfillment. Thus a model can be fully validated.
2.2. Expert comparisons
In order to be able to quickly compare several variants of the depiction of an expert with each other, the architecture of the development tool is designed to be able to manage several expert opinions in the knowledge base. This also makes it possible to draw comparisons between different experts who may differ in their judgment.
In connection with a sensitivity validation, an expert comparison can prove that if an expert’s decision-making behavior is depicted using a fuzzy model, this model reacts validly to changes, whereas if other modelling procedures are used to depict the same decision-making behavior, investment projects that differ slightly from one another can receive completely different recommendations (on the implications resulting from the different modelling procedures see [1,4]).
The following example shows this based on a test case of Stiftung Warentest. In the course of this study it was examined which proposals were received by an investor who wanted to invest for his retirement provision in the long term and who presented himself as “risk-conscious” [24]. Investment proposals with a mixture of bond funds and share funds, where the proportion of share funds was between 30 and 80 percent, received the rating “very good” from Stiftung Warentest [24].
In this comparison, the model presented, which depicts the decision-making behavior of the expert consulted, is referred to as “Expert A” for simplification purposes. On the diagnoses and conclusions of the expert which are described below in this section, see [5].
The verbal evaluations of Expert A are described with fuzzy intervals, following the concepts of [2] and [3], cf. Figure 6 [1].
For comparison a copy of this model was created which is referred to below as “Expert B”. The state variables were then modified in this copy. The values of Expert B’s state variables are described – as in the “first” or “classic” expert systems – with classic intervals, as shown in Figure 7 [1]. No further changes were made to the copy.
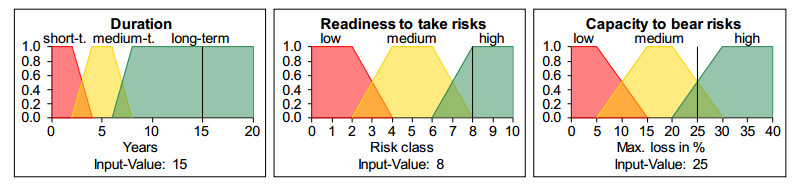
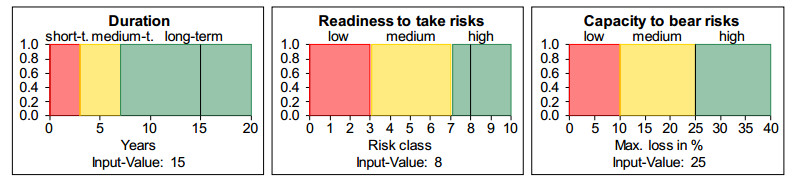
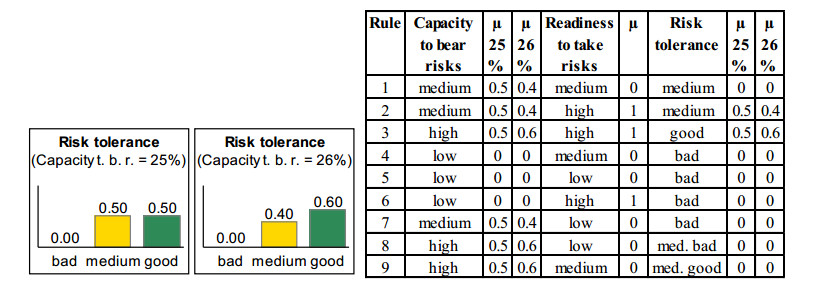
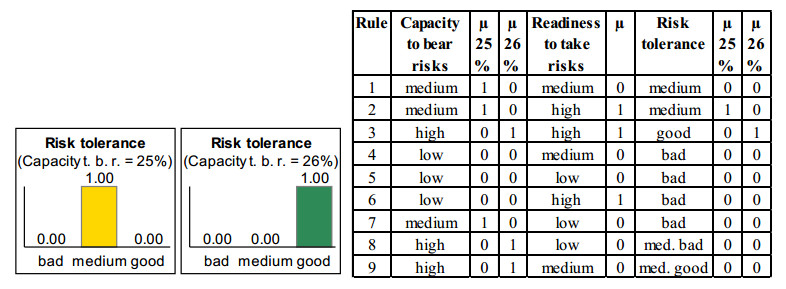
Since both experts are significantly more cautious than Stiftung Warentest and only make similar recommendations when the conditions are better (see Section 2.1), the initial situation of the comparison was not represented with a clearly medium risk tolerance of the investor, which the expert would describe as “risk-conscious”; instead, the risk profile was depicted somewhat better: the readiness to take risks is at risk class 8, which both experts evaluate as clearly high, and the capacity to bear risks is 25%, which Expert A evaluates as medium to high and expert B as clearly medium, cf. Figure 6 and Figure 7. Subsequently, the investment strategy evaluations of the two experts were compared after changes in the boundary areas of the evaluation intervals. Figure 8 and Figure 9 show how the evaluation of the risk tolerance at analysis level 1 changes for both experts when the capacity to bear risks is increased from 25% to 26%.
While Expert A evaluates the risk tolerance only slightly better, Expert B no longer evaluates it as medium but as good. This is because Expert B no longer evaluates a capacity to bear risks of 26% as medium but as high (cf. Figure 7) and thus Rule 2 is no longer fulfilled, but Rule 3 (cf. Figure 9).
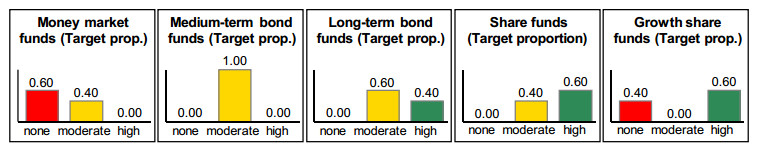
At analysis level 2, in the case of Expert A, there are only minor changes to the recommended asset class proportions because he evaluates the risk tolerance only slightly better. Figure 10 and Figure 11 show his evaluations of money market, bond and share funds at a capacity to bear risks of 25% and 26%. Using share funds as an example, Table 2 shows that in the underlying rule matrices for the evaluation of asset classes, the membership values and degrees of fulfillment change only slightly.
According to Expert A, with the given risk tolerance and duration there is no asset class that should take up a high proportion of the portfolio. Medium-term bond funds are too unprofitable to be an investment focus. However, the given constellation is already somewhat too good for a high proportion of long-term bond funds, as the investor could take higher risks. The better the conditions for a risky investment become, the more it is the case that long-term bond funds should only be included in a moderate amount in a portfolio, only for diversification purposes – share funds increasingly represent an alternative with higher return potential.
Thus, as can be seen from the comparison of Figure 10 with Figure 11, evaluation of share funds improves as the capacity to bear risks increases, while that of long-term bond funds deteriorates. However, the existing risk tolerance is not yet sufficient for a high proportion of share funds. This correctly reflects the more cautious approach of the expert consulted compared to Stiftung Warentest. He only recommends a high proportion of share funds if there is a clearly good risk tolerance with a long duration (see Rule 6 in Table 2).
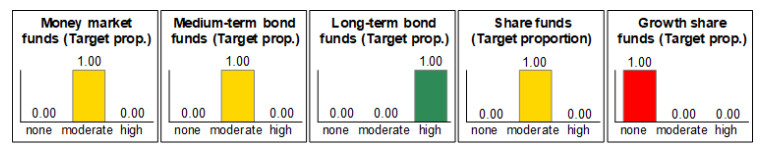
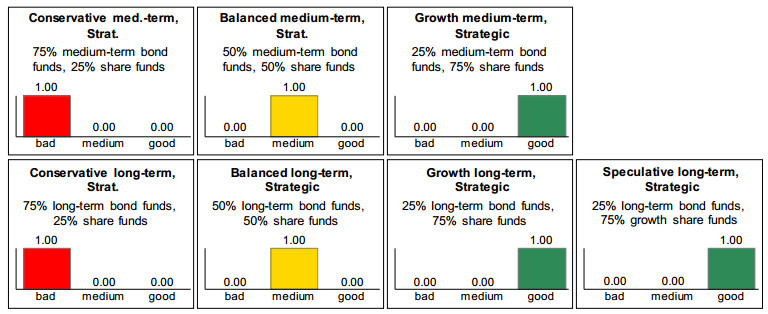
In the case of Expert B, by contrast, the asset class evaluations change significantly because he no longer evaluates the risk tolerance as medium but as good, cf. Figure 9. Expert B therefore no longer recommends a moderate but a high proportion for share funds, cf. Table 3. The evaluations of other asset classes also change just as significantly, cf. Figure 12 compared with Figure 13.
A comparison of the evaluations of both experts shows that when verbal evaluations are described with the help of fuzzy intervals, as is the case with Expert A, very detailed, differentiated evaluations can also be depicted (on this and on the following explanation see [13,20]). There are not only evaluations in the form “none to moderate” or “moderate to high”, but – as with growth share funds – also those in the form “both none and high”. This evaluation reflects the fact that, in the opinion of the consulted expert, there are both aspects for and against the inclusion of this asset class in the portfolio. Since growth share funds involve higher risks than standard share funds, the expert refrains from investing in more constellations than is the case with standard share funds.
In his opinion, the partially fulfilled high risk tolerance speaks for an investment, but the partially fulfilled medium risk tolerance speaks against it, since a medium risk tolerance is no longer compatible with the high-risk content of growth share funds.
In the case of Expert B, in contrast, only one rule is fulfilled in every analysis field, since the linguistic evaluations in his state variables are depicted over disjoint classic intervals (on this and on the implications described below see [13,20,25]). Differentiated evaluations are therefore not depicted and it may occur that an evaluation changes significantly with a minimal change in an input parameter, as is the case in the example of growth share funds (from “none” to “high”).
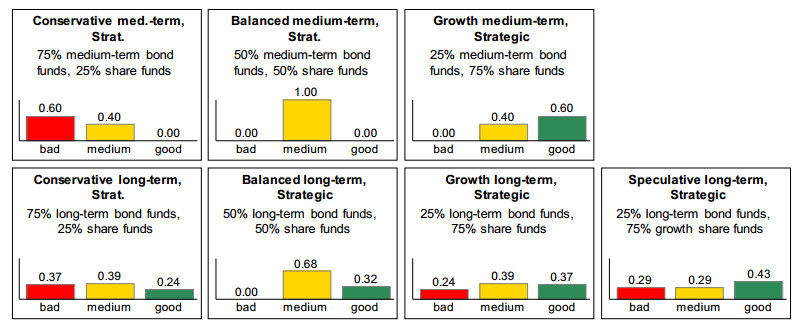
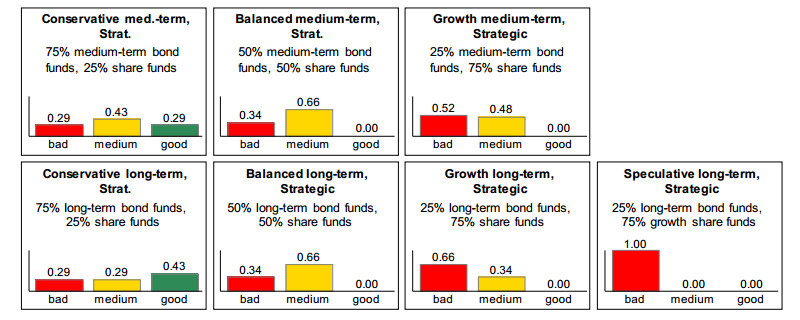
The evaluations of the strategies at analysis level 3 result from the asset class proportions recommended at analysis level 2, see chapter 2. In the case of Expert A, in turn these evaluations change only slightly, since his asset class evaluations have changed only slightly, cf. Figure 14 compared with Figure 15.
Since there is no asset class for which the expert recommends a high proportion under the given conditions, there is no ideally suited strategy among those depicted in the model. The strategy “Growth medium-term”, which has a 75% proportion in standard share funds, is evaluated best of all strategies. It is somewhat less risky than a strategy with an 80% share proportion, which is the maximum which a strategy could feature in order to be rated as (clearly) good by Stiftung Warentest.
Nevertheless – and despite the fact that the investor has already been depicted with a better risk tolerance than in the test case – the expert does not yet evaluates the strategy as clearly good, as he is much more cautious. This is also reflected in the fact that he evaluates the two strategies “Growth long-term” and “Speculative long-term”, which also have an share fund proportion of 75%, less favorably than the strategy “Growth medium-term”, since, unlike the latter, they are more risky with long-term bond funds (instead of medium-term bond funds) or growth share funds (instead of standard share funds). All other investment strategies are evaluated as “bad to medium” or “predominantly medium” because they have too little return potential under the given conditions.
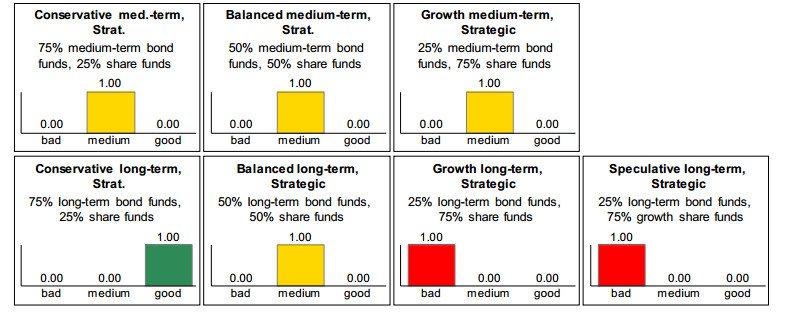
While Expert A’s evaluations of investment strategies hardly change, the slight change in the capacity to bear risks leads to completely different recommendations in the case of Expert B, cf. Figure 16 compared with Figure 17. For example, the two strategies “Growth long-term” and “Speculative long-term” are now clearly evaluated as good, whereas they were previously clearly evaluated as bad.
However, not only can there be extreme improvements in the evaluations, but also extreme deteriorations, as can be seen from the example of the strategy “Conservative long-term”, which is now evaluated as clearly bad, whereas it was previously evaluated as clearly good.
In contrast, Expert B’s evaluations of investment strategies would not change, even in the event of a major change in the capacity to bear risks, if this did not result in leaving the state evaluation class “medium capacity to bear risks”– since all values within a classic interval receive the same evaluation [13,25]. This would be the case, for example, with an increase from 11% to 25%, because both feature values are clearly evaluated as medium by expert B (see Figure 7). This behavior is also a major shortcoming of earlier expert systems [1].
The fuzzy modelling in expert A, on the other hand, shows a behavior as is expected from a valid model in a sensitivity validation, not only with small but also with large changes. With a significant increase in the capacity to bear risks from 11% to 25%, which does not lead to any change for Expert B, the evaluation of risk tolerance also changes significantly in the fuzzy model. Figure 18 shows a factor variation of the capacity to bear risks over the corresponding range.
For values greater than 15% and less than 21%, the evaluation of the risk tolerance does not change according to the expert’s specifications and corresponds to the 15% evaluation presented. With a capacity to bear risks of 11%, the evaluation of the risk tolerance is significantly worse than with 25%. For this reason, strategies with a share fund component are only evaluated as “poor to medium”, and the higher the share component in the strategy and thus the associated risk, the worse they are evaluated, cf. Figure 19. If a strategy contains growth share funds which are riskier than share funds, it is even rated as clearly poor, which also correctly reflects the opinion of the expert consulted.
2.3. Progression analyses
With the help of progression analyses, it is possible to graphically analyze the extent to which the degrees of fulfillment of the linguistic evaluations of evaluation variables change when input parameters are varied.
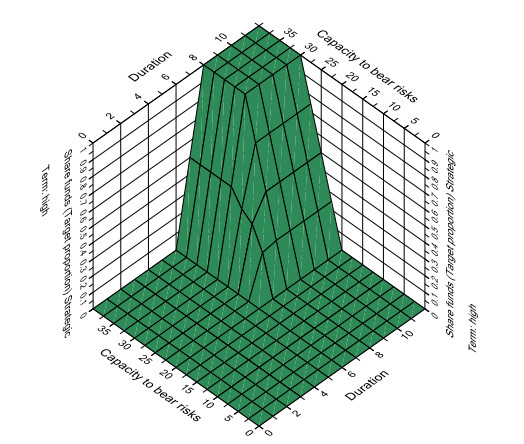
The example in Figure 20 shows a three-dimensional progression analysis which is used to validate the behavior of the model. This analysis makes it possible to identify constellations in which a high proportion of share funds is recommended. The figure shows the extent to which the term “high proportion” of the variable “Share funds (target proportion) strategic” is fulfilled if the duration and capacity to bear risks are changed. In this analysis, the investor has a maximum readiness to take risks.
It can be seen that, starting from a sufficiently long duration and a sufficiently high capacity to bear risks, the degree of fulfillment for the recommendation of a high share proportion gradually increases. For example, the degree of fulfillment increases from 0 to 0.04 if a duration of 6 years is extended by 30 days given a capacity to bear risks of 30%. In the case of a significant change, such as an extension of the duration from 4 years to 7 years (with the same capacity to bear risks), the degree of fulfillment also changes significantly, from 0 to 0.5 before.
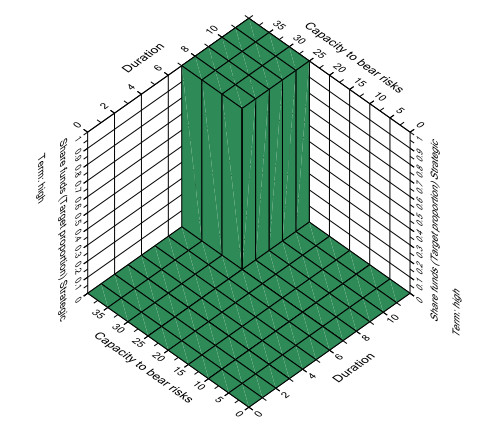
Figure 21 shows the identically configured progression analysis for the case in which the verbal evaluations of the state variables in the expert’s decision-making are represented in the form of disjoint classic intervals instead of fuzzy intervals, as presented in Section 2.2 (on this and the implications described below see [13,20,25]).
This modelling results in only two different evaluations in all constellations: either a high proportion of share funds is clearly recommended (degree of fulfillment = 1) or clearly not (degree of fulfillment = 0). It can be seen that in numerous constellations, minimal changes result in significant leaps in the recommendation. For example, with a capacity to bear risks of 25% (or higher), extending an investment period of 7 years by a single day results in a clear recommendation to invest a high proportion in a risky form of investment, whereas this was clearly discouraged previously. In contrast, given the same capacity to bear risks, a significant extension of the investment period from, for example, 4 years to 7 years would not lead to a change in the recommendation.
A comparable behavior can also result from a change in the capacity to bear risks. While, for example, with a duration of 7 years – or longer – a significant improvement in the capacity to bear risks from 15% to 25% does not lead to change in evaluation, the recommendation changes if the capacity to bear risks increases slightly from 25% to 26%.
The two progress analyses illustrate in a further way the advantages of a rule-based fuzzy model which were already shown in the factor variations and in the expert comparison. In addition, progression analyses show that the sudden change of recommendations in a “classic” modelling can be caused by a minimal change of a single input parameter, whereas this does not occur in a fuzzy model even if several input parameters are changed slightly at the same time.
3.
Conclusion
Through a sensitivity validation with visualization of all interim and final evaluations, a comprehensive understanding of the processes of a fuzzy model can be gained. As a result, well-founded statements about the validity of a concrete fuzzy system are possible, as shown for the asset allocation model presented here.
The validation instruments developed make it possible to prove that the asset allocation model, which is based on the fuzzy logic concepts described above, depicts the expert's decision-making behavior transparently and realistically and thus reacts to changes in the input parameters exactly as one would expect from the expert: the valuations of the investment strategies change to the extent that the parameters of the investment project or investor profile change.
In addition, the validation tools also make it possible to uncover the weaknesses of a model and thereby raise awareness of the serious problems that can arise if the decision-making behavior of an expert is not depicted realistically – as was shown for the case where “classic intervals” were used to depict expert knowledge. It can then easily occur that the results are not trustworthy. In numerous constellations, a model can then show completely unexpected, incomprehensible and disproportionate reactions to a minimal change in just one single feature, even to the point of recommendations being made that contradict those made before the change.
It should be emphasized that a realistic representation of expert knowledge, as can be achieved by a fuzzy model using the approaches presented, does not automatically lead to a model delivering good results. The recommendations of a fuzzy model always depend on the individual views of an expert and his financial institution, which are not based on generally valid algorithms. If the institution does not offer appropriate investment strategies or the expert's evaluations are not accurate, then the model will not provide good recommendations either.
Conflict of interest
The author declares that there is no conflict of interest.









 DownLoad:
DownLoad: