1.
Introduction
The first cases of the previously unknown severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) occurred in China in late 2019, but were not recognized at that time as infections with the novel coronavirus (2019-nCov). The genetic sequence of SARS-CoV-2 was identified in early January 2020. SARS-CoV-2 is thought to have a zoonotic origin, but the route of transmission from natural reservoirs to humans remains unclear. The novel coronavirus has been found in domestic and farm animals, that have been in contact with infected humans in several countries. Potential intermediate hosts include mink, pangolins, rabbits, and domesticated cats, which can become infected with SARS-CoV-2. Viruses derived from Chinese and Malayan pangolins were found to have high genomic similarity to SARS-CoV-2 [1], and it is conceivable that raccoon dogs may have played a significant role in the development of the pandemic [2]. Environmental samples taken from the huanan wholesale seafood market in Wuhan city, where seafood, wild, and farmed animal species were sold in December 2019, were tested positive for SARS-CoV-2, implying that this market played a role in the initial amplification of the outbreak [3]. Nonetheless, it is not yet clear how the infection was introduced into the market [1].
Originating from China, the virus spread across the whole world via air-borne virus infection from the end of January 2020. Between 31 December 2019 and the 26 calendar week in 2021,184,424,524 cases and 3,986,982 deaths were registered worldwide [4]. Governments around the globe took measures to combat the infectious disease in their own countries, which included temporary lockdowns of the population and shut-downs of certain production activities [5,6]. The development and efficient distribution of vaccines, that are also effective against several mutated virus variants, and the fast and safe vaccination of large parts of populations worldwide is a current worldwide challenge. Worldwide percentages of populations fully vaccinated until July 16th 2021 include 70.41% in Malta, 68.27% in Iceland, 67.52% in the United Arab Emirates, 57.54% in Israel, 52.60% in the United Kingdom, 48.87% in the United States, 47.82% in Spain, 44.66% in Germany, 43.69% in Austria, 41.86% in Switzerland, 40.63% in Italy, 35.80% in Sweden and 25.92% in Finland. Very low immunisation rates can be found in African, South Asian and some South American countries [7].
The transition dynamics of the model created in this paper contain distinct degrees of intervention measures like non-pharmaceutical interventions (NPIs), isolation and vaccination programs in order to reflect distinct degrees of intervention measures.
2.
The SVICDR model
In compartmental models, individuals may be in a finite number of discrete states, some of which are simply labels specifying the various characteristics of individuals, some of which change over time, such as age class, some of which are fixed, such as sex or species, and some of which indicate the progress of an infection [8], p 873]. The transitions of individuals between different compartments can be expressed by systems of ODEs. Such a compartmental model assumes a homogeneous population, which can be viewed as one in which individuals mix uniformly and randomly [9]. For a homogeneous population, it can be assumed that all susceptible individuals in the same compartment at any point in time have the same probability of coming into contact with any other individual in the population and that individuals differ only in their disease state. Next, we summarize the assumptions of the SVICDR model and describe the considered compartments.
2.1. Model assumptions
In the basic form of Kermack and McKendrick's SIR model, no births and no deaths are included in the system. The basic version of the model also assumes that the population size remains constant and that recovered individuals are completely immune, so that they can never contract the disease again [10], p 10–13]. These two assumptions are modified in the SVICDR model as follows:
Death rates are included in the model because of the nonnegligible number of infected persons who died worldwide for reasons related to the coronavirus (2.16%) [4]. First, a natural mortality rate μ is included. It is the rate at which persons die per unit time from causes unrelated to SARS-CoV-2. Disease-related deaths are accounted for using mortality rates λ1 for infected non-ICU patients and λ2 for ICU patients.
Whereas lethality is the proportion of confirmed cases who died among all infected cases in a population with respect to a given infectious disease within a given period of time [11] mortality is the proportion of confirmed cases that died among all individuals in a population. The case-fatality rate (CFR) is a measure used to represent the lethality of a disease. It is used in this work to describe the transition of individuals from the infected to the COVID-19-induced deceased compartment.
To calculate the CFR of novel coronavirus with respect to a given population, the number of confirmed deceased cases is divided by the number of confirmed infected cases. The rate can be related to a specific time period. Thus, the CFR indicates the proportion of confirmed infections that are fatal [12], p 32]. The difference between a lethality rate and the CFR is that the divisor of the lethality rate is more general and can still be specified. The rationale for using the CFR instead of other lethality rates is that the number of all infected persons is unknown [13], so usually only detected cases can be counted as infected cases.
We note that various data sources may treat deaths of persons whose demise was actually caused by or who died in association with SARS-CoV-2 infection as COVID-19 deaths. The German Robert Koch-Institute records deaths of persons with verified SARS-CoV-2 infection as COVID-19 deaths.
In general, when CFR is used as an indicator of SARS-CoV-2 lethality, it is very likely to overestimate the actual lethality rate because a large proportion of infected individuals remain undiagnosed because they are not included in the population of confirmed cases. In most cases, only symptomatic cases are tested and detected. In addition, people who have died from comorbidities may be counted as COVID-19 deaths. However, a CFR may underestimate the region-specific lethality rate for a given period in that the cumulative number of deaths may continue to increase as the number of patients in ICUs increases.
Nationwide testing programs and the recognition of region-specific case-notification rates seem significant to find an appropriate lethality measure.
Permanent cure is not necessarily assumed, so a certain small proportion of cured individuals per unit time will experience an effect of declining immunity and re-infection. This small proportion transits from the recovered back to the infected state per unit of time.
2.2. Compartments and transition rates in the SVICDR model
The SVICDR model consists of a susceptible, a vaccinated, an infected, an intensive care, a deceased, and a recovered compartment. In addition to the control measure of vaccination, the possibility of quarantine is also included in the model. It is significant to note that positively tested individuals are defined as confirmed cases in the established model.
The compartment S contains the susceptibles of the population. For 2019-nCoV, this is all residents of the country or region under consideration except those who have already become infected or recovered from the disease. The class S does not need to include all susceptibles in the system, as susceptible individuals may be quarantined in general, including self-quarantine. Inflicted quarantine is the temporary segregation of persons suspected of being infected.
For the vaccinated compartment an all-or-nothing vaccine is assumed. Consequently, all vaccinated individuals will be become fully immune with a certain probability. In this model, vaccination causes full protection from infection for a fraction V of the susceptible class per unit time t, while the fraction 1−V gains no protection. Vaccinated individuals thus transit from compartment S to a vaccinated compartment V at the rate V in the model considered. This rate is defined as a time-dependent function V(t) if a fluctuating vaccination strategy or an increasing number of available doses is assumed. It is not assumed that the immunizing vaccination effect can wane and that antibody levels in vaccinated individuals can fall below a critical level. Thus, individuals are unable to transit back from compartment V into S. Booster vaccinations after several years are possible in this case to maintain vaccine protection.
An alternative to an all-or-nothing vaccination schedule is a nonrandom vaccination schedule in which all vaccinated individuals respond identically to vaccination in terms of protection against infection and protection against transmission [14]. A special case is a leaky vaccine scenario, in which vaccinated individuals do not achieve complete protection. This may mean, for example, that vaccination has no effect on the ability to transmit the disease. For all of these vaccination regimens, a threshold parameter can be derived that determines the probability of a large outbreak and the proportion of the population that will be infected by the disease outbreak [14].
The infected compartment I consists of individuals who have contracted the infection and are infected. It comprises infected individuals whether or not they are capable of transmitting the infection or showing symptoms. The transmission rate describing the transition from S to I is the time-dependent continuous function θI(t), cf. Subsection 3.3. It is affected by the transmission risk β, the contact rate function γ(t), and the quarantine rate function q(t).
Let the CFR of individuals in compartment I equal MI and the average time from infection to recovery equal TI. Let there be a fraction κ of infected individuals per moment of time transits to compartment C with intensive care patients. Individuals in the I compartment die for reasons related to SARS-CoV-2 at a rate of
are admitted to an intensive care unit (ICU) at a rate
and recover at a rate
Infected SARS-CoV-2 cases may be transferred to an intensive care unit (ICU). We include a corresponding intensive care compartment C in the model because it allows us to predict the number of future patients in the ICU. The letter C stands for critical cases. Let the CFR of ICU patients be MC and the average time from ICU admission to recovery be TC>TI. Individuals in the ICU die from causes related to SARS-CoV-2 at a rate of
and recover at a rate
The death rates for compartment I and C underlie CFRs MI and MC, respectively, which result in individuals with rates λ1 and λ2 entering the deceased compartment D. Thus, the deceased compartment D(t) contains all individuals classified as deceased COVID-19 deaths by time t from the data source chosen for implementation.
In this compartment model, recovery of an individual is identified with the attainment of a level of virus in the individual that makes it impossible or extremely unlikely to transmit the infection to susceptible individuals. Recovery is not equated with the disappearance of symptoms or the complete loss of infectivity.
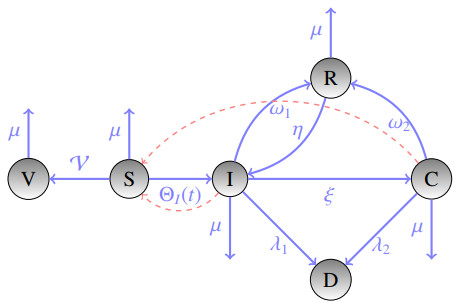
The dynamics of this model with pooled infected compartments arising from the system (16) are visualized in Figure 1. Blue arrows from one compartment to another indicate a transition, where the compartment from which a red dashed arrow emanates can infect susceptibles.
As described above, the abbreviation S stands for the susceptible, V for the vaccinated, I for the infected, C for the intensive care, R for the recovered and D for the deceased compartment. A symbol table with the definitions of all the model parameters can be found in Table 1 of this paper. Let us note that a larger compartment model with 13 compartments, from which the presented SVICDR model can be derived as a submodel, is derived concisely in [15].
If the time to switching to the next compartment tD is is exponentially distributed with a probability density function p(t)=1De−tD and G(t)=P(tD>t) is the corresponding survival function, the average time of sojourn in the regarded compartment is
The average time to recovery of compartments I and C is the average length of the infectious period TI and the average length of stay in the intensive care unit TC, respectively. In the case of respiratory infections that are predominantly spread via aerosols — such as Covid-19 — the infectivity is highest with the onset and during the course of the clinically symptomatic phase: coughing, sneezing, etc. This is no different with SARS-Cov-2, cf. [16].
Although it is not clear exactly how long these periods are, different studies revealed that infectivity reaches its maximum shortly before or on symptom onset, that is, around the time when the incubation period, i.e., the period between infection and the onset of symptoms, ends. A statistical analysis based on clinical and epidemiological data from SARS-CoV-2 cases suspected or confirmed between 21 January to 14 February 2020 in a Chinese hospital specialized for treating COVID-19 patients found, among other aspects, that infectiousness peaked at 2 days before to 1 day after symptom start [17]. A novel mechanistic approach inferring the infectiousness profile of SARS-COV-2-infected individuals using data from known infector–infectee pairs indicates that a higher proportion of transmissions occur prior to symptoms than predicted by existing methods [18]. Moreover, a systematic literature search comprising the results of 113 studies conducted in 17 countries suggests that the viral load of SARS-CoV-2 peaks from upper respiratory tract samples around the time of symptom onset or a few days after, and becomes undetectable within about two weeks [19].
It is also certain that the infectivity of an individual decreases over time, and severely ill individuals are infectious longer than individuals with mild symptoms [13].
As indicated above, the rate at which recovered compartment R is achieved by infected non–ICU cases is ω1 and by ICU patients ω2. Once infected, that is, once in compartment I, individuals are certain to reach the recovered compartment R after some time unless they die.
Based on current knowledge, it is possible for symptoms to reappear at any time point and even for susceptibility to be regained by (some) individuals due to a lessening of the protective effect of recovery. A mathematical modeling framework capable of describing immunity as decreasing and building over time seems reasonable [20]. In this work, a fraction η of recovered individuals whose immune status has fallen below a certain critical value returns to the I compartment per unit time.
In a longitudinal cohort study, the incidence of PCR-confirmed SARS-CoV-2 infection was assessed in seropositive and seronegative health care workers screening 12,541 asymptomatic and symptomatic individuals at Oxford University Hospitals using an enzyme-linked immunosorbent assay (ELISA) against trimeric spike immunoglobulin G (IgG). Baseline antibody status was determined by anti-spike and anti-nucleocapsid IgG assays, and employees were followed for up to 31 weeks. Results suggested that a previous infection resulting in antibodies to SARS-CoV-2 provides protection against re-infection for at least 6 months in most individuals [21].
3.
Transmission dynamics in the SVICDR model
In the proposed model, the quarantine and contact rates used are assumed to be cosine functions and defined in Subsection 3.2. Contact here includes contact with any other individuals in the population under consideration. The resulting transmission rate of the model is derived in Subsection 3.3.
3.1. The transmission risk
Let ce denote the average number of all contacts between a susceptible and an infectious person in the population under consideration per unit time. It is also called the effective contact rate of a population. In addition, a certain condition can be imposed, such as a sufficiently small distance between the two individuals involved, see also [22] for the social awareness aspect. Let s be the average number of acquired secondary infections per unit time in the population under consideration. Here, the transmission risk β with respect to a given infection and population is defined by the ratio of s to ce, i.e., β=s/ce.
The above definition of transmission risk can also be called secondary attack rate, which allows statements about the contagiousness of an agent. Let γ=ˉγN(t) be the number of contacts an individual makes per unit time t. Where ˉγ is the per capita contact rate. The effective contact rate ce is less than or equal to the total contact rate γ.
Multiplying the per capita contact rate ˉγ by β yields the rate ˜β, that is, the rate at which susceptible individuals are infected per unit time: ˜β=βˉγ.
Since the number of susceptibles who get infected per infectious individual per unit of time t is
where S(t)/N(t) is the proportion of susceptibles within the population, the term ˜βI(t)S(t) represents the number of susceptibles infected by individuals in compartment I at time t, where ˜βI(t) describes the corresponding infectivity [10], p 10].
Transmission risks posed by different compartments are different. In Section 2.2, six compartments were presented, of which compartments I and C are the infected states in the SVICDR model presented. Since no subdivision into noninfectious and infectious sub-compartments is made here, compartments I and C are simultaneously the so-called infectious states, since individuals in them can be infectious. With respect to the compartments K∈{I,C}, the number of individuals infected by a compartment K at time t is defined as
The difference between the transmission risks posed by I and C must be expressed. Hence, a factor ϵK∈[0,1] is multiplied by the transmission risk β to obtain the specific transmission risk emanating from class K. A compartment where susceptible individuals have a higher risk of infection on contact than another class is interpreted as a compartment that poses a higher risk of transmission. Since ICU patients are more isolated than other infected individuals, the following inequality between the two modifiers can be deduced: 1≥ϵI>ϵC>0.
3.2. Contact and quarantine rates
The course of the SARS-CoV-2 incidence in Germany implies that the restrictive measures of the respective federal state increased until April 2020, were continuously reduced between May and September 2020, expanded again strongly during the second major wave between October 2020 and February 2021, and decreased again from the end of May 2021.
The initial time point considered, to which the initial contact rate c0 and quarantine rate q0 refer, is the beginning of the 10th calendar week in 2020. The value γ(t) is the average number of contacts of an individual in the population in week t. The value q(t) denotes the average proportion of individuals quarantined in week t. The form of the contact and quarantine rate functions is as defined in the Eqs (9) and (10).
For example, under no-pandemic conditions, the average number of contacts per person per week can be assumed to be greater than 100 (i.e., greater than an average of 14 contacts of any type per person per day) and the quarantine rate to be zero or very slightly greater than zero. Under pandemic conditions, the contact rate should be assumed to be significantly less than this and the quarantine rate should be assumed to be greater than this, in accordance with high vigilance, standoff regulations, and more extensive intervention measures, if necessary. Increased government intervention and precautionary measures should generally lead to an increase in the q1 parameter in the q(t) rate and a decrease in the c1 parameter in the γ(t) rate.
3.3. Transmission rate
Recalling the discussion in Subsection 3.1, the number of individuals infected with K ∈{I,C} per unit time is
If a bilinear incidence is assumed, it can be seen that the number of susceptibles infected at time t is given by
Incorporating the quarantine rate q(t) into Eq (12), the transition from the class S to I can be derived:
The number of individuals moving from the compartment S to I is:
A compartment Sq reached by susceptibles who are quarantined and thus cannot be infected per moment of time t could be included in the model. To include this compartment Sq in the implementation, reliable data on the number of individuals in preventive quarantine per unit time would need to be available.
4.
Transition dynamics in the SVICDR model
Since no tourism and births are considered and individuals in the considered population may die and thus leave the system, the total number of individuals is not assumed to be constant N at all time points, but is described by a time-dependent function N(t). We obtain the SVICDR model and it holds
A standard incidence is used in the implementation. Thus, when multiplying the transmission rate by the size of the susceptible compartment at time t, S(t) is normalized to the size of the total population minus the size of the deceased compartment at time t.
On the one hand, the use of a standard incidence requires the calculation of the time derivative of the time-dependent relation S(t)/N(t). On the other hand, constancy can be achieved by adding the value μN as a recruitment rate to the ODE related to the susceptible compartment. The resulting ODE system for the SVICDR model reads
here, the rate of transition from the compartment S to I is defined by
The basic reproduction number is defined as the expected number of secondary infections caused by the first infected individual introduced into a population of only susceptible individuals without immunized population members and in the absence of controlling interventions. For an arbitrary system of ODEs of a compartment model the basic and control reproduction numbers can be computed with the aid of the technique of so-called next generation matrices (NGMs) [8]. Using the function f:Rn→Rn, that maps the state variables to their derivations, the dynamics of the system of ODEs can be written as
of which Xp+1,…,Xn are the infected states. Let Fi be the flux of newly infected individuals in the compartment i, and V+i (V−i) the other entering (leaving) fluxes related to the compartment i, i∈{1,…,n}. All three are non-negative functions. Then the infected subsystem can be separated as [23]
An endemic equilibrium (EE) point is a steady-state solution where the disease persists in the population, which is the case when R0>1. A disease-free equilibrium (DFE) point of an ODE system corresponding to a compartment model is a steady-state solution where there is no disease i.e., R0<1. A DFE point is given by X∗=(X1∗,…,Xp∗,0,…,0), where the zero appears n−p times, for which it holds that [23]
with J1 and J2 two resulting matrices. It holds that
and the linearised system at the DFE can be written by means of the linearisation of F and V :
Consequently, it holds that X′=(E+T)X [24]. The matrix T corresponds to the transmissions and the matrix E to the transitions in the system. Let σ(Q) denote the spectrum of any square matrix Q, then the spectral radius of Q is
and the stability modulus of Q is defined by
If α(T)<0, then the basic reproduction number R0 linked to the DFE X∗ of the underlying system of ODEs is defined as [23]
The matrix KL is called the next-generation matrix (NGM) with large domain. Equivalent to KL, the NGM with classical domain can be defined as
Using this NGM technique, setting η=0 and omitting for simplicity the time reference t, the basic reproduction number R0SVICDR of the SVICDR model can be derived as, cf. [15]
Next, the normalized forward sensitivity index is used for a sensitivity analysis of a basic reproduction number R0 depending on a certain model parameter. This index is defined as [25]
where p is a selected model parameter. A positive (negative) sensitivity index means that the prevalence of the disease increases (decreases) if the value of the respective parameter is increased. For instance, with respect to Eq (18) the normalized forward sensitivity index of R0SVICDR depending on γ is
The message propagation technique, applicable to compartment models in which contacts are modeled as a network, even allows upper bounds on the size of disease outbreaks in the form of upper bounds on the probability that a given individual will ever contract the disease [26].
Adding the recruitment rate μN, the equilibrium conditions for the model (16) are given by
where Θ∗I=θ∗I(ϵII∗+ϵCC∗). Substitution of the fourth of these conditions into the last gives
Then, substituting the Eq (22) and the fourth equation of the system (21) into the third yields
This indicates that either I∗=0 (point of the DFE) or
(endemic equilibrium point). Regarding the first equation in (21) we see
such that S∗=μN∗V+μ in the DFE. Rearranging terms in the second equation in (21), we obtain that
It follows that the DFE point is
The endemic equilibrium exists in this case if and only if S∗ is less than μN∗V+μ.
5.
Numerical methods
The ODE system given in Section 4 is solved by an explicit nonstandard finite difference (NSFD) scheme designed in Section 5.2. The discrete ℓ2 -error between the reported time series data and the compartment size data output by the NSFD scheme is calculated using the nonlinear least squares (NLS) method in MATLAB, see Subsection 5.1.
5.1. The nonlinear least squares approach to compartment models
The term measurement describes a quantification of a certain state variable, and Di(tj), j∈{1,…,l}, i∈{1,…,N} be the measurement with respect to the state variable xi representing the size of the compartment Ki at a time tj∈[t0,tl] in this context. Let the measured data for the ith compartment and the jth time point be represented in the vector D(i)j:=Di(tj).
Subsequently, a measurement function Φ(t) exists that maps a point in time tj∈[t0,tl] into a measured s -dimensional data set:
The complete set of measured data covering all compartments and all points in time t∈[t0,tl] is saved as a matrix of the size l×s, that can be transformed into a vector ˆΦ of the form ˆΦ:=[Φ(t0),…,Φ(tl)]⊤∈Rn with n=ls.
Next, let Yi(tj,ϑ) be the program output data for the compartment Ki, i∈{1,…,s} and the time tj, j∈{1,…,l}, which is abbreviated as Y(i)j:=Yi(tj,ϑ). Consequently, a model function Y(t,ϑ) exists that maps a point in time tj into a set of generated data for a given parameter vector ϑ :
The complete set of data provided by the model, which includes all s compartments and all time points t∈[t0,tl], is stored as a matrix of size l×s, which is transformed into a vector ˆY of the form
A model output data set ˆY(ϑ) obtained from the integration of a system of ODEs with certain initial conditions can be fitted as optimally as possible to a given time series data set ˆΦ by optimizing the adjustable part of the model parameters ϑ. Thus, let the adjustable part of the parameter vector ϑ to be optimized be ϑ1∈Rm1, and let the fixed part of ϑ be ϑ2∈Rm2 with m1+m2=m. In the following, an entry of the vector ˆΦ is denoted by ˆΦk, k∈{1,…,n} and an entry of the vector ˆY(ϑ) is denoted by ˆYk(ϑ), k∈{1,…,n}.
A nonlinear optimization problem is an NLS problem if the objective function f has the form of so-called squared residuals. We assume for each of the s compartments K1,…,Ks the same l observation points in time. Let the mentioned residuals be denoted by r, with r:Rm→Rn, for which it holds
The objective function of the respective least squares problem is defined as
Expressed mathematically and using the Euclidean norm, the resulting unconstrained optimization problem has the objective function
5.2. A nonstandard finite difference scheme for the SVICDR model
Finite difference methods are a class of numerical techniques to solve differential equations by approximating the derivatives with finite difference quotients.
In addition to properties such as stability and continuity, qualitative properties such as positivity preservation and correct asymptotic long-term behavior are also important, eg., in biological systems where the positivity of the number of individuals in the compartments must be preserved. This is exactly where nonstandard finite difference (NSFD) procedures come into play to meet these requirements.
A numerical scheme for a system of first-order differential equations is called NSFD scheme if at least one of the following conditions described in [27] is satisfied:
● First-order derivatives are approximated by the generalized forward difference method (forward Euler method) dundt≈un+1−unϕ(h), where un=u(tn) and ϕ≡ϕ(h) is the so-called denominator function with ϕ(h)=h+O(h2).
● The nonlinear terms are approximated in a non-local way, e.g. by a suitable function of several grid points, like u2(tn)≈unun+1 or u3(tn)≈u2nun+1.
According to [27], further basic rules of NSFD are the equivalence between the orders of the discrete derivatives and the orders of the corresponding derivatives appearing in the differential equations, non-trivial denominator functions of the discrete representations for the derivatives, etc.
In order to be able to derive the denominator function ϕ the following consideration is made. It is defined that ˜N=N−D=S+V+I+C+R, and an actually negligible recruitment rate μ is added to the system [28]. Adding the differential equations of the model yields
that is solved by
with ˜N0=S(0)+V(0)+I(0)+C(0)+R(0).
The transmission rate in the nth step is defined as
With the aid of these and the denominator function, an NSFD scheme can be established for the SVICDR model (16):
Analogously to the continuous model (16), adding the Eq (37) yields
The denominator function can be derived by comparing Eq (38) with the discrete version of Eq (35), that is
such that the denominator function is defined by
This means that the solution of Eq (39) is exactly the discrete version of Eq (35) if we use the denominator function given in Eq (40). In other words, using the NSFD the long term behaviour of the total population is properly modelled. An even more accurate way to compute the denominator function would take into account the transition rate Υi at which the ith compartment is entered by individuals for all model compartments Ki, i=1,2,…, cf. [29]. In this case the parameter μ occurring in the denominator function in Eq (40) would be replaced by a parameter T∗. T∗ could be determined as the minimum of the inverse transition parameters:
The designed NSFD scheme (37) is formally implicit. However, it can be easily rearranged to obtain a scheme that can be evaluated sequentially in an efficient explicit way, i.e., a solution of a nonlinear system is avoided. Here we give this rearranged NSFD scheme for the SVICDR model (37):
The NSFD scheme (42) is positivity preserving, i.e. for positive data it always produces non-negative solutions since all parameters and the denominator function are non-negative (if ϵI is sufficiently small). Thus negative values for the solution are avoided. Moreover, stability with respect to the maximum norm is ensured, cf. [29].
6.
Results
Online sources accessed to obtain compartment size data related to Germany include the Robert Koch-Institute [30,31], the German Interdisciplinary Association for Intensive Care and Emergency Medicine (DIVI) [32], and the German COVID-19 Vaccination Dashboard [33]. Data are for March 2020 through June 2021. The corresponding Matlab scripts can be found in [34].
Table 1 shows all parameters used in the implementation of the SVICDR model. It contains all parameter definitions, parameter calculation formulas, and parameter values used to fit the ODE system to the observed pandemic situation in Germany.
The vaccination rate is the exponential function v(t)=0.001⋅et/11. Figure 2 shows v(t) and the proportion of actually secondarily vaccinated individuals in the German population between spring 2020 and summer 2021.
As Figure 2 shows, the proportion of effective second vaccinations in the German population is about 3.5% in calendar week 11 in 2021 (mid-March), 11% in calendar week 20 (mid-May), 25% in calendar week 29 (end of June), and 40% in calendar week 28 (mid-July). The vaccination rate v(t) yields higher values than the actual immunisation rate until calendar week 23 (early June), i.e., 7% in calendar week 11 and 16% in calendar week 20, but slightly lower values than these from then on, i.e., 27.6% in calendar week 25 and 38.4% in calendar week 28.
The following Figures 3–7 show the results of the differently chosen bounds of the estimated parameters. The aim was to create different scenarios of the courses of the pandemic wave in autumn 2021. Four different values for the parameter c1 with the same fixed bounds for the other estimated parameters were used to create Figure 3. The parameter β was optimized in different program runs in a range between 0.03 and 0.049.
It can be seen that higher values of β, c1, ϵC and ϵI result in comparatively higher curve levels. Figure 3 shows that there is a peak of varying magnitude in calendar week 34 in 2021. In the upper left plot, there is a comparatively small peak of 14,340 infected individuals, while in the upper right plot it is 43,530, in the lower left plot it is 22,960, and in the lower right plot it is 80,040. Despite the smaller value of c1 in the upper right compared to the lower left diagram, here the much higher transmission risk leads to a peak almost twice as high.
In 2020, 15,921 new infections were observed in Germany in calendar week 40, 26,111 in calendar week 41, 42,055 in calendar week 42, and 74,848 in calendar week 43, and a peak number of 174,772 in calendar week 51 [30]. It should be noted that the number of individuals in the infected compartment is likely to be 1.3 to 2.3 times higher than the number of new infections per unit time.
In 2021, high numbers of second COVID-19 vaccinations should lead to a decrease in incidence compared with 2020. Nonetheless, mutant variants, such as the delta variant (B.1.617.2) in particular, that accounted for 37% of SARS-CoV-2-positive cases in Germany in calendar week 24 in 2021, may be more resistant to given vaccines as well as more dangerous to unvaccinated individuals [35].
One possible factor increasing the transmission risk β and the re-infection rate η is an increased proportion of mutations with higher transmissibility than the originally known novel coronavirus among all infections. According to preliminary results, COVID-19 vaccines approved in Germany immunize the vaccinated more effectively against the Alpha (B.1.1.7) than against the Delta variant of concern, although high protection against B.1.617.2 appears to be present in fully vaccinated individuals [35].
If a leaky vaccination was assumed without introducing any leaky-vaccinated compartment, the transmission risk β emerging from vaccinated people in a subsequent infected state would be reduced. In this case, a poorly organized vaccination strategy would result in a comparatively large transmission risk.
Compared to Figure 3, the bounds of parameters β and ϵI are changed in the scenario presented in Figure 4. The estimated parameter values obtained in the four resulting plots are very similar among themselves. The only clear difference between the four plots is the value of the parameter c1 shaping the contact rate function, which is fixed. The value c1=38 causes local maxima of 58 and local minima of 18 contacts, whereas the value c1=47 results in local maxima of 67 and local minima of 27 contacts per week. It can be noted that the increase of c1 from 38 to 40 (42, and 45, respectively) leads to an increase of 29,900 (70,600, and 162,600, respectively), i.e. to a tripling (almost sevenfold, and almost 16–fold, respectively) of the size of the local maximum reached in calendar week 34/35 (end of August).
In the Figures 5 and 6, the bound of the parameter q1 is set to [0.01,0.1] to obtain the upper left plot, [0.01,0.25] to obtain the upper right plot, [0.01,0.5] to obtain the lower left plot, and [0.01,0.7] to obtain the lower right plot. The other model parameters remain at very similar or the same level in the four plots. Assigning q1 to a value in the interval (0,0.1) as in the upper left diagram can be considered as a scenario of lighter NPIs or a baseline scenario.
Values q1∈(0.1,0.5) as in the other three graphs correspond to intervention scenarios of varying magnitude, including increased testing activity leading to more case isolations, more actual quarantines imposed on contacts of infected cases, curfews, and remote work in possible sectors. Adopting control measures such as closing schools, universities, restaurants, and other facilities can be considered "partial quarantine'' for affected individuals. This type of quarantine is not imposed directly by the state or an institution and is not a self-quarantine, but ensures that individuals have fewer contacts and leave the house less often.
A scenario characterized by the absence of a broad quarantine program, but primarily increased awareness in response to the pandemic itself and initial recommendations from the media or health institutions, does not result in a substantial change in the parameter q1, but in a decrease in c1.
In Figures 5 and 6 it can be observed that an increase in q1 leads to an earlier reaching of the peak as well as to a larger local maximum. The peak in the size of the infected compartment occurs between calendar weeks 35 and 36 (cf. Figure 5) and the peak in the size of the intensive compartment occurs 1–2 weeks later between calendar weeks 36 and 38 (cf. Figure 6) in September 2021. The respective delay in ICU admission after infection appears reasonable.
An increase in the peak size between the upper left diagram (q1=0.055387) and the upper right diagram (q1=0.124728) of 23 (24)%, the lower left diagram (q1=0.279607) of 51 (61)%, and the lower right diagram (q1=0.356349) of 63 (77)% is discernible in Figure 6 (Figure 5). The corresponding increase in the transmission risk β outweighs the increase in q1.
In Figure 7 the parameter ϵI is fixed to the value 0.175. In several program runs, this value was found to yield comparatively reasonable curve shapes and peak height ranges in the four plots when the bound of the contact rate parameter c1 is raised to the interval [50,60]. While 117,400 infected persons (upper left plot of Figure 7) are not unlikely in calendar week 34 in 2021,346,500 infected persons i.e. c1=60 (lower right plot of Figure 7) are considered unlikely because of the large proportion of vaccinated persons in the population. A number of more than 200,000 infected persons should be considered high, since the peak size in the German pandemic so far was about 175,000 weekly new infections in December 2020 [30].
A comparison of the lower right plot of Figure 7 with the lower right plot of Figure 5 proves that increasing β and c1 leads to a large increase in peak height despite the simultaneous slight increase in q1 and decrease in ϵI. It amounts to 31% in this case, i.e., almost one third. It is noticeable that the local minima in all four plots per figure in the Figures 3–7 reach very similar levels between calendar weeks 27 and 28, although stronger local maxima in the autumn of 2021 are accompanied by somewhat weaker local minima in the summer of 2021. To facilitate validation, we added a plot with some description (Figure 8) displaying the real course of size of compartment I over 20 weeks, which data have meanwhile become available for: In order to be able to better validate the accuracy of the model in the distinct parameter value scenarios, meanwhile available compartment size data for I provided by the Robert Koch-Institute [30] are plotted against the time in Figure 8. It can be seen that a local maximum was attained in calendar week 36 (beginning of September). This was predicted accurately (plus or minus 1–2 weeks) in the Figures 3–7. The point of time of the minimum of 9165 infected individuals in calendar week week 26 was also predicted precisely. However, the size of this minimal value was predicted as I(t)∈(50,000,100,000), larger than it actually is according to Figure 8. Comparing Figure 3 with only small peaks to the Figures 4–8, it becomes clear that values of β∈∼[0.04,0.06]. Comparing it to Figure 7, values of ϵI>0.2 seem to bring about the most reasonable results for β<0.5 and c1<50. Regarding Figure 8, the assignment c1=45 in Figure 4 seems to be too large to lead to an accurate result with the given ϵI,ϵC,β, but c1=40 is a better choice. Some q1∈(0.12,0.2) seems to result in the most realisitc predicted scenarios for c1=43,β∈(0.4,0.5) and the respective ϵI,ϵC. With some larger β=0.055 and the fixed q1=0.375,ϵI=0.175 as in Figure 7, the contact rate parameter assignment c1=53 yields the most reasonable prediction of 159,700 infected people at the peak time.
To show an exemplary result of a baseline method, we added the predicted plot (Figure 9) of the course of the infected compartment I and analyzed it: The method of NSFD to numerically solve differential equations by constructing a discrete model can be replaced by other numerical integration schemes like Runge-Kutta-based methods. In this case the Dormand-Prince Runge-Kutta (RKDP) algorithm was used as a baseline method in the form of the Matlab solver ode45 for this purpose. Figure 9 shows a predicted future scenario for the infected compartment I using the parameter boundaries stated below the figure. Several more plots resulting from the usage of ode45 can be found in [15], p 112–126].
Similarly to Figure 4 but different to Figure 6 and Figure 7, none of the optimized parameters β, c1, q1, ϵI, ϵC was fixed to a single value for all four generated plots. In the given scenario, basically the different allocations of c1 determine the peak sizes. With the assignment c1=8. An increase of 2.8% in the peak size between the upper left and right, 15.1% between the upper and lower left and 25.9% between the upper left and lower right diagrams of Figure 9 can be noted. Concerning the usage of the RKDP method, it is striking that the lower bound of β and the values assigned to c1 have to be strongly diminished compared to the NSFD implemenations in order to obtain reasonable local maxima of less than 300,000 to 400,000 weekly infected people in calendar week 32.
7.
Conclusions
Since the application of the NSFD scheme for the SVICDR model leads to realistic results and this method has a number of favorable properties such as preservation of positivity and correct long-term behavior, the performance of NSFD schemes applied to other compartment models should be investigated.
Our implementation based on the model-specific NSFD scheme shows that increasing the q1 parameter in the quarantine rate function q(t) or decreasing the c1 parameter of the contact rate function γ(t) leads to containment of infection counts. We found that program runs with lower bounds on q1 resulted in later peak performances. We note that an increase in quarantine rates is usually accompanied by a decrease in contact rates in terms of an intervention strategy, so that the containment effect of an increased q1 is again maintained.
A change in the vaccination strategy or testing policy may indirectly affect quarantine rates because quarantine or testing policies may be adjusted to reflect the general vaccination status of the population.
In this work, a specific exponential vaccination rate was used, which fits well with the previous course of vaccination development in Germany. Program runs demonstrated that changing only the parameter vb in the vaccination rate v(t)=vAet/vB changes the maximum achieved number of infections in the expected direction (i.e., a moderately increased vb causes a slightly higher incidence due to slower functional growth). If the bounds on other parameters are set further, a program run with increased vb may result in comparatively lower infection rates through the simultaneous optimization of other estimated parameters such as transmission risk β or reinfection rate η.
A reduced transmission risk β always favors a scenario with reduced infection, ICU, and case-fatality rates. The calculation of sensitivity indices (see Section 4) of estimated model parameters as a function of the model-specific basic reproduction number according to [15], p 100] shows the large influence of the transmission modification factors ϵI and ϵC on the forward normalized sensitivity indices of β, γ(t), and q(t).
A possible extension of the SVICDR model is to divide the infected compartment I into an asymptomatic compartment and a symptomatic compartment. The associated goal would be to track the evolution of asymptomatic transmissions and their proportion of all observed transmissions.
Another interesting research question is the extent to which declining immunity in recovered and fully vaccinated individuals may influence future pandemic evolution. There are few approaches to compartmental models of declining immunity in the literature [36]. For example, the level of antibodies as a function of elapsed time can be modeled by a probability distribution. In addition, models with lag differential equations take into account a lag representing the average duration of disease-induced immunity. They are characterized by a higher degree of accuracy than SIR models. The distribution of immune status, i.e., antibody levels, could be described based on a within-host submodel for continuous decay and occasional boosting [20].
Finally, the major future advance is to use PDEs instead of comparatively simple ODEs for disease modeling. In this way, the spatial dependence of pandemic spread could be studied in much more detail. Then the network is defined by a metric graph, i.e., a graph where the connections between nodes (called bonds) are intervals rather than just undirected connections. The blocking measures and mobility restrictions or impacts of travel activities can then be modeled in a much more sophisticated way by using appropriate, specially designed constraints at the branch points of the metric graph. These conditions accurately model the spatial effects of the restrictions or relaxations, much better than simply adjusting the transition rates as in the ODE case before. However, these branch point conditions are quite complicated and computationally expensive.
Acknowledgments
The authors acknowledge support from the Open Access Publication Fund of the University of Wuppertal.
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad:




















