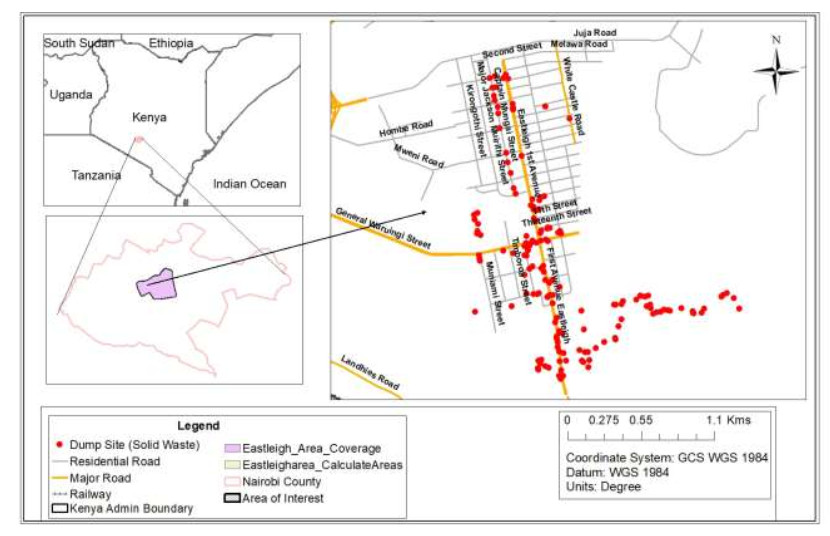
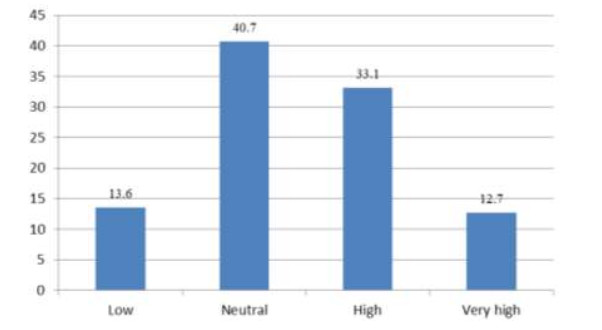
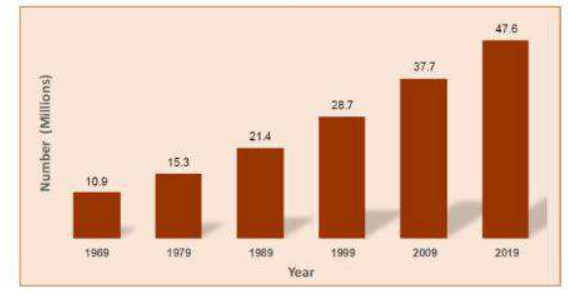
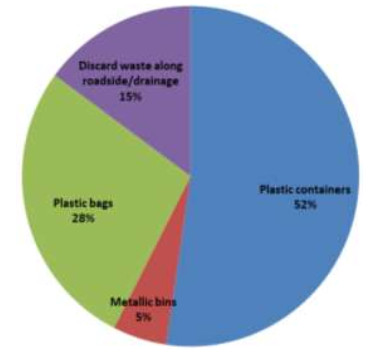
Solid waste management is a documented threat to health and the environment to many countries in sub-Saharan Africa. Rapid industrial development and urbanization have seen a rise in urban population which translates to massive production of solid waste. Though most urban and city planners have adopted new technologies such as landfills and incineration these alone cannot work without training residents on best practices that will guide them on how to manage their waste. Both health and environmental implications are associated with solid waste management and amounting in urgency especially in developing countries. The study aimed to assess the methods used by residents of Eastleigh South Ward in Nairobi County to dispose of their solid waste at the household level. Various waste disposal methods were documented during field observation and interviews while secondary data was obtained from records and reports on the management of waste in Nairobi County. About 48% of the resident indicated they discard waste along the road in heap/drainage, further 35% indicated putting waste in dust bins which eventually ends up in undesignated areas. The study also documents challenges related to waste management including infrequent /irregular waste collection, illegal dumping, low levels of information on poor waste disposal, and lack of concern among residents. Other challenges included irresponsible waste management approaches by the Nairobi County Government as well reluctance to pay private garbage collectors and high cost of disposal services charged by private garbage collectors. Promoting awareness through public education on the management of solid waste will enhance proper solid waste management practices. The study further recommends allocation of more resources to allow for effective management of solid waste.
1.
Introduction
The concept of embedded tensors initially emerged in the research on gauged supergravity theory [1]. Using embedding tensors, the N=8 supersymmetric gauge theories as well as the Bagger-Lambert theory of multiple M2-branes were investigated in [2]. See [3,4,5] and the references therein for a great deal of literature on embedding tensors and related tensor hierarchies. In [6], the authors first observed the mathematical essence behind the embedding tensor and proved that the embedding tensor naturally produced Leibniz algebra. In the application of physics, they observed that in the construction of the corresponding gauge theory, they focused more on Leibniz algebra than on embedding tensor.
In [7], Sheng et al. considered cohomology, deformations, and homotopy theory for embedding tensors and Lie-Leibniz triples. Later on, the deformation and cohomology theory of embedding tensors on 3-Lie algebras were extensively elaborated in [8]. Tang and Sheng [9] first proposed the concept of a nonabelian embedding tensor on Lie algebras, which is a nonabelian generalization of the embedding tensors, and gave the algebraic structures behind the nonabelian embedding tensors as Leibniz-Lie algebras. This generalization for embedding tensors on associative algebras has been previously explored in [10,11], where they are referred to as average operators with any nonzero weights. Moreover, the nonabelian embedding tensor on Lie algebras has been extended to the Hom setting in [12].
On the other hand, Filippov [13] first introduced the concepts of 3-Lie algebras and, more generally, n-Lie algebras (also called Filippov algebras). Over recent years, the study and application of 3-Lie algebras have expanded significantly across the realms of mathematics and physics, including string theory, Nambu mechanics [14], and M2-branes [15,16]. Further research on 3-Lie algebras could be found in [17,18,19] and references cited therein.
Drawing inspiration from Tang and Sheng's [9] terminology of nonabelian embedding tensors and recognizing the significance of 3-Lie algebras, cohomology, and deformation theories, this paper primarily investigates the nonabelian embedding tensors on 3-Lie algebras, along with their fundamental algebraic structures, cohomology, and deformations.
This paper is organized as follows: Section 2 first recalls some basic notions of 3-Lie algebras and 3-Leibniz algebras. Then we introduce the coherent action of a 3-Lie algebra on another 3-Lie algebra and the notion of nonabelian embedding tensors on 3-Lie algebras with respect to a coherent action. In Section 3, the concept of 3-Leibniz-Lie algebra is presented as the fundamental algebraic structure for a nonabelian embedding tensor on the 3-Lie algebra. Naturally, a 3-Leibniz-Lie algebra induces a 3-Leibniz algebra. Subsequently, we study 3-Leibniz-Lie algebras induced by Leibniz-Lie algebras. In Section 4, the cohomology theory of nonabelian embedding tensors on 3-Lie algebras is introduced. As an application, we characterize the infinitesimal deformation using the first cohomology group.
All vector spaces and algebras considered in this paper are on the field K with the characteristic of 0.
2.
Nonabelian embedding tensors on 3-Lie algebras
This section recalls some basic notions of 3-Lie algebras and 3-Leibniz algebras. After that, we introduce the coherent action of a 3-Lie algebra on another 3-Lie algebra, and we introduce the concept of nonabelian embedding tensors on 3-Lie algebras by its coherent action as a nonabelian generalization of embedding tensors on 3-Lie algebras [8].
Definition 2.1. (see [13]) A 3-Lie algebra is a pair (L,[−,−,−]L) consisting of a vector space L and a skew-symmetric ternary operation [−,−,−]L:∧3L→L such that
for all li∈L,1≤i≤5.
A homomorphism between two 3-Lie algebras (L1,[−,−,−]L1) and (L2,[−,−,−]L2) is a linear map f:L1→L2 that satisfies f([l1,l2,l3]L1)=[f(l1),f(l2),f(l3)]L2, for all l1,l2,l3∈L1.
Definition 2.2. 1) (see [20]) A representation of a 3-Lie algebra (L,[−,−,−]L) on a vector space H is a skew-symmetric linear map ρ:∧2L→End(H), such that
for all l1,l2,l3,l4∈L. We also denote a representation of L on H by (H;ρ).
2) A coherent action of a 3-Lie algebra (L,[−,−,−]L) on another 3-Lie algebra (H,[−,−,−]H) is defined by a skew-symmetric linear map ρ:∧2L→Der(H) that satisfies Eqs (2.2) and (2.3), along with the condition that
for all l1,l2∈L and h1,h2,h3∈H. We denote a coherent action of L on H by (H,[−,−,−]H;ρ†).
Note that Eq (2.4) and ρ(l1,l2)∈Der(H) imply that
Example 2.3. Let (H,[−,−,−]H) be a 3-Lie algebra. Define ad:∧2H→Der(H) by
Then (H;ad) is a representation of (H,[−,−,−]H), which is called the adjoint representation. Furthermore, if the ad satisfies
then (H,[−,−,−]H;ad†) is a coherent adjoint action of (H,[−,−,−]H).
Definition 2.4. (see [21]) A 3-Leibniz algebra is a vector space L together with a ternary operation [−,−,−]L:L⊗L⊗L→L such that
for all li∈L,1≤i≤5.
Proposition 2.5. Let (L,[−,−,−]L) and (H,[−,−,−]H) be two 3-Lie algebras, and let ρ be a coherent action of L on H. Then, L⊕H is a 3-Leibniz algebra under the following map:
for all l1,l2,l3∈L and h1,h2,h3∈H. This 3-Leibniz algebra (L⊕H,[−,−,−]ρ) is called the nonabelian hemisemidirect product 3-Leibniz algebra, which is denoted by L⋉ρH.
Proof. For any l1,l2,l3,l4,l5∈L and h1,h2,h3,h4,h5∈H, by Eqs (2.1)–(2.5), we have
Thus, (L⊕H,[−,−,−]ρ) is a 3-Leibniz algebra. □
Definition 2.6. 1) A nonabelian embedding tensor on a 3-algebra (L,[−,−,−]L) with respect to a coherent action (H,[−,−,−]H;ρ†) is a linear map Λ:H→L that satisfies the following equation:
for all h1,h2,h3∈H.
2) A nonabelian embedding tensor 3-Lie algebra is a triple (H,L,Λ) consisting of a 3-Lie algebra (L,[−,−,−]L), a coherent action (H,[−,−,−]H;ρ†) of L and a nonabelian embedding tensor Λ:H→L. We denote a nonabelian embedding tensor 3-Lie algebra (H,L,Λ) by the notation HΛ⟶L.
3) Let HΛ1⟶L and HΛ2⟶L be two nonabelian embedding tensor 3-Lie algebras. Then, a homomorphism from HΛ1⟶L to HΛ2⟶L consists of two 3-Lie algebras homomorphisms fL:L→L and fH:H→H, which satisfy the following equations:
for all l1,l2∈L and h∈H. Furthermore, if fL and fH are nondegenerate, (fL,fH) is called an isomorphism from HΛ1⟶L to HΛ2⟶L.
Remark 2.7. If (H,[−,−,−]H) is an abelian 3-Lie algebra, then we can get that Λ is an embedding tensor on 3-Lie algebra (see [8]). In addition, If ρ=0, then Λ is a 3-Lie algebra homomorphism from H to L.
Example 2.8. Let H be a 4-dimensional linear space spanned by α1,α2,α3 and α4. We define a skew-symmetric ternary operation [−,−,−]H:∧3H→H by
Then (H,[−,−,−]H) is a 3-Lie algebra. It is obvious that (H,[−,−,−]H;ad†) is a coherent adjoint action of (H,[−,−,−]H). Moreover,
is a nonabelian embedding tensor on (H,[−,−,−]H).
Next, we use graphs to describe nonabelian embedding tensors on 3-Lie algebras.
Theorem 2.9. A linear map Λ:H→L is a nonabelian embedding tensor on a 3-Lie algebra (L,[−,−,−]L) with respect to the coherent action (H,[−,−,−]H;ρ†) if and only if the graph Gr(Λ)={Λh+h|h∈H} forms a subalgebra of the nonabelian hemisemidirect product 3-Leibniz algebra L⋉ρH.
Proof. Let Λ:H→L be a linear map. Then, for any h1,h2,h3∈H, we have
Thus, the graph Gr(Λ)={Λh+h|h∈H} is a subalgebra of the nonabelian hemisemidirect product 3-Leibniz algebra L⋉ρH if and only if Λ satisfies Eq (2.6), which implies that Λ is a nonabelian embedding tensor on L with respect to the coherent action (H,[−,−,−]H;ρ†). □
Because H and Gr(Λ) are isomorphic as linear spaces, there is an induced 3-Leibniz algebra structure on H.
Corollary 2.10. Let HΛ⟶L be a nonabelian embedding tensor 3-Lie algebra. If a linear map [−,−,−]Λ:∧3H→H is given by
for all h1,h2,h3∈H, then (H,[−,−,−]Λ) is a 3-Leibniz algebra. Moreover, Λ is a homomorphism from the 3-Leibniz algebra (H,[−,−,−]Λ) to the 3-Lie algebra (L,[−,−,−]L). This 3-Leibniz algebra (H,[−,−,−]Λ) is called the descendent 3-Leibniz algebra.
Proposition 2.11. Let (fL,fH) be a homomorphism from HΛ1⟶L to HΛ2⟶L. Then fH is a homomorphism of descendent 3-Leibniz algebra from (H,[−,−,−]Λ1) to (H,[−,−,−]Λ2).
Proof. For any h1,h2,h3∈H, by Eqs (2.7)–(2.9), we have
The proof is finished. □
3.
3-Leibniz-Lie algebras
In this section, we present the concept of the 3-Leibniz-Lie algebra, which serves as the fundamental algebraic framework for the nonabelian embedding tensor 3-Lie algebra. Then we study 3-Leibniz-Lie algebras induced by Leibniz-Lie algebras.
Definition 3.1. A 3-Leibniz-Lie algebra (H,[−,−,−]H,{−,−,−}H) encompasses a 3-Lie algebra (H,[−,−,−]H) and a ternary operation {−,−,−}H:∧3H→H, which satisfies the following equations:
for all h1,h2,h3,h4,h5∈H.
A homomorphism between two 3-Leibniz-Lie algebras (H1,[−,−,−]H1,{−,−,−}H1) and (H2,[−,−,−]H2,{−,−,−}H2) is a 3-Lie algebra homomorphism f:(H1,[−,−,−]H1)→(H2,[−,−,−]H2) such that f({h1,h2,h3}H1)={f(h1),f(h2),f(h3)}H2, for all h1,h2,h3∈H1.
Remark 3.2. A 3-Lie algebra (H,[−,−,−]H) naturally constitutes a 3-Leibniz-Lie algebra provided that the underlying ternary operation {h1,h2,h3}H=0, for all h1,h2,h3∈H.
Example 3.3. Let (H,[−,−,−]H) be a 4-dimensional 3-Lie algebra given in Example 2.8. We define a nonzero operation {−,−,−}H:∧3H→H by
Then (H,[−,−,−]H,{−,−,−}H) is a 3-Leibniz-Lie algebra.
The subsequent theorem demonstrates that a 3-Leibniz-Lie algebra inherently gives rise to a 3-Leibniz algebra.
Theorem 3.4. Let (H,[−,−,−]H,{−,−,−}H) be a 3-Leibniz-Lie algebra. Then the ternary operation ⟨−,−,−⟩H:∧3H→H, defined as
for all h1,h2,h3∈H, establishes a 3-Leibniz algebra structure on H. This structure is denoted by (H,⟨−,−,−⟩H) and is referred to as the subadjacent 3-Leibniz algebra.
Proof. For any h1,h2,h3,h4,h5∈H, according to (H,[−,−,−]H) is a 3-Lie algebra and Eqs (3.2)–(3.4), we have
Hence, (H,⟨−,−,−⟩H) is a 3-Leibniz algebra. □
The following theorem shows that a nonabelian embedding tensor 3-Lie algebra induces a 3-Leibniz-Lie algebra.
Theorem 3.5. Let HΛ⟶L be a nonabelian embedding tensor 3-Lie algebra. Then (H,[−,−,−]H,{−,−,−}Λ) is a 3-Leibniz-Lie algebra, where
for all h1,h2,h3∈H.
Proof. For any h1,h2,h3,h4,h5∈H, by Eqs (2.3), (2.6), and (3.5), we have
Furthermore, by Eqs (2.4), (2.5), and (3.5), we have
Thus, (H,[−,−,−]H,{−,−,−}Λ) is a 3-Leibniz-Lie algebra. □
Proposition 3.6. Let (fL,fH) be a homomorphism from HΛ1⟶L to HΛ2⟶L. Then fH is a homomorphism of 3-Leibniz-Lie algebras from (H,[−,−,−]H,{−,−,−}Λ1) to (H,[−,−,−]H,{−,−,−}Λ2).
Proof. For any h1,h2,h3∈H, by Eqs (2.7), (2.8), and (3.5), we have
The proof is finished. □
Motivated by the construction of 3-Lie algebras from Lie algebras [17], at the end of this section, we investigate 3-Leibniz-Lie algebras induced by Leibniz-Lie algebras.
Definition 3.7. (see [9]) A Leibniz-Lie algebra (H,[−,−]H,⊳) encompasses a Lie algebra (H,[−,−]H) and a binary operation ⊳:H⊗H→H, ensuring that
for all h1,h2,h3∈H.
Theorem 3.8. Let (H,[−,−]H,⊳) be a Leibniz-Lie algebra, and let ς∈H∗ be a trace map, which is a linear map that satisfies the following conditions:
Define two ternary operations by
Then (H,[−,−,−]Hς,{−,−,−}Hς) is a 3-Leibniz-Lie algebra.
Proof. First, we know from [17] that (H,[−,−,−]Hς) is a 3-Lie algebra. Next, for any h1,h2,h3,h4,h5∈H, we have
and
Similarly, we obtain
and
Hence Eqs (3.1)–(3.3) hold and we complete the proof. □
4.
Cohomology and infinitesimal deformations of nonabelian embedding tensors on 3-Lie algebras
In this section, we revisit fundamental results pertaining to the representations and cohomologies of 3-Leibniz algebras. We construct a representation of the descendent 3-Leibniz algebra (H,[−,−,−]Λ) on the vector space L and define the cohomologies of a nonabelian embedding tensor on 3-Lie algebras. As an application, we characterize the infinitesimal deformation using the first cohomology group.
Definition 4.1. (see [22]) A representation of the 3-Leibniz algebra (H,[−,−,−]H) is a vector space V equipped with 3 actions
satisfying for any a1,a2,a3,a4,a5∈H and u∈V
For n≥1, denote the n-cochains of 3-Leibniz algebra (H,[−,−,−]H) with coefficients in a representation (V;l,m,r) by
The coboundary map δ:Cn3Leib(H,V)→Cn+13Leib(H,V), for Ai=ai∧bi∈∧2H,1≤i≤n and c∈H, as
It was proved in [23,24] that δ2=0. Therefore, (⊕+∞n=1Cn3Leib(H,V),δ) is a cochain complex.
Let HΛ⟶L be a nonabelian embedding tensor 3-Lie algebra. By Corollary 2.10, (H,[−,−,−]Λ) is a 3-Leibniz algebra. Next we give a representation of (H,[−,−,−]Λ) on L.
Lemma 4.2. With the above notations. Define 3 actions
by
for all h1,h2∈H,l∈L. Then (L;lΛ,mΛ,rΛ) is a representation of the descendent 3-Leibniz algebra (H,[−,−,−]Λ).
Proof. For any h1,h2,h3,h4,h5∈H and l∈L, by Eqs (2.1), (2.3)–(2.6), and (2.9), we have
and
which imply that Eqs (4.1) and (4.2) hold. Similarly, we can prove that Eqs (4.3)–(4.5) are true. The proof is finished. □
Proposition 4.3. Let HΛ1⟶L and HΛ2⟶L be two nonabelian embedding tensor 3-Lie algebras and (fL,fH) a homomorphism from HΛ1⟶L to HΛ2⟶L. Then the induced representation (L;lΛ1,mΛ1,rΛ1) of the descendent 3-Leibniz algebra (H,[−,−,−]Λ1) and the induced representation (L;lΛ2,mΛ2,rΛ2) of the descendent 3-Leibniz algebra (H,[−,−,−]Λ2) satisfying the following equations:
for all h1,h2∈H,l∈L. In other words, the following diagrams commute:
Proof. For any h1,h2∈H,l∈L, by Eqs (2.7) and (2.8), we have
And the other equation is similar to provable. □
For n≥1, let δΛ:Cn3Leib(H,L)→Cn+13Leib(H,L) be the coboundary operator of the 3-Leibniz algebra (H,[−,−,−]Λ) with coefficients in the representation (L;lΛ,mΛ,rΛ). More precisely, for all ϕ∈Cn3Leib(H,L),Hi=ui∧vi∈∧2H,1≤i≤n and w∈H, we have
In particular, for ϕ∈C13Leib(H,L):=Hom(H,L) and u1,v1,w∈H, we have
For any (a1,a2)∈C03Leib(H,L):=∧2L, we define δΛ:C03Leib(H,L)→C13Leib(H,L),(a1,a2)↦δΛ(a1,a2) by
Proposition 4.4. Let HΛ⟶L be a nonabelian embedding tensor 3-Lie algebra. Then δΛ(δΛ(a1,a2))=0, that is, the composition C03Leib(H,L)δΛ⟶C13Leib(H,L)δΛ⟶C23Leib(H,L) is the zero map.
Proof. For any u1,v1,w∈V, by Eqs (2.1)–(2.6) and (2.9) we have
Therefore, we deduce that \delta_\Lambda (\delta_\Lambda(a_1, a_2)) = 0. □
Now we develop the cohomology theory of a nonabelian embedding tensor \Lambda on the 3-Lie algebra (L, [−, −, −]_L) with respect to the coherent action (H, [−, −, −]_H; \rho^{\dagger}) .
For n\geq 0 , define the set of n -cochains of \Lambda by \mathcal{C}^n_\Lambda(H, L): = \mathcal{C}^n_{\mathrm{3Leib}}(H, L). Then (\oplus_{n = 0}^{\infty}\mathcal{C}^n_\Lambda(H, L), \delta_\Lambda) is a cochain complex.
For n\geq 1 , we denote the set of n -cocycles by {\bf Z}^n_\Lambda(H, L) , the set of n -coboundaries by {\bf B}^n_\Lambda(H, L) , and the n -th cohomology group of the nonabelian embedding tensor \Lambda by
Proposition 4.5. Let H\stackrel{\Lambda_1}{\longrightarrow}L and H\stackrel{\Lambda_2}{\longrightarrow}L be two nonabelian embedding tensor 3-Lie algebras and let (f_L, f_{H}) be a homomorphism from H\stackrel{\Lambda_1}{\longrightarrow}L to H\stackrel{\Lambda_2}{\longrightarrow}L in which f_H is invertible. We define a map \Psi:\mathcal{C}^{n}_{\Lambda_1}(H, L)\rightarrow \mathcal{C}^{n}_{\Lambda_2}(H, L) by
for all \phi\in \mathcal{C}^{n}_{\mathrm{\Lambda_1}}(H, L), \mathfrak{H}_i = u_i\wedge v_i\in \wedge^2 H, 1\leq i\leq {n-1} , and w\in H . Then \Psi: (\mathcal{C}^{n+1}_{\mathrm{\Lambda_1}}(H, L), \delta_{\Lambda_1})\rightarrow (\mathcal{C}^{n+1}_{\mathrm{\Lambda_2}}(H, L), \delta_{\Lambda_2}) is a cochain map.
That is, the following diagram commutes:
Consequently, it induces a homomorphism \Psi^* from the cohomology group \mathrm{H}\mathrm{H}^{n+1}_{\mathrm{\Lambda_1}}(H, L) to \mathrm{H}\mathrm{H}^{n+1}_{\mathrm{\Lambda_2}}(H, L) .
Proof. For any \phi\in \mathcal{C}^{n}_{\mathrm{\Lambda_1}}(H, L), \mathfrak{H}_i = u_i\wedge v_i\in \wedge^2 H, 1\leq i\leq {n} , and w\in H , by Eqs (4.6)–(4.8) and Proposition 2.11, we have
Hence, \Psi is a cochain map and induces a cohomology group homomorphism \Psi^*: \mathrm{H}\mathrm{H}^{n+1}_{\mathrm{\Lambda_1}}(H, L) \rightarrow \mathrm{H}\mathrm{H}^{n+1}_{\mathrm{\Lambda_2}}(H, L) . □
At the conclusion of this section, we employ the well-established cohomology theory to describe the infinitesimal deformations of nonabelian embedding tensors on 3-Lie algebras.
Definition 4.6. Let \Lambda: H\rightarrow L be a nonabelian embedding tensor on a 3-Lie algebra (L, [−, −, −]_L) with respect to a coherent action (H, [−, −, −]_H; \rho^\dagger) . An infinitesimal deformation of \Lambda is a nonabelian embedding tensor of the form \Lambda_t = \Lambda+t\Lambda_1 , where t is a parameter with t^2 = 0.
Let \Lambda_t = \Lambda+t\Lambda_1 be an infinitesimal deformation of \Lambda , then we have
for all u_1, u_2, u_3\in H. Therefore, we obtain the following equation:
It follows from Eq (4.9) that \Lambda_1\in \mathcal{C}_\Lambda^1(H, L) is a 1-cocycle in the cohomology complex of \Lambda . Thus the cohomology class of \Lambda_1 defines an element in \mathrm{H}\mathrm{H}_\Lambda^1(H, L) .
Let \Lambda_t = \Lambda+t\Lambda_1 and \Lambda'_t = \Lambda+t\Lambda'_1 be two infinitesimal deformations of \Lambda . They are said to be equivalent if there exists a_1\wedge a_2\in \wedge^2 L such that the pair (id_L+tad(a_1, a_2), id_H+t\rho(a_1, a_2)) is a homomorphism from H\stackrel{\Lambda_t}{\longrightarrow}L to H\stackrel{\Lambda'_t}{\longrightarrow}L . That is, the following conditions must hold:
1) The maps id_L+tad(a_1, a_2):L\rightarrow L and id_H+t\rho(a_1, a_2): H\rightarrow H are two 3-Lie algebra homomorphisms,
2) The pair (id_L+tad(a_1, a_2), id_H+t\rho(a_1, a_2)) satisfies:
for all a, b\in L, u\in H. It is easy to see that Eq (4.10) gives rise to
This shows that \Lambda_1 and \Lambda'_1 are cohomologous. Thus, their cohomology classes are the same in \mathrm{H}\mathrm{H}_\Lambda^1(H, L) .
Conversely, any 1-cocycle \Lambda_1 gives rise to the infinitesimal deformation \Lambda+t\Lambda_1 . Furthermore, we have arrived at the following result.
Theorem 4.7. Let \Lambda: H\rightarrow L be a nonabelian embedding tensor on (L, [−, −, −]_L) with respect to (H, [−, −, −]_H; \rho^{\dagger}) . Then, there exists a bijection between the set of all equivalence classes of infinitesimal deformations of \Lambda and the first cohomology group \mathrm{H}\mathrm{H}_\Lambda^1(H, L) .
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research is supported by the National Natural Science Foundation of China (Grant No. 12361005) and the Universities Key Laboratory of System Modeling and Data Mining in Guizhou Province (Grant No. 2023013).
Conflict of Interest
The authors declare there is no conflicts of interest.

















 DownLoad:
DownLoad: