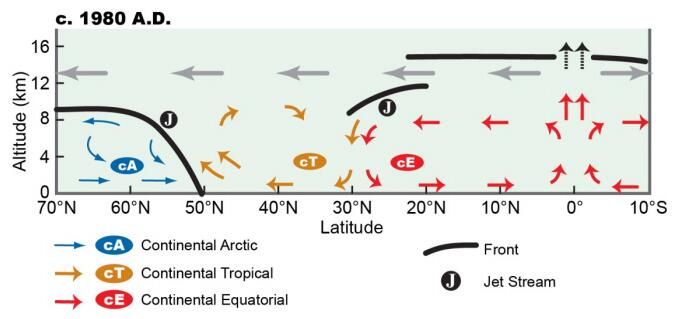
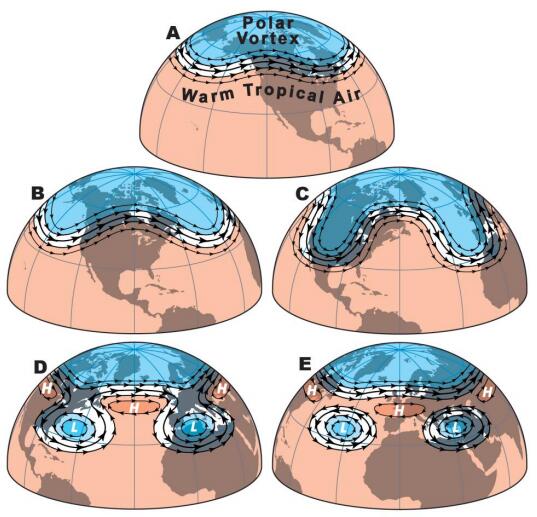
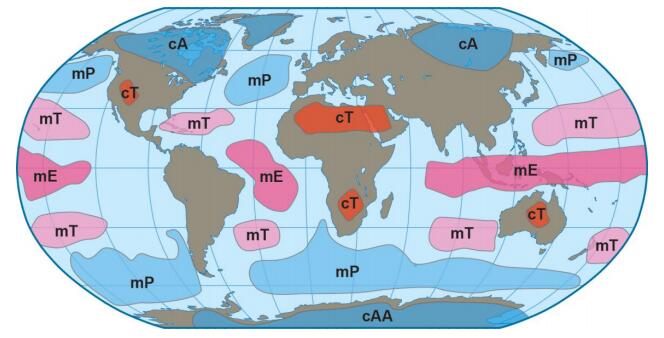
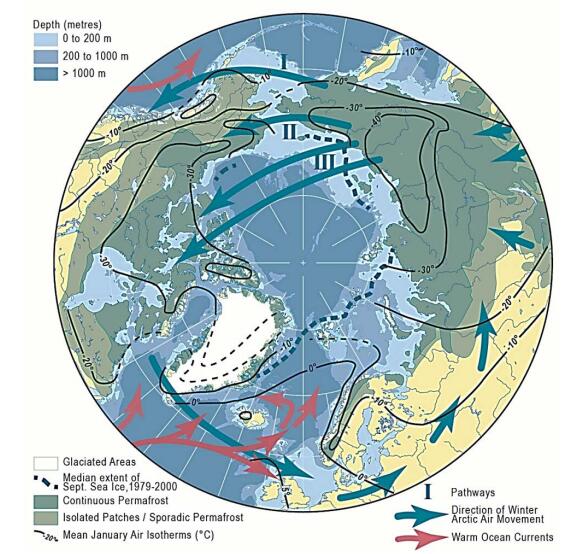
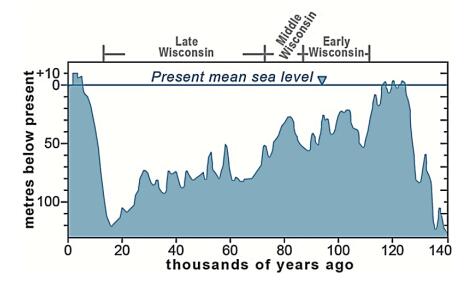
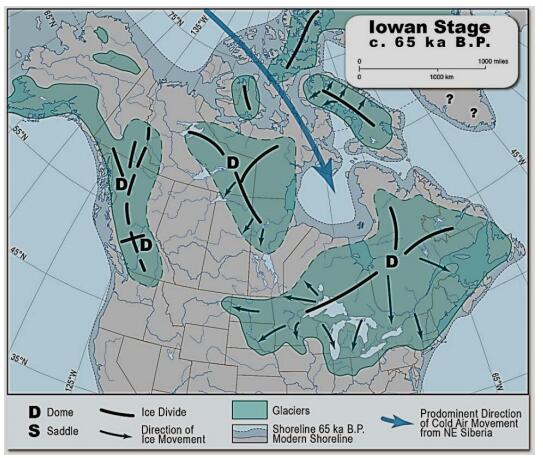
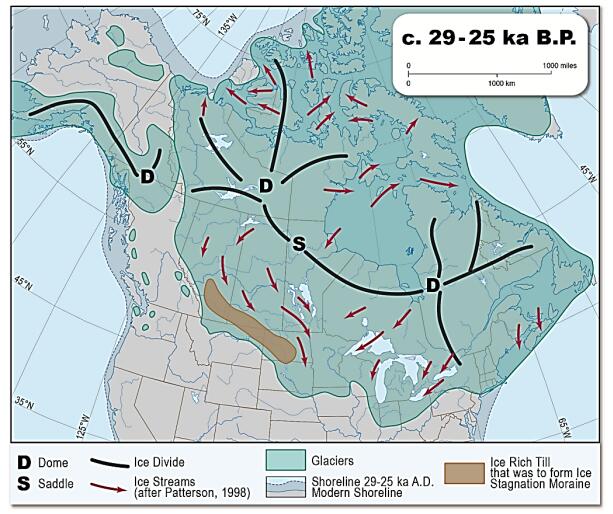
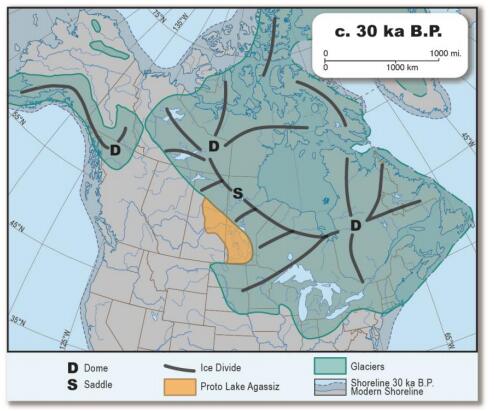
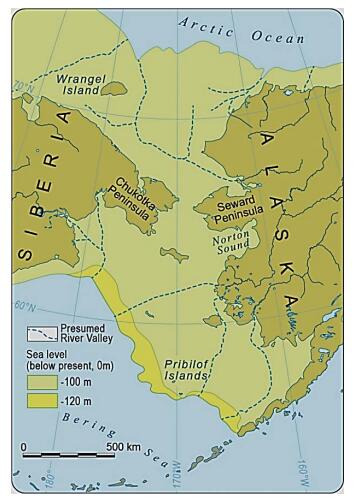
The Arctic air mass is the cold, dry body of air slowly moving eastwards around the North Pole in the northern hemisphere. Its southern boundary consists of four planetary waves known as the Rossby waves that mark the interface with subtropical air bringing heat polewards. The Arctic air mass is constantly being modified by the addition of heat and moisture over the oceans, as well as by winter cooling over the land masses due to limited incoming solar radiation and constant reradiation of heat into the atmosphere. The coldest air in winter is located over northeastern Siberia and moves east, cooling Canada. Warm ocean currents add large quantities of heat to the air mass moving over them, but without this addition of heat, the Arctic air mass becomes significantly colder. Research in Tibet and Northeast Asia on depression of sea level shows that during the Late Wisconsin cold event (65–10 ka B.P.), vast quantities of sea water were sequestered on land primarily as ice sheets, exposing the sea bed in the Bering Strait from 50–10 ka B.P. together with the bottom of the South China Sea between 30–20 ka B.P.. The East China Monsoon failed to reach Tibet and much of Northeast China, resulting in severe cooling of northeast Siberia and northern Tibet. This, in turn, caused severe cooling in eastern Canada together with the development of a vast, predominantly cold-based ice sheet. As the sea levels started to rise (about 19 ka B.P.), the East China Monsoon slowly redeveloped and a gradual warming took place on both continents. However, along the west side of the North American Cordillera, the Late Wisconsin glaciation only began in 29 ka B.P. but continued along the west coast until about 10 ka B.P. This paper explores the relationship of the Late Wisconsin history on the two continents, together with the mechanisms causing the landforms and climatic differences. Finally, the probable effects of these climatic changes on the early peopling of North America are discussed.
1.
Introduction
All graphs considered in this paper are finite, undirected and simple. Let G be a graph with vertex-set V(G) and edge-set E(G). A subset D of V(G) is called a dominating set of G if every vertex of G is either in D or adjacent to a vertex of D. The domination number γ(G) is the cardinality of a minimum dominating set of G.
The domination in graphs is so classic that it has been widely studied in networks theory, while the decision problem for the domination number of a general graph was proved to be NP-complete [8]. On the study of domination, there are three early textbooks compiled by Haynes et al. [13,14] and Henning et al. [17]. Recently, Haynes, Hedetniemi and Henning [11,12] edited two new books on this field once again.
Definition 1.1. [24] (1) A vertex v∈V(G) is called γ-fixed if v belongs to every minimum dominating set of G. (2) A vertex v∈V(G) is called γ-bad if v does not belong to any minimum dominating set of G. (For simplicity, we abbreviate "γ-fixed" and "γ-bad" to "fixed" and "bad" respectively in this paper.)
Definition 1.2. A vertex v∈V(G) is called critical if γ(G−v)<γ(G). In particular, we agree that the single vertex of a trivial graph is critical.
Remark for Definition 1.2: It is easy to see that γ(G−v)<γ(G)⇔γ(G−v)≤γ(G)−1⇔γ(G−v)=γ(G)−1, where γ(G−v)≤γ(G)−1⇒γ(G−v)=γ(G)−1 holds because if not so, then γ(G−v)≤γ(G)−2, and thus G would have a dominating set with cardinality ((γ(G)−2)+|v|)<γ(G), contradicting the minimality of γ(G).
The terms of fixed and bad vertices of graphs were introduced by Samodivkin [24], which can help us to research the constructions of minimum dominating sets of a graph better and shorten the processes of our proofs [7,22,24,25]. (In [28], fixed and bad vertices of a graph are also called universal and idle vertices, respectively.) The notions of domination critical, which include vertex-critical [4] and edge-critical [3,27], are very important to domination of graphs. But in this paper, we are not going to discuss the topic of edge-critical.
Definition 1.3. A graph G is called vertex-critical if every vertex of G is critical.
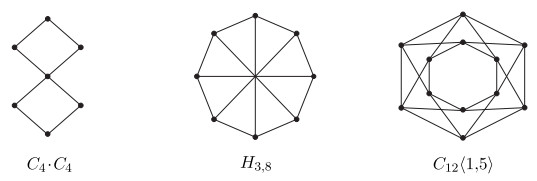
There are lots of nice properties on domination vertex-critical graphs [1,2,19,29,30]. Many of them possess symmetry, and even vertex-transitivity. For example, the graph C4⋅C4 obtained by identifying two vertices of two cycles of orders four, the Harary graph H3,8 and the circulant graph C12⟨1,5⟩ (See Figure 1.).
Trees is a kind of basic graph class often applied to algorithm design. There are a good few results on the study of the constructions for special trees, such as trees with equal domination and total domination numbers [7], trees with equal domination and restrained domination numbers [6], trees with equal total domination and disjunctive domination numbers [18], trees with equal independent domination and weak domination numbers [10], trees with a minimum vertex cover also being a minimum total dominating set [5], trees with two disjoint minimum independent dominating sets [15], trees with the paired domination number being twice the matching number [26], trees without fixed vertices [31], trees without fixed vertices and critical vertices [23,16], trees with unique minimum dominating sets [9,34], trees with equal Roman {2}-domination and Roman domination numbers [21], and trees with total Roman domination number being equal to the sum of domination number and semitotal domination number [20].
Naturally, there are two such questions: Can we exhaustively characterize vertex-critical graphs, as well as graphs without critical vertices? It seems not easy to solve these two questions. Therefore, in this paper, we study on the latter one and focus on the graph class-trees. Via defining 3 operations of graphs, we get a constructive characterization of trees without critical vertices.
2.
Preliminary
2.1. Notations and terminologies
For any u,v∈V(G), denote by dG(u,v) the distance from u to v in G as well as dG(v), NG(v), NG[v] and N2G(v) the degree, open neighborhood, closed neighborhood and 2-open neighborhood of vertex v in G respectively, where the 2-open neighborhood of vertex v in G is defined as N2G(v)={x∈V(G)∣d(x,v)=2}. For any ∅≠X⊆V(G), let G[X] denote the subgraph of G induced by X.
Denote by MDS_(G) the set composed of all the minimum dominating sets of G. That is, MDS_(G)={D∣D is a minimum dominating set of G}. A vertex of degree one (resp. degree zero) in G is called an end-vertex (resp. isolated vertex) of G. Let g be a cut-vertex of G. If a component P of G−g is a path and g is adjacent to an end-vertex of P in G, then we call P as a pendant path of G and say that g and P are linked with each other. A pendant path of G with order l (l≥1) is called an l-pendant path of G. Let P2k+1=v1v2⋯v2k+1 be a path of order 2k+1. Then vk+1 is the center of P2k+1.
Let r be a vertex, l and m be two non-negative integers with l+m≥1. Let P13≅P23≅⋯≅Pl3≅P3 with Pi3=viuiwi, i=1,2,…,l, and P12≅P22≅⋯≅Pm2≅P2 with Pj2=xjyj, j=1,2,…,m. For every 1≤i≤l, link r and ui by an edge. For every 1≤j≤m, link r and xj by an edge. Denote the resulting graph as Rl,m and call r as the root of Rl,m (See Figure 2).
2.2. Some useful results
Now, we give three observations and some known lemmas, which will support our proofs in the next section.
Observation 2.1. Let G be a graph. If G1 and G2 are vertex-induced subgraphs of G such that V(G)=V(G1)∪V(G2), then γ(G)≤γ(G1)+γ(G2) with the equality holding when G1 and G2 are two components of G.
Observation 2.2. Let u∈V(G). If u is adjacent to two end-vertices v and w in G, then v and w are bad in G, and u is fixed in G.
Observation 2.3. Let u be an end-vertex of G with NG(u)={v}. Then u is non-fixed and v is non-bad in G, and |{u,v}∩D|=1 for any D∈MDS_(G).
Lemma 2.4. [3] For any nontrivial tree T and any v∈V(T), v is a fixed vertex of T if and only if γ(T−v)>γ(T).
Lemma 2.5. [32] Let G be a graph with minimum degree at least one. If x is a bad or fixed vertex of G, then all the elements of NG[x] are non-critical vertices of G.
Lemma 2.6. [33] Let G be a graph.
(a) If x is a non-fixed vertex of G, then γ(G−x)≤γ(G).
(b) If x is a bad vertex of G, then γ(G−x)=γ(G).
(c) If x is a non-fixed and non-critical vertex of G, then γ(G−x)=γ(G).
Lemma 2.7. [34] Let T be a tree containing only one vertex u of degree at least 3. Then u is linked with |NT(u)| pendant paths in T.
Lemma 2.8. [34] Let T be a tree with at least two vertices of degree at least 3 and let dT(u,v)=max{dT(x,y)| both x and y are vertices of degree at least 3 in T}. Then u is linked with |NT(u)|−1 pendant paths in T.
Lemma 2.9. [34] Let G0 be a graph without any isolated vertices and possessing a fixed vertex. If G is a graph obtained via linking a fixed vertex of G0 and the single vertex of P1 by an edge, then γ(G)=γ(G0).
Lemma 2.10. [34] Let G0 be a graph without any isolated vertices and possessing a fixed vertex. If G is a graph obtained via linking a fixed vertex of G0 and the center of P3 by an edge, then γ(G)=γ(G0)+1.
3.
Trees without critical vertices
3.1. Nontrivial vertex-critical trees do not exist
We now ask a question: Is there a nontrivial tree only containing critical vertices? Unluckily, the answer to this question is no (See Lemma 3.1).
Lemma 3.1. If dG(u)=1 and v∈NG(u)∪N2G(u), then v is a non-critical vertex of G.
Proof. Suppose to the contrary that v is a critical vertex of G. If v∈NG(u), let D1∈MDS_(G−v). Then by Definition 1.2, we have |D1|=γ(G)−1. Since u is an isolated vertex of G−v, it follows that u is fixed in G−v. Now, if we let D2=(D1−{u})∪{v}, then D2 is a dominating set of G with |D2|=|D1|=γ(G)−1, a contradiction.
If v∈N2G(u), then |D′|=γ(G)−1 for any D′∈MDS_(G−v). Let NG(u)={w}. Since u is still an end-vertex of G−v, it follows from Observation 2.3 that w is a non-bad vertex of G−v. Let D′1∈MDS_(G−v) with w∈D′1. On one hand, we have |D′1|=γ(G)−1. But on the other hand, D′1 is also a dominating set of G, which implies that |D′1|≥γ(G), a contradiction.
Lemma 3.1 tells us that if G is nontrivial and has an end-vertex, then G must have a non-critical vertex. Therefore, a tree is vertex-critical if and only if it is trivial.
3.2. To get larger graphs without critical vertices via operations of graphs
In this subsection, via several operations of graphs, we can get large graphs without critical vertices from small graphs without critical vertices step by step. In particular, these processes of operations are reversible for trees. (Here, large graph represents graph with large order while small graph represents graph with small order.) For a graph G0, we define the following three operations.
Operation i. Link a fixed vertex of G0 and the single vertex of P1 by an edge. Denote the resulting graph by G0∽P1. (Refer to Figure 3 (i)).
Operation ii. Link a fixed vertex of G0 and the center of P3 by and edge. Denote the resulting graph by G0∽P3. (Refer to Figure 3 (ii)).
Operation iii. Link an arbitrary vertex of G0 and the root of Rl,m by and edge. Denote the resulting graph by G0∽Rl,m. (Refer to Figure 3 (iii)).
Remark. In fact, the resulting graph may be not unique. So, "G=G0∽P1" means that "G is obtained from G0 by Operation i".
Lemma 3.2. Let G0 be a graph without any isolated vertices and possessing a fixed vertex, and let G=G0∽P1. Then all the vertices of G0 are non-critical if and only if all the vertices of G are non-critical.
Proof. (⇒) Suppose that V(P1)={v1} and gv1∈E(G). From Lemma 2.9, we have γ(G)=γ(G0)=γ(G−v1). So by Definition 1.2, v1 is a non-critical vertex of G. Also, we have g is a non-critical vertex of G by Lemma 3.1. It remains to prove that x is a non-critical vertex of G for every x∈V(G−v1−g)⊆V(G0). Since all the vertices of G0 are non-critical, we have γ(G0−x)≥γ(G0). Since dG−x(v1)=1, we have v1 is a non-fixed vertex of G−x by Observation 2.3. So there exists D−x∈MDS_(G−x) such that v1∉D−x, and then g∈D−x. Thus D−x∩V(G0−x) is a dominating set of G0−x. Hence γ(G−x)=|D−x|=|D−x∩V(G0−x)|≥γ(G0−x)≥γ(G0)=γ(G), which implies that x is a non-critical vertex of G. The necessity follows.
(⇐) Assume to the contrary that G0 has a critical vertex y0. Since all the vertices of G are non-critical, we have γ(G−y0)≥γ(G). Let D−0∈MDS_(G0−y0). Then |D−0∪{y0}|=γ(G0−y0)+1=γ(G0), which implies that D−0∪{y0}∈MDS_(G0). By the definition of Operation i, g is a fixed vertex of G0. So we have g∈D−0∪{y0}, and g is a non-critical vertex of G0 by Lemma 2.5. Thus g≠y0, and therefore g∈D−0, which implies that D−0 is a dominating set of G−y0. Hence γ(G0−y0)=|D−0|≥γ(G−y0)≥γ(G)=γ(G0), which contradicts the assumption that y0 is a critical vertex of G0. The sufficiency follows.
Lemma 3.3. Let G0 and W be two graphs. Let G be a graph obtained via linking an arbitrary vertex of G0 and an arbitrary vertex of W by an edge. If γ(G)=γ(G0)+γ(W) and all the vertices of G are non-critical, then all the vertices of G0 are non-critical.
Proof. For any y∈V(G0), since all the vertices of G are non-critical, it follows that γ(G−y)≥γ(G). By Observation 2.1, we have γ(G0−y)+γ(W)≥γ(G−y)≥γ(G)=γ(G0)+γ(W). Thus γ(G0−y)≥γ(G0), and so y is a non-critical vertex of G0. The lemma follows.
Lemma 3.4. Let G0 be a graph without isolated vertices and possessing a fixed vertex, and G=G0∽P3.
(a) If all the vertices of G are non-critical, then all the vertices of G0 are non-critical.
(b) When G0 is a tree, (in order to avoid confusion, ) we rewrite T0=G0 and T=G. If all the vertices of T0 are non-critical, then all the vertices of T are non-critical.
Proof. (a) Suppose that P3=v1v2v3 and E(G)−E(G0)−E(P3)={gv2}. Then g is fixed in G0. From Lemma 2.10, we get γ(G)=γ(G0)+1. Item (a) follows by Lemma 3.3.
(b) Firstly, by Observation 2.2, v2 is a fixed vertex of T. So by Lemma 2.5, v1,v2, v3 and g are non-critical vertices of T.
Secondly, we need to show that x is a non-critical vertex of T for every x∈V(T−g)−V(P3). That is, to prove γ(T−x)≥γ(T). Since T0 has no critical vertices, we have γ(T0−x)≥γ(T0). Let D−x∈MDS_(T−x). If g∈D−x, then D−x∩V(T0−x) is a dominating set of T0−x, and so γ(T−x)=|D−x|=|D−x∩V(T0−x)|+|{v2}|≥γ(T0−x)+1≥γ(T0)+1=γ(T). If g∉D−x, then (D−x∩V(T0−x))∪{x} is a dominating set of T0−g. By Lemma 2.4, we have |(D−x∩V(T0−x))∪{x}|≥γ(T0−g)≥γ(T0)+1, which implies that |D−x∩V(T0−x)|≥γ(T0). So γ(T−x)=|D−x|=|D−x∩V(T0−x)|+|{v2}|≥γ(T0)+1=γ(T). Item (b) follows.
Note. In Lemma 3.4 (b), we restrict G0 to be a tree because if G0 is a general graph, then the result maybe not true. (See the following Example 3.5).
Example 3.5. Define G0 and G as shown in Figure 4. Then G=G0∽P3. It is not hard to check that γ(G0)=2, h1 and g are fixed vertices of G0, as well as w1,u1,u2,u3,u4 and h2 are bad vertices of G0. By Lemma 2.5, G0 has no critical vertices. However, since γ(G)=γ(G0)+1=3, we can see that {h2,v2}∈MDS_(G−w1), which implies that w1 is a critical vertex of G.
Lemma 3.6. Let G0 be a graph and G=G0∽Rl,m. Then
(a)γ(G)=γ(G0)+(l+m);
(b) all the vertices of G0 are non-critical if and only if all the vertices of G are non-critical.
Proof. Suppose that E(G)−E(G0)−E(Rl,m)={gr}. Set U={u1,u2,…,ul}, X={x1,x2,…,xm}, Y={y1,y2,…,ym} and Z=X∪Y.
(a) We can easily see that γ(Rl,m)=l+m. So γ(G)≤γ(G0)+(l+m). It remains to prove γ(G)≥γ(G0)+(l+m). Let D∈MDS_(G). If D∩V(G0) can dominate g in G, then D∩V(G0) is a dominating set of G0, and so |D|≥|D∩V(G0)|+|U|+|D∩Z|≥γ(G0)+(l+m); if not, then r∈D and (D∩V(G0))∪{g} is a dominating set of G0, and so |D|=|D∩V(G0)|+|{r}|+|U|+|D∩Z|=|(D∩V(G0))∪{g}|+(l+m)≥γ(G0)+(l+m).
(b) (⇐) The sufficiency follows immediately by Item (a) and Lemma 3.3.
(⇒) We claim that r is a bad vertex of G. Otherwise, let Dr∈MDS_(G) with r∈Dr. If g∈Dr, then Dr−{r} is a dominating set of G, contradicting the minimality of |Dr|. So we have g∉Dr, and then Dr∩V(G0) is a dominating set of G0−g. Thus γ(G0−g)≤|Dr∩V(G0)|=|Dr|−|U|−|Dr∩Z|−|{r}|=γ(G)−(l+m)−1=γ(G0)−1, which implies that g is a critical vertex of G0, contradicting the known condition that G0 has no critical vertices.
Now firstly, for every 1≤i≤l and every 1≤j≤m, we have ui,vi,wi,r,g and xj are non-critical vertices of G by Lemma 2.5.
Secondly, if there exists some 1≤j′≤m such that γ(G−yj′)=γ(G)−1, we can let D−∈MDS_(G−yj′) with r∈D− by Observation 2.3. But then D−∪{yj′}∈MDS_(G) with r∈D−∪{yj′}, contradicting the claim that r is bad in G. So for every 1≤j≤m, we have γ(G−yj)≥γ(G), which implies that yj is non-critical in G.
Finally, it remains to show that γ(G−x)≥γ(G) for every x∈V(G−g)−V(Rl,m)⊆V(G0). Since all the vertices of G0 are non-critical, we have γ(G0−x)≥γ(G0). Let D−x∈MDS_(G−x). If D−x∩V(G0−x) can dominate g, then D−x∩V(G0−x) is a dominating set of G0−x, and so γ(G−x)=|D−x|≥|D−x∩V(G0−x)|+|U|+|D−x∩Z|≥γ(G0−x)+(l+m)≥γ(G0)+(l+m)=γ(G); if not, then we have r∈D−x and (D−x∩V(G0−x))∪{g} is a dominating set of G0−x, and so γ(G−x)=|D−x|=|D−x∩V(G0−x)|+|{r}|+|U|+|D−x∩Z|=|(D−x∩V(G0−x))∪{g}|+(l+m)≥γ(G0−x)+(l+m)≥γ(G0)+(l+m)=γ(G). The necessity follows.
3.3. To construct trees only containing non-critical vertices
Since it is hard to obtain a constructive characterization of graphs without critical vertices, we only solve this problem partly by restricting the graph class to be trees in this subsection.
Theorem 3.7. A nontrivial tree T has no critical vertices if and only if T can be obtained from P2 or P3 by a finite sequence of Operations i–iii.
Proof. Let T be the set of graphs obtained from P2 or P3 by a finite sequence of Operations i–iii. It suffices to prove that T has no critical vertices if and only if T∈T.
(⇐) Assume that T is obtained by doing n times Operations i, ii and iii. We will prove that all the vertices of T are non-critical by induction on n. When n=0, we have T=P2 or T=P3, and the result is true clearly. Suppose that the result is true when n=k(k≥0). Then from Lemmas 3.2, 3.4 (b), and 3.6 (b), we know that the result is also true when n=k+1. By the induction principle, the sufficiency follows.
(⇒) We are going to prove the necessity by induction on |V(T)|. When |V(T)|=2 or 3, the result is true clearly. Suppose that the result is true when |V(T)|<k(k≥4). We consider the case when |V(T)|=k below.
Case 1. T has a pendant path of order at least 3.
Let P3 be a 3-pendant path of T and T0=T−V(P3). Note that P3≅R0,1. So T=T0∽R0,1. By Lemma 3.6 (b), all the vertices of T0 are non-critical. Since |V(T0)|<|V(T)|=k, we have T0∈T by the induction hypothesis. Hence T=T0∽R0,1∈T.
Case 2. T has a vertex u adjacent to an end-vertex w in T and u is fixed in T−w.
Let T0=T−w. Then T=T0∽P1. By Lemma 3.2, T0 has no critical vertices. Since |V(T0)|=k−1<k, we have T0∈T. Hence T=T0∽P1∈T.
Case 3. T has a vertex u of degree 3 which is adjacent to two end-vertices v,w of T and a fixed vertex g of T−{v,u,w} in T.
Let T0=T−{v,u,w}. Then T=T0∽P3. By Lemma 3.4 (a), T0 has no critical vertices. So T0∈T, and hence T∈T.
Case 4. T has a vertex u of degree at least 3 linked with |NT(u)|−1 2-pendant paths.
Let P12,P22,…,Pm2 be the 2-pendant paths linked with u in T, where m=|NT(u)|−1. Then T[{u}∪⋃mj=1V(Pj2)]≅R0,m. Let T0=T−({u}∪⋃mj=1V(Pj2)). Then T=T0∽R0,m. As a consenquence, we have T∈T.
Case 5. All of Cases 1–4 do not occur.
Since |V(T)|≥4 and Case 1 does not occur, T is not a path. So T has at least one vertex of degree at least 3.
Claim 5.1. There does not exist a vertex u adjacent to three end-vertices in T.
Suppose not. Let v1 be an end-vertex which is adjacent to u in T and let T0=T−v1. By Observation 2.2, u is a fixed vertex of T0, which is contrary to the supposition that Case 2 does not occur.
Claim 5.2. There does not exist a vertex u linked with one 1-pendant path P1 and one 2-pendant path P2 in T.
Suppose not. Let V(P2)={x,y} with ux∈E(T). By Observation 2.3, there exists Du∈MDS_(T) such that u∈Du. Let D∗u=(Du−{x,y})∪{y}. Then D∗u−{y} is a dominating set of T−y, which implies that y is a critical vertex of T, contradicting the known condition that T has no critical vertices.
Claim 5.3. T has at least two vertices of degree at least 3.
Suppose, to the contrary, that T has only one vertex c with dT(c)≥3. By Lemma 2.7, c is linked with |NT(c)| pendant paths in T. Since Case 1 does not occur, it follows from Claims 5.2 and 5.1 that all of these |NT(c)| pendant paths are 2-pendant paths. But this contradicts the supposition that Case 4 does not occur.
Claim 5.4. If u and v are two vertices of degree at least 3 in T such that dT(u,v)= max {dT(x,y)|both x and y are vertices of degrees at least 3 in T}, then |NT(u)|=3 and u is adjacent to 2 end-vertices in T.
By Lemma 2.8, u is linked with |NT(u)|−1 pendant paths in T. Since Cases 1 and 4 does not occur, it follows from Claims 5.2 and 5.1 that |NT(u)|=3 and u is adjacent to 2 end-vertices in T.
Now, let u and v be two vertices of T satisfying the supposition of Claim 5.4. Suppose that v1 and w1 are two end-vertices which are adjacent to u in T and NT(u)−{v1,w1}={r}. By Claim 5.4, the equivalent status of v and u, and Observation 2.2, we get that v is a fixed vertex of T−{u,v1,w1}. Since Case 3 does not occur, we have r≠v.
Let Tv be the component of T−r such that v∈V(Tv), {z}=NT(r)∩V(Tv), NT(r)−{z}={u1,u2,…,uq} (where u1=u) and Tu1,Tu2,…,Tuq be the components of T−r such that ui∈V(Tui) for every 1≤i≤q. Furthermore, we may suppose without loss of generality that Tu1,Tu2,…,Tul are not pendant paths of T as well as Tul+1,Tul+2,…,Tul+m are pendant paths of T, where 1≤l≤q and l+m=q.
Claim 5.5. Tui is a 2-pendant path of T for every l+1≤i≤l+m.
Suppose, to the contrary, that Tui′ is a pendant path of T with |V(Tui′)|≠2 for some l+1≤i′≤l+m. By Lemma 3.1, r is a non-critical vertex of T−V(Tui′). Since Case 1 does not occur, we have |V(Tui′)|=1. Let V(Tui′)={w} and T0=T−{u,v1,w1}. By Observations 2.2 and 2.3, one may let Dr∈MDS_(T) with u,r∈Dr. We claim that Dr∩V(T0)∈MDS_(T0). Otherwise there exists D0∈MDS_(T0) such that |D0|<|Dr∩V(T0)|. But then {u}∪D0 would be a dominating set of T with |{u}∪D0|<|{u}∪(Du∩V(T0))|=|Dr|, contradicting the minimality of |Dr|. Thus γ(T)=|Dr|=|{u}|+|Dr∩V(T0)|=1+γ(T0). Since Case 3 does not occur, r is not a fixed vertex of T0. Let ˆDr0∈MDS_(T0) with r∉ˆDr0. Then w∈ˆDr0 and {u}∪ˆDr0∈MDS_(T). Since ({u}∪ˆDr0)−{w} is a dominating set of T−w, it follows that w is a critical vertex of T, a contradiction.
Claim 5.6. For every 2≤i≤l, ui is the unique vertex of V(Tui) satisfying dT(ui)≥3.
Firstly, since Tui is not a pendant path of T, Tui has a vertex with degree at least 3 in T. Secondly, we claim that for every h∈V(Tui)−{ui}, h is not a vertex of V(Tui) with degree at least 3 in T. Otherwise, we have dT(h,v)=dT(h,ui)+dT(ui,v)>dT(ui,v)=1+dT(r,v)=dT(u,v), contradicting the selection of u and v. From these two observations, Claim 5.6 follows.
Since dT(ui,v)=dT(u1,v), we have |NT(ui)|=3 and ui is adjacent to 2 end-vertices in T for every 2≤i≤l by Claim 5.4, which implies that
(See Figure 5.) Let T0=T−({r}∪⋃li=1V(Tui)∪⋃mj=1V(Tul+j)). Then T=T0∽Rl,m. By Lemma 3.6 (b), T0 has no critical vertices. Thus we have T0∈T by the induction hypothesis, and so T∈T.
In conclusion, the result is true when |V(T)|=k. The necessity follows.
4.
Conclusions
We think that it is quite difficult to give a construction for graphs without critical vertices. For further studies, ones may consider to characterize unicyclic graphs without critical vertices, or graphs with domination number 3 and without critical vertices.
Acknowledgments
1. National Natural Science Foundation of China (no. 12061047);
2. Natural Science Foundation of Jiangxi Province (no. 20192BAB211002);
3. Undergraduate Innovation Training Project of Hubei Province (no. 202111072011);
4. Foundation of Cultivation of Scientific Institutions of Jianghan University (no. 06210033).
Conflict of interest
The authors declared that they have no conflicts of interest to this work.









 DownLoad:
DownLoad: