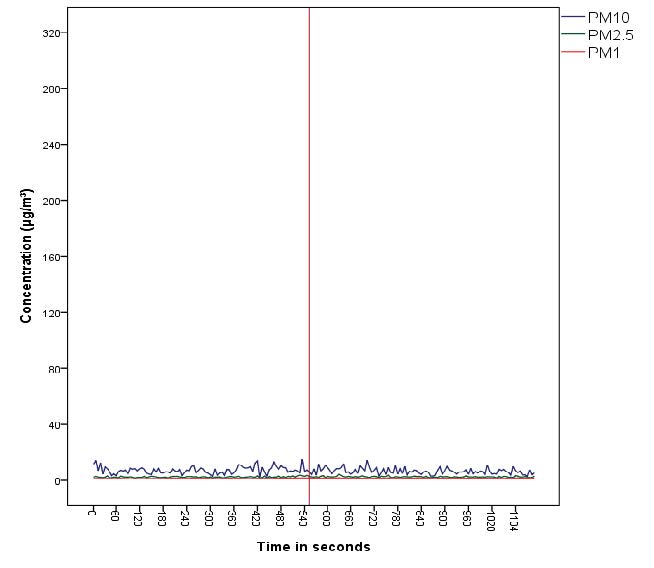
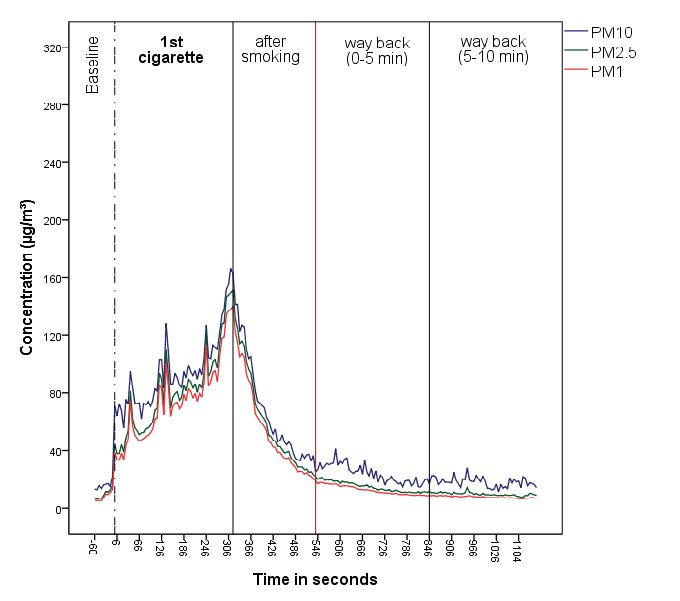
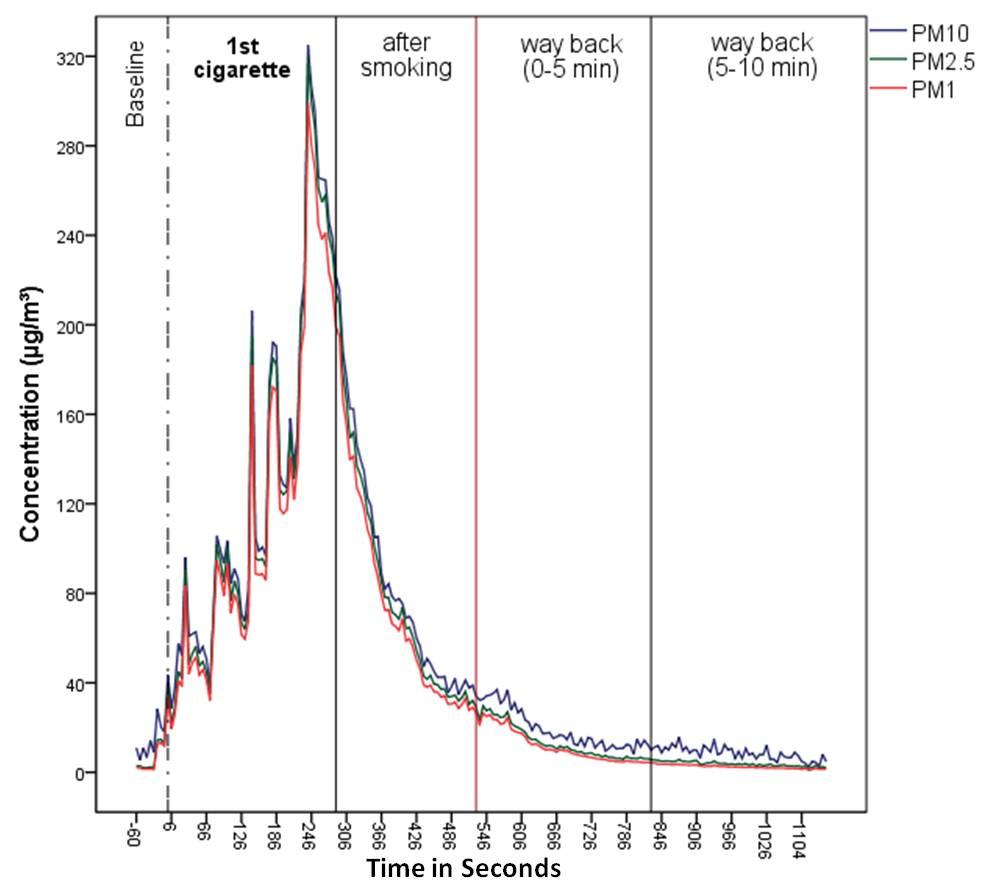
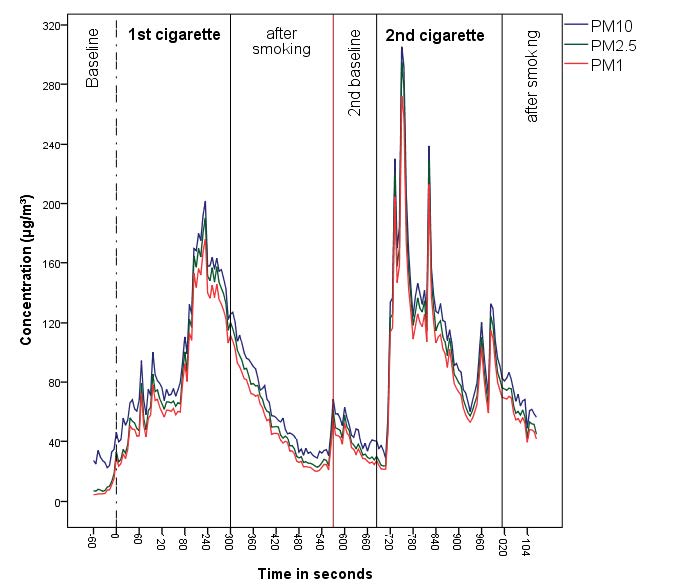
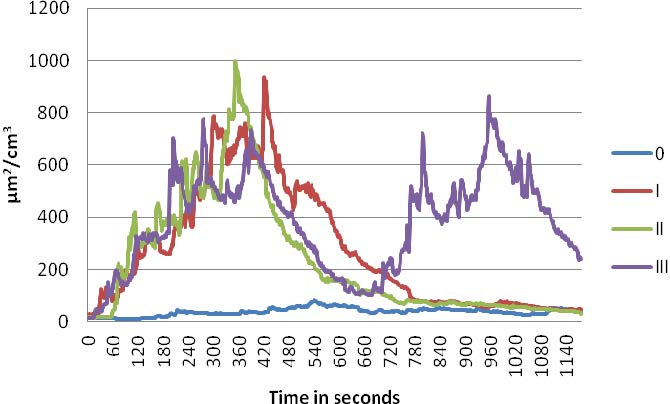
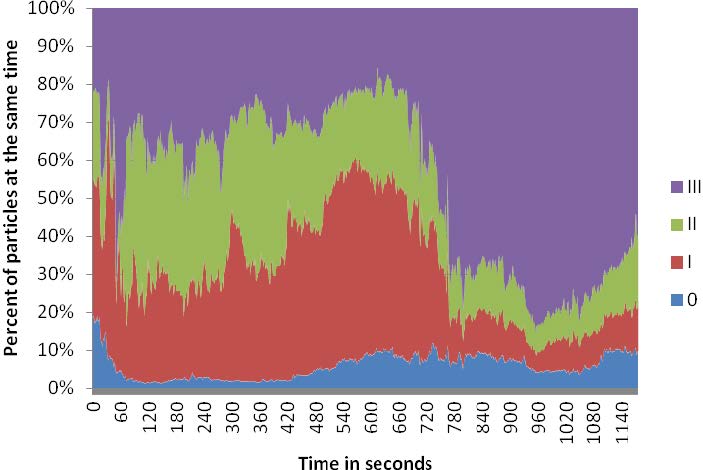
The exposure to particles was measured by a diffusion size classifier (10–300 nm) and an optical particle counter (300 nm–10 μm) at the child’s seat of a car during repeated drives on a fixed route from a suburban domestic area to a school and back. One single cigarette smoked in a car at the front seat during a 10 minute trip, lead to an increase of PM10 on the back seat by a factor of 10.5, for PM2.5 by a factor of 21.3 and for PM1 by a factor of 23.9. Concentrations dropped after opening the back door, but stayed elevated on the way back, compared to outdoor concentrations. Holding the cigarettes to the open window of the front seat did not reduce exposure on the back seat. When a second cigarette was smoked on the way back, PM10 concentrations rose again to 300 μg m−3. While background PM1 made up 19–39% of PM10, PM1 during smoking amounted to 78–89% of PM10. PM1 was highly correlated to particle number (mean 97,701 pt cm−3, SD 82,537) and lung deposited surface area (LDSA, mean 270 cm2 cm−3, SD 229). Positioning of the cigarette at the open window did not decrease the exposure to LDSA at the child’s seat. In conclusion, particles can reach exorbitant high levels at the back seat, when cigarettes are smoked in a small place like a car, even with a 2 inches open window next to the smoker at the front seat. Through smoking in cars parents can harm their or other’s children severely.
1.
Introduction
Topological data analysis (TDA) is an emerging mathematical and statistical field which provides insights into the structure of high-dimensional or complex data. One commonly employed tool in TDA is persistent homology, which measures topological features across spatial scales in data sets such as point clouds [1]. Topological methods for data analysis have recently been reviewed in [2,3] and applications to biological fields such as structural and molecular biology, developmental biology, oncology, and precision medicine were reviewed in [4,5,6]. A common application of persistent homology to biological data analysis is to carry out classification tasks on static experimental or simulated images. Examples include identifying diabetic retinopathy [7], classifying MRI results [8], distinguishing between patterns in wild-type and mutant zebrafish [9], and classifying actin filament networks of plant cells [10], to name a few. Results of persistent homology computation are often summarized in topological summaries, such as the commonly used persistence diagram summary and visualization [11].
Other research directions have focused on understanding how topological features change in biological datasets that evolve over time. Studies [12,13,14] used distances between topological summaries to classify behaviors observed in biological images collected at different time points. The study [15] introduced the concept of vineyards, which are continuous families of persistence diagrams for time-series of continuous functions. Vineyards consist of vines that track points in time-parameterized stacks of persistence diagrams and require constructing simplicial complexes using the sublevel set filtration at each time point. This method was originally applied to protein folding trajectories in [15] and more recently to detecting anomalies in spatially heterogeneous COVID-19 data in [16]. Another study used persistent homology to characterize features of collective aggregation and swarming through time in model simulations [17]. This work introduced a visualization tool called the CROCKER plot, which tracks Betti numbers (the number of topological features in each dimension) through time. Betti numbers are a natural choice for data analysis since the 0th, 1st, and 2nd Betti numbers correspond to the number of connected components, rings, and hollow solids that emerge from aggregation and swarming dynamics. The work in [17] and [18] found that this topology-based approach was able to capture events and structures that standard order parameters like polarization and angular momentum missed, and that it also had predictive value in selecting models describing agent interactions from pea aphid data.
Instead of tracking the number of topological features through time or classifying image patterns at different times, we have previously used persistent homology to track how a given topological feature evolves over time using the Vietoris-Rips filtration [19]. Our motivation was to track the formation and collapse of a single large biological ring channel consisting of actin filaments interacting with myosin motor proteins. This approach involved recording the birth and death information of the ring structures identified at every time step, and then employing a greedy matching algorithm that prioritized tracking the development of the largest ring from one time step to the next. The method was applied to datasets generated using MEDYAN, an agent-based, stochastic modelling framework for simulating complex actin-myosin interactions [20].
Here, we build on the work in [19] to develop general tools for tracking topological features of interest in data from cell biology models and experiments. Specifically, we improve methods applied to filamentous structure data, and propose techniques for tracking multiple significant features through time, with a focus on ring channel dynamics driven by actin-myosin interactions. The methods proposed here apply to simulated data as well as data from imaging experiments, which are noisier than synthetic datasets. The prior work in [19] focused on tracking a single significant ring channel through time in simulated filamentous data, and the point cloud construction involved sampling monomers along these filaments, with no encoded information about monomers that neighbored each other or belonged to the same filament. Here, we take advantage of previously unused filament information by investigating the effects of treating monomers that are neighbors or on the same filament differently from those which are not. In addition to simulation data, we also study applications to experimental work on wound-induced actomyosin contractile rings in Xenopus oocytes [21] and on dorsal closure in the Drosophila melanogaster fruit fly [22]. Notably, the data from dorsal closure contains multiple similar-sized contracting rings, which poses significant challenges to the previous greedy algorithm for tracking emergent holes in [19]. We therefore propose a new framework of matching topological features from consecutive time frames using the Wasserstein distance between persistence diagrams. While the greedy algorithm in [19] matches one topological feature at a time, the algorithm introduced here considers all features simultaneously in assigning a matching between topological summaries at consecutive time points. We find that the new method more accurately tracks the development of multiple topological features present in dorsal closure data [22], and that our analysis can distinguish between control and genetic defects in the closure process.
The manuscript is organized as follows. In Section 2.1, we discuss our data sources, which include both in silico computational models and in vivo experiments. In Section 2.2, we describe our procedure for extracting and processing the data into a time series of point clouds or binary images with an accompanying distance function. Section 2.3 discusses the use of persistent homology to extract 1-dimensional topological features from the data. In Section 2.4, we discuss the Wasserstein, Bottleneck, and greedy matching algorithms for tracking these topological features throughout time. We describe statistical methods to distinguish between significant topological features and noise in Section 2.5. Finally, in Section 3, we apply the proposed methods to simulated and experimental actin-myosin interaction datasets and show how they can provide quantitative characterization of ring channel dynamics and distinction between experimental perturbations.
2.
Materials and methods
2.1. Data
2.1.1. Simulated actin-myosin data
We consider realistic synthetic data corresponding to interactions of cytoskeleton filaments with motor proteins. In particular, we use the MEDYAN agent-based modeling framework, which is a complex stochastic reaction–diffusion model in three dimensions [20]. This model is parameterized for actin-myosin interactions using experimentally-validated length and timescales. As in [19], we use a standard implementation of MEDYAN on a domain of size 2μm×2μm×0.2μm, which corresponds to simulating actin-myosin interactions on a thin patch of the cell cortex. We include interactions of actin filaments with nonmuscle myosin IIA mini-filaments and alpha-actinin cross-linking proteins, as well as growth and depolymerization of actin filaments.
Relevant to our approach, MEDYAN includes a coarse-grained computational model of actin filaments, which tracks elongated cylindrical segments that make up the polymers [20] (we denote these by monomer units). This means that the model simulations output rich location information of the actin monomer units through time, which can be sampled to generate discrete point clouds of actin positions in three dimensions [19]. Additional details on the MEDYAN model and numerical implementation are available in [20]. The dataset used here consists of 200 time frames (collected every 10 seconds). Each time frame contains 3-dimensional position information for 100–450 actin monomer units, depending on the time frame. The standard parameterization of the model shows the formation of an actomyosin ring at the boundaries of the domain, however changes in parameters (such as corresponding to different regulation by motor proteins) can generate different numbers of clusters, rings, asters, bundles, or mesh distributions, which have also been observed in both in vitro and in vivo experiments [23].
2.1.2. Actomyosin contractile ring data
We consider datasets from experiments tracking wound-induced contractile rings in Xenopus oocytes through time. These rings consist of an array of F-actin and myosin Ⅱ motors [21,24]. This study sought to determine how different mechanisms such as contraction of the actomyosin ring and a zone of actomyosin polymerization contribute to wound closure. Generally, it would be useful to understand the patterns of movement of actin and myosin in establishing and closing actomyosin arrays. The fluorescence in these videos of actomyosin behavior corresponds to either actin filaments or to foci of myosin motors; however, the proposed analysis of the fluorescent images and of the emerging protein structures applies similarly to both settings. We focus on a wild-type dataset tracking actin behavior following induction of a wound, and on an experiment that breaks off the contractile ring using cauterization during wound healing as described in [21]. The wildtype dataset consists of a greyscale video with 32 time frames that have dimensions 384×384, while the cauterization dataset is a color video with 39 time frames that have dimensions 400×400. These videos show a thick fluorescent ring that contracts (i.e., whose diameter decreases) throughout the time of the experiment.
2.1.3. Multi-ring dorsal closure data
We also consider datasets from [25] that exhibit closure of multiple biological circular structures throughout time. Dorsal closure occurs during mid-embryogenesis in the Drosophila melanogaster fruit fly and serves as a model of cell sheet movement for wound healing and other developmental processes. The amnioserosa tissue is essential during embryonic development and consists of similarly-shaped cells separated by actomyosin-rich structures [22]. Actin and myosin also contribute to the forces driving the contraction and closure of the amnioserosa and dorsal opening. This experiment aimed to screen genes affecting dorsal closure by systematically removing genomic regions [22]. In combination with fluorescence time-lapse imaging of the dynamics, this experimental approach provided a qualitative investigation into the morphology and dynamics of dorsal closure [22]. The datasets used are greyscale videos with 112–130 time frames that each have dimensions 672×512. These videos show the fluoresced boundaries of the cells in the amnioserosa tissue, as they close in throughout the dorsal closure process. The cells have different shapes and close in at different rates in different parts of the tissue depending on the defect considered. Our method provides a complementary quantitative tool for studying closure both in wild-type conditions as well as in genetic screens associated with closure defects, such as irregular cell shapes or tissues that fall apart [22].
2.2. Image processing
Contractile ring data [21]: First, we smoothed out the images using the remove outliers function in ImageJ with radius 2 and threshold 50 followed by using the despeckle function. Next, we performed the subtract background function using a rolling ball radius of 50 pixels. Subsequently, we applied the morphological gradient function in MorphoLibJ [26], a package for ImageJ, using a 2×2×0 cube as the structuring element. Lastly, we binarized the image using an auto threshold with method intermodes and exported each frame as a PNG image.
Multi-ring dorsal closure data [25]: First, to correct the uneven illumination in the videos, we used ImageJ to perform the subtract background function using a rolling ball radius of 50 pixels (consistent with the processing in [22]); we enabled the smoothing feature while disabling the sliding paraboloid feature. Subsequently, we applied the morphological gradient function in MorphoLibJ [26], using a 2×2×0 cube as the structuring element; this operation highlighted the amnioserosa cell boundaries. Next, we binarized the image using an auto-threshold with method triangle, which provided a balance of retaining thin, sparse features of interest while not picking up too much noise. Lastly, we applied MorphoLibJ's 3D morphological erosion using a 1×1×0 cube as the structuring element; the level of erosion can be adjusted based on preference for thicker, enhanced lines or thinner lines that are closer to the unprocessed data. After creating the binarized AVI, each frame was exported as a PNG image.
2.2.1. Extracting point clouds from binary images
We used Pillow [27], an image processing package for Python, to extract the white pixels corresponding to fluorescent proteins from the binary images. The pixel location data was saved into CSV files of x- and y-coordinates. This approach has the advantage that the data format is identical to the simulation-generated MEDYAN data. We found that both the wound-induced contractile ring and multi-ring dorsal closure videos had tens of thousands of white pixels per frame. Since persistent homology computation for datasets of that size can be computationally expensive, we investigated ways to reduce the size of the point clouds.
As detailed in Section 2.3.1, we used the Python package Ripser to compute Vietoris–Rips persistence diagrams [28,29]. Since this package can compute the homology of a low- to mid-thousands point cloud on the order of seconds on standard computers, one approach is to randomly sample several thousand points from all white pixels in each experimental image. We found that sampling 2000 points at random from each time frame in the wound-induced contractile ring data maintained the appearance of the fluorescent ring.
However, a concern with the multi-ring dorsal closure data was that random sampling would not pick up thinner, sparser fluorescent lines that still outline holes. Therefore, for these datasets, we first compressed the images. Each image was divided into n×n boxes of pixels. If the box contained k white pixels, than the compressed image had a min (2k/n2,1) probability of being converted into a single white pixel in the compressed version. This approach reduced the image size by a factor of n2, and had the advantage that it visually stayed true to the original shape of the image. Taking k/n2 as the probability yielded qualitatively similar images and results. We note that this change in size also changes the interpretation of the persistence scale of the rings (1-dimensional holes) we analyze. For the multi-ring dorsal closure data, we first applied the compression with n=4 to compress the images by a rate of 16. We then randomly sampled 50% of the points from the compressed image at each time. A final option is to add noise from the uniform distribution on [0,1)2 to each point to avoid the formation of many trivial small holes; our results were qualitatively very similar whether we applied this last step or not.
2.3. Topological data analysis
We characterize the emergence, maintenance, or closing of rings in cell biology data using tools from topological data analysis. We specifically use persistent homology techniques to extract information about features such as connected components, loops, or trapped volumes from data represented as a point cloud or as a binary image. The key idea behind persistent homology is to study the data (and the resulting topological features) at multiple scales. To study the underlying topology of the data, the multiple spatial scales are represented by a nested family of simplicial complexes (also called a filtration) constructed based on the data. It is not always clear what type of filtration is most useful for a given application [30]. We discuss the filtration methods that were instructive for our cell biology applications in Sections 2.3.1, 2.3.2 and 2.3.3.
Persistent homology records how the homology of the constructed simplices changes as we vary the spatial length scale of interest, which we call ϵ, in the data. The goal is to identify features that persist across a range of the scale ϵ. The output of the persistent homology computation are pairs of points (ϵbirth,ϵdeath), where ϵbirth is the length scale at which the topological feature is first identified, and ϵdeath denotes the length scale at which the feature dies. The persistence or lifetime of the feature is then given by ϵdeath−ϵbirth. For a given filtration, we are most interested in determining the persistence of the 1-dimensional holes in our data (that is, the birth and death scales for a 1-dimensional loop). We will use a common topological summary, the persistence diagram, to record these lifetime intervals for topological features [11]. We provide a broad introduction to persistence diagrams here.
Definition. A Persistence Diagram is a finite multiset of points in R2 above and on the diagonal y=x, where the x-axis corresponds to ϵbirth and the y-axis corresponds to ϵdeath.
In this work, we will find it useful to define a distance metric between persistence diagrams. Several methods exist for finding bijections between these multisets of points [11,31]. When finding distances between two persistence diagrams, these topological summaries need not have the same numbers of topological features, since points on the diagonal are included as necessary to construct the bijection between points on the two persistence diagrams.
Since we are interested in the dynamics of cell biology processes, our data will consist of time-series datasets. We will use several methods for tracking the most significant 1-dimensional holes through time using persistence diagrams, and we outline these methods in Section 2.4.
2.3.1. Vietoris-Rips filtration
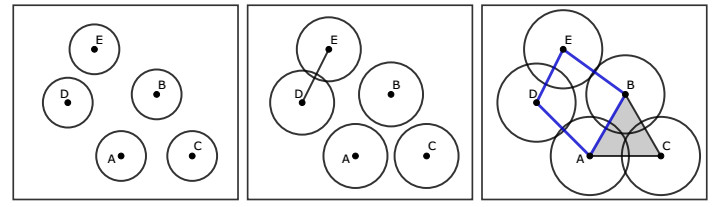
As in [19], we use the Vietoris-Rips (VR) filtration to perform persistent homology calculations, given its computational efficiency. For a given data set consisting of discrete points and for a given proximity parameter ϵ, a VR simplex S is a set of data points such that any two points in S are distance less than ϵ away from each other. The VR complex for a chosen ϵ is the set of all VR simplices with parameter ϵ. The VR filtration is then generated by varying the value of the parameter ϵ. See Figure 1 for a visualization of VR complexes at different scales for a sample point cloud.
VR complexes are an approximation to Čech complexes, which make use of information about the underlying space the data set lives in to retain important properties of the data set (see the Čech theorem [32]). Unfortunately, Čech complexes are computationally expensive to construct. A set S is a simplex in a Čech complex with parameter ϵ if there exists a point, not necessarily in the data set, that is less than distance ϵ away from any point in S. Čech complexes are more computationally expensive than VR since VR complexes are flag complexes, which makes them easier to store and use previous computations [32]. For example, if we previously determined that AB,BC, and CA are 1-simplices, we can immediately conclude that ABC is a 2-simplex in VR. However, additional computation would be needed to determine if ABC is a Čech simplex. In this work, we used the computational package Ripser in Python to compute the VR filtration [28,29].
2.3.2. Vietoris-Rips filtration with neighbor encoding
Implicit in the definition of the VR filtration is the existence of a distance metric between data points. A simple choice of distance function is the standard Euclidean norm, which provides distances between the actin monomer units, as in [19]. However, defining the distance in this way does not take advantage of the information available in simulated MEDYAN data regarding neighboring monomer units or actin units that belong to the same filament. We therefore seek alternatives for our simulated data that encode this additional filament information into the distance calculation. In practice, computation of persistent homology can be carried out given a matrix of pairwise distances between the points in the point cloud. By adjusting this distance matrix, we can establish the "proximity" of certain subsets of monomer units, for example those belonging to the same filaments. This information is not available for the experimental data described in Sections 2.1.2 and 2.1.3, however improvements in image analysis and segmentation could provide access to inferred filament structure information in the future.
We propose two methods of modifying the distance matrix: pairwise neighbor encoding and whole filament encoding. In pairwise neighbor encoding, directly adjacent monomer units in a filament have their distance set to 0. In whole filament encoding, monomer units in the same filament have all their pairwise distances set to 0. The effects of these modifications on the distance matrix are illustrated in a sample matrix in Figure 2. Implementing these encodings is straightforward, since Ripser accepts distance matrices as an argument when computing persistence diagrams.
2.3.3. Flooding filtration
Another filtration method that we investigated for experimental datasets of protein localization is the flooding filtration. This filtration is particularly useful for datasets consisting of binary images. In the case of experimental videos of actomyosin organization, each experimental time frame can be processed (see Section 2.2) to extract a binary image, where pixels with value 1 indicate the presence of fluorescent proteins at that location, while pixels with value 0 correspond to the absence of fluorescent proteins. As in [30], we then generate sequences of binary images that correspond to filtered simplicial complexes in the flooding filtration.
Specifically, the first binary image in the sequence is simply the original binary image extracted from the experimental time frame. To generate the second image, we dilate the first image. The second image in the sequence is initialized with the pixel values from the first image. We then find all pixels within the Moore neighborhood (the eight surrounding pixels) of pixels with value 1 in the first image and we assign them a value of 1 in the second image. This process is repeated for all subsequent flooding rounds, until all pixels in the image have value 1. The simplicial complexes corresponding to each image in the filtered sequence are constructed. As noted in [30], the scale parameter for the application of persistent homology corresponds to discrete flooding rounds in the flooding filtration. The implementation of the flooding filtration follows the computational framework in [30,33].
2.4. Applying persistent homology to time-series data
Given the persistent homology computation for static data using one of the filtrations described in Section 2.3, the next step in our approach is to connect the topological objects identified at each time point through time.
We seek to connect the birth-death pairs summarized in persistence diagrams throughout time in a way that is most likely to track the same significant topological holes as they evolve across consecutive time steps.
The first algorithm we used was developed in [19]. We will refer to this approach as a greedy algorithm, since it prioritizes tracking the most significant topological object through time. After it creates a path through time for the most significant feature, it moves on to the second most significant, and so on. This algorithm requires that the user specifies an application-dependent linkage tolerance parameter. This parameter represents the largest distance between pairs of points in consecutive persistence diagrams that could be connected, and thus restricts the selection of the connecting birth-death pair based on user-provided information about the application domain size. If a birth-death pair does not have any possible corresponding pair within this distance, the algorithm assumes that the current path ends at that time. This matching approach can be computationally expensive, depends on the application-specific linkage parameter, and prioritizes the most significant emergent hole in the simulation [19]. We therefore investigate additional established methods for connecting pairs of points in persistence diagrams.
Definition. The pth Wasserstein Distance and the Bottleneck Distance between two persistence diagrams, X and Y, are given by:
where the infimum is taken over all bijections ϕ between X and Y. We seek the bijection matchings between points in two persistence diagrams that minimize these distances. In practice, implementation of the Bottleneck distance can yield many possible matchings with the same distance. On the other hand, the Wasserstein distance accounts for the contribution from all points [31], so that matching persistence diagrams using the Wasserstein distance is more likely to be unique and yield robust results.
As in previous applications [31], we use q=∞, though we find that using q=2 does not significantly alter the results. On the other hand, there is not much existing investigation of appropriate values of p when using the Wasserstein Distance in applications. The advantage of using this distance metric for matching persistence diagrams is that it considers all points in the persistence diagram when seeking an optimal matching, rather than focusing on the most significant one, as in the greedy algorithm. As a result, these metrics have also been shown to be stable to small perturbations in the point cloud [11,34].
In practice, when matching features in persistence diagrams throughout time using Bottleneck and Wasserstein distance metrics, we used the Persim package in Python. In particular, we used functions persim.bottleneck and persim.wasserstein to generate Bottleneck and Wasserstein matchings of persistence diagrams [35]. Sample code for our analysis framework applied to two example datasets is provided in the Github repository [36].
2.5. Significance for topological features
An important question when characterizing topological features using persistent homology is how to distinguish between significant features and noisy ones. Often, features that have higher persistence (ϵdeath−ϵbirth) are considered significant. This concept is not appropriate for all applications and filtration methods, because sometimes short-lived features can yield very important insights [37,38]. In our examples, the point clouds we consider for our analysis correspond to physical locations of proteins in two or three spatial dimensions. The simplicial complexes we construct are based on the Euclidean distance for the Vietoris-Rips filtration or on the distance between fluorescent pixels in an image for the flooding filtration. Thus, we expect that persistent 1-dimensional holes in our data will correspond to relatively large, biologically significant holes in the application domain.
This raises the question of how to determine the threshold between significant features (sometimes denoted as signal) and noise in topological summaries based on persistent homology [39,40,41]. We follow an approach developed in [19] to determine a threshold for significance in persistence diagrams. This approach involves studying the distribution of spurious feature persistences generated from many random samples drawn from a null model, where there is no expectation of observing a significant topological feature. The first step for this approach is to determine an appropriate null model for the application. We developed the null models differently based on each type of data we analyzed. For experimental video data, we created null models based on the numbers of fluorescent points we extracted from each time frame in our image processing procedure. For instance, for the actomyosin contractile ring data in [21] and the VR filtration, we sampled roughly 2000 points from each video frame. Our null model was generated by randomly simulating a Poisson spatial process with intensity 2000. This choice of null model corresponding to complete spatial randomness follows the approaches of [42,43,44], who were interested in understanding the persistent homology of random simplicial complexes. We generated 100 such null model datasets, computed their persistent homology, and analyzed the distribution of the 1-dimensional topological feature persistences across all simulations. By comparing the departure of the survival function for persistence levels of features from data with the survival function for persistence levels of features that arise in null models, we assign a significance threshold for each application. For the flooding filtration, our approach was only slightly modified. Instead of developing a null model based on the number of fluorescent points extracted, we generated the null model frames based on the number of pixels of value 1 in the binary images extracted from each time frame. We then randomly placed pixels with value 1 on the same domain to construct null frames and repeated the significance testing process outlined above.
For actin-myosin interactions simulated using MEDYAN, the data consists of actin filament structures made up of a sequence of actin monomer segments in three dimensions. Given the filamentous structure of this data, we generated null models by randomly constructing straight filaments in the simulation domain, as previously described in detail in [19]. We then used the same significance testing approach to determine significance thresholds based on this null model.
3.
Results and discussion
3.1. Simulated actin-myosin data
We first applied our methods to synthetic data generated using the MEDYAN simulation platform [20]. In these realistic simulations of complex protein interactions with standard kinetic parameters, we start with randomly oriented short actin filaments and we qualitatively observe the formation of an actomyosin ring structure in the simulation domain [19], as in Figure 4A. The red lines in this figure connect the 3-dimensional locations of actin monomer units that outline the simulated filaments. We therefore expect to track the formation of one significant 1-dimensional hole that increases in persistence for a large portion of the simulated time. We use the VR filtration to analyze this data, along with three methods of filament encoding: the regular distance metric between monomer units (as in [19]), pairwise neighbor encoding (setting the distance between neighboring monomer units to zero), and whole filament encoding (setting the distance between all monomer units on the same filament to zero), as described in Section 2.3.2 and illustrated in Figure 2.
In computing the VR filtration, we sampled 30% of the monomer units from the MEDYAN simulation at each time step, following the approach in [19], although we note that results do not differ significantly when sampling fewer (10%) of the monomer units. A more detailed analysis of the impact of sampling on the point cloud used for each time frame is provided in [19], and Figure 4A is generated using the 30% sampling. Figure 4 shows the resulting paths, corresponding to tracking the most significant 1-dimensional hole in a standard MEDYAN simulation using all three distance metrics. We find that the pairwise neighbor and whole filament encoding lead to slightly smoother paths of the significant feature through time. While the paths tracking the most significant feature largely agree across methods, encoding for neighbor or filament identity in the monomer units makes the persistence metric more robust to noise in the data at each time step. These different methods for neighbor encoding also have the advantage that they share the same spatial scale of the persistence of the most significant feature. We can therefore use the previously-determined significance threshold for MEDYAN-simulated data (dashed line in Figure 4, as obtained in [19]) and observe that the methods predict similar timescales for the emergence of the actomyosin ring structure.
3.2. Contractile wound-induced actin-myosin ring data
We now investigate the application of these methods to experimental data tracking a wound-induced actomyosin ring structure which closes in through time in Xenopus oocytes [21]. For all fluorescence videos considered, we expect to track at most one significant topological loop (1-dimensional hole) which corresponds to the wound healing contractile ring. We seek to characterize the timing of the ring closure using both the VR and flooding filtrations for analyzing these datasets.
For the VR filtration, we sampled 2000 points at random from each video frame to ensure computational efficiency (see Section 2.2); we find that this does not substantially change the aspect of the original fluorescent images. This is not required for the flooding filtration, where we include all fluorescent pixels in each time frame. In connecting 1-dimensional features between consecutive persistence diagrams through time, we find that all matching methods outlined in Section 2.4 give the same results. This is because the wound healing experiments consist of a single significant contracting hole, similar to our simulated data in [19]. Figure 5A, C shows the most significant topological paths extracted using the Wasserstein distance metric between persistence diagrams (see Eq (2.1) with p=2) for wild-type data (in blue), as well as for a perturbation experiment that breaks off the contractile ring using cauterization during wound healing (in green) [21]. As expected, these paths illustrate the closing of the wound through time, represented by the decreasing persistence of the feature. For this data, the most significant paths can be easily identified by finding the path with the highest persistence at some time point in the video, as in our previous work [19] (in this case, the highest persistence is achieved at the initial time point).
To determine a threshold for distinguishing significant 1-dimensional holes from noise (dashed black lines in Figures 5A, C), we generate null models for each filtration method as described in Section 2.5. For the flooding filtration, we consider different numbers of fluorescent pixels in the null model, to account for the varying numbers of fluorescent pixels observed throughout time in the experimental videos. Figures 5B, D show the survival probability at each persistence level for the wild-type data (in blue), compared to the survival distribution for the null models. The persistences extracted from the experimental data clearly depart from the null model distribution. We therefore choose the significance threshold to be the right above the highest persistence value obtained in the null models, i.e., a distance of 12 units between points for the Vietoris-Rips filtration, and 7 flooding steps for the flooding filtration.
Figures 5A, C also show that both filtration methods capture the different closing speeds of the ring formed around the wound in each experiment. In addition, the path corresponding to the cauterized wound is noisier and dips under the significance threshold for each method earlier than in the wild-type experiment, thus illustrating the breaking of the ring structure sooner in this experiment. In [30], for data consisting of images of interconnected blood vessels, the flooding filtration descriptor vectors were not found to be biologically interpretable and did not robustly distinguish between parameters in model simulations of angiogenesis. Here, we find that both the VR and the flooding filtration accurately capture the dynamics of the 1-dimensional hole (wound healing actin-myosin ring) of interest.
3.3. Multi-ring dorsal closure data
We also study the application of the proposed topological methods for time-series data to videos from experiments of dorsal closure during embryo formation in the Drosophila fruit fly [22]. During this developmental process, epithelial cells called amnioserosa cells (AS cells) initially have isotropic circular shapes, but later shorten and ingress from the tissue surface before naturally dying. We are therefore interested in extracting the time paths tracking the closure of multiple significant topological loops in these videos, corresponding to the ingression of multiple AS cells during dorsal closure.
Given the similar insights derived from using the Vietoris-Rips filtration and the flooding filtration in Section 3.2, we focus on results derived using the VR filtration only in this section. As detailed in Section 2.2, we carry out standard image processing of the time-lapse fluorescence microscopy videos. Our sampling of the discrete point clouds generates data consisting of 1500–2500 points extracted from each time frame; see Figure 6A, B for snapshots of three processed time frames from a control dorsal closure experiment in [22]. Since we would like to characterize the closure of multiple AS cells in this experiment, we use the Wasserstein distance matching for connecting birth-death pairs in consecutive persistence diagrams. We use p=2 in Eq (2.1), but find that the results are robust to a range of values of p. This matching approach has the advantage that it does not require specifying a linkage parameter and it does not prioritize finding the single most significant emergent hole as in the greedy algorithm (see Appendix for further comparison between matching methods).
Assigning a level of significance to the topological paths generated for this application is more challenging, since relevant paths for analysis should correspond to AS cells that start as 1-dimensional loops and persist for some length of time of the dorsal closure experiment. We therefore consider both a significance threshold for the maximum persistence of the paths and a minimum time over which the paths persist (which we refer to as minimal path length) in determining significant paths for the dorsal closure application. To understand how the closure paths arise throughout time, we first remove paths that only exist for one time point and those whose maximum persistence does not exceed 1 unit in a control experiment of dorsal closure from [22]; we note that, due to the image processing procedure and given the spatial scale of the imaging experiment, one unit in persistence scale is equivalent to 1.2μm for this application. After this filtering, the remaining 571 paths are characterized in the bar chart in Figure 6C. Many of the paths (orange bars) start from the initial time and last until late into the experiment, as we would expect for the closure of AS cells, which start as isotropic rounded cells in the developmental process studied here. Our method also identifies noisier paths that start later in the experiment (blue and green bars in Figure 6C).
We also seek a threshold for distinguishing significant 1-dimensional holes from noise based on the persistence values of the extracted topological features, as described in Section 2.5. Given the variation in the number of points extracted at each video time frame, we generate null models with different numbers of points drawn randomly in a domain consistent with the experiment. Unlike the case of the wound-induced contractile ring data, where we were interested in tracking one large 1-dimensional hole, here the features of interest are small compared to the spatial size of the domain. It is thus not surprising that the survival probability functions of the persistences levels extracted from the wild-type experimental data are not as clearly distinguished from the null model ones, see Figure 6D. However, the null models corresponding to randomly drawing 2000 or 3000 points in the domain show overall smaller persistence sizes for 1-dimensional loops, and inform our choice for filtering paths based on a maximal persistence level.
Given that many of the remaining paths in Figure 6C are characterized by low maximal persistence and short path lengths, we remove these noisy paths by further filtering by a minimum persistence level of 5 (as inspired by Figure 6D and corresponding to roughly 6μm) and a minimum path length corresponding to a third of the experimental video time. The remaining 39 significant paths start at the initial time of the experiment and are shown in Figure 6E. These paths offer a quantitative representation of the closure of multiple AS cells through time and also illustrate some dampened oscillations in the cells, which are due to the tissue contraction and have been previously reported [22]. It is important to note that we do not claim that each individual path perfectly tracks a single topological feature. This is because different AS cells are very likely to be represented by birth-death pairs of 1-dimensional holes occupying the same parts of the persistence diagram space. Therefore, misidentifications or jumps in the paths as these pairs cross each other in consecutive persistence diagrams are likely. Nonetheless, the method quantifies the overall closure of multiple AS cells, so that averaged measures describing these paths have the potential to distinguish between experimental settings.
To investigate this, we considered time-lapse imaging data from [22] corresponding to both a control (wild-type) experimental setting (Figure 6A, B) and to mutation deficiencies that lead to impacted amnioserosa phenotypes in fruit fly dorsal closure. We focus on some of the most common such defects, which include irregular AS cell shapes and AS tissues falling apart. Figure 7 shows the mean and standard deviation cloud of the persistences at each time point of the significant paths for the control experiment in Figure 6E (blue). The averaged paths shown in green correspond to a video of dorsal closure for the irregular AS cell shape phenotype. In this setting, AS cells are less rounded and ingress and die faster, which is consistent with the lower overall persistence levels and shorter path lengths that our method identifies. Given this observed difference in the experiment, our analysis is based on 38 significant paths identified after filtering by imposing a smaller minimum persistence scale of 2.5 (corresponding to roughly 3μm) and a minimum path length representing a fourth of the experimental video time. Finally, we also include the comparison to the averaged paths shown in orange, which correspond to a video of dorsal closure for the phenotype where the AS cells fall apart. As the cell sheet falls apart, larger holes emerge in the AS tissue, which is consistent with the larger mean path persistences output by our method at later times, as illustrated in Figure 7. The analysis of this experiment is based on 40 significant paths filtered using the same minimum persistence scale and minimum path length used for the control experiment in Figure 6E.
4.
Conclusions
Ring channel dynamics and regulation play key roles in various biological and developmental processes [45]. The interactions of actin filaments cross-linked with myosin motor proteins have been studied using experiments based on fluorescence microscopy as well as using agent-based modeling simulations, yielding complex datasets that track the temporal and spatial dynamics of the interacting proteins. Here, we propose methods based on topological data analysis (in particular, persistent homology) that quantitatively characterize one or multiple ring channel openings or closures in both synthetic data tracking full actin filaments and in noisier experimental data measuring the fluorescence intensity of the proteins in space and time.
For filamentous structure data, the approach we propose goes beyond the prior work in [19] by providing a way to account for actin monomer identity, such as neighbor and filament information, which is available from the rich output of the MEDYAN agent-based model [20]. In applications where identifying a representative loop of the topological feature is relevant, this approach would allow for easier identification of the filaments that gave rise to the structure of interest. While the data considered here comes from complex and realistic simulations of actin filaments with multiple chemical species, there are also in vitro and in vivo model systems where actin can be tagged directly. For instance, recent advances in techniques such as super-resolution microscopy have allowed visualization and tracking of individual actin and myosin filaments in 3 dimensions in epithelial cells of the Drosophila fruit fly [46]. Combining these new experiments with novel filament tracing methods as in [47,48,49] will allow to apply the topology-based filamentous structure analysis proposed here in the same way as done for synthetic datasets.
In applications to experimental data, we propose methods that apply to discrete point clouds extracted from the fluorescence intensity data, as well as methods that apply to binary images extracted from the videos. We show that different filtration methods can be used for computing the persistent homology of data extracted at each time point. Notably, the flooding filtration for binary images gave similar insights as the more commonly-used Vietoris-Rips filtration for point clouds, since the dilation steps in the flooding filtration provide insights into the density of fluorescent proteins throughout space and the holes that form in the image. This is in contrast with insights about data consisting of blood vessels from models of angiogenesis, where the flooding filtration was found to be less informative [30]. Future work could investigate additional filtration methods, such as functional persistence based on nested families of sub- or super-level sets for the pixel values of fluorescence imaging data. We also proposed a new methodology for connecting the identified topological holes through time using the Wasserstein distance metric. This method considers all features simultaneously in assigning a matching between the persistence diagrams from two consecutive time points, rather than prioritizing the most significant ring channel feature as in [19]. In addition, the method does not require specifying a linkage parameter that needs to be customized for each application and is robust to the choice of the Wasserstein distance parameters. Despite being more robust, this approach still lacks stability, as in the case of the vines and vineyards proposed in [15], since it cannot guarantee precise connections of features whose trajectories through time intersect in persistence diagram space.
To give useful insights on the timing of emergence or closure of ring channels, topological methods must be combined with statistical approaches for distinguishing significant hole features from noisy ones. Here we build on the approach in [19] by constructing appropriate null models for each application and generating distributions of persistences that are not expected to generate significant features. The significance thresholds that we identify for separating signal from noise in persistence diagrams give similar timing insights for the biological processes across filtration methods. However, how to estimate appropriate significance thresholds when the topological features of interest are small compared to the domain size remains an open question.
Notably, the methods proposed here can distinguish between and quantitatively characterize different experimental perturbations in the applications considered. For example, the time-dependent persistence paths capture distinct closing rates or times for different wound closure experimental settings. Characterizing patterns of movement of actin in these settings is useful since different mechanisms may contribute to the ring contraction. Both actin and myosin motor fluorescence can be tracked in these experiments, so that the data analysis method proposed here could distinguish between the activity of the two and give insights into their assembly to establish and close actomyosin arrays. In addition, since myosin Ⅱ motors appear in the region bordering the wound in the form of punctae [21], the topology-based method could also give insights into the size and arrangement of these clusters. Similarly, the time-dependent persistence paths also capture different closure behaviors for various genetic screens in dorsal closure experiments. The deficiencies tested in [22] had diverse effects in closure, leading to questions about how to link the tested genes to pathways and structures that coordinate closure. In particular, closure is a robust process, so that understanding mutants that disrupt but still complete closure is of interest. By identifying differences in the timing or closure rate of the process, the methods proposed here can contribute to the understanding of genes that are redundant for closure.
The techniques can be applied with standard image processing analysis of fluorescence imaging videos and thus do not require costly segmentation methods. However, taking advantage of improved segmentation pipelines would likely improve the robustness of the time paths, particularly for instances where multiple ring structures are tracked, as in dorsal closure experiments. In addition, combining these TDA methods with improvements in image analysis [49] would also allow to segment additional biological structures such as the lateral epidermis cells in dorsal closure, and therefore to analyze other genetic defects affecting those phenotypes. Finally, given the availability of more complex 3-dimensional protein interaction data, the TDA methods proposed here naturally extend to investigating higher-dimensional features such as trapped volumes in these datasets.
Acknowledgments
We thank Dr. Mikael Vejdemo-Johansson, Dr. Christopher Tralie, and Dr. Daniel Kiehart for helpful discussions. This project originated as part of the summer 2021 DOmath program sponsored by the Duke University Mathematics Department.
Conflict of interest
All authors declare no conflicts of interest in this paper.
Appendix.
Variants of the greedy matching method
In the application to MEDYAN filamentous data in [19], as well as in our application to the Bement wound closure data explored here, we have found that the greedy matching algorithm proposed in [19] and the Bottleneck matching method work well as long as there is only one significant ring channel to track. However, issues arise with these methods when they are applied to data sets with multiple significant rings, such as the dorsal closure data in [25]. Compared to paths created by the Wasserstein matching method (see Figure 6E), paths from the greedy matching algorithm are notably more erratic: many of the paths feature large jumps in persistence over very short time frames, some paths have persistence close to zero for long periods of time, some paths track an increase in persistence over time despite the data depicting rings closing in, and there are many short-lived paths, among other issues. Figure A1 A illustrates paths generated using greedy matching for the wild-type dorsal closure dataset in Figure 6A, B. The Bottleneck distance is the l∞ analogue of the pth Wasserstein distance, and as a result only considers the effect of the largest distance that any point has moved in consecutive persistence diagrams [31]. We find that it therefore suffers from some of the same limitations as the greedy matching algorithm, such as shorter path lengths, larger jumps in persistence, and smaller overall persistence lengths tracked.
In this section, we note that minor variations in the implementation of the greedy matching algorithm can yield qualitatively different results that improve on the original method. Prior knowledge of data features may help inform the type of variation that would provide an appropriate data analysis approach. We start by reviewing the greedy matching algorithm used here and first proposed in [19]. This method requires choosing a linkage parameter dl.
● Start with the birth-death pairs A={a1,a2,...,an} and B={b1,b2,...,bm} for time frames 0 and 1, respectively.
● Sort the birth-death pairs in A and B by persistence from highest to lowest.
● If n<m, we perform forward matching, i.e.
– Take the pair a1 with the highest persistence in A.
– Find the pair bj that is closest to a1. The L2 or L∞ distance can be used here.
– If ||a1−bj||<dl, then a1 is matched with bj. Else, a1 is matched with the diagonal.
– Repeat the forward matching process for pairs in A and B, after removing pairs that have already been matched.
● If n≥m, we perform backward matching, where we take the pair with the highest persistence in B and match it to the closest point in A.
Besides prioritizing higher persistence birth-death pairs, there are two other aspects in which the greedy method differs from the Wasserstein matching. The first is that the greedy algorithm requires a choice of forward or backward matching at each time point, and the second is that the greedy method strongly prefers to match birth-death pairs to other pairs rather than to the diagonal. To show the effects of these two differences, we consider the following variants of the greedy matching algorithm for the wild-type dorsal closure dataset:
● diagonal-link greedy matching: for forward matching, if ak is closer to the diagonal than to bj, then match ak to the diagonal, and similar for backward matching.
● forward greedy matching: always perform forward matching.
● backward greedy matching: always perform backward matching.
The results of applying these algorithmic variants are illustrated in Figure A1. We find that the diagonal-link matching reduced the number of paths with persistence near zero, the forward matching selected paths with a downward trajectory, and the backwards matching selected paths with an upwards trajectory. While many of the paths still suffer from the same issues as in the original greedy matching, the mean and standard deviation cloud of the persistences appears somewhat closer to the robust prediction in Figure 7 for control data. In particular, the mean closure of the cells using the forward matching is comparable to the one generated by the Wasserstein matching in Figure 7.
However, despite the variations explored in this section, we still recommend the Wasserstein matching method for connecting paths of topological features. Although the greedy variants can perform well, they require tuning the linkage parameter as well as a choice of the appropriate variation. This is in contrast to the Wasserstein matching method, which does not require any a priori assumptions about the data. We have found that the Wasserstein matching method was robust in a variety of applications, without requiring adjustments for new data sets.









 DownLoad:
DownLoad: