Indonesia, which is strongly supportive of renewable energy development, meets its obligation to extensively employ renewable energy through the mandatory mixing of palm oil-derived biodiesel with diesel, a fossil fuel. The success of the program is inseparable from the government's provision of incentives which involve paying the difference in cost between biodiesel and diesel through export taxes collected from producers of palm oil and its derivatives. However, the increase in the government's mandatory target is not in line with the higher revenue obtained with the result that under current policy conditions the government will not be able to provide incentives for the B30 plan during the next few years. This research presents a dynamic simulation modelling of Indonesia's biodiesel program and analyzes the policy applied in support of that program. A system dynamics model is proposed to enable decision-makers to understand the relationship between the different variables inherent in the system and the impact of different variables on the continuity of the biodiesel program in Indonesia. The system dynamics model consists of three sub-models: the palm oil production sub-model, the biodiesel demand and production sub-model and the biodiesel fund management sub-model. Fund management of biodiesel is specifically discussed, starting with the source of funds, through fund management, to the impact of fund availability on the biodiesel mandatory program's continuity. The simulation shows that increasing palm oil production capacity is insufficient in order to ensure the success of the government program. Simulations indicate that the biodiesel program will operate optimally if two prerequisites are satisfied; first, that the levy policy adopted is not dependent upon crude palm oil (CPO) prices and, second, that the provision of incentives is limited solely to those required by the prevailing Public Service Obligation (PSO).
1.
Introduction
Global warming and climate change have numerous impacts on all aspects of human life, while posing a threat to the very survival of the human race. Global warming and air pollution have been identified as the primary drivers of climate change, with CO2 emissions being generally considered by writers on the subject as the primary cause of these problems [1,2]. The major source of GHG emissions is the burning of fossil fuels to generate the energy necessary to support human activities as indicated by the United States Environmental Protection Agency [3]. In 2018, Indonesia’s domestic consumption of fossil fuels as primary energy sources amounted to 96.55% [4] with the largest proportion, up to 41.8% of overall energy consumption, accounted for by the transportation sector [5]. One form of renewable energy that can potentially be developed is biodiesel, a liquid fuel produced primarily from vegetable oils or animal fats, used to power diesel engines after being mixed with diesel-a fossil fuel [6].
Indonesia is one of the countries actively promoting the use of renewable energy. One policy of concern at national level is the development of biodiesel biofuel constituting a mixture of fossil-based diesel fuel with biofuel derived from palm oil, governmental support takes the form of issuing policies, such as regulation No.79 of 2014 [7], which stipulate that national consumption of renewable energy should increase to 23% of total energy use by 2025 with 25% of such renewable energy being derived from biofuels. Since 2009, the Indonesian government (GoI) has been actively involved in setting specific targets for the combining of fossil fuels with biofuels [8].
In Indonesia, oil and gas sector-related imports represent the predominant contributor to the national trade deficit [9]. One potential strategy to reduce these imports is that of using biodiesel as a composite element of a fuel-oil mixture. In 2009, the GoI introduced the specific practice of mixing biodiesel with fossil fuel-derived diesel. The use of this mixture has increased annually but only reached the desired target in 2015 due to the GoI’s repeatedly raising it [8]. The use of biodiesel as a biofuel was almost 40 times higher in 2018, having risen from 95 million liters to 3,650 million liters [8]. The most recent nationally applied policy required that biodiesel (B20) constitute 20% of diesel fuel mixture by 2019, rising to 30% by 2020 [10].
The raw material sourced for biodiesel fuel in Indonesia is palm oil, a major national agricultural sector product. Indeed, until 2019, the country was the largest global producer of this commodity [11]. Several types of vegetable oil, namely; rapeseed, palm, soybean, sunflower, peanut and jatropha, among others, are produced in various parts of the world. Palm oil is the vegetable oil with the highest yield of approximately three to four tons per hectare per year [12], while that of another competing oil is typically less than one tonne/ha/year, which makes palm oil-derived biodiesel more competitive than other forms [13].
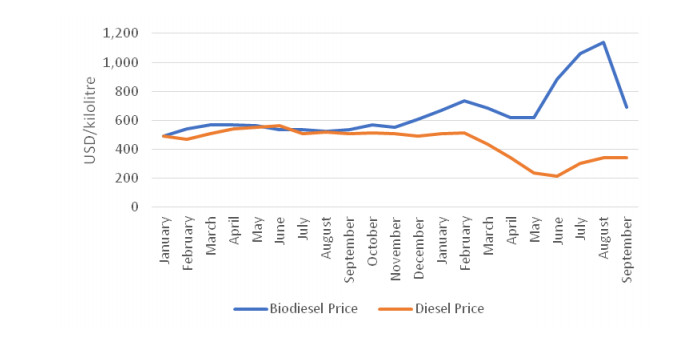
The use of palm oil-sourced biodiesel is of significant economic benefit to palm oil farmers in Indonesia. Moreover, the use of renewable energy also reduces carbon emissions and is, therefore, environmentally friendly. However, despite the benefits of biofuel use, its production is uncompetitive in terms of cost, therefore requiring government intervention. Policy instruments such as mixed mandates, tax credits, exemptions, subsidies, and import tariffs are used to stimulate the international production and consumption of biofuels [14]. Biodiesel use within Indonesia is increasing encouragingly year-on-year [8] owing to official subsidies for its production which ensures no difference to the public in the price of pure diesel or B20 and B30. This form of financial support is provided because the cost of producing biodiesel remains higher than that of pure diesel (see Figure 1). The necessary funds for this subsidy are obtained from levies collected from industries that export palm oil products. However, rising domestic consumption of palm oil as a raw material of biodiesel will increase the need for government subsidies. On the other hand, higher palm oil consumption to meet domestic biodiesel demand has also resulted in a decline in palm oil exports, thereby reducing the amount of revenue collected. The increase in the government’s mandatory target is not in line with the higher revenue obtained with the result that, under the current policy, the government will not be able to provide incentives for the B30 plan over the next few years. Therefore, a policy that supports the continuity of biodiesel consumption in Indonesia is required.
Several studies involving biofuel policy simulations have been conducted. For example, Espinoza et al. (2017) conducted a dynamic simulation of the biodiesel market in Colombia based on publication of that country's policy regarding the mandate to mix diesel with biodiesel [13]. An instrument analysis was subsequently conducted which indicated that the government-implemented structured biodiesel pricing policy rendered the cost of biodiesel to the consumer uncompetitive. Moncada et al. (2017) analyzed the potential development of biofuel production capacity in Germany by conducting policy interventions in the field of bioenergy (biodiesel tax-related intervention) and agriculture (agricultural market liberalization) [14]. Barisa et al. (2015) modeled the system dynamics of the biodiesel market and analyzed various policy support instruments designed to increase the proportion of biofuels within the total fuel demand of the transportation sector in Latvia [15]. Musango et al. (2012) carried out system dynamics modeling to evaluate the impact of developing biodiesel production in the Eastern Cape, South Africa [16]. Research relating to the biofuel policy simulation within the Indonesian context has also been conducted. Indrawan et al. (2017) investigates the use of palm biodiesel in the Indonesian power sector and recommend development policies that support massive biodiesel production [17]. Arrumaisho and Sunitiyoso (2019) undertook an analysis of the biodiesel industry in order to identify both the factors influencing its development in Indonesia and the manner in which these exercise their influence [18]. Wijaya et al. (2017) simulated a system dynamics model as a means of highlighting the policy formulations necessary to satisfy the mandatory biodiesel requirements in Indonesia in order to achieve energy security [19].
Researches that explicitly discuss funding scenarios so that biofuels can compete with fossil fuels have been carried out. Kuo et al. (2019) proposed a biofuel model in Taiwan that takes government subsidy policies using system dynamics into account with limited biofuel resources [20]. Yi et al. (2019) analyze the type of subsidy which more cost-effective for the ethanol industry between investment subsidy, production subsidy, and entry subsidy [21]. Chanthawong et al. (2018) conducted an analysis of various subsidy and taxation scenarios on biofuel policies in Thailand to see their impact on economic, social, and energy indicators [21].
These studies represent a valuable contribution to a policy analysis of the biofuel sector. However, when discussing policies related to subsidies that ensure the competitiveness of bioenergy fuel prices with those of fossil fuels, none of these studies identify either the source of these funds or how they are managed. This paper aims to propose policies capable of achieving national biodiesel energy targets, while specifically discussing biodiesel fund management from the source of funds, through fund management, to the impact of the availability of funds on the continuity of mandatory biodiesel programs. This study has provided an insight into macro-level policy analysis to address this gap with a special focus on implementing the government’s mandate. Therefore, this research will conduct a policy simulation and fund management exercise to satisfy the government's mandatory requirements which have been assessed through system dynamics simulations generated by Vensim software.
In this study, a continuity assessment of mandatory biodiesel funding management in Indonesia will be carried out through reference to a system dynamics model which is defined, designed, and assessed as a tool enabling decision-makers to understand the behavior of the mandatory biodiesel funding management system in Indonesia. A macro view of a specific biodiesel utilization model in Indonesia results from this study by considering government subsidy policies, market demand, and palm oil production capacity. The remaining body of this study is organized in the following manner: section 2 contains a description of biodiesel-related policies in Indonesia, section 3 describes the research methods employed and outlines the calculations produced, section 4 presents the simulations and policy scenario, while section 5 features results and discussions. Finally, the conclusions drawn and opportunities for future studies are presented and discussed in section 6.
2.
Biodiesel development policies in Indonesia
In recent years, various policy initiatives have been launched to promote the development and consumption of renewable energy in Indonesia. For example, as summarized by Silalahi et al. (2019), the use of biofuels is governed by Presidential Decree No.1 of 2006 and supported by other regulations [9]. The target to which the government is actively working is that of renewable energy accounting for 23% of total energy consumption by 2025, with 26% of such energy being derived from biofuels. The biofuels developed in Indonesia include biodiesel and bioethanol which represent mixtures with diesel and gasoline respectively. However, bioethanol use remains limited in scope and has yet to prove successful in terms of mass consumption. In contrast, biodiesel has been used as a diesel fuel mixture. In September 2018, through the issuing of Presidential Decree No.66, the government ultimately instructed all sectors (both PSO and non-PSO) to increase their production of biodiesel mix by 20%, while two years later the target was further increased to 30%.
In 2015, in order to support the continuity of the biodiesel program, the government established the Oil Palm Plantation Fund Management Agency (in Indonesian, Badan Pengelola Dana Perkebunan Kelapa Sawit or BPDPKS), under the auspices of the Ministry of Finance, to oversee palm oil funding [22]. In general, the function of BPDPKS is to collect funds from commercial enterprises which export palm oil plantation commodities and their derivatives which subsequently invested in promoting the uptake of biodiesel biofuels. BPDPKS funding is divided into three forms of financing, namely; palm oil sector research and development (including human resource development funds; research and development funds; promotion funds for oil palm and its derivatives; plantation facilities and infrastructure funds), palm oil rejuvenation and the provision of biodiesel incentives [23]. In supporting the uptake of biodiesel as a fuel, the funds collected by BPDPKS are primarily used to finance incentives. The availability of incentives promoting the use of biodiesel is vital because its price remains relatively higher than that of fossil-derived diesel (see Figure 1). For biodiesel development, funds are not derived from the state revenue and expenditure budget, but from the tax levied on each palm oil commodity exported. Therefore, the financing term for the provision of biodiesel is that of ‘incentive’ rather than ‘subsidy’. Before the formation of BPDPKS, the GoI invariably provided incentives from the state budget to support biodiesel production. In 2015, the abandoning of its policy of subsidizing biodiesel placed small-scale biodiesel companies under pressure with the result that continued production proved so challenging as to culminate in the termination of operations [24]. After the formation of BPDPKS, this institution succeeded in increasing the public consumption of biodiesel [24].
From 2015 onwards, BPDPKS was levied in accordance with Ministry of Finance laws No. 133/PMK.05/2015 [27] and No. 81/PMK.05/2018 [28] at a rate of 50 cents per dollar for CPO and CPKO products, while derivatives were subject to levies of USD 30, USD 20 and USD 0 depending on their type. However, since 2019, Ministry of Finance law No. 136/PMK.05/2019 [29] has required that the tariff be fully applied if the CPO price is above USD 619/ton. If the price is between USD 570 and USD 619, the levy rate falls by half, while if it is below USD 570, no levy is applied.
Oil palm producing plantations in Indonesia fall within one of three categories, namely; private sector-managed, government-managed, and smallholder-managed. In terms of productivity, smallholder-managed plantations record the lowest level [30]. Two BPDPKS programs supportive of biodiesel policy continuity in Indonesia provide incentives to meet the different prices of biodiesel and diesel and for oil palm rejuvenation programs. In terms of the latter, BPDPKS has initiated a support program through the provision of funding totaling USD 1,923 (based on an assumed exchange rate of USD 1 = IDR 13,000) for smallholder palm oil farmers [31]. Given that initial oil palm production dates from 25 years ago, the majority of oil palms in Indonesia need to be replaced since they were planted in the 1980s. However, small-scale farmers generally prefer to avoid replanting due to the loss of income they will incur during the subsequent rejuvenation period required by their plantations. For this reason, BPDPKS exists as an agency that will provide both financial assistance and advice to palm oil farmers.
3.
Method
System dynamics (SD) represent one method of modeling complex systems that promotes understanding of both dynamic complexity and the sources of policy resistance, in addition to the design of more effective policies [32]. In this paper, SD follows the methodology applied by Bautista et al. (2019) [33]. The SD method contains five steps: problem formulation, dynamic hypothesis formulation, description of the model boundary, description of the model structure, and definition of the functions that will describe the selected indicators, testing of the model and, finally, and results analysis.
The first step, problem formulation, involves identifying the purpose and focus of the problem model. A clear purpose is the single most important factor in a study of successful modelling. SD modelers seek to characterize the problem dynamically that, as a pattern of behaviour, unfolds over time and shows how the problem arose and its potential future evolution [33]. The second step consists of dynamic hypothesis formulation whose objective is to define the variables representing each of the dimensions and relations. In this step, conceptualization through a causal loop diagram is developed [32]. In the third step, the description of the model boundary provided identifies the endogenous and exogenous indicators that facilitate an explanation of the problem [33]. The fourth step, description of the model structure, incorporates each indicator in a casual loop diagram using functions (equations or graphic functions). Finally, the fifth step, testing and analysis, validates the model and the system. During the testing phase, comparison with reference modes can be employed to establish whether the model adequately reproduces the problem behaviour for the intended purpose [33].
3.1. Problem formulation
Formulation of the problem investigated by this research comprised a literature review and exploratory study involving the analysis of news and official reports related to the development of the biodiesel program in Indonesia. This problem formulation was undertaken to analyze biodiesel funding, production, and consumption within the country.
The basic reason for promoting biodiesel is its positive impact on the economic, social and environmental sectors. For the past few decades, GoI has been importing diesel because domestic demand far exceeds that of national production. The consumption of biodiesel, one possible means of reducing diesel imports, is widespread within the economic sector primarily because the raw material, palm oil, is one of the mainstay plantation commodities within the country. The use of palm oil as fuel will increase the level of its domestic consumption, while reducing the amount of foreign exchange expended due to the ensuing lower diesel imports, thereby enhancing its economic value. Several studies have also posited that, from a social perspective, the economic activities of oil palm plantations have improved the lives of Indonesians, especially those of oil palm farmers as summarized in [8]. In 2019, the B20 program employed a workforce of 828,488 oil palm farmers [34]. Moreover, from an environmental standpoint, the government has stated that the use of B20 biodiesel in 2019 had reduced GHG emissions of CO2 by 9.91 million tons [34].
An increase in the government’s mandatory target causes domestic CPO consumption to rise dramatically which, conversely, produces a reduction in the quantity available for export. Declining exports, in turn, compromise local levies and the funds available to BPDPKS to subsidize the price difference between diesel and biodiesel with the result that the GoI’s mandatory target cannot be fully achieved. The increase in this target is not in line with the higher revenue obtained. Consequently, under current policy conditions, the government will not be able to provide incentives for the B30 plan during the next few years. To support the GoI's mandatory program, several scenarios will be explored, and the number of unmet biodiesel requests evaluated. Therefore, this research will include both a policy simulation and fund management exercise to satisfy the government’s mandatory requirements.
3.2. Dynamic hypothesis formulation
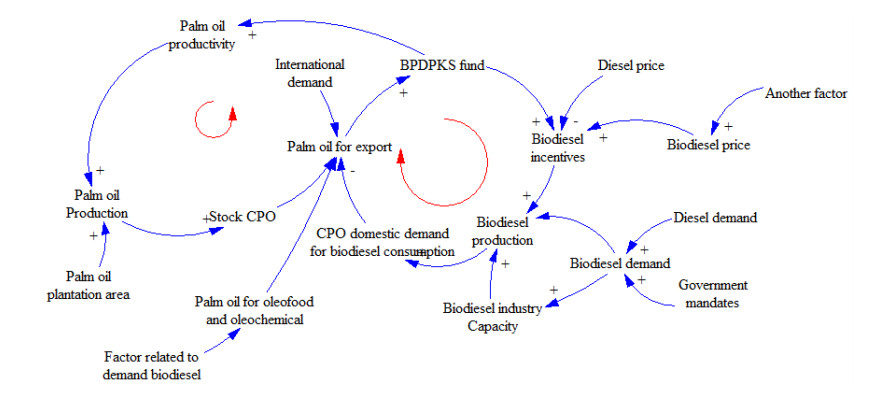
The formulation of dynamic hypotheses involves the causal loop shown in Figure 2. In this diagram, descriptions of dynamic behavior and the interactions between indicators are identified through reference to three sources; the relevant literature, the historical data related to selected indicators, and information regarding the conditions prevailing within Indonesia. The validation of causal loop diagram involved the participation of four experts from BPDPKS and MEMR (the Ministry of Energy and Mineral Resources Republic of Indonesia) who confirmed that the variables and interactions presented reflected Indonesia's actual conditions.
The research hypothesis relating to this dynamic model is based on a framework suitable for assessing the continuity of mandatory governmental programs and the appropriateness of system dynamics as the methodology to be applied. The research framework developed will provide information regarding the continuity of the government's mandatory target. Descriptions of dynamic behavior and interactions between indicators are displayed in an integrated cause and effect diagram contained in Figure 2.
This model contains a reinforcing loop and a balancing loop. Positive feedback loops are also known as reinforcing loops because they will strengthen or proliferate and are usually marked with an R notation. On the other hand, negative feedback loops are typically known as balancing loops because they have a stabilizing effect and are indicated by a B notation.
With regard to the first loop, loop R, if CPO production expands then the amount of exportable CPO will increase because the demand for Indonesian CPO always exceeds production capacity. Consequently, the international market will readily absorb available Indonesian biodiesel. The volume of biodiesel exported will increase the amount of BPDPKS funding which, in turn, provides more financing for the rejuvenation of plantations, thereby increasing palm oil productivity. It should be noted that the funds intended to increase productivity are only channeled to smallholders. The second loop, loop B, performs a balancing function. In this loop, the amount of CPO exported will increase BPDPKS funds, thereby intensifying incentives for biodiesel producers and augmenting the amount of biodiesel produced.
3.3. Description of the model boundary
In the research contained in this paper, palm oil constitutes the raw material for biodiesel. The boundary model is described using 32 exogenous and 51 endogenous indicators as shown in Tables A1 and A2. Exogenous indicators, determined by external conditions and displayed in the form of constants or graphical functions, are those that invariably act as a cause but never as an effect. In contrast, endogenous indicators are ones influenced by one or more other variables and are calculated using equations. Exogenous indicators are determined by external conditions and displayed in the form of constants or graphical functions.
3.4. Description of the model structure and equations
The dynamic model is divided into three sub-models: CPO production, fund management, and biodiesel supply and demand. Each sub-model and equation of the selected indicators are explained in the next section, while the formal structure of stocks and flows are shown in Figures 3–5. In Indonesia, biodiesel production began in 2009, while BPDPKS dates from 2015. Therefore, in this study, the year constituting the initial model time (zero time) is 2015.
3.4.1. Palm oil production sub-model
The oil palm production sub-model employed in Indonesia is shown in Figure 3. The calculation of palm oil production (PoP) is based on the area of cultivation multiplied by the productivity of each form of ownership; smallholder, public, and private (Eq 1) [30]. The annual productivity of public/state owner (StoP) and private (ProP) palm oil producers totaled 3.948 and 3.902 tons per hectare, respectively (2016 data) [35], far higher than that of smallholders (ShP) which stood at 3.147 tons per hectare annually. A review of palm oil productivity data relating to Indonesia confirms that both the land area assigned to plantations and its productivity tend to increase year-on-year [35].
The cause of the low productivity of smallholder oil palm farmers is their limited access to sources of finance and subsidies, making it difficult for them to utilize high quality planting material and replant their unproductive plantations [31]. Low smallholder productivity means that Indonesian palm oil production cannot achieve optimum results, primarily because of the vast area cultivated, approximately 34.7% of the total area under cultivation. Aware of these conditions, the GoI has supported the rejuvenation program by providing funding of USD 1,923 (IDR 25 million) per hectare [31]. However, in Indonesia, the agricultural sector did not immediately take advantage because, according to certain estimates, the rejuvenation of one hectare of land requires a capital investment of USD 4,615 (IDR 60 million) [31]. This represents a figure which small-scale farmers, understandably, find difficult to afford. The level of post-rejuvenation oil palm production in Indonesia cannot be calculated directly, given that the rejuvenation program only commenced in 2017 [36]. However, a pilot project conducted in one Indonesian province indicated that rejuvenation can as much as double productivity [37]. Therefore, within this model, it is assumed that the provision of USD 4,615 of funding per hectare during the four years after replanting will double initial smallholder productivity (ShPi) (Eq 2). Several important equations of this sub-model are shown below:
where: t: time, ProL: privately-owned land, ShL: smallholder land, StoL: state owned land, totrej: total rejuvenated area, unrej: unrejuvenated area, ShGr: current smallholder growth rate.
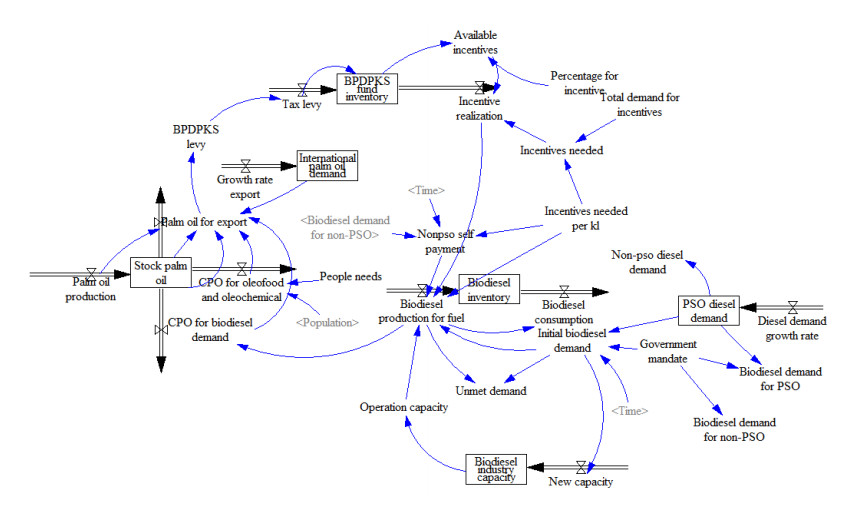
3.4.2. Biodiesel supply and demand sub-model
Figure 4 contains a sub-model for biodiesel supply and demand. The supply of palm oil in Indonesia comprises three downstream products, namely; palm oil earmarked for domestic consumption in the form of oleo food and oleochemicals, palm oil required to satisfy local biodiesel needs, and palm oil destined for export. Domestic demand is estimated on the basis of the level of biodiesel demand in Indonesia under the government's mandate (GovMan) [38].
There are two types of commercial diesel demand within the country, namely PSO demand (DmPso) and non-PSO demand (DmNPso). PSO fuel is a government-subsidized fuel oil intended for certain consumers, including; micro businesses, public transportation and other consumers as governed by the Republic of Indonesia Presidential Regulation No.191 of 2014 [39]. The demand for non-PSO was, on average, 1.2 times that for PSO (Eq 7) [40,41]. In this study, these two types of diesel demand will be differentiated due to the government mandate focusing on them. The research reported here will consider the total capacity of the biodiesel industry (BiodCap). In this study, taking actual data into account, it is assumed that the annual capacity growth rate of the biodiesel industrial (IndGr) is 0.02 taking into account population growth [42] and increasing targets for biodiesel use in Indonesia.
Biodiesel production depend on biodiesel industry capacity, biodiesel demand and government incentives (Eq 3). The government mandate depends on current policy (Eq 4). Biodiesel demand depends on the government mandate and demand from PSOs and non-PSOs (Eq 5). Biodiesel industry capacity depends on current biodiesel capacity and industry growth rates (Eq 6). The important equations in this sub-model comprise the following:
where: BiodProd: biodiesel production for fuel, OprCap: operation capacity, InBiodDm: initial biodiesel demand, IndNeCap: new industrial capacity, IncReal: incentive realization, NpsoP: non-pso self-payment, IncNeed: incentive need.
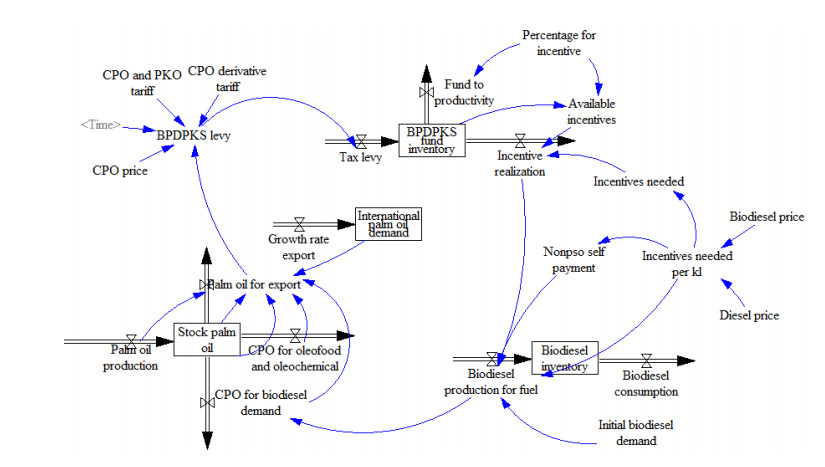
3.4.3. Biodiesel fund management sub model
The fund management model for biodiesel in Indonesia is shown in Figure 5. GoI levies for palm oil products and its derivatives (BLev) are applied to the volume of palm oil and its derivatives exported (PoE) in compliance with current regulations. This levy is directly linked to world CPO prices (CpoPr) in order to avoid exporters of the commodity and its derivatives being disadvantaged. The more pre-export CPO processing is undertaken locally, the lower the levies will be. The percentage of total CPO and PKO exported varies each year, but invariably accounts for less than 33% of the total palm oil exported [35]. Therefore, in this model, it is assumed that the amount exported in the form of CPO/PKO is 1/3 of the total export volume, while the remainder is in the form of its derivatives (Eq 8). The fees collected are subsequently dispersed for two main purposes, namely; for oil palm plantation rejuvenation and available biodiesel incentives which will directly affect the amount of biodiesel produced for diesel fuel blends. In other words, if no incentives are available, no biodiesel will be produced for diesel fuel mixtures. Biodiesel prices depend on the CPO price and conversion of ton cpo to ton kl (Eq 9), while the price of biodiesel is updated every month by MEMR as the monthly market index price of biofuels [25].
Financing for the supply of biodiesel is an incentive rather than a subsidy. Biodiesel incentives represent a form of government alignment for the community. The provision of incentives relating to the distribution of biodiesel constitutes a positive effort by the GoI to encourage domestic adoption of palm oil [43]. The important equations in this sub-model are outlined below:
where: DeTar: CPO/PKO derivatives levy tariff, CpoTar: CPO/PKO levy tariff, BiodPrc: biodiesel price, Cpoconv: conversion from ton of CPO to kiloliter of biodiesel.
3.5. Testing and analysis
In order to validate the constructed system dynamics model three criteria were applied: structural correspondence; behavioural correspondence; and phenomenon correspondence [13,33]. In order to undertake structural correspondence, a comprehensive causal diagram was validated through consultation consisting of personal interviews with four biodiesel experts in Indonesia who confirmed that the variables and relationship between variables reflected the reality of the situation. The correspondence between behaviour and phenomena was measured by the Mean Absolute Percentage Error (MAPE) formula which calculates the accuracy of the model predictions [33]. A MAPE of up to 30% has been defined as valid [44] while, according to [45], forecasting can be regarded as accurate if the MAPE is below 50. Simulations were carried out for the period 2015 to 2050. However, to calculate MAPE, the values generated by the model were compared against only the collected historical value data [13] dating from 2015–2019. The MAPE produced for the most important indicators is displayed in Table 1. Of the MAPE values obtained, all were below 30%. According to these validation criteria, cause and effect relationships and equations met the validation conditions, and the SD model adequately represented evaluation of the biodiesel programme in Indonesia.
4.
Simulation and policy scenario
In this section, the scenarios to be simulated is explained. Scenarios are built on existing policies and potential policy recommendations.
4.1. Mandatory biodiesel policy
There are two types of policies related to the GoI-imposed mandatory biodiesel target up to 2050 that will be simulated. The first is a mandatory policy incorporating a target of 30% during the ten-year period 2020–2030, followed by one of 50% between 2030 and 2050, while the second is a mandatory policy with a target of up to 30% during the two decades after 2030. Indonesia's success in implementing B20 up to 2019 has rendered its government extremely optimistic about the success of the biodiesel program. The first mandatory policy was adopted because the government already had plans to implement B50 in the future [46]. This is a realistic policy because the use of B50 biodiesel blends has been tested on direct injection diesel engines running at a constant speed, and the findings of [47] confirm that B50 achieves a similar performance to diesel.
The mandatory B30 policy has passed its road test which confirmed that all aspects of the diesel-powered vehicle have satisfied the relevant requirements [48]. However, the successful implementation of B30 has yet to be proved because the policy was only introduced in 2020. Moreover, interview results indicated that the possibility of developing biodiesel as a diesel mixture would depend on more than 30% of vehicles undergoing a complex adaptation process. Therefore, the following mandatory policy constitutes a scenario focusing on the implementation of B30 up to 2050.
4.2. Export levy policy
When it was formed in 2015, BPDPKS levied tax regardless of CPO prices. However, in 2018, the regulation was revised due to a decrease in CPO [49]. Therefore, this tax policy will take account of both types of plan.
Under the Type 1 tax policy, if the CPO price is above USD 619/ton, a tax of USD 50 per ton will be applied to CPO and CPKO products, while derivatives are subject to taxes of USD 30, USD 20 and USD 0 according to their respective types. If the price is between USD 570 and USD 619, only half the levy tariff will apply, and if the CPO price is below USD 570, then the levy will be 0.
The Type 2 tax policy is a tax collection policy regardless of CPO prices, namely; for palm oil products and derivatives at a rate of USD 50 per dollar for CPO and CPKO products and for derivatives subject to tax of USD 30, USD 20 and USD 0 depending on their respective types.
4.3. Incentives policy
The financing of the biodiesel supply represents an incentive, rather than a subsidy. Biodiesel incentives constitute a form of government alignment with the community. The GoI does not explicitly allocate funds within the state budget to finance such incentives. Rather, the money required for this purpose is collected from palm oil commodity-exporting companies and managed by the Palm Oil Plantation Fund Management Agency [43]. Incentives are provided to biodiesel produce companies. Any company supplying biodiesel that satisfies the prevailing administrative and quality requirements can become a biodiesel distributor. The degree of incentive provided varies according to the quantity of biodiesel distributed. The volume of biodiesel distributed by each biofuel company depends on its production capacity. The higher the production capacity, the greater the amount of biodiesel that can be distributed.
Biodiesel production costs in Indonesia are lower compared to those of other countries because the fuel is subsidized. This policy has underpinned the country’s rapid industrial growth [50]. Therefore, just as with the sales policy that categorizes diesel type into PSO and non-PSO, two types of incentives are classified, namely; those available to all sectors and others exclusively reserved for the PSO sector. The policies in 4.1–4.3 are combined to produce eight simulated scenarios in Table 2. Incentives are provided only for PSO diesel demand, which means that non-PSO consumers must pay the price of biodiesel consumed according to the market price. In contrast, PSO consumers only pay according to the diesel price.
5.
Results and discussions
In this step, a system dynamics model was implemented by means of Vensim software and adopted to simulate the management of biodiesel funds and consumption within the Indonesian context. The time limit of the system constitutes the simulation between 2015 and 2050. The time unit was that of years, while the Euler integration method was applied. In order to understand the consumption of biodiesel, the model was simulated using eight scenarios as described in Chapter 4. The results of the simulation presented through the important variables are described as follows.
5.1. Palm oil rejuvenation analysis
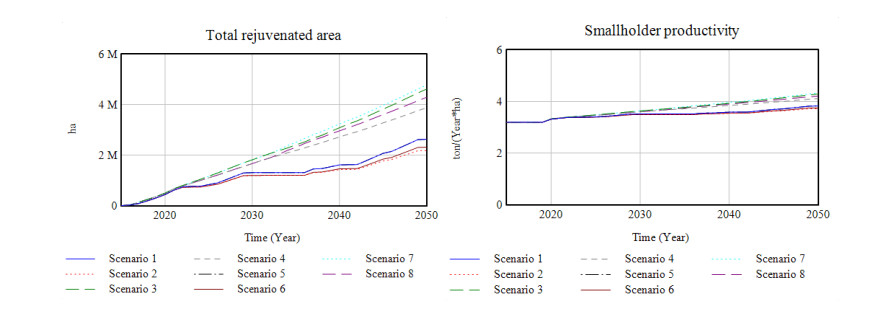
Given the necessary support, smallholder productivity will increase. With consistent rejuvenation assistance, an estimate of smallholder plantation productivity can be produced, as shown in Table 3 and Figure 6. It can be concluded, therefore, that under the current policy (Scenario 1) smallholder productivity could increase to approximately 3.82 tons/ha per year by 2050. However, this level of productivity still falls far short of the Indonesia Palm Oil Association's target of around 6.9 ton/ha per year [51]. If Scenario 8 is applied, it is estimated that smallholder farmer productivity will reach 4.21 tons per hectare per year in 2050. The productivity of smallholders in Scenario 7 is greater than that in Scenario 8 because the levies obtained are higher due to the lower consumption of domestic palm oil which results in the greater availability of rejuvenation funds.
5.2. Unmet demand analysis
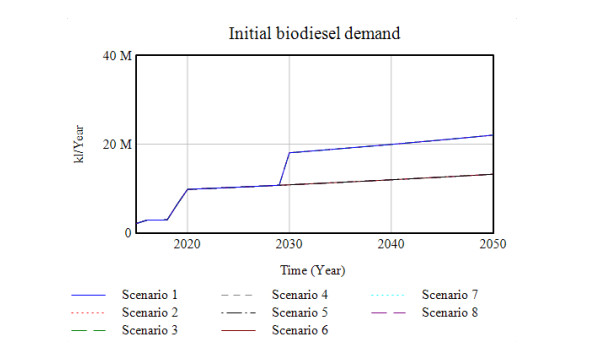
As indicated by the contents of Table 2, eight types of scenario were simulated. Initial biodiesel demand in Indonesia is based on the data shown in Figure 7. Biodiesel demand for Scenarios 1–4 follows a line that culminates in 18 million KL, while demand for Scenario 5–8 follows one that reaches 10 million KL. Maximum palm oil production is achieved in Scenario 8 because of the significant BPDPKS funds collected, thereby increasing the productivity of smallholders who support palm oil production.
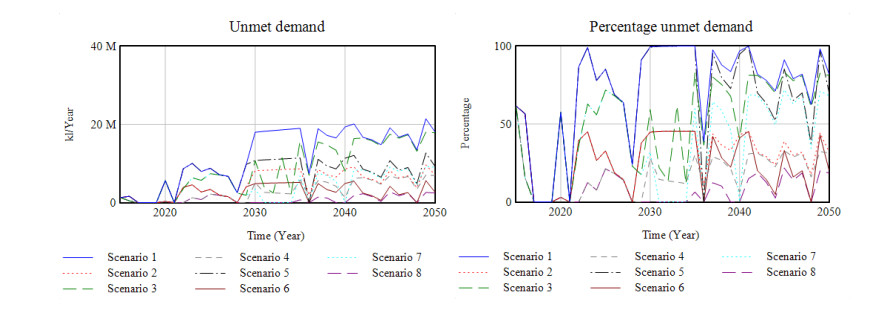
The first issue subjected to analysis was the percentage of unsatisfiable demand occurring between 2020 and 2050. Scenario 1 is based on the current policy up to 2020 within which the percentage of unfulfilled demand can be seen to reach an average of 80.17%, as shown in Figure 8 and Table 4. Scenarios 1 and 5 produce similar unanticipated results for fulfilled demand of approximately 70–80%. Therefore, innovative policies must be implemented to ensure the success of the government's mandatory program.
The simulation results indicate that demand can be maximally satisfied only in Scenarios 4 and 8. This means that the government will be able to successfully implement the biodiesel mandatory B30 policies by providing incentives for both PSO and non-PSO demand as long as BPDPKS collection is not dependent upon the CPO price. In Scenarios 4 and 8 there is a significant difference in unmet demand due not to insufficient funding of incentives, but because of the limited industrial capacity to satisfy domestic biodiesel requirements. This unmet demand means that expansion of the biodiesel industry by 0.02% per year is inadequate to meet the demand for B50 biodiesel, although such capacity will enable the achieving of the B30 target.
If the incentive payment policy is compulsorily applied to all sectors (PSO and non-PSO), then Scenarios 1, 3, 5, and 7 are applied. The minimum unmet demand will be achieved in Scenario 7 (43.32%), followed by Scenario 3 (57.54%). If the policy relating to levies takes the price of CPO into account, then Scenarios 1, 2, 5, and 6 will ensue. In this section, the minimum unmet demand of 27.13% occurs in Scenario 6.
A policy of continuing to impose levies irrespective of the CPO price will encumber the industry, while that of providing only demand-focused incentives for the PSO variety will increase the burden on non-PSO consumers. As seen in Scenarios 4 and 8, if both the B30 and B50 policies are implemented, given an adequate industrial capacity, the demand for all biodiesel will almost reach 100%. However, this will represent a burden on both non-PSO consumers and the biodiesel industry. If a decision is made to impose levies on only one sector, then either Scenarios 2 and 6 that represent a burden for non-PSO consumers or Scenarios 3 and 7 constituting a burden for the CPO industry will ensue. From the contents of Table 4, it is clear that a policy that encumbers non-PSO consumers through the removal of incentives directed at this group will result in a higher level of demand when compared to one hampering the biodiesel industry, irrespective of the CPO price.
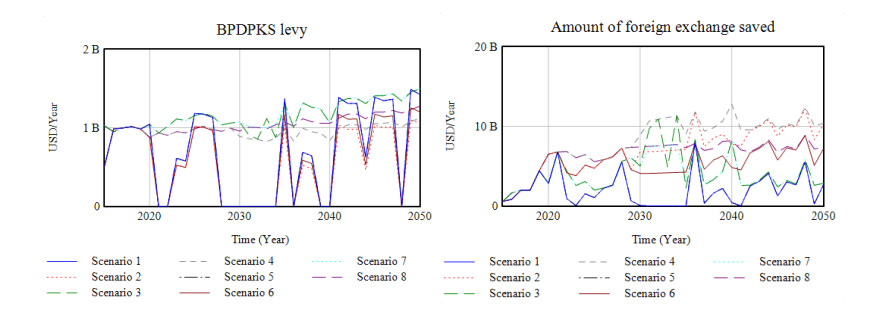
In the various simulated scenarios, the most significant factor influencing the continuity of this program is the number of CPO price-dependant levies received by BPDPKS. On the other hand, CPO is a product with rates that are difficult to predict because they are dependent upon weather conditions and the price of other vegetable oils such as rapeseed and soybean. For this reason, a government initiative is required within which an injection of funds is provided at times that BPDPKS proves unable to collect palm oil. Incentives could be funded by calculating the amount of foreign exchange saved by the state, which far exceeds the financial resources necessary to manage BPDPKS finances (see Figure 9). This figure indicates that the amount of foreign exchange saved is much greater than the BPDPKS levy. This means that even if the palm oil industry’s collection policy depends on the CPO price to ensure that the palm oil industry is not disadvantaged, the government can use funds resulting from the foreign exchange saved that far exceed those required by BPDPKS. With the injection of funds, the productivity of palm oil smallholders will increase, thereby satisfying the demand for biodiesel.
6.
Conclusions
In this study, the system dynamics model for Indonesia’s biodiesel fund management is presented. This model is in line with government regulations that implement B30 as from 2020 [10] and the government's plan to implement biodiesel utilization up to B50 [46]. It has been established that under current policy conditions the government will be unable to provide incentives for the B30 plan during the next few years.
This study aimed to identify the optimum scenarios for sustainable biodiesel consumption in Indonesia. Fund management of biodiesel incentives ensuring that biodiesel prices are competitive with fossil fuel is specifically discussed, starting with the source of funds, through fund management, to the impact of fund availability on the biodiesel mandatory program's continuity. This specific discussion of fund management differentiates it from other studies and represents the novelty of this research.
The system dynamic model developed in this paper provides insight on the funding system. Biodiesel utilization in Indonesia is characterized as dynamics and complex that requires system dynamics as a policy tool. The model built has considered specific indicators that affect biodiesel's development as fuel in Indonesia. Also, the model already contains the current policy schemes applied in Indonesia and considers the government's future policy plans.
The simulation results indicate that several policy scenarios are required to meet the GoI’s target with regard to biodiesel consumption. First, in order to render B30 and B50 programs implemented up to and including 2050 successful, the GoI must pursue a policy of levies regardless of CPO prices and pay incentives only for PSO consumption. Second, if a decision is made to impose levies on only one sector, then a policy weighing more heavily on non-PSO consumers through the removal of incentives directed at this group will result in higher biodiesel consumption when compared to one burdening the biodiesel industry, irrespective of the CPO price. Third, the capacity of biodiesel refineries must be expanded, either through the construction of new plants or an expansion in existing capacity by 2030.
The results of this study indicate several possible future areas for investigation. Firstly, the dynamic model presented could be modified to analyze different policies prior to their implementation in order to assess their probable respective impacts. Secondly, future research could be undertaken to complement other relevant variables, for example, the distribution problem affecting the biodiesel industry in Indonesia or the capacity of the country’s biodiesel industry. Thirdly, for an assessment of the sustainability of the biodiesel program, research into the impact of biodiesel policies on social and environmental systems in Indonesia is required.
Acknowledgments
This study was partly financed by research grant from the Ministry of Research, Technology and Higher Education of the Republic of Indonesia.
Conflict of interest
The authors declare no conflict of interest.
Appendix










 DownLoad:
DownLoad: