Since 2007 Reunion Island, a French overseas region located in the Indian Ocean, aims to achieve energy self-sufficiency by 2030. The French government has made this insular zone an experimental territory for renewable energy resources (RES) by implementing great powers photovoltaic (PV) plants. However, the performance of PV conversion is highly climate dependent, and there have been many research contributions to show that the two main factors that influence PV cell efficiency are solar radiation and cell temperature. Moreover, considering the high variability of environmental factors on PV plants, the high penetration of PV in electric systems may threaten the stability and reliability of the electrical power grid. In this study, a linear relation analysis of time series data collected over one year is performed in order to investigate the dependent variable of PV power output from explanatory variables such as solar irradiance, cell temperature, wind speed and humidity. The originality of this paper is to apply cointegration methods, usual tools of econometrics, to PV systems. More precisely, this research work lies in the use a robust statistical method to model a vector cointegrating relationship linking the PV power output and the four environmental parameters mentioned above, to make accurate forecasts in a tropical area. The Johansen vector error correction model (VECM) cointegration approach is used to determine the most appropriate PV power output forecasting when the desired model is concerned with N explanatory variables and for N > 2. This long run equilibrium relationship has been tested over many years of data and the outcome is more than reliable when comparing the model to measured data.
Nomenclature: ACF: AutoCorrelation Function; ADF: Augmented Dickey Fuller; AIC: Akaike Information Criteria; AR: Auto-Regressive; ARIMA: Auto-Regressive Integrated Moving Average; ARMA: Auto-Regressive Moving Average; ARX: Auto-Regressive eXogenous; CARDS: Coupled Auto-Regressive and Dynamical System; DF: Dickey Fuller; DW: Durbin Watson; ECM: Error Correction Model; EG: Engle Granger; G: Solar irradiance; HQ: Hannan-Quinn; Humi: Relative Humidity; JB: Jarque Bera; LB: Ljung Box; LM: Lagrange Multiplier; MAE: Mean Absolute Error; MBE: Mean Bias Error; P: Power output; PACF: Partial AutoCorrelation Function; RMSE: Root Mean Square Error; SARIMA: Seasonal Auto-Regressive Integrated Moving Average; SIC: Schwartz Information Criteria; Swind: Speed of wind; T: Cell temperature; VAR: Vector Auto Regression; VARX: Vector Auto-Regressive eXogenous; VECM: Vector Error Correction Mechanism
1.
Introduction
To avoid an energy crisis created by the exhaustion of the fossil fuels, many countries have introduced renewable energy policies. For example, Reunion Island, a French overseas territory in the Indian Ocean, aims to achieve electrical [1] autonomy by 2030. Among renewable energy sources (RES), solar energy is considered as a strong potential and availability on Reunion Island. That is why, the French government has made this insular zone an experimental territory for RES by implementing great powers photovoltaic (PV) plants more than 194 MW in 2019. However, due to the high variability of environmental factors [2,3] on PV cell efficiency, the high penetration of PV in electric systems may threaten the stability and reliability of the electrical power grid for smart buildings or smart city applications. Indeed, one of Reunion island project is to build up active micro-grids or virtual PV power plants to feed in power to all devices and appliances of a smart building. Therefore, PV systems operating under real field conditions are of great importance for obtaining accurate prediction of their efficiency and power output. In this context, an accurate forecasting [4,5,6] of the PV power generation can improve system reliability and power quality, and reduce the impact of uncertainties on the grid. However, the accuracy of PV power output forecasts from inclined building mounted modules for optimal energy extraction [7] are not just based on climatic conditions [8,9,10], because its fluctuation is due to several factors such as solar irradiance, temperature, wind speed, humidity and dust [11]. Over the last decade, a large number of solar PV power generation forecasting techniques [12,13,14] have been modeled. The state-of-the-art techniques to produce power forecasts for PV has been described and classified [5] in three main approaches : physical, statistical and hybrid methods. Sobri et al. [6] also reviewed PV power output forecasting techniques but classified them into three different major methods: statistical-time series methods, physical methods and ensemble methods. Among the statistical-time series approach, classical regression methods, which have been studied, take advantage of the correlation nature of meteorological parameters using prediction models as input [15,16,17]. However, regression between non-stationary series [18,19] may conclude on the existence of two variables even though there is no real relationship between them. The goal of this study is to parameterize, and to our knowledge for the first time in an insular zone, the more realistic relationship between PV plant power output and relevant meteorological factors such as incoming irradiation, cell temperature, wind speed and humidity using a powerful statistical technique.
The proposed method falls into the category of multiple linear regression methods. There have been some recent studies concerning PV power generation estimate thanks to a relationship between a dependent variable (PV power) and independent variables, called predictors. Antonanzas et al. [5] made a classification:
● Linear stationary models. Auto-Regressive methods (AR) [20] models the PV power output as a linear combination of the lagged values of its predictors, simple Moving Average (MA) [21], the Auto-Regressive Moving Average (ARMA) [22] models combining the two last methods, AR eXogenous (ARX) [20] methods adds exogenous data to an AR model, ARMAX [21] an ARMA model with exogenous data and also the Vector AR (VAR) and Vector ARX (VARX) [23].
● Linear non-stationary models. Auto-Regressive Integrated Moving Average (ARIMA) [24] techniques model a stochastic process combining AR component to a MA component, the Seasonal ARIMA (SARIMA) [25] which introduce a seasonal component and the coupled auto-regressive and dynamical system (CARDS) [26] model.
Researches classified the forecasting of PV power production in different categories based on the needs of the PV production and transport actors. In general, PV power forecasting depends on the meteorological and solar irradiance data, the type of method used to forecast and the forecasting horizon. Zamo et al., Kostylev et al. and Das et al. [27,28,29] proposed a classification for these forecasting time horizon:
● Very short-term forecast horizon: a few second to one hour, used for electricity dispatch in real time and energy smoothing.
● Short-term forecast: for one hour, several hours up to a day ahead, to guarantee system commitment and scheduling
● Medium-term forecast: multiple days to months ahead, to ensure power system planning
● Long-term forecast: months to one to several years, to find and assess potentially resourceful sites.
This statistical method aims at creating a medium-term forecast model of the hourly production of PV electricity for the next days, in order to answer needs of electricity grid managers, energy traders and producers. Parametrized and regressive model such as the one proposed is best built for short and medium-term forecast horizon [30].
In this paper, a linear relation analysis of time series data collected over a year is performed, and the dependent variable of PV power output P is investigated on explanatory variables such as solar irradiation, cell temperature, wind speed and humidity. These four variables are denoted respectively as G, T, swind and humi. For that, the stationarity of each previous cited time series is tested. Then, the Augmented Dickey Fuller (ADF) test is used to determine the method of regression estimation between the PV and all influencing variables. A former study [31] using a robust statistical technique has shown a relationship between P and T in a non-tropical zone. The statistical method used was the Engle & Granger (EG) cointegration technique. The disadvantage of the EG method is that it does not distinguish several cointegration relationships. For instance, the study of N variables simultaneously, with N > 2, may lead to up to N-1 cointegration relations, and the method of EG allows to obtain only one cointegration equation. To overcome this difficulty, an original statistical study of the Johansen technique [32,33] is proposed. The Johansen cointegration approach is suggested to determine the most appropriate PV power output-forecasting model. Even though the Johansen approach for cointegration has been a popular tool in applied economics [34], it has never been applied to renewable energy technologies and even less to PV systems for forecasting.
For optimal energy extraction, the PV design for this study is a building mounted on the grid connected system where the modules that make up the PV plant are at a tilted angle of 21°, same as Reunion Island latitude. The polycrystalline PV cells of 180W each are equipped with solar irradiance, cell temperature and wind sensors. For this study, the sample of one year daily means data is retrieved among 7 years of measurements from the COREX building located at La Possession in the west coast of the island and all tests are performed under 64-bit Eviews software 9 environment of HIS Global Incorporation. This paper is part of a European project1, one of the main focuses of which is PV power output-forecasting in tropical island environments.
1 French acronym for Supervision, Dynamic Management and Optimization of Urban Micro grids for Island Electricity Self-sufficiency.
The rest of the paper is organized as follows. Section 2 explains the effect of environmental factors on PV systems. Section 3 describes time series and their properties, and statistical techniques used in this study to link PV power output and environmental parameters (explanatory variables). Section 4 deals with the principle of cointegration and vector error correcting model for the determination of the short and long run relationship between the explanatory variables. In section 5, the Johansen cointegration approach is detailed whereas Section 6 shows the application of this approach to experimental data. Section 7 presents obtained experimental results. Finally, a discussion is proposed in Section 8 and appropriate conclusions and future works are given in Section 9.
2.
Effect of environmental factors on PV systems
2.1. Solar radiation effect
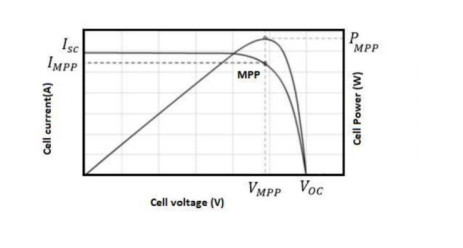
Light can be considered to consist of a stream of tiny particles of energy called photons which when fall on a PV cell convert photonic energy into electrical energy. The PV characteristic current—voltage (I—V) curve and power-voltage (P-V) is illustrated in Figure 1. The most relevant parameters used to evaluate the performance of solar cells are the short-circuit current (ISC) and the open-circuit voltage (VOC). The conversion efficiency (η) is determined from these parameters and is calculated as the ratio between the generated power at the maximum power point (PMPP) and the incident solar irradiance (W/m2). As indicated in Figure 1, the greater is the power of the solar radiation, the greater is PMPP. Therefore, solar irradiance is an environmental factor that is considered in this study.
2.2. Temperature effect
Solar irradiance is the biggest environmental factor for solar cells that convert light into electricity. PV modules generate electrical power proportionally of the solar radiation while considering the PV module performance is sharply sensitive to cell temperature. Solar irradiance and cell temperature are two factors, which affect the performance of a PV cell. The PV cell temperature affects negatively its voltage and positively its current.
Whereas manufacturers only provide PV characteristics under laboratory Standard Testing Conditions (STC), in real conditions, the PV cell temperature T also has great influence [35,36] on the power output P. In tropical zone, cell temperatures can reach or even exceed 70 ℃ compared to 25 ℃ STC conditions. T is required to calculate the power loss, usually between -0.35 and -0.5%/℃. This means that every 10 ℃ in excess results in a decrease in P between 3.5 and 5%. As P changes with temperature fluctuations, this parameter must be taken into account to optimize the annual yield and to analyze electrical grid temporal stability of their supply.
Although T is one of the most important factors that affect the performance of the PV modules, additional physical conditions such as humidity, wind and dust have drastic impact on P.
2.3. Humidity effect
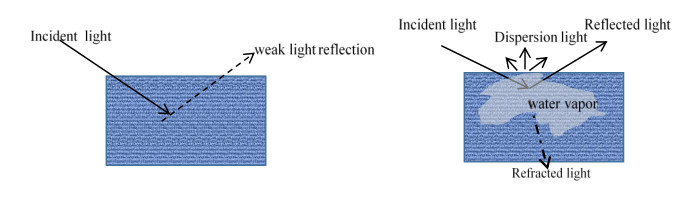
Humidity is the amount of steam present in air. Figure 2a shows the low percentage of reflected light due to the glazing cover when most of the incident photonic energy is converted into electrical energy.
Small steam particles in the atmosphere cause light diffraction or scattering, and thus altering direct PV irradiation. Figure 2b shows light refraction due to steam that greatly reduces light intensity to the solar cells leading to reducing power output. Additionally, reflection and dispersion of the striking light to these water molecules that act as a prism is subjected to more losses of the total energy which is not subjected to conversion by the PV module.
Tropical regions such as Reunion Island in the Indian Ocean are frequently humid areas. This environmental factor creates obstacles and much sharper drop in irradiance levels resulting in a PV efficiency decrease mainly on open circuit voltage and short circuit current.
2.4. Wind effect
As the wind cools well by ventilation the solar modules, this factor reduces the temperature impact. Higher is the wind speed, better is the conversion efficiency. Consequently, the impact of the wind effect is opposite to solar irradiation and temperature effects. As indicated by manufacturers, PV modules that are cooled by 1 ℃ should increase the efficiency up to 0.05% with increasing percentage over time. It has also been shown that adaptive cooling mechanism [37] for PV modules can reduce thermal losses below 5% compared to uncool PV systems. Wind speed also has other effects on PV modules such as an increase in wind speed improves short circuit current and open circuit voltage. Such experiment has been conducted to show the effect of the wind speed on the output of modules. The wind effect on photonic particles is similar to that on propagating electromagnetic radio waves [38]. Collisions between particles of the air and photonic particles result in a change of direction of the latter in an opposite direction. Thereby, air temperature, humidity and wind are three environmental factors considered in this study.
2.5. Dust effect
The effect of dust particles deposits on PV modules has the effect of decreasing the electrical energy output by reducing the amount of absorbed solar radiation. The quantity of dust on PV modules has been studied [39] where a decrease in electrical energy output has been observed varying between 3% and 11% depending on this quantity. Although Piton de la Fournaise Volcano in Reunion Island is still under activity generating the dust, this factor is not considered in this study yet.
3.
Time series & properties
3.1. Time series
A time series is a set of observations on the values that a variable takes at different times. Time series data are collected at regular time intervals such as for instance daily, weekly or annually [40]. A time series is stationary if its mean and variance are constant over time, and the value of the covariance between two time periods depends only on the distance or gap or lag between the two time periods and independently of the actual time [41]. If a time series is stationary, that is it does not require any differencing. In this case, it is said to be integrated of order zero and denoted I(0). If a time series is not stationary in the sense just defined, it is called a non-stationary time series. Usually, if a non-stationary time series has to be differenced d times to make it stationary, that time series is integrated of order d noted as I(d). For example, if a time series has to be differenced twice, that is taking the first difference of the first derivatives to make it stationary, it is called second order integrated time series denoted as I(2). Although the interest is in stationary time series, non-stationary time series are often encountered. Let's explain this process through a random walk model and finally define conditions for stationarity. Considering yt as a variable following a random walk where yt is regressed at time t on its value lagged one period, as given in Eq 1:
where εt is a white noise error term with the mean of zero and the variance σ2. From Eq 1, by proceeding by recurrence Eq 2 can be obtained as follows:
where εi is given as NID (0, σ2) and NID represents normally and independently distributed with a mean value of zero and a constant variance. This process is non-stationary as shown in Eq 3 where Var stands for variance.
From Eq 3 is deduced that the variance of yt process is a time function. Considering that t increases, its variance increases indefinitely, and thus violating a condition of stationarity.
A time Series is stationary if it has the following conditions:
- constant mean for all time t,
- Var (yt) is a finite constant independent of t,
- Cov (yt, yt-1) is a finite function which is independent of t.
It is also interested to express Eq 1 in a differential form as given in Eq 4:
If yt is non-stationary, its first derivatives is stationary and correspond to the first derivatives of a random walk-time series which are stationary.
3.2. Properties of time series
Regression analysis of time series is used to discover or to verify the predicted relationships and properties of integrated series have to be verified. Regression of a non-stationary time series on another non-stationary time series can produce a spurious regression [42]. To avoid the spurious regression problem from such regression, we must transform non-stationary time series to make them stationary. Several statistical tests have to be executed to determine if a time series is stationary. Unit root test has become one of the most widely used methods for testing the stationarity of a time series. To explain the idea behind the unit root test, a general form of Eq 5 is used as follows:
which can be transformed as Eq 6
where Δ is the first difference operator. The unit root test is a hypothesis test with the following hypothesis: if β = 1, there is a unit root and the time series is non-stationary which refers to the null hypothesis H0. The alternative hypothesis H1 is that β < 1 and the time series is stationary.
3.2.1. Residual diagnostics
The serial correlation in residual from estimated equation test is based on the hypothesis testing. There many residual tests, first order, second order or squared residuals. The following sections describe only some tests and their outcome interpretations that are used in this study to determine the most perfect model between PV output and climate parameters in a tropical zone. The goal of this section is to give the guideline about serial correlation. Only if a model is free from serial correlation or heteroscedasticity, then it can be used for forecasting.
3.2.2. Augmented dicker fuller
Dickey Fuller (DF) test is the simplest approach to test for a unit root. In case of autocorrelation problem of εt, DF developed a test called Augmented Dickey Fuller (ADF) test [43]. As an example, the outcome of the ADF test applied to the variable P, using the Eviews software, is represented in Table 1. If the null hypothesis is true, which expresses itself P has a unit root, such series is a non-stationary one. The ADF test is based on t-statistic approach and probability approach as represented in Table 1, respectively. DF tabulated critical values are chosen significance level at 1%, 5% and 10%, respectively. To check the unit root test, the calculated t-statistic with its corresponding probability, which is indicated as statistic ADF test in Table 1, has to be compared to the critical values, and mainly at 5% level. According to the guideline, if the test statistic value is greater than the 5% level critical value as well as for probability value, the null hypothesis cannot be rejected. Therefore, power series are non-stationary series. In Table 1, the ADF t-statistic value which is -1.000357 greater than -1.941740 value at 5% level as well as for the probability value at 28.44%.
The same test was repeated for the first difference of P. It can be deduced from the corresponding outcome given in Table 2 where D(P) or I(1) series is stationary at first difference.
3.2.3. Correlogram
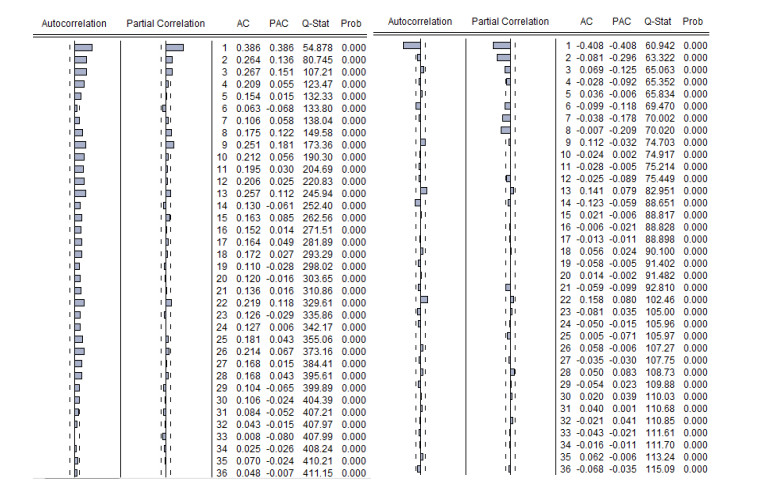
Another visual diagnosis tool identified as the first step for the stationary test can be done by computing the autocorrelation function (ACF), and the partial autocorrelation function (PACF). This graphical tool is known as correlogram or Ljung Box (LB) statistics [44]. The following figures show correlograms of a time series. Autocorrelation and partial autocorrelation functions characterize the pattern of temporal dependence in the series. Autocorrelation and partial autocorrelation give the impression that the residuals are purely random. Correlogram is simply plots of ACFs and PACFs against the lag length given as the arithmetical progression 1 to 36 in each above table. The solid vertical line in this diagram represents the zero axis and observations between spikes above or below the line are positive and negative values, respectively. For stationary time series, the correlogram tapers off quickly, whereas it dies off gradually for non-stationary time series. For example, Figure 3(a) represents a non-stationary time series correlogram, similar to a purely white noise process and the autocorrelations at various lags hover around zero. Figure 3(b) represents a typical stationary series, as the autocorrelation coefficient starts at quite a high value and declines very slowly toward zero as the lag lengthens. Finally, we can simply point out the statistical significance of the autocorrelation coefficients given by the Eq 7, where k is the lag number:
The sample autocorrelation coefficients are normally distributed with zero mean and a variance equal to one over the sample size N. We conclude this visual diagnostic from Figure 3 by specifying that, if the time series is not stationary at level, it has to be differenced once or more times to achieve stationarity. Furthermore, correlograms of both autocorrelation and partial autocorrelation must indicate that residuals are purely random.
3.2.4. Q-Statistic
An alternative to LB statistics is the Q statistics developed by Box and Pierce is a joint hypothesis test of all the correlation coefficients instead of individual tests [45].
As seen in Figure 3, due to the large number of samples in this study, the Q-stat values differ consistently between the two tables at lag order 36. Although each corresponding probability value is significant, only Figure 3(b) is acceptable due to stationary criteria.
3.2.5. Durbin—Watson & LM tests
Durbin Watson (DW) statistics is a way for detecting serial correlations in a regression model of for example three variables (POWER, IRRA and TEMP) as given in Eq 8.
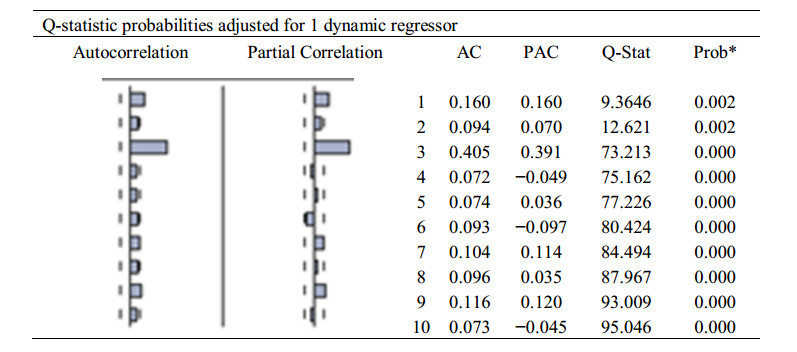
where Power is the dependent variable, and Power (-1) is the one-period lag dependent variable. Eq 8 is also known as an autoregressive (AR) model. DW can be used only if there is only one lag in the AR model. For several-periods lag, Q-statistics and Lagrange Multiplier (LM) tests have to be applied to the AR and to the outcome. The corresponding probabilities obtained using Eviews software are represented in Table 3(a) for the LM tests, and Table 3(b) for the Q-statistics tests. If the null hypothesis H0 is true, there no serial correlation. If the alternative hypothesis H1 is true, there is a serial correlation. However, all probability values being less than 5%, H0 can be rejected, or rather H1 is accepted. Indeed, there is serial correlation in the AR model.
Usually, the LM test is used for higher order errors with variables that are dependent on longer periods of time. This is the purpose of the Breush-Godfrey test for the estimation of least squares or second-order least squares. The result is given in Table 4.
Analyzing the observed R squared and the corresponding probability, less than 5% significant level, the null hypothesis can be rejected. Therefore, there is a serial correlation in the AR model. According to both tests, there is a serial correlation in the AR model, which cannot be used for forecasting.
3.2.6. Histogram—Normality test & jarque bera statistic
If residuals are normally distributed, a bell form shaped curve can be superimposed on the histogram [46]. Plotting residuals of the latter is a rough method to test the normality hypothesis. The histogram is usually given with significant value of the Jarque Bera (JB) statistics which has two degrees of freedom for the null hypothesis of normality, i.e., the residuals are normally distributed. JB must be used for very large samples. Considering the great number of observations, this is very suitable for this study. The JB formula for the null hypothesis of normality is given in Eq 9:
where S is the skewness coefficient (symmetrical form), K is the kurtosis coefficient (flattening form) and n is the sample size. For example, the JB is expected to be null if S = 0 and K = 3 for a normality test.
The horizontal axis of the histogram represents variables of interest such as an ordinary least squares residuals values. The vertical axis is the expected value of this variable if it were normally distributed. Figure 4 represents the histogram with a normal distribution considering the JB value and the corresponding probability value, indicating the null hypothesis of normal distribution for this large number of observations, cannot be rejected.
More probability distributions shall be used in this study. Some definitions and technical terms are explained in the following section for a better understanding, and results outcomes through different Eviews tables.
3.2.7. Further definitions of statistical distributions
(a) Chi-Square
Considering random variables such as x1, x2, x3… xn that are normally and independently distributed. xi follows the normal distribution given as in Eq 10:
where μ and σ2 are the mean value and variance of x, respectively. Variances measure the dispersal of the data points around the mean. If data fall far from the mean value, variance shall increase.
The chi-square denoted as χ2 is given by the Eq 11:
where n denotes the degree of freedom. This test is sometimes referred to as the median test. Chi-squares are specifically tabulated for different uses of the null hypothesis.
(b) Coefficient of Determination
A linear regression model is given as in Eq 12:
where et is the residual term. The sum squared residual SSR is given in Eq 13:
The coefficient of determination R2 is used to evaluate the goodness-of-fit of a regression model. Its value lies between 0 and 1. If this value is closer to 1, better is the fit. However, R2 is a measure of the accuracy of the relationship between the model and the dependent variable. However, it is not a formal test for relationship determination as expressed by the Eq 14:
where TSS is the total sum of squares given as in Eq 15:
where ˉyt is the estimated value, and et=yt−ˉyt is the difference between the observed value of the variable and the adjusted value using the estimated coefficient of the model.
(c) F-Statistic
The F-statistic denoted as F test is a joint test that indicates whether a linear regression model provides a better fit to the data than a model that contains no independent variables. The F-test is related to the R-squared as given in Eq 16:
where k is the degree of freedom and N the number of observations. The F-test as already mentioned is based on the hypothesis test. The null hypothesis H0 of F-test states that the model with no independent variables fits the data as well as the model under test. If the F-test is significant, then it can be concluded that the correlation between the model under test and the dependent variable is statistically significant. Consequently, R2 value from Eq 16 is not equaled to zero. The F-test is given with its corresponding probability value at a significant level. If the probability value is less than the significance level, then data provide sufficient evidence to conclude that the regression model fits the data better than the model with no independent variables.
(d) Lag length criteria
To determine the best relationship between the model and the dependent variable is to choose the optimal lag length as an essential element for relationship stability. Including too many lagged terms will consume degrees of freedom and possibility of multicollinearity whereas too few lags will lead to specification errors. Several criteria have been defined such as Akaike, Schwartz, Hannan and probably at a lesser extent the Durbin Watson. Akaike and Schwartz make it possible to intercede when introducing one or more explanatory variables, between the loss of degrees of freedom and the information endowment. The lower the lag length is, the better the model is. In this study, the Akaike information criteria (AIC) and Schwartz information criteria (SIC) are considered and will be indicated in the outcome table form of Eviews software for all regression determination. The AIC is defined as in Eq 17:
The SIC relationship is similar to AIC with a half value of exponential term. However, it should be noted that for both AIC and SIC the lowest lag length should give a better model. Table 5 is an example of the results that come up for a regression test under Eviews. All the specified parameters are indicated in this table with the corresponding values. Similar tables will be seen in this study and must be analyzed if the values are statistically significant.
4.
Properties of cointegration and error correction mechanism
4.1. Properties of cointegration
The method of cointegration in regression analysis is based on an assumption of stationary increments with fixed time lag called I(d). These terminology and notation have been established in upper sections. The development of the cointegration technique is based on I(d) integration to infer a short time as well as long-time equilibrium relations between non-stationary variables via regression analysis. Here, it should be pointed out that the regression of a non-stationary time series (on another non-stationary time series) may produce a spurious regression. One way to lookout against it is to find out if the time series are cointegrated. A combination of two or more individual non-stationary series may result in a stationary series. The properties of cointegration are explained as follows.
When regressing using the least squares regression including two non-stationary variables as given in Eq 12, and rewritten as integrated order I(1) in Eq 18:
et is non-stationary and auto correlated as the DW is very small. Basically, Granger demonstrated that if Pt and Gt are I(d) series, a linear combination of et is also I(d) that may result in a spurious regression. The last one is characterized by a high R2 and t Student value even though there is no meaningful relationship between the two variables. To avoid such situation, regression is performed on variables in first difference which are stationary (ΔPt and ΔGt are I(0)) as represented in Eq 19:
However, sometimes a regression with variables at level is preferred rather than at first difference. In that case, it is important to know how to regress non-stationary variables, and if the regression is not a spurious regression. Then, the concept of cointegration is applied.
The idea behind cointegration is as follows: in a short term Gt and Pt may have a divergent evolution but they will evolve together in the long term. There exist then a long-term relationship between Pt and Gt that is stable denoted as the cointegration relationship given as in Eq 20:
A summary of cointegration concepts and conditions is given below:
Cointegration of two or more-time series suggests that there is a long-run, or equilibrium, relationship between them. The two cointegration conditions are, firstly, these series have to be of the same integrated order I(d). Secondly, a linear combination of these series allows to reduce the integrated series to a lower order.
To reconcile the short-run behavior with its long-run behavior, an error correction mechanism (ECM) has been developed by Engle & Granger (EG).
4.2. Error correction mechanism
In this section, to help understanding, only two variables P and G are considered to have only one cointegration relationship between them. The same principle is extended to five variables in the final study. If two variables P and G are cointegrated (Pt – ˆa Gt –b is I(0)), then the relationship between them can be expressed as an ECM, such as Eq 21:
where must have a negative sign, Pt behaves as spring recall force and can go back to its long-term equilibrium value given as (aG(t-1) + b). Otherwise the specification of ECM type is not valid. The ECM allows to model jointly short-term dynamics (variables in first difference) and long-term dynamics (variables at level).
The short-term dynamic is given as in Eq 22(a):
The long-term dynamic is given as in Eq 22(b) as cointegration of two-time series suggests that there is a long-run, or equilibrium, relationship between them.
Eq 22(b) is deduced from Eq 22(a) as for the long term by using Pt-1 = Pt and Gt-1 = Gt.
This EG method is valid when the number of variables N is equal to two but as N > 2, up to N-1 cointegration relations can exist. Therefore, EG method is a limited technique, as the study of N variables simultaneously does not make it possible to distinguish several cointegration relations. To overcome this difficulty, the study of a multivariate approach of Johansen cointegration is proposed as discussed in the next section.
5.
Johansen VECM cointegration
The Johansen test can be considered as a multivariate generalization of the augmented Dickey-Fuller test, but the former is a strategic test that makes it possible to estimate all cointegrating vectors when more than two variables are considered. In this study, the Johansen test is applied to 5 variables where Power (P) is the dependent variable, whereas irradiation (IRRA), temperature (Temp), wind speed (Wind), humidity (Humi) are explanatory variables. Indications in brackets are notation used in Eviews software for this study.
It should be recalled that if non-stationary series are integrated of the first order I(1) and found to be cointegrated, a vector error correction mechanism (VECM) can be used so as to enable the examination of short run as well as long-run dynamics of the cointegration series. This is the subject of the next section.
5.1. Multiple cointegration equation
Considering a vector auto regression (VAR) Pt of order p and N variables of non-stationary I(1) as given in Eq 23:
where the matrix rank are respectively, Pt (N, 1), A1 (N, N), Pt -1 (N, 1)……. Ap (N, N), Pt (N, 1) and εt (N, 1). For example, considering 5 variables lagged 2, Eq 23 is transformed as in Eq 24:
And in the matrix form as represented in Eq 25:
The system equations are given in Eq 26:
This first difference VAR (2) model can be written in a vector error correction model (VECM) as a function of only Pt−1 as in Eq 27:
where Π=A1+A2−I and I is the unit matrix. Eq 27 can also be written as function of Pt-1 and Pt-2 as given in Eq 28:
If the coefficient matrix Π has reduced rank r < k, where k is the vector variables of I(1), r is the number of cointegration equations. The matrix Π can be written in terms of vector of adjustment parameters α and matrix of cointegration vectors β' given by Eq 29:
where α is a (N, r) matrix with r < N, and β' has r cointegration vectors such that 0 < r < N as to highlight the VECM model. If this is applied for N = 5 as for this study. It results in Eq 30:
To estimate a VECM model, the matrix rank must be equal to r, meaning that Π has r non zero Eigen values and thus β'.
The Johansen test and estimation strategy which is a maximum likelihood test makes it possible to estimate all cointegrating vectors for N variables, which all have unit roots and there are at most N-1cointegrating vectors. The Johansen test provides estimates of all cointegrating vectors if cointegration relationship does exist, and a rank test is useful. Thereby, if:
- Rank (Π) = 0, then r = 0 meaning that none cointegration relationship and VECM cannot be applied,
- Rank (Π) = r, and meaning that variables are cointegrated and the number of cointegration relationship is equal to r. VECM model can be estimated.
- Rank (Π) = N, meaning that none cointegration relationship.
Johansen procedure is based on the maximum Eigenvalue and Trace tests that are conducted on the error correction model foundation. For both test statistics, the initial Johansen test is a null hypothesis test of no cointegration against the alternative of cointegration.
The first test of maximum Eigenvalues is to determine whether the rank of the matrix is zero, and the null hypothesis is rank (Π) = 0 whereas the alternative hypothesis is rank (Π) = 1.
The second test of Trace is to determine whether the rank of the matrix is r0, the null hypothesis is rank (Π) = r0 and the alternative hypothesis is that r0 < rank (Π)
≤ r, where r is the maximum number of possible cointegration vectors.
The Johansen technique described in this section is basic and further discussions or more technical details are beyond the scope of this paper. Interested readers can consult literatures [47,48,49].
The Johansen test that will be conducted in the following sections is summarized below in five steps.
- Step 1: Performing series stationarity (correlogram & ADF) tests to determine whether there is cointegration relationship or not.
- Step 2: If step1 is true, meaning that series are of the same order of integration and cointegration is likely, therefore VECM model can be estimated. Determining the lag length using Akaike and Schwarz criteria.
- Step 3: Implementing the Johansen test to determine the amount of cointegration relationships.
- Step 4: Identifying the cointegration relationships or long-term relationships between variables.
- Step 5: Estimating the VECM model by maximum likelihood method, test validations by visual diagnostic or correlogram, and checking that residuals from the model are white noise.
6.
Applying Johansen tests to experimental data
Data that is used for this study comes from a building-mounted PV plant designed for a grid connected system. Inclined at 21°, which is Reunion Island latitude, for optimal energy extraction, the modules that make up the PV plant are polycrystalline type of 180 W each, equipped with solar, temperature and wind sensors. For this study, the sample of one-year daily mean data of year 2012, with 365 observations, is retrieved among 7 years of measurements from the COREX building, located at La Possession in the west coast of the island. The determined cointegrating relationship is then applied and compared to other data in real conditions for the years 2013 to 2018. With a 10-minute sampling step, this represents more than 17, 000 data per year. This cointegration relationship is also applied to the second half of year 2019 to make the PV output prediction. The following notations are used for each variable: POWER, IRRA, TEMP, WIND, and HUMI.
6.1. Visual diagnostic of stationary series of the 5 variables
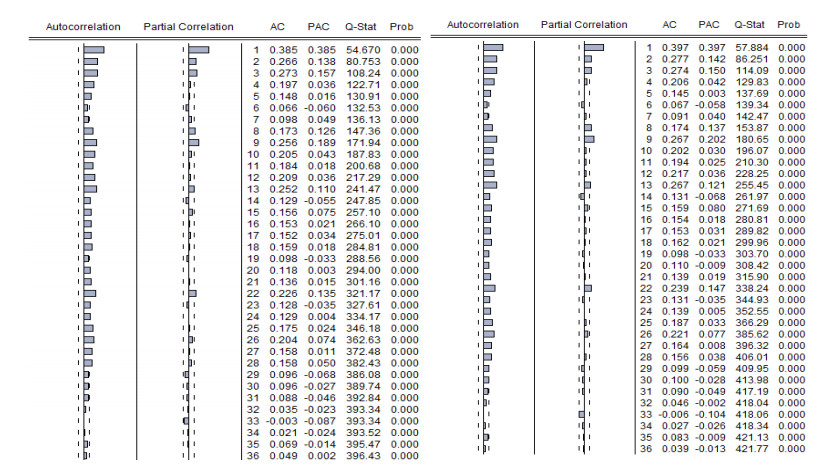
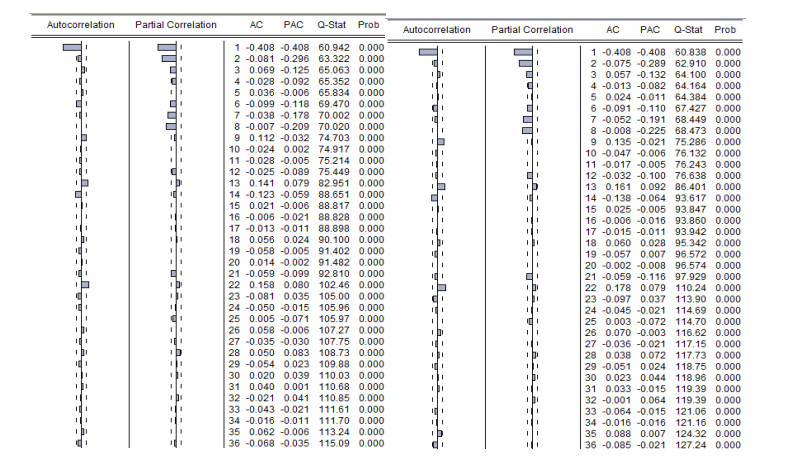
As mentioned in step 1, the following Figures 5(a) and (b) show the correlograms of non-stationary series of Power and Irra (irradiation) at level as explained in section 3.2.3. Similar figures for other variables at level such as Temp, Wind and Humi (humidity) are given in appendix 1. The autocorrelation coefficient starts at a high value and declines very slowly toward zero as the lag increases the autocorrelation coefficients at various lags are high even up to lag 26 for correlograms. The last values in the Q-stat columns are significant indicating serial correlation in the residuals. More precisely, if we consider that at level each series is a non-stationary series as a visual diagnostic.
Figures 6(a) and (b) show stationary series of first difference of variable Power and Irra, as the spikes are beyond the vertical line of the autocorrelation column, except for the first value, which means that we have to consider the first lag as it will be indicated by the ADF test. These correlograms seem to indicate white noise time series. Similar diagrams of first difference of variables Temp, Wind & Humi are shown in appendix 2.
6.2. Augmented dickey fuller test of the 5 variables
The ADF test is applied to verify the null hypothesis of whether there is a unit root in a time series as explained in section 3.2.2. In this section, only the stationary outcome of each series is displayed and the header portion of each Table 6 (a) and (b) indicates the null hypothesis test for Power and IRRA and is rejected if the ADF t-statistic value is less at 5% significant level. Similar figures of the ADF test at first difference for other variables of Temp, Wind and Humi are indicated in appendix 3.
As all series are of the same order of integration that is I(1), cointegration is probable (OR expected). Therefore, VECM model can be estimated. The next section goes to step 2.
6.3. Lag length determination
As indicated in section 3.2.7(d), the AIC and SC are used to determine the lag length. As a reminder, lower is AIC value, better is the model. To determine the lag length, it is assumed that variables are not cointegrated, and the unrestricted vector auto-regression is processed under the Eviews software with a corresponding number of lag. The outcome for lag 1, that is p = 1, is indicated in Table 7(a) and (b).
The AIC value indicated in Table 7(a) is for each system. For Power as the dependent variable, the corresponding AIC is 18.67, whereas in Table 7(b), the value of the AIC is for the whole VAR system and this is the chosen one. For the test with lag = 2, AIC value of the system is greater than for p = 1. The result obtained is not represented here. In Table 7(a), it can be noted that values in brackets '()' are standard errors while values in square brackets '[]' are the corresponding t-statistic value. Table 8 shows the result obtained for another test that confirms the order determination by comparing various criteria.
The star "*" indicates the lag order selected by the following criterion and their corresponding definition: LR is the likelihood ratio, FPE is final prediction error and HQ is the Hannan-Quinn criterion. Therefore, the lag length for p = 1 will be used from now on in this study. The next section goes to step 3.
6.4. Determining of the number of cointegration relationships
As explained in section 4.2, the number of cointegration relationships is based on both the Trace and the Eigen value tests. This is reported in two blocks through Eviews software, denoted the Trace statistics and the maximum Eigenvalue statistics, respectively. For this study, this test is performed with the deterministic trend assumption, which means that there is no intercept or trend in the cointegration equation or VAR test. The two outcome blocks of this test through Eviews are indicated in Table 9 (a) and (b). In Table 9 (a), the header portion indicates the concerning series with the lag length equal to one and no deterministic trend. The columns of each block are as follows. The first column is the number of cointegration relations under the null hypothesis. The second column is the ordered Eigenvalues of the Π matrix as explained in section 4.2. The third column is the test statistic and the fourth column is the 5% critical value. The Trace test indicates 4 cointegration equations at 5% significant level as the probability value is nearly 47% and greater than 5%. The star "*" denotes rejection of the hypothesis at 5% level. Therefore, all variables such POWER, IRRA, TEMP, level of HUMI and SWIND are linked by a long run relationship.
In Table 9(b), the maximum eigenvalue test indicates four equations at 5% level. The outcome of this test is in line with what is indicated in section 5.1.The Johansen VECM test is then performed through Eviews with one lagged. The final outcome is given in Table 10 (a), (b) and (c). The entire Eq 26 in section 5.1 can be deduced from Table 10. The target model D (POWER) which is the dependent variable given in Eq 31 (a) (b), (c) between Table 10a & c. D (POWER) is identified as ΔP.
Eq 31(c) is the long-term relationship as each variable at (t-1) is equal to each variable at t.
It should be noted that Eq 31(c) is determined with one outlier in square brackets '[]' removed from the number of observations. An outlier may be defined as an observation with a large residual that represents the difference (positive or negative) between the actual value and the estimated value from the regression model. When the residual is large, it is in comparison with the other residuals. Usually, a large residual catches attention because of its rather large vertical distance from the estimated regression line. The relationship of ΔP is deduced from Table 10(c) using the error correction model where the values in brackets '()' is the standard error, and the values in square brackets '[]' is the t statistic value. There is no probability value to determine whether each coefficient is significant.
This is done by using system equations through Eviews, where the residual of the cointegration equation can be derived when D (POWER) is the dependent variable. This allowed to determine the residual of the cointegration equation as given in Eq 32:
The probability of each coefficient C (1) to C (9) is given in Table 11.
From sections 4 and 5, the coefficient of C(1) which is the speed of adjustment towards the long run relationship, must be of negative sign and statistically significant whereas coefficients from C(2) to C(9) are short run coefficients. Negative implies a departure in one direction. The correction would have to pull back to the other direction. In this case, this is satisfying for the model as it implies that the model is converging in the long-run equilibrium. To test the short run causality, the Wald test was performed as given in the next section.
6.5. Wald test
The Wald statistic test is a joint test for short run coefficients and the null hypothesis is that all short run coefficients are jointly zero. In this case C (2) = … C (9) = 0. This is given in Table 12, where probability of the chi-square value as explained in section 3.2.7, is greater than 5% significant level, meaning that there is no short-run relationship as all coefficients C(2) to C(9) are zero. The null hypothesis cannot be rejected.
6.6. Lagrange multiplier test and jarque bera statistic
The long run relationship of Eq 31(c) is significant. However, the residual property of white noise needs to be tested. This is verified using the LM test as described in section 3.2.5, and the outcome is given in Table 13.
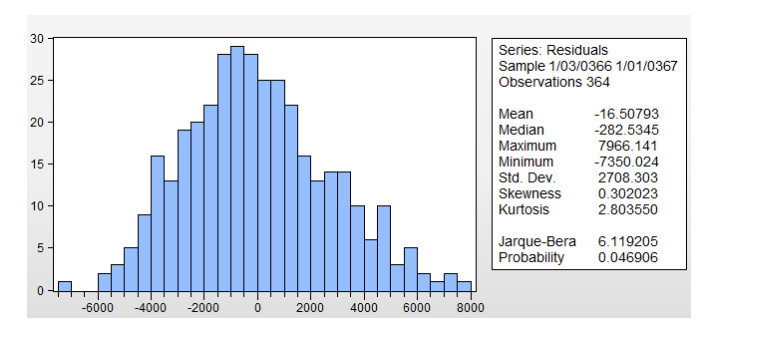
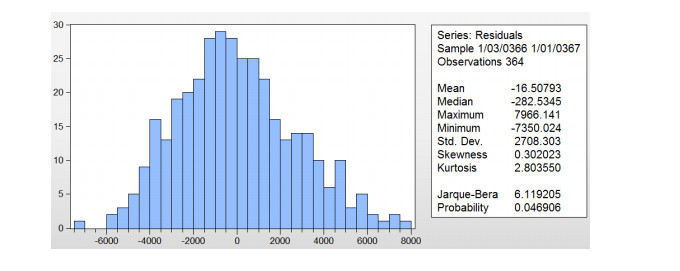
The observed R squared and the corresponding probability which is greater than 5% significant level mean that the null hypothesis can be rejected, and the AR model has serial correlation. To see if the residual is normally distributed, the Jarque Bera statistic is applied as displayed in Figure 7.
As explained in section 3.2.6, the Jarque Bera coefficient is very significant due to the large number of observations, and the bell shape indicates that the residual follows a normal distribution. The obtained model outcome is good. The stability diagnostic needs to be tested to make sure that the model is dynamically stable. For this purpose, the CUSUM test is performed.
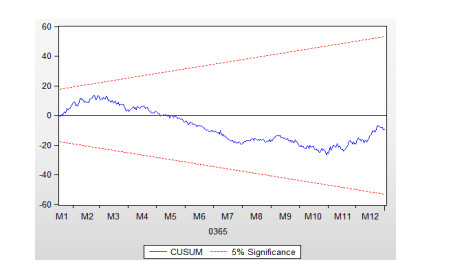
6.7. The CUSUM test
The CUSUM test (Durbin Test) is based on the cumulative sum of the recursive residuals. It plots the cumulative sum together with the 5% critical lines. The test attains parameter stability if the cumulative sum goes inside the area between the two critical lines. In Figure 8, the blue curve, also known as the trade line, lies between the red boundaries. Therefore the model is set to be dynamically stable.
The residual is a random or white noise process. The final long run relationship of this study linking the environmental parameters to the power output in a tropical zone is given in Eq 33:
This equation is then applied for several years of data, and the outcome is compared to real data. This is given is the next section.
7.
Experimental results
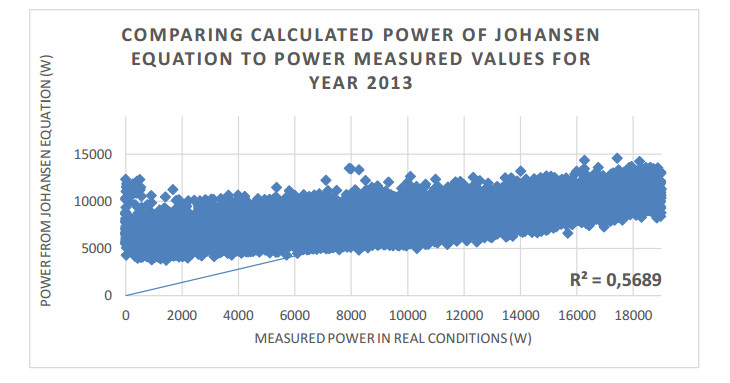
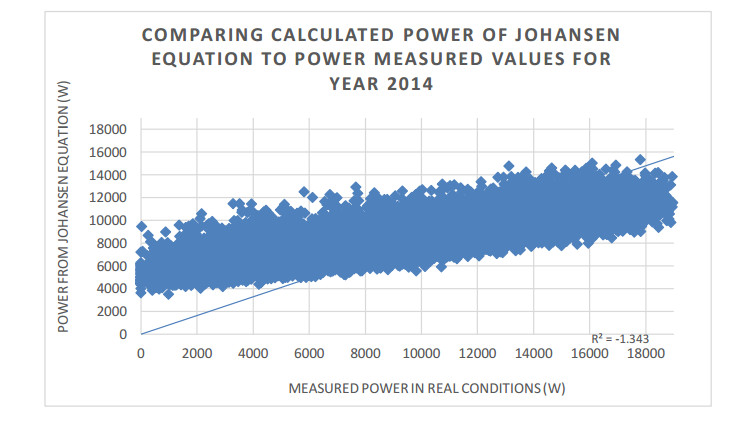
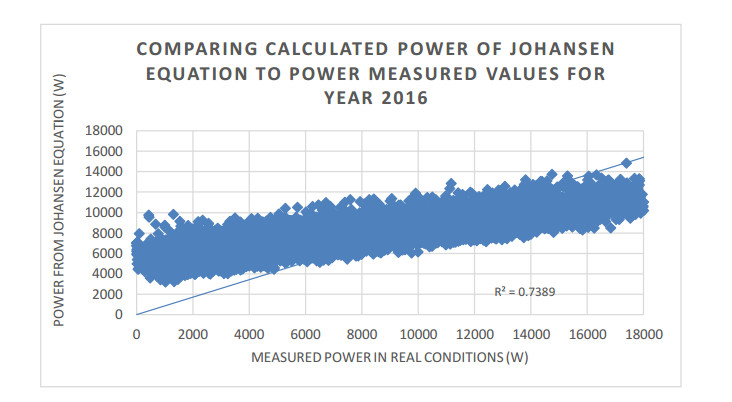
We used the model cointegration regression of Eq 33 determined from year 2012 to calculate the power output for each year of 2013, 2014 and 2016. The goal was to design a model from data of year 2012 and trying to forecast the power output from the model for the following years. Then, we compared each year Johansen cointegration power output to the measured power output in real conditions of the corresponding year. Figure 9(a), (b), (c) represent the plot of each year with the corresponding R2 value. The year sample time is 10 minutes giving more than 17, 000 values per year.
The accuracy of the fit for a regression model is characterized by the coefficient of determination R2 or Pearson's correlation coefficient [50]. It shows how correlated the forecasted and real values are. Applying the Johansen cointegration equation to the different years, it can be observed that R2 is between nearly 65% and 74%. The R2 value could have been better but the data has been randomly chosen. Some data are far from the regression lines as in Figure 9(b) and (c), but can be explained by the fact that these data were related to a few days before and after a storm period.
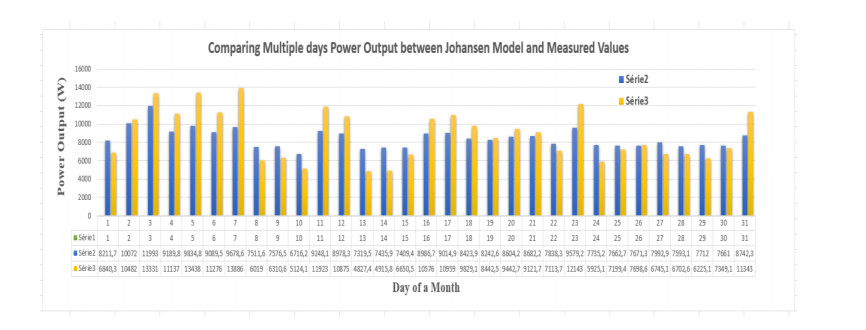
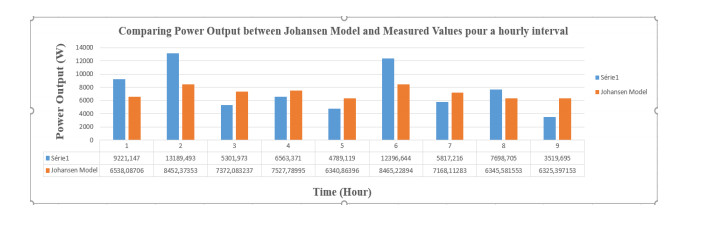
We then applied the Johansen cointegration model for a long-term forecasting that is multiple days ahead. This is represented in Figure 10, where the yellow and blue colors of the bar chart are respectively for the measured power output and Johansen model power output. The x axis is the day number of a particular month. For this test, we used the month of January 2016.
The values below the bar chart diagram are real power output (yellow series) and model power output (blue series).
We also applied the test for an immediate-short-term forecasting that is hours ahead. This is represented in the bar chart diagram of Figure 11. The blue bar chart (series 1) is the measured power output and the orange one (series 2) is the Johansen cointegration power output model. The horizontal axis is an hourly interval of a particular day. For this test we have used data of 11th April 2014 from 9 a.m. to 5 p.m.
This is a promising model which obviously need to be improved nothing when comparing the bar chart diagrams at various time interval forecasting.
8.
Discussion
The Johansen cointegration principle is an appropriate applied method to determine the cointegration relationship between PV output and environmental parameters such as solar irradiation, module temperature, wind speed and relative humidity.
The present work focuses on the methodology used for developing the forecasting method and therefore does not address more general questions such as the precise sensitivity of the environmental factors, the effect of a very long (multiple years) training data or the quantitative comparison with other similar researches. Nevertheless, the following observations can be drawn from this study:
● Indeed, it provides more efficient estimators and can also be carried out when distributions of residuals are not normal and heteroscedastic.
● The weakness of the Johansen approach is that it is sensitive to the lag length. This last one has been determined in a systematic and accurate manner to make the technique perfectly reliable.
● The Johansen cointegration relationship is determined from data of a specific year, and the outcome has been applied and compared to other years of data under real conditions. Like all the current statistical methods of solar photovoltaic generation forecast, it uses past meteorological parameters, hourly irradiance and hourly PV power output to reconstruct the relationship, which means that it is severely dependent of in-site data and requires a sufficient of past measures to be more precise.
● This multiple linear regression between PV power output and the four chosen environmental parameters has a prediction accuracy for the following years between 65% and 74% (Figures 9(a)–9(c)). The precision is not as high as we expected but can be explained by the fact that this model is a regression model which as we know is better suited for short-term or medium-term forecast and not long term forecast. However, the performance accuracy is higher since we deal with short term forecast (Figure 11). Its performance is hardly comparable as it is to Machine Learning (ML) or deep learning models such as Artificial Neural Networks (ANN) or Support Vector Machine (SVM) which are widely use nowadays but by building a hybrid model combining the Johansen cointegration principle and a Machine Learning technique the model's performance can be widely improved.
● In this research, the four environment factors namely solar irradiation, module temperature, wind speed and relative humidity were chosen because their data were available from various sensors on site. Solar irradiation and cell temperature are the two most sensitive factors in the PV power generation.
The main goal is this paper was to propose an original statistical approach that can estimate and forecast PV generation based on meteorological parameters in a tropical island such as Reunion Island.
9.
Conclusion and perspectives
Johansen cointegration principle has been applied to non-stationary economic variables for cointegration analysis of equilibrium relationships, but has never been applied to renewable energy domain. The determined model is free from serial correlation or heteroscedasticity and it can then be used for forecasting. The outcomes show that the Johansen test is an appropriate applied model able to build a cointegration relationship between PV output generation and meteorological parameters such as solar radiation, module temperature, wind speed and humidity. This promising model is only at the beginning of a new facet of research with multidisciplinary competence in this field.
In future research works, the cointegration equation determined in this paper requires improvement by additional robust statistical methods and more robust residual tests, including additional environmental parameters such as ambient temperature, dust, as well as physical effects of air convention, heat transfer by conduction and radiation to PV technology. The resulting cointegration equation should then be applied to a residential area where the consumption profile of residents is known, in order to integrate other back up energy systems such as wind turbines, fuel cells, biomass to move towards smart buildings.
A thorough benchmarking of statistical multiple linear and non-linear regression in order to forecast PV power generation will be proposed in a future work for the sake of comparing this proposed method with several statistical regression forecast models, according to some objective criterion. In order to characterize the quality of the forecasts of each of these models, commonly used error metrics such as: Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Bias Error (MBE) or their relative counterparts (rRMSE, RMAE, rMBE) will be applied.
The evaluation of the performance of the final model did not consider possible interactions among independent variables or even powered variables. In the next paper, these interactions will be discussed.
This regression model as it is does not possess evolutionary techniques such as heuristics and artificial intelligence (neural networks, etc.). A future work will tackle this problem by building a hybrid model combining the Johansen cointegration principle and a Machine Learning technique and therefore will be able to consider more accurately the climate variability and climate change effect.
From the perspective side in a near future, the mathematical aspects behind the statistical theories will be computed in line code using Python 3.7 and integrated on an FPGA chip in order to be applied at minute sampling time to make accurate daily prediction. The whole process should be identified as the RTF (Ramenah-Tanougast-Fanchette) respectively for physical aspects, statistical technique, FPGA implementation and artificial intelligence for predictive principle of energy systems to smart building and smart city. The international University of Mascareignes of Republic of Mauritius in the Indian Ocean has been approached in order to perform the final test.
Acknowledgements
This project has received funding from the Reunion Island Region under grant number DIRED/20171399 and the European Commission—European Regional Development Fund (ERDF) Operational Program 2014–2020. An appreciation is addressed to COREX group which allowed to have access to the climate and power data. A special acknowledgement is extended to UEM.
Conflict of interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: