Abbreviation List
AEOE Aqueous enzymatic oil extraction
ASE Accelerated solvent extraction
BP British petroleum
FAME Fatty acid methyl esters
FFA Free fatty acid
IRAR Infrared radiation assisted reactor
L. Linnaeus
MAAEE Microwave-assisted aqueous enzymatic extraction
MAE Microwave-assisted extraction
PSE Pressurized solvent extraction
SFE Supercritical fluid extraction
TAG Triacylglycerol
UAE Ultrasound-assisted extraction
1. Introduction
Energy demand is expected to increase due to rapid population growth, expanding urbanization and better living standards [1]. Fossil fuels remain the dominant source of energy [2] though it is non-renewable and has negative impact on global climate [3]. According to BP's Energy Outlook to 2035 [2], world energy consumption is projected to increases by 34% between 2014 and 2035, and fossil fuels remain the dominant source of energy (accounting for almost 80%) powering the global economy in 2035 (down from 86% in 2014). The transport sector, which heavily depends on oil-derived liquid products such as gasoline and diesel, globally occupies the third place when total energy consumption and greenhouse gas (GHG) emissions are considered (after the industry and the building sectors). This consumption level is predicted to increase by 60% by 2030 [4].
Rapid growth in both global energy demand and carbon dioxide emissions associated with the use of fossil fuels has driven the search for alternative energy sources which are renewable and have a lower environmental impact [5,6]. Thus, it has become apparent that biodiesel is destined to make a substantial contribution to the future energy demands of domestic and industrial economies [6]. Biodiesel is produced from vegetable oil or animal fat reacts in the presence of a catalyst (usually a base) with an alcohol (usually methanol) to give the corresponding alkyl esters (for methanol, fatty acid methyl esters) [7]. Biodiesel is non-toxic, biodegradable and a portable fuel produced from renewable sources [3,8] and it is one of the technically and economically feasible options to tackle the fast depletion of fossil fuels and environmental pollution [1]. The other benefit of biodiesel fuel is that it can be used in any mixture with petro diesel fuel, as it has very similar characteristics [3].
The potential feedstocks for biodiesel production are edible (first generation feedstocks) and non-edible vegetable oils (second generation feedstocks), wasted oils and animal fats [9] First-generation biofuels are directly related to a biomass that is generally edible, and are usually produced from edible oils, such as soybeans, palm oil, sunflower, safflower, rapeseed, coconut and peanut [4,10]. Second-generation biofuels are fuels that are produced from a wide array of different feedstock, ranging from lignocellulosic feedstocks to municipal solid wastes. Third-generation biofuels are related to algae which have been considered as emerging non-edible oil sources of growing interest because of their high oil content and rapid biomass production [10,11,12] but could also to a certain extent be linked to utilization of CO2 as feedstock [10]. However, the first generation biofuels seems to create some skepticism to scientists. There are concerns about environmental impacts and carbon balances, which sets limits in the increasing production of biofuels of first generation. The main disadvantage of first generation biofuels is the food-versus-fuel debate, one of the reasons for rising food prices is due to the increase in the production of these fuels [9,13,14]. Therefore, non-edible biodiesels feedstocks get great attention to overcome the problem that occurs due to continuous utilization of edible oils for biodiesel [13].
In the different literature, various biodiesel feedstocks: edible oils, non-edible oils, animal fats, waste oils and algal biomass and methods of biodiesel production from these feedstocks were well described and reviewed. However, the preparation of different feedstocks for oil extraction, oil extraction methods from different feedstocks, advantages and disadvantages of the extraction methods and ways to improve them are, to our knowledge, not yet well reviewed. Thus, the aim of this review is to identify the major biodiesel feedstocks, oil extraction and separation methods, the advantages and disadvantages of various oil extraction methods, particularly that of non-edible oils, and suggest how to optimize the appropriate method (s) to enhance the sustainability of biodiesel production and utilization.
2. Biodiesel and Its Feedstock
Biodiesel is defined as the mono-alkyl ester of long chain fatty acids derived from renewable lipid feedstock such as vegetable oils or animal fats [15]. Biodiesel is a non-toxic, biodegradable and renewable fuel that can be produced from a range of organic feedstock including fresh or waste vegetable oils, animal fats, and oilseed plants [16] (the reaction for biodiesel formation is shown in Figure 1).
The major components of plant oils and animal fats are triacylglycerol (TAGs); the esters of fatty acids and glycerol. The TAGs, also known as triglycerides, consists of different fatty acid composition which influences both physical and chemical properties of plant oils and animal fats [15,18,19]. There are two kinds of fatty acids: saturated fatty acids containing carbon-carbon single bond, and unsaturated fatty acids which include one or more carbon-carbon double bond. The major components of biodiesel are straight fatty acid chain and the common fatty acids are palmitic acid (C16:0), stearic acid (C18:0), oleic acid (C18:1), linoleic acid (C18:2) and linolenic acid (C18:3). The other fatty acids which are also present in several plant oils include myristic acid (C14:0), palmitoleic acid (C16:1), arachidic acid (C20:0), and erucic acid (C22:1) [11,18,19]. According to Sajjadi et al. [17], physico-chemical properties of oils from different sources differ, and it is noteworthy that although some oils may be extracted from a unique root, their compositions are significantly dependent on the main parts from which the oil is extracted.
2.1. Different types of oils
Globally, there are more than 350 oil-bearing crops identified as potential sources for biodiesel production [13,17]. The availability of wide range of biodiesel feedstocks is one of the most significant factors that enables the sustainable production of biodiesel [20,21,22]. According to Avhad and Marchetti [18], satisfactory replacement of petroleum diesel with biodiesel depends on two basic requirements: first is its easy availability and environmentally acceptability, and the second is being economically reasonable. Availability of feedstock for producing biodiesel depends on the regional climate, geographical locations, local soil conditions and agricultural practices of any country [13].
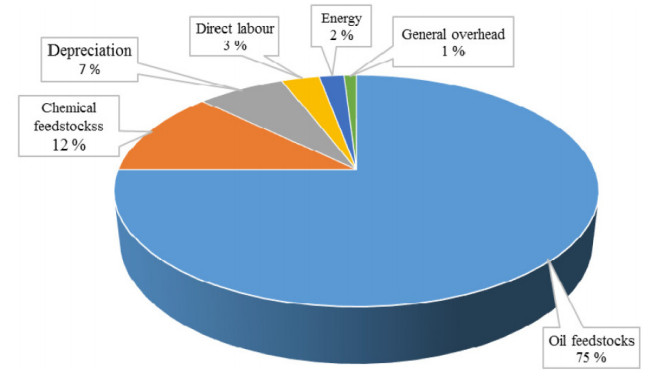
From the literature, it has been found that feedstock alone represents about 75% of the overall biodiesel production cost [13,23,24] as presented in Figure 2. Therefore, minimizing the cost of biodiesel production has been the main agenda for biodiesel producers in order to be competitive with petroleum-derived diesel [25]. Hence, it is crucial to employ inexpensive feedstocks to replace expensive refined oils [4,13]. Using low-cost triglyceride sources such as waste cooking oil and animal fats is also important to minimizing the total cost as these wastes are three times cheaper than refined oils, and are abundantly available [25].
Feedstocks of biodiesel can be divided into four main categories: edible vegetable oil, non-edible oils, waste or recycled oils, and animal fats [13,18,23,26,27,28]. Accordingly, some forms of plant oils, animal fats, and other feedstocks that are used for producing biodiesel are listed in Table 1.
|
Edible oils
|
Non-edible oils
|
Animal fats
|
Other sources
|
| Barley |
Abutilon muticum
|
Beef tallow |
Cyanobacteria |
| Canola |
Aleurites moluccana
|
Chicken fat |
Bacteria |
| Coconut |
Camelina (Camelina Sativa) |
Fish oil |
Cooking oil |
| Corn |
Coffee ground (Coffea arabica) |
Pork lard |
Fungi |
| Groundnut |
Cotton seed (Gossypium hirsutum) |
Poultry fat |
Latexes |
| Palm and palm kernel (Elaeis guineensis) |
Croton megalocarpus
|
Waste salmon |
Microalgae (Chlorellavulgaris) |
| Peanut |
Cynara cardunculus
|
|
Miscanthus |
| Pumpkin seed |
Jatropha curcas
|
|
Pomace oil |
| Rapeseed (Brassica napus
L.) |
Jojoba (Simmondsia chinensis) |
|
Poplar |
| Rice bran oil (Oryza sativum) |
Karanja or honge (Pongamia pinnata) |
|
Soapstocks |
| Safflower (Carthamus tinctorius) |
Mahua (Madhuca indica) |
|
Switchgrass |
| Sesame (Sesamum indicum
L.) |
Moringa (Moringa oleifera) |
|
Tall oil |
| Sorghum |
Nagchampa (Calophyllum inophyllum) |
|
Tarpenes |
| Soybeans (Glycine max) |
Neem (Azadirachta indica) |
|
|
| Sunflower (Helianthus annuus) |
Pachira glabra
|
|
|
| Wheat |
Passion seed (Passiflora edulis) |
|
|
|
Pongamia (Pongamia pinnata) |
|
|
|
Rubber seed tree (Hevca brasiliensis) |
|
|
|
Terminalia belerica
|
|
|
|
Tobacco seed |
|
|
2.1.1. Edible plant oils
Edible oils resources such as soybeans, palm oil, sunflower, safflower, rapeseed, coconut and peanut are considered as the first generation biodiesel feedstocks because they were the first crops to be used for biodiesel production [13]. Edible oil contents of seeds and kernels of some plants are shown in Table 2. Currently, more than 95% of the world biodiesel is produced from edible oils such as rapeseed (84%), sunflower oil (13%), palm oil (1%), soybean oil and others (2%) [4,13]. Plantations of these feedstock plants have been also well established in many countries around the world such as Malaysia, USA and Germany [13]. However, continuous large-scale usage of edible plant oils for biodiesel production raises many concerns such as food versus fuel crisis and major environmental problems such as deforestation and destruction of vital soil resources, conversion of much available farm lands to oil bearing plants [13,14].
Table 2. Species name and oil content of edible and non-edible plant [6,11,12,13,30,37,38,39,40,41,42,43,44,45,46,47,48,49,50].
| Type of oil
|
Common name
|
Species name
|
Oil content of seed/kernel (wt%)
|
Reference
|
| Seed
|
Kernel
|
| Edible |
Coconut |
Cocos Nucifera L.
|
63–65 |
63.1 (± 2.8)
|
[6,38]
|
|
|
Corn |
Zea mays
|
24.44 |
- |
[39]
|
|
|
Hemp seed |
Cannabis Sativa L.
|
22–38 |
- |
[40]
|
|
|
Mustard seed |
Brassica nigra
|
33 |
- |
[41]
|
|
|
Olive |
Olea europaea
|
45–70 |
- |
[37]
|
|
|
Palm |
Elaeis guineensis
|
30–60 |
- |
[6]
|
|
|
Peanut |
Arachis hypogea L.
|
45–55 |
47–61 |
[6,37]
|
|
|
Pumpkin seed |
Cucurbita maxima
|
31.5 |
43.69 (± 3.92)
|
[42,43]
|
|
|
Rapeseed |
Brassica napus
|
38–46 |
- |
[6]
|
|
|
Rice bran |
Oryza sativa
|
15–23 |
- |
[37]
|
|
|
Safflower seed |
Carthamus tinctorius
|
35 |
- |
[44]
|
|
|
Sesame seed |
Sesamum indicum
|
58 |
- |
[45]
|
|
|
Soybean |
Glycine max
|
18–20 |
- |
[46]
|
|
|
Sunflower |
Helianthus annuus
|
25–35 |
50 |
[37,47]
|
| Non-edible |
Castor |
Ricinuscommunis L.
|
45–50 |
- |
[30]
|
|
|
Cottonseed |
Gossypium hirsutum L.
|
18–25 |
31.42 |
[37,48]
|
|
|
Desert date |
Balanites aegyptiaca
|
45–50 |
36–47 |
[12]
|
|
|
Jatropha |
Jatropha curcas L.
|
20–60 |
40–60 |
[12,30,49]
|
|
|
Jojoba |
Simmondisa chincnsis
|
45–50 |
- |
[37]
|
|
|
Karanja |
Pongamia pinnata
|
30–40 |
30–50 |
[30]
|
|
|
Linseed |
Linum usitatissimum
|
35–45 |
- |
[30]
|
|
|
Mahua |
Madhuca indica
|
35–40 |
50 |
[30]
|
|
|
Neem |
Azadirachta indica
|
20–30 |
25–45 |
[30]
|
|
|
Polanga |
Calophyllum inophyllum
|
65 |
22 |
[12]
|
|
|
Caster |
Ricinus communis
|
45–50 |
- |
[11]
|
|
|
Rubber seed |
Hevea brasiliensis
|
40–60 |
40–50 |
[12]
|
|
|
Tobacco |
Nicotiana tabacum L.
|
30–43 |
- |
[37]
|
|
|
|
Nicotiana tabacum
|
36–41 |
17 |
[11,12]
|
|
|
|
Zanthoxylum bungeanum
|
24–28 |
25 |
[12]
|
|
|
Tung |
Vernicia montana
|
16–18 |
- |
[37]
|
|
|
Ethiopian mustard |
Brassica carinata
|
42 |
2.2–10.8 |
[12]
|
|
|
Sea mango |
Cerbera odollam
|
54 |
6.4 |
[12]
|
|
|
Croton oil plant |
Croton tiglium
|
30–45 |
50–60 |
[50]
|
The prices of vegetable oil have also increased dramatically in the last few decades and this will affect the economic viability of biodiesel industry [13,14,51]. Furthermore, the use of such edible oils to produce biodiesel is not feasible in the long term due to the growing gap between demand and supply [13]. Thus, the current use of the food-grade plant oils as a feedstock for producing biodiesel are considered to be not worthy and stipulates search for relatively less expensive resources [13,18].
The average fatty acid composition of different edible vegetable oils are shown in Table 3. The dominant fatty acids of edible oils are oleic acid (C18:1), linoleic acid (C18:2), palmitic acid (C16:0) and staeric acid (C18:0). The fatty acid composition of edible oils from different plants seeds differ. For example, caprylic acid, which is the lightest compound is only available in wheat grain (11.4 wt%) and coconut oils (8.45 wt%) [17]. According to Sajjadi et al. [17], generally is assumed that the compositions of fatty acids compositional profiles do not change during the conversion of the feedstocks to fuel via transesterification and thus, greatly affect the quality of biodiesel to be produced.
Table 3. Comparison of the fatty acid composition of the selected edible oils.
| Source
|
Fatty Acids Composition
|
Reference
|
| C14:0
Myristic acid
|
C16:0
Palmitic acid
|
C16:1
Palmitoleic acid
|
C18:0
Stearic acid
|
C18:1
Oleic acid
|
C18:2
Linoleic acid
|
C18:3
Linolenic acid
|
C20:0
Arachidic acid
|
C22:0
Behenic acid
|
C20:1
Gadoleic acid
|
C22:1
Erucic acid
|
C24:0
Lignoceric acid
|
C8:0
Capryli acid
|
Waste
coconut oil |
0.50 |
21.40 |
0.20 |
3.00 |
27.50 |
47.40 |
- |
- |
- |
- |
- |
- |
8.45 |
[52]
|
| Corn |
- |
- |
11.67 |
1.85 |
25.16 |
60.60 |
0.48 |
0.24 |
- |
- |
- |
- |
- |
[15]
|
| Hempseed |
- |
6.0–8.5 |
- |
2.5–3.0 |
12.0–15.0 |
52.0–56.0 |
- |
0.5–0.8 |
- |
- |
- |
- |
- |
[53]
|
| Mustard seed |
0.05 |
5.54 |
0.21 |
1.51 |
8.83 |
10.79 |
20.98 |
1.21 |
1.09 |
5.27 |
37.71 |
1.68 |
- |
[41]
|
| Olive |
- |
11.60 |
1.00 |
3.10 |
75.00 |
7.80 |
0.60 |
0.30 |
0.10 |
- |
- |
0.50 |
- |
[54]
|
| Palm |
0.70 |
36.70 |
0.10 |
6.60 |
46.10 |
8.60 |
0.30 |
0.40 |
0.10 |
0.20 |
- |
0.10 |
- |
[54]
|
| Peanut |
0.20 |
8.0 |
- |
1.80 |
53.30 |
28.40 |
0.30 |
0.90 |
3.00 |
2.40 |
- |
1.80 |
- |
[54]
|
| Pumpkin seed |
- |
13.80 |
- |
11.20 |
29.50 |
45.5 |
- |
- |
- |
- |
- |
- |
- |
[42]
|
| Rapeseed |
- |
- |
3.49 |
0.85 |
64.40 |
22.30 |
8.23 |
- |
- |
- |
- |
- |
- |
[15]
|
| Rice bran |
- |
22.00 |
- |
3.00 |
38.00 |
35.00 |
- |
- |
- |
- |
- |
- |
- |
[55]
|
| Safflower seed |
- |
11.07 (± 0.10)
|
- |
4.37 (± 0.10)
|
12.76 (± 0.22)
|
69.65 (± 0.24)
|
0.49 (± 1.15)
|
0.78 (± 0.05)
|
0.59 (± 0.09)
|
- |
- |
0.29 (± 0.13)
|
|
[56]
|
| Sesame |
- |
9.80 (± 0.21)
|
- |
6.3 (± 0.15)
|
41.82 (± 0.91)
|
40.50 (± 1.01)
|
0.32 (± 0.01)
|
0.67 (± 0.03)
|
- |
- |
- |
- |
- |
[57]
|
| Sunflower |
- |
16.29 (± 0.54)
|
- |
6.66 |
22.70 (± 0.07)
|
44.13 (± 0.60)
|
8.97 (± 0.52)
|
0.62 (± 70.11)
|
0.63 (± 70.02)
|
- |
- |
- |
- |
[55]
|
| Soybean |
- |
6.14 |
0.09 |
4.11 |
34.30 |
51.17 |
2.23 |
0.17 |
0.41 |
- |
0.53 |
- |
- |
[58]
|
| Wheat grain |
0.13 |
17.71 |
0.2 |
0.78 |
16.5 |
56 |
2.9 |
- |
- |
- |
- |
- |
11.4 |
[17]
|
One of the possible solutions to reduce the utilization of the edible oil for biodiesel production is by exploiting non-edible oils. They got great attention as the plants from which these oils obtained are easily available in many parts of the world [6,13,59]. These plants can grow on wastelands that are not suitable for food crops, eliminate competition for food, reduce deforestation rate, and their oils are very economical compared to edible oils [13].
2.1.2. Non-edible plant oils
Non-edible plant oils which are known as the second generation feedstocks can be considered as promising substitutions for traditional edible food crops for the production of biodiesel [6]. Recently, these oils have gained enormous attention as a new generation feedstock because of their high oil content, easy availability, and having the advantage that it could be grown on lands which are not suitable for agriculture [6,13]. Non-edible oil bearing plants could also be grown with less intensive attention; thus, reducing the cost of cultivation [6,12,13,18]. Therefore, production of biodiesel from non-edible oils is an effective way to overcome the associated problems with edible oils [6]. Some of the main and most investigated non-edible plant oils for biodiesel production include jatropha seed oil [32,36], karanja oil [33], jojoba oil [34], linseed oil [35], cottonseed oil [60], amongst others (Table 1).
During selection of any feedstock as a biodiesel source, the amount of oil that can be obtained from the seeds or kernel is an important parameter. Estimated oil contents of seed and kernel of some non-edible vegetable oil were shown in Table 2 [6,12]. Moreover, fatty acid composition is an important characteristic of biodiesel feedstock as it determines the efficiency of process to produce biodiesel. It has been observed that the percentage and type of fatty acid compositions depends mainly on the plant species as well as their growth conditions [6].
The fatty acid composition and distribution of non-edible oils are generally aliphatic compounds with a carboxyl group at the end of a straight chain [4]. Ong et al. [19] reported that the presence of fatty acid compositions has interfered fuel properties and quality of biodiesel. It has also been found that the biodiesel with a high level of methyl oleate (mono unsaturated fatty acid) might have excellent characteristics in ignition quality, fuel stability and flow properties at low temperature [19,61].
Generally, non-edible oil is composed of a high number of double carbon chain (polyunsaturated acid) which indicate that the these oil group has a greater degree of unsaturated fatty acid than saturated carbon chain [19,62]. Moreover, it was reported that cetane number, heat of combustion, melting point, and viscosity of neat fatty compounds increase with increasing chain length and decrease with increasing unsaturation [62,63] of the fatty acid methyl esters (FAME) molecule. Therefore, structural fatty acid composition will affect the physico-chemical properties of biodiesel such as cetane number, cold flow properties, heat of combustion and viscosity [6,61,62]. Fatty acid compositions of various non-edible oils that were found to be suitable for production of biodiesel are shown in Table 4.
Table 4. Comparison of the fatty acid composition of the selected non-edible plant oils [4,17,30,32,34,37,64,65,66,67,68,69,70].
| Feed stocks
|
Fatty Acids
|
Reference
|
| C14:0
Myristic acid
|
C16:0
Palmitic acid
|
C16:1
Palmitoleic acid
|
C18:0
Stearic acid
|
C18:1
Oleic acid
|
C18:2
Linoleic acid
|
18:3
Linolenic acid
|
C20:0
Arachidic acid
|
C22:0
Behenic acid
|
C20:1
Gondoic acid
|
C22:1
Erucic acid
|
C18:1
Riconoleic acid
|
| Caster seed |
- |
1.00 |
- |
- |
3.00 |
5.00 |
1.00 |
- |
- |
- |
- |
89.00 |
[64]
|
| Cottonseed |
1.00 |
25.80 |
0.60 |
2.5 |
16.4 (± 0.8)
|
51.50 |
0.20 |
0.20 |
0.20 |
- |
- |
- |
[65]
|
| Desertdate kernel |
- |
15.40 (± 0.26)
|
- |
19.01 (± 0.29)
|
25.74 (± 0.35)
|
39.85 (± 0.48)
|
- |
- |
- |
- |
- |
- |
[66]
|
| Jatropha |
- |
15.20 |
0.70 |
6.80 |
44.60 |
32.20 |
- |
0.40 |
- |
- |
- |
- |
[32,34]
|
| Jojoba |
- |
1.20 |
- |
- |
10.70 |
- |
- |
9.10 |
- |
59.50 |
12.30 |
- |
[67]
|
| Karanja |
- |
11.65 |
- |
2.4–8.9 |
51.59 |
16.46 |
2.65 |
- |
- |
- |
- |
- |
[68]
|
| Linseed |
- |
5.10 |
0.30 |
2.5 |
18.90 |
18.10 |
55.10 |
- |
- |
- |
- |
- |
[69]
|
| Mahua |
- |
17.80 |
- |
14.00 |
46.30 |
17.90 |
- |
- |
- |
1.7 |
- |
- |
[70]
|
| Moringa |
- |
7.60 |
1.40 |
5.5 |
66.60 |
8.10 |
0.20 |
5.80 |
- |
- |
- |
- |
[71]
|
| Neem |
0.2–0.26 |
14.9 |
0.1 |
20.6 |
43.9 |
17.9 |
0.4 |
1.6 |
0.3 |
- |
- |
- |
[72]
|
| Polonga |
- |
12.01 |
- |
12.95 |
34.09 |
38.26 |
0.30 |
|
|
- |
- |
- |
[68]
|
| Rubber seed |
2.2 |
10.2 |
- |
8.7 |
24.6 |
39.6 |
16.3 |
- |
- |
- |
- |
- |
[73]
|
| Tobaco |
0.14 |
8.46 |
- |
3.38 |
11.24 |
75.58 |
1.14 |
- |
- |
- |
- |
- |
[74]
|
| Tung |
- |
4.00 |
- |
1.00 |
8.00 |
4.00 |
3.00 |
- |
- |
- |
- |
- |
[37]
|
2.1.3. Waste oils and animal fats
The residual obtained after using oil for the cooking purposes is generally discarded with no further application [18]. Over the last few years, waste cooking oil has been considered as a possible feedstock for biodiesel production due its low cost, and as its biofuel was found to fulfill the requirements specified by European standard for biodiesel (EN) and American Society for Testing and Materials (ASTM) standards [75]. However, waste oil is highly impure consisting mainly of high free fatty acid (FFA), and thus, could be categorized in two groups based on its FFA content: the yellow grease (FFA < 15%), and the brown grease (FFA > 15%). These oils after the filtration and purification processes could be used for biodiesel production [18].
Animal fats such as tallow [76], chicken fat [77], lard [78] and yellow grease [79] are also considered as feedstocks. According to Adewale et al. [80], animal fat wastes are low cost, mitigate environmental damage and increase the quality of the resultant biodiesel fuel. However, it has been reported that these may not be plentiful enough to satisfy the global energy demand. Moreover, biodiesel derived from animal fats has a relatively poor performance in cold weather. Furthermore, the transesterification process is difficult for some types of fats due to the presence of a high amount of saturated fatty acids. [4,13].
2.1.4. Algae as biodiesel feedstocks
The amounts of oily crops, both edible and non-edible, animal fats and waste cooking oils are limited, so it is unlikely to provide worldwide biodiesel production demand. The search for other renewable sources is needed to provide the required amount of oily feedstocks. In recent years a high interest towards producing biodiesel from microalgae has been developed. The advantages of using microalgae for biodiesel production are: much higher biomass productivities than land plants, some species can accumulate up to 20–50% triacylglycerol, no agricultural land is required to grow the biomass and they required only sunlight and a few simple and cheap nutrients [81].
3. Oil Extraction Methods
One of the important steps in the production of biodiesel is oil extraction, and different methods and techniques of oil extraction are in use [4,12,13]. Preparation of feedstocks and various oil extraction methods are discussed in the following parts.
3.1. Feedstock preparation
The pre-requisite for oil extraction is seed preparation [4,13,82]. The preparation of seeds involves removal of outer layers of the fruit to expose the kernels or seeds, and its drying to reduce moisture content [82]. The seeds are separated from fruits, and the fruits that do not dehisce are cracked open manually. The separated seeds or kernels are sieved, cleaned and stored at room temperature [13].
According to Atabani et al. [13,82] seeds can be either dried in the oven or sun dried to appropriate moisture. The kernels or seeds have to be prepared in such a way that they contain optimum moisture content for high oil extraction. For instance, Jahirul et al. [82] has found that seed kernel of beauty leaf (C. inophyllum) prepared to 15% moisture content provided the highest oil yields in both mechanical and solvent extraction methods. The drying process should be checked very carefully by weighing the trays several times in a day whenever possible and after reaching the desired dryness; the trays are stored in a refrigerated room [4]. Mechanical expellers or presses can be fed with either whole seeds or kernels or a mix of both, but common practice is to use seeds only. However, for chemical extraction only kernels are employed [83].
3.2. Extraction methods
After preparation, the raw material is ready for oil extraction. There are three main methods that have been identified for oil extraction: (ⅰ) mechanical extraction, (ⅱ) chemical or solvent extraction, and (ⅲ) enzymatic extraction [4,6,13]. Moreover, accelerated solvent extraction (ASE), supercritical fluid extraction (SFE) as well as microwave-assisted extraction (MAE) methods are frequently used [4]; however, they are not as common or well known as the first three mentioned alternatives
It has been observed that mechanical pressing and solvent extraction are the most commonly used methods for commercial oil extraction [6]. According to Atabani et al. [13], the main products during oil extraction are the crude oil, and the important by-products are such as seeds or kernel cakes. Seed cakes can be used as fertilizers for soil enrichment [6], feed for poultry, fish and swine, and some oil cakes have also application in fermentation and biotechnological processes [84].
3.2.1. Mechanical oil extraction
Mechanical press oil extraction is the most conventional technique. A manual ram press or an engine driven screw press can be used [4]. Jahirul et al. [82] and Bhuiya et al. [85] used a Mini 40 screw press to extract oil from beauty leaf kernels (C. inophyllum). It has been found that engine driven screw press can extract 68–80% of the available oil while the ram presses only achieved 60–65%. Oil extraction efficiencies calculated from data reported in more recent studies are found to generally correspond to these ranges, although the efficiency range of engine driven screw presses can be broadened to 70–80% [4,6,13]. This broader difference is due to the fact that seeds can be subjected to a different number of extractions through the expeller [82,85]. Calculated oil yields (% of contained oil) of mechanical extraction method is presented in Table 5.
Table 5. Calculated oil yields (% of contained oil) of mechanical extraction methods [6,82,83,86].
| Press type
|
Oil yield (%)
|
Necessary treatment
|
| Engine driven screw press |
68.0 |
Filtration and degumming |
| 80.0 |
| 79.0 |
| Ram press |
62.5 |
|
The oil extracted by mechanical presses needs further treatment of filtration and degumming in order to produce a more pure raw material [6,87]. Another problem associated with conventional mechanical presses is that the design of mechanical extractor is suited for some seeds, and therefore, the oil yield is affected if that mechanical extractor is used for other seeds [4,6,13,87]. It has been also found that pretreatment of seeds before applying mechanical extractor increases the amount of oil recovery [6,83]. For instance, by cooking jatropha seeds in water for one hour at 70 ℃ and using screw pressing, Beerens [88] obtained oil yield of 89% after single pass and 91% after dual pass compared to 79% and 87% oil yield recovery of untreated seeds, respectively. Therefore, several other methods have been proposed recently for oil extraction such as solvent extraction, enzymatic extraction and microwave assisted techniques in order to improve the oil extraction yield.
3.2.2. Solvent oil extraction (chemical extraction)
Solvent extraction is the process in which the oil is removed from a solid by means of a liquid solvent, it is also known as leaching [4]. The chemical extraction using n-hexane method results in the highest oil yield which makes it the most commonly used solvent [4,13]. Jahirul et al. [82] has used n-hexane to extract the oil from Australian native beauty leaf seeds (Calophyllum inophyllum), although the cost of oil extraction technique by mechanical screw press is low it is ineffective due to relatively lower oil yields. On the contrary, the chemical oil extraction method was found to be very effective because of high oil yield and for its consistent performance.
It has been observed that there are many factors affecting the rate of solvent extraction such as particle size, the type of solvent used, temperature and agitation speed [6,13]. The solvent has to be selected in such a way that it would be a good selective solvent and its viscosity would be sufficiently low to circulate freely. Sayyar et al. [89] extracted J. curcas oil by n-hexane and petroleum ether and found that the extraction yield with n-hexane to be about 1.3% more than that of petroleum ether (47.3% and 46.0% wt, respectively) under similar conditions. The authors recognized n-hexane as a more preferable solvent for extraction of jatropha oil as compared to petroleum ether. In the extraction of olive oil using organic solvents like hexane, ethanol, petroleum ether, isopropyl alcohol and carbon tetrachloride by a Soxhlet extractor, Banat et al. [90] did also obtain the highest oil yield (12.7%) by n-hexane. However, it has been observed that this method consumes much more time compared to other techniques. The solvent extraction is only economical attractive at a large-scale of production (more than 50 ton biodiesel per day) as reported [13]. In addition, n-hexane solvent extraction has a negative environmental impact because of the wastewater generation, higher specific energy consumption and higher emissions of volatile organic compounds and human health impacts [6]. According to Achten et al. [83] and Mahanta and Shrivastava [91], there are three other types of solvent extraction technique: hot water extraction, soxhlet extraction and ultrasonication technique that could be use instead of hexane solvent extraction.
Jahirul et al. [82] reported that in oil extraction from beauty leaf seeds(Calophyllum inophyllum) by mechanical method (using the screw press) and chemical extraction (using hexane as a solvent), each method has advantages and disadvantages. The advantages and disadvantages of oil extraction by mechanical extraction and chemical extraction from beauty leaf seeds is presented in Table 6.
Table 6. Advantages and disadvantages of mechanical and chemical oil extraction methods for beauty leaf seeds [82].
| Mechanical Extraction
|
Chemical Extraction
|
| Advantages
|
Disadvantages
|
Advantages
|
Disadvantages
|
√ Virgin oil is more sought after
√ No potential for solvent contamination
√ Relatively inexpensive after initial capital costs
√ Minor consumables cost |
· Generally ineffective for processing Beauty Leaf seed
· Time and labor intensive
· Relatively low oil yields
· Operators require experience to achieve best results
· High dependence on kernel moisture content |
√ Repeatable and reproducible results and process
√ High oil yields
√ Relatively simple and quick
√ Hexane can be recovered and reused, reducing cost significantly |
· Less sought after than virgin oil
· Potential for solvent contamination
· Safety issues and environmental concerns regarding the use of hexane
· Very costly if the hexane cannot be recovered |
3.2.3. Accelerated solvent extraction (ASE)
Accelerated solvent extraction (ASE) is also referred to as pressurized solvent extraction (PSE) is another modern oil extraction technique which uses organic and/or aqueous solvents at elevated temperatures and pressures [4]. It has been observed that high temperature accelerates the extraction rate, while elevated pressure prevents boiling at temperatures above the normal boiling point of the solvent.
Khattab and Zeitoun [92] have extracted oil of flaxseed by different methods by supercritical fluid extraction (SFE), accelerated solvent extraction (ASE) and conventional solvent extraction (SE) and found the highest oil yield (42.40%) by SE using n-hexane which did not differ significantly from the one obtained by accelerated solvent extraction ASE in terms of oil quantity (41.90%) and their physicochemical properties and fatty acid profiles. The supercritical fluid extraction (SFE), however, showed significantly lower oil yield (36.49%) in this particular oil extraction from flaxseed. Sarip et al. [93] have also extracted crude palm oil from palm mesocarp by using hot compressed water extraction method and obtained 70 ± 0.5% of the oil with averaged free fatty acid of 0.81 ± 0.08%. Moreover, it was also reported that ASE has been used for the extraction of different materials including wheat germ [94] and flaxseed hulls [95]. In ASE, time as well as solvent consumption is significantly reduced compared to the other solvent extraction techniques [92,94].
3.2.4. Enzymatic oil extraction
Aqueous enzymatic oil extraction (AEOE) method is a promising technique for extraction of oil from plant materials [96,97]. In this method, enzymes should be used to extract oil from crushed seeds [91]. Aqueous enzymatic oil extraction can also be used in combination with other methods of oil extraction. For instance, Shah et al. [97] used a combination of ultrasonication and aqueous enzymatic oil extraction (using an alkaline protease at pH = 9.0) method to extract oil from J. curcas seeds and obtained 74% of the seed oil which is very large compared to the 17–20% oil extracted by aqueous oil extraction alone. Moreover, using of ultrasonication also resulted in reducing the process time from 18 to 6 h. The main advantages of using enzymatic oil extraction are that it is environmental-friendly and does not produce volatile organic compounds. However, the long process time is the main disadvantage associated with this technique [91].
Table 7 shows the reaction temperature, reaction pH, time consumption and oil yield of different chemical and enzymatic extraction methods tested on J. curcas. It has been found that the chemical extraction using n-hexane method results in the highest oil yield which makes it the most commonly used method. Moreover, the negative environmental impacts associated with solvent extraction can be reduced significantly by using AEOE technique although the later method takes long time to complete the process [83,91].
Table 7. Reported oil yields percentage for different chemical and enzymatic extraction methods and different reaction parameters for J. curcas.
| Extraction technique
|
Reaction temperature (℃)
|
Reaction pH
|
Time consumption (h)
|
Oil yield (%)
|
Reference
|
| n-Hexane oil extraction (Soxhlet) apparatus |
- |
- |
24 |
95–99 |
[86]
|
| First acetone, second n-hexane |
- |
- |
48 |
- |
[98]
|
| AOE |
50 |
9 |
6 |
38 |
[83,97]
|
| AOE with 10 min of ultrasonication as pre-treatment |
50 |
9 |
6 |
67 |
[83,97]
|
| AEOE (hemicellulase or cellulase)
|
60 |
4.5 |
2 |
73 |
[6,13,83]
|
| AEOE (alkaline protease)
|
60 |
7 |
2 |
86 |
[6,13,83]
|
|
|
50 |
9 |
6 |
64 |
[83]
|
| AEOE (alkaline protease) with 5 min of ultrasonication as pre-treatment |
50 |
9 |
6 |
74 |
[83,97]
|
| Three-phase partitioning |
25 |
9 |
2 |
97 |
[83,99]
|
3.2.5. Supercritical fluid extraction (SFE)
Supercritical fluid extraction (SFE) technique is used to avoid the use of organic solvents and to increase the speed of extraction [4]. SFE using CO2 has numerous advantages over the solvent extraction [92,100]. It uses CO2as a solvent which is a nontoxic, inexpensive, nonflammable, and nonpolluting supercritical fluid solvent for the extraction of natural products, and also almost 100% oil can be extracted by this method [100].
Maran and Priya [101] have used a supercritical fluid extraction (at 44 MPa, 49.8 ℃, and 0.64 g/min of CO2 flow rate and within 81 min) method for extraction of oil from muskmelon seed (Cucumis melo) and produced slightly higher oil yield (48.11 ± 0.04%) than that of Soxhlet extraction method (46.83 ± 0.29%). Moreover, these authors reported that the fatty acids composition of muskmelon seed oil extracted by SFE was similar to that of Soxhlet extraction. However, the main limitation of the SFE is the high cost at production scale, not only due to the use of high pressure equipment but also because of the raw material should be freeze dried to reduce its moisture to values below 20%, as high water concentration in fluid phase negatively affects the oil yield [102,103].
3.2.6. Microwave-assisted extraction (MAE)
Microwave-assisted extraction (MAE) also called microwave extraction, is a new extraction technique, which combines microwave and traditional solvent extraction [104]. MAE has been recognized as a technique with several advantages over other extraction processes, such as reduction of costs, shorter time, less solvent, higher extraction rate, better products with lower cost, reduce energy consumption and CO2emissions [104,105]. In microwave-assisted aqueous enzymatic extraction (MAAEE) of pumpkin seed oil by using mixtures of cellulose, pectinase and proteinase (w/w/w), Jiao et al. [106] obtained the highest oil recovery of 64.17%. The authors also reported that there were no significant variations in physicochemical properties of MAAEE and soxhlet extracted oils, and thus, MAAEE is a promising and environmental-friendly technique for pumpkin seed oil extraction. Moreover, it has been found that the MAE method needs a few minutes compared to SFE and the apparatus of MAE extraction is simpler and cheaper, and can be used with a variety of materials with less limit of the polarity of extractants [104]. Therefore, MAE extraction is an interesting alternative to conventional liquid solvent extraction methods, especially in the case of plant material [4,104]. In microwave-assisted solvent extraction of oil from soybeans and rice bran by using solvent (ethanol) to feedstock ratio of 3:1, the maximum oil yields of 17.3% and 17.2% at 20 min and 120 ℃ were achieved as compared to 11.3% and 12.4% using control extraction for soybeans and rice bran, respectively [107].
4. Advantages and Disadvantages of Main Oil Extraction Methods
From the above discussions, it is possible to observe that each method of oil extraction has its own advantages and disadvantages. The advantages and disadvantages of the main three oil extraction methods: mechanical, chemical or solvent and ASE are summarized in Table 8.
Table 8. Advantages and disadvantages of main three oil extraction methods [4,82,108].
| Methods
|
Advantages
|
Disadvantages
|
| Oil press | √ Virgin oil is more sought after | · Generally ineffective in beauty leaf oil extraction |
| √ No potential for solvent contamination | · Time and labor intensive |
| √ Relatively inexpensive after initial capital costs | · Relatively low oil yields |
| √ Minor consumable costs | · Operators require experience to achieve best results |
| √ Whole seeds or kernels can be processed | · High dependence on kernel moisture content |
| √ No environmental problem regarding the use of screw press | · Relatively dirty process
· Filtration or degumming process pf oil is required
· Low and inconsistent oil production
· High oil loss |
| n-Hexane | √ Repeatable and reproducible results and process | · Less sought after than virgin oil |
| √ High oil yields | · High potential for solvent contamination |
| √ Relatively simple and quick | · Safety issues and environmental concerns |
| √ Suitable for bulk oil extraction | · Very costly if the hexane cannot be recovered |
| √ Low capital investment | · High hexane requirement |
| √ No especial equipment required ü Hexane can be recovered and reused, reducing cost significantly | · Only kernel can be processed |
| ASE | √ Automatic technique | · Very high initial cost |
| √ Condition can be optimized | · High preparation required |
| √ More efficient | · Special equipment and skill required |
| √ Clean process | · Potential for solvent contamination |
| √ Relatively less solvent consumption ü Less time and labor incentives ü High oil yield | · Only kernel can be processed |
5. Single and Combined Oil Extraction Methods to Reduces Problems of Extraction
Traditional oil extraction methods have their own advantages and disadvantages. To overcome the disadvantages and improve the strong sides, different oil extraction methods are combined. Moreover, to decrease the environmental impacts of solvents of chemical extraction, different methods of oil extraction have been developed. For instance, Conte, et al. [109] have extracted safflower oil by Soxhlet extraction, ultrasound-assisted extraction (UAE) and pressurized liquid extraction (PLE) techniques (using pressurized ethanol). Soxhlet and ultrasound-assisted extractions gave maximum global oil yield of 36.53% and 30.41%, respectively (70 ℃ and 240 min) while a maximum global yield for pressurized liquid extraction would be 25.62% [109]. According to the authors, although traditional extraction methods (Soxhlet and UAE) showed maximum global oil yields, the advantages derived from PLE make it a promising alternative for the extraction of essential oil from vegetable matrices due to the reduction of solvent consumption and extraction time.
At optimal conditions of sonication, ultrasonic-assisted extraction (UAE) of raspberry seed oil was able to provide a higher content of beneficial unsaturated fatty acids, whereas conventional Soxhlet extraction resulted in a higher amount of saturated fatty acids [110]. Ultrasound-assisted extraction gave grape seed oil yield (14% w/w) similar to Soxhlet extraction in 6 hours, and no significant differences for the major fatty acids was observed in oils extracted by both methods. The advantage of using ultrasound is that it's lower solvent consumption and a shorter extraction time [111].
6. Future Prospective of Oil Extraction Methods
Biodiesel production from non-edible feedstocks is increasingly attractive alternative to both fossil diesels and renewable fuels derived from food crops. Thus, one of the current research focus in biodiesel production is optimization of oil extraction methods from non-edible oils sources, characterization the oils and suitability test for biodiesel [112], and searching for appropriate methods of biodiesel production from these oils [4,17]. Non-edible biodiesel feedstocks include non-edible oils, animal fats and waste oils [4,13] and algal biomass [10,11,12]. Some of the recently optimized non-edible seed oil extraction methods include extraction from seeds of waste date pits (Phoenix dactylifera L.) [112], Sesame (Sesamum indicumL.) [113], jatropha seed kernels [114], beauty leaf seed(Calophyllum inophyllum) [85], Moringa oleifera [115] and karanja (Pongamia pinnata) [116].
According to Sajjadi et al. [17], animal fats are important feedstocks for biodiesel production as their cost is substantially lower than the cost of vegetable oil. However, many types of animal fats contain high amount of saturated fatty acids, which make the transesterification process difficult. To overcome such problems, various biodiesel production methods have been optimized by different investigators. For instance, Kumar and Math [117] investigated the combined effects of catalyst (NaOH) concentration, reaction time and methanol quantity on biodiesel yield from waste animal fat at 55 ℃ to 60 ℃, and obtained the maximum animal fat methyl ester yield of 91% v/v, at 35% v/v methanol and 0.46% w/v catalyst within 90 minutes. Chakraborty and Sahu [118] have also carried out a study on the impacts of methanol to goat tallow molar ratio, infrared radiation assisted reactor (IRAR) temperature and H2SO4 concentration on the tallow conversion to biodiesel. Under optimal conditions, 96.7% FFA conversion was achieved within 2.5 h at 59.93 wt.% H2SO4, 69.97 ℃ IRAR temperature and 31.88:1 methanol to tallow molar ratio. According to the authors, infrared radiation strategy could significantly reduce the reaction time compared to conventionally heated reactor while providing appreciably high biodiesel yield. Nuhu and Kovo [119] used a two-step transesterification to produce biodiesel from chicken fat due to the presence of high FFA (4.16%) in the feedstock, and the first esterification step was a pretreatment process that could reduce the FFA to 0.43%. The second step, the transesterification reaction, yielded 93.4% fat methyl ester from 50g of chicken fat at 60 ℃ reaction temperature and within 2 hours corresponding to 6:1 molar ratio of oil-to-methanol and 1% wt catalyst concentration.
From various types of biomass, microalgae have the potential of becoming a significant energy source for biofuel production in the coming years. Currently, researches are mainly focusing on optimization of cultivation methods and the conversion of microalgae to biodiesel (lipids for biodiesel production) [120]. Martinez-Guerra and Gude [121] has also wrote that algal biodiesel production will play a significant role in sustaining future transportation fuel supplies, and a large number of researchers around the world are investigating into making this process sustainable by increasing the energy gains and by optimizing resource-utilization efficiencies. Some of the studies that focus on optimization of biodiesel production from microalgae include the investigations by Misau et al. [122], Gülyurt et al. [123], Barreiro, et al. [120] and Rajendran et al. [124].
7. Conclusions
The increasing demand of energy, where the major part of that energy is derived from fossil sources and the problem associated with petroleum fuels have led to search for renewable alternative energy sources of which biodiesel is a promising alternative. The potential feedstock of biodiesel include, edible and non-edible oils, animal fats, waste oils and algal biomass. However, nowadays, more than 95% of the world biodiesel is produced from edible oils and this resulted in food versus fuel debates, rising in the price of oil and environmental problems. To overcome these problems, it is important to use relatively cheaper and non-edible biodiesel feedstock such as non-edible oils, waste animal fats and waste oils.
Many non-edible plat oils have fatty acid composition and other physico-chemical properties that enable them to be suitable for biodiesel production as that of edible oils. Moreover, many potential non-edible plant oil for biodiesel have been identified, and the oil extraction and biodiesel production methods have also been optimized. Methods to extract oil from waste animal fats and refining animal oils and waste oils, and converting them to biodiesel were also optimized by different scholars.
The major oil extraction methods are mechanical extraction, chemical or solvent extraction, and enzymatic extraction. From these methods, chemical or solvent oil extraction method, particularly, Soxhlet extraction by using hexane as solvent, is the most widely used method due to its efficiency of oil extraction. However, chemical oil extraction method has a negative environmental impact. There are also other oil extraction method such as accelerated solvent extraction, supercritical fluid extraction, microwave-assisted extraction and ultrasonic-assisted extraction.
All oil extraction methods have their own advantages and disadvantages. Therefore, by combining the appropriate oil extraction methods, it is possible to reduce the disadvantages and improve the oil extraction efficiency and reduce the negative environmental impacts. Furthermore, for non-edible and low-cost biodiesel feedstocks gradually gain acceptance and well establish and continue to settle in the biodiesel market, various aspects must be scrutinized and studied. Researches that focus on the study of low-cost biodiesel feedstocks, various efficient and environmental-friendly oil extraction techniques, and study of oil yield and fatty acid profiles of non-edible oils, animal fats and waste oils and efficient and cost effective biodiesel conversion technologies are crucial. It can also be concluded that the emphasis must be given to those feedstocks which are neither compete with food crops nor lead to land clearing, and provide significant greenhouse-gas reductions.
Acknowledgments
The authors would like to express their gratitude to the EnPe/NORHED project of Norad at the Norwegian University of Life Sciences, Faculty of Sciences and Technology for their financial support.
Conflict of Interest
All authors declare no conflicts of interest in this paper.










 DownLoad:
DownLoad: