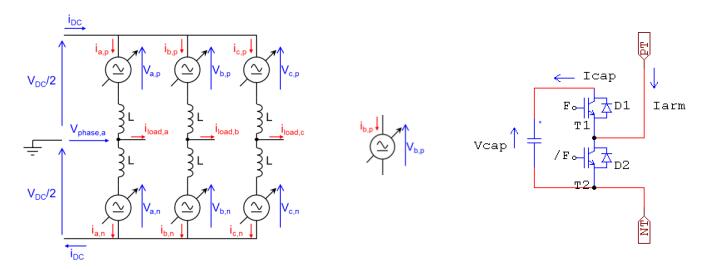
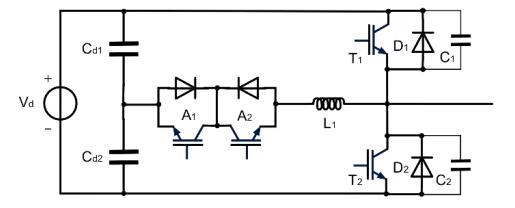
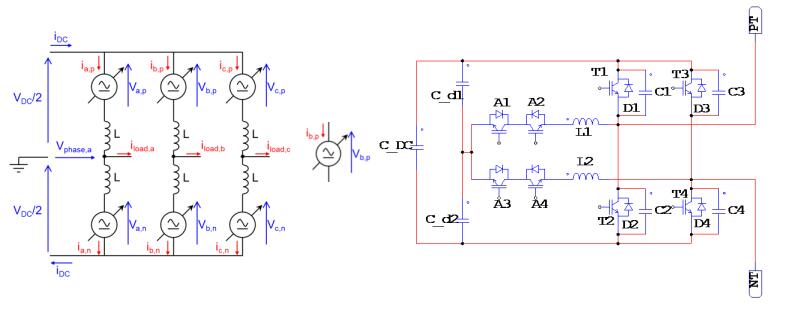
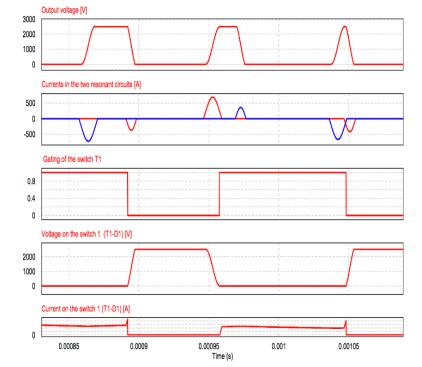
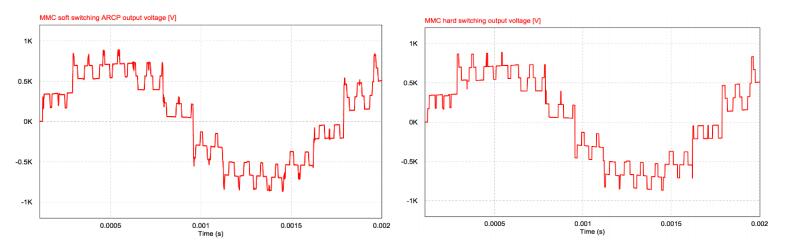
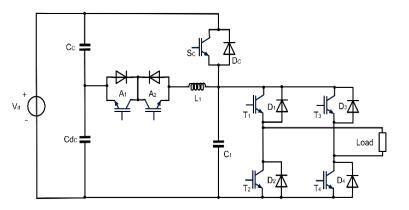
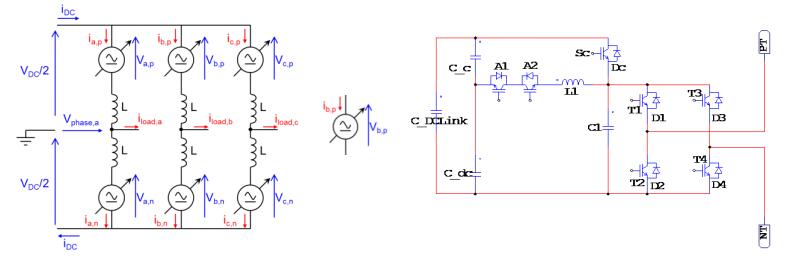
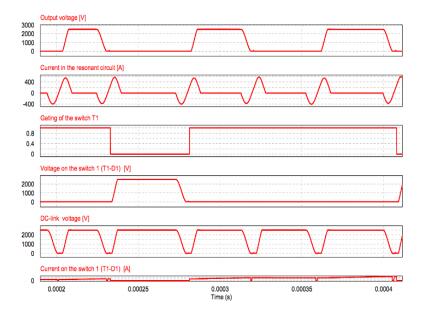
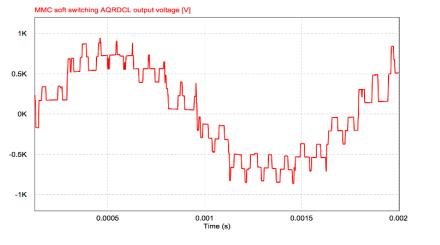
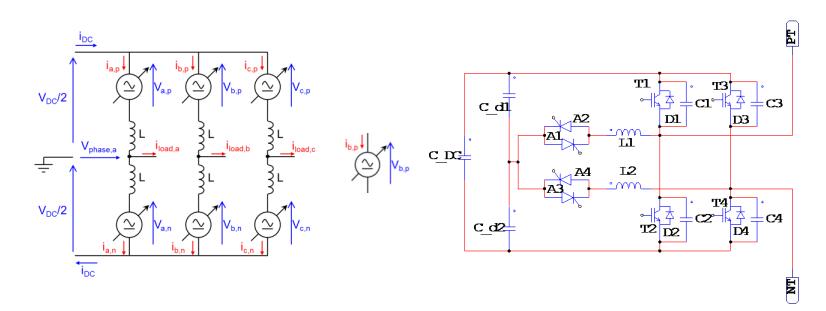
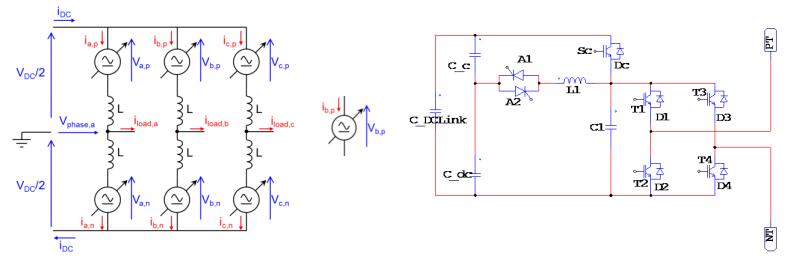
The Modular Multilevel Converter (MMC) concept is a modern energy conversion structure that stands out for a number of interesting features that opens wide application chances in Power Systems, for example for efficient grid integration of renewable sources. In these high-voltage, high-power application fields, a high efficiency is mandatory. In this regard, an interesting and promising development opportunity could be to make soft-switching the elementary converters of the submodules (cells), half H-bridges or full H-bridges, obtaining at the same time the advantage of increasing the switching frequency. The-Active Resonant Commutated Pole Converter (ARCP) or the Auxiliary Quasi Resonant DC-link Inverter (AQRDCL) soft-switching topologies appear adequate for this purpose. This paper is dedicated to examining these development possibilities.
1.
Introduction and setting of the problem
Homogenization theory has become an important tool in the investigation of processes taking place in highly heterogenous media ranging from soil to the most advanced aircraft the construction of which uses composite materials. So far, the problems solved by means of homogenization have mainly involved deterministic partial differential equations (PDEs) and the homogenization of PDEs with randomly oscillating coefficients; the great wealth of results obtained over several decades on problems of diverse classes and methodologies can be found for instance in [9,6,40,41,23,34,22,49,31,17,4,32,36,46,50,33], for the deterministic case and [13,14,18,20,24,37,19,47,48]. for the random case. Fundamental methods were subsequently developed such as the method of asymptotic expansions ([9], [6], [40], [41]), the two scale-convergence ([4], [32]), Tartar method of oscillating test functions and H-convergence ([49]), the asymptotic method for non periodically perforated domains ([23], [46]), G-convergence ([36]) and Γ-convergence developed by De Giorgi and his students; relevant extensions of some of these methods, including their random counterparts, have also emerged in recent times. One rapidly developping important branch of homogenization is that of numerical homogenization; see [1], [2].
However physical processes under random fluctuations are better modelled by stochastic partial differential equations (SPDEs). It was therefore natural to consider homogenization of this very important class of PDEs. Research in this direction is still at its infancy, despite the importance of such problems in both applied and fundamental sciences. Some relevant interesting work have recently been undertaken, mainly for parabolic SPDEs; see for instance [3,8,10,11,21,43,44]. We also note the closely related work [3,25,15,16] dealing with stochastic homogenization for SPDEs with small parameters. The list of references is of course not exhaustive, but a representation of the main trends in the field.
The homogenization of hyperbolic SPDEs was initiated in [27], [28,29], [30] where the authors studied the homogenization of Dirichlet problems for linear hyperbolic equation with rapidly oscillating coefficients using the method of the two-scale convergence pioneered by Nguetseng in [32] and developed by Allaire in [4] and [5]; they also dealt with the linear Neumann problem by means of Tartar's method and obtained the corresponding corrector results within these settings; [30] deals with a semilinear hyperbolic SPDE by Tartar's method.
In the present work, following the two-scale convergence method, we investigate the homogenization of a non-linear hyperbolic equation with nonlinear damping, where the intensity of the noise is also nonlinear and is assumed to satisfy Lipschitz's condition. Our investigation relies on crucial compactness results of analytic (Aubin-Lions-Simon's type) and probabilistic (Prokhorov and Skorokhod fundamental theorems) nature. It should be noted that these methods extend readily to the case when Lipschitz condition on the intensity of the noise is replaced by a mere continuity. In contrast to the linear and the semilinear cases considered in previous papers, the type of nonlinear damping and nonlinear noise in the present paper leads to new challenges in obtaining uniform a priori estimates as well as in the passage to the limit. It should be noted that the process of damping in mechanical systems is a crucial stabilizing factor when the system is subjected to very extreme tasks; mathematically this translates in some regularizing effects on the solution of the governing equations.
We are concerned with the homogenization of the initial boundary value problem with oscillating data, referred to throughout the paper as problem (Pϵ):
where uϵt denotes the partial derivative ∂uϵ/∂t of uϵ with respect to t, ϵ>0 is a sufficiently small parameter which ultimately tends to zero, T>0, Q is an open and bounded (at least Lipschitz) subset of Rn, W=(W(t))(t∈[0,T]) an m-dimensional standard Wiener process defined on a given filtered complete probability space (Ω,F,P,(Ft)0≤t≤T); E denotes the corresponding mathematical expectation. For a physical motivation, we refer to [27,28], where the authors discussed real life processes of vibrational nature subjected to random fluctuations; for instance the nonlinear term B(t,uϵt) stands for damping effects, the term f(t,x,x/ε,∇uϵ) is the oscillating regular part of the force acting on the system and depending linearly on ∇uϵ, while the term g(t,x,x/ε,uϵt)dW represents the oscillating random component of the force; it depends on uεt. More precise assumptions on the data will be provided shortly.
Few words about the difference between the current work and previous works by the authors on homogenization of SPDEs. Compared to [27,28,29,30], the structure of problem (Pε) is dominated by nonlinear terms such as the damping B(t,uϵt), leading to Lp(Q)-like norms whose combination with the predominently L2-like norms coming from the other terms requires special care, both in the derivation of the a priori estimates, as well as in the passage to the limit. Though, two-scale convergence method is also used in the paper [27], the model there is essentially linear. The works [43,44] deal with stochastic parabolic equations in domains with fine grained boundaries, where no conditions of periodicity hold and the methodology implemented there is a stochastic counterpart of Kruslov-Marchenko's [23] and Skrypnik's [46] homogenization theories based on potiential theory; for instance the homogenized problems in [43,44] involve an additional term of capacitary type. The investigation of a hyperbolic counterpart of these works has still not been undertaken and is somehow overdue. Finally, compared with the above mentioned works, the current paper involves a simpler proof of the convergence of the stochastic nonlinear term (its integral) thanks to a blending of two-scale convergence with a regularizing argument and a result on convergence of stochastic integrals due to Rozovskii [39,Theorem 4,P 63].
We now introduce some functions spaces needed in the sequel.
For 2≤p≤∞, we define the Sobolev space
where the derivatives exist in the weak sense, and Lp(Q) is the usual Lebesgue space. For p=2,W1,2(Q) is denoted by H1(Q). By W1,p0(Q) we denote the space of elements ψ∈W1,p(Q) such that ψ|∂Q=0 with the W1,p(Q)-norm. By (ϕ,ψ) we denote the inner product in L2(Q) and by ⟨.,.⟩ we denote the duality pairing between W1,p0(Q) and W−1,p′(Q) (1p+1p′ = 1). We also consider the following spaces, H(Q)={u∈H1(Q)|MQ(u)=0} where MQ(u) is the mean value of u over Q, C∞per(Y) the subspace of C∞(Rn) of Y- periodic functions where Y=(0,l1)×...×(0,ln). Let H1per(Y) be the closure of C∞per(Y) in the H1-norm, and Hper(Y) the subspace of H1per(Y) with zero mean on Y.
For a Banach space X, and 1≤p≤∞, we denote by Lp(0,T;X) the space of measurable functions ϕ:t∈[0,T]⟶ϕ(t)∈X and p-integrable with the norm
When p=∞, L∞(0,T;X) is the space of all essentially bounded functions on the closed interval [0,T] with values in X equipped with the norm
For 1≤q,p<∞, Lq(Ω,F,P,Lp(0,T;X)) ((Ω,F,P) is a probability space with a filtration {Ft}t∈[0,T]) consists of all random functions ϕ:(ω,t)∈Ω×[0,T]⟶ϕ(ω,t,⋅)∈X such that ϕ(ω,t,x) is progressively measurable with respect to (ω,t). We endow this space with the norm
When p=∞, the norm in the space Lq(Ω,F,P,L∞(0,T;X)) is given by
It is well known that under the above norms, Lq(Ω,F,P,Lp(0,T;X)) is a Banach space.
We now impose the following hypotheses on the data.
(A1) Aϵ(x)=A(xϵ)=(ai,j(xϵ))1≤i,j≤n is an n×n symmetric matrix, the components ai,j, are Y−periodic and there exists a constant α>0 such that
(A2) B(t,⋅):u∈W1,p0(Q)⟶W−1,p′(Q) such that
(ⅰ) B(t,⋅) is a hemicontinuous operator, i.e. λ⟶⟨B(t,u+λv),w⟩ is a continuous operator for all t∈(0,T) and all u,v,w∈W1,p0(Q);
(ⅱ) There exists a constant γ>0 such that ⟨B(t,u),u⟩≥γ‖u‖pW1,p0(Q) for a.e.t∈(0,T) and all u∈W1,p0(Q);
(ⅲ) There exists a positive constant β such that ‖B(t,u)‖W−1,p′(Q)≤β‖u‖p−1W1,p0(Q) for a.e.t∈(0,T) and all u∈W1,p0(Q);
(ⅳ) ⟨B(t,u)−B(t,v),u−v⟩≥0, for a.e.t∈(0,T) and all u,v∈W1,p0(Q);
(ⅴ) The map t⟶B(t,u) is Lebesgue measurable in (0,T) with values in W−1,p′(Q) for all u∈W1,p0(Q).
(A3) We assume that f(t,x,y,w) is measurable with respect to (x,y) for any (t,w)∈(0,T)×Rn, continuous with respect to (t,w) for almost every (x,y)∈Q×Y, and Y-periodic with respect to y. Also there exists an Rn-valued function F=(Fi(t,x,y))1≤i≤n such that f(t,x,y,w)=F(t,x,y)⋅w. Furthermore,
for any (t,w,ε)∈(0,T)×L2(Q)×(0,∞), with the constant C independent of ε and t. A sufficient requirement for this condition to hold is that Fi(t,⋅)∈L∞(Q×Y) for any t∈(0,T).
(A4) aϵ(x)∈H10(Q), bϵ(x)∈L2(Q), for any ϵ>0.
(A5) g(t,x,y,ϕ) is an m-dimensional vector-function whose components gj(t,x, y,ϕ) satisfy the following conditions:
● gj(t,x,y,ϕ) is Y-periodic with respect to y, measurable with respect to x and y for almost all t∈(0,T) and for all ϕ∈L2(Q),
● gj(t,x,y,ϕ) is continuous with respect to ϕ for almost all (t,x,y)∈(0,T)×Q×Y, and there exists a positive constant C independent of t, x and y, such that
and
● gj(t,x,y,⋅) satisfies Lipschitz's condition
with the constant L independent of t, x and y.
If ||gj(t,x,y,0)||L2(Q×Y)<∞ for any i=1,...,m and any t∈(0,T), the condition (1) is redundant since it follows from the Lipschitz condition (2).
From now on we use the following oscillating functions
We now introduce our notion of solution; namely the strong probabilistic one.
Definition 1.1. We define the strong probabilistic solution of the problem (Pϵ) on the prescribed filtered probability space (Ω,F,P,{Ft}t∈[0,T]) as a process
satisfying the following conditions:
(1) uϵ,uϵt are Ft−measurable,
(2)
(3) ∀t∈[0,T], uϵ(t,.) satisfies the identity
The problem of existence and uniqueness of a strong probabilistic solution of (Pϵ) was dealt with in [38]. The relevant result is
Theorem 1.2. Suppose that the assumptions (A1)−(A5) hold and let p≥2. Then for fixed ϵ>0, the problem (Pϵ) has a unique strong probabilistic solution uϵ in the sense of Definition 1.1.
Our goal is to show that as ϵ tends to zero the sequence of solutions (uϵ) converge in a suitable sense to a solution u of the following SPDE
where A0 is a constant elliptic matrix defined by
χ(y)∈Hper(Y) is the unique solution of the following boundary value problem:
for any λ∈Rn and Y=(0,l1)×...×(0,ln),
a and b are suitable limits of the oscillating initial conditions aϵ and bϵ, respectively, ˜W is an m-dimensional Wiener process
2.
A priori estimates
Here and in the sequel, C will denote a constant independent of ϵ. In the following lemma, we obtain the energy estimates associated to problem (Pϵ).
Lemma 2.1. Under the assumptions (A1)-(A5), the solution uϵ of (Pϵ) satisfies the following estimates:
and
Proof. The following arguments are used modulo appropriate stopping times. Itˆo's formula and the symmetry of A give
Integrating over (0,t),t≤T, we get
Using the assumptions (A1), (A2)(ii), (A5) and taking the supremum over t∈[0,T] and the expectation on both sides of the resulting relation, we have
where
Using assumptions (A3), thanks to Cauchy-Schwarz's and Young's inequalities, we have
where ϱ>0. Thanks to Burkholder-Davis-Gundy's inequality, followed by Cauchy-Schwarz's inequality, the last term in 5 can be estimated as
Again using Young's inequality and the assumptions (A5), we get
for ϱ>0. Combining the estimates 6, 7, 5 and assumption (A5) and taking ϱ sufficiently small, we infer that
Using Gronwall's inequality, we have
and subsequently
The proof is complete.
The following lemma will be of great importance in proving the tightness of probability measures generated by the solution of problem (Pϵ) and its time derivative.
Lemma 2.2. Let the conditions of Lemma 2.1 be satisfied and let p≥2. Then there exists a constant C>0 such that
for any ϵ>0 and 0<δ<1.
Proof.. We consider that div(Aϵ∇ϕ) has been restricted to the space W−1,p′(Q) and that the restriction induces a bounded mapping from W1,p0(Q) to W−1,p′(Q).
Assume that uϵt is extended by zero outside the interval [0,T] and that θ>0. We write
Then
Firstly, thanks to assumption (A1), we have
where we have used the fact that p′≤2.
Secondly, we use assumption (A2)(iii), estimate 4 and H¨older's inequality to get
Thirdly,
where we have used assumption (A3).
Using 10, 11 and 12 in 9 raised to the power p′, for fixed δ>0, we get
We now estimate the term involving the stochastic integral.
We use the embedding
to get the estimate
Thanks to Fubini's theorem and H¨older's inequality, we have
where we have used Burkholder-Davis-Gundy's inequality. We now invoke assumption (A5) and estimate 3 to deduce from 14 and 15 that
For the first term in the right-hand side of 13, we use Fubini's theorem, H¨older's inequality and estimate 3 to get
The second term on the right hand side of 13 is estimated using 4 and we get
Combining 13, 16, 17 and 18, and taking into account the fact that the similar estimates hold for θ<0, we conclude that
This completes the proof.
3.
Tightness property of probability measures
The following Lemmas are needed in the proof of the tightness and the study of the properties of the probability measures generated by the sequence (W,uϵ,uϵt).
We have from [45]
Lemma 3.1. Let B0, B and B1 be some Banach spaces such that B0⊂B ⊂B1 and the injection B0⊂B is compact. For any 1≤p,q≤∞, and 0<s≤1 let E be a set bounded in Lq(0,T;B0)∩Ns,p(0,T;B1), where
Then E is relatively compact in Lp(0,T;B)
The following two lemmas are collected from [12]. Let S be a separable Banach space and consider its Borel σ-field to be B(S). We have
Lemma 3.2. (Prokhorov) A sequence of probability measures (Πn)n∈N on (S,B(S)) is tight if and only if it is relatively compact.
Lemma 3.3. (Skorokhod) Suppose that the probability measures (μn)n∈N on (S,B(S)) weakly converge to a probability measure μ. Then there exist random variables ξ,ξ1,…ξn,…, defined on a common probability space (Ω,F,P), such that L(ξn)=μn and L(ξ)=μ and
the symbol L(⋅) stands for the law of ⋅.
Let us introduce the space Z=Z1×Z2, where
and
We endow Z with the norm
Lemma 3.4. The above constructed space Z is a compact subset of L2(0,T;L2(Q))×L2(0,T;L2(Q)).
Proof. Lemma 3.1 together with suitable arguments due to Bensoussan [7] give the compactness of Z1 and Z2 in L2(0,T;L2(Q)).
We now consider the space X=C(0,T;Rm)×L2(0,T;L2(Q))×L2(0,T;L2(Q)) and B(X) the σ−algebra of its Borel sets. Let Ψϵ be the (X,B(X))-valued measurable map defined on (Ω,F,P) by
Define on (X,B(X)) the family of probability measures (Πϵ) by
Lemma 3.5. The family of probability measures {Πϵ:ϵ>0} is tight in (X,B(X)).
Proof. We carry out the proof following a long the lines of the proof of [27,lemma 7]. For δ>0, we look for compact subsets
such that
This is equivalent to
which can be proved if we can show that
Let L_{\delta } be a positive constant and n\in \mathbb{N} . Then we deal with the set
Using Arzela's theorem and the fact that W_{\delta } is closed in C(0,T;\mathbb{R}^{m}) , we ensure the compactness of W_{\delta } in C(0,T;\mathbb{R}^{m}) . From Markov's inequality
where \eta is a nonnegative random variable and k a positive real number, we have
But
where (2k-1)!! = 1\cdot 3\cdot \cdot \cdot (2k-1) and W_{i} denotes the i-th component of W .
For k = 4 , we have
Choosing (L_{\delta })^{4} = \dfrac{(\sum n^{-2})^{-1}}{3CT^{2}\delta } , we have
Now, let K_{\delta },\,\,M_{\delta } be positive constants. We define
Lemma 3.4 shows that D_{\delta } is compact subset of L^{2}(0,T;L^{2}(Q)), for any \delta >0 . It is therefore easy to see that
Markov's inequality 19 gives
for K_{\delta } = M_{\delta } = \frac{6C}{\delta }.
Similarly, we let \mu _{n},\,\,\nu _{m} be sequences of positive real numbers such that \mu _{n},\,\,\nu _{n}\rightarrow 0 as n\rightarrow \infty , \sum_{n}\frac{\mu _{n}^{p^{\prime }/p}}{\nu _{n}}<\infty (for the series to converge we can choose \nu _{n} = 1/n^{2} , \mu _{n} = 1/n^{\alpha } , with \alpha p^{\prime }/p>4 ) and define
Owing to Proposition 3.1 in [7], B_{\delta } is a compact subset of L^{2}(0,T;L^{2}(Q)) for any \delta >0 . We have
Again thanks to 19, we obtain
for K_{\delta }^{\prime } = \frac{9C}{\delta } , L_{\delta }^{\prime } = \frac{ 9C}{\delta } and M_{\delta }^{\prime } = \dfrac{9C\sum \frac{\mu _{n}^{p^{\prime }/p}}{\nu _{n}}}{\delta } . This completes the proof.
From Lemmas 3.2 and 3.5, there exist a subsequence \{\Pi _{\epsilon _{j}}\} and a measure \Pi such that
weakly. From lemma 3.3, there exist a probability space (\tilde{\Omega},\tilde{\mathcal{F}},\tilde{\mathbb{P}}) and \mathcal{X} -valued random variables (W_{\epsilon _{j}},u^{\epsilon _{j}},u_{t}^{\epsilon _{j}}),\,\,(\tilde{W},u,u_{t}) such that the probability law of (W_{\epsilon _{j}},u^{\epsilon _{j}}, u_{t}^{\epsilon _{j}}) is \Pi _{\epsilon _{j}} and that of (\tilde{W},u,u_{t}) is \Pi . Furthermore, we have
Let us define the filtration
We show that \tilde{W}(t) is an \tilde{\mathcal{F}_{t}} -wiener process following [7] and [42]. Arguing as in [42], we get that (W_{\epsilon _{j}},u^{\epsilon _{j}},u_{t}^{\epsilon _{j}}) satisfies \tilde{\mathbb{P}}-a.s. the problem \left( P_{\epsilon _{j}}\right) in the sense of distributions.
4.
Two-scale convergence
In this section, we state some key facts about the powerful two-scale convergence invented by Nguetseng [32].
Definition 4.1. A sequence \{v^{\epsilon}\} in L^{p}(0,T;L^p(Q))(1<p<\infty) is said to be two-scale converge to v = v(t,x,y),\,\ v\in L^{p}(0,T;L^p(Q\times Y)), as \epsilon \rightarrow 0 if for any \psi = \psi(t,x,y)\in L^p((0,T)\times Q ;C_{\text{per}}^{\infty }(Y)) , one has
where \psi^{\epsilon}(t,x) = \psi(t,x, \frac{x}{\epsilon}) . We denote this by \{v^{\epsilon}\}\rightarrow v \,\,\,\text{2-s in}\,\,\, L^{p}(0,T;L^p(Q)) .
The following result deals with some of the properties of the test functions which we are considering; it is a modification of Lemma 9.1 from [17,p.174].
Lemma 4.2. (i) Let \psi \in L^{p}((0,T)\times Q;C_{per}(Y)),\,\,1<p<\infty . Then \psi (\cdot,\cdot,\frac{\cdot}{\epsilon })\in L^{p}(0,T;L^{p}(Q)) with
and
Furthermore if \psi \in L^{2}((0,T)\times Q;C_{per}(Y)) , then
(ii) If \psi (t,x,y) = \psi _{1}(t,x)\psi _{2}(y),\,\ \psi _{1}\in L^{p}(0,T;L^{s}(Q)),\,\psi _{2}\in L_{per}^{r}(Y),\,\,1\leq s,r<\infty are such that
then \psi (\cdot,\cdot,\frac{\cdot}{\epsilon })\in L^{p}(0,T;L^{p}(Q)) and
The following theorems are of great importance in obtaining the homogenization result; for their proofs, we refer to [4], [17] and [26].
Theorem 4.3. Let \{u^{\epsilon}\} be a sequence of functions in L^{2}\left(0,T;L^{2}(Q)\right) such that
Then up to a subsequence u^{\epsilon} is two-scale convergent in L^{2}\left(0,T;L^{2}(Q)\right) .
Theorem 4.4. Let \{u^{\epsilon }\} be a sequence satisfying the assumptions of Theorem 4.3. Furthermore, let \{u^{\epsilon }\}\subset L^{2}\left( 0,T;H_{0}^{1}(Q)\right) be such that
Then, up to a subsequence, there exists a couple of functions (u,u_{1}) with u\in L^{2}(0,T;H_{0}^{1}(Q)) and u_{1}\in L^{2}((0,T)\times Q;H_{{\text{per}}}(Y)) such that
The following lemma is crucial in obtaining the convergence of the stochastic integral in the next section
Lemma 4.5. The oscillating data given in (A5) satisfies the following convergence
Proof. Test with \psi \left( t,x,\frac{x}{\varepsilon }\right) , where \psi \left( t,x,y\right) \in L^{2}\left( \left( 0,T\right) \times Q,C_{per}^{\infty }\left( Y\right) \right) , as follows:
where
Then
thanks to the Lipschitz condition on g\left( t,x,\cdot \right) . Now due to the strong convergence 20 of u_{t}^{\varepsilon }-u_{t} to zero in L^{2}\left( \left( 0,T\right) \times Q\right) , \mathbb{\tilde{P}} -a.s., we get that I_{1}^{\varepsilon }\rightarrow 0 , \tilde{\mathbb{P}}-a.s.
Now we can apply 2-scale convergence for the limit of I_{2}^{\varepsilon } and indeed
Therefore
and this implies the result.
Remark 1. From the assumption (A5), 28 and 23, we have the following strong convergence
5.
The homogenization result
We will now study the asymptotic behaviour of the problem (P_{\epsilon_j}) , when \epsilon_j \rightarrow 0 .
Theorem 5.1. Suppose that the assumptions on the data are satisfied. Let
Then there exist a probability space \left( \tilde{\Omega},\tilde{\mathcal{F}},\tilde{\mathbb{P}},\left( \tilde{\mathcal{F}}_{t}\right) _{0\leq t\leq T}\right) and random variables (u^{\epsilon _{j}},u_{t}^{\epsilon _{j}},W_{\epsilon _{j}}) and (u,u_{t},\tilde{W}) such that the convergences 20 and 26 hold. Furthermore (u,u_{t},\tilde{W}) satisfies the homogenized problem (P) .
Proof. From estimates 3 and 4 and assumption (A2)(iii) , we have the following convergences
Now let us identify the limit in 35. By arguing as in [38,Lemma 2.6,p. 51], we get
Having this in hand, let v\in L^{p}(0,T;W_{0}^{1,p}(Q)) and define
From the monotonicity assumption (A2)(iv) , we have \chi _{\epsilon _{j}}\geq 0 . Now using 34, 35 and 36 to pass to the limit in 37, we get
For \lambda >0 and w\in L^{p}(0,T;W_{0}^{1,p}(Q)) , we can chose v(t) = u_{t}(t)-\lambda w(t) . Hence
Using the hemicontinuty assumption (A2)(i) , we have
Now, from assumptions (A2)(ii) and (A2)(v) , we use the Lebesgue dominated convergence theorem to pass to the limit in 38. This implies
But the inequality 39 is true for all w(t)\in L^{p}(0,T;W_{0}^{1,p}(Q))) . Therefore
Testing problem (P_{\epsilon _{j}}) by the function \Phi \in C^{\infty}_{\text{c}}((0,T)\times Q) and integrating the first term in the right-hand side by parts, we have
Using estimate 3, the convergence 20 and Theorems 4.3 and 4.4, we show the two-scale convergence
Let \Phi ^{\epsilon _{j}}(t,x) = \phi (t,x)+\epsilon _{j}\phi _{1}(t,x,\frac{x}{\epsilon _{j}}), where \phi \in C^{\infty}_{\text{c}}((0,T)\times Q) and \phi _{1}\in C^{\infty}_{\text{c}}((0, T)\times Q;C_{\text{per}}^{\infty }(Y)) . Then we can still consider \Phi ^{\epsilon _{j}} as test function in 40. Thus
Let us deal with these terms one by one, when \epsilon _{j}\rightarrow 0 . Thanks to estimate 22 and convergence 33, we have
The second term can be written as follows,
Since A_{\epsilon _{j}}\in L^{\infty }(Y) and \nabla _{x}\phi (t,x)+\nabla _{y}\phi _{1}(t,x,y)\in L_{\text{per}}^{2}(Y;C(Q\times (0,T))) , we regard A_{\epsilon _{j}}[\nabla _{x}\phi (t,x)+\nabla _{y}\phi _{1}(t,x,\frac{x}{\epsilon _{j}})] as a test function in the two-scale limit of the gradient in the first term in 42. Therefore
Thanks to H \ddot{o} lder inequality, 22 and the fact that A_{\epsilon _{j}}\nabla u^{\epsilon _{j}} is bounded in L^{\infty }(0,T; L^{2}(Q) , we have
Again, thanks to estimate 22 and convergence 35, we have
Let us write
where we have used the assumption (A3). It is easy to see that the second term in 43, converges to zero. For the first term in the right-hand side of 43, we readily have
Concerning the stochastic integral, we have
We deal with the term involving \phi \left( t,x\right) . We have
In view of the unbounded variation of W_{t}^{\varepsilon }-\tilde{W}_{t} , the convergence of the first term on the right-hand side of 46 needs appropriate care, in order to take advantage of the \mathbb{\tilde{P}}- a.s. uniform convergence of W_{t}^{\varepsilon } to \tilde{W}_{t} in C\left(
\left[ 0,T\right] \right) . We adopt the idea of regularization of g\left( t,x,\frac{x}{\varepsilon },u_{t}^{\varepsilon }\right) with respect to the variable t , by means of the following sequence
where \rho is a standard mollifier.
We have that g_{\lambda }^{\varepsilon }\left( u^{\varepsilon }\right) \left( t\right) is a differentiable function of t and satisfies the relations
and for any \varepsilon >0
We split the first term in the right-hand side of 46 as
Owing to 49, and Burkholder-Davis-Gundy's inequality, it readily follows that the second term in 50 is bounded by a function \sigma _{1}\left( \lambda \right) which converges to zero as \lambda \rightarrow 0 . In the first term in the same relation, we take advantage of the differentiability of g_{\lambda }^{\varepsilon } with respect to t in order to integrate by parts. As a result we get
Thanks to the conditions on \phi and g and the uniform convergence obtained from the application of Skorokhod's compactness result, namely
we get that both terms on the right-hand side of 51 are bounded by the product \sigma _{2}\left( \lambda \right) \eta _{1}\left( \varepsilon \right) such that \sigma _{2}\left( \lambda \right) is finite and \eta _{1}\left( \varepsilon \right) vanishes as \varepsilon tends to zero. Summarizing these facts, we deduce from 50 that
Thus, we infer from 46 that
Taking the limit in 54 as \varepsilon \rightarrow 0 , we get
but the left-hand side of this relation being independent of \lambda , we can pass to the limit on both sides as \lambda \rightarrow 0 , to arrive at the crucial statement
Owing to 27; that is
we can call upon the convergence theorem for stochastic integrals due to Rozovskii [39,Theorem 4,p. 63] to claim that
Hence, we deduce from 55 that,
For the second term in 45, thanks to Burkholder-Davis-Gundy's inequality, the assumptions on g^{\epsilon _{j}} and 22, we have
Combining the above convergences, we obtain
Choosing in the first stage \phi = 0 and after \phi _{1} = 0 , the problem 57 is equivalent to the following system of integral equations
and
By standard arguments (see [17]), equation 58 has a unique solution given by
where \chi (y), known as the first order corrector, is the unique solution to the following equation:
As for the uniqueness of the solution of 59, we prove it as follows. Using 60 in 59, one obtains that 59 is the weak formulation of the equation
where
and
But the initial boundary value problem corresponding to 62 has a unique solution by [38]. It remains to show that u(x,0) = a(x) and u_{t}(x,0) = b(x) . Notice that equation 40 is valid for \Phi ^{\epsilon _{j}}(t,x) = \phi (t,x)+\epsilon _{j}\phi _{1}(t,x,\frac{x}{ \epsilon _{j}}) where \phi \in C^{\infty }_{\text{c}}((0,T)\times Q) and \phi _{1}\in C^{\infty }_{\text{c}}((0,T)\times Q;C_{\text{per}}^{\infty }(Y)) , such that \phi (0,x) = v(x) and \phi (T,x) = 0 . Thus, we have
where we pass to the limit, to get
The integration by parts, in the first term gives
In view of equation 57, we deduce that
for any v\in C^{\infty }_{\text{c}}(Q) . This implies that u_{t}(x,0) = b(x) . For the other initial condition, we consider \Phi ^{\epsilon _{j}}(t,x) = \phi (t,x)+\epsilon _{j}\phi _{1}(t,x,\frac{x}{\epsilon _{j}}) as a test function in 40, where \phi \in C^{\infty }_{\text{c}}((0,T)\times Q) and \phi _{1}\in C^{\infty }_{\text{c}}((0,T)\times Q;C_{\text{per}}^{\infty }(Y)) , such that \phi (0,x) = 0,\phi _{t}(0,x) = v(x) and \phi (T,x) = 0 = \phi _{t}(T,x) . Integration by parts in the first term of 40, gives
Passing to the limit in this equation, we obtain
We integrate by parts again to obtain
Using the same argument as before, we show that u(x,0) = a(x) . We note the triple \left( \tilde{W},u,u_{t}\right) is a probabilistic weak solution of (P) which is unique. Thus by the infinite dimensional version of Yamada-Watanabe's theorem (see [35]), we get that \left( W,u,u_{t}\right) is the unique strong solution of (P) . Thus up to distribution (probability law) the whole sequence of solutions of (P_{\epsilon }) converges to the solution of problem (P) . Thus the proof of Theorem 5.1 is complete.
6.
Convergence of the energy
Let us introduce the energies associated with the problems (P_{\epsilon _{j}} ) and ( P ), as follows:
But from It \hat{o} 's formula, we have
Thus
The vanishing of the expectation of the stochastic integrals is due to the fact that (g^{\epsilon }(u_{t}^{\epsilon }),\tilde{u}_{t}^{\epsilon }) and (g(u),u_{t}) are square integrable in time. We want to prove that the energy associated with the problem ( P_{\epsilon _{j}} ), uniformly converges to that of the corresponding homogenized problem ( P ). For this purpose we need to assume some stronger assumptions on the initial data. We have the following result
Theorem 6.1. Assume that the assumptions of Theorem 5.1 are fulfilled and
Then
where u is the solution of the homogenized problem.
Proof. Thanks to the convergences 20, 44, 29, 66 and 67, we show that
Now we need to show that \left( \mathcal{E}^{\epsilon _{j}}(u^{\epsilon _{j}})(t)\right) , is uniformly bounded and equicontinuous on [0,T] and hence Arzela-Ascoli's theorem concludes the proof. We have
Thanks to the assumptions on the data (A3),\,(A4) and (A5) , the a priori estimates 3 and 4, we show that
For any h>0 and t\in \lbrack 0,T] , we get
Again assumptions (A3), (A5) and Cauchy-Schwarz's inequality, give
This implies the equicontinuity of the sequence \{\mathcal{E}^{\epsilon _{j}}(u^{\epsilon _{j}})(t)\}_{\epsilon _{j}} , and therefore the proof is complete.
7.
The corrector result
In this section, we establish a corrector result stated in the following
Theorem 7.1. Let the assumptions of Theorems 5.1 and 6.1 be fulfilled. Assume that \nabla _{y}\chi (y)\in \lbrack L^{r}(Y)]^{n} and \nabla u\in L^{2}(0,T;[L^{s}(Y)]^{n}) with 1\leq r,s<\infty such that
Then
Proof. It is easy to see that
Then convergence 20 gives
Thus 68 holds. Similarly we show that
It remains to show that
We have
Again
Now from the ellipticity assumption on the matrix A , we have
Let us pass to the limit in this inequality. We start with
From the convergence of the energies in Theorem 6.1 and using 63 and 60, we have
Next, using the two-scale convergence of \nabla u^{\epsilon _{j}} , with the test function A\left( y\right) \left( \nabla u(t,x)+\nabla _{y}u_{1}(t,x,y)\right) , we obtain
Now, let us write
For u_{1} given by 60, we have
Now using (ii) of Lemma 4.2, for p = 2 , we obtain
Combining 71, 72 and 73 with 70, we deduce that
Thus the proof is complete.
As a closing remark, we note that our results can readily be extended to the case of infinite dimensional Wiener processes taking values in appropriate Hilbert spaces; for instance cylindrical Wiener processes.
Acknowledgments
The authors express their deepest gratitude to the reviewers for their careful reading of the paper and their insightful comments which have improved the paper. Part of this work was conducted when the first author visited the African Institute for Mathematical Sciences (AIMS), South Africa, he is grateful to the generous hospitality of AIMS.













 DownLoad:
DownLoad: