Forecasting the total electricity production in South Africa: Comparative analysis to improve the predictive modelling accuracy

1.   Introduction

The monthly, quarterly and annual time series data display seasonality, fluctuation, nonlinearities, and so on. The total electricity production data often has some characteristics, such as seasonal patterns, trends and nonlinearity. To overcome the issue and obtain more accurate forecasts, the various models have been applied in the past several decades. Traditionally, the univariate time series models are often included in forecasting comparisons: the sARIMA model and the HW model. The main advantage of using univariate time series models is that they do not consider the relationship between dependent and independent variables, but they are used to predict the future values of a time series by using only historical data. One of the most important issues in model selection is to determine the appropriate approach to utilize forecasting. The sARIMA and the HW models are widely used forecasting methods which can capture the seasonality. For the sARIMA and the HW models, the parameters representing the differential or seasonal need to be estimated. The popularity of the sARIMA and the HW models is not only due to their success in forecasting, but also their simplicity and analytical ability. However, empirical findings demonstrate that the sARIMA and the HW models have a drawback. For example, both models only assume the linear form of the model. The nonlinear patterns cannot be captured by the sARIMA and the HW models. On the other hand, the nonlinear models, such as the ANN and the ANFIS, can only capture nonlinearity in data. For this reason, the nonlinear models are not able to model the linear part in data. Due to the shortcomings of linear and nonlinear models, the hybrid forecasting approach has come to the forefront over the past decade.

The motivation of this study is based on the following remarks:

− The study by Makridakis et al. ^[1] manifests that the complex models usually fit past data well, but forecasting the future, the simple models are often more accurate;

− Khashei and Bijari ^[2] put forward an approach to encourage motivation for combining different single methods to benefit from their strength of capturing different characteristics of the time series data.

Thus, the aim of this study is to forecast the total electricity production in South Africa under two different types of approaches. The first approach assumes that simple forecasting models may perform better than the models of complex form. The second approach assumes that the hybrid models may have better out-of-sample forecasting performances than simple models. The main reason for using hybrid models is that forecasting accuracy can be enhanced by using the linear and the non-linear features.

The forecasting models found in the literature are divided in two main frames: simple models and complex models. For this study, the focus is on the forecasts by sARIMA and Holt-Winter's as simple models and by hybrid models, such as the ANN based sARIMA, the ANN based HW models, the ANFIS based sARIMA and the ANFIS based HW models. The ARIMA model is one of the most optimal forecasting models in the literature. Besides being simple and useful, the Holt-Winters method and its versions, 'additive' and 'multiplicative', are significantly robust for a wide range of energy applications. Bianchi et al. ^[3] provide the evidence that the Holt-Winters method performs as well as or better than more complex methods. De Gooijer and Hyndman ^[4] claim that the ARIMA is a robust method to deal with trend and seasonality. Armstrong ^[5] reports that the ARIMA model improve forecasting accuracy but there is a little evidence that supports this claim. Chen et al. ^[6] find that the sARIMA is the most appropriate model for forecasting inbound air travel arrivals to Taiwan. Gelper et al. ^[7] put forward that the Holt-Winters method is a useful method if data shows trend and seasonality. Permanasari et al. ^[8] indicate that the ARIMA model has better forecasting performance than the Holt-Winters method by using disease incidence, especially for the seasonal disease. Omane-Adjepong et al. ^[9] state that the sARIMA model yields more accurate forecasts than the seasonal additive and multiplicative Holt-Winters methods. Rahman and Ahmar ^[10] show that the Holt-Winters additive type is better than the ARIMA model for the total primary energy consumption data. de Oliveira and Oliveira ^[11] use the combination of decomposition and bootstrap agammaegating techniques to improve forecasts based on the univariate models, such as the sARIMA model, the HW additive and multiplicative models and the ETS model for electric energy demand across different countries. González et al. ^[12] employ the Hilbertian autoregressive moving aveage (ARMX) model to forecast electricity price. In terms of the linearity, much attention has been directed in recent literature to the linear quantile regression to model electricity demand. Lebotsa et al. ^[13] employ partially linear additive quantile regression to forecast the short-term electricity demand.

The study, by Darbellay and Slama ^[14], discussed that the ANN model can be useful for nonlinear process. Chatfield ^[15,16] questioned whether the concerns with the ANN model were exaggerated regarding the perfect forecasting technique. There is no doubt that Chatfield was not the only one in awe of the forecasting performance of ANN model. This was followed by several papers discussing that naïve models' forecasting performance, such as random walk, can beat the ANNs ^{[17,18,19,20,21]}. The authors of ^[2,22,23] show that ANNs produce promising results compared to the traditional time series models, such as the ARIMA model. Besides the ANN model, there is a large body of literature to attest to the fact that grey prediction model has significant impact on electricity consumption forecasting. Ding et al. ^[24] use a new grey model to forecast China's electricity consumption. Hu ^[25] forecasts electricity consumption by using the ANN based grey forecasting method. In terms of the comparison between the ANFIS model and the ARIMA model, there exist various results in the literature. Tektaş ^[26] show that the ANFIS model has better results than the ARIMA model in terms of forecasting performance. Yayar et al. ^[27] conclude that the ANFIS model is more appropriate than the ARIMA in point of the forecasting of electric consumption. Yadav and Balakrishnan ^[28] find that the ANFIS model performs better than the ARIMA model. However, Hernandez et al. ^[29] argue that the ARIMA model is better than the ANFIS model in terms of forecasting. Lusis et al. ^[30] in their study state that the support vector regression model (SVR) has higher accuracy for a day-ahead load forecast. Luo et al. ^[31] show that even if the SVR model is most robust rather than the multiple linear regression model and the ANN model, all models do not satisfy forecasting when the scale of the data integrity attacks becomes large. Li et al. ^[32] suggest that the combination of ensemble empirical mode decomposition (EEMD) and random forest model to forecast daily electricity consumption shows the best forecasting performance, in comparison to others, such as a back-propagation neural network (BPNN) and least square support vector machine (LSSVM). Chen et al. ^[33] suggest that their proposed method based on the combination of EMD and extreme learning machine (ELM) provides better forecasting performance than all other three methods, such as radial basis function kernel (RBF) based ELM, universal kernel function (UKF) based ELM and mixed-ELM, in terms of electric load forecasting.

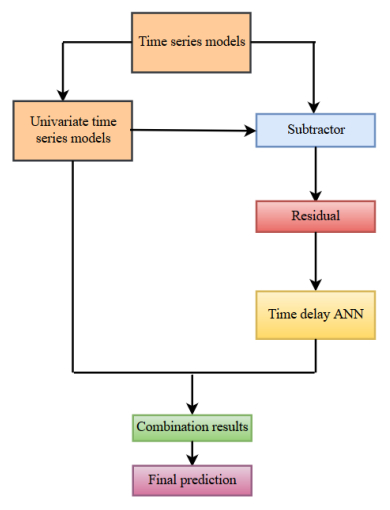
There is known fact that the series generated from linear process might be inappropriate for most real-world problems that are non-linear ^[34,35]. As seen in many studies, the literature holds different views in respect to the forecasting performances of linear and non-linear models. A time series usually consists of the linear and the nonlinear parts. Herein, one particular type of model that has come into prominence is the hybrid model. The hybrid model is a forecasting technique that combined other individual models. In this study, the ARIMA and Holt-Winters models for the linear part of a time series data were used, and the ANN and the ANFIS models are used to handle the non-linear part that corresponds to error term for a time series data. The process for the hybrid models used in this study was presented in Figure 1.

Figure 1.  The process for hybrid model.

DownLoad: Full-Size Img PowerPoint

As seen in the literature above, there are widely studied the linear and the nonlinear models to forecast different data in energy sector. These models can be either univariate or multivariate models (such as multivariate linear quantile regression for linear model and grey forecasting approach for nonlinear model). The reason of focusing on the univariate models is that the univariate models outperform than the multivariate models in terms of out-of-sample forecasting ^[36]. Moreover, the study by Kunst ^[36] explains the possible reasons why the multivariate models have not been used in this study: 1) it is clearly seen that the number of parameter to be estimated in multivariate model is more than the univariate ones. Each parameter to be added to the model, which refers to unknown quantity, results in additional source of error; 2) in terms of the multivariate models, there are not only more model structures than univariate ones (which will cause model selection problem), but also there are decision-making issues which need to be faced according to the selection of independent variables which have impact on the dependent or the output variables (for example, in the context of technical economic analysis, the various inputs need to be used to mathematical modeling of the combined methanol-electricity production plant ^[37]). However, in the light of the forecasting process, the inaccurate selection of the independent variables will increase the noise, and this will lead to the poor forecasts.

The rest of the paper is organized as follows: In Section 2, the descriptive statistics of the dataset was briefly introduced. Section 3 of the paper provides necessary description of the ARIMA, the Holt-Winters, the ANN and the ANFIS models. The forecasted results are presented in Section 4. Section 5 contains conclusion.

2.   Datasets

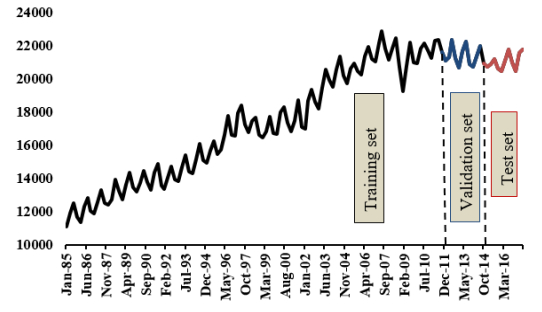
In this study, the quarterly total electricity production in South Africa for the period from January 1985 (1985:Q1) to September 2017 (2017:Q3) were used. The data are provided from the internet page of Federal Reserve Economic Data. In addition to the data, R program is used to forecast total electricity production. Figure 2 shows the time-series plot of the data.

Figure 2.  The quarterly total electricity production (Gigawatt hours-GWh).

DownLoad: Full-Size Img PowerPoint

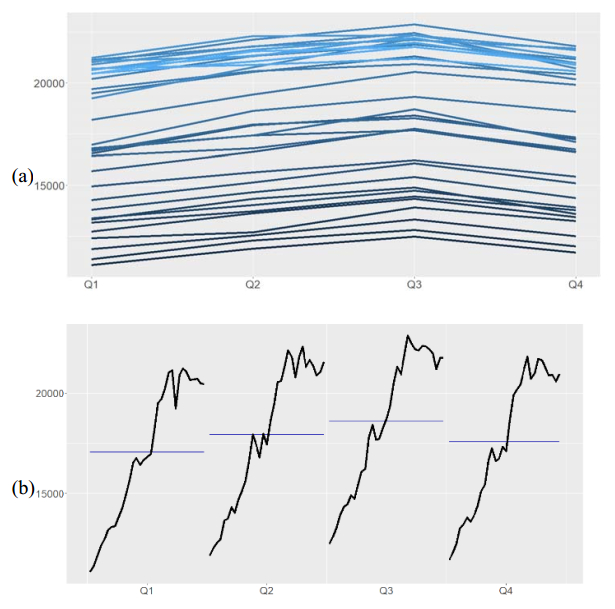
According to Figure 2, the total electricity production decreases in December. In South Africa, the summers last from November to January, and the summers are hot and generally dry. According to World Meteorological Organization ^[38], January 2013 was the hottest month. The electricity production indeed declines in dry, hot months if river flows ebb ^[39]. Because South Africa is a water scarce country and has limited water storage, the total electricity production forecasting is important for both future planning and policy ^[40]. Since the data shows the seasonal pattern, the sARIMA and the HW models are applied to capture the seasonality. Figure 3-a allows the underlying seasonal pattern to be seen more clearly. According to Figure 3-a, the total electricity production has consistently increased over the years as the lower (darker) lines represent earlier years, and the higher (lighter) lines represent recent years. Moreover, Figure 3-b shows the changes in seasonality over time. Table 1 shows the descriptive statistics of the data and confirms the left skewness and platykurtic distribution. The data with low kurtosis, the less than number three, tends to have light tails, or lack of outliers. This finding supports our aim which is to hold all data points in the model. Otherwise, the outliers in dataset need to be removed, and it is known fact that they can have significant adverse impact on our forecasts.

Figure 3.  Seasonal plots of the total electricity production in South Africa (GWh).

DownLoad: Full-Size Img PowerPoint

Table 1.  Descriptive Statistics.

Mean	Maximum	Minimum	Std. Dev.	Skewness	Kurtosis
17800.330	22868.000	11073.000	3442.301	−0.287	1.676
LB-Q (12)	p-value	J-B Test	p-value	ARCH (12)	p-value
1207.133	0.000	11.36815	0.0034	3.687	0.978

---

 | Show Table

DownLoad: CSV

3.   Methodologies

As a comparison, the HW model by Holt ^[41] and Winters ^[42], the sARIMA model by Box and Jenkins ^[43], the ANN model by Rumelhart et al. ^[44] and the ANFIS model by Jang ^[45] were applied to the total electricity production. In this study, the HW model was used because it is not only a widely used tool for forecasting method which can handle trend and seasonal variation, but also outperforms the sophisticated ones according to Makridakis and Hibon ^[46]. On the other hand, the forecasting competition between simple and hybrid models has attracted considerable academic attention. In recent years the ANN and the ANFIS models have shown better modeling performance than the other nonlinear models when dealing with modeling the nonlinear patterns in data. Moreover, the ANN and the ANFIS models have their popularity in terms of their applications and are also well embedded in the literature. Therefore, the ANN based on sARIMA, the ANN based on HW models, the ANFIS based on sARIMA model and the ANFIS based on HW models in forecasting the total electricity production have been used to allow for fair competing in the study. In this part, the basic framework of modelling approaches of the sARIMA model, the HW model, the ANN model and the ANFIS model are briefly described. To better understand the methodological baseline, the two utmost important criteria are considered to guide methodology selection. First, the methodology selection is based on the forecasting related literature. The second criteria to the methodology selection is based on the data characteristics.

Figure 4.  Framework of methodology.

DownLoad: Full-Size Img PowerPoint

3.1.   sARIMA model

Autoregressive Moving Average Model (ARMA) has become considerably important tool in forecasting of economic time series. The autoregressive part is called as Autoregressive model (AR), and the moving average part is called as Moving Average (MA) model. In AR model, the output variable is a linear function of the previous behaviors of itself. In MA model, the output variable is a linear function of the current and various past values of a stochastic term. In ARMA (p, q) model, p and q are the orders of AR and MA models respectively. The ARMA (p, q) model is defined as follows ^[47]:

If the observed data is non-stationary, taking differencing (d) can be used to eliminate non-stationarity. The model is then referred as an ARIMA model. The ARIMA (p, d, q) model is given as follows ^[47]:

where y_t denote a series of values for a time series of interest, and e_t denotes a series of random disturbances and is assumed to be white noise. Let be B the backward shift (or lag) operator.

In this study, the sARIMA model which includes additional seasonal terms in the ARIMA model was used because the quarterly total electricity production data was used as output variable. The sARIMA (p, d, q) (P, D, Q) model can be written as ^[48]:

where p is non-seasonal AR order; d is non-seasonal differencing; q is non-seasonal MA order; P is seasonal AR order; D is seasonal differencing; Q is seasonal MA order; and S is time span of repeating seasonal pattern.

3.2.   HW model

The HW model, which can deal with a time series containing both trend and seasonality, is an extension of the Exponential Smoothing (ES) model. The HW model has two versions, additive and multiplicative. In this study, both additive and multiplicative versions of HW exponential smoothing model have been applied in the forecast of total electricity production. The general forecast functions for the additive and multiplicative HW models are as follows ^[49].

Additive formulation of HW:

Multiplicative formulation of HW:

where ${\ell _t}$ is the component of level, ${b_t}$ is the component of the slope, and ${s_{t + h - m}}$ is the relevant seasonal component. The crude oil prices are denoted by ${y_1}, \ldots, {y_n}$ and the seasonal period is m (e.g., m = 12 for monthly data). Let ${\hat y_{t + h|t}}$ be the h-step forecast made using data to time t.

3.3.   ANN model

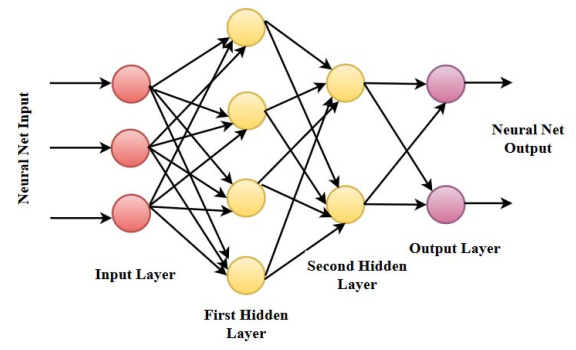
The most widely used ANNs in the forecasting field are multi-layer perceptrons (MLPs) in literature ^[50,51]. The ANN model can be divided into four stages: (1) the topology design stage consist of the choice of the ANN type, the number of its layers, the number of neurons in each layer, its inputs and outputs, the selection of training, validation and test samples; (2) in the training stage, the neural network learns the potential relationship between input variables and output variable, and the learning process is continued till it finds the minimum error; (3) in the validation stage, connection weights are adjusted with unknown data; and (4) the test stage is applied to evaluate the performance of the net with the test sample. Figure 5 shows the ANN architecture with two hidden layer nodes. In the ANN framework, while the total electricity production was considered as output variable, the all other explanatory variables that are the lagged values of the output variable were included in the model as input variables. Specifically, the determination of the number of hidden layers are very important. The theoretical findings show that there is no reason to use more than two hidden layers in the ANN model ^[52]. Moreover, Kurkova ^[53] provides the evidence that a feedforward neural network with two hidden layers should be used to countervail the lost efficiency in the usage of regular activation function. Nevertheless, the other reason of using two hidden layers is to severely reduce the total number of necessary hidden nodes. The final ANN model is four layered network which consist of lagged output units as inputs (from one-time lagged to four-time lagged), two hidden layers, and one output unit. The ANN (I × H1 × H2 × O) notations were used to represent the number of input variables (I), hidden units in each layer (H1and H2), and the output unit (O).

Figure 5.  ANN architecture with two hidden layers.

DownLoad: Full-Size Img PowerPoint

3.4.   ANFIS model

This method based on the theory of fuzzy set and fuzzy logic is proposed by Jang ^[45]. This method is composed of ANN system and FIS system. The ANN model is known as statistical data modelling tool. It refers to learning algorithm which can capture the complex patterns in the relationship between input and output data. The FIS comprises membership function, fuzzy logic operator and if-then rules. Figure 6 shows the ANFIS architecture. In addition to the other models, the ANFIS model which takes the advantages of using neural networks and fuzzy logic at the same time, was carried out to check whether it has the best performances among the six implemented models. In this study, genfis3 function of Fuzzy toolbox of MATLAB was performed to generate a FIS using fuzzy c-means clustering (FCM) by extracting a set of rules that models the data behavior. The function requires separate sets of input and output data as input arguments. the lagged values of total electricity production series were used as input variables.

Figure 6.  An ANFIS architecture for a two rule Sugeno system.

DownLoad: Full-Size Img PowerPoint

3.5.   Hybrid model

For time series forecasting, two types hybrid models are employed as alternatives to widely used the ARIMA and the HW models. Recently, combined models with both linear and non-linear models have been attracted much attention. Zhang ^[54] used hybrid ARIMA-ANN model to handle both linear and non-linear parts of the data. The linear part was modelled by ARIMA, and the non-linear part was modelled by the ANN model. In this study, the same process detailed as below was followed.

where ${L_t}$ is the linear component and ${N_t}$ is the non-linear component. Firstly, the sARIMA and the HW models for the linear component were used and then the non-linear relationship will be appeared in the residual of linear component modelling.

The non-linear function by ANN and ANFIS models are described as follows:

where $f$ is non-linear function and ${\xi _t}$ is a random error. The Equation (6) can be re-written for the hybrid model as follows:

In Equation (9), ${\hat N_t}$shows the forecasted value corresponding to ${\varepsilon _t}$ from Equation (8). To sum up, the following steps for the hybrid methodology can be written. The utilized neural network algorithm used in hybrid methodology is presented in Table 2.

Table 2.  Neural Network Algorithm utilized in Hybrid Methodology.

Hybrid Methodology
1. Given a time series x = [x1, x2, …, xn]. 2. Determine the training set (82%) and validation test (9%) size as in-sample, and test size (9%) as out-of-sample. 3. Normalize the time series data using min-max normalization using the following formula:                          zi = (xi-min(x))/(max(x)-min(x)) 4. Determine the best simple individual models and their parameters using the normalized vector in-sample period. 5. Obtain the forecasts using selected simple individual models. 6. De-normalize the forecasts to find $\widehat {{L_t}}$ in Equation (7). 7. Obtain residuals $\left({{\varepsilon _t}} \right)$ by subtracting simple models' forecasts from actual values in Equation (7). 8. Select the best lag number to determine the number of inputs on the data of residual series. 9. Normalize the residual series using min-max normalization. 10. Obtain forecasts using ANN and ANFIS models. 11. De-normalize the forecasts to obtain $\widehat {{N_t}}$ from Equation (8). 12. Combine the simple models' forecasts with ANN and ANFIS models' forecasts as in Equation (9).
input: ${{\rm{ \mathit{ ε} }}_{{\rm{i}}, {\rm{j}}}}$:the errors obtained by subtracting jth model predictions from actual values, ${\zeta _m}$: model building period (training period), ${\zeta _v}$: validation period, ${\zeta _t}$: test period, i: the number of observed predictions, j: the number of univariate models, ${h_1}\left({{\rm{the}}\; {\rm{number}}\; {\rm{of}}\; {\rm{nodes}}\; {\rm{in}}\; {\rm{first}}\; {\rm{hidden}}\; {\rm{layer}}} \right) = c\left({1, 2, \ldots, 12} \right)$, ${h_2}\left({{\rm{the}}\; {\rm{number}}\; {\rm{of}}\; {\rm{nodes}}\; {\rm{in}}\; {\rm{second}}\; {\rm{hidden}}\; {\rm{layer}}} \right) = c\left({1, 2, \ldots, 12} \right)$, k: the time delay number of ${{\rm{ \mathit{ ε} }}_{{\rm{i}}, {\rm{j}}}}$.
1: Given ${{\rm{ \mathit{ ε} }}_{{\rm{i}}, {\rm{j}}}}$, ${\zeta _m}$, ${\zeta _v}$ 2: foreach $j$ do                 foreach k do                         create datamatrix =cbind(Lag(${\rm{(}}{{\rm{ \mathit{ ε} }}_{{\rm{i}}, {\rm{j}}}}, {\rm{}}k = 1, ..4)$, ${{\rm{ \mathit{ ε} }}_{{\rm{i}}, {\rm{j}}}}$)                 end for         end for 3: Run neural network model $\left\{ {{{\rm{ \mathit{ ε} }}_{{\rm{i}}, {\rm{j}}; {\zeta _m}}}, {h_1}, {h_2}, {{\varepsilon '}_{{\rm{i}}, {\rm{j}}; {\zeta _m}}}} \right\}$ 4: Compute $MA{E_{{\zeta _v}, {{\varepsilon '}_{i, j}}, {h_1}, {h_2}}}$ 5: Save minimum $MA{E_{{\zeta _v}, {{\varepsilon '}_{i, j}}, {h_1}, {h_2}}}$ to determine the optimum number of nodes in each hidden layer 6: Run neural network model $\left\{ {{{\rm{\varepsilon }}_{{\rm{i,j}};{\rm{}}{\zeta _m} + {\zeta _v}}},\;\;{h_1},{h_2},\varepsilon _{{\rm{i}},{\rm{j}};{\rm{}}{\zeta _m}}^{\rm{'}}} \right\}$ output: Optimal model − optimal ${{{\rm{ \mathit{ ε} '}}}_{{\rm{i}}, {\rm{j}}}}$ with optimum ${{h_1}}$ and ${{h_2}}$

---

 | Show Table

DownLoad: CSV

4.   Results and Discussions

The data are divided into two parts, i.e. training and testing datasets. The total electricity production data from 1985:Q1 to 2014:Q3 are used as training datasets, and the data from 2014:Q4 to 2017:Q3 are used as testing data sets. The different parameters of p, d, q, P, D, Q and S were experimented in order to determine the best model that will give the best forecast. The KPSS unit root test and AIC information criteria were used to determine the degree of differencing d and the appropriate seasonal orders for the purpose of choosing the best sARIMA model. In the light of the findings, sARIMA (1, 0, 0) (0, 1, 1) ^[4] is considered the best for total electricity production by using R software which supports the automatic search on determining the parameters.

The HW model is a triple exponential smoothing forecast method that has the capability to handle trend and seasonality effectively. It is a five-step process in which practitioners must calculate the specific factors at each step (1) seasonal indices; (2) overall smoothing of trend level; (3) trend factor; (4) smoothing of seasonal indices; and (5) generating of forecasts. Both multiplicative HW and additive HW models are used.

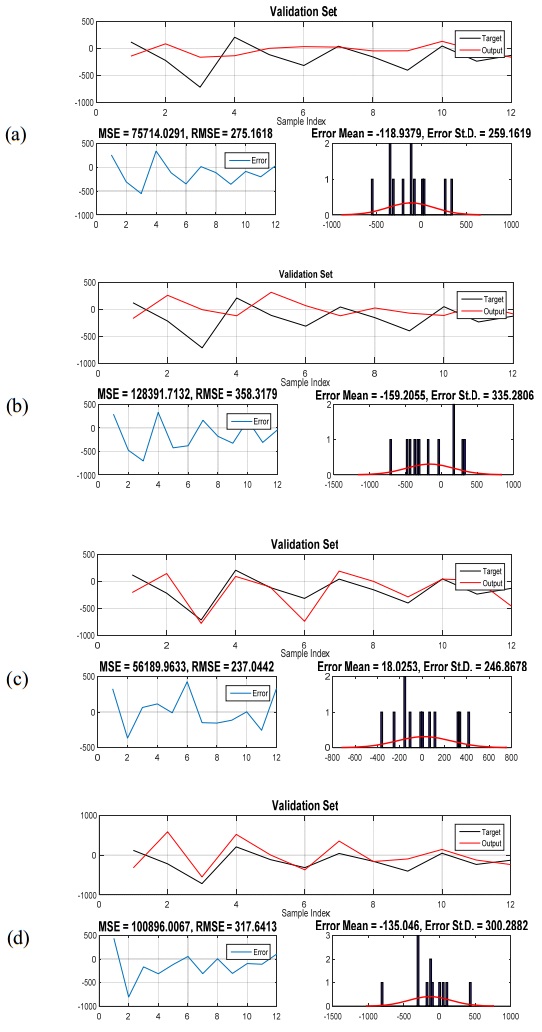
The ANN model can be divided into four stages: (1) the topology design stage consist of the choice of the ANN type, the number of its layers, the number of neurons in each layer, its inputs and outputs, the selection of training, validation and test samples; (2) in the training stage, the neural network learns the potential relationship between input variables and output variable, and the learning process is continued till it finds the minimum error; (3) in the validation stage, connection weights are adjusted with unknown data; and (4) the test stage is applied to evaluate the performance of the net with the test sample. In this study, 107 observations for training set, 12 observations for validation set and 12 observations for testing set were used. The training dataset are used to learn or develop candidate models, validation set used to select a model and test set is used for assessing model performance on future data. Table 3 shows the validation set performance of the ANN based on sARIMA.

Table 3.  Validation Set Performance of ANN based on sARIMA.

Validation Set Performance
Lag	Hidden Layer 1	Hidden Layer 2	MAE
1	9	4	262.138
2	2	9	261.9352
3	5	2	233.5972
4	6	4	243.0433

---

 | Show Table

DownLoad: CSV

As results reported in Table 3 show that one to four lagged of total electricity production are used as input variables. The ANN (I × H1 × H2 × O) notations were used to represent the number of input variables (I), hidden units in each layer (H1 and H2), and the output unit (O). Finally, ANN (3 × 5 × 2 × 1) model used to forecast the non-linear part of the data.

The validation set performance of ANN based on multiplicative HW model is given in Table 4. Based on the results of Table 4, one to four lagged total electricity production are chosen as input variables. ANN (3 × 8 × 9 × 1) model used to forecast the non-linear part of the data.

Table 4.  Validation Set Performance of ANN based on Multiplicative HW.

Validation Set Performance
Lag	Hidden Layer 1	Hidden Layer 2	MAE
1	9	6	242.2049
2	4	8	245.0679
3	8	9	230.3607
4	1	7	233.0093

---

 | Show Table

DownLoad: CSV

The validation set performance of ANN based on multiplicative HW model is given in Table 5. According to results of Table 5, it is evident that the number of input variables is three and the best model is chosen as ANN (3 × 8 × 3 × 1) model used to forecast the non-linear part of the data.

Table 5.  Validation Set Performance of ANN based on Additive HW.

Validation Set Performance
Lag	Hidden Layer 1	Hidden Layer 2	MAE
1	9	6	217.1001
2	2	9	218.1105
3	8	3	200.2002
4	1	7	205.1442

---

 | Show Table

DownLoad: CSV

In regard to ANFIS model, it is applied by using the MATLAB program. In this study, one factor – the lagged values of total electricity production itself –was used as inputs for forecasting the total electricity production. The first 117 of data is used as training set to optimize the model parameters, 12 of data is used as validation set and the last 12 serves as the test set. The used steps are as follows:

Table 5.  Validation Set Performance of ANN based on Additive HW.

Validation Set Performance
Lag	Hidden Layer 1	Hidden Layer 2	MAE
1	9	6	217.1001
2	2	9	218.1105
3	8	3	200.2002
4	1	7	205.1442

---

 | Show Table

DownLoad: CSV

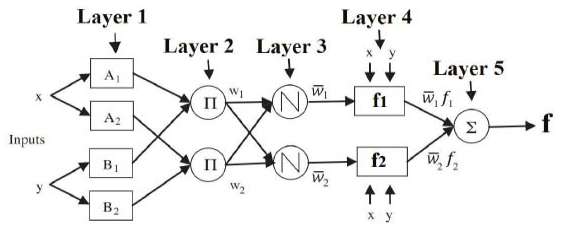
First, in order to determine that the number of input variables and the number of clusters for fuzzy c-means clustering (FCM), the ANFIS based sARIMA model has been conducted in terms of validation sets. The selection is made by minimum root mean square performance metrics (RMSE). Figure 7 shows the best model with three input variables (including 1, 2 and 3 lagged total electricity production, respectively) and FCM is equal to three.

Figure 7.  Validation set performance of ANFIS based on sARIMA. (a) one lag and FCM is equal 6; (b) two lag and FCM is equal 3; (c) three lag and FCM is equal 3; (d) four lag and FCM is equal 3.

DownLoad: Full-Size Img PowerPoint

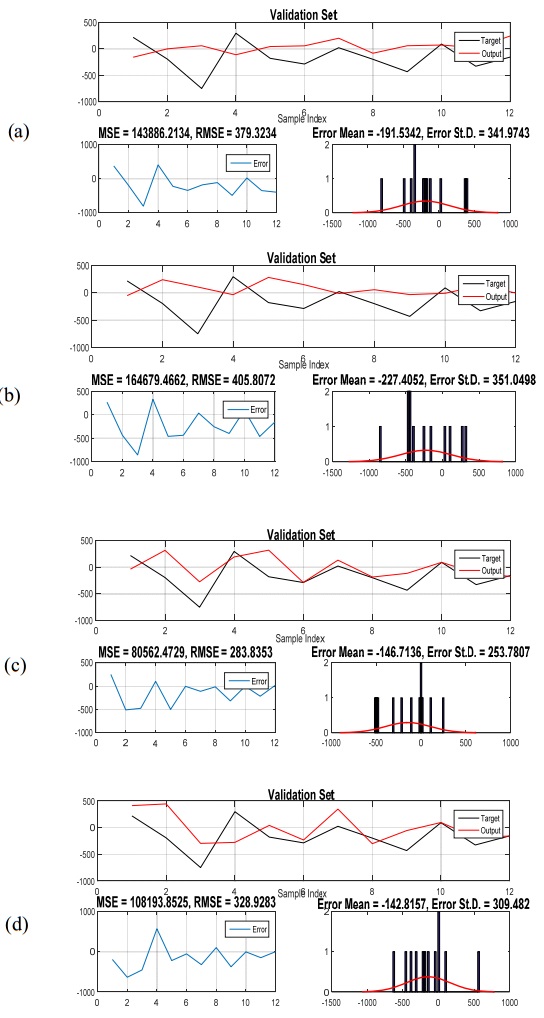
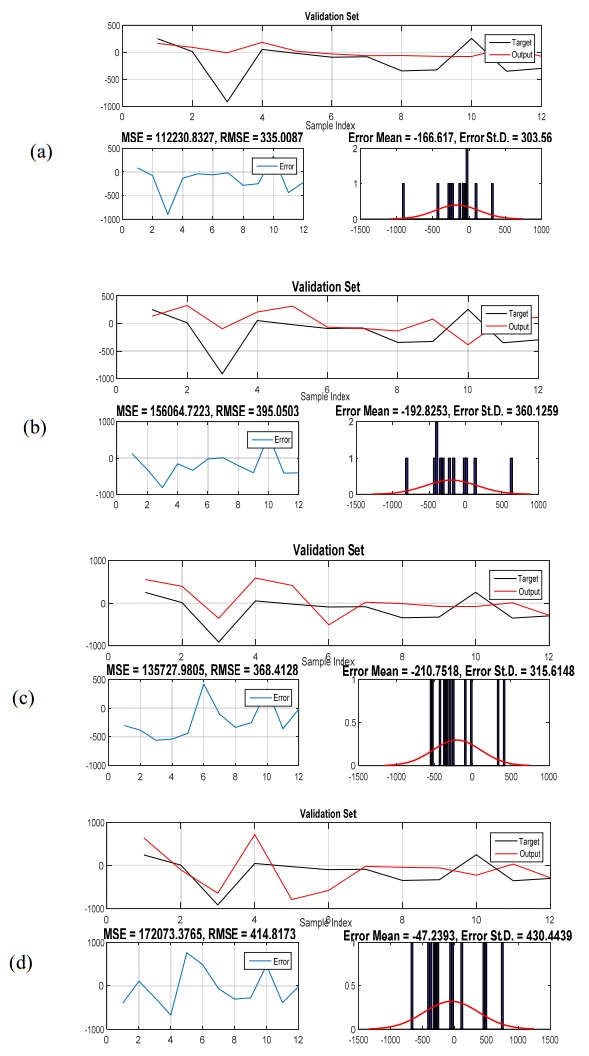
The same process is applied to the ANFIS based on multiplicative HW model and the ANFIS based on additive HW model to find out whether the hybrid models perform better than simple linear models. Figure 8 and Figure 9 show the results of the ANFIS based on multiplicative HW model and the ANFIS based on additive HW model, respectively. The best model for the ANFIS based on multiplicative HW model is selected with minimum RMSE that is the one with one input variable (one lagged total electricity production) and three numbers of clusters. The validation set results for the ANFIS based on additive HW model show that three input variables (including 1, 2 and 3 lagged total electricity production respectively) and five numbers of clusters are selected according to RMSE measure.

Figure 8.  Validation set performance of ANFIS based on multiplicative HW. (a) one lag and FCM is equal 3; (b) two lag and FCM is equal 5; (c) three lag and FCM is equal 3; (d) four lag and FCM is equal 3.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Validation set performance of ANFIS based on additive HW. (a) one lag and FCM is equal 6; (b) two lag and FCM is equal 4; (c) three lag and FCM is equal 5; (d) four lag and FCM is equal 5.

DownLoad: Full-Size Img PowerPoint

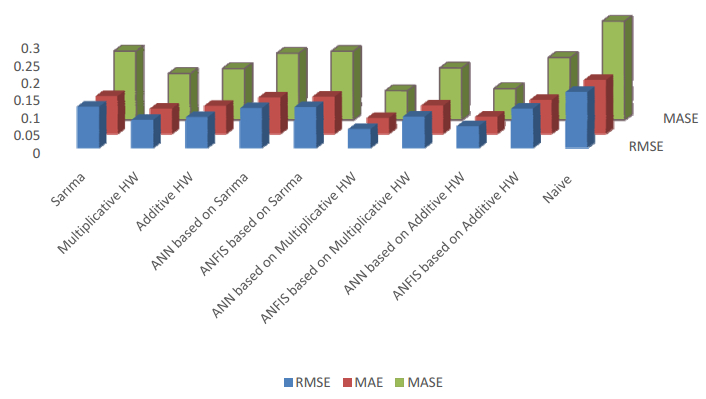
After forecasting the linear and non-linear parts of the data, the forecasts by hybrid models are calculated. Table 6 shows the out-of-sample forecasting of all models involved in this study. In order to evaluate the model performances, the following three indices, RMSE, the mean absolute error (MAE) and mean absolute scale error (MASE) were applied in this study. The RMSE, MAE and MASE are defined by following equation:

Table 6.  Comparison of out-of-sample forecasting performances.

Models	RMSE	MAE	MASE
sARIMA	1,188	1,085	0,198
Multiplicative HW	0,813	0,727	0,133
Additive HW	0,888	0,807	0,148
ANN based on sARIMA	1,145	1,048	0,192
ANFIS based on sARIMA	1,176	1,076	0,197
ANN based on Multiplicative HW	0,543	0,460	0,084
ANFIS based on Multiplicative HW	0,902	0,814	0,149
ANN based on Additive HW	0,629	0,493	0,090
ANFIS based on Additive HW	1,130	0,977	0,179
Naïve	1,605	1,552	0,284
Note: Naïve model is random walk model and is used as benchmark model. Entries represent the forecasting accuracy metrics values (divided by 1000 for RMSE and MAE).

---

 | Show Table

DownLoad: CSV

where ${{A_i}}$ presents the actual value, ${{F_i}}$ presents the forecast value and m represents the seasonal period.

The results from Table 6 indicate that the hybrid models by using the ANN model are superior to simple models, such as the sARIMA model and both multiplicative and additive HW models. However, the hybrid models by using ANFIS model falls behind the simple models in terms of forecasting performance. This finding supports Makridakis et al. ^[1]'s finding, as they mentioned that simple model is better than complex model. However, if the hybrid model including the ANN model is used for forecasting the total electricity production, it is obvious that the forecast accuracy can be improved. In addition, Diebold- Mariano (DM) statistical test proposed by Diebold and Mariano ^[55] was employed to show whether there is any statistical difference between the models in terms of forecasting performances.

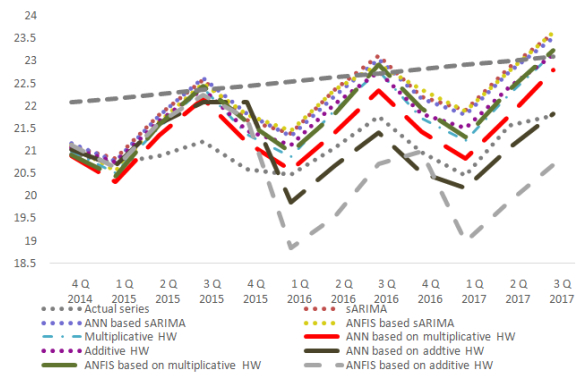
According to Table 6 and 7, the best forecasting performance is achieved by using the ANN based on multiplicative HW hybrid model. Moreover, the ANN based additive HW model can be chosen for forecasting the total electricity production in South Africa. The results confirm that the hybrid models are better than the univariate time series models for the total electricity production forecasting in South Africa. Figure 10 shows the plot of forecasts by the simple models and the hybrid models.

Table 7.  Diebold-Mariano test for comparing predictive accuracy.

Model 2/Model 1	ANN based on Multiplicative HW
sARIMA	−5.290 (0.000)*
ANN based on sARIMA	−5.465 (0.000)*
ANFIS based sARIMA	−5.247 (0.000)*
HW Multiplicative	−4.555 (0.000)*
HW Additive	−4.089 (0.000)*
ANN based on Additive HW	−0.251 (0.403)
ANFIS based on Multiplicative HW	−5.446 (0.000)*
ANFIS based on Additive HW	−2.655 (0.011)**
Naïve	−6.364 (0.000)*
Note: The null hypothesis is that Model 1 is less accurate than Model 2. Model 1 represents. ANN based on Multiplicative HW. * and ** indicate that the null hypothesis is rejected by 1% and 5% significance level respectively.

---

 | Show Table

DownLoad: CSV

In addition to Figure 10, Figure 11 also shows that the success of the hybrid models can be attributed to its ability to more closely track the actual values than simple models. The hybrid models show better forecasting performance in almost all forecast point. Figure 12 also confirms that the hybrid models produce more accurate forecasts than the simple models in terms of the accuracy metrics.

Figure 10.  The plot of the forecasts.

DownLoad: Full-Size Img PowerPoint

Figure 11.  Multiple forecasts comparison for each forecast point.

DownLoad: Full-Size Img PowerPoint

Figure 12.  Out-of-sample forecasting performances in terms of accuracy metrics.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

The hybrid models are capable of improving the forecasting performances where simple models fall short in terms of forecasting accuracy. Ten different forecasting models, the sARIMA model, the multiplicative HW model, the additive HW model, the ANN based on sARIMA model, the ANN based on multiplicative HW model, the ANN based on additive HW model, the ANFIS based on sARIMA model, the ANFIS based on multiplicative HW model, the ANFIS based on additive HW model, and the naïve model as benchmark, were applied to forecast the total electricity production data. For this study, three different models are considered for forecasting with simple models, the ANN based linear models and the ANFIS based linear models. The forecasting results show that the best linear model is the multiplicative HW model and the best hybrid model is the ANN based on multiplicative HW model. This result is compatible with the expectation which may sign that the selection of the best linear model from the other linear models in terms of out-of-sample forecasting performance is significantly important when combining the models. The ANN based on multiplicative HW model, which shows the higher forecasting accuracy has superior capability in modeling the total electricity production over the linear models in terms of all the evaluation criteria. Thus, the hybrid model not only provides better forecasting performance, but also shows better statistical interpretation. However, this accuracy is achieved at the expense of computational complexity. Hence, it is recommended to use ANN based linear models only in those models in which the hybrid models are useful in extracting advantages of individual models for forecasting the total electricity production with higher forecasting accuracy. Especially, since the ANN based both multiplicative and additive HW models have the best forecasting performance, an interesting direction of further research is to investigate whether both multiplicative and additive HW models can be efficiently combined with the other nonlinear models. Additionally, the success of the hybrid models depends on how well the linear and nonlinear components are forecasted. This finding points out the usability of different linear and nonlinear forecasting models which give new incentives for further researches.

Conflict of interest

The author declares no conflict of interest in this paper.